大学物理课件毕奥萨伐尔定律
合集下载
大学物理8-3 毕奥-萨伐尔定律
上页 下页 返回 退出
而k
0 4
故
dB
0 I d l sin
4 πr
2
-7 2 4 π 10 N A 其中 0 ,称为真空中的磁导率。
磁感应强度的矢量式:
0 Idl er dB 2 4π r
Biot-Savart定 律的微分形式
Biot-Savart定 律的积分形式
I qnvS
电流元在P点产生的磁感应强度
dB
0 qnvSdl sin
r
2
4π
设电流元内共有dN个以速度v运动的带电粒子:
d N nS d l
每个带电量为 q的粒子以速度 v通过电流元所 在位置时,在P点产生的磁感应强度大小为
0 qv sin dB B dN 4π r2
r
dl
r d dB B
P
I
电流元在给定点所产生的磁感应强度的大小与 Idl 成正比,与到电流元的距离平方成反比,与电 流 元 和矢径夹角的正弦成正比 于r 。 dB 方 向 垂 直 与 Idl 组成的平面,指向为由 Idl 经 角转向 r 时 右螺旋前进方向。
I d l sin dB k r2
dB
0 R nI d l
2
2( R l )
2
2 3/ 2
2
0 R nIdl B dB L L 2( R 2 l 2 ) 3 / 2
上页 下页 返回 退出
. . .. . . . . . . . . . . . .
A2 dB
q
r
q
垂直于纸面向内
v
普通物理PPT课件7.2 毕奥-萨伐尔定律.ppt

解 三段直导线在圆心处 产生的磁场为零.
B
dB
0 4
Idl r
r3
1o 2
A
dB
0 4
Idl R2
B1
0 1 4
I1dl R2
0 4
I1l1 R2
B2
0 2 4
I2dl R2
0 4
I2l2 R2
•
I
U R
U
l
s
I1 l2 I2 l1
B B1 B2 0
要求能计算载流直导线、载流圆线 圈和载流圆弧的组合所产生的磁场。
B dB// dBcos
cos R r
B
0 IR 4 r 3
2R
dl
0
0 IR 2
2r 3
0 IR 2
3
2( R2 x2 )2
特例:圆心处 x 0
B 0I
2R
例3 如图所示,两根长直导线沿半径方向接到 粗细均匀的铁质圆环上的A和B两点,并与很 远处的电源相接, 试求环中心o点处的磁感应 强度.
载流直导线
B
0I
4πd
(cos1
cos 2
)
载流圆线圈轴线上
B
0 IR2
2(R2 x2 )3
2
载流圆线圈圆心处
B 0I
2R
一段圆弧圆心处
B 0I 2 2R
解
dB
0 4
Idl sin
r2
B
B dB 0
A
4
BIdl sin
A r2
l r0ctg r r0 sin
dl
r0
sin 2
d
B 0 2 I sin d
毕奥萨伐尔定律介绍课件

定律的物理意义
物理意义
毕奥-萨伐尔定律揭示了电流在空间 中产生磁场的基本规律,对于电磁场 理论的发展和应用具有重要意义。
应用举例
在电磁学、电机学、变压器、电磁铁 等领域中,毕奥-萨伐尔定律被广泛应 用于分析和计算磁场分布。
Part
02
毕奥萨伐尔定律的推导
毕奥萨伐尔的生平与贡献
毕奥出生于1774年,是 法国物理学家和数学家。
在物理学中的应用
01
02
03
描述磁场分布
毕奥-萨伐尔定律可以用来 描述磁场在空间中的分布 ,特别是在电流和磁铁附 近产生的磁场。
计算磁场力
根据毕奥-萨伐尔定律,可 以计算磁场对电流和磁铁 的作用力,即洛伦兹力和 安培力。
解决电磁问题
在解决电磁学问题时,毕 奥-萨伐尔定律常与其他电 磁学定律一起使用,以完 整地描述电磁场的行为。
毕奥萨伐尔定律介绍 课件
• 毕奥萨伐尔定律概述 • 毕奥萨伐尔定律的推导 • 毕奥萨伐尔定律的应用 • 毕奥萨伐尔定律的实验验证 • 毕奥萨伐尔定律的扩展与展望
目录
Part
01
毕奥萨伐尔定律概述
定义与公式
定义
毕奥-萨伐尔定律描述了电流在空间中产生的磁场分布,特别是电流元在空间中产生的磁 场。
公式
毕奥和萨伐尔通过实验观 测到电流在空间中产生磁 场的现象。
毕奥萨伐尔定律的数学表达形式
毕奥萨伐尔定律可以用数学公式 表示,描述了电流产生的磁场的
大小和方向。
这个定律在电磁学中非常重要, 是研究电磁场和电磁力的基础。
通过应用毕奥萨伐尔定律,可以 解决许多与电流和磁场相关的问
题。
Part
03
毕奥萨伐尔定律的应用
大学物理课件-毕-沙-拉定律

×
O
x
Bx
dBx
0 2R
I
0
sind
0 I 2R
dBy
0 2R
I
cosd
By
dBy
0 2R
I
cosd 0
0
例7 四條相互平行的載流長直導線如圖所示,電流均為I,正方形
邊長為2a,求正方形中心的 B
1
2
B4 B3
4 B1 B2 3
B 0I 0I 2 x 2 2a
Bo 0
I
I1
U Ii R
U R li
2rU
Rli
2r
B0
Bi
0li 4r 2
2rU
Rli
0U
2rR
例2 一無限長直載流導線被彎成如圖所示的形狀,通以
電流I,則 Bo
3
1
2 R
3
I
I
2
R
1
B1 B3 0
Bo
B2
0I
2R
3
2
0I
12R
Bo
0I
2R
0I 2 R
(5) x>>R
B
0 IR 2
2(x2 R2)32
則每個運動電荷產生的電流元在P點產生的磁感應強度為:
運動電荷的磁場:
B
dB dN
0 4
qv r0 r2
適用條件:
v <<C
運動電荷的磁場
B
0
4π
qv
r2
r0
大小:
B 0 4
q v sin(v , r0 ) r2
方向:垂直於
v
和
r0所確定的平面,右手螺旋
毕奥萨伐尔定律.ppt

第七章 恒定磁场
7
物理学
第五版
7-4 毕奥-萨伐尔定律
4.由叠加原理求出磁感应强度的分布;
若各电流产生的
dB 方向一致,直接用
B
若各电流产生的 dB方向不一致,按照所选取
dB
的坐标系,求出
dB
的各方向的分量,(注意是
否具有对称性)然后各方向分别进行积分。
这样做的目的是将磁感应强度的矢量积分变 为标量积分。有时在积分过程中还要选取合适的积 分变量,来统一积分变量。
B 0I
2R
B
I
❖ 载流圆弧:
圆心角
B 0I 0I 2R 2 4R
第七章 恒定磁场
B
I
17
物理学
第五版
7-4 毕奥-萨伐尔定律
(1)
R
B0
x
推
Io
广 (2)
I
R
组
o×
合 (3) I
R ×o
B0
0I
2R
B0
0I
4R
B0
0I
8R
第七章 恒定磁场
18
物理学
第五版
7-4 毕奥-萨伐尔定律
(4) I
第七章 恒定磁场
33
B 0nI
O
x
第七章 恒定磁场
30
物理学
第五版
7-4 毕奥-萨伐尔定律
四 运动电荷的磁场
dB
0
Idl
r
4π r3
Idl
qnSvdl
dB
0
4π
nSdlqv r3
r
j
S
dl
其中: I qnvS
dN nSdl
《大学物理》毕奥—萨伐尔定律
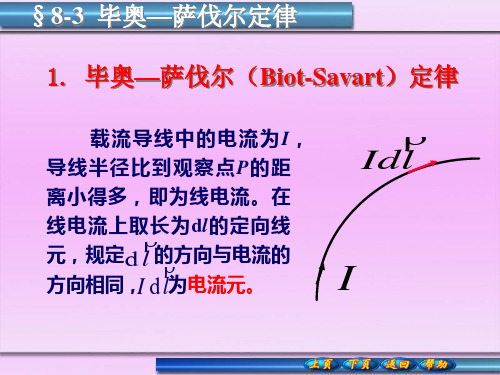
d B//
,,由所于以各圆P电点流电元流的的具大磁有小场对为B方称:向性不,相其同电,流可元分的解为逐对d抵B和d消B
B
LdB//
dB sin 0
L
4
L
Id r2
l
sin
0I sin 4r 2
2R
dl
0
0I sin 4r 2
2R
载流圆线圈轴线上的磁场
I dl
r
R
IO
x
d B
dB
dr
带电圆环旋转时产生的电流强 度为
R r.o
q
B
R 0
o
2
2rdr
2r
1 2
oR
s
dI
补充例题3一半径为R的均匀带电半圆弧,单位长度
上的电量为,绕其直径所在的直线以角速度匀速
转动,求圆心o处的磁场。
解 半圆弧旋转起来,象一个球面,可划分为若
干圆电流积分。
R o
r x
o
dI Rd λ
B
dB
L
0 L 4
I d l sin
r2
I
dl L
lr
O
d 1
P
2d
B
载流长直导线的磁场
B
dB
L
0 L 4
I d l sin
r2
I
由几何关系有:
sin cos r d sec
dl L
l d tan dl d sec2 d l r
B 0 I d l sin
E
1
4 0
q r3
r
q
r
P
v
B
E
运动电荷的磁场
大学物理毕奥-萨伐尔定律

1
2
2
I
2 B
B 0I
4πr
3)延长线上的磁场
B=0
I
A
B
1
A
→r
r
*p
B
+P
2、圆形载流导线(圆电流)轴线上的磁场(R, I)
Id l
o
IR
r dB d B
x
*
p dBx
x
dB'
解: (1)如图建立坐标系
(2)在导线上取电流元 Idl
dB
0
4π
Idl sin 900 r2
0 4
Idl r2
20
2
0, B 向外
0, B 向内
例7(例11-2) 一半径为R的无限长的半圆形金属薄片,沿轴 通有I 的电流,设电流在金属片上均匀分布,试求圆柱轴线上 任意一点P的磁感应强度.
解:将电流分割成许多无限长载流直导
线,电流为dI
I
利用无限长载流直导线的磁感应强度公式
B 0I
2πr
dB 0dI 2R
电流元中的运动电荷数
dN nSdl
电流元
Idl vSnqdl qv dN
将
Idl qv dN
代入上式得
从微观上看,电流元的dB就是dN个运动电荷共同产生的磁场
运动电荷的磁场
B
dB
0
qv r0
dN 4π r2
r0为电荷q到场点的矢径方向的单位矢量, 方向垂直于V,r确定的平面
是低速(v c)情形下匀速运动点电荷产生的磁场。
电流元 在空间P点产生的 磁感应强度 为
dB
k
Idl r2
r
0
第八讲 磁感应强度 毕奥萨伐尔定律

y o
r
a
I
建立坐标系
θ
Idl
z
分析对称性、写出分量式 由对称性: B y Bz 0
19
B0
B dBx dB cos
21
国防科大
B dBx dB cos
0 I cosdl 4 r 2 I a I 0 2 cos dl 0 2 2a 4r r 4 r
0 Idl ( I ' dl 'r ) dF 4 r3 r x x ' , 4 10 N A I ' dl '( Idl r ') dF ' 0 4 r '3 r ' r
7 0
提出寻找电流、电流之间的相互作用的定量规律问题。
dB p
I ' dl 'r B dB 4 r
0 3
r
Biot-savert定律
dl '
I ' dl '
r
实验表明磁场满足叠加原理:
dl '
I'
dB p
点电荷的场强+场强叠加原理
1 dq E dE r 4 r
cos
a r
r ( x 2 a 2 )1 2
dB
例3. 在Bohr氢原子模型中,电子在圆轨道上绕核转动,试 证明电子的轨道磁矩 与轨道角动量 L 之间有关系:
x P
x
θ
dB
e L 2m
L
e为电子电荷,m为电子质量。 解:
Ia 2 0 Ia 2 0 3 2( x 2 a 2 )3 2 2r
r
a
I
建立坐标系
θ
Idl
z
分析对称性、写出分量式 由对称性: B y Bz 0
19
B0
B dBx dB cos
21
国防科大
B dBx dB cos
0 I cosdl 4 r 2 I a I 0 2 cos dl 0 2 2a 4r r 4 r
0 Idl ( I ' dl 'r ) dF 4 r3 r x x ' , 4 10 N A I ' dl '( Idl r ') dF ' 0 4 r '3 r ' r
7 0
提出寻找电流、电流之间的相互作用的定量规律问题。
dB p
I ' dl 'r B dB 4 r
0 3
r
Biot-savert定律
dl '
I ' dl '
r
实验表明磁场满足叠加原理:
dl '
I'
dB p
点电荷的场强+场强叠加原理
1 dq E dE r 4 r
cos
a r
r ( x 2 a 2 )1 2
dB
例3. 在Bohr氢原子模型中,电子在圆轨道上绕核转动,试 证明电子的轨道磁矩 与轨道角动量 L 之间有关系:
x P
x
θ
dB
e L 2m
L
e为电子电荷,m为电子质量。 解:
Ia 2 0 Ia 2 0 3 2( x 2 a 2 )3 2 2r
大学电磁学课件5.2毕奥—萨伐尔定律

µ 0 nI
µ
0
B
nI 2
A1
O
A2
例题1 一个半径R为的塑料薄圆盘 电量+q均匀 为的塑料薄圆盘, 例题 1. 一个半径 为的塑料薄圆盘 , 电量 均匀 分布其上, 分布其上 , 圆盘以角速度 ω绕通过盘心并与盘面垂直 的轴匀速转动。求圆盘中心处的磁感应强度。 的轴匀速转动。求圆盘中心处的磁感应强度。 解 : 带电圆盘转动形成圆电流, 带电圆盘转动形成圆电流 , 处宽度为d 的圆环作圆电 取距盘心 r 处宽度为dr的圆环作圆电 流,电流强度 + + + + + + + + +o + + + + + ω
毕奥—萨伐尔定律是一个实验定律,它是由一些简 单的、典型的载流导体所产生的磁场为基础,经分 析、归纳出的定律,而不是由电流元直接得出的, 事实上,也不可能得到单独的电流元。 实验表明,磁场和电场一样,遵从叠加原理,即任 v 意载流导线在空间某点的磁感应强度 B等于所有电 流元在该点的磁感应强度矢量和
v v ˆ µ 0 Id l × e r dB = 4π r2
I
r Idl θ
r r
•P
r dB
r r 式中dB 是电流元Idl在场中任一点P产生的磁感应强度, r µ0 ˆ 为由er 指向P点的单位矢量, 称为真空磁导率,是 Idl µ 0 = 4π × 10 −7 T ⋅ m ⋅ A −1 一个有量纲的常数,
本节讲授
第五章
恒定电流的磁场
§5.2 毕奥—萨伐尔定律 毕奥—
主讲: 主讲:物电学院副教授 尹绍全
一.毕奥-萨伐尔定律 毕奥-
电流周围有磁场,稳恒电流的磁场是稳恒磁场。 电流周围有磁场,稳恒电流的磁场是稳恒磁场。由 于稳恒电流总是闭合的,且形状各异, 于稳恒电流总是闭合的,且形状各异,所以要想求得总 磁场分布,必须先研究一小段电流的磁场。 磁场分布,必须先研究一小段电流的磁场。沿电流方向 r 称作电流元 电流元。 取一小段电流 Idl ,称作电流元。 1820年 法国科学家毕奥、 1820年,法国科学家毕奥、萨伐尔和拉普拉斯在实 验基础上,分析总结出电流元产生磁场的规律: 验基础上,分析总结出电流元产生磁场的规律:毕 萨伐尔定律( 以下简称毕—萨定律),其内容如 萨定律), 奥—萨伐尔定律( 以下简称毕 萨定律),其内容如 萨伐尔定律 下: r 产生的磁感强度为: 电流元 Idl 在场点 P产生的磁感强度为: 产生的磁感强度为
µ
0
B
nI 2
A1
O
A2
例题1 一个半径R为的塑料薄圆盘 电量+q均匀 为的塑料薄圆盘, 例题 1. 一个半径 为的塑料薄圆盘 , 电量 均匀 分布其上, 分布其上 , 圆盘以角速度 ω绕通过盘心并与盘面垂直 的轴匀速转动。求圆盘中心处的磁感应强度。 的轴匀速转动。求圆盘中心处的磁感应强度。 解 : 带电圆盘转动形成圆电流, 带电圆盘转动形成圆电流 , 处宽度为d 的圆环作圆电 取距盘心 r 处宽度为dr的圆环作圆电 流,电流强度 + + + + + + + + +o + + + + + ω
毕奥—萨伐尔定律是一个实验定律,它是由一些简 单的、典型的载流导体所产生的磁场为基础,经分 析、归纳出的定律,而不是由电流元直接得出的, 事实上,也不可能得到单独的电流元。 实验表明,磁场和电场一样,遵从叠加原理,即任 v 意载流导线在空间某点的磁感应强度 B等于所有电 流元在该点的磁感应强度矢量和
v v ˆ µ 0 Id l × e r dB = 4π r2
I
r Idl θ
r r
•P
r dB
r r 式中dB 是电流元Idl在场中任一点P产生的磁感应强度, r µ0 ˆ 为由er 指向P点的单位矢量, 称为真空磁导率,是 Idl µ 0 = 4π × 10 −7 T ⋅ m ⋅ A −1 一个有量纲的常数,
本节讲授
第五章
恒定电流的磁场
§5.2 毕奥—萨伐尔定律 毕奥—
主讲: 主讲:物电学院副教授 尹绍全
一.毕奥-萨伐尔定律 毕奥-
电流周围有磁场,稳恒电流的磁场是稳恒磁场。 电流周围有磁场,稳恒电流的磁场是稳恒磁场。由 于稳恒电流总是闭合的,且形状各异, 于稳恒电流总是闭合的,且形状各异,所以要想求得总 磁场分布,必须先研究一小段电流的磁场。 磁场分布,必须先研究一小段电流的磁场。沿电流方向 r 称作电流元 电流元。 取一小段电流 Idl ,称作电流元。 1820年 法国科学家毕奥、 1820年,法国科学家毕奥、萨伐尔和拉普拉斯在实 验基础上,分析总结出电流元产生磁场的规律: 验基础上,分析总结出电流元产生磁场的规律:毕 萨伐尔定律( 以下简称毕—萨定律),其内容如 萨定律), 奥—萨伐尔定律( 以下简称毕 萨定律),其内容如 萨伐尔定律 下: r 产生的磁感强度为: 电流元 Idl 在场点 P产生的磁感强度为: 产生的磁感强度为
毕奥萨伐尔定律介绍课件

02
该定律主要描述了电流元在空间 中产生的磁场分布规律,对于理 解电磁场的产生、传播以及电磁 感应等电磁现象具有重要意义。
毕奥萨伐尔定律的重要性
毕奥萨伐尔定律是电磁学核心理论之一,为研究电磁场的性质和行为提供了重要的 基础。
该定律对于现代电磁技术,如电磁感应、电磁波传播、电子设备等,都具有重要的 应用价值。
力学
在研究天体运动和物体运 动时,毕奥萨伐尔定律可 以用来描述物体的运动轨 迹和相对运动。
量子力学
在量子力学中,毕奥萨伐 尔定律可以用来描述微观 粒子的波粒二象性。
在工程中的应用
航空航天工程
毕奥萨伐尔定律在航空航天工程 中有重要的应用,如计算飞行器
的轨迹和空气动力学性能。
机械工程
在机械设计中,毕奥萨伐尔定律 可以用来分析机器的运动状态和
毕奥萨伐尔定律的物理意义
磁场产生
毕奥萨伐尔定律揭示了电流在空间中 产生磁场的过程,当电流通过导线或 导线网络时,会在周围空间产生磁场 。
磁场方向
根据毕奥萨伐尔定律,磁场的方向与 电流的方向垂直,可以用右手定则来 判断。
毕奥萨伐尔定律的适用条件
真空或电介质
毕奥萨伐尔定律适用于真空中的电流在空间中产生磁场的情况,或者适用于电 介质中的情况。
实验验证
介绍了毕奥萨伐尔定律的实验验证方法和结果,以及该定律在实验 中的应用。
毕奥萨伐尔定律在现代的应用
经典应用
介绍了毕奥萨伐尔定律在经典物理学中的应用, 如电磁学、光学和力学等。
现代应用
重点介绍了毕奥萨伐尔定律在现代物理学中的应 用,如量子力学、相对论和宇宙学等。
应用前景
探讨了毕奥萨伐尔定律在未来科技中的应用前景 ,如新材料、新能源和生物医学等领域。
该定律主要描述了电流元在空间 中产生的磁场分布规律,对于理 解电磁场的产生、传播以及电磁 感应等电磁现象具有重要意义。
毕奥萨伐尔定律的重要性
毕奥萨伐尔定律是电磁学核心理论之一,为研究电磁场的性质和行为提供了重要的 基础。
该定律对于现代电磁技术,如电磁感应、电磁波传播、电子设备等,都具有重要的 应用价值。
力学
在研究天体运动和物体运 动时,毕奥萨伐尔定律可 以用来描述物体的运动轨 迹和相对运动。
量子力学
在量子力学中,毕奥萨伐 尔定律可以用来描述微观 粒子的波粒二象性。
在工程中的应用
航空航天工程
毕奥萨伐尔定律在航空航天工程 中有重要的应用,如计算飞行器
的轨迹和空气动力学性能。
机械工程
在机械设计中,毕奥萨伐尔定律 可以用来分析机器的运动状态和
毕奥萨伐尔定律的物理意义
磁场产生
毕奥萨伐尔定律揭示了电流在空间中 产生磁场的过程,当电流通过导线或 导线网络时,会在周围空间产生磁场 。
磁场方向
根据毕奥萨伐尔定律,磁场的方向与 电流的方向垂直,可以用右手定则来 判断。
毕奥萨伐尔定律的适用条件
真空或电介质
毕奥萨伐尔定律适用于真空中的电流在空间中产生磁场的情况,或者适用于电 介质中的情况。
实验验证
介绍了毕奥萨伐尔定律的实验验证方法和结果,以及该定律在实验 中的应用。
毕奥萨伐尔定律在现代的应用
经典应用
介绍了毕奥萨伐尔定律在经典物理学中的应用, 如电磁学、光学和力学等。
现代应用
重点介绍了毕奥萨伐尔定律在现代物理学中的应 用,如量子力学、相对论和宇宙学等。
应用前景
探讨了毕奥萨伐尔定律在未来科技中的应用前景 ,如新材料、新能源和生物医学等领域。
比奥-萨伐尔定律课件

长直导线、电源、测量 仪表(如电流表、电压
表、磁力计等)。
将电源与长直导线连接, 确保电流能够流通。
观察并记录导线受到的 力、电流和电压等数据。
改变电流大小或导线长 度,重复上述步骤。
实验结果与结论
分析数据
对比在不同实验条件下导 线受到的力、电流和电压 的变化,分析其规律性。
得出结论
根据实验数据和规律,得 出比奥-萨伐尔定律的正确 性和适用范围。
03
解方程是推导过程中的一个重要步骤,需要仔细处理。
推导的结论
• 通过推导,我们得到了比奥-萨伐尔定律的公式:E=πr^2dB/dt。这个公式告诉我们线圈中产生的电动势E与磁感应强度B 的变化率dB/dt成正比,与线圈的半径r的平方成正比,与线圈的匝数N成正比。
03
比奥-萨伐尔定律的应用
在物理中的应用
多尺度分析
将比奥-萨伐尔定律与多尺度分析方法相结合,研究不同时间尺度 和空间尺度下的系统行为,揭示其内在机制和演化规律。
未来的研究方向
1 2 3
复杂网络中的比奥-萨伐尔定律
研究复杂网络中的传播机制和演化规律,对比奥 -萨伐尔定律进行更深入的探讨。
跨学科研究
将比奥-萨伐尔定律与其他学科领域相结合,如 物理学、生物学、社会学等,拓展其应用范围和 理论内涵。
实际应用
了解地球磁场对输电线路、 电机等电气设备的影响, 为实际工程应用提供理论 支持。
05
比奥-萨伐尔定律的扩展与展望
扩展的理论与模型
广义比奥-萨伐尔定律
将原有的定律扩展到更广泛的领域,包括非线性、非平衡态和复 杂系统的情况,提供更全面的理论框架。
引入随机因素
考虑随机扰动和噪声对系统的影响,建立更贴近实际的模型,提高 预测的准确性和可靠性。
磁场强度毕奥萨伐尔定律及运动电荷产生的磁场 ppt课件

当电荷运动速度与磁场方向一致时电荷受力为当把运动电荷放在磁场中后它会受到一种与其速度有关的力这个力称为洛仑兹力三磁感应强度描述磁场性质的基本物理量
磁场 磁场强度 毕奥—萨伐尔定律
ppt课件
1
前言 静止的电荷周围—电场。 运动的电荷周围—电场和磁场。
静止电荷对静止电荷和运动电荷的作用,均满足 库仑定律。运动荷对静止电荷的作用不遵守库仑定律, 而高斯定律仍然成立。
dB
L
oIdl rˆ L 4r 2
2.分割电流元;
3. 确定电流元的磁场 dB
0 4
Id l r
r3
4.求 B 的分量 Bx 、By 、Bz ;
5.由 B
Bx2
By2
Bz2
求总场。
ppt课件
9
例1:一段有限长载流直导线,通有电流为 I ,求距 a 处
q
t
qN
qnV ppt课件
nqvS
20
在该d导B体上4选0 I取d一rl3个r电流元 Idl ,它产生的磁场为:
电流元产生的磁场相当于电流 元内 dN 个运动电荷产生的磁场。 Idl
而电荷元内电荷的数目为:
dN = ndV = nSdl
dN
r
S
P
dB
反,相互抵消。B 0, B ppt课件 Bx2 B2 B x 14
B dB x dB sin
Idl
sin R
r
B
dB
x
2R
0
0I 4r 2
Rdl r
R
Io
0IR 4r 3
磁场 磁场强度 毕奥—萨伐尔定律
ppt课件
1
前言 静止的电荷周围—电场。 运动的电荷周围—电场和磁场。
静止电荷对静止电荷和运动电荷的作用,均满足 库仑定律。运动荷对静止电荷的作用不遵守库仑定律, 而高斯定律仍然成立。
dB
L
oIdl rˆ L 4r 2
2.分割电流元;
3. 确定电流元的磁场 dB
0 4
Id l r
r3
4.求 B 的分量 Bx 、By 、Bz ;
5.由 B
Bx2
By2
Bz2
求总场。
ppt课件
9
例1:一段有限长载流直导线,通有电流为 I ,求距 a 处
q
t
qN
qnV ppt课件
nqvS
20
在该d导B体上4选0 I取d一rl3个r电流元 Idl ,它产生的磁场为:
电流元产生的磁场相当于电流 元内 dN 个运动电荷产生的磁场。 Idl
而电荷元内电荷的数目为:
dN = ndV = nSdl
dN
r
S
P
dB
反,相互抵消。B 0, B ppt课件 Bx2 B2 B x 14
B dB x dB sin
Idl
sin R
r
B
dB
x
2R
0
0I 4r 2
Rdl r
R
Io
0IR 4r 3
毕奥萨伐尔定律PPT课件

B 0I
2πr
I B
I XB
电流与磁感强度成右螺旋关系
8
第8页/共31页
例2 有一无限长通电 的扁平铜片,宽度为a, 厚度不计,电流I 在铜 片上均匀分布,求铜片 外与铜片共面、离铜片 边缘为b 的点P(如图) 的磁感强度.
I
P b*
a
9
第9页/共31页
解 建立坐标如图
dx
dI I dx a
*
P
y
0I
4 π r0
(cos1
cos2
)
B 的方向沿 x 轴的负方向
6
第6页/共31页
B
0I
4 π
z
无限长载流长直导线
D 2
I
xo
C 1
B
×
P
y
1 0 2 π
B 0I
2 π r0
半无限长载流长直导线
1
π 2
2 π
BP
0I
4πr
7
第7页/共31页
无限长载流长直导线的磁场
R
1
x1 o* 2
x2 x
×× ××× × ×× ××× ×× ×
23
第23页/共31页
讨论
B
0nI
2
cos2
c os 1
(1)P点位于管内轴线中点 1 π 2
cos 1 cos 2
cos2
l/2
l / 22 R2
B
0nI
cos2
0nI
2
l l 2 / 4 R2 1/2
若 l R
4a
2. 圆 电流轴 线IR上2i 磁场:
P
B
0
2( R 2
大学物理-毕奥-萨伐尔定律
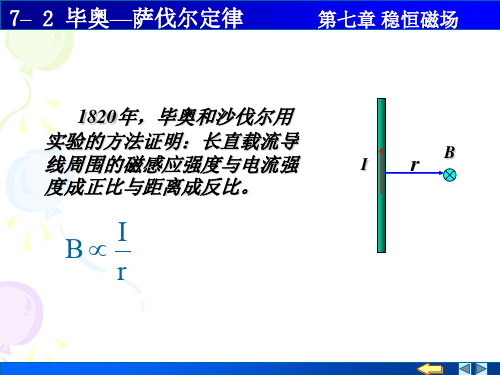
磁感强度叠加原理 B dB
0I
4π
dl
r
r3
7– 2 毕奥—萨伐尔定律
第七章 稳恒磁场
dB
0
4π
Idl
r
r3
毕奥—萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
1
8
2
+
7
Idl + 3
R
6
+4
5
1、5 点 :dB 0
3、7点
:dB
0 Idl
4π R2
7– 2 毕奥—萨伐尔定律
第七章 稳恒磁场
1820年,毕奥和沙伐尔用 实验的方法证明:长直载流导 线周围的磁感应强度与电流强 度成正比与距离成反比。
B I r
I
rB
7– 2 毕奥—萨伐尔定律
第七章 稳恒磁场
拉普拉斯对此结果作了分析,得出了 电流元产生的磁场的磁感应强度表达式。
电流元
Idl
I
dl
(4)写出总磁感应强度的大小和方向,或写成矢量 式。
7– 2 毕奥—萨伐尔定律
第七章 稳恒磁场
导线1,2和3在P点产生的磁 场方向均垂直纸面向内, 大小均为
B1
B2
B3
0 I 4r
cos1
cos2
0 I
4 a 2 tg300
cos 300 cos1500
30I 2a
1
x1 o p 2
x2
x + + + + + + + + + + + + + + +
0I
4π
dl
r
r3
7– 2 毕奥—萨伐尔定律
第七章 稳恒磁场
dB
0
4π
Idl
r
r3
毕奥—萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
1
8
2
+
7
Idl + 3
R
6
+4
5
1、5 点 :dB 0
3、7点
:dB
0 Idl
4π R2
7– 2 毕奥—萨伐尔定律
第七章 稳恒磁场
1820年,毕奥和沙伐尔用 实验的方法证明:长直载流导 线周围的磁感应强度与电流强 度成正比与距离成反比。
B I r
I
rB
7– 2 毕奥—萨伐尔定律
第七章 稳恒磁场
拉普拉斯对此结果作了分析,得出了 电流元产生的磁场的磁感应强度表达式。
电流元
Idl
I
dl
(4)写出总磁感应强度的大小和方向,或写成矢量 式。
7– 2 毕奥—萨伐尔定律
第七章 稳恒磁场
导线1,2和3在P点产生的磁 场方向均垂直纸面向内, 大小均为
B1
B2
B3
0 I 4r
cos1
cos2
0 I
4 a 2 tg300
cos 300 cos1500
30I 2a
1
x1 o p 2
x2
x + + + + + + + + + + + + + + +
大学物理课件-2毕奥-萨伐尔定律

1 2
0I
2R1
(每202长1/3/1度8 相等的圆弧在O处产生的磁场大小相同);20
方向:垂直纸面向外。
大线圈在O处产生的磁场大小为: B0大
方向:垂直纸面向里。
1 2
0 I
2R2
、
B0 B0小 B0大
方向:垂直纸面向外。
0I
4
1 [ R1
1 ]
R2
(2) B0
BB00'' 大 小
B0小 B0大
以电荷为q速度为的正电荷作研究对象在电流元中其电流为i102021318lqns单个载流子产生的磁场112021318一个以速度v作匀速直线运动的电荷q与电流元是相当的在dt时间内粒子位移为dlvdt等效电流元为idlidtvqv根据毕奥萨伐尔定律在距它r处点p所激励的磁感应强度为
20XX年复习资料
它们的方向均垂直纸面向里。
B B '
‘
02021/3/108小
B0’大
ቤተ መጻሕፍቲ ባይዱ
0 I
4
1 [ R1
1 ]
R2
方向均垂直纸面向里21。
相信梦想是价值的源泉,相信眼光决定未来的一 切,相信成功的信念比成功本身更重要,相信人 生有挫折没有失败,相信生命的质量来自决不妥
协的信念。
谢谢观看
2021/3/18
22
电流元在空间某点产生的磁感应强度大小与电流
元大小成正比,与电流元和由电流元到点P的矢
量平方间成夹反角比正;弦d成B垂正直比于,I与dl电和流r元 所到组点成P的的距平离面,的
指向满足右手定则。
Idl r
dB k
2021/3/18
r3
其中: k = 0 /4 真空磁导率 : 0=410-7TmA-31
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Bz dBz
(1)取电流元 I dy 方向沿Z轴负向,各电流元相同。
(2)统一变量B来自0 I2π r
I
B
I
X
B
电流与磁感强度成右螺旋关系
半无限长载流长直导线的磁场
π 1 2 2 π
BP
0 I
4π r
I
o
r
* P
I R o
x
*
B
x
B
0 IR 2
(x 2 R 2)2 2
0 Idl r dB 3 4π r
1
毕奥—萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
8 2
d 1、5 点 : B 0
3、7点 :dB +3
+
7
Id l
R
6
0 Idl
4π R
0
2
2、4、6、8 点 :
+4
5
dB
0 Idl
4π R
2
sin 45
毕奥---萨伐尔定律应用举例 解题步骤
0 IR 2
2x
3
, B
0 IS
2π x
3
(1) I (2 )
R B x 0 0 I o B0 2R
I
(4)
BA
d (5) I *A
R1
0 I
4π d
R
o (3) I R
B0
0 I
4R
R2
*o
B0
o
0 I
8R
B0
0 I
4 R2
0 I
4 R1
0 I
4π R1
x
O
已知,实验表明,受力 总是垂直于 的大小及 间的夹角有关,当
所决定的平面, 时受力最大。
的 大小及方向由下式定义:
Fmax
v
q
+
B
单位 特斯拉 1(T ) 1N/A m
1 特斯拉 ( T ) = 104 高斯( G )
Biot-Savart’s law
一 毕奥—萨伐尔定律 (电流元在空间产生的磁场)
magnetic induction
在通有电流导线的周围, 小磁针会发生偏转 ;
运动电荷会受某种力的作用。
理论和实验证明 电流(或运动的电荷) 能产生一种有别于静电场 的另一种场,称为磁场。
运动电荷 (电流)
磁场
运动电荷 (电流)
空间某点的磁场大小和方向,用磁感应强度 B 来描述。
运动正电荷 力的大小与 某点
1.选取合适的坐标系、选取合适的电流元——根据已知电流的 分布与待求场点的位置;
2.写出电流元产生的磁感应强度——根据毕奥-萨伐尔定律;
3.计算磁感应强度的分布——叠加原理; 4.一般说来,需要将磁感应强度的矢量积分变为标量积分,并 选取合适的积分变量,来统一积分变量。
B x dBx
B y dBy
运动电荷 静电荷 电场 静电场 磁场 稳恒磁场 稳恒电流
学习方法: 类比法
Contents 磁感应强度 magnetic induction 毕奥 - 萨伐尔定律 Biot-Savart’s law
chapter 9
磁场高斯定理与安培环路定理 Gauss theorem and Ampere circuital theorem in magnetic field 运动电荷的磁场 magnetic field of moving charge
Id l
dB
4π r 0 Idl r dB 4π r 3
2
dB
0 Idl sin
dB
P *
r
Id l
I
0 4π 10 7 N A 2 真空磁导率
r
任意载流导线在点 P 处的磁感强度
磁感强度叠加原理
0 I dl r B dB 3 4π r
如图所示,有一长为l , 半径为R的载流密绕直螺 线管,单位长度的匝数为n,通有电流I. 设把螺线管 放在真空中,求管内轴线上一点处的磁感强度.
(1) 无限长的螺线管
(2)半无限长螺线管
B 0 nI
x1 0, x2
1 B 0 nI 2
1 0 nI 2
B
0 nI
0 Idl r ˆ 比较: B d 2 4π r
类似处:
dE
1 dq ˆ r 2 4 π 0 r
⑴都是元场源产生场的公式:一个是电流元产生磁场, 一个是电荷元产生电场。 ⑵大小都和 r2成反比。 ⑶与叠加原理一起使用,原则上可求解任意分布的磁场或电场。
不同处:
dE的方向与ˆ相同; r dB的方向与ˆ垂直,且与 l 垂直。 r Id
3
B0
0 I
2R
B0 讨 1)若线圈有N 匝 B 3 2R 2 2 2 (x R ) 2 论
N 0 IR 2
0 IN
2)x 0 B 的方向不变( I 和 B 成右螺旋关系)
3)若导线为一段 圆弧,张角为θ, 4)x R B
0 I 0 I B0 2 R 2 4R
