2015中考专题+第四讲+直线与圆的位置关系(培优)
初三数学培优之直线与圆的位置关系(2)
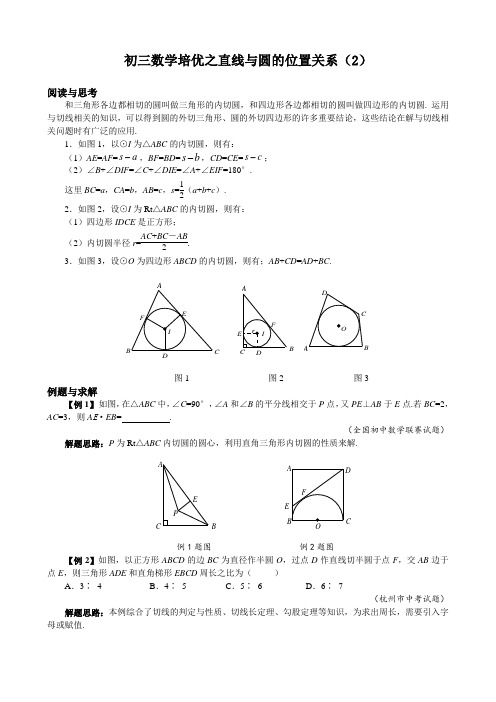
初三数学培优之直线与圆的位置关系(2)阅读与思考和三角形各边都相切的圆叫做三角形的内切圆,和四边形各边都相切的圆叫做四边形的内切圆. 运用与切线相关的知识,可以得到圆的外切三角形、圆的外切四边形的许多重要结论,这些结论在解与切线相关问题时有广泛的应用.1.如图1,以⊙I 为△ABC 的内切圆,则有:(1)AE =AF =a s -,BF =BD =b s -,CD =CE =c s -; (2)∠B +∠DIF =∠C +∠DIE =∠A +∠EIF =180°.这里BC =a ,CA =b ,AB =c ,s =12(a +b +c ).2.如图2,设⊙I 为Rt △ABC 的内切圆,则有: (1)四边形IDCE 是正方形; (2)内切圆半径r =AC +BC -AB2.3.如图3,设⊙O 为四边形ABCD 的内切圆,则有;AB +CD =AD +BC .CB图1 图2 图3例题与求解【例1】 如图,在△ABC 中,∠C =90°,∠A 和∠B 的平分线相交于P 点,又PE ⊥AB 于E 点.若BC =2,AC =3,则A E ·EB = .(全国初中数学联赛试题)解题思路:P 为Rt △ABC 内切圆的圆心,利用直角三角形内切圆的性质来解.P E BCAOEDC例1题图 例2题图【例2】如图,以正方形ABCD 的边BC 为直径作半圆O ,过点D 作直线切半圆于点F ,交AB 边于点E ,则三角形ADE 和直角梯形EBCD 周长之比为( )A .3∶ 4B .4∶ 5C .5∶ 6D .6∶ 7(杭州市中考试题)解题思路:本例综合了切线的判定与性质、切线长定理、勾股定理等知识,为求出周长,需要引入字母或赋值.【例3】如图,已知∠ACE=∠CDE=90°,点B在CE上,CA=CB=CD,过A、C、D三点的圆交AB 于F.求证:F是△CDE的内心.(全国初中数学联赛试题)解题思路:即要证F为△CDE角平分线的交点,将问题转化为角相等问题的证明,充分运用与圆相关的角的性质.ADFBC E【例4】如图,不等边△ABC内接于⊙O,I是其内心,且AI⊥OI.求证:AB+AC=2BC.(四川省竞赛试题)解题思路:从外心、内心出发,添加辅助线,充分运用圆的性质,由角的关系导出线段的关系.【例5】如图,已知Rt△ABC中,CD是斜边AB上的高,O、O1、O2分别是△ABC、△ACD、△BCD 角平分线的交点.求证:(1)O1O⊥CO2;(2)OC=O1O2.(武汉市选拔赛试题)解题思路:在直角三角形中,斜边上的高将它分成的两个直角三角形和原三角形相似,得对应角相等.故通过证交角等于90°的方法得两线垂直,再用全等三角形证两线段相等.B【例6】如图,已知直径与等边三角形ABC 的高相等的圆与AB 和BC 边相切于点D 和E ,与AC 边相交于点F 和G . 求∠DEF 的度数.(浙江省竞赛试题)解题思路:若要运用切线的性质,则需确定圆心,这是解本例的关键.GFA BEDC能力训练A 级1.如图,⊙I 是Rt △ABC 的内切圆,切点为D 、E 、F ,若AF 、BE 的长是方程x 2-13x +30=0的两根,则S △ABC 的值是 . (泰州市中考试题)F(第1题图) (第2题图) (第3题图)2.如图,Rt △ABC 中,∠C =90°,BC =5,⊙O 内切Rt △ABC 的三边AB 、BC 、CA 于D 、E 、F ,半径r =2,则AC = . (杭州市中考试题) 3.如图,已知直线6+-=x y 与x 轴交于点A ,与y 轴交于点B ,点P 为x 轴上可以移动的点,且点P 在点A 的左侧,PM ⊥x 轴,交直线6+-=x y 于点M . 有一个动圆O ′,它与x 轴、直线PM 和直线6+-=x y 都相切,且在x 轴上方.当⊙O ′与y 轴也相切时,点P 的坐标是 .(青岛市中考试题)4.如图,已知△ABC 的内切圆O 与各边相切于D 、E 、F ,那么点O 是△DEF 的( ) A .三条中线的交点 B .三条高的交点C .三条角平分线的交点D .三条边的垂直平分线的交点(四川省中考题)CC(第4题图) (第5题图)5.如图,AD 是△ABC 的角平分线,⊙O 过点A 且和BC 相切于点D ,和AB 、AC 分别交于点E 、F .若BD =AE ,且BE =a ,CF =b ,则AF 的长为( )A .1+52 aB .1+32 aC .1+52bD .1+32b6.若0°<α<90°,那么以sin α、cos α、tan α·cot α为三边的△ABC 的内切圆半径r 与外接圆半径R 之和是( ) (安徽省竞赛试题)A .sin α+cos α2B .tan α+cot α2C .2sin αcos αD .1sin α+cos α7.如图,设AD 是△ABC 的中线,△ABD 、△ADC 的外心分别为E 、F ,直线BE 与CF 交于点G . 若DG =12BC ,求证:∠ADG =2∠ACG .(“我爱数学”夏令营竞赛试题)8.如图,BC 是⊙O 的直径,AB 、AD 是⊙O 的切线,切点分别为B 、P .过C 点的切线与AD 交于点D .连结AO 、DO .(1)求证:△ABO ∽△OCD ;(2)若AB 、CD 是关于x 的方程x 2-52(m -1)x +(m -1)2=0的两个实数根,且S △ABO +S △OCD =20,求m 的值.OBDCPA(第7题图) (第8题图) (第9题图)9.如图,以坐标原点O 为圆心,6为半径的圆交y 轴于A 、B 两点,AM 、BN 为⊙O 的切线,D 为切线AM 上的一点(D 与A 不重合),DE 切⊙O 于点E ,与BN 交于点C ,且AD <BC . 设AD =m ,BC =n .(1)求m ·n 的值;(2)若m ,n 是方程2t 2-30t +k =0的两根,求:①△COD 的面积;②CD 所在直线的解析式;③切点E 的坐标.(辽宁省中考题)10.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…,⊙O n为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切,…,⊙O n-1与⊙O n相外切,⊙O1,⊙O2,…,⊙O n都与AB相切,且⊙O1与AC相切,⊙O n与BC相切.求这些等圆的半径r(用n表示).(河北省竞赛试题)AF G(第10题图)(第11题图)11.如图,四边形A1A2A3A4内接于一圆,△A1A2A3、△A2A3A4、△A3A4A1的内心分别是I1、I2、I3.求证:(1)A2、I1、I2、A3四点共圆;(2)∠I1I2I3=90°.(四川省竞赛试题)B级1.如图,AC⊥BC,BC=a,AC=b,⊙O的半径为r,那么满足关系式r=aba+b的图形是.(把正确的所有图形的序号填在横线上)BACAB①②③④2.已知在△ABC中,∠C=90°,AC=4,BC=3,CD为AB上的高. O1、O2分别为△ACD、△BCD的内心,则O1O2= .(太原市竞赛试题)3.如图,半圆与两直角边相切,且圆心O在直角三角形ABC的斜边AB上.若直角三角形面积为S,斜边长为c,则半圆的半径r= .(五城市联赛试题)4.已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O 的切线分别交过A、B两点的切线于D、C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP·PC为定值;④P A为∠NPD的平分线.其中一定成立的是()A.①②③B.②③④C.①③④D.①④BBC(第3题图) (第4题图) (第5题图) (第6题图)5.如图,半圆O 的直径在梯形ABCD 的底边AB 上,且与其余三边BC 、CD 、DA 相切,若BC =2,DA =3,则AB 的长( )A .等于4B .等于5C .等于6D .不能确定(全国初中数学联赛试题)6.如图,在矩形ABCD 中,连结AC .如果O 为△ABC 的内心,过O 作OE ⊥AD 于点E ,作OF ⊥CD 于F ,则矩形OFDE 的面积与矩形ABCD 的面积的比值为( )A .12B .23C .34 D .不能确定,与AB 、BC 的长度有关(《学习报》公开赛试题) 7.一条直线DE 平分△ABC 的周长,同时直线DE 又平分了△ABC 的面积. 求证:直线DE 经过△ABC 的内切圆圆心O .(全国初中数学联赛试题)8.如图,AB 、BC 、CD 分别与圆相切于E 、F 、G ,AB =BC =CD . 连结AC 与BD 相交于点P ,连结PF. 求证:PF ⊥BC . (江苏省竞赛试题)BD BFPG A E C(第8题图) (第9题图)9.如图,在△ABC 中,CH 为高,R 、S 分别为△ACH 和△BCH 的内切圆与CH 的切点.若AB =1995,AC =1994,BC =1993,则RS 可表示成mn,其中m ,n 是互质的正整数.求m +n 的值.(美国中学生数学邀请赛试题)10.如图,△ABC 的三边满足关系式BC =12(AB +AC ),O 、I 分别为△ABC 的外心、内心.∠BAC 的外角平分线交⊙O 于E ,AI 的延长线交⊙O 于D ,DE 交BC 于H .求证:(1)AI =BD ;(2)OI =12AE.(湖北省选拔赛试题)KC(第10题图) (第11题图) (第12题图)11.如图,在平面直角坐标系中,A 、B 两点的坐标分别为A (-2,0)、B (8,0).以AB 为直径的半圆P 与y 轴交于点M ,以AB 为一边作正方形ABCD .(1)求C 、M 两点的坐标;(2)连接CM ,试判断直线CM 是否与⊙P 相切?说明你的理由;(3)在x 轴上是否存在一点Q ,使得△QMC 的周长最小?若存在,求出点Q 的坐标;若不存在,请说明理由.(南宁市中考试题)12.如图,⊙O 是等边△ABC 的内切圆,与AB 、AC 两边分别切于D 、E 两点,连结DE . 点P 是劣弧 ⌒DE 上的一个动点(不与D 、E 重合),过点P 作PM ⊥AB 于M ,PN ⊥AC 于N ,PK ⊥BC 于K ,PK 交DE 于L 点.求证:(1)PL 2=PM ·PN ;(2)PK =PM +PN .(黄石二中理科实验班自主招生考试试题)。
《直线与圆的位置关系》优秀课件

掌握直线与圆的位置关系的定义 、分类和判定方法,理解其几何 意义和实际应用。
直线与圆的位置关系的重要性
基础概念
直线与圆的位置关系是解析几何中的 基础概念,是后续学习曲线与方程、 极坐标等知识的基础。
实际应用
在几何作图、工程绘图、物理学等领 域中,直线与圆的位置关系有着广泛 的应用。
教学方法与手段
相切线的定义
直线与圆只有一个公共点 ,即直线与圆相切。
相切线的性质
相切线与圆心的距离等于 圆的半径。
相切线的应用
在几何图形中,相切线可 以用于求解与圆相关的最 值问题,如圆的面积、周 长等。
相交线的性质及应用
相交线的定义
直线与圆有两个公共点,即直线与圆相交。
相交线的性质
相交线与圆心的距离小于圆的半径。
03
直线与圆的位置关系的判定方 法
代数法
定义
通过解直线与圆方程组成的方程 组,利用解的情况判断直线与圆
的位置关系。
步骤
将直线方程代入圆方程,消去一 个变量后得到一个关于另一个变 量的二次方程。根据二次方程的 判别式判断直线与圆的位置关系
。
结论
若判别式小于0,则直线与圆相 离;若判别式等于0,则直线与 圆相切;若判别式大于0,则直
线与圆相交。
几何法
定义
通过观察直线与圆心的距离和圆 的半径,判断直线与圆的位置关
系。
步骤
计算直线到圆心的距离d,比较d 与圆的半径r的大小。若d小于r, 则直线与圆相交;若d等于r,则直 线与圆相切;若d大于r,则直线与 圆相离。
结论
几何法适用于判断直线与圆的位置 关系,但需要一定的观察和计算能 力。
本节内容通过具体例题的解析,让学生掌握直线与圆位置关系的判定方法,同时培养了学 生的分析问题和解决问题的能力。
《直线与圆的位置关系》优质课件

汇报人:日期:CATALOGUE目录•教学目标与重点难点•教学内容与过程•教学方法与手段•教学资源与反思•作业布置与反馈•教学案例与拓展•总结与展望教学目标与重点难点使学生掌握直线与圆的位置关系的判断方法,理解点到直线的距离公式,并能够进行简单的应用。
知识与技能通过实例演示和探究活动,培养学生的数学思维能力和自主学习能力。
过程与方法让学生感受到数学与生活的紧密联系,培养学生对数学的兴趣和自信心。
情感态度与价值观教学目标重点难点直线与圆的位置关系的判断方法,点到直线的距离公式。
难点如何应用点到直线的距离公式解决实际问题。
教学内容与过程回顾初中已学过的直线与圆的位置关系引出高中阶段需要进一步学习的直线与圆的位置关系展示生活中的直线与圆的实例,激发学生对该主题的兴趣复习导入介绍直线与圆位置关系的种类:相交、相切、相离引导学生通过实验和推理,理解直线与圆位置关系的判定方法和性质通过观察和操作,让学生感受直线与圆的位置关系探索新知设计不同难度的练习题,让学生动手操作,加深对直线与圆位置关系的理解通过小组合作、讨论,引导学生自主解决问题,培养学生的合作精神和解决问题的能力巩固练习归纳小结回顾本节课学习的重点内容,引导学生总结直线与圆位置关系的判定方法和性质强调本节课学习的意义和作用,激发学生对数学的兴趣和热情教学方法与手段通过展示直线和圆的模型和图像,帮助学生理解直线与圆的位置关系。
直观演示法探究式教学法归纳总结法引导学生通过观察、思考和实践,自主探究直线与圆的位置关系的特点和规律。
将学生探究的结果进行归纳和总结,形成系统化的知识结构。
030201使用PPT等多媒体手段,展示直线与圆的图像和动画,帮助学生更好地理解。
多媒体辅助展示直线和圆的模型,让学生更直观地感受直线与圆的位置关系。
实物展示组织学生进行小组讨论和交流,鼓励学生互相学习和分享经验。
互动交流教学资源与反思深入剖析教材,理解教材的编排思路和用意,挖掘教材中的重点和难点。
直线与圆的位置关系ppt课件

新知讲解
想一想:自一点引圆的切线的条数 (1)若点在圆外,则过此点可以作几条切线? 若点在圆外,则过此点可以作圆的两条切线. (2)若点在圆上,则过此点只能作几条切线? 若点在圆上,则过此点只能作圆的一条切线,且此点是切点. (3)若点在圆内,则过此点能作几条切线? 若点在圆内,则过此点不能作圆的切线,即可以作0条. 问题:如何刻画直线与圆相切? 公共点的个数只有1个; 圆心到直线的距离等于半径.
2
因此所求切线l的方程为y=-2x或y= 1 x.
2
新知讲解
例2:已知直线l经过点 O (0,0),且与圆C:(x-1)2 + (y-3)2 =5相切,求直线l的方程.
解法2:当直线l的斜率不存在时,直线l的方程为x=0,圆
心C(1,3)到直线l的距离为1≠ 5 ,不合题意.
当直线l的斜率存在时,设直线l的方程为y=kx,即kx-y=0,
新知讲解
例2:已知直线l经过点 O (0,0),且与圆C:(x-1)2 + (y-3)2 =5相切,求直线l的方程.
思路1 直线与圆相切
直线的方程,
圆的方程
0
直线方程
思路2
d r
新知讲解
例2:已知直线l经过点 O (0,0),且与圆C:(x-1)2 + (y-3)2 =5相切,求直线l的方程.
当堂检测
1.(1)直线x+y-2=0与圆x2+y2=2的位置关系为__相__切____ (2)直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为___相__离___ (3)直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系为__相__交____
直线与圆的位置关系知识点及例题

直线与圆的地点关系一、知识点梳理1、直线与圆的地点关系:r为半径, d 为圆心到直线的距离图形名称相离相切相交判定d>r d=r d<r交点个数无 1 个 2 个例 1、以下判断正确的选项是()①直线上一点到圆心的距离大于半径,则直线与圆相离;②直线上一点到圆心的距离等于半径,则直线与圆相切;③直线上一点到圆心的距离小于半径,? 则直线与圆订交.A.①②③B.①②C.②③D.③例 2、过圆上一点能够作圆的______条切线;过圆外一点能够作圆的_____条切线;?过圆内一点的圆的切线______.例 3、以三角形一边为直径的圆恰巧与另一边相切,则此三角形是_______.例 4、以下直线是圆的切线的是()A.与圆有公共点的直线B.到圆心的距离等于半径的直线C.垂直于圆的半径的直线D.过圆直径外端点的直线例 5.如下图,Rt△ABC中,∠ACB=90°,CA=6,CB=8,以C为圆心,r为半径作⊙C,当r为多少时,⊙C 与 AB相切2、切线的判断:( 1)依据切线的定义判断:即与圆有一个公共点的直线是圆的切线.( 2)依据圆心到直线的距离来判断:即与圆心的距离等于半径的直线是圆的切线.( 3)依据切线的判断定理来判断:即经过半径的外端而且垂直于这条半径的直线是圆的切线.判断切线经常用的协助线作法:( 1)若直线与圆有公共点时,协助线的作法是“连结圆心和公共点”,再证明直线和半径垂直.(2)当直线与圆并无明确有公共点时,协助线的作法是“过圆心向直线作垂线”再证明圆心到直线的距离等于圆的半径 .例 6、判断以下命题能否正确( 1)经过半径的外端的直线是圆的切线( 2)垂直于半径的直线是圆的切线;( 3)过直径的外端而且垂直于这条直径的直线是圆的切线;( 4)和圆有一个公共点的直线是圆的切线;( 5)以等腰三角形的极点为圆心,底边上的高为半径的圆与底边相切.例 7.OA均分∠BOC,P是OA上任一点(O除外),若以P为圆心的⊙P与OC相离,?那么⊙P与OB的地点关系是()A.相离B.相切C.订交D.订交或相切例 8、如下图,在直角坐标系中,⊙M的圆心坐标为(m,0),半径为2,?假如⊙M与y轴所在直线相切,那么m=______,假如⊙ M与 y 轴所在直线订交,那么m? 的取值范围是_______.例 9、如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC?的延伸线于点E,连结 BC.( 1)求证: BE为⊙ O的切线;1(2)假如 CD=6, tan ∠ BCD= ,求⊙ O的直径.2例 10、如图,已知:△ABC内接于⊙O,点D在OC的延伸线上,sinB=1,∠D=30°.2( 1)求证: AD是⊙ O的切线;(2)若 AC=6,求 AD的长.例 11、如图,P为⊙O外一点,PO交⊙O于C,过⊙O上一点A作弦AB⊥PO于E,若∠ EAC=∠ CAP,求证: PA是⊙ O的切线.3、切线的性质:1、经过切点的半径垂直于圆的切线,经过切点垂直于切线的直线必经过圆心关于切线的性质可分解为:过圆心、过切点、垂直于切线这三个条件中随意两个作为条件,就能够推出第三个作为结论4、切线长定理:切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长切线长定理:从圆外一点能够引圆的两条切线,它们的切线长相等,这点和圆心的连线均分两条切线的夹角.例 12、如图 1, PA、 PB是⊙O 的两条切线、 A、 B 为切点。
中考复习直线与圆的位置关系ppt课件

2023/10/11
活动2:求圆 请根据下列条件分别计算出⊙O的半径
(1)如图4,在△ABC中, AC是⊙O的直径, ⊙O与BC相切于点C,与AB相交于点D, 且AB=10,BC=8;
(2)如图5,在△ABC中,圆心O在AC上, ⊙O与AB,BC分别切于点D,C, 且AB=10,BC=8;
(3)如图6,△ABC中, ∠C=90° ,⊙O与△ABC三边分别切于点D,E,F,且 AB=10,BC=8;
练习反馈
5.如图,四边形ABCD的边AB、BC、CD、DA和圆⊙O分别相
切于点L、M、N、P, 求证: AD+BC=AB+CD
C N
证明:由切线长定理得 D
∴AL=AP,LB=MB,NC=MC,
M
DN= DP
P
O
AL
B
∴AL+LB+NC+DN=AP+MB+MC+DP
即 AB+CD=AD+BC
2023/10/11
• 易证EQ=EA, FQ=FB, • PA=PB • ∴ PE+EQ=PA=12cm • PF+FQ=PB=PA=12cm
• ∴周长为24cm
A
EO
Q
P
FB
2023/10/11
练习反馈
• 7. (2018•泰安)如图, ⊙M的半径为2,圆心M的坐标为(3 ,4),点 P是⊙M上的任意一点, PA⊥PB,且PA 、PB与x轴分别交于A 、B两点, 若点A、点B关于原点O对称,则AB的最小值为( )
2023/10/11
图8
练习反馈
• 1.如图,直线AB经过⊙O上的点C,并且OA=OB, • CA=CB,求证直线AB是⊙O的切线.
《直线与圆的位置关系》优秀课件

环境保护
通过观察直线与圆的位置关系, 可以判断环境监测设备的准确性
和灵敏度。
解析几何在生活中的应用
金融投资
解析几何可以应用于金融领域,例如利用线性回 归模型进行股票价格预测等。
建筑设计
解析几何在建筑设计中被广泛应用于确定建筑物 的位置、高度和形状,以确保美观和功能性。
医学影像
解析几何在医学影像领域的应用,例如CT、MRI 等图像的生成和处理。
判断方法
利用圆心到直线的距离大 于圆的半径,即d > r。
性质
直线与圆相离时,直线被 圆截得的线段长度为无穷 大。
04
案例分析与应用
直线与圆位置关系的实际应用
航海导航
利用直线与圆的位置关系,确定 船只与目标之间的距离和方向,
确保安全航行。
工业制造
在机械加工、制造等领域,直线 与圆的位置关系可用于确定工件
直线与圆位置关系的判断方法
介绍判断直线与圆位置关系的方法,包括圆心到直线的距离、直线与圆的交点个 数等。
解题思路与方法
解题思路
明确解题思路,包括分析问题、建立 模型、求解和整合答案等步骤。
方法总结
总结解决直线与圆位置关系问题的方 法,包括代数法和几何法两种。
问题建模与求解
典型例题解析
选取具有代表性的例题,进行详细解析,包括题目分析、建 模、求解和答案整合等。
培养解决复杂问题的能力 加强数学思维和方法的训练
拓展直线与圆位置关系的应用领域 学习其他几何图形的基础知识
与其他同学的互动交流
分享学习心得和经验,互相启发
合作完成一些实际问题的解决方 案
分组合作,互相学习,共同进步
讨论直线与圆位置关系的应用案 例
直线与圆的位置关系

利用消元法,得到关于另一个元的一元二次方程
代数法主要步骤:
比较Δ与0的大小: 当Δ<0时,直线与圆相离;当Δ=0时, 直线与圆相切 ;当Δ>0时,直线与圆相交。
求出其Δ的值
把直线方程与圆的方程联立成方程组
!
添加标题
几何法主要步骤:
!
添加标题
利用点到直线的距离公式求圆心到直线的距离
!
添加标题
作判断: 当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交
直线与圆的 位置关系直线与圆的
单击此处添加副标题
1
2
3
4
5
6
我们把太阳看作一个圆,把地平线看作一条直线可以发现,太阳与地平线有三种位置关系:
分 析
章节一
直线与圆的位置关系:
直线与圆相交;
直线与圆相切;
直线与圆相离。
思 考
现在,如何用直线的方程和圆的方程判断它们之间的位置关系?
1、看由它们的方程组成的方程组有无实数解;
分析:
例1 已知直线 和圆心为C的圆 ,判断直线l与圆的位置关系;如果相交,求 它们交点的坐标.
①
②
消去y,得
因为
所以,直线l与圆相交,有两个公共点.
解法一: 由直线与圆的方程,得
01
课本第140页 习题4.2 (A组)第 1、2、3 题
Thank you
谢谢!谢谢!
方法一
方法二
在初中,我们怎样判断直线与圆的位置关系?
A B C 返回 例1
直线与圆相切,只有一个公共点;
单击此处添加正文,文字是您思想的提炼,为了演示发布的良好效果,请言简意赅地阐述您的观点。
直线与圆的位置关系课件

直线与圆相离
1
外切
直线与圆相离,并且与圆有且仅有一
外离不相交
2
个切
分离。
3
外离相离
直线与圆没有任何交点或切点,但它 们还是有一定的接近性。
直线与圆相切
1
切点性质
直线与圆相切于一个切点,切点在圆上。
2
法线性质
直线在切点处垂直于圆的切线。
圆的定义和特征
圆
圆是由一条曲线围成的,所有 点到圆心的距离相等。
球体
球体是三维空间中由一条曲线 围成的,所有点到球心的距离 相等。
气旋
气旋是带状大气旋转体,呈圆 形或类似圆形的自然现象。
直线与圆的位置关系分类
1 相离
直线和圆没有交点,彼 此没有相交。
2 相切
直线切到圆的边界,只 有一个接触点。
3 相交
3
角度性质
直线与半径的夹角等于切线与半径的夹角,并且都是直角。
直线与圆相交
1
交点性质
直线与圆相交于两个交点,交点分别
切线性质
2
在圆内和圆外。
直线通过切点,既是直线也是圆的切
线。
3
夹角性质
直线与切线的夹角等于直线与半径的 夹角。
直线与圆相切的性质
1 唯一性
直线和圆之间最多只能有一个切点。
2 切点位置
切点在圆上,与圆的切线垂直。
3 切线方向
切线通过切点,既是直线也是圆的切线。
直线与圆相交的性质
1 交点个数
2 切点位置
直线和圆相交于两个交 点,分别在圆内和圆外。
切点在圆上,与圆的切 线垂直。
3 夹角性质
直线与切线的夹角等于 直线与半径的夹角。
直线与圆的位置关系初中

直线与圆的位置关系初中在数学的世界里,直线和圆就像是两个不同性格的小伙伴,彼此间的关系可是五花八门,各种各样,真是让人忍俊不禁。
你想啊,直线就像一个永远走不尽头的奔放青年,而圆呢,恰好是那种温柔婉约的小姐姐,总是围着自己的心情转。
就这样,两者在平面上相遇,仿佛一场奇妙的舞会。
嘿,今天就来聊聊这两位主角的关系,看看它们到底会擦出什么样的火花。
咱们得说说这俩人相遇的基本情况。
直线和圆的关系可分为三种,真是让人感慨万千。
第一种情况,直线与圆的关系相当亲密,咱们称之为“相切”。
这时候,直线就像是轻轻碰了碰圆的边缘,哦,那种亲密感就好比是老朋友久别重逢,瞬间感受到的温暖。
直线和圆有一个共同的点,简直就像是一对亲密无间的小伙伴,给人一种“我们只需这一点,就够了”的感觉。
然后再看看第二种情况,直线和圆的关系就没那么紧密了,这就是“相交”。
嘿,这时候的直线可就不止轻轻碰一碰了,它干脆直接穿过了圆圈,就像一条勇敢的鱼逆流而上。
这样一来,直线和圆就像是在进行一场热烈的辩论,各说各话,产生了两个交点,简直就像两位辩手在台上你来我往,谁也不让谁,场面可谓是火药味十足,热闹非凡。
最后一种情况就有点尴尬了,直线和圆的关系是“相离”。
这就像两个性格迥异的小伙伴,虽然同处一个空间,但彼此之间却是天各一方,根本没有任何交集。
就像是坐在不同的桌子上,各自吃着不同的美食,似乎彼此都不想打招呼。
这样一来,虽然都在同一个平面上,但直线和圆却好像两条平行线,永远也不会有交集,简直让人感到一丝淡淡的悲凉。
大家是不是觉得直线和圆之间的关系就像是生活中的人际关系呢?有时候我们遇到的人可能只是擦肩而过,毫无交集;可能会在某个瞬间和某人心意相通;而又会与某人撞个正着,产生一段深刻的联系。
不同的关系都是人生的一部分,直线和圆的相遇与离散,也正是生活的缩影。
嘿,别忘了数学可不仅仅是公式和定理,生活中的这些简单的几何图形也充满了故事。
直线和圆,代表着我们生活中的许多关系,它们教会我们,生活就是要不断地相遇、相切、相离。
直线与圆的位置关系---获奖课件

二、直线和圆的位置关系(用圆心o到直线l的
距离d与圆的半径r的关系来区分)
r
d
∟
直线和圆相离
d >r
数形结合
直线和圆相切
d
r
d= r
以数解形,以形助数
直线和圆相交
d <r 数量关系
d
r
位置关系
试一试
1、已知圆的直径为13cm,设直线和圆心的距离 为d : (1)若d=4.5cm ,则直线与圆 相交 , 直线与圆 2 个公共点. 有____
大 漠 孤 烟 直 , 长唐 河王 落维 日 圆
·
:
你能从日落的自然现象中,找出哪些基本的平面 几何图形? 圆
海/地平面
直线
今天老师和同学们一起来探究
操作与思考
(地平线)
请同学们利用手中的工具再现日落的 O 整个情景
● ●
O
(地平线)
一、直线与圆的位置关系(用公 共点的个数来区分)
探索新知
来判断;
圆心到直线的距离d与半径r (2)根据性质,由______________________ 的关系来判断。
典例分析
例:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径的圆与AB 有怎样的位置关系?为什么? (1)r=2cm;(2)r=2.4cm (3)r=3cm.
教材P46
(1)直线和圆没有公共点时, 叫做直线和圆相离。 (2)直线和圆有唯一个公共点, 叫做直线和圆相切,
这条直线叫圆的切线, 这个公共点叫切点。 (3)直线和圆有两个公共点, 叫做直线和圆相交, 这条直线叫圆的割线, 这两个公共点叫交点。
快速判断下列各图中直线与圆的位置 关系l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四讲直线与圆的位置关系【知识点】※1. 直线和圆相交、相切相离的定义:(1)相交: 直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线.(2)相切: 直线和圆有惟一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,惟一的公共点做切点.(3)相离: 直线和圆没有公共点时,叫做直线和圆相离.※2. 直线与圆的位置关系的数量特征:设⊙O的半径为r,圆心O到直线的距离为d;①d<r <===> 直线L和⊙O相交.②d=r <===> 直线L和⊙O相切.③d>r <===> 直线L和⊙O相离.※3. 切线的总判定定理:经过半径的外端并且垂直于这个条半径的直线是圆的切线.※4. 切线的性质定理:圆的切线垂直于过切点的半径.※推论1 经过圆心且垂直于切线的直线必经过切点.※推论2 经过切点且垂直于切线的直线必经过圆心.※分析性质定理及两个推论的条件和结论间的关系,可得如下结论:如果一条直线具备下列三个条件中的任意两个,就可推出第三个.①垂直于切线; ②过切点; ③过圆心.※5. 三角形的内切圆、内心、圆的外切三角形的概念.和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心, 这个三角形叫做圆的外切三角形.※6. 三角形内心的性质:(1)三角形的内心到三边的距离相等.(2)过三角形顶点和内心的射线平分三角形的内角.由此性质引出一条重要的辅助线: 连接内心和三角形的顶点,该线平分三角形的这个内角.【例题分析】1.(2014•德州,第22题10分)如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.(1)求AC、AD的长;(2)试判断直线PC与⊙O的位置关系,并说明理由.2. 如图,直线与⊙O 相切于点D ,过圆心O 作EF ∥交⊙O 于E 、F 两点,点A 是⊙O 上一点,连接AE ,AF ,并分别延长交直线于B 、C 两点; (1)求证:∠ABC+∠ACB=90°;(2)若⊙O 的半径5=R ,BD=12,求tan ∠ACB 的值.3.如图,AB 为的直径,点C 在⊙O 上,点P 是直径AB 上的一点(不与A ,B 重合),过点P 作AB 的垂线交BC 的延长线于点Q 。
(1)在线段PQ 上取一点D ,使DQ=DC ,连接DC ,试判断CD 与⊙O 的位置关系,并说明理由。
(2)若cosB=35,BP=6,AP=1,求QC 的长。
4.如图,AB 为O ⊙的直径,点C 为O ⊙上一点,若BAC CAM ? ,过点C 作直线垂直于射线AM ,垂足为点D .(1)试判断CD 与O ⊙的位置关系,并说明理由;(2)若直线与AB 的延长线相交于点E ,O ⊙的半径为3,并且30CAB °∠=. 求CE 的长.B 第23题图D CA5.(2014•广东,第24题9分)如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB 于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)(2)求证:OD=OE;(3)求证:PF是⊙O的切线.6.如如图,AB是⊙O的直径,点F,C是⊙O上两点,且==,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.(1)求证:CD是⊙O的切线;(2)若CD=2,求⊙O的半径.7.如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.(1)求证:BC平分∠PDB;(2)求证:BC2=AB•BD;(3)若PA=6,PC=6,求BD的长.8.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)求证:CD2=CA•CB;(2)求证:CD是⊙O的切线;(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=2\3,求BE的长.9.如图,在△ABC中,AB=AC,以AB为直径作半圆⊙0,交BC于点D,连接AD,过点D 作DE⊥AC,垂足为点E,交AB的延长线于点F.(1)求证:EF是⊙0的切线.(2)如果⊙0的半径为5,sin∠ADE=4\5,求BF的长.10.如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.(1)求证:AP是⊙O的切线;(2)OC=CP,AB=6,求CD的长.11.如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.(1)求证:CG是⊙O的切线.(2)求证:AF=CF.(3)若∠EAB=30°,CF=2,求GA的长.12.如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.(1)求证:DE是⊙O的切线;(2)求tan∠ABE的值;(3)若OA=2,求线段AP的长.【课后练习】图①图②已知A 、D 是一段圆弧上的两点,且在直线l 的同侧,垂线,垂足为B 、C ,E 是BC 上一动点,连结AD 、AE 、DE ,(1)如图①,如果AB=6,BC=16,且BE:CE=1:3,求AD 的长。
(2)如图②,若点E 恰为这段圆弧的圆心,则线段AB 、BC 、CD 之间有怎样的等量关系?请写出你的结论并予以证明。
再探究:当A 、D 分别在直线l 两侧且AB ≠CD ,而其余条件不变时,线段AB 、BC 、CD 之间又有怎样的等量关系?请直接写出结论,不必证明。
B 卷(共50分)一、填空题:(每小题4分,共20分) 21.化简:22221369x y x y x y x xy y +--÷--+=_______ 22.如图,A 、B 、c 是⊙0上的三点,以BC 为一边,作∠CBD=∠ABC,过BC 上一点P ,作PE∥AB 交BD 于点E .若∠AOC=60°,BE=3,则点P 到弦AB 的距离为_______. 23.已知21(123...)(1)n a n n ==+,,,,记112(1)b a =-,2122(1)(1)b a a =--,…,122(1)(1)...(1)n n b a a a =---,则通过计算推测出n b 的表达式n b =_______.(用含n 的代数式表示)24.如图,正方形OABC 的面积是4,点B 在反比例函数(00)ky k x x=><,的图象上.若点R 是该反比例函数图象上异于点B 的任意一点,过点R 分别作x 轴、y 轴的垂线,垂足为M 、N ,从矩形OMRN 的面积中减去其与正方形OABC 重合部分的面积,记剩余部分的面积为S .则当S=m(m 为常数,且0<m<4)时,点R 的坐标是________________ (用含m 的代数式表示)25.已知M(a ,b)是平面直角坐标系xOy 中的点,其中a 是从l ,2,3三个数中任取的一个数,b 是从l ,2,3,4四个数中任取的一个数.定义“点M(a ,b)在直线x+y=n 上”为事件Q n (2≤n≤7,n 为整数),则当Q n 的概率最大时,n 的所有可能的值为______.B二、(共8分)26.某大学毕业生响应国家“自主创业”的号召,投资开办了一个装饰品商店.该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30,且x 为整数);又知前20天的销售价格1Q (元/件)与销售时间x(天)之间有如下关系:11Q 302x =+ (1≤x≤20,且x 为整数),后10天的销售价格2Q (元/件)与销售时间x(天)之间有如下关系:2Q =45(21≤x≤30,且x 为整数).(1)试写出该商店前20天的日销售利润1R (元)和后l0天的日销售利润2R (元)分别与销售时间x(天)之间的函数关系式;(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润. 注:销售利润=销售收入一购进成本.三、(共10分)27.如图,Rt△ABC 内接于⊙O,AC=BC ,∠BAC 的平分线AD 与⊙0交于点D ,与BC 交于点E ,延长BD ,与AC 的延长线交于点F ,连结CD ,G 是CD 的中点,连结0G .(1)判断0G 与CD 的位置关系,写出你的结论并证明;(2)求证:AE=BF ; (3)若3(2OG DE ⋅=,求⊙O 的面积。
四、(共12分)28.在平面直角坐标系xOy 中,已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为M,若直线MC 的函数表达式为3y kx =-,与x轴的交点为N ,且。
(1)求此抛物线的函数表达式;(2)在此抛物线上是否存在异于点C 的点P ,使以N 、P 、C 为顶点的三角形是以NC 为一条直角边的直角三角形?若存在,求出点P 的坐标:若不存在,请说明理由;(3)过点A 作x 轴的垂线,交直线MC 于点Q.若将抛物线沿其对称轴上下平移,使抛物线与线段NQ 总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?。
