习题1-7 无穷小的比较
合集下载
1-7无穷小的比较
一、无穷小的比较
1 例如, 例如 当x → 0时, x , x , sin x , x sin 都是无穷小 . x 2 x 观 lim = 0, x 2比3 x要快得多 ; 察 x→0 3 x 各 sin x 极 sin x x ; = 1, lim x→0 x 限 1 2 x sin x = lim sin 1 0 lim 比. 比 . 2 x→0 x→0 x x 0 , 快 .
x
例２ 解
ex − 1 . 求 lim x →0 x
令 e x − 1 = u, 即 x = ln(1 + u),
则当 x → 0 时, 有 u → 0,
ex − 1 u = lim Q lim = lim u→ 0 x →0 u→ 0 ln(1 + u ) x
=
u→ 0
1 ln(1 + u)
1 u
这里仅证1), (2)式 (
(1)不妨设m ≥ n, ο (xm ) ο (xn ) lim = lim n + n n x→0 x →0 x x x ο (xm ) ο (xn ) = lim n + lim n x →0 x →0 x x ο (xn ) ο (xm ) xm = lim m ⋅ n + lim n = 0 + 0 = 0. x →0 x x →0 x x 因此ο ( x m ) + ο ( x n ) = ο ( x l ).l = min(m, n).
x
1 x2
sin x ⋅ tan x − sin x tan x − sin x x 2 ⋅sin x
=e .
1 2
注意 : 在求幂指函数的极限 lim f ( x ) g ( x ) 时, 可以用等价无穷小替 换指数g ( x)中的因子, 但是一般情况下不可以用等价无穷小替换 底f ( x)中的因子. 因为求幂指函数的极限 lim f ( x) g ( x ) 时, 可采用对数法转化为求极
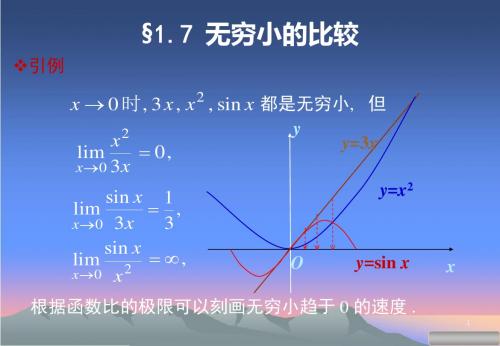
1 例如, 例如 当x → 0时, x , x , sin x , x sin 都是无穷小 . x 2 x 观 lim = 0, x 2比3 x要快得多 ; 察 x→0 3 x 各 sin x 极 sin x x ; = 1, lim x→0 x 限 1 2 x sin x = lim sin 1 0 lim 比. 比 . 2 x→0 x→0 x x 0 , 快 .
x
例２ 解
ex − 1 . 求 lim x →0 x
令 e x − 1 = u, 即 x = ln(1 + u),
则当 x → 0 时, 有 u → 0,
ex − 1 u = lim Q lim = lim u→ 0 x →0 u→ 0 ln(1 + u ) x
=
u→ 0
1 ln(1 + u)
1 u
这里仅证1), (2)式 (
(1)不妨设m ≥ n, ο (xm ) ο (xn ) lim = lim n + n n x→0 x →0 x x x ο (xm ) ο (xn ) = lim n + lim n x →0 x →0 x x ο (xn ) ο (xm ) xm = lim m ⋅ n + lim n = 0 + 0 = 0. x →0 x x →0 x x 因此ο ( x m ) + ο ( x n ) = ο ( x l ).l = min(m, n).
x
1 x2
sin x ⋅ tan x − sin x tan x − sin x x 2 ⋅sin x
=e .
1 2
注意 : 在求幂指函数的极限 lim f ( x ) g ( x ) 时, 可以用等价无穷小替 换指数g ( x)中的因子, 但是一般情况下不可以用等价无穷小替换 底f ( x)中的因子. 因为求幂指函数的极限 lim f ( x) g ( x ) 时, 可采用对数法转化为求极
高数同济17无穷小的比较
注意 对于代数和中各等价无穷小一般不能替换.
若 ~ , ~ 且 与 不等价 , 则 - ~ - ,
下页
13
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
当x 0时,
arctan x ~ x ,
arcsin x ~ x , tan x ~ x ,
例13
x 0
lim
1 x si n x lim2 3 lim 1 x 0 x 0 2 x x
15
结束
内容小结 1. 无穷小的比较
设 , 对同一自变量的变化过程为无穷小, 且
0
是 的高阶无穷小 是 的低阶无穷小 是 的同阶无穷小 是 的等价无穷小 是 的 k 阶无穷小
1 2 e - 1 ~ x , 1 - cos x ~ x , (1 + x ) - 1 ~ x . 2
注意 对于代数和中各等价无穷小一般不能替换.
若 ~ , ~ 且 与 不等价 , 则 - ~ - ,
下页
12
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
下页
9
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
当x 0时,
arctan x ~ x ,
arcsin x ~ x , tan x ~ x ,
x
1 2 e - 1 ~ x , 1 - cos x ~ x , (1 + x ) - 1 ~ x . 2
例9
tan2 2 x 求 lim . x 0 1 - cos x
若 ~ , ~ 且 与 不等价 , 则 - ~ - ,
下页
13
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
当x 0时,
arctan x ~ x ,
arcsin x ~ x , tan x ~ x ,
例13
x 0
lim
1 x si n x lim2 3 lim 1 x 0 x 0 2 x x
15
结束
内容小结 1. 无穷小的比较
设 , 对同一自变量的变化过程为无穷小, 且
0
是 的高阶无穷小 是 的低阶无穷小 是 的同阶无穷小 是 的等价无穷小 是 的 k 阶无穷小
1 2 e - 1 ~ x , 1 - cos x ~ x , (1 + x ) - 1 ~ x . 2
注意 对于代数和中各等价无穷小一般不能替换.
若 ~ , ~ 且 与 不等价 , 则 - ~ - ,
下页
12
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
下页
9
常用等价无穷小:
sin x ~ x , ln( 1 + x ) ~ x ,
当x 0时,
arctan x ~ x ,
arcsin x ~ x , tan x ~ x ,
x
1 2 e - 1 ~ x , 1 - cos x ~ x , (1 + x ) - 1 ~ x . 2
例9
tan2 2 x 求 lim . x 0 1 - cos x
无穷小的比较
【例42】
二、 等价无穷小
【例43】
二、 等价无穷小
二、 等价无穷小
【例44】
试证明：如果α~β，则α－β是比α(或β)高阶的无穷小.反之， 如果α－β是比α(或β)高阶的无穷小，则α~β .
谢谢聆听
x~x,1 cos x~12x2,ln(1+x)~x,ex－1~x,ax －1~xln a,n1+x－1~1nx.
二、 等价无穷小
注
当x→0时，x为无穷小.在常用等价无穷小中，用任 意一个无穷小f(x)代替x后，上述等价关系依然成立.
例如，x→0时，有sinx3~x3, e－x2－1~－x2,ln (1+4x)~4x，等等.
一、 无穷小阶的定义
定义14
设α，β是自变量在同一变化过程中的两个无穷小，且α≠0. (1) limβα=0，则称β是比α高阶的无穷小，记为β=o(α). (2) limβα=∞，则称β是比α低阶的无穷小. (3) limβα=c(c≠0)，则称β与α是同阶无穷小 limβα=1，则称β与α是等价无穷小，记为α~β. (4) limβαk=c(c≠0,k>0)，则称β是α的k阶无穷小.
二、 等价无穷小
定理22
设α，α′，β，β′是自变量在同一变化过程中的无穷小，且 α~α′，β~β′，limβ′α′存在，则
定理22表明，在求两个无穷小之比的极限时，分子及分母都 可以用等价无穷小代换.因此，若无穷小的代换运用得当，则可简 化极限的计算.
二、 等价无穷小
定理23
α与β β=α+o(α).
一、 无穷小阶的定义
例如，就前述三个无穷小x，x2， sin x(x→0)而言，x2是比x高阶的无穷 小，x是比x2低阶的无穷小，而sinx与x 是等价无穷小.
无穷小量的比较
错 解 当x 0时, tan x ~ x, sin x ~ x.
x x 原式 lim 3 0. x 0 (2 x )
解
当x 0时, sin 2 x ~ 2 x ,
1 3 tan x sin x tan x(1 cos x ) ~ x , 2 1 3 x 1 2 . 原式 lim 3 x 0 ( 2 x ) 16
tan x sin x 例1. 求 lim . 3 x 0 x
解: 原式
xx 原式 lim 3 x 0 x
lim
2 x 1 x 2 x 0
x3
目录
上一页 下一页
退 出
tan2 2 x 例３ 求 lim . x 0 1 cos x
1 2 解 当x 0时, 1 cos x ~ x , tan 2 x ~ 2 x . 2 ( 2 x )2 原式 lim 8. x 0 1 x2 2
2 2
定义:设, 是同一过程中的两个无 穷小, 且 0.
(1) 如果 lim 0，就说 是比 高阶的无穷小, 记作 o( )；
( ２ ) 如果 lim ，就说 是比 低阶的无穷小． ( 3) 如果 lim C 0, 就说 与 是同阶的无穷小 ; 特殊地， 如果 lim 1, 则称 与 是等价的无穷小 ; 记作 ~ ;
o()，即 o()．
o( ) o( ) lim （１＋ ） 1， lim lim ~ ． 目录 上一页 下一页 退 出
意义：用等价无穷小可给出函数的近似表达式． 1 2 例如, 当x 0时, sin x ~ x , 1 cos x ~ x . 2 sin x x o( x ), 1 y x2
x x 原式 lim 3 0. x 0 (2 x )
解
当x 0时, sin 2 x ~ 2 x ,
1 3 tan x sin x tan x(1 cos x ) ~ x , 2 1 3 x 1 2 . 原式 lim 3 x 0 ( 2 x ) 16
tan x sin x 例1. 求 lim . 3 x 0 x
解: 原式
xx 原式 lim 3 x 0 x
lim
2 x 1 x 2 x 0
x3
目录
上一页 下一页
退 出
tan2 2 x 例３ 求 lim . x 0 1 cos x
1 2 解 当x 0时, 1 cos x ~ x , tan 2 x ~ 2 x . 2 ( 2 x )2 原式 lim 8. x 0 1 x2 2
2 2
定义:设, 是同一过程中的两个无 穷小, 且 0.
(1) 如果 lim 0，就说 是比 高阶的无穷小, 记作 o( )；
( ２ ) 如果 lim ，就说 是比 低阶的无穷小． ( 3) 如果 lim C 0, 就说 与 是同阶的无穷小 ; 特殊地， 如果 lim 1, 则称 与 是等价的无穷小 ; 记作 ~ ;
o()，即 o()．
o( ) o( ) lim （１＋ ） 1， lim lim ~ ． 目录 上一页 下一页 退 出
意义：用等价无穷小可给出函数的近似表达式． 1 2 例如, 当x 0时, sin x ~ x , 1 cos x ~ x . 2 sin x x o( x ), 1 y x2
第一章 习题1-7 无穷小的比较
① arcsin x;
2 ② (1 x ) 1; 2
③ cos(x ) 1;
2
④ tan(x ).
3
x2 x4 2 解： arcsin x ~ x ; (1 x ) 1 ~ ; cos( x ) 1 ~ ; tan( x 3 ) ~ x 3 . 2 2
当 x 0 时的等价无穷小按低阶 到高阶次序为： ①
3 2
( x) 是比 x 高阶的无穷小 .
( 2) lim
( x)
x
x 0
e 3 x arcsin x 1 e3x 1 arcsin x lim lim lim 3 1 4. x 0 x 0 x 0 x x x
( x) 是与 x 同阶的无穷小 .
高等数学作业讲评
第一章 习题 1-7 无穷小的比较 1. (1) 如果当 x x0 时，无穷小 ( x) 等价于 f ( x), 那么求极限时 可以用 ( x) 替代以下哪个函数中的 ( x) ？ f ( B )
A. lim f ( x) x f ( x) ; B. lim . 2 2 x x0 x x0 x x 解： 等价无穷小只能在乘积 中进行因子替换故应选 B. . (2) 我们要熟记哪些在 0 时常见的等价无穷小？ x x2 1 cos x ~ ; tan x ~ x ~ arctan x; 答： sin x ~ x ~ arcsin x; 2 x x x n e 1 ~ x; a 1 ~ x ln a; ln(1 x) ~ x; 1 x 1 ~ . n (3) 将下列 x 0 时的等价无穷小按低阶 到高阶次序排列起来： (提示：先用 等价无穷小替换 ) 1
n
(6) lim tan 3x tan x . 6 x
2 ② (1 x ) 1; 2
③ cos(x ) 1;
2
④ tan(x ).
3
x2 x4 2 解： arcsin x ~ x ; (1 x ) 1 ~ ; cos( x ) 1 ~ ; tan( x 3 ) ~ x 3 . 2 2
当 x 0 时的等价无穷小按低阶 到高阶次序为： ①
3 2
( x) 是比 x 高阶的无穷小 .
( 2) lim
( x)
x
x 0
e 3 x arcsin x 1 e3x 1 arcsin x lim lim lim 3 1 4. x 0 x 0 x 0 x x x
( x) 是与 x 同阶的无穷小 .
高等数学作业讲评
第一章 习题 1-7 无穷小的比较 1. (1) 如果当 x x0 时，无穷小 ( x) 等价于 f ( x), 那么求极限时 可以用 ( x) 替代以下哪个函数中的 ( x) ？ f ( B )
A. lim f ( x) x f ( x) ; B. lim . 2 2 x x0 x x0 x x 解： 等价无穷小只能在乘积 中进行因子替换故应选 B. . (2) 我们要熟记哪些在 0 时常见的等价无穷小？ x x2 1 cos x ~ ; tan x ~ x ~ arctan x; 答： sin x ~ x ~ arcsin x; 2 x x x n e 1 ~ x; a 1 ~ x ln a; ln(1 x) ~ x; 1 x 1 ~ . n (3) 将下列 x 0 时的等价无穷小按低阶 到高阶次序排列起来： (提示：先用 等价无穷小替换 ) 1
n
(6) lim tan 3x tan x . 6 x
1-7无穷小的比较
常用的等价无穷小.
当x0时,
sinx ~ x,
tgx ~ x,
arctgx ~ x,
arcsinx ~ x,
ex–1 ~ x,
ln(1+x) ~ x,
1
cos
x
~
x2 2
(1 x)k 1 ~ kx, (k R, k 0)
事实上, 当 y > 0时, y = elny. 从而,
lim
一般, 设变量u从初值u0变到终值u1, 记u=u1u0, 称为变量u的增量(改变量).
u可正, 可负, 还可为0. 另外, u1 = u0+ u
设f (x)在U(x0)有定义, xU(x0), 记 x =xx0 称为自变量x在x0处增量(改变量). 且 x = x0 + x
记 y = f (x) f (x0) = f (x0 + x) f (x0) 称为y在x0处相应于x的增量(改变量).
sin
a
2
1) bx
1 2
lim
x0
(a a
2
b)x bx
=1
例3.
求
lim
x
x2
ln(1
3 x3
).
解:
lim x2 ln(1
x
3 x3
)
lim
x
x
2
3 x3
lim
x
3 x
=0
或,
lim x2 ln(1
x
3 x3
)
lim
x
3 x
如图
y f (x) = |x|
o
x
1-7无穷小量、比较、替换
蚌埠学院 高等数学
14
当x 时，ln(1 1)与 1 是同阶无穷小． x 3x
2020年1月11日星期六
蚌埠学院 高等数学
4
例1.证明:当x 0时, x2 tan 3 x为x的五阶无穷小.
解
x2 tan3 x
lim
x0
x5
lim( tan x )3 1 x0 x
故当x 0时, x2 tan3 x为x的5阶无穷小.
10
注意：不能滥用等价无穷小代换.
无穷小代换原则：积商可部分代换，
和差只能总体代换.
例5.
求
lim
x0
tan x sin sin3 2x
x
.
错解 当x 0时, tan x ~ x,sin x ~ x.
原式
lim
x0
xx (2x)3
0.
解 当x 0时, sin 2x ~ 2x,
常用等价无穷小:
当x 0时,
y
y 1 x2 2
y 1 cos x
O
x
x ~ sin x ~ tan x ~ arcsin x ~ arctan x ~ ln(1 x)
x ~ ex 1, 1 cos x ~ 1 x2, (1 x)a 1 ~ ax (a 0) 2
2020年1月11日星期六
记作 o( )（ ; 是比 低阶的无穷小）
(2) 如果lim C(C 0), 就说与是同阶的无穷小;
特殊地 如果lim )
如果
lim
k
C(C 0, k
0), 就说是的k阶的
无穷小.
2020年1月11日星期六
无穷小的比较公式
无穷小的比较公式在数学中，无穷小是一种特殊的数值概念，它可以用来描述接近于零的量。
无穷小的比较公式是用来比较两个无穷小的大小关系的公式。
在本文中，将详细介绍无穷小的比较公式，并给出一些具体的例子。
1.高阶无穷小比低阶无穷小大2.函数与它的微分比无穷小大3.无穷小的乘积是无穷小4.极限运算首先来看第一种形式，即高阶无穷小比低阶无穷小大。
假设有两个无穷小量a和b，如果当x趋近于其中一点时，a/x和b/x的极限都为零，且a/x的阶数高于b/x的阶数，则有a比b大。
举个例子，考虑函数f(x)=x和g(x)=x^2，当x趋近于零时，f(x)/x 的极限为1，g(x)/x的极限为0，因为x^2的阶数比x的阶数高，所以可以得出x^2是一个比x大的无穷小。
第二个形式是函数与它的微分比无穷小大。
如果函数f(x)在其中一点处可微分，且其微分f'(x)在该点处不为零，那么当x趋近于该点时，f(x)与f'(x)的比值趋近于零，即f(x)/f'(x)的极限为零。
举个例子，考虑函数f(x)=x^2，它在x=0处可微分，且其导数f'(x)=2x在该点处不为零。
当x趋近于零时，f(x)/f'(x)=x^2/(2x)=x/2的极限为零。
因此，x^2是一个比2x大的无穷小。
第三个形式是无穷小的乘积是无穷小。
如果a是一个无穷小，b是一个有界函数，那么a乘以b也是一个无穷小。
考虑两个无穷小量a和b，其中a是一个无穷小，b是一个有界函数。
当x趋近于其中一点时，a的极限为零，而b的取值在一些区间内有限。
因此，a乘以b的极限仍为零，即a乘以b也是一个无穷小。
最后一个形式是极限运算。
如果有两个无穷小量a和b，且a比b大，那么a和b之间的任何有限运算后的结果仍然是一个无穷小。
举个例子，考虑两个无穷小量a=x，b=x^2、根据前面的分析，x^2是一个比x大的无穷小。
那么，无论我们对a和b进行加法、减法、乘法或除法，结果仍然是一个无穷小。
同济大学高等数学第七版1-7无穷小的比较 PPT
1 - cos x ~ 1 x2 , 所以 当x 0时有 2
1- cos x 1 x2 o( x2 ). 2
16
定理2 (等价无穷小替换定理)
设
~ ,
~
且
lim
A(或),
则
lim
lim
A(或).
证
lim
lim(
t
1)
n 1 1 n
12
13
二、利用等价无穷小替换求极限
定理1 ~ － o().
即 两个等价无穷小的差一定是一个更高 阶的无穷小，反之亦然。
原因？ 他们太接近了，所以它们的差远远小于 它们之中的任何一个。
定理1 ~ o().
14
定理1 ~ o().
证 设 ~ , 则
lim
-
lim
- 1
lim
-1
0,
因此 - o( ), 即 o(lim
lim
o( )
lim1
o( )
1,
lim x 2 0,
x0 x
x2 0比x 0要快得多;
lim sin x 1, sin x 0与x 0快慢相仿;
x0 x
4
无穷小的比较
定义 设, 是同一过程中的两个无穷小, 且 0.
(1) 如果lim 0, 就说是比 高阶的无穷小;
记作 o( );
原式
lim
x0
x- x (2 x)3
1- cos x 1 x2 o( x2 ). 2
16
定理2 (等价无穷小替换定理)
设
~ ,
~
且
lim
A(或),
则
lim
lim
A(或).
证
lim
lim(
t
1)
n 1 1 n
12
13
二、利用等价无穷小替换求极限
定理1 ~ － o().
即 两个等价无穷小的差一定是一个更高 阶的无穷小，反之亦然。
原因？ 他们太接近了，所以它们的差远远小于 它们之中的任何一个。
定理1 ~ o().
14
定理1 ~ o().
证 设 ~ , 则
lim
-
lim
- 1
lim
-1
0,
因此 - o( ), 即 o(lim
lim
o( )
lim1
o( )
1,
lim x 2 0,
x0 x
x2 0比x 0要快得多;
lim sin x 1, sin x 0与x 0快慢相仿;
x0 x
4
无穷小的比较
定义 设, 是同一过程中的两个无穷小, 且 0.
(1) 如果lim 0, 就说是比 高阶的无穷小;
记作 o( );
原式
lim
x0
x- x (2 x)3
无穷小的比较
β α′ β′ = lim ⋅ lim ⋅ lim β′ α α′ β′ = lim = A (或∞ ). α′
10
无穷小的比较
等价无穷小替换定理说明, 等价无穷小替换定理说明,两个无穷小之 比的极限, 比的极限,可由它们的等价无穷小之比的极限 型未定式的极限运算带来方便. 给 0 型未定式的极限运算带来方便. 代替. 代替.
无穷小的比较
ln(1 + x ) ~ x , sin x ~ x , tan x ~ x ,
ln 1 + x + 2 sin x 1. 求 lim x →0 tan x ln 1 + x + 2 sin x 解 lim x →0 tan x ln 1 + x 2 sin x = lim + lim x →0 x → 0 tan x tan x
1 100 同阶无穷小. x → ∞时, 是 的 同阶无穷小 x x 1 − cos x 1 因为 lim = , 2 2 x→0 x 2
所以当 x → 0时, 1 − cos x是x的 二阶无穷小 时 二阶无穷小.
4
无穷小的比较
常用等价无穷小
当x →0时
tan x ~ x ,
sin x ~ x ,
x →0
x3 x
x →0
x
x
2
∴ tan x − sin x为x的三阶无穷小 .
6
无穷小的比较
二、利用等价无穷小替换求极限
定理1 定理1 β ~ α ⇔ 证 ⇒设 α ~ β, 则 β −α β β = lim − 1 = lim lim − 1 = 0, α α α 因此 β − α = o (α ), 即 β = α + o (α ).
10
无穷小的比较
等价无穷小替换定理说明, 等价无穷小替换定理说明,两个无穷小之 比的极限, 比的极限,可由它们的等价无穷小之比的极限 型未定式的极限运算带来方便. 给 0 型未定式的极限运算带来方便. 代替. 代替.
无穷小的比较
ln(1 + x ) ~ x , sin x ~ x , tan x ~ x ,
ln 1 + x + 2 sin x 1. 求 lim x →0 tan x ln 1 + x + 2 sin x 解 lim x →0 tan x ln 1 + x 2 sin x = lim + lim x →0 x → 0 tan x tan x
1 100 同阶无穷小. x → ∞时, 是 的 同阶无穷小 x x 1 − cos x 1 因为 lim = , 2 2 x→0 x 2
所以当 x → 0时, 1 − cos x是x的 二阶无穷小 时 二阶无穷小.
4
无穷小的比较
常用等价无穷小
当x →0时
tan x ~ x ,
sin x ~ x ,
x →0
x3 x
x →0
x
x
2
∴ tan x − sin x为x的三阶无穷小 .
6
无穷小的比较
二、利用等价无穷小替换求极限
定理1 定理1 β ~ α ⇔ 证 ⇒设 α ~ β, 则 β −α β β = lim − 1 = lim lim − 1 = 0, α α α 因此 β − α = o (α ), 即 β = α + o (α ).
1-8无穷小的比较
三、证明：若 , 是无穷小，则 ~ 0( ) . 四、设 f(x)= lim
2 n x 2n 1 求：1、 f ( x ) 的表达式 . 2、确定 a, b 的值,使得lim f ( x ) f (1) ，
x 1
x 1
x
2 n 1
sin
x cos( a bx )
一、无穷小的比较
1 例如, 当x 0时, x , x , sin x , x sin 都是无穷小. x 2 x 2 lim 0, x 比3 x要快得多; 观 x0 3 x 察 各 lim sin x 1, sin x与x大致相同 ; 极 x0 x 1 2 限 x sin x lim sin 1 0 lim 不存在. 不可比. x 0 （ 型）x 0 x 2 x 0 极限不同, 反映了趋向于零的“快慢”程度不 同.
tan x sin x 例５ 求 lim . 3 x 0 sin 2 x
错 解 当x 0时, tan x ~ x , sin x ~ x .
x x 原式 lim x 0 3 0. (2 x )
解
当x 0时, sin 2 x ~ 2 x ,
1 3 tan x sin x tan x(1 cos x ) ~ x , 2 1 3 x 2 1. 原式 lim 3 x0 ( 2 x ) 16
练 习 题
(1 ax ) 1 6、lim =_________. x 0 x
1 n
7、当 x 0 时， a x 3 a ( a 0) 对于 x 是_______阶无穷小 . n 8、当 x 0 时，无穷小 1 cos x 与 mx 等价，则 m _______,n _______ . 二、求下列各极限： tan x sin x lim 1、 x 0 ； 3 sin x e e lim 2、 ； sinx sin x 3、lim ； x0 x tan x tan a 4、lim ； xa xa
高等数学1-7-无穷小的比较_OK
lim
1 cos x
x0 (1 cos x)x(1 cos x)
x2
lim x0 (1
2 cos x)x (
x)2
2
lim
1
1 函数与极限
29
x0 (1 cos x ) 2
三、小结
1.无穷小的阶的比较
反映了同一过程中, 两无穷小趋于零的速度快慢, 但 并不是所有的无穷小都可进行比较. 高(低)阶无穷小; 等价无穷小; 同阶无穷小.
1
1 函c数o与s极x限~
x2 2
等价无穷小 6
2
（5） lim ln(1 x) x0 x
lim
ln(1
x)
lim
ln(1
x)
1 x
ln[lim
(1
x)
1 x
]
x0 x
x0
x0
ln e 1. 故 ln(1 x) ~ x(x 0) 等价无穷小
（6）
ex 1 lim
x0 x
令 ex 1 u,
ex 1
lim sin x(1 cos x) 1 x0 (1 sin x) cos x x3
lim sin x 1 cos x
1
x x0
x2 (1 sin x) cos x
1 2
1
原式 e2.
函数与极限
27
【例7 】求
lim 1 x sin x 1 x0 x arctan x
解 因为当x→0
1 xsin x 1 ~ xsin x ,arctanx ~ x 2
x0
x
x0 x(1 cos x)
lim sin2 x lim sin x sin x
x0 x(1 cos x) x0 x 1 cos x
高数 无穷小的比较
x 1
x 1
lim f ( x ) f ( 1) .
练习题答案
3 一、1. ； 2
0, m n 2. 1, m n ； 3. 2； , m n
a 6. ； n
2. e ； 7. 3；
4. ；
5. x ；
1 8. , 2. 2
1 二、1. ； 2
tan 2 x 例３ 求 lim . x 0 1 cos x
2
1 2 解 当x 0时, 1 cos x ~ x , tan 2 x ~ 2 x . 2 2 (2 x ) 原式 lim 8. x0 1 2 x 2
若未定式的分子或分母为若干个因子的乘积，则 可对其中的任意一个或几个无穷小因子作等价无 穷小代换，而不会改变原式的极限．
故当 x 时 f ( x ) 和 g ( x ) 不能比较.
练 习 题
一、 填空题： tan 3 x 1. lim =__________. x 0 sin 2 x arcsin x n 2. lim =________. m x 0 (sin x ) ln(1 2 x ) 3. lim =_________. x 0 x 1 x sin x 1 4. lim =________. 2 x 0 x arctan x x n 5. lim 2 sin n =________. n 2
例如，
x2 lim 0， x 0 3 x
即 x o( 3 x ) ( x 0).
2
当 x 0 时，x 2 是比 3 x 高阶的无穷小;
sin x lim 1， x 0 x
即 sin x ~ x ( x 0).
当 x 0 时， x 与 x 是等价无穷小． sin
x 1
lim f ( x ) f ( 1) .
练习题答案
3 一、1. ； 2
0, m n 2. 1, m n ； 3. 2； , m n
a 6. ； n
2. e ； 7. 3；
4. ；
5. x ；
1 8. , 2. 2
1 二、1. ； 2
tan 2 x 例３ 求 lim . x 0 1 cos x
2
1 2 解 当x 0时, 1 cos x ~ x , tan 2 x ~ 2 x . 2 2 (2 x ) 原式 lim 8. x0 1 2 x 2
若未定式的分子或分母为若干个因子的乘积，则 可对其中的任意一个或几个无穷小因子作等价无 穷小代换，而不会改变原式的极限．
故当 x 时 f ( x ) 和 g ( x ) 不能比较.
练 习 题
一、 填空题： tan 3 x 1. lim =__________. x 0 sin 2 x arcsin x n 2. lim =________. m x 0 (sin x ) ln(1 2 x ) 3. lim =_________. x 0 x 1 x sin x 1 4. lim =________. 2 x 0 x arctan x x n 5. lim 2 sin n =________. n 2
例如，
x2 lim 0， x 0 3 x
即 x o( 3 x ) ( x 0).
2
当 x 0 时，x 2 是比 3 x 高阶的无穷小;
sin x lim 1， x 0 x
即 sin x ~ x ( x 0).
当 x 0 时， x 与 x 是等价无穷小． sin
§1.7 无穷小的比较
arcsin x ~ x ,
arctan x ~ x , ln(1 + x ) ~ x ,
1 1 + x − 1 ~ x, 2 1 2 1 − cos x ~ x . 2
n
e − 1 ~ x,
x
1 1 + x − 1 ~ x, n
5
无穷小的比较
lim
1 − cos x 1 = 2 x →0 2 x
21
极限存在准则 两个重要极限
思考题
1. 求极限 lim ( 3 + 9 )
x x → +∞ 1 x x
x
1 1 2. 求极限 lim cos + sin x →∞ x x
3. 2002年考研数学二 8分 年考研数学二, 分 年考研数学二
xn ( 3 − xn )( n = 1,2,L), 证明数列{ xn }的极限存在 , 并求此极限 . 答案 : 3 2
§1.7 无穷小的比较
无穷小的比较 利用等价无穷小替换求极限 小结 思考题 作业
函数与极限 第一章 函数与极限
1
无穷小的比较
一、无穷小的比较
时 如,当x → 0时, x ,
观 察 各 极 限
x2 = 0, lim x→0 3 x
sin x lim = 1, x →0 x
2
1 x , sin x , x sin x
10
β β′ β′ 若 ~α′, β~β′, 且lim 存 , 则lim =lim . α 在 α α′ α′
例
求lim tan 2x . x→0 sin 5x 解 当x→0时, tan 2x~2x, sin 5x~5x, 所以 → 时 , , lim tan 2x = lim 2x = 2 . x→0 sin 5x x→0 5x 5
无穷小阶的比较
的无穷小来代替，这样可以简化很多函数极限的计算．下面给出一些常用的等价无
穷小公式（当 x 0 时）：
（1） sin x ~ x ；
（2） arcsin x ~ x ；
（3） tan x ~ x ；
（4） arctan x ~ x ；
（5）1 cos x ~ 1 x2 ； 2
（6） n 1 x 1 ~ 1 x ． n
高等数学
无穷小阶的比较
例如，因为
lim
x0
2x x2
，所以当
x
0
时，
2x
是比
x2
低阶的无穷小，反过来
x2
是比 2x 高阶的无穷小，即 x2 o(2x) ；因为 lim sin x 1 ，lim tan x 1 ，所以当 x 0
x0 x
x0 x
时， sin x ， tan x 与 x 是等价无穷小，即 sin x ~ x ， tan x x ．
无穷小阶的比较
例 4 求 lim tan 2x ． x0 sin 3x
解 因为当 x 0时， tan 2x ~ 2x ， sin3x ~ 3x ，所以 lim tan 2x lim 2x 2 ． x0 sin 3x x0 3x 3
无穷小阶的比较
例 5 求 lim 1 x2 1 ． x0 1 cos x
无穷小阶的比较
例 1 证明：当 x 0 时，1 cos x ~ 1 x2 ． 2
证明
因为
lim
x0
1
cos x2
x
lim
x0
2 sin 2 x2
x 2
lim
x0
sin x
x 2
2
1，
2
七节无穷小的比较-精品
lim（１＋o()） 1，
因此~．
例2 因为当 x0时 , six~ nx , ta x~ n x ,
arx c~x s,i1 n co x~ s 1x 2. 当 x 0 时 有 2
sixn xo (x ), taxn xo(x), arx cs x io (n x ),1coxs1x2o(x2).
解 在x0处没有,定义
且limsin1不存.在 x0 x
y sin 1 x
x0为第二类间. 断点
这种情况称为的振荡断间点.
注意 可去间断点只要改变或者补充间断处函 数的定义, 则可使其变为连续点. 在此例中, 令f(1)2, 则f(x)2 x, 0x1,
1x, x1,
在x1处的连.续
跳跃间断点 如果 f(x)在点 x0处,左 右极限都
存在 ,但f(x0)f(x0),则称x0为 点函f(数 x)的
taxnsinx为x的三阶无 . 穷小
定理 1 与是等价无穷小必 的要 的条 充件 分 为o().
证 必要性 设~，
lim
lim
1
0，
因 此 o ( ) ， 即 o ( ) ．
充分性 设 o()．
lim limo()
f (x0)
那么就称函 y 数f (x)在点x0连续。
""定义 :
0,0,使x当 x0时 , 恒f有 (x)f(x0).
例1 试证函 f(x数 )xsin1x, x0, 在x0 0, x0,
处连. 续
证 limxsin10,
x0
x
又f(0)0, lim f(x)f(0), x 0
1-7无穷小与无穷大
x
1
～
例3 x 1时,无穷小1 x和1 x3是否同阶，
是否等价？
解 xlim111xx3
通过商的 极限说明 阶的高低
lim x1 (1
1 x x)(1 x
x2)
1. 3
故当x1时, 1x 与1x3 是同阶无穷小 但不等价.
3. 常用的等价无穷小
当 x 0时，
f (x) M
①
则称函数
当
( x )时为无穷大, 记作
( lim f ( x) )
x
若在定义中将 ①式改为 f ( x) M ( f ( x) M ),
则记作 lim f ( x) ( lim f ( x) ).
x x0
x x0
( x )
lim f ( x) 是一个记号，在“ ”
x x0
极限定义下，lim f ( x)不存在；
x x0
4°若
lim
x x0
f ( x) , 则称直线
x x0
为曲线 y f ( x) 的铅直渐近线 .
5° 无穷大与无界函数的关系
lim f ( x)
x x0
,
则称
是比
低阶的无穷小;
(3)若
lim
C 0,
则称 是
的同阶无穷小，
记作 O( )
(4)若lim 1,则称 是 与 等价的无穷小, 记作
~ 或 ~
(5)若
lim k
C 0, 则称
是关于
的 k 阶无穷小.
例如 , 当 x 0 时
1.7 无穷小的比较
lim 0
o( ) 或 o( )
证 很简单
lim 1 lim(1 ) 0 lim 0 o( ) 例如 sin x x 所以 x sin x o( x)
2 3
2
October, 2004
例1
证明： n
x 1 x 1 ( x 0) n
x t 1
n
解 令
n
1 x t
x 0 t 1
t 1 1 x 1 t 1 lim lim n lim n t 1 1 x 0 x t 1 t 1 n (t 1) n n
October, 2004
例3
tan 2 x 计算： lim Nhomakorabeax 0sin 5 x
解
因为 x0 时
tan 2x 2x
所以
sin 5x 5x
tan 2 x 2x 2 lim lim x 0 sin 5 x x 0 5 x 5
October, 2004
课内练习
ln(1 x ) 计算： lim x 0 1 cos x
1.7 无穷小的比较
Ranks of Infinitesimals
October, 2004
无穷小的比较 设 lim 0
lim 0
(1) lim 0 是比 高阶的无穷小 记 o( ) 此时 lim 也说 是比 低阶的无穷小 o( ) 0 注意： lim
2 3
x 0
x x x
2 3
2
低阶无穷小＋高阶无穷小 等价于 低阶无穷小
o( )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§1.7无穷小的比较
一、判断题
1、γβα,,是同一极限过程中的无穷小，且,~,~γββα则必有γα~。
[ ]
2、0→x 时330tan sin sin ~,lim
lim 0sin x x x x x x x x x x →∞→--∴== [ ] 3、已知11cos lim 0=-→x
x x ，由此可断言，当)1(cos ,0x x x -→与时为等价无穷小。
[ ] 4．当0→x 时，x 3sin 与1-x e 是同阶无穷小 。
[ ]
5．当1→x 时，31x - 是1-x 的高阶无穷小。
[ ]
二、单项选择题
1、x →0时，1—cos x 是x 2的 。
(A)高阶无穷小 (B)同阶无穷小，但不等价 (C)等价无穷小 (D)低阶无穷小
2、当x →0时，（1—cos x ）2是sin 2x 的 。
(A)高阶无穷小 (B)同阶无穷小，但不等价 (C)等价无穷小 (D)低阶无穷小
3、如果应满足则高阶的无穷小是比时c b a x c
bx ax x ,,,111,2+++∞→ 。
(A)1,1,0===c b a (B) 0,1,a b c ==为任意常数
(C) 为任意常数c b a ,,0≠ (D) 都可以是任意常数c b a ,,
4、1→x 时与无穷小x -1等价的是 。
(A)()3121x - (B) ()x -121 (C) ()
2121x - (D) x -1 5．下列极限中，值为1的是 。
(A) x x x sin 2lim π∞→ (B) x x x sin 2lim 0π→ (C) x x x sin 2lim
2
ππ→ (D) x x x sin 2lim ππ→
B 组
三、设当0→x 时，)1ln()cos 1(2x x +-是比n x x sin 高阶无穷小；而n x x sin 又是比)1(2-x e 高阶的无穷小，求n 。