电磁场理论-07 导行电磁波
导行电磁波

2 av 4 E 1 * i 0 ˆj S1 Re E1 H1 Re z sin k1z cos k1z 0 1 2
在纯驻波情况下,只有电能和磁能的相互交换而无能量传输。
电磁场与电磁波
第七章
平面电磁波的反射与折射,导行电磁波
图7-3 驻波和行驻波的电磁场振幅分布
Ei0 Er0
1
2
Et0
解得:
2 1 Er0 Ei0 2 1 22 Et 0 Ei0 2 1
Er0 2 1 令: Ei0 2 1
反射系数 :分界面上反射波电场 强度与入射波电场强度之比。
Et 0 22 T Ei0 2 1
电磁场与电磁波
第七章
平面电磁波的反射与折射,导行电磁波
例:有一频率 f 100MHz ,x 方向极化的均匀平面波, 从空气垂直入射到 z 0 的理想导体表面上, 设入射波电 场强度振幅为 6mV/m, 试写出: (1) 入射波电场强度 Ei 和 磁场强度 H i 的复数和瞬时表达式; (2) 反射波电场强度 Er 和磁场强度 H r 的复数和瞬时表达式; (3) 空气中的 合成场 E 和 H ; (4)空气中离界面第一个电场强度波腹 点的位置;
透射系数 T :分界面上透射波电场 强度与入射波电场强度之比。
Er
z
Hr
反射波与折射波的特性由分界面两侧媒质的参数确定。
电磁场与电磁波
第七章
平面电磁波的反射与折射,导行电磁波
二、平面波对理想导体表面的垂直入射
jk1z ˆ 入射波: E x E e i i0 E i 0 jk1z 1 ˆ ˆ H i z Ei y e
电磁场理论-导行电磁波

第7章 导行电磁波
上式给出了 g、 和 c 之间的关系。 c 由导波系统的截 面形状、尺寸和模式决定,可以根据具体导波结构求出。 对于 TEM 模, c ,所以 g
可见,TEM 模的波导波长等于填充相同介质的无界空 间中的波长。
(3) 相速
由vp
,可得
TE
和
TM
波相速:
vp
v
v
1 ( c )2
第七章 导行电磁波
第7章 导行电磁波
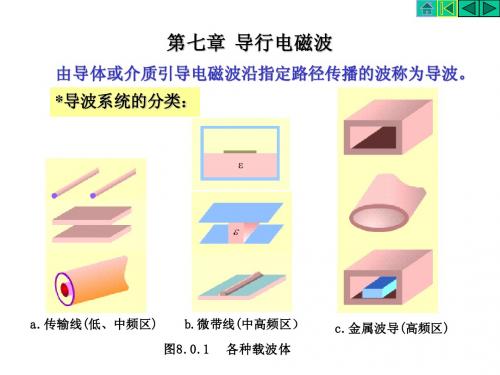
电磁波除了在无限空间传播外,还可以在某种特定 结构的内部或周围传输,这些结构起着引导电磁波传输 的作用,这种电磁波称为导行电磁波(简称导波),引导 电磁波传输的结构称为导波结构。导波结构可以由金属 材料构成,也可以由介质材料构成,还可以由金属和介 质共同构成。这里主要讨论在其轴线方向上截面形状、 面积以及所填充媒质均不变的均匀导波结构。无限长的 平行双导线、同轴线、金属波导、介质波导以及微带传 输线等等都是常用的导波结构。
0
,可得:
对 TM 模
Ez 0
对 TE 模,由
(k 2
2
)Et
j
ez
t Hz
t Ez
可得
(k
2
2
)n
Et
j
n ez t H z
n t Ez
j
n ez t H z
0
j n ez t H z
j (n t Hz )ez j
(n ez )t H z
j
H z n
ez
H z 0 n
第7章 导行电磁波
第7章 导行电磁波
1、纵向分量与横向分量的关系
导波结构中电磁场满足无源区域的麦克斯韦方程组:
H
电动力学教程 第7章 导行电磁波

对于TEM波,λc=∞,
0 g r r
7.2 矩形波导
矩形波导的结构如图所示,假定其内的填充介质为理想
介质。矩形波导内只能传播TE波或TM波而不能传播TEM波。 7.2.1 矩形波导中的TM波
2 Ez 2 Ez 2 k c Ez 0 2 2 x y
Ez ( x, y ) X ( x)Y ( y )
1 2
m n a b
2
2
截止波长
c
fc
2 m n a b
2 2
式中 v 1/ 为无限大介质中的电磁波的波速。
截止状态
当工作频率低于截止频率时,即 f < fc,γ为正实数,此
3. 横磁波(TM波)
7.1.1 横电磁波(TEM波)
根据纵横关系,横向场分量不为0的条件是
2 γTEM k2 0
即
γTEM jk jω με
定义 :导行波的波阻抗 Z
导波系统中,沿波的传播方向构成右手螺旋关系的横 向电场和横向磁场之比,即 x
Ey Ex Z Hy Hx
z
y
m n kc k k a b
2 x 2 y
在矩形波导中TE波的传输常数为
2 2 kc2 k 2 k x ky k2
m n 2 a b
2
2
(2) 当y=0时,Ez=0,
Ez c2c3 sin kx x 0
欲使上式对所有 x值都成立,则c3应为零。此时c2不能为零, 因为若c2等于零,则Ez在非边界处也恒为零,这与TM波的 情况不符,因此只能取c3等于零。
第七章导行电磁波

第七章导行电磁波§.1导行电磁波及其导行系统1导行电磁波就是在导行系统(统称传输线,有时指波导)中传输的电磁波,简称导波。
2在一个实际射频、 微波系统里,传输线是最基本的构成,它不仅起连接信号作用,而且传 输线本身也可以成为某些元件,如电容、电感、变压器、谐振电路、滤波器、天线等等。
3传输线的主要指标:1)损耗。
损耗来源于导体、介质、辐射、模式转换; 2)色散和单模工作频带宽度。
取决于传输线的结构; 3)制造成本。
取决于是否可以集成。
4几种典型微波传输线,结构演化、特点。
1)双线;2 )同轴线;3)波导;4 )微带线;5) 介质波导与光纤;6)空间。
§2导波的一般分析方法1导波的一般分析方法:先求出场纵向分量,然后由场纵向分量导出其余的场横向分量。
2导波场横向分量与场纵向分量关系: Step1 :设导波的传播方向(纵向)为z 方向,传播无衰减,传输线横截面保持不变,则有E 二 E °(x,y )e$zzH 二 H °(x, y )e 』zZ( 1) 式中k z 是导波沿传播方向(z 方向)的传播常数,有 国2氏=k 2= k ; + k ; = k ; + k ; (2) 把(1)式代入直角坐标系中的波动方程,简化后可得喘 +k ;E =0(3)可 T H +k ;H =oStep2:将(1)式代入Maxwell 方程组的两个旋度方程,直角坐标系中展开后可得场横向分 量与场纵向分量关系:在圆柱坐标系里也能导出类似的关系式。
3由场纵向分量导出场横向分量方法的好处: 1)简化计算:六个分量的求解简化为两个分量的求解。
场纵向分量相当于位函数。
2)便于波型分类 4导波波型的分类:E xkz 牡E z +觎cH z "k ; 、dx k z 纲E y;:E z .」汩z k z ex■yH x<k z cy H y--;:E z 'H zk z ::x1) TE 波(横电波,或H 波):E z =0,电磁场只有五个分量 2) TM 波(横磁波,或 E 波):H z =0电磁场只有五个分量3) TEM 波:E z =0和H z = 0,电磁场只有四个分量欲横向场存在,由(4)式可知,必须k T = 0,这样首先方程(3)变为^2E =0和=0这样TEM 波的电磁场在横截面上的分布满足拉普拉斯方程,因此 TEM 波的电磁场在横截面上的特性与静电场、静磁场一样。
第七章导行电磁波

h2u2
h1u1
(7-1-12b)
第七章 导行电磁波
13
§7.2 导行波波型的分类以及导行波的传输特性
7.2.1 导行波波型的分类
导行波的波型是指能够单独存在于导行系统中的电磁波的场
结构形式,也称为传输模式。导行波波型大致分为三类。
1.TEM波
若电场和磁场在传播方向上的分量 Ez 0 、Hz 0 ,
用以引导电磁波传输的装置称为导波装置,或称为传输 线或导行系统。在导波装置中沿一定方向传输的电磁波称为 导行电磁波。如果导波装置的横截面尺寸、形状、介质分布、 材料及边界均沿传输方向不变,则称之为规则导波装置。常 用的导行系统如图7-1所示。其中最简单、最常用的是矩形波 导、圆柱形波导和同轴线。
如果将一段波导的两端短路或开路,就可以构成微波谐 振器。
波kc为色0散,波因。而对,于其T相EM速波和,群k速c 都0是,频则率有的,函v数p ,v即g TEv波和TcrMr ,
第七章 导行电磁波
10
j由横乘向以方式程(7(7-1-1-9-9aa)) ,和对(式7-1(-97c-)1-9可c )以作求得E T e、z HT运,算 用,
然后两式相加,并利用矢量恒等式 (A ) A A A B C ( A C ) B ( A B ) C ,整理可得
(7-1-7b) (7-1-7c)
T 2H z (u1,u2)kc 2H z(u1,u2)0
(7-1-7d)
第七章 导行电磁波
8
矢量方程(7-1-7a)和(7-1-7c)的求解比较困难,因此 通常并不直接求解 ET 和 HT ,而是结合导行系统的边界条
第七章 导行电磁波

欲使上式对于所有的 x 值成立,要求C2 = 0或 C3 = 0 。 E 当C2 = 0时,z = 0,这与TM波情况不符,因此,只能 取 C3 = 0 。此时 E z = C 2 C 4 sin k x x sin k y y 或者写成 E z = E 0 sin k x x sin k y y (7-28) 当 x = a 时, z = 0 。由式(7-28)得 E
(7-32)
Hx = j
ωεE 0 nπ
Ex =
γ E z
2 kc
x
(7-14a) (7-14c)
Ey =
γ Ez
2 kc
y
(7-14b) (7-14d)
Ey =
γ Ez
2 kc y
jωε Ez Hy = 2 kc x
对于TE波,根据方程(7-8b)和导波系统的边 界条件,求出 Hz 后,再考虑到 Ez =0 ,可得TE波的 其他横向场分量为
2 E + k 2E = 0
2 H + k 2 H = 0
在直角坐标系下,矢量拉普拉斯算符可分解为与横 截面坐标有关的 2 和与纵坐标有关的 2 两部分, xy z 即 2 2 2 2 2 2
= x
2
+
y
2
+
z
2
= xy + z
代入波动方程得 2 E + k c2 E = 0 即 xy 同理可得磁场的类似方程
显然,平行双导线、同轴线以及带状线等能够 建立静电场,因此他们可以传播TEM波,而由单根导 体构成的金属波导中不可能存在静电场,因此金属 波导不可能传播TEM 波。 由式(7-5)可知,对于TM波,根据方程(7-8a)和 导波系统的边界条件,求出 E z 后,再考虑到 Hz = 0 , 可得TM波的其他横向场分量为
福州大学电磁场 第七章 导行电磁波
j
+
sin βz' e j
U ( z' ,t ) = 2 U m cos βz' cos(ωt + ) I ( z' ,t ) = 2U m Z0
+
+
sin βz' cos(ωt + +
π
2
)
2π 2π λ Zin( z' ) = jZ0c tan( z' ) = jZ0 tan( ( z'+ )) λ λ 4
=
1
5、导波波长
2π λg = β
ε
6、反射系数 反射系数定义为反射波电压(电流)与入射波电压(电 反射系数定义为反射波电压(电流)与入射波电压( 的比值。 流)的比值。 电压
U ( z' ) ρ u ( z' ) = + U ( z' )
Um 2Γz' = +e Um
= ρLe
2Γz'
其中
ρ
Um L= + Um
UL Z0 cos( ω t + β z' + )
U ( z' , t ) = U L cos( ω t + β z' + )
I ( z' , t ) =
L1 Zin ( z' ) = Z0 = C1
行波状态无损耗线特点: 行波状态无损耗线特点: (1)沿线电流、电压振波不变。 沿线电流、电压振波不变。 电流、电压同相。 (2)电流、电压同相。 沿线各点的输入阻抗等于特性阻抗。 (3)沿线各点的输入阻抗等于特性阻抗。
图8.4.2 由端电压确定积分常数
第七章 导行电磁波 - 部分

由和及可得A=D=0;由和 可得:
mp kx = a
(m = 1, 2, 3L )
np ky = b
(n = 1, 2, 3L )
TE 波
最终解得TE波的Hz分量为:
Hz 0
骣 mp 鼢 骣 np 珑 = H 0 cos 珑 x 鼢 cos y 鼢 鼢 珑 b 桫a 桫
利用横向场与纵向场分量间的关系可得:
2 ?T E
0
2 ?T H
0
导波的一般分析方法
对于沿z 向均匀一致的波导,静态场Es满足:
Ñ 2E s = 0
类似的,恒定磁场Hs满足:
Ñ 2H s = 0
TEM波满足的横向算子场方程与上述两个方程完全相同, 边界条件也一样,其解也必然一样。 任一波导,若其结构能够支持静态场分布,即在横截面 上可建立满足二维拉普拉斯方程的场分布,则此波导可 传播TEM波;否则只能传播TE、TM或混合模式波。
kz = 骣 mp 鼢 骣 np 鼢 k2 - 珑 珑 鼢 珑 b 桫a 鼢 桫
2 2
对于一定的波导和模式,随频率不同,kz 可能为虚数、 实数和零。
截止频率与截止波长
k>kT, kz为实数,波可以传播;反之, kz为虚数,波 沿z 轴指数衰减,无法传播,这种现象称为截止。 当k=kT时, kz =0,在z 向不能形成导波,是导波在波 导中传播与截止的临界情况,故kT称为截止波数,一般 记为kc,它所对应的频率为截止频率fc。
m = - Z TEM = - Z 0 e
矩形波导中的导波
矩形波导的横截面为封闭的金属框,因此不支持静态场
2 E 分布,即 压T 2 0,压T H
0 ,故仅能传输TE或TM波而
电磁场与波课件教学PPT-第七章 导行电磁波-精品文档

2Exk2Ex0, 2Hxk2Hx0 —— 横向场方程 2Eyk2Ey0, 2Hyk2Hy0
2 E z k 2 E z 0 , 2 H z k 2 H z 0—— 纵向场方程
利用解形式化简为:
由于
Ez(x,y,z)Ez(x,y)ez Hz(x,y,z)Hz(x,y)ez
xa
O
边界条件:Ez |x00 Ez |xa0 Ez |y00 Ez |yb0
分离变量法求解偏微分方程: E z(x,y)f(x)g(y)
第七章 导行电磁波
16
电磁场与电磁波
偏微分方程化为微分方程求解:
f
(x)kx2
f
(x)
0
g(y)ky2g(y) 0
f(0)0, f(a)0 g(0)0, g(b)0
H z y
)
Ex
k
1
2 c
(
E z x
j
H z) y
Ey
1
k
2 c
(
E z y
j
H z) x
kc2 2 k2
9
电磁场与电磁波
2. 场方程(分析方法)
根据亥姆霍兹方程 2 E k 2 E 0 , 2 H k 2 H 0 其场分量形式即为:
电磁场与电磁波
分类分析时变电磁场问题
共性问题
个性问题
0 t
电磁波的
j 典型代表 t
均匀平面波
电磁波的 传输
波导
电磁波的 辐射
天线
第4章
√
第5、6章
√√
第7章
第七章 导行电磁波
第七章导行电磁波

x,
y)e
j (tz )
Ez0 y
jβE
0 y
jω
μH
0 x
,
H
0 z
y
jβH
0 y
jωεEx0
约去ej(t-z)
jβEx0
Ez0 x
jω
μH
0 y
,
jβH
0 x
H
0 z
x
jωεE
0 y
(7-1-13)
E
0 y
x
Ex0 y
jω
μH
0 z
,
H
0 y
x
H
0 x
y
jωεEz0
2020/7/19
7
联立式(7-1-13)中的各式,可求得
向存在纵向分量电场。
2020/7/19
9
一、矩形波导中电磁场的求解
1.分离变量法求解波动方程 思路:先求电场、磁场纵向分量Ez和Hz,然后求其它横向分量。 由式(7-1-11):
2
E
0 z
x 2
2
E
0 z
y 2
h2
E
0 z
0,
2
H
0 z
x 2
2
H
0 z
y 2
h2
H
0 z
0
(7-2-1)
Ez0 ,
H
Ey x
Ex y
j H z
,
H y x
H x y
j Ez
Ex Ex0 ( x, y)e , j(tz) Ey Ey0 (x, y)e j(tz) , Ez Ez0 (x, y)e j(tz)
Hx
H
0 x
工程电磁场之七均匀传输线中的导行电磁波

2. 无损耗均匀传输线方程
ET 0
ET
1
i
2
i
因此在z=C的任意xy平面内,定义两导线之间的电压
u ( z, t ) 2 1
0 ucb uda E dl dz t cbad
u 0 i L0 z t t
单位长度 的磁通
特点
沿线各点入端阻抗等于特性阻抗,与线长无关,这 种情况称为传输线匹配;
② 终端短路时的入端阻抗
ZL 0
Z i jZ 0 tan
2
l jX
上 页 下 页
第 七 章
均匀传输线中的导行电磁波
特点 终端短路的无损耗均匀传输线的入端阻抗具有纯电抗性质
0l
4 l
4
2
0 X
返 回
下 页
第 七 章
均匀传输线中的导行电磁波
7.0
引言
1. 传输线的定义和分类 定义
用以引导电磁波,将电磁能或电磁信号从一点定向 地传输到另一点的电磁器件称为传输线。要求达到 最大效率的传输能量。 一般按传输线上传递电磁波的类型分为:
分类
① 传递横电磁波(TEM波)的平行双线 、同轴电缆 、 平行板等双导体系统传输线。工作频率为米波段 (受限于辐射损耗)。 ② 传递横电波(TE波)或横磁波(TM波)的单导体系 统,如金属波导和介质波导等。工作频率为厘米波段
d B a
dz
c
b
上 页 下 页
第 七 章
均匀传输线中的导行电磁波
z z2
0dz
cbad
A dl ( A
Az1 )dz L0idz
第7章导行电磁波

2 式中: x k y 2 k 2 k2
由边界条件来确定四个待确定量C1,C2,C3,C4 .
由边界条件可知,在导体边界面上,电场切向为零。
Ez Ez
x 0, a y 0,b
0 0
n x sin y b
由上边界条件,可确定出Ez的解为:
双导线 同轴线 带状线 微 带 矩形波导 圆波导 光 纤
3Hz 300THz
30Hz
300Hz
3kHz
30kHz
300kHz
3MHz
30MHz
300MHz
3GHz
30GHz
300GHz
3THz
30THz
音频 VF
甚低频 VLF
低 频 LF
中 频 MF
高 频 HF
甚高频 VHF
特高频 UHF
超高频 SHF
本章主要内容: 导行电磁波的一般特性 矩形波导中电磁波的特性 谐振腔 分析方法: 导行波是在有限区域内传播的电磁波,因此场量必 须满足波动方程,同时还必须满足一定的边界条件。 本章通过求解特定边界条件下的波动方程,得到导 波场的解,从中可以分析得出在各种导波装置中波的 性质。
7.1 导行电磁波概述
TEM波的相速为:v p
k
1
TEM波的波阻抗为:
H z H y j Ex y
ZTEM
Ex TEM j Hy j TEM
Ez Ex j H y x
TEM波的波阻抗与媒质本征阻抗相等。 相伴的磁场
通过数学变形,可以得到用纵向场分量Ez 、Hz 分 量表示的横向场量,即:
Ez H z 1 Ex 2 ( j ) 2 k x y Ez H z 1 Ey 2 ( j ) 2 k y x H z Ez 1 ( j ) 和 Hx 2 2 k x y H z Ez 1 Hy 2 ( j ) 2 k y x
第七章 导行电磁波

矩形波导形状如下图示,宽壁的内尺寸为 a ,窄壁的内尺寸为 b 。 已知金属波导中只能传输 TE 波
y
及TM 波,现在分别讨论他们在矩形 波导中的传播特性。
b z
,
a x
若仅传输 TM 波,则 Hz = 0 。按 照纵向场法,此时仅需求出 Ez 分量, 然后即可计算其余各个分量。
H 0 nπ
Ey j
H 0 mπ
mπ nπ jk z z x cos y e sin a a b
式中 m, n 0, 1, 2, ,但两者不能同时为零。由上式可见,与TM波一 样,TE波也具有前述多模特性,但此时m 及 n不能同时为零。因此,TE
式中 kc2 k 2 kz2
电磁场与电磁波 这样,只要求出 z 分量,其余分量即可根据上述关系求出。z 分量 为纵向分量,因此这种方法又称为纵向场法。
在圆柱坐标系中,同样可用 z 分量表示 r 分量和 分量。其关系
式为
Er 1 Ez H z j k j z 2 kc r r
电磁场与电磁波
类似地可以导出矩形波导中TE波的各个分量为
mπ nπ jk z z H z H 0 cos x cos y e a b
Hx j Hy j Ex j
k z H 0 mπ mπ nπ jk z z x cos y e sin 2 kc a a b k z H 0 nπ mπ nπ jk z z x sin y e cos 2 kc b a b kc2 kc2 mπ nπ cos x sin b a b y e jk z z
电磁场理论 第七章-导行电磁波

y b x a o z
m n H z ( x, y) H m cos( x) cos( y) a b
kcmn ( m 2 n 2 ) ( ) a b
m 0, 1 , 2, 3 n 0, 1 , 2, 3
电磁场理论
第7章 导行电磁波
14
所以TE波的场分布
m n H z ( x, y, z ) H m cos( x) cos( y)e z a b m m n H x ( x, y , z ) 2 H 0 sin( x) cos( y )e z kc a a b
m 2 n 2 ( ) ( ) a b
kcmn 2
2 2 1 2 kcmn f cmn (m a) (n b)2
结论:在矩形波导中,TE10模的截止频率最低、截止波长最 长。
电磁场理论
第7章 导行电磁波
18
m 2 n 2 2 当 kcmn < k 时, mn kcmn k 2 j 2 ( ) ( ) j mn a b
Ez n m n E y ( x, y , z ) 2 2 Em sin( x) cos( y)e z kc y kc b a b j Ez j n m n H x ( x, y , z ) 2 2 Em sin( x) cos( y)e z kc y kc b a b j Ez j m m n H y ( x, y , z ) 2 2 Em cos( x)sin( y )e z kc x kc a a b H z ( x, y , z ) 0
2 2 2 2
—— 横向场方程
2 Ez k 2 Ez 0, 2 H z k 2 H z 0 —— 纵向场方程
第七章导行电磁波详解

2 Ez0 z 2
2 Ez0 y 2
h2 Ez0
0
,
2
H
0 z
z 2
2
H
0 z
y 2
h
2
H
0 z
0
(7-1-11)
2020/9/30
8
§7-2 矩形波导中的电磁场
空心波导中能否传输TEM波呢?
假设它能够传TEM波。在波导任意横
截面上作闭合环路L,沿L对磁场进行
环路积分。TEM波只有横向场分量Ex, Ey和Hx,Hy。横截面上磁场线是闭合 曲线,因此沿任意闭合回路L磁场强度
y 2
y)
h2E 0 (x,
y)
0
(7-1-8)
h k2 2 k2 2
(7-1-9)
h称为2E特0 征值2E,0 是h2待E 0定 0的, 常2数H 。0 用2EH0
x2 y2
x2 y2
、H 0代表E 0
0
h2H 0 0
(
x,
y)、H 0 (x, (7-1-10)
y
)
分解成标量方程,即
2020/9/30
H
0 x
j h2
β
H
0 z
x
ωε
Ez0 y
,
H
0 y
j h2
β
H
0 z
y
ωε
Ez0 x
Ex0
j h2
β
Ez0 x
ωμ
H
0 z
y
,
E
0 y
j h2
β
Ez0 y
ωμ
H
0 z
x
(7-1-14)
结论
求出电场、磁场的纵向分量Ez和Hz,即可求得其它横向分量。
第七章 导行电磁波

j E z 2 ,H k c y
j E z 2 k c x
Ex Z TM H
k
2 c x
E z E z ,Ey 2 x k c y
Z TM
j y 1 ez E
E H
14
TE 波
E z 0, H z 0
H z 1 E z E y 2 ( j ) kc y x
2 2 2 k k c
11
导波的分类 如果 Ez= 0, Hz= 0,E、H 完全在横截面内,这种被称为横 电磁波,简记为 TEM 波; 如果 Ez 0, Hz= 0 ,传播方向只有电场分量,磁场在横截面 内,称为横磁波,简称为 TM 波或 E 波; 如果 Ez= 0, Hz 0 ,传播方向只有磁场分量,电场在横截面 内,称为横电波,简称为 TE 波或 H 波。
H x ,y ,z )H x ,y ) e z( z(
z
16
7.2 矩形波导
结构:如图 所示,a ——宽边尺寸、 b ——窄边尺寸 特点:可以传播TM 波和TE波,不能传播TEM波 7.2.1 矩形波导中的场分布 1. 矩形波导中TM 波的场分布
对于TM 波,Hz= 0,波导内的电磁场由Ez 确定 方程
n m n H y ( x, y, z ) 2 H 0 cos( x ) sin( y )e z kc b a b j n m n E x ( x, y, z ) 2 H 0 cos( x ) sin( y )e z kc b a b j m m n E y ( x, y, z ) 2 H 0 sin( x ) cos( y )e z kc a a b E z ( x, y, z ) 0
第07章导行电磁波-精品文档

令 kc2 k2 2,称为截止波数,则有: T 2 e (x ,y ) k c 2 e (x ,y ) 0 (5 )
同理,有: T 2 h (x ,y ) k c 2 h (x ,y ) 0 (6 )
7.2 导行波的分析方法和分类
这样,可由上面两个方程得到 e ( x , y )和 h ( x , y ) 各分量的标量波
圆波导
带状线
微带
介质波导 光纤
7.2 导行波的分析方法和分类
一、导行波的分析方法
为分析方便,对任意截面的均匀波导,选 z 方向为波导的轴
线方向,也即传输方向,横截面所在平面为 xoy 平面,如图,并
作如下假定:(1)波导的横截面形状和媒质特性不沿轴线 z 变化。
(2) 波导内壁是理想导体,即;波导内填充均匀、线性、各
7.1 引言
这种“路”的分析方法,也称为长线理论。事实上,“场”的方 法和“路”的方法是紧密相关,互相补充的。
“电磁波沿传输线传输”问题是一类典型而简单的电磁场边值 问题,它可以分为两个方面来研究。一方面是研究电磁场的横向分 布特性,即研究与传输线轴线相垂直的传输线横截面上的场分布; 另一方面是研究电磁场沿传输线轴线,即纵向的传播特性。下面我 们将从这两方面作详细讨论。
梯 度 定 义 式
令 ET ExxˆEyyˆ,则有:
E Tk 1 c 2( T E zj z ˆ T H z) (1 1 )
7.2 导行波的分析方法和分类
同理,有:H T H x x ˆ H y y ˆ k 1 c 2 ( T H z j z ˆ T E z) ( 1 2 )
(9 a) (9 b )
H xk 1 c 2(j E y z H xz) H yk 1 c 2(j E x z H yz)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传输线中向+z 或 -z 方向传播的导行波
类比
无界空间中向+z 或 -z 方向传播的均匀平面波
无源时谐 波动方程 z方向的 边界条件 表示式中与 z 有关的部分 x、y 方向的 边界条件 表示式中与 x,y 有关的部分
2 2 k E 0 0 E H k H 0 2 H k 2 H 量 E z、H z的有、无来对导行波进行分类
1) Ez 0,H z 0 :横电磁波,TEM波 2) Ez 0,H z 0 :横电波,TE波(或H波) Transverse Electric 3) Transverse Magnetic
Ez 0,H z 0 :横磁波,TM波(或E波)
4) Ez 0,H z 0 : 混合波 TE波+TM波
6.1.2
导行波的传播特性
一、各种波(或称模式(mode))的传播特性
1、 TEM波:Ez 0,H z 0
由公式(7-19) : 欲使E t x, y 0和H t x, y 0
2 2 2 k 2 0 jk 须有:kc 0 kc z 因此: E r E x, y e E x, y e jkz
结论:
• 随 z 增大,电场的相位逐渐滞后,因此该TEM 导行波向 z 方向传播。
• TEM波始终是传播的。
2、TE波和TM波:
由公式(7-19) :
2 须有: kc 0
欲使E t x, y 和H t x, y 有意义
2 kc k2
2 j k 2 kc j
求解,得
2 2 kx k2 k y c H z x, y H 0 cos(k x x x ) cos(k y y y )
X x A cos(k x x x ) Y y B cos(k y y y )
4、 H z x , y , z H z x , y e z
2、截止波数、截止频率、截止波长、
• 截止(或临界)波数:kc
k kc , 则是传输波 k kc , 则是凋落波
• 截止(或临界)频率: kc 2f c f c
f f c , 则k kc , 是传输波
kc 2
2 kc c • 截止(或临界)波长: c kc
H 0 cosk x x x cos k y y y e
5、根据纵向场法,可由 H z 推出 E x、E y、H x、H y 的表示式,其结果为教材P180页式 (7-59);
z
6、这些表达式中, k x、k y、 x、 y 是待定常数, 要根据边界条件来确定它们;
(此划分界限并不十分严格)
6.1 规则传输线的分析方法和一般特性
规则传输线:
横截面的形状、尺寸及 媒质参数不随传输线纵向坐标 变化的无限长、直传输线。
y
z (纵向) 模型假设:
x
1、传输线所用导体为理想导体,所用介质为理想介质。
2、求解传输线中的电磁场时假设传输线中无源。
6.1.1 规则传输线中的电磁波 一、求解方法:
• TEM导行波的相移常数等于无界理想介 质中的相移常数; • TEM 导行波的相速度与频率无关,是 非色散波。
2、TE、TM波:
2 相移常数为 k 2 kc
vp
k
2 2 kc
( 2f
)
2
2 kc
1、TE、TM波的相速度与频率有关,是色散波,传输 线对于TE、TM波是色散传输系统。这是由传输线这种 几何结构造成的,称为几何色散。而导电媒质中的色散 称为媒质色散。 2、色散现象导致传输线传输信号的失真,所以传输线不 宜传输带宽较大的信号。
3、了解:群速度、能速度
四、波导波长:传输线中相邻的同相位点之间的距离 2 2 • TEM模: g g
相移常数
k
(λ为无界空间中的波长)
• TE、TM模:
2 k kc 2
g
2
五、波阻抗:
某个传输波的横向电场与横向磁场的绝对值 之比。
Et Z Ht
求出
3、纵向场法
• 直角坐标表示式: ˆ E y x, y y ˆ E z x, y z ˆ E x , y E x x , y x ˆ H y x, y y ˆ H z x, y z ˆ H x , y H x x , y x • 纵向场法:
一、场分量求解
E z ( x, y ) 0,H z ( x, y ) 0 1、 TE模: 2、由纵向场法,求出 H z 就可求出 E、H 3、 采用分离变量法,求 H z ( x, y ) : H z x, y X x Y y
代入
2 2 H x , y k t z c H z x, y 0
无源时谐Maxwell方程
H r jE r E r jH r H r 0 E r 0
无源时谐波动方程
2
2 E r k E r 0 2 2 H r k H r 0
小结:
1、传输线中有TEM、TE、TM三种波;
2、TEM波总是非色散的传输波;
3、TE、TM波有截止、传输两种状态。
4、频率大于传输线的截止频率的TE或TM波才可 以在传输线中传输,因此对于TE、TM波而言, 传输线相当于一个高通滤波器;
5、TE、TM波在传输时会出现色散现象,导致信 号失真,因此传输线对于TE 、TM波来说是窄带 器件;
传输线的种类:
双线
同轴线
矩形波导
圆波导
(外壁、内芯为金属, (两根金属线) 之间可填充介质) (外壁为金属,内部可填充介质)
带线
微带线
介质波导
光纤
(由金属、介质构成)
(主要由介质构成)
从减少传输线损耗和结构工艺的可实现 性等方面考虑,不同频段、不同需求,使 用不同的传输线。
米波、分米波以下:双线、同轴线 厘米波:空心金属波导、带状线、微带线 毫米波:空心金属波导、介质波导、微带线 光波:光纤
2 2 t E x , y kc E x , y 0 时,由
• kc 在求解方程 x、y方向的边界条件确定。
• k 2 f 2 , 一旦传输线中所填充 媒质的参数 、 确定,k 就只随导行波的频率 f 或 波长λ变化。 • kc值一旦确定 ,则导行波是传输的还是凋落的,就取 决于频率或波长。
向+ z 传播的 均匀平面波
向+ z 传播的导行波
无界,无变化
e
jkz
γ值待定,与x、y方向 边界条件有关
无界,无变化 z 类比: e
无界、无变化 常矢量
有界、有变化
x, y的矢函数: E x, y
E x, y e z H x, y e z
E r 结论:导行波的表示式: H r
第六章 导行电磁波
主要内容:
一般导波传输线的特性分析 金属矩形波导 同轴线 平面传输线 波导的激励与耦合
传输线(transmission line ):用来传输电磁能量的线路 称为传输线或称波导(waveguide)(广义的)。 传输线能导引电磁波沿传输线的纵向方向前进。
被导引的电磁波称为导行波(guided-wave)。
k
求 解
传输线的边界条件: 1、z方向无界、无变化 2、xoy平面上有媒质交界面 求出无源时谐波动方程的通解,再根据边界条件 确定通解中的待定常数。
二、求解传输线的无源时谐波动方程
1、求解思路:
(1)分离变量法(教材P168) (2) 类比方法: ①传输线的无源时谐波动方程与无界空间中的无源时 谐波动方程完全相同, ②传输线与无界空间一样在 z 方向无界、无变化, ③传输线中导行波向 +z 或 -z 方向传播,
Ez Hz
E x、 E y H x、H y
求解:
求出
• 求解纵向分量 E z、H z
2 2 E x , y k t z c E z x, y 0
2 2 t H z x , y kc H z x , y 0
① kc
x、y 方向的边界条件
② Ez ③ Hz
E i x, y, z, t
z
任意固定时刻,传输波电场的任 意分量沿传输线纵向的分布情况
• 情况2:
为实数
z z
E i x, y, z, t
当k kc , , e e E x, y, z E x, y e z 为凋落波 瞬时表示式:E x, y, z, t E x, y e z cost
注: H0也是待定常数,它体现导行波的幅度(即能量大小),
由辐射源的强度决定。它仅是一个与x、y、z无关的常系数,不 影响导行波的空间分布规律,因此目前不用确定它。
2 t
2 z 2 2 E x , y e k E x , y e z 0 z 2 2 E x, y k E x, y 0 2
kc
x、y 方向的边界条件
① kc 求解: ② E x, y ③ H x, y
z
任意固定时刻,凋落波电场的任意分量 沿传输线纵向的分布情况 注意:由于表示式中没有相移因子,所以凋落波并不是 边传输边衰减的电磁波,而是幅值沿 z 方向逐渐减小的一 种场分布。将凋落波这种不能传播的非波动状态称为截止 ( cutoff )状态。
