2014年春季新版新人教版七年级数学下学期6.1、平方根导学案18
七年级数学下册6.1平方根学案(新版)新人教版

6.1.3 平方根(课时3) 备课组长审核签名 【学习目标】 1.了解平方根的概念;掌握平方根的特征. 2.能利用开平方与平方互为逆运算的关系,求某些非负数的平方根. 3.通过对平方根的学习,培养学生从多方面、多角度分析问题、解决问 题的思想意识,养成全面分析问题的习惯.【学习重点】平方根的概念和求数的平方根. 【学习难点】平方根和算术平方根的联系与区别. 【学前准备】认真阅读课本P44---P461. 填表:x 8 -8 53 53-2x 16 0.36定义:如果 ,那么这个数就叫做a 的 或二次方根.即:如果a x =2,那么x 叫做a 的 .a 的平方根记为 .求一个数a 的平方根的运算,叫做 ,其中a 叫做 .归纳:平方与开平方互为 运算,如3±的平方是 ;9的平方根是 .练习:2的平方根是 ;25±表示 ,它的值为 .2.试一试,求下列各数的平方根.(注意书写格式)(1)100; (2) 169; (3) 25.0; (4)412; (5)0.解:(1)因为100)(2=,所以100的平方根是 ,即=±100 ;(2)(3)(4)(5)思考:(1)一个正数的平方根有几个?它们有何关系?(2)0的平方根是多少?(3)负数有没有平方根?为什么?3.判断下列说法是否正确,并口述理由.(1)3-的平方9,所以9的平方根是3-; ( ) (2)1的平方根是1; () (3)-1的平方根是-1; ( ) (4)5是25的算术平方根; ( )(5)65是3625的一个平方根;( ) (6)0的平方根与算术平方根都是0. ()【课堂探究】例1说出下列各式的意义,并求它们的值:(1)36; (2)81.0-; (3)949±. 学习小组长评价和签字 完成 订正 签字思考:平方根和算术平方根两者有什么区别和联系呢? 例2 如果一个数的平方根是31-+a a 和,求a 的值及这个数.【随堂检测】1.下列各数有平方根吗?如果有求出它的平方根,如果没有,说明理由. (1)64; (2)49; (3)0.04; (4)-4; (5)2)3(-.2.计算下列各式的值(1)9; (2)49.0-; (3)8164±.3.判断下列各式计算是否正确,并说明理由.(1)24±=; ( ) (2)24±=-. ( ) (3)24±=±; ( )4. 求满足下列各式的x 的值:(1) 92=x ; (2)092=-x ; (3) 0942=-x ; (4)9)1(2=-x .5.如果一个数的平方根是3+a 和152-a ,求a 的值及这个数.【归纳总结】1.正数的平方根有 个,它们互为 ;0的平方根是 ;负数 平方根.课后作业0603--平方根 (课时3)班级: 座号: 姓名:1.2-表示( )A .2的平方根B .2的算术平方根C .2的负的平方根D .将2开平方2.下列说法正确的是( )A .4的平方根是2B .4的算术平方根是-2C .8的平方根是4D .9的平方根是3±3. 9的平方根是( )A .81±B .9C .3±D .34.下列各数中,没.有.平方根的是( ) A .25 B .0 C .-1 D .41 5.7的平方根是( ) A . 7± B .7 C .7±D .7- 6.下列计算中,正确的是( )A .39±=B .43169=C .3)3(2-=-D .24±= 7.144的平方根是 ;算术平方根是 .169的平方根是 ;算术平方根是 . 8.一个数的平方根是412-+m m 和,求=m ,这个数是 .9.如果一个正方形的面积为a ,那么这个正方形的边长为 .10.计算:4= ,=-36.0 ,=±2516 . 11.求下列各数的平方根.(1)49; (2)254; (3)6101; (4)0016.0.12.求满足下列各式的x 的值:(1) 92=x ; (2)092=-x ; (3) 0942=-x ; (4)9)1(2=-x .13.如果一个数的平方根是3+a 和152-a ,求a 的值及这个数.14.(1)22= ,2)3(-= ,25= ,2)6(-= ,27= ,20= .对于任意数a ,2a = .(2)2)4(= ,2)9(= ,2)25(= ,2)36(= ,2)49(= ,2)0(= .对于任意非负数a ,2)(a .*15.阅读: 1.4142≈,所以2的整数部分是1,小数部分是12-.(1)33的整数部分是 ,小数部分是 .(2)已知m 是10的整数部分,n 是10的小数部分,求1)10(--m n 的平方根.16。
初中数学人教新版七年级下册6.1 第1课时 算术平方根导学案

初中数学人教新版七年级下册实用资料
)2=0.0025.
x叫
.
___________________________________________________________________________
问题:下列各式中哪些有意义?哪些无意义?为什么?
-
例4.若=0,求m+n的值.
方法总结:几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
1.若|a+3|=0 ,则a=______.
1.填空:(看谁算得又对又快)
(1) 一个数的算术平方根是3,则这个数是.
(2) 一个自然数的算术平方根为a,则这个自然数是;和这个自然数相邻的下一个自然数是.
(3)81的算术平方根为.
(4)2的算术平方根为.
2.求下列各数的算术平方根:
(1)169; (2)49
64
; (3) 0.0001.
3.下列式子表示什么意义?你能求出它们的值吗?
例4 下列式子表示什么意义?你能求出它们的值吗?
4.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
5.【拓展题】已知|x+2y|+
7
3)
5(2=
+
-+z
y
x
,求x-3y+4z的值. “备课大师”全科【9门】:免注册,不收费!/。
人教版初一数学下册6.1平方根(1)导学案

6.1平方根(1)导学案学习目标:1.经历算术平方根概念的形成过程,了解算术平方根的概念2. 会求某些正数(完全平方数)的算术平方根并会用符号表示学习重点:会求正数(完全平方数)的算术平方根并会用符号表示学习难点:会求正数(完全平方数)的算术平方根并会用符号表示一【问题导学】(一)学校要举行美术作品比赛,小明很高兴.他想裁出一块面积为25平方分米的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取___________ 分米?(二)(自主完成下表)二【自主学习】自主学习:算术平方根的定义(自学课本40页例1以上部分)回答下列问题:(1)定义:一般地,如果一个_______ 的等于a,即 _____________ ,那么这个_______ 叫做a 的算术平方根。
a的算术平方根记作,读作________________ ,a叫做___________ 。
★规定:0的算术平方根是。
正数_____ 的平方等于9,我们把正数________ 叫做______ 的算术平方根.正数_____ 的平方等于16,我们把正数_______ 叫做______ 的算术平方根.(2 )结合算术平方根的定义填空:被开方数a的取值范围是 _________ ;算术平方根x的取值范围是 _____________ 。
总结:(1)算术平方根具有双重非负性,对于.a,要求__________ ,.一a >0,即只有 _______ 才有算术平方根,而且算术平方根是_____________ 的。
负数为什么没有算术平方根?因为x2=a,其中a是平方运算的结果,要么是__________ ,要么是 _____ ,所以负数没有算术平方根。
温馨提示:关键词语正数”例如:32 = 9,实际上______________ 的平方也等于9,但是只有才叫做9的算术平方根。
(3 )跟踪练习:下列各式中哪些有意义?哪些无意义?为什么?5 , - 3 , 、-3 , (-3)2(4)算术平方根的表示方法:①0.25的算术平方根表示为 _______ ;②0的算术平方根表示为_____ ;③a(a > 0)的算术平方根表示为_________ .三【课堂练习】1、求下列各数的算术平方根: (1)0.0001 (2)2解••• ____ =0.0001••• 0.0001的算术平方根是 ______ 即3、求下列各式的值:(5) J o.01 = _______ ; (6) T 32 = ________. ( 7) J 0= ________总结:正数有_个算术平方根,它为 ____________ ; 0的算术平方根为 _____ ;负数 ________ 算术 平方根 四【课堂小结】本节课你学到了 ________________________________________________________________________ 五【达标检测】 一、填空1、 屮11= ______ ; ((_81)2= ________ ; V 0.0064 = ________2、 ,81的算术平方根是 _________ . ■. 16的算术平方根是 ________ 。
人教版数学七年级下册 6.1《平方根》导学案设计
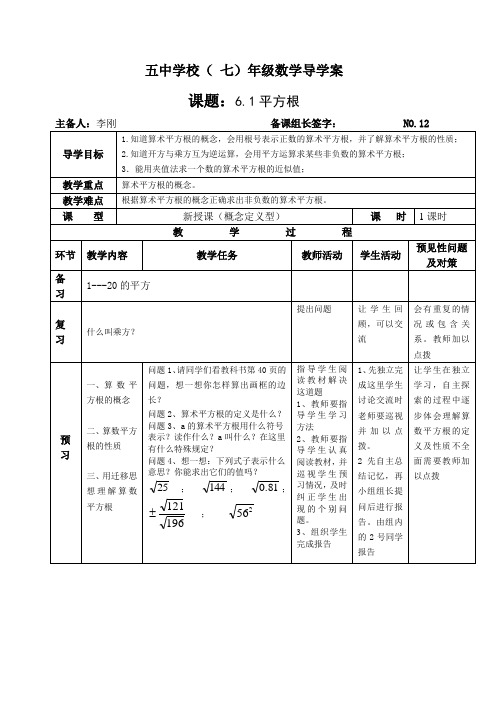
五中学校(七)年级数学导学案课题:6.1平方根研习问题5求下列各数的算术平方根:(1)100; (2)1; (3)6449;(4)0.0001 (5)问题6怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?(课本第41页的探究)(1)、除了课本上的方法外,你还有其他的方法吗?(2)、这个大正方形的边长是多少呢?(3)、这个大正方形的边长是(),表示( )的算术平方根,它到底是个多大的数?你能求出它的值吗?(4)阅读教材41-42页的内容,然后自己推导一下2的值。
(5)什么叫无限不循环小数?请你举出几个无理数。
(6)你对正数a的算术平方根a的结果有怎样的认识呢?总结:a的结果有()种情况:当a是完全平方数时,a是一个()数;当a不是一个完全平方数时,a是一个( )数。
问题7指出下列各数的整数和小数部分分别是多少?3136,2;31、组织学生组间交流及展现。
2、教师及时点拨、追问、纠错。
3、精讲如何估算2的大小。
4、讲解无限不循环小数的特点组内交流独立完成后,分小组报告学生在自主学习的基础上,对于不能独立解决的问题进行组间交流,在报告过程中,由同组进行补充。
学生对于“2是4的平方根”和“4的平方根是2”这两种说法容易混淆.教师要根据平方根的定义讲清因为正数有两个平方根,所以必须说“4的平方根是正负2”认真听取别人的经验,方法,把自己对问题的认识与大家共享。
有错误教师订正时习习题1.1必做:第1、2、4、5 选做题:第3题教师布置规范程度差板书设计6.1平方根1、定义4、归纳5、应用举例2、性质3、扩展与延伸教学反思组长签字:领导签字:。
人教版七年级数学下册6.1算术平方根导学案

1 人教版义务教育课程标准实验教科书七年级下册6.1《算术平方根》导学案一、学习目标(1)了解算术平方根的概念,会用根号表示正数的算术平方根,了解算术平方根的非负性。
(2)会用平方运算求某些非负数的算术平方根。
(3)通过用类比的方法探寻出算术平方根的概念及表示方法,并能自我总结出算术平方根的非负性和应用平方运算求算术平方根。
在体验问题解决的过程中,发展学生抽象思维、数感和符号感。
二、自学内容阅读课本P68页,并回答下列问题(1)如果一个________的______等于a ,那么_________就叫做______的算术平方根。
(2)正数a 的算术平方根怎样表示?为什么规定:0的算术平方根为0。
(3) 读作_______,表示_______;a 的取值范围是_________.(4)仿照例题(1)的格式探求下列各数的算术平方根:36;121;49。
(5)求算术平方根的运算与求平方运算有什么关系 三、探究学习象52=25,那么5就叫做25的算术平方根102=100,那么10就叫做100的 算术平方根你能否用自己的语言来描述一下,如何理解“算术平方根”?四、巩固测评1、求下列各数的算术平方根:① 100; ② ; ③ 0.0001;① 0.0025; ② 121; ③ 32;2、下列式子表示什么意思?你能求出它们的值吗?3、下列各数没有算术平方根的是( )A. 0B.16C.-4D.24、若数a 的算术平方根等于3,则a 的值是( )a 644981.0025111252 A.3 B. -3 C. -9 D.95.判断题(1)的算术平方根是± ; ( ) (2)5是 的算术平方根 ; ( )(3)一个正数的算术平方根总小于它本身; ( )6.填空题(1)正数的算术平方根总是 数,0的算术平方根是 ,算术平方根等它本身的数有 ;(2) 的算术平方根是 ;(3) 的算术平方根的相反数的绝对值是7、下列各式中哪些有意义?哪些无意义?为什么?;— ; 五、思考题 (1)81 的算术平方根是的值是的算术平方根是六、拓展延伸(3)如果,那么x= ,y=(4) 的算术平方根等于2七、学习心得 123456例2:求下列各式的值, (4121()25-()24-491533-23)(-8181().1-_______1有意义时,当x x ()____________,212的取值是此时的最小值是a a ++0+=。
人教版数学七年级下册--6.1 平方根(1)-算术平方根 导学案

第六章 实数 6.1平方根 【教学目标】知识与技能1. 了解算术平方根的概念。
2. 会用根号表示正数的算术平方根。
3. 了解开方与乘方的互逆运 算;会用平方运算求某些非负数的算术平方根。
过程与方法通过生活中的实例,总结出算术平方根的概念,通过计算非负数的算术平方根,真正掌握算术平方根的意义。
情感、态度与价值观通过学习算术平方根,认识数与人类生活的密切联系,建立初步的数感和符号感,发展抽象思维,为学生以后学习无理数做好准备。
【教学重难点】重点: 算术平方根的概念和求法难点: 会用平方运算求某些非负数的算术平方根【导学过程】【知识回顾】写出下列各数是哪个正数的平方① 16 ② 49 ③ 100 ④94 ⑤ 169 ⑥2581 ⑦ 2.5 ⑧ 2.25 【新知探究】探究一、问题1:(P40)提问:怎样算出画框的边长?依据是什么?如何用式子表示?探究二、算术平方根的概念1、归纳:一般地, 叫做a 的算术平方根.a 的算术平方根记为a ,读作“ ”,a 叫做 .规定:0的算术平方根是 .也就是,在等式2x =a (x ≥0)中,规定 x=2、 试一试:你能根据等式:212=144说出144的算术平方根是多少吗?并用等式表示出来.3、1.252. 0.00253.1649探究三、例1 求下列各数的算术平方根:(1) 100; (2) 1; (3) 6449; (4) 0.0001 探究四、算术平方根的有意义的条件 (1)负数有算术平方根吗? (2)、a 是什么数?(3),a 中的a 可以取任何数吗?【知识梳理】本节课你学到了什么?有什么收获和体会?还有什么困惑?1.一般的说,一个 数x 的平方等于a,即x 2=a,那么这个 数x 就叫着a 的 。
2. a 的算术平方根记为 ; 0的算术平方根是 。
3. 一个 数越大,这个 数的算术平方根就越 。
【随堂练习】3. 4的算术平方根是 ;2581的算术平方根是 ; 2 97的算术平方根是 ; 2.25的算术平方根是 ;1000的算术平方根是 。
人教版七年级数学下册6.1平方根导学案

课题:6.1平方根学习目标1.理解一个数平方根的意义;会用根号表示一个数的平方根;2.掌握平方根与算术平方根联系与区别3.通过本节的训练,提高学生的逻辑思维能力;培养学生的探究能力和归纳问题的能力。
学习重点:平方根和算术平方根的概念及求法.学习难点:平方根与算术平方根联系与区别.学习方法:归纳法.学习过程一、问题导入①填空: ( )2=9;( )2=100 ( )2=0 ( )2=0.0081②填表:二、概念归纳①如果一个数的平方等于a,那么这个数就叫做a的或.即:如果x2=a,那么x叫做 , 求一个数a的平方根的运算,叫做②根据上图可知:平方与开平方互为。
根据这种运算关系,可以求一个数的三、重点探究①a可以取任何数吗?答:被开方数a是,即a 0;(填不等号)②正数a有个平方根,用a表示其中正的平方根(即是 ),读作“根号a”,另一个负的平方根记为a-,其中a叫做。
”表示正数a的平方根,读作“”。
③ 0有个平方根,是;负数平方根.四、基础训练①9的平方根是,9的算术平方根是;11的平方根是,11的算术平方根是②在x2, -│-2│中,是非负数的有个,分别是③求下列各数的平方根(1)900 (2)1 (3) 4964(4) 1.21 (6)214(5)0五、达标训练成立, 则x 的取值范围是②求下列各式的值 (1);③求满足下列各式的x 的值:(1) x2 =25 (2) x 2 -81=0 (3) 4x 2-9=0④.若一个正方形的面积变为原来的4倍,则它的边长变为原来的多少倍?若一个正方形的面积变为原来的 9倍,则它的边长变为原来的多少倍?若一个正方形的面积变为原来的m 倍,则它的边长变为原来的多少倍?六、拓展训练①分别求出下列各数在哪两个整数之间.②(2002,南昌中考)若m,n 满足2(1)0m -=,的平方根是( ) A.±4 B.±2 C.4 D.2-的值为( ) A.1 B.2 C.3 D.以上均不12对④(学科综合)在物理学中,用电器中的电阻R与电流I,功率P•之间有如下的一个关系式:•P=I2R,,现有一用电器,电阻为18欧,该用电器功率为2400瓦,求通过用电器的电流I.。
人教版数学七年级下册- 6.1《平方根》导学案(2)

【学习目标】
1.了解平方根的概念,并会用符号表示。2)会求一个数的平方根。3)理解平方根与算术平方根的区别;了解开方与乘方之间是互为逆运算的关系
2.自主、合作、交流
3.培养学生的分析能力和归纳能力
【重 点】
会利用开方与乘方之间的互逆运算关系,求某些非负数的算术平方根和平方根。
【难 点】
掌握求一个数的平方根的方法,并理解平方根的意义。
【学习过程】
一复习导入:(2分钟)
1)如果一个数的平方等于9,那么这个数是多少?
(2)填表:
1
16
36
49
二、自主学习内容、指导、检测:(15分钟)
探究一、
1、一般地, 如果一个数 的平方等于 ,即,那么这个数 就叫做 的,记为,读作。例如和是9的平方根,也就是说是9的平方根。
(2).填空:
(1)121的平方根是,121的算术平方根是;
(2)0.36的平方根是,0.36的算术平方根是;
(3)的平方根是8和-8,的算术平方根是8;
(4)的平方根是 和 ,的算术平方根是 .
2、根据上面的计算,思考回答:(1)正数有几个平方根? 他们有什么关系?
(2)0 的平方根是多少?
(3)负数有平方根吗?
3、归纳:
探究三:1、求下列各数中的 值:
① ② ③ ④
2、已知︱a-2︱+ =0,求 的平方根.
3、一个正数 的两个平方根分别是 和 ,求a和x的值。
3、释疑点拨:(3分钟)
1、例:你能说出下列各式表示的意思吗?你能求出它们的值吗?
(1) ;(2) ;(3)
2、 有意义吗? 何时才有意义?为什么?
3、议一议:平方根与算术平方根有什么异同?
2014年春季新版新人教版七年级数学下学期6.1、平方根导学案19

平方根(二) 【第二课时】一、复习:1、求下列各式的值:(1)1 (2)81 (3)94 (4)64492、2的值是多少?二、自学检测1、思考:-4有算术平方根吗?2、要使代数式23x -有意义,则x 的取值范围是( )A. 2x ≠B. 2x ≥C. 2x >D. 2x ≤三、巩固训练:非负数a 的算术平方根表示为___,225的算术平方根是____,0的算术平方根是____ 1612181___,____,_____2581==-=16的算术平方根是_____, 0.64-的算术平方根____若x 是49的算术平方根,则x =( )A. 7B. -7C. 49D.-49四、课堂检测1、若47x -=,则x 的算术平方根是( ) A. 49 B. 53 C.7 D 53.2、若()2130x y x y z -+++++=,求,,x y z 的值。
回到引言:宇宙的第一速度U 12=gR 宇宙的第二速度U 22=2gR ,其中g=9.8 R ≈6.4×106,则有U 12≈9.8×6.4×106≈6.272×107 U 22≈9.8×2×6.4×106≈1.2544×108因为U 1 U 2是6.272×107与1.2544×108的平方根,所以U 1=37109.710272.6⨯±≈⨯±U 2=481012.1102544.1⨯±≈⨯± 因为U 1>0 ,U 2>0 ∴U 1≈7.9×103 U 2≈1.2×104五、拓展探究1、已知21a -的算术平方根是3,31a b +-的算术平方根是4,c 是13的整数部分,求2a b c +-的算术平方根2、若a 是30的整数部分,b 是30的小数部分,试确定a 、b 的值。
2014年春季新版新人教版七年级数学下学期6.1、平方根导学案1

6.1 平方根第1课时 平方根(1)学前温故1.计算:(1)12=____,(-1)2=____.(2)⎝ ⎛⎭⎪⎫122=____,⎝ ⎛⎭⎪⎫-122=____. 2.计算:102=____,1002=______,1 0002=______.新课早知1.如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x 叫做a 的__________.a 的算术平方根记为a ,读作“根号a ”,a 叫做__________.规定:0的算术平方根是____.2.3的算术平方根是________.3.无限不循环小数是指小数位数______,且小数部分________的小数.4.如果被开方数的小数点向左(或向右)移动2位,它的算术平方根的小数点就相应地向左(或向右)移动______.5.举出一例无限不循环小数:__________.答案:学前温故1.(1)1 1 (2)14 142.100 10 000 1 000 000新课早知1.算术平方根 被开方数 0 2. 33.无限 不循环4.1位 5.3,5,7等.1.求一个数的算术平方根【例1】 求下列各数的算术平方根:(1)0.64; (2)4936; (3)81; (4)(-3)2. 分析:按照算术平方根的定义,只要找到一些正数的平方分别等于上面的几个数,那么这几个正数分别就是上面几个数的算术平方根.解:(1)因为0.82=0.64,所以0.64的算术平方根是0.8,即0.64=0.8; (2)因为⎝ ⎛⎭⎪⎫762=4936,所以4936的算术平方根是76, 即4936=76; (3)因为92=81,所以81的算术平方根是9,即81=9;(4)因为(-3)2=9,而32=9,因此32=(-3)2,所以(-3)2的算术平方根是3,即(-3)2=3.2.运用估算的数学方法确定一个数的整数部分与小数部分 【例2】 已知m 是15的整数部分,n 是15的小数部分,求8m -n 的值. 分析:解题的关键是求出m 和n .解:∵9<15<16,即3<15<4,∴15的整数部分m =3,15的小数部分n =15-3.∴8m -n =8×3-(15-3)=24-15+3=27-15.1.9的算术平方根是( ).A .3B .-3C .81D .-812.下列说法正确的是( ).A .5是25的算术平方根B .±4是16的算术平方根C .-6是(-6)2的算术平方根D .0.01是0.1的算术平方根3.估计20的算术平方根的大小在( ).A .2与3之间B .3与4之间C .4与5之间D .5与6之间4.5的算术平方根是________.5.用两张边长为5 cm 的正方形纸片重新剪开并拼接成一个较大的正方形,其边长约为__________.(精确到0.01 cm )6.求下列各数的算术平方根:(1)900; (2)196; (3)0; (4)⎝ ⎛⎭⎪⎫-232. 7.求下列各式的值: (1) 1.44; (2)(-0.1)2;(3)0.81-0.04; (4)1214. 答案:1.A2.A 因为52=25,所以A 正确;因为一个正数的算术平方根是一个正数,所以B ,C错误;因为0.012=0.000 1≠0.1,所以D 错误.3.C4. 55.7.07 cm 较大正方形的面积为2×52=50, 故其边长为50≈7.07(cm ).6.解:(1)∵302=900,故900的算术平方根是30, 即900=30;(2)∵142=196,故196的算术平方根是14,即196=14;(3)∵02=0,故0的算术平方根是0,即0=0;(4)∵⎝ ⎛⎭⎪⎫-232=⎝ ⎛⎭⎪⎫232, 故⎝ ⎛⎭⎪⎫-232的算术平方根是23,即⎝ ⎛⎭⎪⎫-232=23. 7.解:(1) 1.44=1.2;(2)(-0.1)2=0.01=0.1;(3)0.81-0.04=0.9-0.2=0.7;(4)1214=494=72.。
数学七年级下册第六章第1课时《算术平方根》导学案

6.1(1)算术平方根学习目标:1、掌握算术平方根的概念及意义;2、能够用算术平方根的概念求一些特殊的非负数的算术平方根。
学习重点:算术平方根的概念会求非负数的算术平方根。
学习难点:利用平方和开平方互为逆运算的关系求一个非负数的算术平方根,并明白负数为什么没有算术平方根。
学习过程:一、学习准备:1、口算下列各题:①求1~20的整数的平方。
2、课前预习P40~P41,并完成下列问题:①小欧想裁出一个面积是25dm ²的正方形布块,它的边长应该是多少?为什么? ②完成下列表格:二、解读教材:1、完成填空:①( )²=1;②( )²=4;③( )²=0;④( )²=0.04;⑤( )²=121;⑥( )²=3649。
【括号内填非负数】 2、上面式子的共同特点:都是知道一个数的平方的结果,求 。
3、如果一个数x 的 等于a ,即 ,那么这个 叫做a 的 。
概念对应:例如:5²=25,∴ 是 的算术平方根; 仿上边的例子再举一例:4、算术平方根的表示方法:a 的算术平方根记作: ,读作: ,其中的a 叫作 数。
即兴对位,例:25的算术平方根记作: ,读作: ;8的算术平方根记作: ,读作: ;反过来:169表示的意义是 ,它的值是 。
为什么? 规定:0的算术平方根是 。
5、思考:负数有算术平方根吗?为啥?三、挖掘教材:1、说出下列式子的意义:3: ;-3: 。
2、如何求(-4)²的算术平方根?3、猜想:20这个数介于哪两个整数之间?4、4的算术平方根是: 。
四、例题解析:1、求下列各数的算术平方根:①100; ②6449; ③0.0001; ④(-3)4;注意:解题格式2、求下列各式的值: ①23-)(; ②432; ③0.0001的算术平方根;④猜想42的值及意义;五、达标练习: 1、填空:①( )²=64;②( )²=121;③( )²=256169; 2、求下列各数的算术平方根:①64; ②169; ③256169; ④0.0025; ⑤3²; ⑥13、求下列各式的值: ①259; ②-22; ③25-)(4、比较下列各数的大小:1,3,2,0.01,-5。
【最新文档】新人教版七年级数学下册《6.1平方根》导学案-word范文 (2页)

【最新文档】新人教版七年级数学下册《6.1平方根》导学案-word范文本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!
== 本文为word格式,下载后可方便编辑和修改! ==
新人教版七年级数学下册《6.1平方根》导学案
【学前准备】
1.81的算术平方根是.
2.平方得81的数有几个?分别是什么?它们有什么关系?
【导入】
【自主学习,合作交流】
任务一:探究平方根
1.阅读课本40例1之上的内容,完成下列问题
1)什么是平方根?并举例说明
2)什么是开平方运算?开平方运算与平方运算是什么关系?
3)16的平方根是,16的算术平方根是
平方根与算术平方根的联系与区别是什么?
任务二:阅读40页例4内容完成下列问题
1.仿例完成
1)0.042)3)144
2.平方根具有什么性质(完成46页归纳)
3.平方根如何表示?
4.仿例5完成
【当堂测试】
1.判断下列说法是否正确:。
2014年春季新版新人教版七年级数学下学期6.1、平方根导学案8

课题:算术平方根的应用自研课(时段:晚自习时间:10分钟)
1、旧知链接:求下列各数的算术平方根:(1)9 (2)0 (3
(4
2、新知自研:自研教材P41-P44的内容,完成课本43页探究的表格。
3、教具准备:制作两个面积为1的正方形。
展示课(时段:正课时间:60分钟)
【学习主题】1.
2.理解正数a、b
训练课(时段:晚自习 , 时间:20分钟)
“日日清巩固达标训练题”
自评: 师评: 基础题:
1.
)
A 、1和2
B 、2和3
C 、3和4
D 、4和5 2. 的值( )
A 、在
1~2之间
B 、在2~3之间
C 、在3~4之间
D 、在4~5之间
3.
1.3110.1311≈≈,则x=
4.
,小数部分是 。
5.
0.79 。
6.的值在整数 与整数 之间。
发展题:
7.
设x 、y ,试表示出
x 、y 的值。
提高题:
8.先阅读,再回答问题:
1
,
2
3。
依
n 为正整数)的整数部分为多少,并说明理由。
培辅课(时段:大自习附培辅单)
1、今晚你需要培辅吗?(需要,不需要)
2、效果描述:
反思课
1、病题诊所:
2、精题入库:
【教师寄语】新课堂,我展示,我快乐,我成功………今天你展示了吗!!!。
人教版数学七年级下册第18课时《6.1平方根(第3课时)》教案

人教版数学七年级下册第18课时《6.1平方根(第3课时)》教案一. 教材分析《6.1平方根(第3课时)》是人教版数学七年级下册的一节重要课程。
本节课主要内容是让学生掌握平方根的概念,会求一个数的平方根,以及了解平方根的性质。
通过本节课的学习,学生能够进一步理解平方根的概念,提高解决问题的能力。
二. 学情分析学生在学习本节课之前,已经学习了有理数、实数等基础知识,对数的运算和性质有一定的了解。
但部分学生对平方根的概念和性质可能理解不深,求平方根的方法也需要进一步巩固。
因此,在教学过程中,教师需要关注学生的学习情况,针对性地进行讲解和辅导。
三. 教学目标1.让学生掌握平方根的概念,会求一个数的平方根。
2.使学生了解平方根的性质,能够运用平方根解决实际问题。
3.培养学生的逻辑思维能力,提高学生解决问题的能力。
四. 教学重难点1.平方根的概念和性质。
2.求一个数的平方根的方法。
五. 教学方法1.情境教学法:通过生活中的实例,引导学生理解平方根的概念和性质。
2.互动教学法:教师与学生互动,让学生在探讨中掌握求平方根的方法。
3.练习法:通过大量练习,巩固学生对平方根知识的掌握。
六. 教学准备1.教学课件:制作课件,展示平方根的概念和性质。
2.练习题:准备一些有关平方根的练习题,用于课堂练习和课后作业。
七. 教学过程1.导入(5分钟)教师通过一个生活实例引入本节课的主题,如:“一块正方形的面积是25平方米,求这块正方形的边长。
”让学生思考,引出平方根的概念。
2.呈现(10分钟)教师讲解平方根的概念和性质,让学生了解平方根的定义,以及如何求一个数的平方根。
3.操练(10分钟)教师提出一些有关平方根的问题,让学生独立解答。
如:“求16、25、9的平方根。
”教师巡回指导,帮助学生解决问题。
4.巩固(10分钟)教师学生进行小组讨论,分享求平方根的方法和心得。
然后,全班交流,总结平方根的性质。
5.拓展(10分钟)教师提出一些拓展问题,如:“一个数的平方根有两个,分别是正数和负数。
人教版七年级数学(下册)导学案 6.1 第1课时 算术平方根

第1课时 算术平方根【学习目标】1、理解数的算术平方根的概念,并会用符号表示。
2、理解平方与开平方是互为逆运算。
3、会求一些非负数的算术平方根。
【学习重点和难点】1.学习重点:算术平方根的概念。
2.学习难点:算术平方根的概念。
【学习过程】一、自主探究学校要举行美术作品比赛,小鸥很高兴.他想裁出一块面积为25平方分米的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少分米?(一)说这块正方形画布的边长应取多少分米?你是怎么算出来的?答:因为52=25,所以这个正方形画布的边长应取5分米。
这个实例中的问题、填表中的问题实际上是一个问题,什么问题?它们都是已知正方形面积求边长的问题.通过解决这个问题,我们就有了算术平方根的概念.正数3的平方等于9,我们把正数3叫做9的算术平方根.正数4的平方等于16,我们把正数4叫做16的算术平方根.说说6和36这两个数?说说1和1这两个数?同桌之间互相说一说5和25这两个数.(同桌互相说)说了这么多,同学们大概已经知道了算术平方根的意思.那么什么是算术平方根呢?还是先在小组里讨论讨论,说说自己的看法.(三)什么是算术平方根呢?如果一个正数的平方等于a ,那么这个正数叫做a 的算术平方根请大家把算术平方根概念默读两遍.(生默读)如果一个正数的平方等于a ,那么这个正数叫做a 的算术平方根.为了书写方便,我们把a (板书:a 的.(指准上图)看到没有?这根钓鱼杆似的符号叫做根号,a a 的算术平方根.根号被开方数a二、边学边练1、 求下列各数的算术平方根: (1)4964; (2)0.0001. (要注意解题格式,解题格式要与课本第40页上的相同)精练2、填空:(1)因为_____2=64,所以64的算术平方根是____________;(2)因为_____2=0.25,所以0.25的算术平方根是____________;(3)因为_____2=1649,所以1649的算术平方根是____________. 3、求下列各式的值:=______;=______;______;______;=______;______. 4、根据112=121,122=144,132=169,142=196,152=225,162=256,172=289,182=324,192=361,填空并记住下列各式:=_______,=_______,_______,=_______,_______,_______,_______,_______,_______.(学生记住没有,教师可以利用卡片进行检查,并要求学生课后记熟)5、辨析题:卓玛认为,因为(-4)2=16,所以16的算术平方根是-4.你认为卓玛的看法对吗?为什么?三、我的感悟这节课我的最大收获是: 我不能解决的问题是:四、课后反思。
人教版数学七年级下册---导学案-6.1平方根(第2课时)

6.1平方根(第2课时)【学习目标】1.利用算术平方根的意义,掌握比较两数大小的方法,提高计算能力和应用能力。
2.通过交流,讨论与探索等过程,学会应用算术平方根解决问题。
3.激情投入,培养严谨的数学思维习惯。
【学习重点】理解算术平方根的意义,能运用算术平方根解决一些简单的应用题。
【学习难点】运用算术平方根解决一些简单的应用题。
【知识链接】1.a怎么读?2.若a有意义,则a的取值范围是什么?3.求下列各数的算术平方根:(1)625;(2)0.008;(3)6;(4)0【自习】阅读教材P41-----441.剪一剪,拼一拼,怎样把两个面积为1的小正方形通过剪、拼,从而得到一个面积为2的大正方形?大正方形的边长是多少?2.无限不循环小数是指小数位数,且小数部分的小数3.通过对2的探究,你能总结出估计一个带根号的无限不循环小数的大小的方法吗?4.阅读教材中的“探究”,思考并进行分析探究,你能发现什么规律?5.7的整数部分是,小数部分是。
6.13在整数_____和______之间。
7.比较大小:3____2【自疑】等级: 组长签字:【自探】活动一:问题1: 1,2,25,4,9,16的算术平方根分别是多少?问题2: 1,2,25,4,9,16的算术平方根的大小与被开方数的大小有什么关系?问题3: 12=1,22=4,由此可确定2与1, 2有何关系?问题4: 试确定2与1.4, 1.5的大小关系。
问题5: 再逐步细化范围,可得2414.1=1.999396,2415.1=2.2002225, 由此判定:2的范围是什么?问题6:如此进行下去,可以得到更精确的2的近似值,2是怎样的数?活动二:试比较下列各数的大小; (1)4与15(2)27与6.【自测】1.下列四个数中,比0小的数是( )A . 32 B.-3 C. D.1 2..估计30的值( )A.在3到4之间。
B.在4到5之间。
C.在5到6之间。
D.在6到7之间。
七年级数学下册 6.1 平方根与算术平方根导学案(新版)新人教版

1. 实数在数轴上的位置如图,那么化简 的结果是()
A. B. C. D.
7.已知 ,你能求出x,y的值吗?
8. ,你能求出 的值吗?
升研
(10min)
《平方根与算术平方根》小测验
1 .判断正误
(1)5是25的算术平方根.()(2)4是2的算术平方根.()
(3)6是 的算术平方根.()(4) 是 的算术平方根.()
0的平方根是________;0的算术平方根是______;
-1.5是______的平方根。
3. =_______( 表示144的________);
- =_______(- 表示144的_______);
± =________(± 表示144的_______)。
(二)基础练习
求下列各数的平方根:
64:_______; :_______;0.36:_______;324:_______。
(5) 是 的一个平方根.()(6)81的平方根是9.()
2.填空题
(1)如果一个数的平方等于a,这个数就叫做.
(2)一个正数的平方根有个,它们互为.
(3)0的平方根是,0的算术平方根是.
(4)一个数的平 方为 ,这个数为 .
(5)若a= ,则a2=;若 =0,则a=.若 =9,则a=.
(6)一个数x的平方根为 ,则.
2. =________; =_______;- =_______;
3. 表示10的__________, 表示_________ _________。
4. =________;± =_______; =_______;
=________; (a<0)=_______。
5.五块同样大小的正方形钢板的面积是320m2,求钢板边长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题
班级
【学习目 标】
1.了解平方根的概念,并会用符号表示。2)会求一个数的平方根 。3)理解平方根与算术平方根的区别;了解开方与乘方之间是互为逆运算的关系
2.自主、合作、交流
3.培养学生的分 析能力和归纳能力
【重点】
会利用开方与乘方之间的互逆运算关系,求某些非负数的算术平方根和平方根。
【难点】
掌握求一个数的平方根 的方法,并理解平方根的意义。
【学习过程】
一复习导入:(2分钟)
1)如果一个数的平方等于9,那么这个数是多少?
(2)填表:
1
16
36
49
二、自主学习内容、指导、检测:(15分钟)
探究一、
1、一般地,如果一个数 的平方等于 ,即 ,那么这个数 就叫做 的,记为,读作。例如和是9的平方根,也就是说是9的平方根。
4、(-3)2的平方根是( ) A.3B.-3C.±3D.±9
5、求下列各式中x的值:
(1)169x2=100(2)x2-3=0
6、若 +2 =b+2,求 、 的值;
五、课堂小结:(2分钟)
平方根的概念和简单计算
6、课后巩固:(3分钟)
课后3题、4题
7、学习反思
学法指导
复习提问,巩固所学知识
学生阅读教材,自主完成本内容
3、议一议:平方根与算术平方根有什么异同?
4、训练提升:(20分钟)
1、判断下列说法是否正确
(1)5是25的算术平方根()(2) 是 的一个平方根()
(3) 的平方根是-4()(4) 0的平方根与算术平方根都是0()
2、 的平方根是; 的平方根是,算术平方根是; =; ; =;
3、若 ,则 , 的平方根是 ;
3、归纳:
探究三:1、求下列各数中的 值:
① ② ③ ④
2、已知︱a-2︱+ =0,求 的平方根.
3、一个正数 的两个平方根分别是 和 ,求a和x的值。
3、释疑点拨:(3分钟)
1、例:你能说出下列各式表示的意思吗?你能求出它们的值吗?
(1) ;(2) ;(3)
2、 有意义吗? 何时才有意义?为什么?
学生独立完成,小组交流、讨论
小组交流、讨论、共同完成,实现生生互助的教学模式
学生总结,互相补充,培养分析归纳能力
【教学反思】
名人名言或名人故事:知之为知之,不知为不知,是知也。
(21的算术平方根是;
(2)0.36的平方根是,0.36的算术平方根是 ;
( 3)的平方根是8和-8,的算术平方根是8;
(4)的平方根是 和 ,的算术平方根是 .
2、根据上面的计算,思考回答:(1)正数有几个平方根?他们有什么关系?
(2)0的平方根是多少?
(3)负数有平方根吗?
2、求一个数 的的运算,叫做开平方;与开平方互为逆运算;
探究二、
1、例:求出下列各数的平方根:
(1)100;(2) ;(3)0.25;(4)0; (5)11; (6)
精炼:
(1).填空:
(1)因为()2=49,所以49的平方根是;
(2)因为()2=0,所以0的平方根是;
(3)因为()2=1.96,所以1.96的平方根是;
