广西2018秋九年级数学上册第4章锐角三角函数4.4解直接三角形的应用第1课时作业课件(新版)湘教版
九年级数学上册 第4章 锐角三角函数 4.4 解直角三角形的应用教学课件 (新版)湘教版.pptx

右边的路BD陡些. 如何用数量来刻画哪条路陡呢?
9
二、新课讲解
α
如上图所示,从山坡脚下点 A 上坡走到点B时,
升高的高度h(即线段BC的长度)与水平前进的距
离l(即线段AC 的长度)的比叫作坡度,用字母i表
示,即
i
=
h l
(坡度通常写成1:m的形式).
13
二、新课讲解
分析:这艘船继续向东航行是否安全,取决于灯 塔C到AB航线的距离是否大于30km.如果 大于30km,则安全,否则不安全.
解: 作CD⊥AB,交AB延长线于点D . 设CD=xkm.
在Rt△ACD中, ∵ tanCAD CD , AD
∴
AD
CD tanCAD
x tan30
.
14
二、新课讲解
AC
1,
因此, A,B两点之间的水平距离AC约为2264 m.
6
二、新课讲解
例1 如图所示, 在离上海东方明珠塔底部1 000 m 的
A 处,用仪器测得塔顶的仰角∠BAC 为25°,仪器 距地面高AE 为1.7 m.求上海东方明珠塔的高度BD (结果精确到1 m). 分析:在直角三角形中, 已知一角和它的邻边, 求对边利用该角的正切 即可.
3. 某次军事演习中,有三艘船在同一时刻向指挥所报告: A船说B船在它的正东方向,C船在它的北偏东55°方向; B船说C船在它的北偏西35°方向;C船说它到A船的距离 比它到B船的距离远40km. 求A,B两船的距离(结果精 确到0.1km).
i=1:2
11
二、新课讲解
解: 用 α 表示坡角的大小,由题意可得
tanα
精品学习2018年秋九年级数学上册第4章锐角三角函数4.4解直角三角形的应用教案新版湘教版

4.4 解直角三角形的应用第1课时俯角和仰角问题教学目标【知识与技能】比较熟练地应用解直角三角形的知识解决与仰角、俯角有关的实际问题.【过程与方法】通过学习进一步掌握解直角三角形的方法.【情感态度】培养学生把实际问题转化为数学问题的能力.【教学重点】应用解直角三角形的知识解决与仰角、俯角有关的实际问题.【教学难点】选用恰当的直角三角形,分析解题思路.教学过程一、情景导入,初步认知海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行,你认为货轮继续向东航行途中会有触礁的危险吗?你是如何想的?与同伴进行交流.【教学说明】经历探索船是否有触礁危险的过程,进一步体会三角函数在解决实际问题中的应用.二、思考探究,获取新知1.某探险者某天到达如图所示的点A处,他准备估算出离他的目的地——海拔为3500m 的山峰顶点B处的水平距离.你能帮他想出一个可行的办法吗?分析:如图,BD表示点B的海拔,AE表示点A的海拔,AC⊥BD,垂足为点C.先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可以求出A、B之间的水平距离AC.【归纳结论】当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫作仰角,在水平线下方的角叫作俯角.2.如图,在离上海东方明珠塔底部1000m的A处,用仪器测得塔顶的仰角为25°,仪器距地面高为1.7m.求上海东方明珠塔的高度.(结果精确到1m)解:在Rt△ABC 中,∠BAC =25°,AC =1000m ,因此tan25°=BC AC =BC1000∴BC =1000×tan25°≈466.3(m),∴上海东方明珠塔的高度(约)为466.3+1.7=468米.【教学说明】利用实际问题承载数学问题,提高了学生的学习兴趣.教师要帮助学生学会把实际问题转化为解直角三角形问题,从而解决问题.三、运用新知,深化理解1.如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC =1200米,从飞机上看地平面控制点B 的俯角α=16°31′,求飞机A 到控制点B 的距离.(精确到1米)分析:利用正弦可求. 解:在Rt△ABC 中sin B =AC AB∴AB =ACsin B =12000.2843≈4221(米) 答:飞机A 到控制点B 的距离约为4221米.2.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m.这栋高楼有多高(结果精确到0.1m)?分析:在Rt△ABD 中,α=30°,AD =120.所以可以利用解直角三角形的知识求出BD ;类似地可以求出CD ,进而求出BC .解:如图,α=30°,β=60°,AD =120.∵tan α=BD AD ,tan β=CD AD,∴BD =AD tan α=120×tan30°=120×33=403,CD =AD tan β=120×tan60°=120×3=120 3.∴BD =BD +CD =403+1203=1603≈227.1 答:这栋高楼约高277.1m. 3.如图,在离树BC 12米的A 处,用测角仪测得树顶的仰角是30°,测角仪AD 高为1.5米,求树高BC .(计算结果可保留根号)分析:本题是一个直角梯形的问题,可以通过过点D 作DE ⊥BC 于E ,把求CB 的问题转化求BE 的长,从而可以在△BDE 中利用三角函数.解:过点D 作DE ⊥BC 于E ,则四边形DECA 是矩形,∴DE =AC =12米.CE =AD =1.5米.在直角△BED 中,∠BDE =30°,tan30°=BE DE,∴BE =DE ·tan30°=43米.∴BC =BE +CE =(43+32)米.4.广场上有一个充满氢气的气球P ,被广告条拽着悬在空中,甲乙二人分别站在E 、F 处,他们看气球的仰角分别是30°、45°,E 点与F 点的高度差AB 为1米,水平距离CD 为5米,FD 的高度为0.5米,请问此气球有多高?(结果保留到0.1米)分析:由于气球的高度为PA +AB +FD ,而AB =1米,FD =0.5米,故可设PA =h 米,根据题意,列出关于h 的方程可求解.解:设AP =h 米,∵∠PFB =45°, ∴BF =PB =(h +1)米,∴EA =BF +CD =h +1+5=(h +6)米, 在Rt△PEA 中,PA =AE ·tan30°, ∴h =(h +6)tan30°,∴气球的高度约为PA +AB +FD =8.2+1+0.5=9.7米.【教学说明】巩固所学知识.要求学生学会把实际问题转化成数学问题;根据题意思考题目中的每句话对应图中的哪个角或边,本题已知什么,求什么.四、师生互动、课堂小结先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充. 课后作业布置作业:教材“习题4.4”中第2、4、5题. 教学反思本节课我们学习了有关仰角、俯角的解直角三角形的应用题,对于这些问题,一方面要把它们转化为解直角三角形的数学问题,另一方面,针对转化而来的数学问题应选用适当的数学知识加以解决.第2课时 坡度和方位角问题教学目标【知识与技能】1.了解测量中坡度、坡角的概念;2.掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度、与弧长的有关实际问题.【过程与方法】通过对例题的学习,使学生能够利用所学知识解决实际问题. 【情感态度】进一步培养学生把实际问题转化为数学问题的能力. 【教学重点】能利用解直角三角形的知识,解决与坡度、与弧长有关的实际问题. 【教学难点】能利用解直角三角形的知识,解决与坡度、与弧长的有关实际问题. 教学过程一、情景导入,初步认知如图所示,斜坡AB 和斜坡A 1B 1,哪一个倾斜程度比较大?显然,斜坡A 1B 1的倾斜程度比较大,说明∠A 1>∠A .从图形可以看出,B 1C 1A 1C 1>BCAC,即tan A 1>tan A . 【教学说明】通过实际问题的引入,提高学生学习的兴趣. 二、思考探究,获取新知1.坡度的概念,坡度与坡角的关系.如上图,这是一张水库拦水坝的横断面的设计图,坡面的铅垂高度与水平前进的距离的比叫作坡度(或坡比),记作i ,即i =AC BC,坡度通常用l ∶m 的形式,例如上图中的1∶2的形式.坡面与水平面的夹角叫作坡角,记作α.从三角函数的概念可以知道,坡度与坡角的关系是i =tan B ,显然,坡度越大,坡角越大,坡面就越陡.2.如图,一山坡的坡度为i =1∶2,小刚从山脚A 出发,沿山坡向上走了240米到达点C ,这座山坡的坡角是多少度?小刚上升了多少米?(角度精确到0.01°,长度精确到0.1米)3.如图,一艘船以40km/h 的速度向正东航行,在A 处测得灯塔C 在北偏东60°方向上,继续航行1h 到达B 处,这时测得灯塔C 在北偏东30°方向上,已知在灯塔C 的四周30km 内有暗礁.问这艘船继续向东航行是否安全?【教学说明】教师引导学生分析题目中的已知条件分别代表的是什么,将图形中的信息转化为图形中的已知条件,再分析图形求出问题.学生独立完成.三、运用新知,深化理解1.如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m ,测得斜坡的倾斜角是24°,求斜坡上相邻两树的坡面距离是多少(精确到0.1m).分析:引导学生将实际问题转化为数学问题画出图形.解:已知:在Rt△ABC 中,∠C =90°,AC =5.5,∠A =24°,求AB . 在Rt△ABC 中,cos A =AC AB, ∴AB =ACcos A = 5.50.9135≈6.0(米). 答:斜坡上相邻两树间的坡面距离约是6.0米.2.同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图水库大坝的横断面是梯形,坝顶宽6m ,坝高23m ,斜坡AB 的坡度i =1∶3,斜坡CD 的坡度i =1∶2.5,求斜坡AB 的坡面角α,坝底宽AD 和斜坡AB 的长(精确到0.1m).解:作BE ⊥AD ,CF ⊥AD , 在Rt△ABE 和Rt△CDF 中,BE AE =13,CF FD =12.5∴AE =3BE =3×23=69(m).FD =2.5CF =2.5×23=57.5(m).∴AD =AE +EF +FD =69+6+57.5=132.5(m). 因为斜坡AB 的坡度i =tan α=13≈0.3333,所以α≈18°26′. ∵BE AB=sin α, ∴AB =BEsin α=230.3162≈72.7(m). 答:斜坡AB 的坡角α约为18°26′,坝底宽AD 为132.5米,斜坡AB 的长约为72.7米.3.庞亮和李强相约周六去登山,庞亮从北坡山脚C 处出发,以24米/分钟的速度攀登,同时,李强从南坡山脚B 处出发.如图,已知小山北坡的坡度i =1∶3,山坡长为240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A ?(将山路AB 、AC 看成线段,结果保留根号)解:过点A 作AD ⊥BC 于点D ,在Rt△ADC 中,由i =1∶3得tan C =13=33, ∴∠C =30°.∴AD =12AC =12×240=120(米).在Rt△ABD 中,∠B =45°,∴AB =2AD =1202(米).1202÷(240÷24)=1202÷10=122(米/分钟)答:李强以122米/分钟的速度攀登才能和庞亮同时到达山顶A .4.某公园有一滑梯,横截面如图所示,AB 表示楼梯,BC 表示平台,CD 表示滑道.若点E ,F 均在线段AD 上,四边形BCEF 是矩形,且sin∠BAF =23,BF =3米,BC =1米,CD =6米.求:(1)∠D 的度数;(2)线段AE 的长.解:(1)∵四边形BCEF 是矩形,∴∠BFE =∠CEF =90°,CE =BF ,BC =FE , ∴∠BFA =∠CED =90°, ∵CE =BF ,BF =3米,∴CE =3米,∵CD =6米,∠CED =90°, ∴∠D =30°. (2)∵sin∠BAF =23,∴BF AB =23,∵BF =3米,∴AB =92米, ∴AF =(92)2-32=352米, ∴AE =35+22米.5.日本福岛发生核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海检船,在相关海域进行现场监测与海水采样,针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估.如图,上午9时,海检船位于A 处,观测到某港口城市P 位于海检船的北偏西67.5°方向,海检船以21海里/时的速度向正北方向行驶,下午2时海检船到达B 处,这时观察到城市P 位于海检船的南偏西36.9°方向,求此时海检船所在B 处与城市P 的距离.(参考数据:sin36.9°≈35,tan36.9°≈34,sin67.5°≈1213,tan67.5°≈125)分析:过点P 作PC ⊥AB ,构造直角三角形,设PC =x 海里,用含有x 的式子表示AC ,BC 的值,从而求出x 的值,再根据三角函数值求出BP 的值即可解答.解:过点P 作PC ⊥AB ,垂足为C ,设PC =x 海里.在Rt△APC 中,∵tan A =PC AC, ∴AC =PCtan67.5°=5x 12在Rt△PCB 中,∵tan B =PC BC, ∴BC =xtan36.9°=4x 3∵从上午9时到下午2时要经过五个小时, ∴AC +BC =AB =21×5, ∴5x 12+4x3=21×5, 解得x =60. ∵sin∠B =PCPB, ∴PB =PCsin B =60sin36.9°=60×53=100(海里) ∴海检船所在B 处与城市P 的距离为100海里. 【教学说明】通过练习,巩固本节课所学内容. 四、师生互动、课堂小结先小组内交流收获和感想而后以小组为单位派代表进行总结.教师作以补充. 课后作业布置作业:教材“习题4.1”中第1、6、7题. 教学反思通过本节课的学习,使学生知道坡度、坡角的概念,能利用解直角三角形的知识解决与坡度、坡角有关的实际问题,特别是与梯形有关的实际问题,懂得通过添加辅助线把梯形问题转化为直角三角形来解决.复习与提升教学目标【知识与技能】1.了解锐角三角函数的概念,熟记30°、45°、60°的正弦、余弦和正切的函数值. 2.能够正确地使用计算器,由已知锐角的度数求出它的三角函数值,由已知三角函数值求出相应的锐角的度数.3.会用解直角三角形的有关知识解决简单的实际问题. 【过程与方法】通过锐角三角函数的学习,进一步认识函数,体会函数的变化与对应的思想. 【情感态度】通过解直角三角形的学习,体会数学在解决实际问题中的作用. 【教学重点】会用解直角三角形的有关知识解决简单的实际问题. 【教学难点】会用解直角三角形的有关知识解决简单的实际问题. 教学过程 一、知识结构【教学说明】引导学生回顾本章知识点,使学生系统地了解本章知识及它们之间的关系. 二、释疑解惑,加深理解 1.正弦的概念: 在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦.记作sin α,即: sin α=角α的对边斜边.2.余弦的概念:在直角三角形中,我们把锐角α的邻边与斜边的比叫作角α的余弦.记作cos α.即 cos α=角α的邻边斜边.3.正切的概念: 在直角三角形中,我们把锐角α的对边与邻边的比叫作角α的正切.记作tan α,即: tan α=角α的对边角α的邻边4.特殊角的三角函数值:5.我们把锐角α的正弦、余弦、正切统称为角α的锐角三角函数. 6.解直角三角形的概念:在直角三角形中,利用已知元素求其余未知元素的过程,叫作解直角三角形. 7.仰角、俯角的概念:当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫作仰角,在水平线下方的角叫作俯角.8.坡度的概念:坡面的铅垂线高度与水平前进的距离的比叫作坡度(或坡比);记作i ,坡度通常用l ∶m 的形式;坡面与水平面的夹角叫作坡角,记作α.坡度越大,坡角越大,坡面就越陡.【教学说明】引导学生回忆本章所学的有关概念,知识点.加深学生的印象. 三、运用新知,深化理解1.已知,如图,D 是△ABC 中BC 边的中点,∠BAD =90°,tan B =23,求sin∠DAC .解:过D 作DE ∥AB 交AC 于E , 则∠ADE =∠BAD =90°, 由tan B =23,得AD AB =23,设AD =2k ,AB =3k ,∵D 是△ABC 中BC 边的中点,∴DE =32k∴在Rt△ADE 中,AE =52k ,∴sin∠DAC =DE AE =32k 52k =35.2.计算:tan 230°+cos 230°-sin 245°tan45° 解:原式=(33)2+(32)2-(22)2×1 =13+34-12=7123.如图所示,菱形ABCD 的周长为20cm ,DE ⊥AB ,垂足为E ,sin A =35,则下列结论正确的个数为( )①DE =3cm ;②BE =1cm ;③菱形的面积为15cm 2;④BD =210 cm.A .1个B .2个C .3个D .4个分析:由菱形的周长为20cm 知菱形边长是5cm.在Rt△ADE 中,∵AD =5cm ,sin A =35, ∴DE =AD ·sin A =5×35=3(cm). ∴AE =AD 2-DE 2=4(cm).∴BE =AB -AE =5-4=1(cm).菱形的面积为AB ·DE =5×3=15(cm 2).在Rt△DEB 中,BD =DE 2+BE 2=32+12=10(cm).综上所述①②③正确.【答案】C4.如图所示,一艘轮船位于灯塔P 的北偏东60°方向,与灯塔P 的距离为80海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处,求此时轮船所在的B 处与灯塔P 的距离(结果保留根号).分析:由题意知,在△ABP 中∠A =60°,∠B =45°,∠APB =75°联想到两个三角板拼成的三角形.因此很自然作PC ⊥AB 交AB 于C .解:过点P 作PC ⊥AB ,垂足为C ,则∠APC =30°,∠BPC =45°,AP =80,在Rt△APC 中,cos∠APC =PC PA. ∴PC =PA ·cos∠APC =403, 在Rt△PCB 中,cos∠BPC =PC PB , ∴PB =PCcos∠BPC =403cos45°=40 6 ∴当轮船位于灯塔P 南偏东45°方向时,轮船与灯塔P 的距离是406海里.【教学说明】通过上面的解题分析,再对整个学习过程进行总结,能够促进理解,提高认知水平,从而促进数学观点的形成和发展.四、复习训练,巩固提高1.如图,△ABC 是等边三角形,P 是∠ABC 的平分线BD 上一点,PE ⊥AB 于点E ,线段BP 的垂直平分线交BC 于点F ,垂足为点Q .若BF =2,则PE 的长为( )A .2B .2 3C .3 3D .3分析:∵△ABC 是等边三角形,点P 是∠ABC 的平分线上一点,∴∠EBP =∠QBF =30°,∵BF =2,FQ ⊥BP ,∴BQ =BF ·cos30°=2×32= 3. ∵FQ 是BP 的垂直平分线,∴BP =2BQ =2 3.在Rt△BEP 中,∵∠EBP =30°,∴PE =12BP = 3. 【答案】C2.如图,为了测量某山AB 的高度,小明先在山脚下C 点测得山顶A 的仰角为45°,然后沿坡角为30°的斜坡走100米到达D 点,在D 点测得山顶A 的仰角为30°,求山AB 的高度.(参考数据:3≈1.73)解:过D 作DE ⊥BC 于E ,作DF ⊥AB 于F ,设AB =x ,在Rt△DEC 中,∠DCE =30°,CD =100,∴DE =20,CE =50 3.在Rt△ABC 中,∠ACB =45°,∴BC =x .则AF =AB -BF =AB -DE =x -50,DF =BE =BC +CE =x +50 3.在Rt△AFD 中,∠ADF =30°,tan30°=AFFD ,∴x -50x +503=33. ∴x =50(3+3)≈236.6.答:山AB 的高度约为236.6米.3.如图,小红同学用仪器测量一棵大树AB 的高度,在C 处测得∠ADG =30°,在E 处测得∠AFG =60°,CE =8米,仪器高度CD =1.5米,求这棵树AB 的高度(结果保留两位有效数字,3≈1.732).解:根据题意得:四边形DCEF 、DCBG 是矩形,∴GB =EF =CD =1.5米,DF =CE =8米.设AG =x 米,GF =y 米,在Rt△AFG 中,tan∠AFG =tan60°=AG FG =x y =3,在Rt△ADG 中,tan∠ADG =tan30°=AG DG =x y +8=33, 二者联立,解得x =43,y =4.∴AG =43米,FG =4米.∴AB =AG +GB =43+1.5≈8.4(米).∴这棵树AB 的高度约为8.4米.五、师生互动,课堂小结师生共同总结,对于本章的知识.你掌握了多少?还存在哪些疑惑?同学之间可以相互交流.课后作业布置作业:教材“复习题4”中第1、3、6、8、12、14题.教学反思根据学生掌握的情况,对掌握不够好的知识点、题型多加练习、讲解.力争更多的学生学好本章内容.。
湘教版九年级数学XJ版上册精品教学课件 第4章 锐角三角函数 解直角三角形的应用(1)

3.国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对 钓鱼岛进行常态化立体巡航,如图①.在一次巡航过程中,巡 航飞机飞行高度为2001米,在点A测得高华峰顶点F的俯角为 30°,保持方向不变前进1200米到达B点后测得F点俯角为 45°,如图②.请据此计算钓鱼岛的最高海拔高度为多少 米.(结果保留整数,参考数值:≈1.732,≈1.414)
课堂小结
利用仰俯角解 直角三角形
仰角、俯角的概念
运用解直角三角形解决 仰角、俯角问题
解:设PD=x米,∵PD⊥AB,∴∠ADP=∠BDP=90°,
x
在Rt△PAD中,tan∠PAD= AD ,∴AD= 在∴又RD∵tB△A=BP=taBnD82x0中6..05,米°≈t,0a.xn5∴∠0=P542BxDx.+=2Dxx=B 8,0.0,
tan3x8.5°≈0.x80=54x,
解得x≈24.6,即PD≈24.6米,∴DB=2x=49.2米.
自学互研
知识模块一 建立直角三角形模型
一棵大树在一次强台风中于高地面5m处折断倒下,倒下 部分与地面成30°夹角,这棵大树在折断前的高度为多少?
解:设大树的根部为点A,折断处为点B,
倒下后树梢与地面接触处为点C.
则在△ABC中有∠A=90°,
∠C=30°,AB=5m,
∵sinC=
AB BC
∴BC= AB
AC 1000
从而,BC=1000×tan25°≈466.3(m)
BD=466.3+1.7=468(m).
答:上海东方明珠塔的高度BD 为468m.
A 25° E
B C
CHale Waihona Puke D范例如图,在离树BC 12米的A处,用测角仪测得树顶的仰角 是30°,测角仪AD高为1.5米,求树高BC.(计算结果可保留根 号)
九年级数学上九年级数学上第4章锐角三角函数4.4解直角三角形的应用目标一坡角的应用课湘教

3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022年3月11日星期五12时42分34秒12:42:3411 March 2022 4、享受阅读快乐,提高生活质量。下午12时42分34秒下午12时42分12:42:3422.3.11
Байду номын сангаас
解:在 Rt△ABC 中,∵cos α=AACB,∴AC=AB·cos α, 当 α=50°时,AC=AB·cos α≈6×0.64=3.84(m), 当 α=75°时,AC=AB·cos α≈6×0.26=1.56(m). 即要想使人安全地攀上斜靠在墙面上的梯子的顶端, 梯子底端与墙面的距离应该在 1.56 m~3.84 m 之间, 故当梯子底端离墙面 2 m 时,此时人能够安全使用这 架梯子.
6 【2020·湘潭】为了学生的安全,某校决定把一段如 图所示的步梯路段进行改造.已知四边形 ABCD 为 矩形,DE=10 m,其坡度为 i1=1: 3,将步梯 DE 改造为斜坡 AF,其坡度为 i2=1:4,则斜坡 AF 的 长是_2_0_._6_2_m__.(结果精确到 0.01 m, 参考数据: 3≈1.732, 17≈4.123)
4 【2020·自贡】如图,我市在建高铁的某段路基横 断面为梯形ABCD,DC∥AB,BC长6米,坡角β为 45°,AD的坡角α为30°,则AD长为__6___2___米 (结果保留根号).
5 【2020·泰安】如图,某校教学楼后面紧邻着一个山坡,坡 上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26 m, 斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学 校决定对该斜坡进行改造.经地质人员勘测,当坡角不超 过50°时,可确保山体不滑坡.如果改造时保持坡脚A不 动,则坡顶B沿BC至少向右移___1_0____m时, 才能确保山体不滑坡.(取tan 50°≈1.2)
九年级数学上册 第4章 锐角三角函数 4.4 解直角三角形的应用教学课件上册数学课件

二、新课讲解
分析:这艘船继续向东航行是否安全,取决于灯 塔C到AB航线的距离是否大于30km.如果 大于30km,则安全,否则不安全.
解: 作CD⊥AB,交AB延长线于点D . 设CD=xkm. 在Rt△ACD中, ∵ tanCADCD, AD ∴ ADtan CD CADtan x30.
12/11/2021
二、新课讲解
解:∵ BD = 3500 m, AE = 1600 m,
AC⊥BD, ∠BAC = 40°,
在Rt△ABC中,
tanBAC= BC= BD- AE=tan44000° AC AC
33550000--1166000000.8833991,即AC222266( 44(mm))
12/11/2021
二、新课讲解
如右图所示,BD表示点B的海拔, AE 表示点A 的海拔,AC⊥BD,垂足为 点C. 先测量出海拔AE,再测出仰角 ∠BAC,然后用锐角三角函数的知识就 可求出A,B两点之间的水平距离AC.
12/11/2021
二、新课讲解
如 图 , 如 果 测 得 点 A 的 海 拔 AE 为 1600m,仰角 ΒAC 40 ,求出A,B两点 之间的水平距离AC(结果保留整数).
示,即
i=
h l
(坡度通常写成1:m的形式).
在上图中,∠BAC 叫作坡角(即山坡与地平面的 夹角),记作 α ,显然,坡度等于坡角的正切,即
i = h = tanα. l
坡度越大,山坡越陡.
12/11/2021
二、新课讲解
例2 如图,一山坡的坡度为i=1:2.小刚从山脚A出发, 沿山坡向上走了240m到达点C.这座山坡的坡角是多 少度?小刚上升了多少米?(角度精确到0.01°,长 度精确到0.1m)
2018年秋九年级数学上册第4章锐角三角函数4.3解直角三角形教案1(新版)湘教版

4. 3解直角三角形教学目标【知识与技能】使学生理解直角三 角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角 互余及锐角三角函数解直角三角形.【过程与方法】通过综合运用勾股定理, 直角三角形的两个锐角互余及锐角三角函数解直角三角形, 步培养学生分析问题、解决问题的 能力.【情感态度】渗透数形结合的数学思想,培养学生良好的学习习惯. 【教学重点】直角三角形的解法.【教学难点】 三角函数在解直角三角形中的灵活运用.教学过程一、 情景导入,初步认知1. 什么是锐角三角函数?2. 你知道哪些特殊的锐角三角函数值?【教学说明】通过复习,使学生便于应用.二、 思考探究,获取新知1.在三角形中共有几个元素?2•直角三角形 ABC 中,/ C = 90°, 呢? (1)边、角之间的关系:. / A 的对边Sin A = ^边"/ A 的对边tan A =/ A 的邻边 (2)三边之间的关系: a 2+ b 2= c 2(勾股定理) ⑶锐角之间的关系: / A +/ B = 90°.吗? 6. 如图,在 Rt △ ABC 中,/ C = 90°,/ A = 30°, a = 5.求/ B b 、c .a 、b 、c 、/ A 、/ B 这五个元素间有哪些等量关系cos A = / A 的邻边斜边3•做一做:在直角三角形 ABC 中, 吗?4.做一做:在直角三角形 ABC 中, 元素吗? 5.想一想:在直角三角形 ABC 中,已知两边,你能求出这个直角三角形中其他的元素 已知一角一边,你能求出这个直角三角形中其他的 已知两角,你能求出这个直角三角形中其他的元素4 2解:•••/ B = 90°—/ A = 60°,口 b又 T tan B = -, ab = a • tan B = 5 • tan60 ° = 5・-J3.•' sin A=- c二 c = SiKA = sin30 ° = 10.【归纳结论】像这样,在直角三角形中,利用已知元素求其余未知元素的过程,叫作解 直角三角形.7•在解直角三角形中,两个已知元素中至少有一条边.【教学说明】我们已掌握 Rt △ ABC 勺边角关系、三边关系、角角关系,利用这些关系, 在知道其中的两个元素(至少有一个是边)后,就可求出其余的元素.这样的导语既 可以使 学生大概了解解直角三角形的概念,同时又陷入思考,为什么两个已知元素中必有一条边呢?激发了学生的学习热情.三、运用新知,深化理解 1.见教材P122例2.2•已知在厶ABC 中,/ C 为直角,/ A 、/ B 、/ C 所对的边分别为 a 、b 、c , c = 8 3, / A = 60°,求/ B 、a 、b .解:a = c sin60 ° = 8 3X = 12,1b =c cos60°= 8 3X ^ = 4,/ B = 30°.3•已知在厶ABC 中,/ C 为直角,/ A 、/ B 、/ C 所对的边分别为 a 、b 、c , a = 3 6, / A = 30°,求/ B 、b 、c .解:/ B = 90°— 30°= 60°,b = a tan B = 3:::” 3 = 9 2,c = a 2 + b 2= , (3 ..,6) 2+( 9 2) 2=54+ 162 = 216= 6 6.(另解:由于 c = sin A ,所以 sn~A =。
2018年秋九年级数学上册第4章锐角三角函数4.4解直角三角形的应用4.4.1仰角、俯角
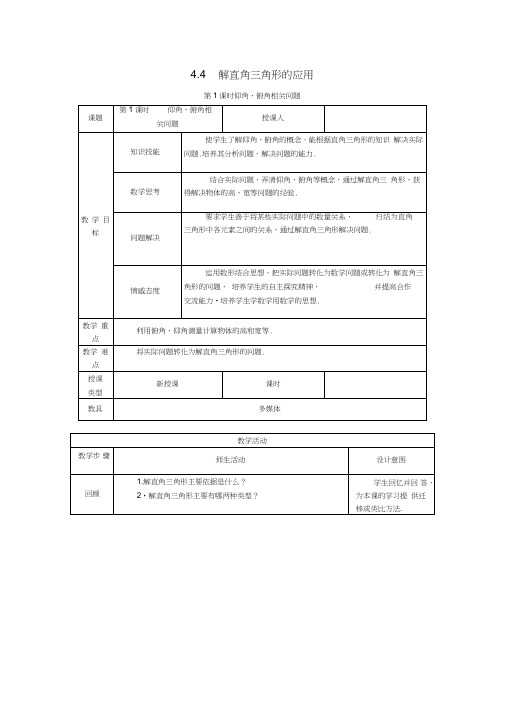
4.4 解直角三角形的应用第1课时仰角、俯角相关问题活动- ' .创设情境导入新课【课堂引入】1.肖颖的教室在教学楼的二楼,一天,他站在教室的窗台前看操场上的旗杆,心想:站在地面上可以利用解直角三角形求得旗杆的高吗?他望着旗杆顶端和旗杆底部,测得视线与水平视线之间的夹角各一个,但是,这两个角怎样命名区别呢?如图4—4 —15,/ CAE / DAE在测量中分别叫什么角呢?图4 —4 —15[答案:仰角和俯角]【探究1】(多媒体出示)1.[嘉兴中考]如图4—4—16,在地面上的点A处测得树顶B的仰角为a , AC= 7米,则树高BC为_7tan a_米.图4—4—16活动实践探究交流新知【探究2】(多媒体出示)2.—棵树AC在地面上的影子BC为10米,如图4 —4 —17①,在树影一端B测得树顶A的仰角为45 °,则树高是多少米?如图②,若一只小鸟从树顶A看树影BC的顶端B的俯角为60 °,则树高是多少米?(精确到1米)[答案:10米17米]图4—4 —17【活动总结】(1)弄清题中仰角和俯角的概念,然后根据题意画出图形,建立数学模型.(2)将实际问题中的数量关系转化为解直角三角形中各元素之间的关系,当有些图形不是直角三角形时,可适当添加辅助线,把它们分割成直角三角形或矩形.鼓励学生独立解决问题,让学生先讨论,教师再给出答案,目的是让学生对仰角、俯角有比较清楚的认识•1.探究1直接根据仰角的意义,求树高.2 •本活动的设计意在引导学生通过自主探究,合作交流,使其对具体问题的认识从形象到抽象,训练学生能从实际问题中抽象出数学知识.旨在培养学生发现问题的意识;提高学生的抽象思维能力,同时也为后续解直角三角形的应用奠定基础.3 .归纳总结主要是把解直角三角形的应用条理化,是知识的一次升华,培养学生的概括能力,突出教学重点.(3)解非直角三角形常见的添辅助线的方法:①通过作 高构造直角三角形;②利用图形本身的性质, 如等腰三角形 顶角平分线垂直于底边构造直角三角形.【应用举例】例1[襄阳中考]如图4— 4— 18,在建筑平台的顶部C 处,测得大树 AB 的顶部A 的仰角为45 °,测得大树 AB 的底部B 的俯角为30°,已知平台的高度 CD 为5 m 则大 树的高度为_(5 + 5_护)_ m 结果保留根号).[解析] 如图4— 4— 19,作CEL AB 于点E ,则/ACE =45°,/ BCE= 30°, BE = CD= 5 m 先在 Rt ^ BCE 中求出 CE 的长,再在 Rt △ ACE 中求出AE 的长.活动开放 训练 体现 应用认真审题是解题的 关键,通过运用一元 一次方程的概念,学 会解决简单的问 题.采取启发式教学 发挥学生的潜能•变式 如图4一 4一 20,线段AB, CD 分别表示甲、乙两 幢楼,AB 丄BD, CD L BD,从甲楼顶 A 测乙楼顶C 的仰角a =30°,已知甲楼高15米,两楼水平距离为24米,求乙楼 的高•[答案:(8』3+ 15)米]【拓展提升】例2如图4— 4— 21,为了测量顶部不能达到的建筑物 AB 的高度,在地平面上取一点 C,用测量仪测得 A 点的仰角 为45°,再向远处走20米取一点D,使点D 在BC 的延长线 上,此时测得A 的仰角为30°,已知测量仪的高为 1.5米, 求建筑物AB 的高度.例3主要是利用俯角构建直角 三角形和一次方程, 从而求水下深度.B图4— 4hB D 图 4— 4图 4— 4— 20图4—4 —21[答案:(10 . 3+ 11.5)米]例3 [河南中考]在中俄"海上联合——2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A 正上方1000米的反潜直升机B测得潜艇C的俯角为68° .试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数.参考数据:sin68°~ 0.9 ,cos68°~2.5 , . 3^ 1.7)图4—4 —22[答案:潜艇C离开海平面的下潜深度约为308米]活动四:课堂总结反思【当堂训练】1. 教材P126练习中的T1, T2.2. 教材P129习题4.4中的T3, T4, T5.当堂检测,及时反馈学习效果.【知识网络】提纲挈领,重点突出._______视线解n侑[阳形的城仰侑、硏川£仰仰、帕仰问题】直问燉_「~ 0.4 ,tan68°海平面。
九年级数学上册 第4章 锐角三角函数 4.4 解直角三角形的应用教案 (新版)湘教版

4.4 解直角三角形的应用教学目标1.使学生理解直角三角形的意义;2.使学生能够用直角三角形的三个关系式解直角三角形;3.通过列方程解直角三角形,培养学生运用代数方法解几何问题的能力;4.培养学生运用化归的思想方法将未知的问题转化为已知的问题去解决. 教学重点和难点正确运用直角三角形中的边角关系解直角三角形是重点;选择适当的关系式解直角三角形是难点. 教学过程设计一、直接运用三个关系解直角三角形 1.定义.由直角三角形中已知的边和角,计算出未知的边和角的过程,叫做解直角三角形. 2.解直角三角形依据.图6-32,直角三角形ABC 的六个元素(三条边,三个角),a,b,c 分别为∠A ,∠B ,∠C 所对的边,除直角C 外,其余五个元素之间的关系如下:(1)三边之间的关系:a 2+b 2=c 2(勾股定理) (2)锐角之间的关系: ∠A +∠B =90°. (3)边角之间的关系: sinA =c aA =∠斜边的对边;cosA =c bA =∠斜边的邻边;tanA =baA A =∠∠的邻边的对边;cotA =abA A =∠∠的对边的邻边;这三个关系式中,每个关系式都包含三个元素,知其中两个元素就可以求出第三个元素 .(1)是已知两边求第一边;(2)是已知一锐角求另一角;(3)是已知两边求锐角,已知一边一角求另一边.这些关系式是解直角三角形的依据,已知其中两个元素(至少有一个是边)就可以求出其余的三个未知元素. 3.例题分析.例1 △ABC 中,∠C 为直角,∠A ,∠B ,∠C 所对的边分别为a,b,c,且b =3,∠A =30°,解这个直角三角形.分析:①未知元素是∠B ,a ,c ; ②∠B 最容易求,∠B =90°-∠A ;③由tanA =b a,可以求a ; ④由cosA =ca,可以求c ;解:①∠B =90°-∠A =90°-30°=60°; ②因不tanA =ba , 所以a =b ·tanA =3×tan30°=3333=⨯; ③因为cosA =ca,问:(1)用cotA 是否可以求出a?从而说明要优选关系式. (2)求c 边还可以用什么方法?(答:也可以用勾股定理求得)练习1 在△ABC 中,∠C =90°,c =2,∠B =30°,解这个直角三角形. (答:∠A =60°,a =,b =1.)例2 在△ABC 中,∠C =90°,,求∠A 、∠B 、c 边.分析:此题解法灵活性很强.求c 边可根据求得,也可先用正(余)切求出∠A(或∠B),再用正余弦求得c 边。
