立体几何中有关“角”的几个结论
立体几何应记住的结论

立体几何应记住的结论:
1. 设正三角形边长为a ,则三角形高为
a 2
,外接圆的半径为
a 3
,内接圆的半径为
a 6
,面积为
2
a 4
2. 内接于球内的正方体1111ABC D A B C D -的边长为a ,球的半径为R ,则2R =
即R ,2
=
3. 设正方体的边长为a ,则以正方体顶点为顶点的正四面体的体积为
3
13
a , 三个侧面为
直角三角形,底面为面对角线的正三棱锥的体积为
3
16
a 。
4. 设正四面体的边长为a ,则正四面体的高为
a 3
,外接球的半径为
a 4
,即高与
半径的比为
43
;
5. 设正六边形1
1111A B C D E F A B C D E F -
的边长为
a ,则对角线B D a =,
AD 2a =,外接圆的半径为a ,0
A B D 90∠=;
6. 底面边长为a 的正三棱锥的侧面都是直角三角形,;体积为3
1
6
a
7. 边长为a 3
12
a
正方体的截面的形状:
1. 三角形,.截面可以是等边三角形,等腰三角形,锐角三角形,但不是直角三角形,钝
角三角形,
2. 四边形:截面可以是平形四边形,矩形,菱形,正方形,梯形,等腰梯形,它们至少一
组对边平行,
3. 五边形:截面五边形必须有两组分别平行的边,同时有两个相同的角,截面不可能是正
五边形。
4.六边形:截面五边形必须有两组分别平行的边,同时有两个相同的角,截面可以是正六
边形。
立体几何常考定理的总结(八大定理)
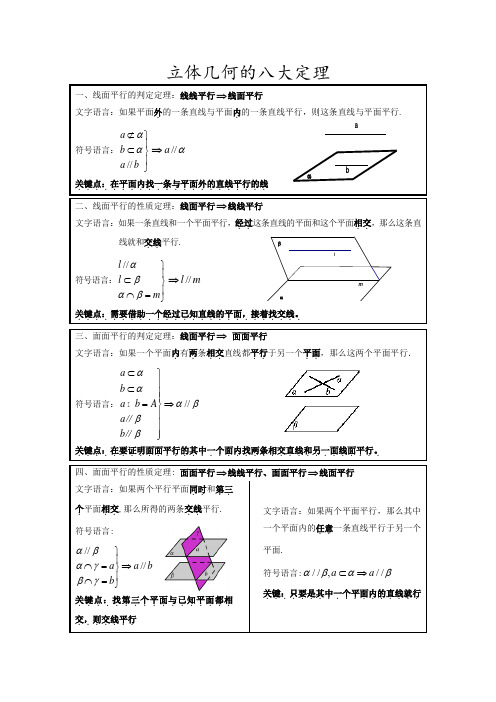
lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点:....在需要证明的两个平面中找线面垂直................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
《立体几何中的向量方法》角的计算

b a
a, b
|
a, b
a
b
结论:
| cos a, b |
|
例一:Rt ABC中,BCA 900 , 现将 ABC沿着平面ABC的法向量
解:以点C为坐标原点建立空间直角坐标
取 平移到A1B1C1位置,已知 BC CA CC1, A1B1、AC1的中 1 取A1B1、AC1的中点D1、F1,求BD1与AF1所成的角的余弦值. 1 z
3. 直三棱柱ABC-A1B1C1中, A1A=2, BAC 900 AB=AC=1, 则AC1与截面BB1CC1所成角的余弦 3 10 值为_________ .
10
三、面面角: 二面角的范围: [0, ]
①方向向量法:
将二面角转化为二面角的两个面的方向向量 (在二面角的面内且垂直于二面角的棱)的 夹角。如图,设二面角 l 的大小为 , 其中 AB l , AB , CD l , CD
空间向量的引入为代数方法处理立体 几何问题提供了一种重要的工具和方法, 解题时,可用定量的计算代替定性的分析, 从而避免了一些繁琐的推理论证。求空间 角与距离是立体几何的一类重要的问题, 也是高考的热点之一。我们主要研究怎么 样用向量的办法解决空间角的问题。
空间的角:
空间的角常见的有:线线角、线面角、面面角。 空间两条异面直线所成的角可转化为两条相 交直线所成的锐角或直角。故我们研究线线角 时,就主要求[0, 2 ]范围内 的角; 斜线与平面所成的角是指斜线与它在面内 的射影所成锐角,再结合与面垂直、平行或在 面内这些特殊情况,线面角的范围也是 [0, ] ;
2
2 2
C
高考数学立体几何中与角有关的四大定理及其证明
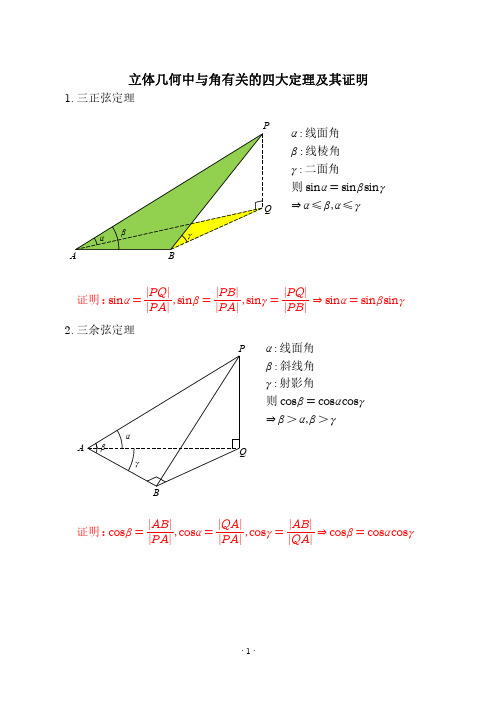
则 cosθ = cos2β + cos2γ - 2cosαcosβcosγ sinα
证明:设 ∠HAC = θ1,∠HAB = θ2 ⇒ α = θ1 + θ2,
由三余弦定理得:
cos β cosγ
= =
cosθ cosθ
cosθ1 cosθ2
① ②
由①和②得 cosθ = cosβ = cosγ ③ cosθ1 cosθ2
α
Aβ
γ
P α : 线面角 β : 斜线角 γ : 射影角 则 cosβ = cosαcosγ ⇒ β > α,β > γ
Q
B
证明:cosβ =
AB PA
,cosα =
QA PA
,cosγ =
AB QA
⇒ cosβ = cosαcosγ
·1·
3. 三夹角公式
P
θ
Aβ
γ
α
C H
B
若 θ 为 PA 与平面 ABC 的夹角
⋅
HO BO
AH AO
⋅
BH BO
= cosθ - cosθ1cosθ2 sinθ1sinθ2
注:若 φ =
π 2
,
则该定理退化为三余弦定理
·3·
立体几何中与角有关的四大定理及其证明
1. 三正弦定理
β α
A
γ
B
P
α : 线面角 β : 线棱角 γ : 二面角 则 sinα = sinβsinγ Q ⇒ α ≤ β,α ≤ γ
证明:sinα =
PQ PA
,sinβ =
PB PA
,sinγ =
PQ PB
⇒ sinα = sinβsinγ
立体几何中的夹角、距离、向量归纳

D BA C α一、空间中各种角包括:异面直线所成的角、直线与平面所成的角以及二面角 1、异面直线所成的角(1)异面直线所成的角的范围是]2,0(π。
(2)求两条异面直线所成的角的大小一般方法是通过平行移动直线,把异面问题转化为共面问题来解决(3)具体步骤如下:①利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选择在特殊的位置上;②证明作出的角即为所求的角; ③利用三角形来求角 2、直线与平面所成的角(1)直线与平面所成的角的范围是]2,0[π。
(2)求直线和平面所成的角用的是射影转化法。
(3)具体步骤如下:①找过斜线上一点与平面垂直的直线;②连结垂足和斜足,得出斜线在平面的射影,确定出所求的角;③把该角置于三角形中计算。
3、二面角(1)二面角的范围在课本中没有给出,一般是指],0(π,解题时要注意图形的位置和题目的要求。
(2)作二面角的平面角常有三种方法图一 图二 图三 ①棱上一点双垂线法:在棱上任取一点,过这点在两个平面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角; 如图一示②面上一点三垂线法:自二面角的一个面上一点向另一面引垂线,再由垂足向棱作垂线得到棱上的点(即垂足),斜足与面上一点连线和斜足与垂足连线所夹的角,即为二面角的平面角; 如图二示③空间一点垂面法:自空间一点作与棱垂直的平面,截二面角得两条射线,这两条射线所成的角就是二面角的平面角 如图三示1、点到直线的距离:点P到直线a 的距离为点P到直线a 的垂线段的长,常先找或作直线a 所在平面的垂线,得垂足为A,过A作a 的垂线,垂足为B连PB,则由三垂线定理可得线段PB即为点P到直线a 的距离。
在直角三角形PAB中求出PB的长即可。
例1、在△ABC 中,AB=2,BC=3,AC=4,求点A 到BC 的距离。
解:作BC AD ⊥,垂足为D ,又 AB=2,BC=3,AC=4, 874322432cos 222222=⨯⨯-+=⋅-+=∴BC AC AB BC AC C815)87(1sin 2=-=∴C41538154321sin 4321=⨯⨯⨯=⨯⨯=∴∆C S ABC AD BC S ABC ⋅=∆21又 2153415322=⨯==∴∆BCS AD ABC∴点A 到BC 的距离为2152、点到平面的距离:点P到平面α的距离为点P到平面α的垂线段的长.常用求法①作出点P到平面的垂线后求出垂线段的长;②转移法,如果平面α的斜线上两点A,B到斜足C的距离AB,AC的比为n m :,则点A,B到平面α的距离之比也为n m :.特别地,AB=AC时,点A,B到平面α的距离相等;③体积法例2、如图,在长方体1111D C B A ABCD -中,,22,2,51===AA BC AB E 在AD 上,且AE=1,F 在AB 上,且AF=3,(1)求点1C 到直线EF 的距离;(2)求点C 到平面EF C 1的距离。
立体几何的八个判定定理

立体几何的八个判定定理立体几何的八个判定定理是指由英国数学家约翰·威尔逊(John Wallis)在17th century所提出的一套定理。
其中包括:(1)贝瑟尔定理:任意一个平面三角形的内角之和等于180度。
(2)杨氏定理:任意一个对角相交的多边形,其内部角之和等于其外部角之和。
(3)特斯克定理:在同样边上的三个面有关的角相加等于180度。
(4)柯尔定理:在同样边上的四个面有关的角相加等于360度。
(5)高斯定理:任意一个多面体的角之和等于360度乘以面的数量。
(6)伯尔定理:任意一个多边形的角之和大于360度。
(7)双旋定理:任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。
(8)欧几里得定理:任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。
贝瑟尔定理是最重要的立体几何判定定理,表明任意一个平面三角形的三个内角之和都等于180度。
这个定理是用来表示平面三角形的构成的,而这个定理也被用来表示一个多边形的构成。
杨氏定理是贝瑟尔定理的推广,即任意一个对角相交的多边形,其内部角之和等于其外部角之和。
特斯克定理是杨氏定理的一个特殊情况,表示在同样边上的三个面有关的角相加等于180度。
柯尔定理也是杨氏定理的一个特殊情况,表示在同样边上的四个面有关的角相加等于360度。
高斯定理是一个重要的立体几何判定定理,即任意一个多面体的角之和等于360度乘以面的数量。
这个定理与贝瑟尔定理的相似之处在于,它们都可以用来表明多面体的构成,它们都表示了一个多面体的性质。
伯尔定理是高斯定理的一个推广,表明任意一个多边形的角之和大于360度。
双旋定理是一个重要的立体几何判定定理,表明任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。
欧几里得定理也是一个重要的立体几何判定定理,表明任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。
总的来说,立体几何的八个判定定理是一个重要的数学工具,它们不仅可以帮助人们更好地理解多面体和多边形的构造,还可以帮助人们解决一些复杂的问题,比如求解三角形的面积,求解多面体的体积等等。
高中数学必修二立体几何角的问题-教师版(含几何法和向量法)

立体几何线线、线面、面面所成角的问题几何法1、两异面直线及所成的角:不在同一个平面的两条直线,叫做异面直线,已知异面直线a,b,经过空间任一点O 作直线a '∥a ,b '∥b ,我们把a '与b '所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).如果两条异面直线所成的角是直角,我们就说这两条直线互相垂直.2、直线和平面所成的角:一条直线PA 和一个平面α相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A 叫做斜足。
过斜线上斜足以外的一点向平面引垂线PO ,过垂足O 和斜足A 的直线 AO 叫做斜线在这个平面上的射影。
平面的一条斜线和它在平面内的摄影所成的锐角,叫做这条直线和这个平面所成的角。
一条直线垂直于平面,我们就说它们所成的角是直角。
一条直线和平面平行,或在平面内,我们说它们所成的角是00.3、二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
在二面角βα--l 的棱l 上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱l 的射线OA 和OB ,则射线OA 和OB 构成的∠AOB 叫做二面角的平面角。
二面角的大小可以可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度。
常见角的取值范围:① 异面直线所成的角⎥⎦⎤ ⎝⎛20π,,直线与平面所成的角⎥⎦⎤⎢⎣⎡20π,,二面角的取值范围依次[]π,0② 直线的倾斜角[)π,0、到的角[)π,0、与的夹角的取值范围依次是⎥⎦⎤⎢⎣⎡20π,4、点到平面距离:求点到平面的距离就是求点到平面的垂线段的长度,其关键在于确定点在平面内的垂足,当然别忘了转化法与等体积法的应用. 向量法1、两异面直线及所成的角:设异面直线a ,b 的夹角为θ,方向向量为a ,b ,其夹角为ϕ,则有cos cos a b a bθϕ⋅==.2、直线和平面所成的角:设直线l 的方向向量为l ,平面α的法向量为n ,l 与α所成的角为θ,l 与n 的夹角为ϕ,则有sin cos l n l nθϕ⋅==.3、二面角:设1n ,2n 是二面角l αβ--的两个面α,β的法向量,则向量1n ,2n 的夹角(或其补角)就是二面角的平面角的大小.若二面角l αβ--的平面角为θ,则1212cos n n n n θ⋅=.4、点到平面距离:点P 是平面α外一点,A 是平面α内的一定点,n 为平面α的一个法向量,则点P 到平面α的距离为cos ,n d n nPA⋅=PA 〈PA 〉=.例题例1.长方体ABCD -A 1B 1C 1D 1中,AB =AA 1=2,AD =1,E 为CC 1的中点,则异面直线BC 1与AE 所成角的余弦值为( )A.1010B.3010C.21510D.31010 解析:建立空间直角坐标系如图.则A (1,0,0),E (0,2,1),B (1,2,0),C 1(0,2,2).BC 1→=(-1,0,2),AE →=(-1,2,1),cos 〈BC 1→,AE →〉=BC 1→·AE →|BC 1→|·|AE →|=3010.所以异面直线BC 1与AE 所成角的余弦值为3010.答案:B例 2.已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E 为BC 的中点.(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角. 证明:在ADE ∆中,222AD AE DE =+,∴AE DE ⊥ ∵PA ⊥平面ABCD ,DE ⊂平面ABCD ,∴PA DE ⊥又PA AE A ⋂=,∴DE ⊥平面PAE (2)DPE ∠为DP 与平面PAE 所成的角在Rt PAD ∆,PD =Rt DCE ∆中,DE =在Rt DEP ∆中,2PD DE =,∴030DPE ∠=例3.如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD . (1)若G 为AD 的中点,求证:BG ⊥平面PAD ; (2)求证:AD PB ⊥;(3)求二面角A BC P --的大小.证明:(1)ABD ∆为等边三角形且G 为AD 的中点,∴BG AD ⊥ 又平面PAD ⊥平面ABCD ,∴BG ⊥平面PAD(2)PAD 是等边三角形且G 为AD 的中点,∴AD PG ⊥ 且AD BG ⊥,PG BG G ⋂=,∴AD ⊥平面PBG ,PB ⊂平面PBG ,∴AD PB ⊥(3)由AD PB ⊥,AD ∥BC ,∴BC PB ⊥ 又BG AD ⊥,AD ∥BC ,∴BG BC ⊥∴PBG ∠为二面角A BC P --的平面角在Rt PBG ∆中,PG BG =,∴045PBG ∠=例4.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一点,且A 1G =λ(0≤λ≤1),则点G 到平面D 1EF 的距离为( D ) A.3 B.22C.32λ D.55练习:1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点,(1)求证:EFGH 是平行四边形;(2)若BD=AC=2,EG=2。
立体几何二面角5种常见解法

立体几何二面角5种常见解法立体几何二面角大小的求法二面角的类型和求法可用框图展现如下:直接在二面角的棱上取一点(特殊点),分别在两个半平面内作 棱的 垂线‘得出平面角,用定义法时‘要认真观察图形的特T 生;例、如图,已知二面角a-a-p 等于120° ,PA 丄a ,A ea,PB 丄例、在四棱锥P-ABCD 中,ABCD 是正方形,PA 丄平面ABCD , 一、定义法: - —面角I可见楼型—不见棱型解法 垂线法 *垂面法积法十P ,Bep.求 z APB 的大"、.PA=AB=a,求二面角B-PC-D的大小二、三垂线定理法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;例、在四棱锥P-ABCD中,ABCD是平行四边形,PA丄平面ABCD,PA=AB=a,z ABC=30°,求二面角P-BC-A 的大小。
例、(2003北京春)如图,ABCD-AiBiCiDi是长方体,侧棱AA】长为1, 底面为正方体且边长为2,E是棱BC的中点,求面GDE与面CDE所成二面角的正切值・DAB例、△ ABC 中,Z A=90°,AB=4,AC=3,平面ABC 外一点P 在平面ABC内的射影是AB中点M,二面角P-AC-B的大小为45°。
求(1 )二面角P—BC—A的大小;(2)二面角C—PB—A的大小例、(2006年陕西试题)如图4,平面丄平面,n =h AG ,BG ,点A在直线I上的射影为Al,点B在I的射影为Bl,已知AB=2 ? AA 1=1,BBi=2,求:二面角Ai —AB — Bi 的大小.A三、垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半 平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的 平面与棱垂直;例、空间的点P 到二面角 I 的面、及棱I 的距离分别为四、射影法:(面积法)利用面积射影公式S 射=$原85 ,其中为平面角的大小,此方法不必在图形中画出平面角;例、在四棱锥P-ABCD 中,ABCD 为正方形,PA 丄平面ABCD ,PA=AB= a ,求平面PBA 与平面PDC 所成二面角的大小。
立体几何中的一个“四角”定理

z, 则〔 )P = x sec a ,RP = x tan a , 〔 p 二 x sec
1一 cost a 一 。 os2# 一 cost Y+ 2cos a cos 床osy 推论 2 设 〔 )A , OB , OC 是不共面的三条射 线, 艺BOC 二 a , 艺C OA = #, 乙AOB = Y, 直线 OA 与平面 BOC 所在的角为 S , 则 1一 cost a 一 cost# 一 cost Y+ 2cosacos#cosY sin&=
ao. 则 二 面 角 M-AB- N 的 取 值 范 围 是 〔 要, 司 . 一 “ . ‘ ”一 一 产 ’ ‘- - - - 一 一 ’” ‘ 一 犷 、 ~ ’ “~ ~ ‘2 ’ 刁 ’
M 所成的角为 S , 利用图 1 , 过点 Q 作平面M 的垂 线 ( 设垂足为 S) , 可知 S 在直线 PR 上, 由此易证 sins = sin角inO ( 4) 联立 ( 1) , (4) 二式 , 消去 e ,t 得
据此, 可获立几中关 于 ( 任意 ) 四面体的一个 优美的体积公式 : 推论3 设四面体立 于一个 顶点处 的三条棱 长分别为 a ,b, 。 且三个面
积公式 为
V =
月 ,RQ = x tan 尽 余弦定理分别用于 △POQ, , L PRQ , 得 PQ2 = (x seca)2+ (x sec 角2 一 2x seca x
coso) , ( 1) 式也成立, 因而当 a E (0 , 二 )、 月 任C o, 1一 。 osea 一 cos2p 一 cost Y+ 2cos a cosgcosY n〕 时, ( 1) 式成立. 事实上, 在如 图 2 所示 的四面体 中, 底面 于是, 对于文首考题, 只需在 ( 1) 式中令 a = 450, Y妻 45。 对任意 RE 【 。 , 司 都成立, 可得 , OBC 上的高 h = a sin民由推论 2 及体积公式 V cosy = cos450coso+ sin450sin床ose 簇 cos450 一 李 , sina . * 立 得 . 0 cos450( 1 一 co确 = co t 4 50t a n
高中数学必修二立体几何角的问题-学生版(含几何法和向量法)

立体几何线线、线面、面面所成角的问题几何法1、两异面直线及所成的角:不在同一个平面的两条直线,叫做异面直线,已知异面直线a,b,经过空间任一点O 作直线a '∥a ,b '∥b ,我们把a '与b '所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).如果两条异面直线所成的角是直角,我们就说这两条直线互相垂直.2、直线和平面所成的角:一条直线PA 和一个平面α相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A 叫做斜足。
过斜线上斜足以外的一点向平面引垂线PO ,过垂足O 和斜足A 的直线 AO 叫做斜线在这个平面上的射影。
平面的一条斜线和它在平面内的摄影所成的锐角,叫做这条直线和这个平面所成的角。
一条直线垂直于平面,我们就说它们所成的角是直角。
一条直线和平面平行,或在平面内,我们说它们所成的角是00.3、二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
在二面角βα--l 的棱l 上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱l 的射线OA 和OB ,则射线OA 和OB 构成的∠AOB 叫做二面角的平面角。
二面角的大小可以可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度。
常见角的取值范围:① 异面直线所成的角⎥⎦⎤ ⎝⎛20π,,直线与平面所成的角⎥⎦⎤⎢⎣⎡20π,,二面角的取值范围依次[]π,0② 直线的倾斜角[)π,0、到的角[)π,0、与的夹角的取值范围依次是⎥⎦⎤⎢⎣⎡20π,4、点到平面距离:求点到平面的距离就是求点到平面的垂线段的长度,其关键在于确定点在平面内的垂足,当然别忘了转化法与等体积法的应用. 向量法1、两异面直线及所成的角:设异面直线a ,b 的夹角为θ,方向向量为a ,b ,其夹角为ϕ,则有cos cos a b a bθϕ⋅==.2、直线和平面所成的角:设直线l 的方向向量为l ,平面α的法向量为n ,l 与α所成的角为θ,l 与n 的夹角为ϕ,则有sin cos l n l nθϕ⋅==.3、二面角:设1n ,2n 是二面角l αβ--的两个面α,β的法向量,则向量1n ,2n 的夹角(或其补角)就是二面角的平面角的大小.若二面角l αβ--的平面角为θ,则1212cos n n n n θ⋅=.4、点到平面距离:点P 是平面α外一点,A 是平面α内的一定点,n 为平面α的一个法向量,则点P 到平面α的距离为cos ,n d n nPA⋅=PA 〈PA 〉=.例题例1.长方体ABCD -A 1B 1C 1D 1中,AB =AA 1=2,AD =1,E 为CC 1的中点,则异面直线BC 1与AE 所成角的余弦值为( )A.1010B.3010C.21510D.31010例2.已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E 为BC 的中点.(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角.例3.如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD . (1)若G 为AD 的中点,求证:BG ⊥平面PAD ; (2)求证:AD PB ⊥;(3)求二面角A BC P --的大小.例4.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一点,且A 1G =λ(0≤λ≤1),则点G 到平面D 1EF 的距离为( ) A.3 B.22 C.32λ D.55练习:1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点,(1)求证:EFGH 是平行四边形;(2)若BD=AC=2,EG=2。
二级结论专题9 立体几何

二级结论专题9立体几何二级结论1:三余弦定理与三正弦定理【结论阐述】三余弦定理(又称最小角定理):如图①,AB 是平面的一条斜线,BC 是平面内的一条直线,OA ⊥平面π于O ,OC BC ⊥于C ,则cos =cos cos ABC OBC OBA ∠∠⋅∠,即斜线与平面内一条直线夹角γ的余弦值等于斜线与平面所成角α的余弦值乘以射影与平面内直线夹角β的余弦值:cos =cos cos γα⋅β;说明:为方便记忆,我们约定γ为线线角,α为线面角,β为射影角,则由三余弦定理可得线面角是最小的线线角,即平面的斜线和它在平面内的射影所成的角,是这条斜线和这个平面内任一条直线所成角中的最小者.三正弦定理(又称最大角定理):如图②,设二面角--AB θδ的平面角为α,AC ⊂平面θ,CO ⊥平面δ,OB AB ⊥,设=,=CAB CAO ∠β∠γ,则sin =sin sin γα⋅β.说明:为方便记忆,我们约定α为二面角,β为线棱角,γ为线面角,则由三正弦定理可得二面角是最大的线面角,即对于一个锐二面角,在其中一个半平面内的任一条直线与另一个半平面所成的线面角的最大值等于该二面角的平面角.【应用场景】空间三类角,即两条异面直线所成角、直线与平面所成角、二面角是立体几何的核心内容,也是高考重点考查的内容之一,几乎在每一份数学高考试卷中都会涉及.建立空间直角坐标系,通过空间向量的坐标运算,是求解空间三类角问题的常用方法.但此法存在两个缺陷:一是若图形不规则或不容易建立坐标系,则该法常常行不通;二是运算量较大.运用“最小(大)角”定理和“三余(正)弦”定理,不仅关联了线线角、线面角和二面角,而且利用它解决立体几何中的三类角问题,不需要建立坐标系,运算量也很小.【典例指引1】(2022年高考浙江卷8)1.如图,已知正三棱柱1111,ABC A B C AC AA -=,E ,F 分别是棱11,BC A C 上的点.记EF 与1AA 所成的角为α,EF 与平面ABC 所成的角为β,二面角F BC A --的平面角为γ,则()A .αβγ≤≤B .βαγ≤≤C .βγα≤≤D .αγβ≤≤【典例指引2】(2019年高考浙江卷8)2.设三棱锥V ABC -的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P AC B --的平面角为γ,则A .,βγαγ<<B .,βαβγ<<C .,βαγα<<D .,αβγβ<<【针对训练】(2018年高考浙江8)3.已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则A .123θθθ≤≤B .321θθθ≤≤C .132θθθ≤≤D .231θθθ≤≤(2022·浙江·高三开学考试)4.在正方体1111ABCD A B C D -中,M 是棱11A D 上的点且1112A M MD =,N 是棱CD 上的点,记MN 与BC 所成的角为α,MN 与底面ABCD 所成的角为β,二面角M CD A --的平面角为γ,则()A .αβγ≥≥B .αγβ≥≥C .γαβ≥≥D .γβα≥≥(2022·北京大兴·高一期末)5.如图,在正方体1111ABCD A B C D -中,M 是棱AB 的中点.令直线1D M 与1AA 所成的角为1θ,直线1D M 与平面1111D C B A 所成的角为2θ,二面角1D AM C --的平面角为3θ,则()A .123θθθ>=B .132θθθ>>C .123θθθ=<D .132θθθ<<(2022·河南新乡·高二期末)6.已知直线l 是平面θ的斜线,且与平面θ交于点M ,l 在平面θ上的射影为m ,在平面θ内过点M 作一条直线n ,直线n 和直线m 不重合,直线l 与平面θ所成的角为α,直线m 与直线n 所成的角为β,直线l 与直线n 所成的角为γ,则()A .cos cos cos αβγ=⋅B .cos cos cos βαγ=⋅C .cos cos cos γαβ=⋅D .以上说法都不对(2022·山西省长治市第二中学校高一期末)7.在空间,若60,AOB BOC COA ∠=∠=∠=︒直线OA 与平面OBC 所成角为θ,则cos θ=()A .13B .12C .2D .38.如图所示,在侧棱垂直于底面的三棱柱111ABC A B C -中,P 是棱BC 上的动点,记直线1A P 与平面ABC 所成的角为1θ,与直线BC 所成的角为2θ,则1θ,2θ的大小关系是A .12θθ=B .12θθ>C .12θθ<D .不能确定(2022·江西省万载中学高二期中)9.已知点A 、B 分别在二面角l αβ--的两个面α、β上,AC ⊥l ,BD ⊥l ,C 、D 为垂足,AC BD CD ==,若AB 与l 成60º角,则二面角l αβ--为()A .30ºB .45ºC .60ºD .120º10.已知二面角AB αβ--是直二面角,P 为棱AB 上一点,PQ 、PR 分别在平面α、β内,且45QPB RPB ∠=∠=︒,则QPR ∠为()A .45°B .60°C .120°D .150°11.ABC 的AB 边在平面α内,C 在平面α外,AC 和BC 分别在与平面α成30 和45 的角,且平面ABC 与平面α成60 的二面角,那么sin ACB ∠的值为()A .1B .13C .3D .1或13(2022·上海市七宝中学高二开学考试)12.正方体中1111ABCD A B C D -,过1D 作直线l ,若直线l 与平面ABCD 中的直线所成角的最小值为6π,且直线l 与直线1BC 所成角为π4,则满足条件的直线l 的条数为_________.(2022·河南省上蔡第一高级中学高三月考)13.在四面体SABC 中,SA ⊥平面,,ABC AB AC SB SC BC ⊥===若直线l 与SA 所成的角为6π,则直线l 与平面SBC 所成角的取值范围是__________.(2022·浙江宁波·高二期末)14.已知三棱锥-P ABC 的棱长均为1,BC ⊂平面,E α为PB 中点,l α⊥.记l 和直线AE 所成角为θ,则该三棱锥绕BC 旋转的过程中,sin θ的最小值是___________.15.三角形ABC 的一条边AB 在平面α内,π=2A ∠,=AB a ,AC ,若AC 与平面α所成角为π4,则直线BC 与平面α所成角的正弦值为___________.二级结论2:多面体的外接球和内切球【结论阐述】类型一球的内切问题(等体积法)例如:如图①,在四棱锥P ABCD -中,内切球为球O ,求球半径.方法如下:------=++++P ABCD O ABCD O PBC O PCD O PAD O PABV V V V V V即:-11111=++++33333P ABCD ABCD PBC PCD PAD PAB V S r S r S r S r S r ⋅⋅⋅⋅⋅,可求出.类型二球的外接问题1.公式法正方体或长方体的外接球的球心为其体对角线的中点2.补形法(补长方体或正方体)①墙角模型(三条线两个垂直)题设:三条棱两两垂直②对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB=CD ,AD=BC ,AC=BD )3.单面定球心法(定+算)步骤:①定一个面外接圆圆心:选中一个面如图:在三棱锥-P ABC 中,选中底面ABC ∆,确定其外接圆圆心1O (正三角形外心就是中心,直角三角形外心在斜边中点上,普通三角形用正弦定理定外心2=sin a r A);②过外心1O 做(找)底面ABC ∆的垂线,如图中1PO ⊥面ABC ,则球心一定在直线(注意不一定在线段1PO 上)1PO 上;③计算求半径R :在直线1PO 上任取一点O 如图:则==OP OA R ,利用公式22211=+OA O A OO 可计算出球半径R .4.双面定球心法(两次单面定球心)如图:在三棱锥-P ABC 中:①选定底面ABC ∆,定ABC ∆外接圆圆心1O ;②选定面PAB ∆,定PAB ∆外接圆圆心2O ;③分别过1O 做面ABC 的垂线,和2O 做面PAB 的垂线,两垂线交点即为外接球球心O .【应用场景】多面体外接球问题是立体几何中的重难点内容之一,在高考中频繁出现.解决此类问题的关键是确定球心的位置,运用常见模型可以很方便的确定球心的位置从而准确求解.【典例指引1】(2022·山西吕梁·一模)16.在《九章算术·商功》中,将四个面都为直角三角形的四面体称为鳖臑,如图在鳖臑ABCD 中,AB ⊥平面BCD ,1AB BC CD ===,BC CD ⊥,则鳖臑ABCD 内切球的表面积为()A .3πB .(3π-C .12πD .(3π+【典例指引2】17.已知三棱锥-P ABC ,在底面ABC 中,30A =,1BC =,PA ⊥面ABC ,PA =则此三棱锥的外接球的表面积为()A .163πB .C .323πD .16π【针对训练】(2022·湖北黄冈·高一期末)18.若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积是球体积两倍时,该圆锥的高为()A .2B .4CD .(2022·青海·海南藏族自治州高级中学高三开学考试)19.如图正四棱柱1111ABCD A B C D -中,底面面积为36,11A BC V 的面积为棱锥111B A B C -的外接球的表面积为()A .68πB .C .172πD .(2022·全国·高三专题练习)20.已知四面体-P ABC 中,PA ⊥平面ABC ,2PA AB ==,BC =,且3tan2ABC ∠=,则四面体-P ABC 的外接球的表面积为()A .15πB .17πC .18πD .20π(2022·江苏·金陵中学高一期末)21.前一段时间,高一年级的同学们参加了几何模型的制作比赛,大家的作品在展览中获得了一致好评.其中一位同学的作品是在球当中放置了一个圆锥,于是就产生了这样一个有趣的问题:已知圆锥的顶点和底面圆周都在球O 面上,若圆锥的侧面展开图的圆心角为23π,面积为3π,则球O 的表面积等于()A .818πB .812πC .1218πD .1212π(2022·云南·弥勒市一中高二阶段练习)22.设直三棱柱111ABC A B C -的所有顶点都在一个球面上,且球的体积是3,1AB AC AA ==,120BAC ∠=︒,则此直三棱柱的高是()A .1B .2C .D .4(2022·重庆·西南大学附中高一期末)23.已知正方形ABCD 中,2AB =,E 是CD 边的中点,现以AE 为折痕将ADE V 折起,当三棱锥D ABE -的体积最大时,该三棱锥外接球的表面积为()A .525π48B .5π4C .25π4D .25π(2022·广西·柳铁一中高三阶段练习)24.在三棱锥A BCD -中,3AB AD BC ===,5CD =,4BD =,AC =锥外接球的表面积为()A .63π10B .64π5C .128π5D .126π5(2022·江西省南丰县第二中学高一学业考试)25.已知四棱锥S ABCD -,SA ⊥平面ABCD ,AB BC ⊥,BCD DAB π∠+∠=,2SA =,BC =S BC A --的大小为3π.若四面体S ACD -的四个顶点都在同一球面上,则该球的体积为()A .3B .C .10πD .323π二、填空题(2022·河南焦作·一模)26.已知三棱锥-P ABC 的每条侧棱与它所对的底面边长相等,且ABC 是底边长为2的等腰三角形,则该三棱锥的外接球的表面积为___________.(2022·河南驻马店·高三期末)27.在三棱锥-P ABC 中,底面是以AB 为斜边的等腰直角三角形,4AB =,PA PB PC ===-P ABC 外接球的表面积为______.(2022·全国·模拟预测)28.已知A 、B 、C 、D 为空间不共面的四个点,且2BC BD AB ===A BCD -体积最大时,其外接球的表面积为______.(2022·安徽马鞍山·一模)29.三棱锥-P ABC 中,PAC △是边长为2AB BC ==,平面PAC ⊥平面ABC ,则该三棱锥的外接球的体积为______30.在三棱锥P -ABC 中,PA ,PB ,PC 两两垂直,1PA =,2PB =,3PC =,则该三棱锥的外接球的表面积为()A .494πB .56πC .3D .14π(2022·湖北荆州·高一期中)31.如图,在一个底面边长为2的正四棱锥P ABCD -中,大球1O 内切于该四棱锥,小球2O 与大球1O 及四棱锥的四个侧面相切,则小球2O 的表面积为______.答案第1页,共23页参考答案:1.A【分析】先用几何法表示出αβγ,,,再根据边长关系即可比较大小.【详解】如图所示,过点F 作FP AC ⊥于P ,过P 作PM BC ⊥于M ,连接PE,则EFP α=∠,FEP β=∠,FMP γ=∠,tan 1PE PE FP AB α==≤,tan 1FP AB PE PE β==≥,tan tan FP FPPM PEγβ=≥=,所以αβγ≤≤,故选:A .2.B【解析】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半.【详解】方法1:如图G 为AC 中点,V 在底面ABC 的投影为O ,则P 在底面投影D 在线段AO 上,过D 作DE 垂直AE ,易得//PE VG ,过P 作//PF AC 交VG 于F ,过D 作//DH AC ,交BG 于H ,则,,BPF PBD PED α=∠β=∠γ=∠,则cos cos PF EG DH BDPB PB PB PBα===<=β,即αβ>,tan tan PD PDED BDγ=>=β,即y >β,综上所述,答案为B.方法2:由最小角定理βα<,记V AB C --的平面角为γ'(显然γ'=γ)由最大角定理β<γ'=γ,故选B.方法3:(特殊位置)取V ABC -为正四面体,P 为VA 中点,易得cos sin sin α=α=β=γ= B.【点睛】常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便解法.3.D【分析】分别作出线线角、线面角以及二面角,再构造直角三角形,根据边的大小关系确定角的大小关系.【详解】设O 为正方形ABCD 的中心,M 为AB 中点,过E 作BC 的平行线EF ,交CD 于F ,过O 作ON 垂直EF 于N ,连接SO 、SN 、OM ,则SO 垂直于底面ABCD ,OM 垂直于AB ,因此123,,,SEN SEO SMO θθθ∠=∠=∠=从而123tan ,tan ,tan ,SN SN SO SO EN OM EO OMθθθ====因为SN SO EO OM ≥≥,,所以132tan tan tan ,θθθ≥≥即132θθθ≥≥,选D.【点睛】线线角找平行,线面角找垂直,面面角找垂面.4.B【分析】作MH AD ⊥于H ,过N 作//NE BC 交AB 于E ,过M 作MF NE ⊥于F ,可得MNF α=∠,MDA γ=∠,MNH β∠=,在正方体中求得它们的正切值比较大小后可得结论.【详解】作MH AD ⊥于H ,则1//MH AA ,1A M AH =,从而1HD MD =,而1AA ⊥平面ABCD ,因此有MH ⊥平面ABCD ,过N 作//NE BC 交AB 于E ,过M 作MF NE ⊥于F ,则MNF α=∠,tan MF MNF FN∠=,由正方体性质易知MDA ∠为二面角M CD A --的平面角,即MDA γ=∠,1113tan 223AA MH MDA DH A D ∠===,NF ⊂平面ABCD ,则MH NF ⊥,同理MH HN ⊥,MF MH M = ,,MF MH ⊂平面MFH ,所以NF ⊥平面MFH ,又HF ⊂平面MFH ,所以FN HF ⊥,所以HDNF 是矩形,FN DH =,由MH ⊥平面ABCD 知MNH β∠=,tan MH MNH HN∠=,由MF MH ≥,HN HD ≥得MF MH MH FN HD NH ≥≥,即tan tan tan αγβ≥≥,,,αβγ均为锐角,所以αγβ≥≥,N 与D 重合时,三角相等.故选:B .5.B【分析】取11A B 的中点N ,再根据几何关系,结合线线角线面角与二面角的定义,分析123,,θθθ的正切值大小结合正切的单调性判断即可【详解】取11A B 的中点N ,连接如图.易得1//AA MN ,故直线1D M 与1AA 所成的角11D MN θ=∠.又直线1D D ⊥平面1111D C B A ,故1D M 与平面1111D C B A 所成的角21MD N θ=∠.又AB ⊥平面11AA D D ,故二面角1D AM C --的平面角3145D AD θ=∠=o .因为1111tan 1D N D A MN MNθ=>=,3tan 1θ=,21tan 1MN D N θ=<,故132tan tan tan θθθ>>,又123,,θθθ均为锐角,故132θθθ>>故选:B6.C【分析】过直线l 上一点A (与M 不重合)作平面θ的垂线交平面θ于O ,过点O 在平面θ内作直线n 的垂线交直线n 于点N ,连接ON ,求出cos α、cos β、cos γ的表达式,由此可得出合适的选项.【详解】如图,过直线l 上一点A (与M 不重合)作平面θ的垂线交平面θ于O ,过点O 在平面θ内作直线n 的垂线交直线n 于点N ,连接ON ,由线面角的定义可得AMO α=∠,则cos MO AMα=,因为AO ⊥平面θ,MN ⊂平面θ,AO MN ∴⊥,ON MN ⊥ ,AO ON O = ,MN ∴⊥平面AON ,AN ⊂ 平面AON ,AN MN ∴⊥,所以,cos cos MN OMN OM β=∠=,cos cos MN AMN AMγ=∠=,因此,cos cos cos γαβ=.故选:C.7.D 【分析】根据线面角定义,结合线面垂直的判定定理进行求解即可.【详解】如图,过点A 作AH ⊥平面BOC 于H ,连接OH ,则AOH ∠为直线OA 与平面OBC 所成的角θ,分别作HE OB ⊥,交OB 于点E ,HF OC ⊥,交OC 于点F ,连接AE 、AF ,因为OB ⊂平面BOC ,所以AH OB ⊥,因为,,AH HE H AH HE =⊂ 平面AEH ,所以OB ⊥平面AEH ,而AE ⊂平面AEH ,所以AE OB ⊥,同理AF OC ⊥,因为60AOB AOC ∠=∠=︒,OEA OFA ∠=∠,OA OA =,所以OEA △≌OFA ,所以AE AF =,OE OF =,所以EH FH =,则OH 为BOC ∠的角平分线,由60BOC ∠=︒,可得30FOH ∠=︒,令HF a =,则2OH a =,OF =,即OE OF ==,在直角三角形AOE 中,因为60AOB ∠=︒,所以cos 60AO ==︒,于是在直角三角形AOH 中,cosOH AOH OA ∠==即cos 3θ=.故选:D8.C【详解】分析:首先要明确有关最小角定理,之后对其中的角加以归类,从而得到两角的关系,即可得结果.详解:根据线面角是该直线与对应平面内的任意直线所成角中最小的角,所以有12θθ<,故选C.点睛:该题考查的是有关角的大小的比较问题,在思考的过程中,需要明确角的意义,从而结合最小角定理,得到结果.9.D【分析】由题意画出图形,作出直线AB 与l 所成角及二面角l αβ--的平面角,设AC BD CD a ===,由已知直线AB 与l 所成角大小,即可求解二面角l αβ--的大小.【详解】解:如图,在β内,过B 作//BE DC ,且BE DC =,连接,CE AE ,由BD l ⊥,则四边形DCEB 为矩形,可得CE l ⊥,CE BD CD ==,AC l ⊥ ,得ACE ∠为二面角l αβ--的平面角,且l ⊥平面ACE即BE ⊥平面ACE ,则BE AE⊥设AC BD CD a ===,则CE BE a ==,又直线AB 与l 所成角为60º,60ABE ∴∠=︒,得AE ,∴在ACE △中,2221cos 22AC CE AE ACE AC CE +-∠=-⋅.120∴∠=︒ACE 故二面角l αβ--的大小为120︒.故选:D .10.B【解析】在正方体中构造符合条件的图形,由正方体的性质即可求解.【详解】以正方体为模型,构造满足条件的几何图形如下图所示,连接QR ,由正方体的性质可得PQR 为等边三角形,故60QPR ∠=︒,故选:B.【点睛】本题主要考查了直二面角,正方体的性质,属于中档题.11.D【分析】从C 向平面α作垂线CD ,作CE AB ⊥,证得DE AB ⊥,分ABC ∠为锐角和钝角,由线面角及二面角结合勾股定理及余弦定理求解即可.【详解】从C 向平面α作垂线CD ,连接,AD BD ,作CE AB ⊥,连接DE ,AB α⊂,则CD AB ⊥,,,CD CE C CD CE ⋂=⊂平面CDE ,则AB ⊥平面CDE ,又DE ⊂平面CDE ,则DE AB ⊥,如图所示:设,45,,30,22CD h CBD BC CAD AC CD h =∠=︒=∠=︒==,CED ∠是二面角的平面角,60,CED CE ∠=︒=,由勾股定理,AE BE ==,当ABC ∠为锐角,CE 在ABC 内,AB AE BE =+=,))()2222,h =+ 即222AB BC AC =+,90,sin 1ACB ACB ∴∠=︒∠=;当ABC ∠为钝角,CE 在ABC 之外,3AB AE BE h =-=,根据余弦定理,2222cos ,AB AC BC AC BC ACB =+-∠())222222cos3h h h ACB ⎛⎫=+-⨯⨯∠ ⎪ ⎪⎝⎭cos 3ACB ⇒∠=,1sin 3ACB ∠,综上:sin ACB ∠的值为1或13.故选:D .12.2【分析】作出辅助线,得到1DD 为轴的圆锥母线(母线与1DD 成60︒)是直线l 的运动轨迹,1D A 为轴的圆锥母线(母线与1D A 成45︒)是直线l 的运动轨迹,两个圆锥的交线即为满足条件的直线l 的条数.【详解】设立方体的棱长为1,过1D 作直线l ,若直线l 与平面ABCD 中的直线所成角的最小值为6π,即l 与平面ABCD 所成角为6π,1DD 为轴的圆锥母线(母线与1DD 成60︒)是直线l 的运动轨迹,连接1D A ,由题意得11D A BC ∥,直线l 与直线1BC 所成角为π4,直线l 与直线1D A 所成角为π4.此时1D A 为轴的圆锥母线(母线与1D A 成45︒)是直线l 的运动轨迹,两个圆锥相交得到两条交线.故答案为:213.,62ππ⎡⎤⎢⎣⎦【分析】设BC 的中点为D ,连接,SD AD ,根据等腰与直角三角形的性质可得ADS ∠为二面角S BC A --的平面角,3ASD π∠=,且直线l 不妨看作以SA 为轴,轴截面的顶角为3π的圆锥母线所在的直线,进而求得线面角的最大值与最小值即可.【详解】如图,设BC 的中点为D ,连接,SD AD .因为SA ⊥平面,ABC SB SC ==AB AC =,所以,AD BC BC SD ⊥⊥,所以ADS ∠为二面角S BC A --的平面角.又,AB AC BC ⊥=1AB AC AD SA ====,故3ASD π∠=.直线l 不妨看作以SA 为轴,轴截面的顶角为3π的圆锥母线所在的直线,所以直线l 与平面SBC 所成角的最小值为366πππ-=,最大值为362πππ+=,故直线l 与平面SBC 所成角的取值范围是,62ππ⎡⎤⎢⎥⎣⎦.故答案为:,62ππ⎡⎤⎢⎥⎣⎦14【分析】把l 和直线AE 所成角转化为AE 与平面α所成角,结合线面角的性质可求答案.【详解】设AE 与平面α所成角为1θ,因为l α⊥,l 和直线AE 所成角为θ,所以1sin cos θ=θ;取CD 的中点F ,连接,EF AF ,因为,E F 分别为中点,所以//EF BC ,AEF ∠或其补角是AE 与BC 所成角;在AEF △中,12AE AF EF ===,所以cos 6AEF ∠=且AEF ∠为锐角.三棱锥绕BC 旋转的过程中,由线面角的性质可知,1AEF θ≤∠,所以1cos cos 6AEF θ≥∠=,即sin θ15【分析】过点C 作CO α⊥,垂足为O ,连,OA OB ,则CBO ∠是直线BC 与平面α所成的角,CAO ∠是AC 与平面α所成的角,利用直角三角形可求出结果.【详解】解:过点C 作CO α⊥,垂足为O ,连,OA OB,则CBO ∠是直线BC 与平面α所成的角,CAO ∠是AC 与平面α所成的角,则π=4CAO ∠,∵AC ,∴==CO OA a ,在直角三角形ABC 中,π=2A ∠,=AB a,AC∴BC ,在直角三角形COB中,sin =CO CBO BC ∠∴直线BC 与平面α.16.B 【分析】根据鳖臑的性质,结合四面体内切球的性质、棱锥的体积公式、棱锥和球的表面积公式进行求解即可.【详解】解:因为四面体ABCD 四个面都为直角三角形,AB ⊥平面BCD ,BC CD ⊥,所以AB BD ⊥,AB BC ⊥,BC CD ⊥,AC CD ⊥,设四面体ABCD 内切球的球心为O ,则()13ABCD O ABC O ABD O ACD O BCD ABC ABD ACD BCD V V V V V r S S S S ----=+++=+++△△△△内,所以3ABCDV r S =内,因为四面体ABCD的表面积为1ABCD ABC ABD ACD BCD S S S S S =+++=△△△△,又因为四面体ABCD 的体积16ABCD V =,所以312V r S ==内,所以24(3S r ππ==-球,故选:B【点睛】关键点睛:利用棱锥的等积性进行求解是解题的关键.17.D【分析】利用正弦定理求出ABC 的外接圆半径为1,结合PA ⊥面ABC ,PA =接球半径,进而求出外接球的表面积.【详解】设ABC 的外接圆半径为R ,因为30A = ,1BC =,由正弦定理得:122sin sin 30BC R A ===︒,所以ABC 的外接圆半径为1,设球心O 在ABC 的投影为D ,则DA =1,因为PA ⊥面ABC ,PA =12OD PA ==2OA ==,即此三棱锥的外接球的半径为2,故外接球表面积为24π216π⨯=.故选:D 18.B【分析】先设出未知量,即圆锥半径为r ,圆锥高为h ,分析组合体轴截面图,找出h 与r 的一组关系式,再根据题意中圆锥与球体的体积关系找出另一组h 与r 的关系式即可求出答案.【详解】如下图组合体的轴截面,设圆锥半径为r ,圆锥高为h ,则CF r =,1AO h =-,AC ,由sin sin OAE CAF =∠∠得OE CFOA CA=,代入得222220h r hr h --=①,由“该圆锥体积是球体积两倍”可知23142(1)33V r h =⋅=⨯⨯ππ,即28hr =②,联立两式得4h =.故选:B19.C【分析】根据正四棱柱的性质求得棱柱的高,三棱锥111B A B C -的外接球即为正四棱柱的外接球,棱柱的对角线即为其外接球的直径,求得球半径后可得表面积.【详解】设正四棱柱1111ABCD A B C D -的高为h ,因为正方形ABCD 的面积为36,所以11116A B B C ==,在111Rt A B C △中,由勾股定理得11A C =在1Rt BCC 中,由勾股定理得22136BC h =+,11A B BC =,因为11 A BC △的面积为所以12⋅=10h =,依题意,三棱锥111B A B C -的外接球即为正四棱柱1111ABCD A B C D -的外接球,其半径为12R ==,所以三棱锥111B A B C -的外接球的表面积为24172ππ⋅=.故选:C .20.B【分析】根据题意可求得ABC 的外接圆半径,再根据勾股定理求出四面体-P ABC 的外接球的半径,即可求解.【详解】解:如图所示:在ABC 中,3tan 2ABC ∠=,又22sin cos 1ABC ABC ∠+∠= 且()0,ABC π∠∈,故解得:cos ,sin 1313ABC ABC ∠=∠=,由余弦定理得:2222cos AC AB BC AB BC ABC =+-⋅⋅∠,即222222=913AC =+-⨯⨯,故3AC =,设ABC 的外接圆半径为r ,则2sin 13ACr ABC===∠,设ABC 的外接圆圆心为1O ,四面体-P ABC 的外接球球心为O ,则222222211117124OA OO O A PA r ⎛⎫=+=+=+= ⎪⎝⎭⎝⎭,∴四面体-P ABC 的外接球的表面积为:174=174ππ⨯.故选:B.21.A【分析】设球半径为R ,圆锥的底面半径为r ,利用扇形的弧长和面积公式求得R ,即可求解.【详解】圆锥的顶点和底面圆周都在球O 面上,圆锥的侧面展开图的圆心角为23π,面积为3π,设母线为l ,则212323l ππ⨯⨯=,可得:3l =,由扇形的弧长公式可得:223r l ππ=,所以1r =,圆锥的高1OO ==,由()222r RR +=,解得:R =所以球O 的表面积等于2818144328R πππ=⨯=,故选:A 22.B【分析】先确定底面ABC 的外接圆圆心及半径,再确定球心位置,并利用球心和圆心的连线垂直于底面,得到直角三角形,利用勾股定理求解.【详解】设12AB AC AA m ===,三角形ABC 外接圆1O 的半径为r ,直三棱柱111ABC A B C -外接球O 的半径为R .因为120BAC ∠=︒,所以30ACB ∠=︒,于是24sin 30r ABm ==︒,2r m =,12O C m =.又球心O 到平面ABC 的距离等于侧棱长1AA 的一半,所以1OO m =.在1Rt OO C 中,由22211OC OO O C =+,得2224R m m =+,R =.所以球的体积34)33V π==,解得1m =.于是直三棱柱的高是122AA m ==.故选:B.23.C【分析】设棱锥D ABE -的外接球球心为O ,半径为R ,则OM ⊥平面BCEF ,因为ABE 的面积为定值,所当高最大时,三棱锥D ABE -的体积最大,过D 作DF AE ⊥于F ,设点M 为ABE 的外心,则有222222(),DF OM FM R OM EM R -+=+=通过计算可得点M 为外接球的球心,从而可求得结果【详解】解:过D 作DF AE ⊥于F ,设点M 为ABE 的外心,G 为AE 的中点,连接,MG MF ,因为正方形ABCD 中,2AB =,E 是CD 边的中点,所以1DE =,则AE BE ===,2EG =,AD DE DF AE ⋅=所以EF ===12MG EG ==,54EM =,所以2510FG EG EF =-=,所以20FM =,设棱锥D ABE -的外接球球心为O ,半径为R ,则OM ⊥平面BCEF ,设OM x =,因为ABE 的面积为定值,所当高最大时,三棱锥D ABE -的体积最大,此时平面ADE ⊥平面BCEF ,因为DF AE ⊥,平面ADE 平面BCEF AE =,所以DF ⊥平面BCEF ,所以222222(),DF OM FM R OM EM R -+=+=,所以2222()DF OM FM OM EM -+=+,所以2222DF DF OM FM EM -⋅+=,所以461252558016OM -⨯+=,解得0OM =,所以ABE 的外心为三棱锥D ABE -外接球的球心,所以54R EM ==所以三棱锥外接球的表面积为2252544164R πππ=⨯=24.D【分析】由已知条件先判定出球心的位置,然后运用正弦定理、余弦定理和勾股定理计算出球的半径,即可计算出外接球的表面积.【详解】如图,由3AB BC ==,AC =,得222AB BC AC +=,∴AB BC ⊥,由3BC =,4BD =,5CD =,得222BC BD CD +=,∴BC BD ⊥,又AB BD B = ,∴BC ⊥平面ABD ,设ABD △的外心为G ,过G 作底面的垂线GO ,使12GO BC =,则O 为三棱锥外接球的球心,在ABD △中,由3AB AD ==,4BD =,得2223341cos 2339BAD +-∠==⨯⨯,sin BAD ∠=,设ABD △的外接圆的半径为r ,则r =,32OG =,∴2223126220OB ⎛⎫=+= ⎪⎝⎭.∴三棱锥外接球的表面积为21261264π4ππ205R =⨯=.25.A【分析】先确定出三角形ACD 外接圆的圆心O ',然后过O '作垂直于平面ABCD 的垂线l ,再过SA 中点M 向l 作垂线,垂足即为球心,根据线段长度可求解出球的半径,则球的体积可求.【详解】因为AB BC ⊥,BCD DAB π∠+∠=,所以222CDA ππππ∠=--=,所以CD AD ⊥,所以ACD 外接圆的圆心为AC 的中点,记为O ',过O '作直线l 使得l ⊥平面ABCD ,取SA 中点M ,过M 作MO l ⊥垂足为O ,则OA OS OC OD ===,所以O 为四面体S ACD -外接球的球心,因为,,SA BC AB BC SA AB A ⊥⊥= ,所以BC ⊥平面SAB ,BC SB ⊥,又AB BC ⊥,所以二面角S BC A --的平面角为SBA ∠,所以3SBA π∠=,因为2SA =,所以3tan3SA AB π==,所以2AC ==,所以112AO MO AC '===,又因为112AM SM OO AS '====,所以AO ==所以四面体S ACD -外接球的体积为34=33π,故选:A.26.34π【分析】把三棱锥放入一个长方体中,转化为求长方体外接球的半径即可得解.【详解】三棱锥-P ABC 可以嵌入一个长方体内,且三棱锥的每条棱均是长方体的面对角线,如图,设PA BC ==,PB AC PC AB x ====,长方体交于一个顶点的三条棱长为a ,b ,c ,则122ABCS =⨯=△,解得5x =.由题得(222218a b PA +===,22225a c AC +==,22225b c PC +==,解之得3a =,3b =,4c =.所以该三棱锥的外接球的半径为R ==,所以该三棱锥的外接球的表面积为2244342S R πππ⎛⎫==⨯= ⎪ ⎪⎝⎭.故答案为:34π27.169π9##169π9【分析】取AB 的中点D 可得PD AB ⊥,由222PD CD PC +=得PD CD ⊥,根据线面垂直的判断定理得PD ⊥平面ABC ,得三棱锥-P ABC 外接球的球心O 在线段PD 上,由()2222R PD OD OD AD =-=+可得答案.【详解】如图,取AB 的中点D ,连接PD ,CD .由题意可得2AD BD CD ===,因为PA PB =,所以PD AB ⊥,因为PA =,所以3PD =,所以222PD CD PC +=,所以90PDC ∠= ,即PD CD ⊥.因为AB CD D = ,所以PD ⊥平面ABC ,设三棱锥-P ABC 外接球的球心为O ,由题意易得三棱锥-P ABC 外接球的球心O 在线段PD 上,如下图则三棱锥-P ABC 外接球的半径R 满足()2222R PD OD OD AD =-=+,解得56=OD ,所以513366=-=R ,216936R =;若三棱锥-P ABC 外接球的球心O 在线段PD 的延长线上,如下图,则三棱锥-P ABC 外接球的半径R 满足()2222=+=+R PD OD OD AD ,()22232+=+OD OD ,无解;所以,三棱锥-P ABC 外接球的表面积2169π4π9S R ==.故答案为:169π9.28.18π【分析】由题可得当BA 、BC 、BD 两两垂直时,三棱锥的体积最大,将三棱锥补形为一个长宽高分别为.【详解】当BA 、BC 、BD 两两垂直时,如图三棱锥A BCD -的底面BCD △的面积和高同时取得最大值,则三棱锥的体积最大,此时将三棱锥补形为一个长宽高分别为长方体的外接球即为三棱锥的外接球,球的半径r =,表面积为24π18πr =.故答案为:18π.29【分析】计算出外接球的半径,进而求得外接球的体积.【详解】等边三角形PAC 的高为πsin 33⨯==,等边三角形PAC 的外接圆半径为222sin6π=三角形ABC 的外接圆半径为22sin3π=,设12,O O 分别是等边三角形PAC 、等边三角形ABC 的中心,设O 是三棱锥-P ABC 的外接球的球心,R 是外接球的半径,则2222215R OA R ==+=⇒=,所以外接球的体积为34π3R =.故答案为:330.D 【分析】将三棱锥P -ABC 补全为长方体,长方体的外接球就是所求的外接球,长方体的对角线就是外接球直径,计算出半径后可得表面积.【详解】将三棱锥P -ABC 补全为长方体,则长方体的外接球就是所求的外接球,设球半径为R ,则()222224214R R PA PB PC ==++=,所以球的表面积为2414S R ππ==.故选:D .31.2π【分析】设O 为正方形ABCD 的中心,AB 的中点为M ,连接PM ,OM ,PO ,可画出内切球的切面图,分别求出大球和小球的半径分别为2R =和4r =,从而求出小球2O 的表面积.【详解】设O 为正方形ABCD 的中心,AB 的中点为M ,连接PM ,OM ,PO ,则1OM =,221013PM PA AM =-=-=,9122PO =-=,如图,在截面PMO 中,设N 为球1O 与平面PAB 的切点,则N 在PM 上,且1O N PM ⊥,设球1O 的半径为R ,则1O N R =,∵1sin 3OM MPO PM ∠==,∴1113NO PO =,则13PO R =,11422PO PO OO R =+==,∴22R =,设球1O 与球2O 相切于点Q ,则22PQ PO R R =-=,设球2O 的半径为r ,同理可得4PQ r =,∴224R r ==,故小球2O 的表面积242r ππ=.故答案为:2π。
立体几何求夹角方法总结

立体几何求夹角方法总结立体几何体现了空间中物体的立体形态,它的重要性在于能够帮助人们更好地理解三维物体,并求出它们之间的夹角,这在数学、物理等领域都有着广泛的应用。
本文将总结出常见的几何求夹角方法,供读者参考。
方法一:向量求夹角向量是几何学中的常用概念,它由矢量和标量组成。
可以通过计算两个向量之间的夹角,得到它们之间的几何夹角。
具体做法如下:1. 求出待求夹角的两个向量;2. 根据向量的标准公式求出它们的数量积;3. 分别计算出两个向量的长度;4. 将数量积和长度带入余弦定理求出夹角。
方法二:平面法线求夹角在三维空间中,可以通过平面的法线向量来计算两个平面之间的夹角。
具体做法如下:1. 求出待求夹角的两个平面的法线向量;2. 根据向量的标准公式求出它们的数量积;3. 分别计算出两个平面的法线向量的长度;4. 将数量积和长度带入余弦定理求出夹角。
方法三:点法线求夹角与平面法线类似,我们也可以通过点和法线向量计算两个平面之间的夹角。
具体做法如下:1. 求出待求夹角的两个平面的任意一点坐标和两个平面的法线向量;2. 根据向量的标准公式求出它们的数量积;3. 分别计算出两个平面的法线向量的长度;4. 将数量积和长度带入余弦定理求出夹角。
方法四:球面三角学法求夹角该方法适用于计算球面上两个点或两个平面之间的夹角,方法稍微复杂。
具体做法如下:1. 求出待求夹角的两个点或平面的经纬度坐标;2. 根据球面三角学公式求出两个点之间的夹角或两个平面之间的夹角;3. 将弧度转化为角度,得到最终的夹角。
综上所述,立体几何求夹角的方法有计算向量之间的夹角、平面法线之间的夹角、点法线之间的夹角和球面三角学法求夹角。
每种方法都有其适用范围和计算步骤,要根据实际情况选择合适的方法进行计算。
立体几何定理大全

立体几何公式大全基本概念公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3: 过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面. 推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.空间两直线的位置关系:空间两条直线只有三种位置关系:平行、相交、异面1、按是否共面可分为两类:(1)共面:平行、相交(2)异面:异面直线的定义:不同在任何一个平面内的两条直线或既不平行也不相交。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线.两异面直线所成的角:范围为 ( 0°,90°) esp。
空间向量法两异面直线间距离:公垂线段(有且只有一条) esp.空间向量法2、若从有无公共点的角度看可分为两类:(1)有且仅有一个公共点-—相交直线;(2)没有公共点-—平行或异面直线和平面的位置关系: 直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行①直线在平面内-—有无数个公共点②直线和平面相交——有且只有一个公共点直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为[0°,90°]最小角定理: 斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角三垂线定理及逆定理: 如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直esp。
立体几何等角定理-定义说明解析

立体几何等角定理-概述说明以及解释1.引言1.1 概述概述部分的内容应该对立体几何等角定理进行简要介绍,突出其重要性和在几何学中的应用。
可以参考以下内容:立体几何是数学中的一个分支,研究空间中的三维图形和体积计算等问题。
在立体几何中,等角定理是一条重要的定理,它探讨了几何体之间的角度关系。
等角定理是指在立体几何中,如果两个几何体具有完全相等的角度,则它们是等角的。
简而言之,等角定理告诉我们,当一个几何体沿着空间中的某个轴旋转时,它的角度保持不变。
这个定理对于解决许多几何题目非常重要。
它可以应用于计算物体的旋转,推导出旋转图形的性质,并且在计算机图形学中有广泛的应用。
在建筑学、工程学和设计领域中,等角定理也被广泛应用于设计和计算三维结构的角度。
本文将介绍立体几何的基本概念,包括空间中的图形和体积计算等内容,然后详细探讨等角定理的定义与原理,以及它在实际问题中的应用举例。
同时,还会介绍等角定理的证明方法,以帮助读者更好地理解和应用这条定理。
总之,通过对立体几何等角定理的研究,我们可以更深入地了解几何体之间角度的关系,进一步提高我们的几何学知识,并且在实际问题中应用这个定理进行计算和设计。
在接下来的正文部分,我们将一步一步地探究等角定理的各个方面,希望读者在阅读完本文之后能够对立体几何等角定理有更全面的了解和应用能力。
1.2 文章结构文章结构部分的内容可以写成以下这样:2. 文章结构本文主要分为三个部分:引言、正文和结论。
2.1 引言部分将对立体几何等角定理的背景和概述进行介绍,让读者对本文的主题有一个整体的了解。
同时还会说明文章的结构和目的,以及对整篇文章进行总结,引导读者进入正文部分。
2.2 正文部分是本文的主体,将对立体几何的基本概念进行阐述,包括对几何的定义和基本性质的介绍。
随后,将详细探讨等角定理的定义与原理,以及它在立体几何中的应用举例。
最后,将介绍一些证明等角定理的方法,帮助读者更好地理解和应用这一定理。
立体几何常见二级结论及应用

立体几何的二级结论结论一: 斜二测画法直观图面积为原图形面积的√24倍备注:在用斜二测画法画直观图时,首先在画直观图的平面上画出对应的x'轴和y'轴,两轴相交于点O',且使∠x'O'y' =45°(或135°),在已知图形平行于x 轴的线段,在直观图中画成平行于x'轴,长度保持不变;在已知图形平行于y 轴的线段,在直观图中画成平行于y'轴,且长度为原来的一半。
结论二:n 面体的表面积为S ,体积为V ,则内切球的半径r=3V S证明:将内切球的球心与n 面体(n ≥4)的各顶点连线,就能将这个多面体分割成n 个棱锥,此时各棱锥的高就是内切球的半径r ;设n 面体体积为V ,各面面积分别为S 1,S 2,……,S n ,各棱锥体积分别为V 1,V 2,……,V n 则有:V=V 1+V 2+……+V n V=13S 1r+13S 2r+……+13S n r V=13r(S 1+S 2+……+S n ) V=13rS 即r=3V S备注:对于棱锥而言,只有三棱锥一定有内切球,内切球的球心在三个侧面与底面形成的三个二面角的角平分面的交点上。
对于n 棱锥(n ≥4),只有正n 棱锥才有内切球。
结论三:设点A 为面上一点,过点A 的斜线AO 在面上的射影为AB ,另外AC 为面上任意一条直线,则∠OAC ,∠BAC 和∠OAB 三角的余弦值存在如下的关系,被称为三余弦定理:cos ∠OAC=cos ∠BAC ·cos ∠OAB 证明:在AC 上找一点C 使得,BC ⊥AC ,连接OC 如下所示:cos ∠OAB=ABOA ①cos ∠BAC=ACAB ②∵ AC ⊥BC ,OB ⊥AC ∴ AC ⊥面OBC ,∴ AC ⊥OC ∴ cos ∠OAC=AC OA ③由①②③可知:cos ∠OAC=cos ∠BAC ·cos ∠OAB例题:已知直线L 与平面α所成角为45°,L 在α内的射影为m ,n 是α内的一条直线,且直线n 与m 所成角为45°,则直线L 与n 所成角为多少? 解:OAB COABC根据三余弦定理可知: cos θ=cos45°·cos45°=12又∵两条直线的夹角范围为[0,90°] ∴ θ=60°结论四:面积射影定理:设平面α外的△ABC 在平面α内的射影为△ABO ,分别记△ABC 与△ABO 的面积为S 和S ’,记△ABC 所在的平面与平面α所成的二面角为θ,则有:cos θ=S’S备注:当二面角的范围为(90°,180]时,cos θ=-S’S证明:过点C 作CD ⊥AB 于点D ,连接OD∵ CD ⊥AB又CO ⊥面ABO ,∴ CO ⊥AB ∴ AB ⊥面CDO ∴ AB ⊥OD∴ 二面角C-AB-D 的平面角即为∠CDOACOBA COBDS △ABC =12CD ·AB ,S △ABO =12OD ·AB∴ S △ABO S △ABC =OD CD=cos ∠CDO 例题:在正三棱柱ABC-A 1B 1C 1中,2AB=AA 1,D 为BB 1上的中点,求平面AC 1D 与平面ABC 所成角的正弦值。
35.立体几何正弦、余弦定理

立体几何正弦、余弦定理正弦定理和余弦定理是解三角形的两个重要工具,它们都有转化(边角转化)和求解(解三角形)两大功能.其中,正弦定理沟通的是边与角的正弦,而余弦定理沟通的是边与角的余弦.二者各有千秋,对于简单的解三角形问题,一个定理即可摆平;对于复杂解三角形问题,或需二者联袂攻克.所以解三角形是正余弦定理的天下!曾几何时,它们还在三角形中鏖战厮杀.待与三角形分别后,我们唏嘘不已,不知何时再与二定理相见?没想到今天竟然与它们邂逅于立体几何!其实,一点也不奇怪,平面的也是立体的,立体几何中也有三角形嗷嗷待解,故而我们又“不知转入此中来”了,正好可以重温一下.一、独立解例1 (河北廊坊2020届高三联考)在三棱柱111C B A ABC −中,3211===AA AC AB ,32π=∠BAC ,⊥1AA 平面ABC ,则该三棱柱的外接球的表面积为( )A .36πB .48πC .72πD .108π分析:例中的三棱柱是一个直棱柱,且高h (侧棱长)已知,故只需求出棱柱底面三角形外接圆半径r ,即可运用公式222r h R +⎪⎭⎫ ⎝⎛=求外接球的半径R .而求r ,可用正弦定理. 解:依题意,ABC ∆外接圆半径330sin 23=︒=r ,所以该三棱柱的外接球的半径233322=+=R ,所以该三棱柱的外接球的表面积为72π.选C .评注:在求几何体的外接球半径时,正弦定理常用来求三角形外接圆的半径,其它功能较少使用.变式1 (河北张家口2020届高三摸底联考)已知三棱锥ABC S −中,⊥SA 平面ABC ,且6π=∠ACB ,1,3==SA AB .则该三棱锥的外接球的体积为( D )A .81313πB .13πC .613π D .61313π 变式2 (江苏镇江2019年高一期中)一个圆锥的底面半径为1,它的正视图是顶角为︒30的等腰解:外接球的球心即为轴截面外接圆的圆心,所以轴截面三角形的外接圆是球的大圆,其半径等于球变式3 (四川攀枝花2018年高二期末)正的边长为2,将它沿高AD 翻折,使点B 与点C 间的距离为3,此时四面体ABCD 外接球表面积为( C )A .677πB .π61919C .7πD .19π 例2 (2019年高考全国Ⅰ卷12)已知三棱锥ABC P −的四个顶点在球O 的球面上,PC PB PA ==,ABC ∆是边长为2的正三角形,FE ,分别是AB PA ,的中点,︒=∠90CEF ,则球O 的体积为( )A .π68B .π64C .π62D .π6分析:先设出棱锥的侧棱长,根据︒=∠+∠180PEC AEC ,用余弦定理表示出CE .然后在CEF Rt ∆中运用勾股定理求出侧棱长,此时可发现棱锥的三条侧棱两两垂直,故而可将其补成长方体求其外接球半径.解:设x PA =,则由︒=∠+∠180PEC AEC ,可得PEC AEC ∠−=∠cos cos ,所以CE x CE x ⨯⨯−+224422CE x x CE x ⨯⨯−+−224222,解得2422+=x CE . 在CEF Rt ∆中,由勾股定理,可得2223244=++x x ,解得2=x ,所以PC PB PA ,,两两垂直,所以球O 的的半径26223=⨯=R ,所以球O 的体积为ππ626343=⎪⎪⎭⎫ ⎝⎛⨯.选D . 评注:本例中的CE 是ACP ∆的中线,用以前号文中介绍过的中线长公式求解更快,即=−+=])4(2[41222x x CE 242+x ,这就是所谓的艺多不压身. 变式4 (百师联盟2020届高三开学摸底大联考)四棱锥P -ABCD 中,底面ABCD 是矩形,其中2,1==BC AB ,⊥PA 底面ABCD ,异面直线AC 与PD 所成的角的余弦值为54,则四棱锥外接球的表面积为( )A .48πB .36πC .8πD .6π分析:由⊥PA 底面ABCD ,且底面ABCD 是正方形,很容易使我们想起用补体法求解.更可喜的是,补体之后,异面直线AC 与PD 所成的角自然出现,为求解进一步带来方便.解:先作出长方体PC ,从中作出四棱锥P -ABCD ,如图所示.连接C B AC 1,,则1ACB ∠就是异面直线AC 与PD 所成的角,设x PA =,则4,12121+=+=x C B x AB ,又因为5=AC 所以在1ACB ∆由余弦定理,可得54452145222=+−−++x x x ,解得1=x ,即1=PA .所以四棱锥外接球的半径2621121222=++=R ,所以四棱锥外接球的表面积为6π.选D . 评注:不用补体,用三角形中位线作异面直线所成的角也可以解出,就是有些困难和麻烦,求半径的公式也得改为222r h R +⎪⎭⎫ ⎝⎛=.在解答几何体外接球问题时,余弦定理常用来求边,做一些基础的准备工作,还是比较低调的.二、牵手解例3 (天津市耀华中学2019年高一期中)已知点A 是以BC 为直径的圆O 上异于C B ,的动点,P 为平面ABC 外一点,且平面⊥PBC 平面ABC ,5,22,3===PC PB BC ,则三棱锥ABC P −外接球的表面积为______.分析:这个棱锥既不是正棱锥,也没有侧棱垂直底面,故无法使用公式法和补体法求解.那只能走一般路子,先找球心,再图求半径.根据题意及球截面的性质,易知球心一定在面PBC 内,且是PBC ∆的外心.因为已知PBC ∆的三边长,故我们可先用余弦定理求出其一个内角的余弦值,进而求其正弦值,最后运用正弦定理求其外接圆半径.解:如图,因为平面⊥PBC 平面ABC ,所以若过点O在平面PBC 内作BC 的垂线,则该垂线一定垂直平面ABC ,设三棱锥ABC P −外接球的球心为1O ,连接O O 1,则⊥O O 1平面ABC ,又因为过点O 的平面ABC 的垂线唯一,所以1O 一定在平面PBC 内,且是PBC ∆的外心.在PBC ∆中,因为5,22,3===PC PB BC ,所以由余弦定理得2222325)22(3cos 222=⨯⨯−+=B ,所以22sin =B ,所以PBC ∆外接圆的半径即三棱锥ABC P −外接球2102225=⨯=R ,所以三棱锥ABC P −外接球的表面积为ππ1021042=⎪⎪⎭⎫ ⎝⎛. 评注:已知ABC ∆的三边长c b a ,,求其外接圆半径可用公式))()((44c p b p a p p abc S abc R −−−==,其中p 是ABC ∆的半周长.不过用这两个公式用于本例中,也不简单,因为有两个边长是无理数.且放白鹿青崖间吧.先用余弦定理求边长或角,再运用正弦定理求三角形外接圆半径,是在外接球问题中正余弦定理联袂的常见分工协作形式.变式5 (广东深圳2018届高三期末质监)在四面体ABC S −中,⊥SA 平面ABC ,32π=∠BAC ,1,2===AB AC SA ,则该四面体的外接球的表面积为( D )A .11πB .328πC .310πD .340π。
立体几何中角的求法

立体几何中角的求法1.异面直线所成角的求法:范围(直线与直线所成角(] 90,0∈θ:(1)平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;(2)补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;2.直线与平面所成的角 范围:(直线与平面所成角[] 90,0∈θ)斜线和平面所成的是一个直角三角形的锐角,它的三条边分别是平面的垂线段、斜线段及斜线段在平面上的射影.通常通过斜线上某个特殊点作出平面的垂线段,垂足和斜足的连线,是产生线面角的关键; 3。
二面角的求法 范围:二面角])180,0[ ∈θ 方法:作,证,算知识:正弦定理,余弦定理,特殊角,反正弦(余弦,正切)(1)定义法:直接在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线,得出平面角,用定义法时,要认真观察图形的特性;(2)三垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;(3)垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直;(4)射影法:利用面积射影公式S 射=S 原cos θ,其中θ为平面角的大小,此法不必在图形中画出平面角; 特别:对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其要考虑射影法)。
(二面角的取值范围[) 180,0∈θ) 1、在正方体1AC 中,求下列线面角 ⑴1DB 与底面AC ⑵1A B 与平面11A B CD2、如图,,,AB ABCD BC CD AB BC AD ⊥⊥=平面 与平面ABCD 所成的角为30o ⑴求AD 与平面ABC 所成的角 ⑵AC 与面ABD 所成的角线线角1. 如图所示,ABCD 是一个正四面体,E 、F 分别为BC和AD 的中点。
