初一数学第一章有理数
初一数学上-第一章:有理数,正数与负数①

第一章:有理数一. 1.1.1 正数与负数(1)定义:①大于0的数是正数。
用“+”表示,如:+6,+0.5注意:但通常当正数在计算中第一个位置出现时,“+”要省略,如+6+7=+13要写成6+7=13②小于0的数是负数。
用“—”表示,如:—6,—3③0既不是正数也不是负数。
注:通俗说法:在一个正数前面加“—”就是负数。
(2)表达的含义:正数和负数是表示实际问题中具有相反意义的两个量。
如:东与西,收入与支出等例:如果向东走5米用“+5米”表示那么向西走10米用“—10米”表示例:1:下列说法正确的是( )A .a -一定是负数 B.一个数不是正数就是负数C.0-是负数 D.在正数前面加“—”号,就成了负数例2:把下列数填到相应的圈里;、π-、 0、a -正数 负数例 3.小优向东走10米记作10+米,那么小优如果向西走3米应该记作__________________.问题1:判断下面每对量是不是具有相反意义的量.(1)节约13m 3水和浪费4m 3的水;(2)电梯上升2层和下降5层;(3)小明向支付宝转入300元后又支出100元..1.下列说法,正确的是()A.加正号的数是正数,加负号的数是负数B.0是最小的正数C.字母a既可是正数,也可是负数,也可是0D.任意一个数,不是正数就是负数2.下列各对关系中,不具有相反意义的量的是()A.运进货物3吨与运出货物2吨B.升温3℃与降温3℃C.增加货物100吨与减少货物2000吨D.胜3局与亏本400元3.(1)如果零上5℃记作+5℃,那么零下3℃记作________ .(2)东、西为两个相反方向,如果-4米表示一个物体向西运动4米,那么+2米表示________ .物体原地不动记为________ .(3)某仓库运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作________ .(4)抗洪期间,如果水位超过标准水位 1.5米记作+1.5 米,那么后来记录的-0.9米表示_________.4.下列各数-2,0,-1/2,-10,3.5中,是正数的有_________. .5.把下列各数填入相应的括号内:-28,20,0,5,0.23,-3.2%,25%,3.14,0.62.正数集合:{ };负数集合:{ }.6.某银行一天内接待了四笔大业务,存款40000元,取款25000元,存款30万元,取款7万元.若存款为正,请你用正、负数表示这四笔款项。
人教版七年级数学上册 第一至第四章全册知识点归纳

人教版初一数学上册知识点归纳七年级数学上册知识点第一章有理数1.1 正数与负数①正数:大于0的数叫正数。
(根据需要,有时在正数前面也加上“+”)②负数:在以前学过的0以外的数前面加上负号“—”的数叫负数。
与正数具有相反意义。
③0既不是正数也不是负数。
0是正数和负数的分界,是唯一的中性数。
注意:搞清相反意义的量:南北;东西;上下;左右;上升下降;高低;增长减少等1.2 有理数1、有理数(1)整数:正整数、0、负整数统称整数;(2)分数;正分数和负分数统称分数;(3)有理数:整数和分数统称有理数。
2、数轴(1)定义:通常用一条直线上的点表示数,这条直线叫数轴;(2)数轴三要素:原点、正方向、单位长度;(3)原点:在直线上任取一个点表示数0,这个点叫做原点;(4)数轴上的点和有理数的关系:所有的有理数都可以用数轴上的点表示出来,但数轴上的点,不都是表示有理数。
3、相反数:只有符号不同的两个数叫做互为相反数。
(例:2的相反数是-2;0的相反数是0)4、绝对值:(1)数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
从几何意义上讲,数的绝对值是两点间的距离。
(2)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。
两个负数,绝对值大的反而小。
1.3 有理数的加减法①有理数加法法则:1、同号两数相加,取相同的符号,并把绝对值相加。
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3、一个数同0相加,仍得这个数。
加法的交换律和结合律②有理数减法法则:减去一个数,等于加这个数的相反数。
1.4 有理数的乘除法①有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数同0相乘,都得0;乘积是1的两个数互为倒数。
乘法交换律/结合律/分配律②有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数;两数相除,同号得正,异号得负,并把绝对值相除;0除以任何一个不等于0的数,都得0。
初一数学知识点(精选5篇)

初一数学知识点(精选5篇)第一章有理数1.整数。
(正整数、0、负整数)2.正数和负数。
3.有理数。
(整数和分数统称有理数)4.自然数。
(非负整数)5.相反数。
(只有符号不同的两个数互为相反数)6.绝对值。
(一个数的绝对值就是表示这个数的点与原点的距离)第二章代数式1.代数式。
(用运算符号把数或表示数的字母连接起来的式子)2.代数式的值。
(求代数式的值就是给代数式中的字母个代数式确定值)第三章实数1.平方根。
(如果一个数的平方等于a,那么这个数就叫做a 的平方根)2.算数平方根。
(一个非负数的正的平方根叫做算数平方根)3.立方根。
(如果一个数的立方等于a,那么这个数就叫做a 的立方根)4.实数。
(有理数和无理数)5.实数的性质。
(实数能进行减、乘、除、加、乘方运算)6.近似数。
(通过四舍五入得到的与精确数接近的数)第四章整式和分式1.整式。
(与有理数相对的数式叫整式)2.分式。
(整式的一部分)3.分式的值为零。
(分子为零且分母不等于零)4.分式的乘除。
(乘除法转化成乘法计算)5.分式的加减。
(异分母的分式加减转化成通分后求和)6.分式方程。
(分母里含有未知数的方程叫分式方程)初一数学知识点篇21.有理数:有理数包括正整数、0和负整数。
有理数可以用分数表示。
2.数轴:数轴是一条直线,它的上面写着从0开始连续不断的点。
数轴上的0是正负数的分界线。
3.相反数:如果两个数的和为0,那么这两个数是一对相反数。
相反数包括正数和负数。
4.绝对值:一个数的绝对值是它离0的距离。
正数的绝对值是它本身,负数的绝对值是它的相反数。
5.代数式:用代数式表示出数量关系和变化规律的式子。
包括等式、不等式、方程、不等式、函数等。
6.整式:整式包括单项式和多项式。
单项式是由数字和字母组成,多项式是由几个单项式组成。
7.分式:分式包括分子和分母。
分子是由数字和字母组成,分母是由分式和整式组成。
8.方程:用方程表示出两个量之间的关系,并且这个方程是一个等式。
初一上期数学第一章 有理数 知识归纳

第一章有理数1.1正数和负数1.正负数正数:大于0的数叫做正数.负数:小于0的数叫做负数.0:非正非负【注】①符号:一个数前面的“+”“-”号叫做它的符号.②正数前面的“+”号可以省略,负数前面的“-”号不可以省略.2.相反意义的量用正数和负数表示具有相反意义的量:如果正数表示某种意义,那么负数表示它的相反意义,反之亦然.【注】“相反意义的量”包括两个方面的含义:一是相反意义;二是要有量.3.“O”的特征(1)0既不是正数,也不是负数,是正数与负数的分界;(2)0是自然数;(3)0的意义:①有时表示没有,如文具盒中有0支铅笔,表示没有铅笔;②有时是一个数,如0度是一个确定的温度;③有时也作为基准,如零上3度.1.2有理数知识点一有理数1、有理数的定义:整数和分数统称为有理数(小数可以化为分数,所以看为为分数)2、有理数的分类:1):按定义⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎭⎬⎫⎪⎩⎪⎨⎧⎭⎬⎫数有限小数或无限循环小负分数正分数分数负整数自然数正整数整数有理数0 2):按正负分⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数正分数正整数正有理数有理数04、四非正数和零统称为非负数;负数和零统称为非正数;正整数和零统称为非负整数(自然数);负整数和零统称为非正整数;【技巧】读的时候,在非正、非负后面加一个“的”知识点二 数轴1、数轴的定义:用一条直线上的点表示数,这条直线叫做数轴。
2、数轴三要素原点、正方向、单位长度称为数轴的三要素,三者缺一不可.【注】单位长度:指所取度量单位的名称,是一条人为规定的代表"1"的线段,这条线段可长可短,按实际情况来规定,同一数轴上的单位长度一旦确定,不能再改变.3、数轴画法首先:画一条水平的直线;其次:在直线上选取一点为原点;再次:确定向右为正方向,用箭头表示出来;最后:根据实际情况,选取适当的长度作为单位长度.4、与有理数的关系(1)有理数和无理数都可以用数轴上的点表示出来.(2)正有理数表示的点位于原点的右边,负有理数表示的点位于原点的左边5、利用数轴比较大小数轴可以用来比较大小,左<右﹔负数<0<正数.知识点三相反数1、定义只有符号不同的两个数叫做互为相反数.【注】①一般地,a和a-互为相反数,a表示任意一个数,可以是正数、负数,也可以是0.②0的相反数是0③“只有符号不同”应与“只要符号不同”区分开﹒④相反数必须成对出现,不能单独存在.2、几何意义一对相反数表示的点在数轴上应分别位于原点两侧;到原点的距离相等;这两点是关于原点对称的.3、求法求任意一个数的相反数,只要在这个数的前面添上“—”号即可.4、相反数的性质(1)若a与b互为相反数,则0=a,则a与b互为相反数.+b=+ba;反之,若0(2)任何一个数都有相反数,而且只有一个.正数的相反数是负数;负数的相反数是正数; 0的相反数仍是0.五、多重符号化简一个正数前面不管有多少个“+”号,都可以全部去掉;一个正数前面有偶数个“―”号,也可以把“―”号全部去掉;一个正数前面有奇数个"―"号,则化简后只保留一个"―"号,即“奇负偶正”(其中“奇偶”是指正数前面的“―"号的个数的奇偶数,“负正"是指化简的最后结果的符号).知识点四 绝对值1、绝对值的定义:一般地,数轴上表示数a 的点与原点的距离叫做数a 的绝对值,记做a (a 可以是正数、负数和0)2、绝对值性质:()()()⎪⎩⎪⎨⎧<-=>=0000a a a a a a3、绝对值具有非负性(1)若有几个非负数的和为0,则这几个非负数均为0。
新人教版初一数学大纲

新人教版初一数学大纲第一章有理数1.1 正数与负数①在以前学过的0以外的数前面加上负号“—”的数叫负数(negative number)。
与负数具有相反意义,即以前学过的0以外的数叫做正数(positive number)(根据需要,有时在正数前面也加上“+”)。
②大于0的数叫正数。
③0既不是正数也不是负数。
0是正数和负数的分界,是唯一的中性数。
④搞清相反意义的量:南北;东西;上下;左右;上升下降;高低;增长减少等1.2 有理数正整数、0、负整数统称整数(integer),正分数和负分数统称分数(fraction)。
整数和分数统称有理数(rational number). 以用m/n(其中m,n是整数,n≠0)表示有理数。
通常用一条直线上的点表示数,这条直线叫数轴(number axis)。
数轴三要素:原点、正方向、单位长度。
在直线上任取一个点表示数0,这个点叫做原点(origin)。
数轴上的点和有理数的关系:所有的有理数都可以用数轴上的点表示出来,但数轴上的点,不都是表示有理数。
只有符号不同的两个数叫做互为相反数(opposite number)。
(例:2的相反数是-2;0的相反数是0)数轴上表示数a的点与原点的距离叫做数a的绝对值(absolute value),记作|a|。
从几何意义上讲,数的绝对值是两点间的距离。
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。
两个负数,绝对值大的反而小。
1.3 有理数的加减法①有理数加法法则:1.同号两数相加,取相同的符号,并把绝对值相加。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3.一个数同0相加,仍得这个数。
加法的交换律和结合律②有理数减法法则:减去一个数,等于加这个数的相反数。
1.4 有理数的乘除法①有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。
初一数学上册

初一上册数学知识点总结第一章有理数一、有理数:1、定义:凡能写成形式的数,都是有理数,整数和分数统称有理数.注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数;p不是有理数;2、有理数的分类:3、注意:有理数中,1、0、-1是三个特殊的数,它们有自己的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有自己的特性;4、自然数➩0和正整数;a>0 ➩a是正数;a<0 ➩a是负数;a≥0 ➩a是正数或0➩a是非负数;a≤0 ➩a是负数或0 ➩a是非正数.二、数轴1、定义:数轴是规定了原点、正方向、单位长度的一条直线。
三、相反数1、只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0。
2、注意: a-b+c的相反数是-a+b-c;a-b的相反数是b-a;a+b的相反数是-a-b;3、相反数的和为0 Û a+b=0 Û a、b互为相反数。
4、相反数的商为-1。
5、相反数的绝对值相等。
四、绝对值1、正数的绝对值等于它本身,0的绝对值是0,负数的绝对值等于它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;2、绝对值可表示为:4、|a|是重要的非负数,即|a|≥0;五、有理数比大小1、正数永远比0大,负数永远比0小;2、正数大于一切负数;3、两个负数比较,绝对值大的反而小;4、数轴上的两个数,右边的数总比左边的数大;5、-1,-2,+1,+4,-0.5,以上数据表示与标准质量的差,绝对值越小,越接近标准。
六、倒数1、定义:乘积为1的两个数互为倒数;2、注意:(1)0没有倒数;(2)若ab=1Û a、b互为倒数;(3)若ab=-1Û a、b互为负倒数.3、等于本身的数汇总:(1)相反数等于本身的数:0 (2)倒数等于本身的数:1,-1 (3)绝对值等于本身的数:正数和0 (4)平方等于本身的数:0,1 (5)立方等于本身的数:0,1,-1.七、有理数加法法则1、同号两数相加,取相同的符号,并把绝对值相加;2、异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;3、一个数与0相加,仍得这个数.八、有理数加法的运算律1、加法的交换律:a+b=b+a ;2、加法的结合律:(a+b)+c=a+(b+c).九、有理数减法法则减去一个数,等于加上这个数的相反数;即a-b=a+(-b).十、有理数乘法法则1、两数相乘,同号得正,异号得负,并把绝对值相乘;2、任何数同零相乘都得零;3、几个因式都不为零,积的符号由负因式的个数决定.奇数个负数为负,偶数个负数为正。
七年级上册第一章内容

七年级上册第一章内容
七年级上册第一章的内容主要是有理数。
这个章节主要包括以下内容:
1. 有理数的概念:包括正数、负数、整数、分数等。
2. 有理数的四则运算:包括加法、减法、乘法和除法。
特别地,加减法主要涉及到绝对值的计算和两数相加的符号法则(同号得正、异号得负);乘除法主要涉及到乘法交换律、乘法结合律和乘法的分配律。
3. 有理数的运算律:包括加法交换律、加法结合律、乘法交换律、乘法结合律和乘法分配律。
4. 有理数的运算顺序:先乘除后加减,并注意括号在运算中的作用。
此外,七年级上册第一章还会介绍数轴的概念,这是理解有理数和四则运算的重要工具。
在学习过程中,应重视理解有理数的意义,掌握四则运算的方法,并注意培养运算的准确性和熟练度。
七年级上册初一数学

第一章有理数1.1 正数与负数①正数:大于0的数叫正数。
(根据需要,有时在正数前面也加上“+”)②负数:在以前学过的0以外的数前面加上负号“—”的数叫负数。
与正数具有相反意义。
③0既不是正数也不是负数。
0是正数和负数的分界,是唯一的中性数。
注意搞清相反意义的量:南北;东西;上下;左右;上升下降;高低;增长减少等1.2 有理数1、有理数(1)整数:正整数、0、负整数统称整数;(2)分数;正分数和负分数统称分数;(3)有理数:整数和分数统称有理数。
2、数轴(1)定义:通常用一条直线上的点表示数,这条直线叫数轴;(2)数轴三要素:原点、正方向、单位长度;(3)原点:在直线上任取一个点表示数0,这个点叫做原点;(4)数轴上的点和有理数的关系:所有的有理数都可以用数轴上的点表示出来,但数轴上的点,不全表示有理数。
3、相反数只有符号不同的两个数互为相反数。
(如2的相反数是-2,0的相反数是0)4、绝对值(1)数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
从几何意义上讲,数的绝对值是两点间的距离。
(2)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。
两个负数,绝对值大的反而小。
1.3 有理数的加减法有理数加法法则:1、同号两数相加,取相同的符号,并把绝对值相加。
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3、一个数同0相加,仍得这个数。
加法的交换律和结合律。
有理数减法法则:减去一个数,等于加这个数的相反数。
1.4 有理数的乘除法有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数同0相乘,都得0。
乘积是1的两个数互为倒数。
乘法交换律、结合律、分配律。
②有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数;两数相除,同号得正,异号得负,并把绝对值相除;0除以任何一个不等于0的数,都得0。
初一数学@有理数的概念
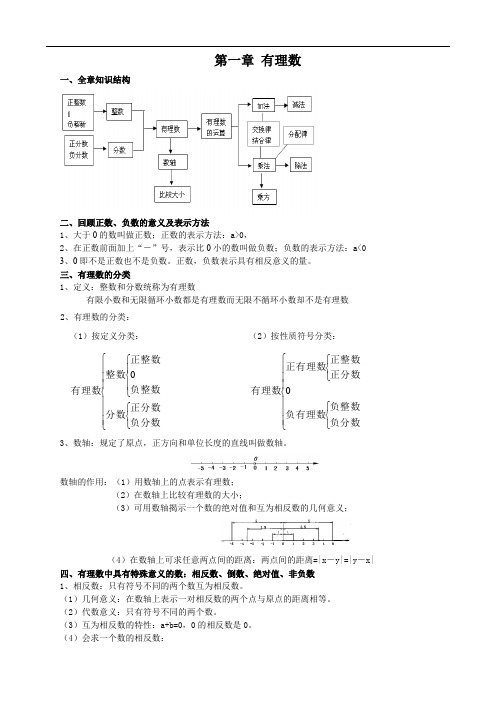
第一章 有理数一、全章知识结构二、回顾正数、负数的意义及表示方法1、大于0的数叫做正数;正数的表示方法:a>0,2、在正数前面加上“-”号,表示比0小的数叫做负数;负数的表示方法:a<03、0即不是正数也不是负数。
正数,负数表示具有相反意义的量。
三、有理数的分类1、定义:整数和分数统称为有理数有限小数和无限循环小数都是有理数而无限不循环小数却不是有理数 2、有理数的分类:(1)按定义分类: (2)按性质符号分类:3、数轴:规定了原点,正方向和单位长度的直线叫做数轴。
数轴的作用:(1)用数轴上的点表示有理数; (2)在数轴上比较有理数的大小;(3)可用数轴揭示一个数的绝对值和互为相反数的几何意义;(4)在数轴上可求任意两点间的距离:两点间的距离=|x -y|=|y -x|四、有理数中具有特殊意义的数:相反数、倒数、绝对值、非负数 1、相反数:只有符号不同的两个数互为相反数。
(1)几何意义:在数轴上表示一对相反数的两个点与原点的距离相等。
(2)代数意义:只有符号不同的两个数。
(3)互为相反数的特性:a+b=0,0的相反数是0。
(4)会求一个数的相反数:⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数正整数整数有理数0⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数正分数正整数正有理数有理数a 的相反数为 a-b 的相反数为 2、倒数:(1)乘积是1的两个数互为倒数 (2)互为倒数的特性: ab=1, (3)0没有倒数(4)互为负倒数: 乘积是-1的两个数互为负倒数; ab=-1 3、非负数:(1)就是大于或等于0的数:a 0(2)数轴上,在原点的右边包括原点的点表示的数 (3)任何数的平方数都是非负数(4)非正数:就是小于或等于0的数:a 0(5)数轴上,在原点的左边包括原点的点表示的数 4、绝对值:(1)几何意义:一个数的绝对值就是它到原点的距离。
(2)代数意义:正数的绝对值是它本身,负数的绝对值是它的相反数,零的绝对值是零。
人教版初中数学--第一章 有理数

(1) 6-9 ;
(2)4-(-7);
(3) (-5)-(-8); (4)0-(-5);
(5) (-2.5)-5.9 ; (6)1.9-(-0.6).
1.3.2 有理数的减法
• 探究:例题 计算(-20)+(+3)-(-5)-(+7) 解=(-20)+(+3)+(+5)+(-7) =[(-20)+(-7)]+(3+5) =-27+8 =-19
1.2.3 相反数
• 观察:数轴上的2与-2,3与-3到原点的距离有什么特征?
2
2
-3 -2 -1
0
12 3
3
3
• 我们看到2和-2,以及3和-3两组数中,虽然2与-2分别在原点的右边与左边,但它们与原点的距离都等于2;
虽然3与-3分别在原点的右边和左边,但它们与原点的距离都等于3.
• 一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示-a和a,我们 说这两点关于原点对称。
另一方面,我们知道 3+(+12)=15 ②
• 由①② ,有
3-(-12)=3+(+12)③
• 规律:减去一个数等于加上这个数的相反数
•
a-b=a+(-b)
1.3.2 有理数的减法
• 练习 • 1计算 • • 2计算 • •
(1) (-3)-(-25); (2)0-7;
(3) 7.2-(-4.8); (4)(-7/2)-21/4
• 0是正数与负数的分界。0℃是一个确定的温度,海拔0表示海平面的平均高 度,0的意义不仅是表示“没有”。
正数与负数--巩固练习
(完整版)人教版初一数学知识点总结
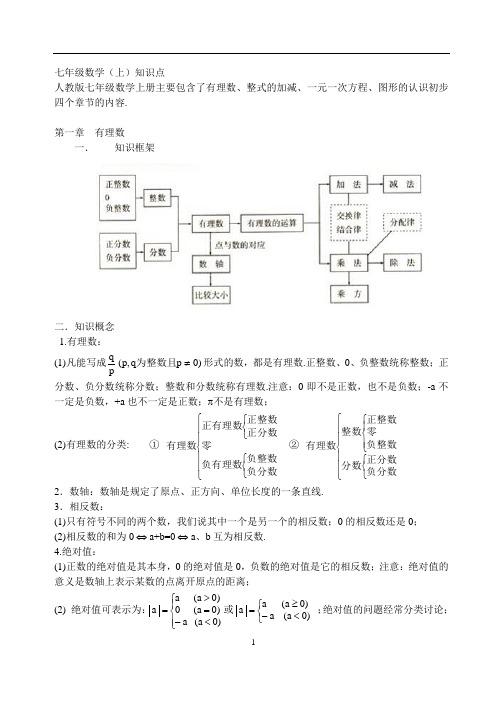
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a . 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初一数学(上下册)目录

初一数学(上下册)目录第一章有理数
第一节有理数的加减法
第二节有理数的乘除法
第三节有理数的乘方
1 乘方
2 科学记数法
3 近似数
第二章整式的加减
第一节整式
第二节整式的加减
第三章一元一次方程
第一节从算式到方程
1 一远一次方程
2 等式的性质
第二节解一元一次方程
1合并同类项与移项
2 去括号与分母
3 实际问题与一元一次方程
第四章图形
第一节几何图形点线面体
第二节直线射线线段
第三节角
1 角
2 角的比较与运算
3 余角与补角
第五章相交线与平行线
第一节1 相交线
2垂线
3同位角内错角同旁内角第二节平行线及其判定
1 平行线
2 平行线的性质
3 命题定理
4 平移
第六章平面直角坐标系
第一节平面直角坐标系
第二节坐标方法的简单应用
第七章三角形
第一节与三角形有关的线段
1 三角形的高线中线和角平分线
2 三角形的稳定性
第二节与三角形有关的角
1 三角形的外角
第二节多边形及其内角和
第八章二元一次方程组
第一节二元一次方程组
第二节消元—二元一次方程组的饿接法第九章不等式与不等式组
第一节不等式
第二节实际问题与一元一次不等式
第三节一元有次不等式组
第十章数据的收集整理与描述
第一节统计调查
第二节直方图。
人教版七年级上册数学 第一章《有理数》第1讲 有理数 (答案+解析)

人教版七年级上册数学第一章《有理数》第1讲有理数(答案+解析)数轴。
在数轴上所表示的数,右边的数总比左边的数大,即从数轴的左边到右边所对应的数逐渐变大,所以正数都大于0,负数都小于0,正数大于负数。
概念剖析:①、画数轴时数轴的三要素原点、正方向、单位长度缺一不可;②、数轴的方向不一定都是水平向右的,数轴的方向可以是任意的方向;③、数轴上的单位长度没有明确的长度,但单位长度与单位长度要保持相等;④、有理数在数轴上都能找到点与之对应,一般地,设a 是一个正数,则数轴上表示数a 的点在原点的右边,与原点的距离是a 个单位长度;表示数a -的点在原点的左边,与原点的距离是a 个单位长度。
⑤、在数轴上求任意两点a 、b 的距离L,则有公式a b L b a L -=-=或,这两个公式选择那个都一样。
知识点四:相反数如果两个数只有符号不同,那么其中一个数就叫另一个数的相反数。
0的相反数是0,互为相反的两个数,在数轴上位于原点的两则,并且与原点的距离相等。
概念剖析:①、“如果两个数只有符号不同,那么其中一个数就叫另一个数的相反数”,不要茫然的认为“如果两个数符号不同,那么其中一个数就叫另一个数的相反数”。
②、显然,数a 的相反数是a -,即a 与a -互为相反数。
要把它与倒数区分开。
③、互为相反数的两个数在数轴上对应的点一个在原点的左边,一个在原点的右边,且离原点的距离相等,也就是说它们关于原点对称。
④、在数轴上离某点的距离等于a 的点有两个。
⑤、如果数a 和数b 互为相反数,则a +b =0;)0(1≠-=ab b a 或)0(1≠-=ab ab ; ⑥、求一个数的相反数,只要在这个数的前面加上“—”即可;例如b a -的相反数是a b -;知识窗口:①一个数前面加上“—”号,该数就成了它的相反数;②一个数前面的符号确定方法:奇数个负号相当于一个负号,偶数个负号相当于一个正号,而与正号的个数无关。
知识点五:绝对值数轴上表示数a 的点与原点的距离叫做数a 的绝对值。
初一数学第一章有理数计算题

初一数学第一章有理数计算题一、有理数加法运算(5题)1. 计算:(-3)+5- 解析:异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
| - 3|=3,|5| = 5,5>3,所以结果为正,5 - 3=2。
- 答案:22. 计算:4+(-7)- 解析:异号两数相加,|4| = 4,| - 7|=7,7>4,取负号,7 - 4 = 3。
- 答案:-33. 计算:(-2)+(-3)- 解析:同号两数相加,取相同的符号,并把绝对值相加。
| - 2|+| - 3|=2 + 3=5,符号为负。
- 答案:-54. 计算:0+(-6)- 解析:0加任何数等于这个数本身,所以0+(-6)=-6。
- 答案:-65. 计算:(-5)+5- 解析:互为相反数的两数相加得0,-5和5互为相反数。
- 答案:0二、有理数减法运算(5题)1. 计算:5-(-3)- 解析:减去一个数等于加上这个数的相反数,所以5-(-3)=5 + 3=8。
- 答案:82. 计算:4 - 7- 解析:4-7=4+(-7),异号两数相加,|4| = 4,| - 7|=7,7>4,取负号,7 - 4=3,结果为-3。
- 答案:-33. 计算:(-3)-(-5)- 解析:(-3)-(-5)=(-3)+5,异号两数相加,| - 3|=3,|5| = 5,5>3,取正号,5 - 3 = 2。
- 答案:24. 计算:0-(-6)- 解析:0-(-6)=0 + 6=6。
- 答案:65. 计算:(-6)-6- 解析:(-6)-6=(-6)+(-6),同号两数相加,| - 6|+| - 6|=6+6 = 12,符号为负。
- 答案:-12三、有理数乘法运算(5题)1. 计算:(-2)×3- 解析:异号两数相乘得负,| - 2|×|3|=2×3 = 6,所以结果为-6。
- 答案:-62. 计算:4×(-5)- 解析:异号两数相乘得负,|4|×| - 5|=4×5 = 20,结果为-20。
初一上册数学总结与复习(含有理数)

初一数学上册知识点总结:有理数第一章有理数1.有理数:(1)凡能写成形式的数,都是有理数,整数和分数统称有理数.注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数; 不是有理数;(2)有理数的分类: ①②(3)注意:有理数中,1、0、-1是三个特殊的数,它们有自己的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有自己的特性;(4)自然数 0和正整数; a>0 a是正数; a<0 a是负数;a≥0 a是正数或0 a是非负数; a≤ 0 a是负数或0 a是非正数.2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)注意: a-b+c的相反数是-a+b-c;a-b的相反数是b-a;a+b的相反数是-a-b;(3)相反数的和为0 a+b=0 a、b互为相反数.(4)相反数的商为-1.(5)相反数的绝对值相等4.绝对值:(1)正数的绝对值等于它本身,0的绝对值是0,负数的绝对值等于它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:或 ;(3) ; ;(4) |a|是重要的非负数,即|a|≥0;5.有理数比大小:(1)正数永远比0大,负数永远比0小;(2)正数大于一切负数;(3)两个负数比较,绝对值大的反而小;(4)数轴上的两个数,右边的数总比左边的数大;(5)-1,-2,+1,+4,-0.5,以上数据表示与标准质量的差,绝对值越小,越接近标准。
6.倒数:乘积为1的两个数互为倒数;注意:0没有倒数; 若ab=1 a、b互为倒数; 若ab=-1 a、b互为负倒数.等于本身的数汇总:相反数等于本身的数:0倒数等于本身的数:1,-1绝对值等于本身的数:正数和0平方等于本身的数:0,1立方等于本身的数:0,1,-1.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b).10 有理数乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个因式都不为零,积的符号由负因式的个数决定.奇数个负数为负,偶数个负数为正。
人教版初一数学上册知识点归纳总结(精华版)

第一章有理数1.有理数: (1)凡能写成)0p q ,p (pq≠为整数且形式的数,都是有理数,整数和分数统称有理数. 注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 (3)注意:有理数中,1、0、-1是三个特殊的数,它们有自己的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有自己的特性;(4)自然数⇔ 0和正整数; a >0 ⇔ a 是正数; a <0 ⇔ a 是负数;a ≥0 ⇔ a 是正数或0 ⇔ a 是非负数; a ≤ 0 ⇔ a 是负数或0 ⇔ a 是非正数. 2.数轴:数轴是规定了原点、正方向、单位长度(数轴的三要素)的一条直线. 3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)注意: a-b+c 的相反数是-(a-b+c)= -a+b-c ;a-b 的相反数是b-a ;a+b 的相反数是-a-b ; (3)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. (4)相反数的商为-1. (5)相反数的绝对值相等 4.绝对值:(1)正数的绝对值等于它本身,0的绝对值是0,负数的绝对值等于它的相反数; 注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或 ⎩⎨⎧≤-≥=)0()0(a a a a a ; (3)0a 1aa >⇔= ;0a 1aa <⇔-=;(4) |a|是重要的非负数,即|a|≥0,非负性; 5.有理数比大小:(1)正数永远比0大,负数永远比0小; (2)正数大于一切负数;(3)两个负数比较,绝对值大的反而小;(4)数轴上的两个数,右边的数总比左边的数大;(5)-1,-2,+1,+4,-0.5,以上数据表示与标准质量的差,绝对值越小,越接近标准。
人教版七年级上册数学知识点归纳:第一章有理数

人教版七年级上册数学知识点归纳第一章有理数一.正数和负数⒈正数和负数的概念负数:比0小的数正数:比0大的数0既不是正数,也不是负数注意:①字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a是正数;当a表示0时,-a仍是0。
(如果出判断题为:带正号的数是正数,带负号的数是负数,这种说法是错误的,例如+a,-a就不能做出简单判断)②正数有时也可以在前面加“+”,有时“+”省略不写。
所以省略“+”的正数的符号是正号。
2.具有相反意义的量若正数表示某种意义的量,则负数可以表示具有与该正数相反意义的量,比如:零上8℃表示为:+8℃;零下8℃表示为:-8℃支出与收入;增加与减少;盈利与亏损;北与南;东与西;涨与跌;增长与降低等等是相对相反量,它们计数:比原先多了的数,增加增长了的数一般记为正数;相反,比原先少了的数,减少降低了的数一般记为负数。
3.0表示的意义⑴0表示“没有”,如教室里有0个人,就是说教室里没有人;⑵0是正数和负数的分界线,0既不是正数,也不是负数。
二.有理数1.有理数的概念⑴正整数、0、负整数统称为整数(0和正整数统称为自然数)⑵正分数和负分数统称为分数⑶正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数。
理解:只有能化成分数的数才是有理数。
①π是无限不循环小数,不能写成分数形式,不是有理数。
②有限小数和无限循环小数都可化成分数,都是有理数。
注意:引入负数以后,奇数和偶数的范围也扩大了,像-2,-4,-6,-8…也是偶数,-1,-3,-5…也是奇数。
2. (1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ①按正、负分类: ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数②按有理数的意义来分:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数总结:①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数(3)注意:有理数中,1、0、-1是三个特殊的数,它们有自己的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有自己的特性;(4)自然数⇔ 0和正整数;a>0 ⇔ a是正数;a<0 ⇔ a是负数;a≥0 ⇔ a是正数或0 ⇔ a是非负数;a≤0 ⇔ a是负数或0 ⇔ a是非正数.三.数轴⒈数轴的概念规定了原点,正方向,单位长度的直线叫做数轴。
初一数学目录

初一数学目录人教版初一数学上册目录:第一章有理数1.1正数和负数阅读与思考用正负数表示加工允许误差1.3有理数的加减法实验与探究填幻方阅读与思考中国人最先使用负数1.4有理数的乘除法观察与思考翻牌游戏中的数学道理1.5有理数的乘方数学活动小结复习题1第二章整式的加减2.1整式阅读与思考数字1与字母X的对话2.2整式的加减信息技术应用电子表格与数据计算数学活动小结复习题2第三章一元一次方程3.1从算式到方程阅读与思考“方程”史话3.2解一元一次方程(一)——合并同类项与移项实验与探究无限循环小数化分数3.3解一元一次方程(二)——去括号与去分母3.4实际问题与一元一次方程数学活动小结复习题3第四章图形认识初步4.1多姿多彩的图形阅读与思考几何学的起源4.2直线、射线、线段阅读与思考长度的测量4.3角4.4课题学习设计制作长方体形状的包装纸盒数学活动小结复习题4部分中英文词汇索引初一数学下册目录:第五章相交线与平行线5.1相交线5.1.2垂线5.1.3同位角、内错角、同旁内角观察与猜想5.2平行线及其判定5.2.1平行线5.3平行线的性质5.3.1平行线的性质5.3.2命题、定理5.4平移教学活动小结第六章平面直角坐标系6.1平面直角坐标系6.2坐标方法的简单应用阅读与思考6.2坐标方法的简单应用教学活动小结第七章三角形7.1与三角形有关的线段7.1.2三角形的高、中线与角平分线7.1.3三角形的稳定性信息技术应用7.2与三角形有关的角7.2.2三角形的外角阅读与思考7.3多变形及其内角和阅读与思考7.4课题学习镶嵌教学活动小结第八章二元一次方程组8.1二元一次方程组8.2消元——二元一次方程组的解法8.3实际问题与二元一次方程组阅读与思考*8.4三元一次方程组解法举例教学活动小结第九章不等式与不等式组9.1不等式阅读与思考9.2实际问题与一元一次不等式实验与探究9.3一元一次不等式组阅读与思考教学活动小结第十章数据的收集、整理与描述10.1统计调查实验与探究10.2直方图10.3课题学习从数据谈节水教学活动小结部分中英文词汇索引。
初一上册数学目录

第一章有理数
1.1 正数和负数
阅读与思考用正负数表示加工允许误差
1.2 有理数
1.3 有理数的加减法
实验与探究填幻方
阅读与思考中国人最先使用负数
1.4 有理数的乘除法
观察与思考翻牌游戏中的数学道理
1.5 有理数的乘方
数学活动
小结
复习题1
第二章整式的加减
2.1 整式
阅读与思考数字1与字母X的对话
2.2 整式的加减
信息技术应用电子表格与数据计算
数学活动
小结
复习题2
第三章一元一次方程
3.1 从算式到方程
阅读与思考“方程”史话
3.2 解一元一次方程(一)——合并同类项与移项
实验与探究无限循环小数化分数
3.3 解一元一次方程(二)——去括号与去分母
3.4 实际问题与一元一次方程
数学活动
小结
复习题3
第四章图形认识初步
4.1 多姿多彩的图形
阅读与思考几何学的起源
4.2 直线、射线、线段
阅读与思考长度的测量
4.3 角
4. 4 课题学习设计制作长方体形状的包装纸盒hv h xccccccccccccccccccccccccccccccccc。
