高考物理竞赛量子力学部分第八章 散射理论ppt课件
合集下载
散射理论 ppt课件
❖ 如果在均匀介质中掺入一些大小为波长数量级 且杂乱分布的颗粒物质，它们的折射率与周围均匀 介质的折射率不同，如胶体溶液、悬乳液、乳状物 等，原来均匀介质的光学均匀性遭到破坏，次波干 涉的均匀性也受到破坏。这种含有不均匀无规则分 布的颗粒物质的介质引起了光的散射。这时，散射 光的强度分布及偏振规律与散射颗粒的大小、颗粒 相对周围介质的折射率有关。
边界条件：
n ( D1 D2 ) , n ( E1 E2 ) 0 n ( B1 B2 ) 0, n ( H 1 H 2 )
❖ 得亥姆霍兹波动方程：
2Ek2E 0 2H k2H 0
散射理论
❖ 当电导率 0 时, k2 2 ,则波动方程为
2E2 E 0
2H 2 H 0
散射理论
❖ 在研究光散射现象时，常常引入散射光强、散 射截面、吸收截面、消光截面以及相应的散射系数 、吸收系数和消光系数等描述散射现象的物理量。 这些物理量与散射颗粒的大小、折射率以及入射光 的波长等因素存在密切的关系
❖ （1）散射截面
❖ 一个散射颗粒在单位时间内散射的全部光能量E sca 与入射光强 I 0 之比称为散射截面，记作 C sca 。
散射理论
散射理论
❖ 光波是电磁波，光波在介质中的传播与介质的特性 有关，并且服从 Maxwell 电磁场方程。因此，光波 在介质中的传播规律。
❖ Maxwell方程组：
E H , • D t
H J E ， • B 0 t
物质方程：
D E r0E, B H r0H J E
❖ 众所周知，在均匀介质中，光线将沿原有的方向 传播而不发生散射现象。当光线从一均匀介质进入 另一均匀介质时，根据麦克斯韦电磁场理论，它只 能沿着折射光线的方向传播，这是由于均匀介质中 偶极子发出的次波具有与人射光相同的频率，并且 偶极子发出的次波间有一定的位相关系，它们是相 干的，在非折射光的所有方向上相互抵消，所以只 发生折射而不发生散射。
高中物理竞赛辅导《量子力学初步》课件
量子力学方程
是否存在一个
根据某种条件可求出微观粒子的
基本算符
量子力学中的
算符是表示对某一函数进行某种数学运算的符号。在量子力学中，一切力学量都可用算符来表示。这是量子力学的一个很重要的特点。
算 符
劈形算符
数学运算符号
拉普拉斯算符
动量算符
动能算符
哈密顿算符
含动、势能
位矢算符
力 学 量 算 符 统称 举 例
（4）
小议链接2
结束选择
请在放映状态下点击你认为是对的答案
下列波函数中合理的是
（1） ；
（2） ；
（3） ；
（4）
小议链接3
结束选择
请在放映状态下点击你认为是对的答案
下列波函数中合理的是
（1） ；
（2） ；
（3） ；
（4）
小议链接4
结束选择
请在放映状态下点击你认为是对的答案
下列波函数中合理的是
（1） ；
（2） ；
自由粒子的
波函数
自由粒子的能量和动量为常量，其波函数所描述的德布
罗意波是平面波。
不是常量，其波函数所描述的德布罗意波就不是平面波。
对于处在外场作用下运动的非自由粒子，其能量和动量
外场不同，粒子的运动状态及描述运动状态的波函数也
不相同。
微观客体的运动状态可用波函数来描述，这是
量子力学的一个基本假设。
量子化等概念。
续上求解
阱内
阱外
只有
因
及
要连续、有限，
薛定谔方程才成立，
在阱外
故粒子在无限深势阱外出现的概率为零。
设质量为 的微观粒子，
处在一维无限深势阱中，
是否存在一个
根据某种条件可求出微观粒子的
基本算符
量子力学中的
算符是表示对某一函数进行某种数学运算的符号。在量子力学中，一切力学量都可用算符来表示。这是量子力学的一个很重要的特点。
算 符
劈形算符
数学运算符号
拉普拉斯算符
动量算符
动能算符
哈密顿算符
含动、势能
位矢算符
力 学 量 算 符 统称 举 例
（4）
小议链接2
结束选择
请在放映状态下点击你认为是对的答案
下列波函数中合理的是
（1） ；
（2） ；
（3） ；
（4）
小议链接3
结束选择
请在放映状态下点击你认为是对的答案
下列波函数中合理的是
（1） ；
（2） ；
（3） ；
（4）
小议链接4
结束选择
请在放映状态下点击你认为是对的答案
下列波函数中合理的是
（1） ；
（2） ；
自由粒子的
波函数
自由粒子的能量和动量为常量，其波函数所描述的德布
罗意波是平面波。
不是常量，其波函数所描述的德布罗意波就不是平面波。
对于处在外场作用下运动的非自由粒子，其能量和动量
外场不同，粒子的运动状态及描述运动状态的波函数也
不相同。
微观客体的运动状态可用波函数来描述，这是
量子力学的一个基本假设。
量子化等概念。
续上求解
阱内
阱外
只有
因
及
要连续、有限，
薛定谔方程才成立，
在阱外
故粒子在无限深势阱外出现的概率为零。
设质量为 的微观粒子，
处在一维无限深势阱中，
高考物理竞赛量子力学部分课程小结精品PPT课件
单粒子行为还是单粒子“系综”的行为？ Von Neumann定理：(d>1)
n
变态变为量子态的方程式，或反之 无相互作用的分开(I)和(II)
无相互作用的分开(I)和(II)
希望能预言某些新的与量子力学结果不同的东西，因为只有这样，才能通过新的实验来检查隐变数理论是否正确，一个成功的隐变数
• 证实由隐变态给出的结果在一定条件下能回 理论，不但应该能解释量子力学可以解释的现象，而且能预言更多更新的现象，而这些新的预言是否成立，依赖于实验。
课程总结
课程总结
课程总结
课程总结
➢量子力学近年来的发展 • 更多的应用 • 量子纠缠和量子信息 • 量子计算 •…
课程总结
欲知后事如何，且聽高等量子力学分解
聰明纍
機關算盡太聰明，反算暸卿卿性命。生前心已 碎，死后性空靈。傢富人寧，終有個傢散人 亡各奔騰。枉費暸，意懸懸半世心；好一似， 蕩悠悠三更夢。忽喇喇似大廈傾，昏慘慘似 燈將盡。呀！一場辛苦忽悲辛。嘆人世，終 難定！
课程总结
Von Neumann定理：(d>1) • 若<1>=1；<cA>=c<A>；若A非负，则
<A>≥0；<A+B+C+…>=<A>+<B>+<C>+… 则必存在<ΔD^2>≠0的可观测量D
课程总结
Gleason修正：(d>2，A,B,C对易算符)
课程总结
➢定域隐变数理论及Bell不等式 • 引入隐变数{λn},(n=1,2,…)，规定它们可能取
新編 “聰明纍”
慾將“變數”說分明，反誤暸卿卿性命。“糾 纏”非“定域”，量子性空靈。天地人靈， 難道是，隂陽互補兩昇騰？枉費暸，先賢門 半世心，依舊是，白濛濛一天霧！休斷言已 “大廈”傾，莫奢談“認識”已盡。呀！算 它“完備”又如何？想“測準”，終難定！
散射理论PPT
有关散射的几个物理量
在研究光散射现象时，常常引入散射光强、散 射截面、吸收截面、消光截面以及相应的散射系 数、吸收系数和消光系数等描述散射现象的物理 量。这些物理量与散射颗粒的大小、折射率以及 入射光的波长等因素存在密切的关系
（1）散射截面
一个散射颗粒在单位时间内散射的全部光能量
入射光强 之I0比称为散射截面，记作
适。用米。氏粒 散子 射线 不度 同大于于瑞1利0 散的射较呈大对微称粒状散分射布称，为常米被氏用散于射
大气中滴粒分布的研究。 一、Mie 散射公式：
不考虑光波的偏振性，将光波作为标量波处理， 取散射颗粒处为坐标原点，入射光沿z 轴正方向传 播，在远离散射体处的散射光波为球面波，
其波源就是散射体。图中,r为散射光观察点与散射体 的距离，散射角为θ，观察点与Z轴组成的平面即为
众所周知，在均匀介质中，光线将沿原有的方向 传播而不发生散射现象。当光线从一均匀介质进入 另一均匀介质时，根据麦克斯韦电磁场理论，它只 能沿着折射光线的方向传播，这是由于均匀介质中 偶极子发出的次波具有与人射光相同的频率，并且 偶极子发出的次波间有一定的位相关系，它们是相 干的，在非折射光的所有方向上相互抵消，所以只 发生折射而不发生散射。
非耗散介质。波的能流为S =E×H，其传播方向即波
矢k 的方向。
当电导率
0时，
k2
2 (
i
), k
kR
ikI
为简单起见，考虑沿X轴方向传播的平面波。
波动方程为
d 2E dx2
2 (
i
)E
0
d 2H dx2
2 (
i
)H
0
其解为
E E0 exp(kI x) exp[i(kR x t)] H H0 exp(kI x) exp[i(kR x t)]
量子力学课件第八章
第八章 WKB 近似WKB （Wenzel ，Kramers, Brillouin ）1方法是得到一维定态Schrödinger 方程的近似解的一种技术（它的基本思想同样可应用于许多其他形式的微分方程和三维Schrödinger 方程的径向部分）。
此法对计算束缚态能量和势垒穿透率都是非常有用的。
它的基本思想如下：假设能量为E 的粒子穿过势能V(x)的区域，其中V(x)为常量。
当E>V 时，则波函数的形式为()ikxx Ae ψ±=，其中k ≡正号表示粒子向右运动，而负号表示它向左运动（当然，通解是两项的线性组合）。
波函数为振荡函数，具有固定的波长（λ=2π/k ）和不变的振幅（A ）。
现在设想V(x)不是一个常量，但是变化相比λ非常缓慢，因此包含许多全波长的区域中的势能可以认为基本上是不变的。
这样，除了波长和振幅随x 缓慢的变化外，可以合理地认为ψ实际上仍然保持正弦形式。
这就是隐藏在WKB 近似后面的核心思想。
它将依赖x 的问题有效地分为两种不同层次：快速振荡和由振幅和波长逐渐变化的调制。
同理，当E<V （其中V 为常量）时，ψ的指数形式为：()xx Ae κψ=其中κ≡如果V(x)不是常量，但是相比1/κ变化很缓慢，除了A 和κ随x 缓慢的变化外，则解可以认为基本上仍然保持指数形式。
现在仍然有一处整个方法不适用的地方，这就是经典转折点的邻域，此处E ≈V 。
因为此处的λ（或者1/κ）趋于无穷大，从而，相比之下V(x)就很难说是“缓慢的”变化了。
我1在荷兰此为KWB ，在法国此为BWK ，在英国此为JWKB （J 为Jeffreys ）们将会看到，对于转折点的恰当地处理将是WKB 近似最难的一个部分，尽管最终的结果形式简洁并易于应用。
8.1经典区域定态Schrödinger 方程()2222d V x E m dx ψψψ-+=可以改写为下列形式：2222d p dx ψψ=- [8.1]其中()p x ≡ [8.2]这是具有总能量E 和势能V(x)的粒子的动量的经典表示式。
量子力学(全套) ppt课件
1 n2
人们自然会提出如下三个问题：
1. 原子线状光谱产生的机制是什么？ 2. 光谱线的频率为什么有这样简单的规律？
nm
3. 光谱线公式中能用整数作参数来表示这一事实启发我们 思考： 怎样的发光机制才能认为原子P的PT课状件态可以用包含整数值的量来描写12 。
从前，希腊人有一种思想认为：
•2.电子的能量只是与光的频率有关，与光强无关，光
强只决定电子数目的多少。光电效应的这些规律是经典
理论无法解释的。按照光的电磁理论，光的能量只决定
于光的强度而与频率无关。
PPT课件
24
（3） 光子的动量
光子不仅具有确定的能量 E = hv，
而且具有动量。根据相对论知，速度 为 V 运动的粒子的能量由右式给出：
nm
11
谱系
m
Lyman
1
Balmer
2
Paschen
3
Brackett
4
Pfund
5
氢原子光谱
n 2,3,4,...... 3,4,5,...... 4,5,6,...... 5,6,7,...... 6,7,8,......
区域 远紫外 可见 红外 远红外 超远红外
RH
C
1 m2
自然之美要由整数来表示。例如：
奏出动听音乐的弦的长度应具有波长的整数倍。
这些问题，经典物理学不能给于解释。首先，经典物理学不能 建立一个稳定的原子模型。根据经典电动力学，电子环绕原子 核运动是加速运动，因而不断以辐射方式发射出能量，电子的 能量变得越来越小，因此绕原子核运动的电子，终究会因大量 损失能量而“掉到”原子核中去，原子就“崩溃”了，但是， 现实世界表明，原子稳定的存在着。除此之外，还有一些其它 实验现象在经典理论看来是难以解释的，这里不再累述。
散射理论
第八章 散射理论本章介绍：前面讨论了薛定谔方程中的束缚态问题。
而对于能量连续的散射态，能级间隔趋于零，因此一般说来，不能用微扰论来处理。
另一方面，微观粒子之间的散射或称碰撞过程的研究，对于了解许多实验现象十分重要，所以，建立一套散射理论无论从实验上看，还是使理论更加完善上看，都是完全必要的。
本章将分别就弹性散射和非弹性散射，按入射粒子的能量高低，分别建立不同的散射理论，并介绍了分波法和玻恩近似两种处理散射问题的近似方法。
§8.1 散射截面§8.2 分波法§8.3 分波法应用实例§8.4 玻恩近似§8.5 质心坐标系与实验坐标系§8.6 全同粒子的散射§8.1 散射截面在经典力学中，弹性散射是按照粒子在散射过程中，同时满足动量守恒和能量守恒来定义的。
在量子力学中，一般说来，除非完全略去粒子之间的相互作用势能，否则，动量将不守恒。
因此，在量子力学中，不可能按经典力学的公式来定义弹性散射。
在量子力学中，如果在散射过程中两粒子之间只有动量交换，粒子由内部运动状态决定，则这种碰撞过程成为弹性散射。
如果在散射过程中粒子内部运动状态有所变化，如激发、电离等则称为非弹性散射。
本章只讨论弹性散射问题。
考虑一束入射粒子流向粒子A 射来，取粒子流入射方向为z 轴。
A 为散射中心。
为讨论方便起见，假定A 的质量比入射粒子大得多，由碰撞引起的A 的运动可以忽略。
应当指出，散射过程是两体问题。
因为它涉及两个互相散射的粒子。
对于两体问题，最好的处理方法是采用质心坐标系。
因为在质心坐标系中，一个两体问题将被归结为一个粒子因为与质心的相互作用而被散射。
另一粒子的运动可对称给出。
从而归结为单体问题。
如果散射中心粒子A 的质量比入射粒子大得多，可以认为质心就在A 上，这样就使问题处理简单多了。
如图所示，入射粒子受A 的作用而偏离原来的运动方向，发生散射。
图中A 角为散射粒子的方向与入射粒子方向的夹角，称为散射角。
年高二物理竞赛康普顿散射课件
EK即为K 壳层电子结合能的数值, 从K 壳层发射出来的最大动能Emax为 :
Emax E EK 41.33KeV
例：钨的K吸收限为0.0178nm，K线系的平均波长为 λKα=0.0211nm，λKβ=0.0184nm，λKγ=0.0179nm。
(1)试画出钨的X射线能级图； (2)若用高压为80keV的X射线管产生的辐射照在钨上，
Wn 80 0 80keV
例：钨的K吸收限为0.0178nm，K线系的平均波长为 λKα=0.0211nm，λKβ=0.0184nm，λKγ=0.0179nm。
EK
1240nm eV 0.0178nm
69.7keV
E=0 EN=-0.4keV
n∞ N, n=4
EK
1240nm eV 0.0211nm
8.5 康普顿散射
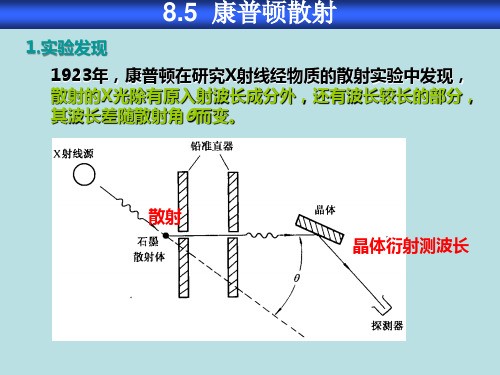
1.实验发现
1923年，康普顿在研究X射线经物质的散射实验中发现， 散射的X光除有原入射波长成分外，还有波长较长的部分，
其波长差随散射角θ而变。
散射
晶体衍射测波长
X射线发射谱线波数同X射线吸收限波数的关系： 如:Kα1线是K能级和LIII能级之间 的跃迁产生的，所以Kα1线的波 数等于K吸收限和LIII吸收限波数 只差。
EK
1240nm eV 0.0178nm
69.7keV
EK
1240nm eV 0.0211nm
58.8keV
EK
1240nm eV 0.0184nm
67.4keV
1240nm
EK
eV 0.0179nm
69.3keV
EL EK EK 10.9keV EM EK EK 2.3keV EN EK EK 0.4keV
讨论：
大学物理竞赛培训量子物理部分资料PPT课件
M B (T )
2hc 25
e hc
1
kT
1
第7页/共123页
普朗克公式→维恩公式
M B (T )
2hc 25
1 e hc kT
1
λ很小或T很小
hc 1
kT
M B (T ) 2hc25ehc kT
令：
C1 2hc2
C2
hc k
即得维恩公式：
M
B
(T
)
C e 5
C2
T
ቤተ መጻሕፍቲ ባይዱ
1
第8页/共123页
普朗克公式→瑞利-琼斯公式
波动观点： 电子密集处波强大， 波幅平方大；电子稀 疏处波强小，波幅平 方小。
可见，电子出现的几率与该处波强成 正比，与波幅平方成正比。
第30页/共123页
测不准关系
x px h
Et
第31页/共123页
自由粒子波函数
x,
t
(
x)e
i
Et
(
x)
0
e
i
px
x,t 2 ----概率密度
第40页/共123页
5）粒子出现的几率密度（概率密度）
n x 2
2 cos a
2n
a
x
n 1,3,5
n x 2
2 sin a
2n
a
x
n 2,4,6
随n和x变化。
xa 2
n x 2 0 此处找不到粒子；
n
粒子在各处出现的概率相等 量子理论→经典理论
第41页/共123页
非对称一维无限深势阱
M B (T )
2hc 25
1 e hc kT
高二物理竞赛课件：量子力学之散射
性质及粒子出射的方向 有关。(,)
• 实际上由 dn / N q(,)d 可以看出 （1） q(,)表明单位时间内沿不同角度(,) 出射粒子数
目的多少，或出射粒子的概率的大小，所以称它为
角分布。
（2）从量纲看，q(,) 具有面积的量纲，因此又称它为
(,) 方向上的微分散射截面，而把
2
Q q( ,)d 0 0 q( ,)sindd
散射体的作用等效于一块横截面积，凡是打在这块面积上 的粒子，都被散射到各个方向上去。
• q(,) 及 Q 都是可由实验测定的量，需要讨论的问题是：
如何从薛定谔方程的解来计算散射截面，以便与实验值相 比较，从而来研究粒子间相互作用的性质及其它问题。所 以说，散射截面是散射理论的核心问题。下面讨论散射截 面与散射粒子的波函数之间的关系。
因为平面波 eikz 可以按着数理方程中的展开公式展开成
一系列球面波的叠加
eikz eikrcos (2l 1)il jl (kr)Pl (cos )
l
式中球贝塞耳函数
的渐j近l (式kr)为
1
l
jl (kr)
2kr
J
l
1 2
(kr
)
r
kr
sin(kr
2
)
所以入射波的渐近式为
eikz r
（4）
称为总散射面积。
“截面”一词，可作如下解释：
• 按着（3）式，在入射粒子流中，每单位时间穿过与入射 方向垂直的 dQ(,) q(,)d 面积的粒子数，即为单位
时间被散射到立体角 d 中去的粒子数 dn ，而单位时间
被散射的总粒子数 则等于单位时间穿过垂直于入射方向
的面积 Q 的入射粒子数。因此，对于入射粒子流来说，
高二物理竞赛光学波散射PPT(课件)
：
As⊥q，ΔEc＝0（ΔEv＝0
），不发生能带起伏，
不引起载流子散射。 所改变的是电子的运动方向，能量基本不变，近似于弹性散射。
纵光学波：离子晶体中起决定作用的散射，晶体中正、负交叉的电荷区形成的电极化电场对电子产生强烈的散射作用，离子晶体中电子迁移率较小。
• 声学波散射几率： 纵光学波：离子晶体中起决定作用的散射，晶体中正、负交叉的电荷区形成的电极化电场对电子产生强烈的散射作用，离子晶体中电子迁移率较小。
po
(1)3 2
(k0T )1 2
exp(
1
1
k0T
)
1
1
f (1 )
k0T
在低温时不起作用， 随着温度的升高， 光学波的散射概率 迅速增大
当长声学波和长光学波两种散射作用同时存在时，晶 格振动对载流子的总散射概率为两种散射概率之和：
P Ps P0
对于不同的半导体，这两种散射的相对强弱不同。 在共价结合的元素半导体中，如Si和Ge，长纵声学波的散射是主要的； 在极性半导体中，长纵光学波的散射是主要的．
长光学波：ωa 大，散射前后电子能量变化大， 是非弹性散射
纵声学波示意图：
膨胀状态--
原子间距增大
压缩状态—
原子间距减小
Ec
B
A
Eg
导带 禁带
Ev
价带
Eg Eg'
禁带宽度随原子间距变化：
？ 疏处禁带宽度减小
密处禁带宽度增大
波状起伏
纵声学波 → 原子疏密变化 → Eg 变化 → 附加势 → 破坏原周期性势场→电子发生散射
长光学波：ωa 大，散射前后电子能量变化大，
横声学波：As⊥q，ΔEc＝0（ΔEv＝0 ），不发生能带起伏，不引起载流子散射。
《量子散射理论》ppt课件
.
弹性散射的严厉解
• 经过围道积分与留数定理给出：
• 代回
• 上面过程也可以作如下等效计算： • 将两个极点添加一个小的虚部，其中为大于0的小数，那么
当时
• 给出与上面一样的，但益处是可以直接作围道积分。 • 进一步写出自在Green函数的算符方式： • 这是一个Green函数的普遍定. 义式，假设回到我们上面的问
与之间满足Dyson方程： 对于我们这里研讨的问题，为以下非齐次方程的解
它的算符方式为
.
弹性散射的严厉解
Lippmann-Schwinger方程：
而由 ，可以推出 或者记为： 。此之谓Dyson方程。 反复选代之，可以得到：
.
BORN近似
对于散射问题，除了个别特殊的势〔如方势阱、库仑势〕外， 我们无法得到准确的解析方式的解，需求借助于各种近似方 法，如Born近似、分波法等。 假设用逐级选代法求解L-S方程： 可以得到的各级近似解如下：
• 在振幅一项中，共包含和这个动量，除始末两个动量之外， 其他个内动量都要积分。
• 由此可见，介于两次散射之间的中间态是“虚态〞，虚态 粒子运动的能量与原始能量相差可以很大，相应地存在时 间极短，符合测不准关系，最后末态能量坚持与初态相等， 这是我们在质心系讨论弹性散射时应该有的结果。
• 下面用一实例演示Born近似下实践问题的处置过程。
.
分波展开和相移
.
分波展开和相移
• 我们还可以引进两个互为复共扼的球Hankel函数：
• 它们与因子乘在一同后分别描写V=0情况下的球面出射波 和〔会聚〕入射波，然而的无奇特性要求限定它们只能以 确定的线性组合方式出现，就是叠加起来得到。假设我们 利用平面波展开式
• 其中是阶Legendre多项式，上式还取定了沿轴方向，假设 放开这一条件，设沿单位矢量方向，那么平面波展开式应 该是如下的方式〔Rayleigh展开式〕
弹性散射的严厉解
• 经过围道积分与留数定理给出：
• 代回
• 上面过程也可以作如下等效计算： • 将两个极点添加一个小的虚部，其中为大于0的小数，那么
当时
• 给出与上面一样的，但益处是可以直接作围道积分。 • 进一步写出自在Green函数的算符方式： • 这是一个Green函数的普遍定. 义式，假设回到我们上面的问
与之间满足Dyson方程： 对于我们这里研讨的问题，为以下非齐次方程的解
它的算符方式为
.
弹性散射的严厉解
Lippmann-Schwinger方程：
而由 ，可以推出 或者记为： 。此之谓Dyson方程。 反复选代之，可以得到：
.
BORN近似
对于散射问题，除了个别特殊的势〔如方势阱、库仑势〕外， 我们无法得到准确的解析方式的解，需求借助于各种近似方 法，如Born近似、分波法等。 假设用逐级选代法求解L-S方程： 可以得到的各级近似解如下：
• 在振幅一项中，共包含和这个动量，除始末两个动量之外， 其他个内动量都要积分。
• 由此可见，介于两次散射之间的中间态是“虚态〞，虚态 粒子运动的能量与原始能量相差可以很大，相应地存在时 间极短，符合测不准关系，最后末态能量坚持与初态相等， 这是我们在质心系讨论弹性散射时应该有的结果。
• 下面用一实例演示Born近似下实践问题的处置过程。
.
分波展开和相移
.
分波展开和相移
• 我们还可以引进两个互为复共扼的球Hankel函数：
• 它们与因子乘在一同后分别描写V=0情况下的球面出射波 和〔会聚〕入射波，然而的无奇特性要求限定它们只能以 确定的线性组合方式出现，就是叠加起来得到。假设我们 利用平面波展开式
• 其中是阶Legendre多项式，上式还取定了沿轴方向，假设 放开这一条件，设沿单位矢量方向，那么平面波展开式应 该是如下的方式〔Rayleigh展开式〕
第八章 散射
l ikr i ( kr ) e 1 等式两 i l 0 2 f ( ) e ( A e A ) Pl l l ikr 边的e r 2ikr l 0 1 l 应该相 i ( kr l l ) i ( kr ) 0 2 2 A Pe A Pe =0 l l l l 等
设
ul ( r ) Rl ( r ) r
d 2ul l (l 1) 2 [k V ( r ) ]ul 0) 2 2 dr r
因为f只是的函数。的渐近式也只与有关 r eik r
Aeikz f ( )
r
对于散射后的波，我们来求径向方程的渐近解：r, V(r ) 0, 方程为
渐近解为
Al 1 ' ( r, ) sin(kr l l ) Pl (cos ) 2 l 0 kr
r
将入射平面波eikz按球面波展开公式
1 e
ikz
1 0 Al jl (kr ) Pl (cos ), kr l 0
1 i i sin ( e e ) 2i
第八章 散射
8.3 玻恩近似
8.1 散射现象的一般描述
原子核物理以及粒子物理的建立和发展都离不开散 射实验及其理论分析。在量子学中，将碰撞现象称为散射
现象。
而当粒子被力场散射时，粒子的能量组成连续谱。
微观粒子的散射也可分为弹性散射和非弹性散射两种：
弹性散射：碰撞前后粒子的性质和内部能级都不变，仅仅发 生整体的动量和能量交换。
d 2ul 2 k ul 0) 2 dr
方程的解为: ul (r ) A sin(kr )
' l ' l
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
▪ 归结为散射相移
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
➢球对称常势阱
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.1 散射问题的一般描述
§8.2 分波法
➢关键：
▪ 入射平面波是{p, Lz, H}的共同本征态
▪ 当势场U=U(r)时，p不再守恒，散射波是 {L^2, Lz, H}的共同本征态
▪ 当将平面波按角动量平方L^2的本征态，即球 面波展开后，对每个分波，因为是{L^2, Lz, H}的本征函数，所以在U(r)作用后，每个分 波只是向前或者向后移动
高考物理竞赛量子力学部分第八章 散射理论ppt课件
第八章 散射理论
复旦大学 苏汝铿
高考物理竞赛量子力学部分第八章 散射理论ppt课件
A bird’s eye view of RHIC
A bird’s eye view of LHC(CERN)
Gold-Gold Collision at RHIC
§8.2 分波法
▪ 要算多少个分波
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
▪ 光学定理
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
➢讨论： ▪ 第l个分波的相移为δl
▪ 只要求出镜像波函数在无穷远处的渐近行为， 与标准形式比较，即可求得相移δl Q
▪ δl正负号的讨论(见下)
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
➢低能散射形状无关近似
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
不同立体角的几率只需考察波函数在无穷 远处的渐进行为
§8.1 散射问题的一般描述
➢定义： ▪ 弹性散射：散射过程中两粒子之间只有动能
交换，而无内部运动状态的变化
➢关键： ▪ 引入质心坐标，将两体问题归结为单体问题
散射图象
§8.1 散射问题的一般描述
§8.1 散射问题的一般描述
§8.1 散射问题的一般描述
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
▪δl正负号的讨论
U(r) > 0 斥力 δl < 0
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
U(r) = 0 δl = 0
U(r) < 0 引力 δl > 0
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
第八章 散射理论
➢问题： ▪ 定态微扰要求分立谱，连续谱怎么办？ ▪ 一般连续谱问题也很难准确求解，也要用
“微扰”如何处理散射问题 ▪ 散射问题是了解复合粒子体系内部分布的有
效手段，也是研究高能物理、宇宙线、重离 子碰撞等许多领域的关键
第八章 散射理论
➢核心： ▪ 求出粒子波散射后，被散射到各个不同方向，
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
➢球对称常势阱
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.1 散射问题的一般描述
§8.2 分波法
➢关键：
▪ 入射平面波是{p, Lz, H}的共同本征态
▪ 当势场U=U(r)时，p不再守恒，散射波是 {L^2, Lz, H}的共同本征态
▪ 当将平面波按角动量平方L^2的本征态，即球 面波展开后，对每个分波，因为是{L^2, Lz, H}的本征函数，所以在U(r)作用后，每个分 波只是向前或者向后移动
高考物理竞赛量子力学部分第八章 散射理论ppt课件
第八章 散射理论
复旦大学 苏汝铿
高考物理竞赛量子力学部分第八章 散射理论ppt课件
A bird’s eye view of RHIC
A bird’s eye view of LHC(CERN)
Gold-Gold Collision at RHIC
§8.2 分波法
▪ 要算多少个分波
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
▪ 光学定理
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
➢讨论： ▪ 第l个分波的相移为δl
▪ 只要求出镜像波函数在无穷远处的渐近行为， 与标准形式比较，即可求得相移δl Q
▪ δl正负号的讨论(见下)
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
➢低能散射形状无关近似
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
不同立体角的几率只需考察波函数在无穷 远处的渐进行为
§8.1 散射问题的一般描述
➢定义： ▪ 弹性散射：散射过程中两粒子之间只有动能
交换，而无内部运动状态的变化
➢关键： ▪ 引入质心坐标，将两体问题归结为单体问题
散射图象
§8.1 散射问题的一般描述
§8.1 散射问题的一般描述
§8.1 散射问题的一般描述
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
▪δl正负号的讨论
U(r) > 0 斥力 δl < 0
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
U(r) = 0 δl = 0
U(r) < 0 引力 δl > 0
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
第八章 散射理论
➢问题： ▪ 定态微扰要求分立谱，连续谱怎么办？ ▪ 一般连续谱问题也很难准确求解，也要用
“微扰”如何处理散射问题 ▪ 散射问题是了解复合粒子体系内部分布的有
效手段，也是研究高能物理、宇宙线、重离 子碰撞等许多领域的关键
第八章 散射理论
➢核心： ▪ 求出粒子波散射后，被散射到各个不同方向，
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论（共69张ppt）