山西省2012届高三年级第四次四校联考(文科数学)
山西省2012届高三四校第四次联考试题理综.pdf

化过程,下列说法不正确的是
A.
B.种群1中A′基因的出现,最可能的来源是基因突变,该来源为生物进化提供了原材料
C.D.
7.化学与人类生产、生活、社会可持续发展密切相关,下列说法正确的是A.“天宫一号”中使用的碳纤维,是一
种新型有机高分子材料.近日台湾爆发的食品添加剂案又一次证明食品中不能添加任何化学添加剂D.食盐中由于含适
滑轮等高的A处由静止释放,当环沿直杆下滑距离也为d时(图中B处),下列说法正确的是(重力加速度为g)。
A.环到达B处时,重物上升的高度为B.环在B处的速度与重物上升的速度大小之比为C. 环减少的机械能大于重物增加
的机械能D.环在B处的速度为
22.(6分)某兴趣小组为测一遥控电动小车的额定功率,进行了如下实验:
工业纯碱中碳酸钠的质量分数(含少量NaCl),准确称量W0 g样品进行实验,下列实验方法所对应的实验方案和测量数
据合理(除W0外)的是
实验方法实验方案测量数据A滴定法将样品配成100 mL溶液,取10 mL,加入甲基橙,用标准盐酸滴定盐酸体积B气
体质量法将样品与盐酸反应,生成的气体全部被碱石灰吸收碱石灰增重C装置质量法将样品放入烧瓶中,置于天平上
随时间的变化如图所示。 0—2min内的平均反应速率v(A)=. 相同温度下,若开始加入(g)的物质b. A的平衡浓度c.达到平衡的时间 d.平衡时的体积分数实验室用Zn和稀硫酸
明确地向人们宣告,天上和地上的物体都遵循着完全相同的科学法则?15.如图所示,一木块在光滑水平面上受到一个
恒力F作用而运动,前方固定一个轻质弹簧,当木块接触弹簧后,下列判断正确的是A.将立即做匀减速直线运动B.将
立即做变减速直线运动C.在弹簧弹力大小等于恒力F时,木块的速度最大D.在弹簧处于最大压缩量时,木块的加速度
山西省四校高三下学期第四次联考(数学文)缺答案

山西省四校高三下学期第四次联考(数学文)本试题分第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间1。
第Ⅰ卷为选择题,第Ⅱ卷为非选择题。
注意事项:1.考生答卷前务必用蓝、黑色墨水笔或圆珠笔将学校名称、姓名、考号填写在试卷上,并用2B 铅笔在机读卡上规定位置涂黑自己的考号和考试科目。
2.选择题选出答案后,用2B 铅笔涂黑机读卡上对应题目的答案标号。
如需改动,用橡皮擦干净后,再选涂其它答案。
3.交卷时只交试卷和机读卡,不交试题,答案写在试题上的无效。
第 Ⅰ 卷 (选择题,共60分)一、选择题。
本大题共12小题.每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.sin15°cos165°的值等于( )A. 14 B.-14 C. 12 D. -122.记函数12xy -=+的反函数为()y g x =,则(5)g = ( )A .2B .一2C .一4D .43.已知集合A={x| |x|<3,x ∈Z},B={1,2,3,4},全集U=AUB ,则集合C U (A ⋂B )的子集个数为( )A .8B .16C .32D .64 4.不等式xx 1log 2-≥1的解集为 ( )A .(]1,-∞-B .[)∞+-,1C .[)0,1-D .(]()∞+-∞-,01,5.已知等差数列{a n }的公差为2,若431,,a a a 成等比数列,则a 2=( )A .-4B .-6C .-8D .-10[6. 函数13-=xy 的定义域为[]2,1-,则其值域为( )A .[]8,2B .[]8,1C .[]8,0D .[]8,1- 7.把曲线cos 210y x y +-=按向量)1,2(-=π平移,得到的曲线方程是( )A .(1)sin 210y x y -+-=B .(1)sin 230y x y -+-=C .(1)sin 210y x y +++=D .(1)sin 210y x y +--=8.高为5,底面边长为43的正三棱柱形容器(下有底),可放置最大球的半径是( )A .23B .2C .223 D .29.10.已知点P (x ,y )在不等式组⎩⎪⎨⎪⎧x -2≤0y -1≤0x+2y -2≥0表示的平面区域上运动,则z =x -y 的取值范围是( )A .[-2,-1]B .[-2,1]C .[1,2]D .[-1,2]11.定义在R 上的函数)(x f 满足0)()2(<'+x f x ,又)3(l og21f a =,))31((3.0f b =,)3(ln f c =,则( )A .c b a <<B .a c b <<C .a b c <<D .b a c <<12.已知点F 1、F 2分别是双曲线2222by a x -=1的左、右焦点,过F 1且垂直于x 轴的直线与双曲线交于A 、B两点,若△ABF 2为锐角三角形,则该双曲线的离心率e 的取值范围是( )A .(1,+∞)B .(1,3)C .(2-1,1+2)D.(1,1+2)第 Ⅱ 卷(非选择题,共90分)二、填空题。
山西省2012届高三年级第四次四校联考理综试题

2012届高三年级第四次四校联考理科综合试题命题:长治二中康杰中学临汾一中忻州一中本试题分第Ⅰ卷和第Ⅱ卷两部分,满分300分,考试时间150分钟。
以下数据可供解题时参考:可能用到的相对原子质量: H-1 N-14 O-16 Na-23 Mg-24 Al-27 Cl-35.5第Ⅰ卷 (选择题,共126分)一、选择题(本大题共13小题,每小题6分。
只有一项是符合题目要求的。
)1.下列有关细胞的叙述中,正确的是A.核孔是生物大分子物质进出的通道,它对物质的通过没有选择性B.卵细胞体积较大有利于和周围环境进行物质交换,为胚胎早期发育提供所需营养 C.有高尔基体的细胞不一定具有分泌功能D.细胞凋亡受基因控制,细胞癌变不受基因控制2.如图是细胞与内环境交换物质的示意图,其中①②③④分别表示体液的成分,a、b分别表示物质运输的途径。
下列有关说法错误的是A.③中产生的热量是维持体温的主要来源之一B.CO2浓度最高的液体是②C.毛细血管壁具体生活的内环境是①②D.若①中胰岛素含量上升,则通过a途径的葡萄糖大于通过b途径的D.若图②中的1个b基因突变为B,则该生物体仍然可以合成出物质乙5.下列有关酶的叙述正确的是A.酶催化效率高是因为其降低活化能更显著B.与光合作用有关的酶分布在叶绿体的内膜、基粒和基质D.细胞质中没有作用于DNA的解旋酶6.右图显示了某种甲虫的两个种群基因库的动态变化过程,有关该图下列说法不正确的是A.图中箭头表示通过迁移,两个种群的基因库之间有机会进行基因交流,由此可知种群1和种群2之间不存在生殖隔离B.种群1中新基因型A′A 的甲虫个体的出现将会使种群1基因库中的基因频率发生改变C.种群1中A′基因的出现,最可能的来源是基因突变,该来源为生物进化提供了原材料D.种群1和种群2中不同的自然选择决定了种群1和种群2甲虫的变异和进化方向7.化学与人类生产、生活、社会可持续发展密切相关,下列说法正确的是A.“天宫一号”中使用的碳纤维,是一种新型有机高分子材料B. 自来水厂在处理水时常加入硫酸亚铁和氯气,能同时达到消毒杀菌和除去水中悬浮杂质的作用C.近日台湾爆发的食品添加剂案又一次证明食品中不能添加任何化学添加剂D.食盐中由于含适量的K131IO3,因而能有效地抵抗核辐射8.下列说法正确的是A.1 mol 蔗糖可水解生成2 mol葡萄糖B.CH3—CH=CH—CH3与C3H6一定互为同系物C.C4H9Cl共有同分异构体9种D.(CH3)2CHCH(CH3)2的名称是2,3 -二甲基丁烷9.M是一种治疗艾滋病的新药(结构简式见右图),下列关于M的说法正确的是B.M能发生加聚反应和取代反应C.M 不能使溴的四氯化碳溶液褪色,也不能使酸性高锰钾溶液褪色D.M的分子式为C13H12O2NF4,分子内至少有13个碳原子在同一平面内1011012.右图是一水溶液在PH 从0至14的范围内,H 2CO 3、HCO -3、CO -23三种成分平衡时的组成百分率,下列叙述正确的是A .等体积的1.0mol·L -1的盐酸和1.0mol·L-1碳酸钠溶液混合时呈中性B .在pH 为6.37及10.25时,溶液中c (H 2CO 3)=c (HCO -3)=c (CO -23) C .若用CO 2和NaOH 反应制取Na 2CO 3,溶液的pH必须控制在12以上D .此图是1.0mol/L 碳酸钠溶液滴定1.0 mol/LHCl 溶液的滴定曲线13. 将a g 镁铝合金投入到x mL 2mol/L 的盐酸中,金属完全溶解后,再加入y mL 1mol/L的氢氧化钠溶液,得到的沉淀量最大且质量为(a +1.7) g ,则下列说法不正确的是A .镁铝合金与盐酸反应时转移的电子数为0.1N AB .x = 2yC .沉淀是Mg(OH)2和Al(OH)3的混合物D .2x = y二、选择题:本题共8小题,每小题6分。
山西省晋中市四校联考度高三数学第一学期联考试题 文【名校特供】

2011-2012学年度第一学期晋中市高三四校联考数学试题(文)本试卷满分150分 考试时间120分钟第Ⅰ卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U R =,集合2{|20}A x x x =->,{|lg(1)}B x y x ==-,则()U C A B等于( ) A.{|20}x x x ><或 B .{|12}x x << C.{|12}x x <≤ D.{|12}≤≤x x 2.下列命题中,真命题是( )A.2,x R x x ∀∈≥ B.命题“若21,1x x ==则”的逆命题C.2,x R x x ∃∈≥D.命题“若,sin sin x y x y ≠≠则”的逆否命题3. 若n s 是等差数列{}n a 的前n 项和,4102=+a a ,则11s 的值为( ) A.22 B.18 C.12 D.444.函数)1(log 221-=x y 的定义域为 ( )A.[)(]2,11,2 -- B.)2,1()1,2( --C.[)(]2,11,2 --D.)2,1()1,2( --5.下列函数中,是奇函数且在区间(0,1)内单调递减的函数是( ) A.12log y x = B.1y x=C.3y x = D.x y tan = 6.已知函数31)21()(x x f x-=,那么在下列区间中含有函数)(x f 零点的是( )A.)31,0(B.)21,31(C.)32,21(D.)1,32(7. 已知函数()f x 是定义在R 上的偶函数,且当0x >时,()ln(1)f x x =+,则函数()f x的大致图像为( )A B C D8.将函数)3cos(π-=x y 的图像上各点的横坐标伸长到原来的2倍(纵坐标不变), 再向左平移6π个单位,所得图像的一条对称轴方程为( )A.9π=xB. 8π=xC. 2π=x D. π=x9.函数x x x y sin cos -=的一个递增区间是( )A.)23,2(ππ B.)2,(ππ C.)25,23(ππ D.)3,2(ππ10.在△ABC 中,如果C A sin 3sin =, 30=B ,那么角A 等于( )A .30 B .45 C .60 D .12011.已知定义在R 上的奇函数)(x f ,满足(4)()f x f x -=-,且在区间[0,2]上是增函数, 则( )A.(25)(11)(80)f f f -<<B. (80)(11)(25)f f f <<-C. (11)(80)(25)f f f <<-D. (25)(80)(11)f f f -<<12.函数32()393,f x x x x =--+若函数()()[2,5]g x f x m x =-∈-在上有3个零点,则m 的取值范围为( )A.[)8,1B.(]1,24-C.[]8,1D.()8,24-第Ⅱ卷 (非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分。
山西数学文精校版-2012普通高等学校招生统一考试

绝密*启用前2012年普通高等学校招生全国统一考试文科数学注息事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合A={x |x 2-x -2<0},B={x |-1<x <1},则 (A )A ⊂≠B (B )B ⊂≠A (C )A=B (D )A ∩B=∅ (2)复数z =-3+i 2+i的共轭复数是(A )2+i (B )2-i (C )-1+i (D )-1-i(3)在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线y =12x +1上,则这组样本数据的样本相关系数为(A )-1 (B )0 (C )12(D )1(4)设F 1、F 2是椭圆E :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,P 为直线x=3a2上一点,△F 1PF 2是底角为30°的等腰三角形,则E 的离心率为( ) (A )12 (B )23 (C )34 (D )45(5)已知正三角形ABC 的顶点A (1,1),B (1,3),顶点C 在第一象限,若点(x ,y )1,粗线画出的是某几何体的三视图,则此几何体的体积为 (A )6 (B )9 (C )12 (D )18(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为(A )6π (B )43π (C )46π (D )63π (9)已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin (ωx ÷φ)图像的两条相邻的对称轴,则φ=(A )π4 (B )π3 (C )π2 (D )3π4(10)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB|=43,则C 的实轴长为(A ) 2 (B )2 2 (C )4 (D )8 (11)当0<x ≤12时,4x <log a x ,则a 的取值范围是(A )(0,22) (B )(22,1) (C )(1,2) (D )(2,2)(12)数列{a n }满足a n +1+(-1)n a n =2n -1,则{a n }的前60项和为 (A )3690 (B )3660 (C )1845 (D )1830第Ⅱ卷本卷包括必考题和选考题两部分。
山西省四校2012届高三第二次四校联考文综

山西省四校2012届高三第二次四校联考文综山西省临汾一中、康杰中学、忻州一中、长治二中2012届高三第二次四校联考文科综合说明:本试卷分第Ⅰ卷和第Ⅱ卷两部分,满分300分,考试时间150分钟。
注意事项:1.考生答卷前务必用蓝、黑色墨水笔或圆珠笔将班级名称、姓名、考号填写在试卷上,并用2B铅笔在机读卡上规定位臵涂黑自己的考号和考试科目。
2.选择题选出答案后,用2B铅笔涂黑机读卡上对应题目的答案标号,如需改动,用橡皮擦干净后,再选涂其它答案。
第Ⅰ卷(选择题共140分)本题共35个小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的。
读“90 附近海平面气压图(单位:hPa)”,回答1~2题。
1.气压最高值出现的纬度和气压值最低处的气压带名称分别是A.50°N、副极地低气压带 B.50°N、赤道低气压带C.60°S、副极地低气压带 D.60°S、赤道低气压带2.由图示气压分布推断,此时A.芬兰的驯鹿北迁 B.智利瓦尔帕莱索附近森林火险等级高C.大陆上等温线向北凸 D.中纬度昼夜差别达一年中最大洞里萨湖是东南亚最大淡水湖,通过洞里萨河同湄公河相连,是湄公河的天然蓄水池。
洞里萨湖湖面最大可达1万平方千米以上,平均水深在10米以上。
洞里萨湖地区交通便捷,船舶吃水4米的船只经各支流可达湖区周围的各省省会。
据此回答3~4题。
3.关于洞里萨湖和洞里萨河的叙述正确的是A.影响洞里萨湖水位变化的主要因素是降水B.洞里萨河一年内流向定期发生变化C.洞里萨河终年流向大致是西北→东南D.该地区通航最佳时间是11月~次年4月4.图示所在地区A.受风力作用影响大 B.农业地域类型主要是商品谷物农业C.地表岩石都是岩浆岩 D.树种繁多,许多树叶有滴水叶尖现象下面左图为“甲乙丙丁四个国家2005年O--5岁、15--65岁、65岁以上三个年龄段的人口比例示意图”,右图为“人口出生率与死亡率变化示意图”,读图完成5~6题。
山西省2012届高三年级第四次四校联考文综试题

2012届高三年级第四次四校联考文综试题命题:长治二中 康杰中学 忻州一中 临汾一中(满分300分,考试时间为150分钟)第Ⅰ卷(单项选择题,共140分)本卷共35小题,每小题4分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
能源消费弹性系数是指能源消费的增长率与GDP 增长率之比。
下图为“我国能源消费弹性系数和GDP 增长率曲线图”。
读图,完成1~2题。
1.下列叙述正确的是A .我国能源消费弹性系数持续上升B .能源利用率越高,能源消费弹性系数越大C .能源消费弹性系数在一定程度上能反映经济结构的变化D .人口数量变化是引起能源消费弹性系数变化的主要因素2.2002—2004年间,我国的能源消费弹性系数较高,最可能的原因是A .科技水平迅速提高B .第三产业比重上升C .使用清洁能源比重上升D .高耗能产业快速发展读“江苏三大名石”图及相关资料,回答3~4题。
3.关于“江苏三大名石”成因的分析,正确的是A .都是外力作用的产物B .雨花石的形成与流水作用有关C .形态都和流水作用有关D .都是内力作用的产物4.从地壳物质循环角度来看,下列转化可能实现的是A .雨花石→砾岩B .太湖石→昆石C .雨花石→昆石D .砾岩→昆石5.候鸟迁徙时间遵循一定的季节规律:越冬时,由温度较低的地区迁往温度较高的地区;繁殖时,由温度较高的地区迁往温度较低的地区。
其迁徙时间一般在3月份前后和9月份前后。
图中箭头表示候鸟9月份迁徙路线的是A6.甲省区总抚养比大大低于全国平均水平,是因为A .社会经济较发达,生育率偏低B .养老体系完善,劳动力抚养负担小C .老年人口比重大,导致死亡率偏高D .该地区经济落后,劳动力迁出7.我国总抚养比有下降趋势,其形成原因可能是A .老人抚养比上升B .年轻劳动力人口数减少C .老年人口数减少D .少年儿童抚养比下降进行交通规划时,需要分析区域的地质地形条件,地基土壤类型承载力越大、地形坡度越小,车辆的通行能力越强。
山西省2012届高三上学期第一、二次四校联考文综试题

山西省2012届高三上学期第一次四校联考地理试题第Ⅰ卷 (选择题,共50分)一、下列各题的四个选项中,只有一项是最符合题意的,请将正确答案填涂在机读卡上(每小题2分,共50分)北京时间2011年9月29日21时16分03秒我国首个空间实验室“天宫一号”在酒泉卫星发射中心载人航天发射场成功发射。
阅读资料,完成1~2题。
1.“天宫一号”发射时,下列说法正确的是A .地球公转速度趋慢B .南极点附近可能出现美丽的极光C .山西昼短夜长,且昼将逐渐变长D .太阳位于开普敦(东一区)的西北方向2.“天宫一号”发射时,与太原属于同一天的地区约占全球的A .1/2B .2/3C .23/24D .全部 读地中海地区冬雨率等值线图,回答3~4题。
(注:冬雨率为冬季降水量占全年降水量的百分率,单位:%)3.图示城市中全年降水量最少的是A .的黎波里 B .罗马 C .巴塞罗纳D .雅典4.根据图中冬雨率等值线总体分布特点,下列说法正确的是A .冬雨率由中心向四周递减B .北部冬雨率较低的原因是受西风影响时间长,降水季节分配较均匀C .南部冬雨率较高的原因是年降水量很少D .东部冬雨率较高的原因是受大西洋影响大,降水季节分配较均匀读“某地对流层气温垂直分布状况图” ,回答5~6题。
5.该地的地形最可能的是A .山地B .平原C .盆地D .高原 6.如该地大力发展工业,由于地形原因最有可能造成的污染是 A .水污染 B .大气污染C .土壤污染D .固体废弃物污染 下图为“某大洋海岸大陆等高线地形图”,左图为丙区域的放大图,其中实线为等高线(单位:米),虚线为地层界线。
读图回答第7~8题。
巴塞罗纳的黎波里罗马 雅典7.下图中能反映左上图地层剖面的示意图是8.若丙地区终年受西风控制,则关于甲、乙两河的叙述,正确的是A .甲河东北岸冲刷严重B .与乙河相比,甲河径流的季节变化更小C .甲河的水能一定比乙河更丰富D .与甲河相比,乙河的航运条件更好读右图,完成9~10题。
山西省2012届高三四校第四次联考试题数学理.pdf

2012届高三年级第四次四校联考 数学(理)试题 (满分150分,考试时间120分钟)命题: 长治二中康杰中学临汾一中 忻州一中一、选择题:本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的 A. B. C. D. 2. 各项都是正数的等比数列中,,则公比 A. B. C. D. 3. A. B. 2 C. D. 4. 若展开式中第四项与第六项的系数相等,则展开式中的常数项的值等于A. 8 B. 16C. 80D. 70 5. 函数,若,则实数的值是 A. B. C. 或 D. 或 6. 命题:使得;命题:若函数 为偶函数,则函数 关于直线对称A. 真B. 真C. 真D. 假 7. 执行右图所给的程序框图,则运行后输出的结果是 A. B. C. D. 8. 由不等式组围成的三角形区域有一个外接 圆,在该圆内随机取一点,该点落在三角形内的概率是 A. B. C. D. 9. 已知A、B、C是圆O:上三点,且=A. B. C. D. 10. 已知三棱锥中,A、B、C三点在以O为球心的球面上, 若, ,三棱锥的体积为,则球O的表面积为 A. B. C. D. 11. 已知数列{an}为等差数列,若0的n的最大值为A. 11 B. 19 C. 20 D. 21 12. 过双曲线的左焦点,作圆:的切线,切点为E,延长FE交双曲线右支于点P,若,则双曲线的离心率为A. B.C. D. 第Ⅱ卷 本卷包括必考题和选考题两部分,第13—21题为必考题,每个试题考生都必须作答,第22—24题为选考题,考生根据要求作答。
二、填空题本大题共4小题,每小题5分,共20分13. 若,则=___________14. 已知为抛物线上不同两点,且直线倾斜角为锐角,为抛物线焦点,若 则直线斜率为 。
15. 某几何体的三视图如图所示,其正视图为矩 形,侧视图为等腰直角三角形,俯视图为直角梯 形,则这个几何体的体积为 。
山西省2012届高三四校第四次联考试题文综
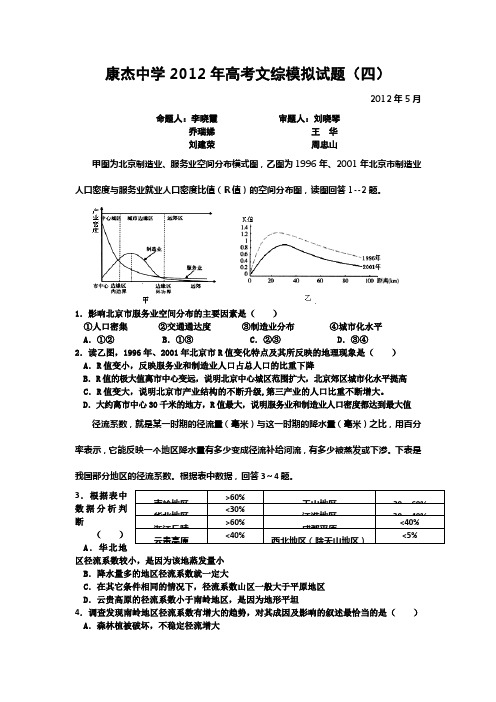
康杰中学2012年高考文综模拟试题(四)2012年5月命题人:李晓霞 审题人:刘晓琴乔瑞娣 王 华刘建荣 周忠山甲图为北京制造业、服务业空间分布模式图,乙图为1996年、2001年北京市制造业人口密度与服务业就业人口密度比值(R 值)的空间分布图,读图回答1--2题。
1.影响北京市服务业空间分布的主要因素是( )①人口密集 ②交通通达度 ③制造业分布 ④城市化水平A .①②B .①③C .②③D .③④2.读乙图,1996年、2001年北京市R 值变化特点及其所反映的地理现象是( )A .R 值变小,反映服务业和制造业人口占总人口的比重下降B .R 值的极大值离市中心变远,说明北京中心城区范围扩大,北京郊区城市化水平提高C .R 值变大,说明北京市产业结构的不断升级,第三产业的人口比重不断增大。
D .大约离市中心30千米的地方,R 值最大,说明服务业和制造业人口密度都达到最大值 径流系数,就是某一时期的径流量(毫米)与这一时期的降水量(毫米)之比,用百分率表示,它能反映一个地区降水量有多少变成径流补给河流,有多少被蒸发或下渗。
下表是我国部分地区的径流系数。
根据表中数据,回答3~4题。
3.根据表中数据分析判断 ( ) A .华北地区径流系数较小,是因为该地蒸发量小B .降水量多的地区径流系数就一定大C .在其它条件相同的情况下,径流系数山区一般大于平原地区D .云贵高原的径流系数小于南岭地区,是因为地形平坦4.调查发现南岭地区径流系数有增大的趋势,对其成因及影响的叙述最恰当的是( )A .森林植被破坏,不稳定径流增大B .降水量增大,地表的侵蚀作用加强C .径流系数增大,水位季节变化减小D .径流系数增大,对当地的气候不会产生影响图4为“欧洲农业集约度的空间变化图”(集约度是指某类事物在特定空间的集中程度。
图中的等值线为集约度指数,指数越大表示集约度越高)。
读图回答5~6题。
5.图中黑影区最主要的农业地域类型是()A.商品谷物农业B.乳畜业C.季风水田农业D.大牧场放牧业6.影响图中集约度指数空间差异的最主要因素是()A.降雨日数B.工业和城市分布C.土壤肥沃程度D.草场分布下面两幅图为我国某地区的山地地形剖面及对应的气候资料图和该山地垂直自然带分习示意图,读图回答7~9题。
山西省临汾一中、康杰中学、忻州一中、长治二中2012届高三第二次四校联考数学(文)试题

山西省临汾一中、康杰中学、忻州一中、长治二中2012届高三第二次四校联考(数学文)(满分150分,考试时间120分钟)一、选择题:本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合∈=y A {Z ∈=x x y ,sin R },则集合A 的子集的个数为( )A .5个B .6个C .7个D .8个 2.若复数iiz 212+-=,则复数z 的虚部为( ) A .i - B .i C . 1- D .13.1)4(cos 22--=πx y 是( )A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为2π的奇函数 D .最小正周期为2π的偶函数 4.已知命题∈∃x p :R ,x x 212<+;命题:q 若012<--mx mx 恒成立,则40m -<≤ 那么( )A .""p ⌝是假命题B .“q ⌝”是真命题C .“p q ∧”为真命题D .“p q ∨”为真命题5.曲线12-+=x xe y x在0=x 处的切线方程为( )A .31y x =-B .31y x =--C .13+=x yD .21y x =--6.设不等式组22,22x y -≤≤⎧⎨-≤≤⎩表示的区域为W ,圆:C 4)2()2(22=-+-y x 及其内部区域记为D .若向区域W 内投入一点,则该点落在区域D 内的概率为( ) A .4π B .8π C .16π D .32π7.在等差数列{}n a 中,若,421053=++a a a 则=13S ( )A .13B .14C .15D .168.执行如图所示的程序框图,输出的S 的值为( )AB .0C D.-9.已知函数⎪⎩⎪⎨⎧<-≥-=2,1)21(,2,)2()(x x x a x f x 满足对任意的实数8题图21x x ≠都有0)()(2121<--x x x f x f 成立,则实数a 的取值范围为( )A .(),2-∞B .]813,(-∞ C .(],2-∞ D .)2,813[10.已知双曲线22221x y a b-=(a >0, b >0)的离心率为2,一个焦点与抛物线216y x =的焦点相同,则双曲线的方程为( )A .16222=-y xB .12622=-y xC .141222=-y xD .112422=-y x 11.在三棱锥A BCD -中,侧棱AB 、AC 、AD 两两垂直,ABC ∆、ACD ∆、ADB ∆ 的( ) A .2π B .6πC. D .24π12.若曲线1C :0222=-+x y x 与曲线2C :0)(=--m mx y y 有4个不同的交点,则实数m 的取值范围为( ) A .)33,0()0,33( -B .)33,33(-C .]33,33[-D .),33()33,(+∞--∞ 二、填空题:本大题共4小题,每小题5分,共20分13.已知 2=a ,4=b ,且)(b a +与a 垂直,则a 与b的夹角为 . 14.,x y 满足约束条件22040y x y x y ≥⎧⎪+≥⎨⎪+-≤⎩,则521-+=y x z 的最小值为 .15.如图为某几何体的三视图,则这个几何体的体积为 .16.已知函数()f x 满足)()1(x f x f -=+,且()f x 是偶函数, 当[0,1]x ∈时,2)(x x f =;若在区间[1,3]-内,函数()()g x f x kx k =--有4个零点,则实数k 的取值范围为 .正视图俯视图侧视图15题图三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)若数列{}n a 满足∈==+n a a a n n (3,111N *). (1)求{}n a 的通项公式;(2)等差数列{}n b 的各项均为正数,其前n 项和为n T ,且153=T ,又112233,,a b a b a b +++成等比数列,求n T .18.(本小题满分12分)若平面向量)2cos ,(cos ),2sin 2,3(x x x-=-=(∈x R ),函数x f ⋅=)(. (1)求函数)(x f 的值域;(2)记△ABC 的内角C B A 、、的对边长分别为c b a 、、,若3)(=A f ,且c b 2=,求角C 的值.19.(本小题满分12分)如图,在四棱锥P ABCD -中,侧面PDC 是边长 为2的正三角形,且与底面垂直;底面ABCD 是菱形,60ADC ∠=,M 为PB 的中点.(1)求四棱锥P ABCD -的体积; (2)求证:PA ⊥平面CDM . 20.(本小题满分12分)甲乙两位学生参加数学竞赛培训,在培训期间他们参加5次预赛成绩记录如下: 甲: 78 76 74 90 82乙: 90 70 75 85 80(1)用茎叶图表示这两组数据;(2)从甲乙两人成绩中各随机抽取一个,求甲的成绩比乙高的概率;(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.21.(本小题满分12分)19题图B已知椭圆)0(12222>>=+b a by a x 经过点)23,1(--M ,离心率为23. (1)求椭圆的方程;(2)设过定点M (0,2)的直线l 与椭圆交于不同的两点A 、B ,且AOB ∠为锐角(其中O 为坐标原点),求直线l 的斜率k 的取值范围.22.(本小题满分12分)设函数322()(0)f x x ax a x m a =+-+>.(1)若函数()f x 在[]1,1x ∈-内没有极值点,求实数a 的取值范围; (2)1a =时函数()f x 有三个互不相同的零点,求实数m 的取值范围;(3)若对任意的[]3,6a ∈,不等式()1f x ≤在[]2,2x ∈-上恒成立,求实数m 的取值范围.2012届高三年级第二次四校联考数学(文)试题参考答案一、选择题:DCADA CACBD BA 二、填空题:13.23π14.27- 15.332 16.1(0,]4. 三、解答题:17.解:(1)由条件可得数列{}n a 是首项为1,公比为3的等比数列.……………2分∴13n na -=.………………4分(2)设数列{}n b 的公差为d ,由315T =可得12315b b b ++=,则25b =.………6分设135,5b d b d =-=+, 又1231,3,9a a a ===,由题意可得()()()2515953d d -+++=+解得10,221-==d d ∵数列{}n b 的各项均为正,∴0d >,∴2d =.………8分则()213222n n n T n n n -=+⨯=+.………………10分18.解:(1)由)3sin(2sin cos 3)(π+=+=x x x x f ,得函数)(x f 的值域为]2,2[-.…………………4分(2)3)(=A f ,23)3sin(=+∴πA . 又),0(π∈A ,3π=∴A .…6分 由c b 2=及A bc c b a cos 2222-+=得 c a 3=则3sin sin ==c a C A ,21sin =∴C ………………………………10分 c a > ,C A >∴,则6π=C .………………………………12分19.解:(1)作PO CD ⊥于O ,则PO=2244ABCD S =⨯⨯=则23323131=⨯⨯=⋅=-PO S V ABCD ABCD P . ………………4分 (2)连接OA . 由侧面PDC 与底面ABCD 垂直, 则PO ⊥平面ABCD ,所以PO CD ⊥.又由060ADC ∠=,1,2DO AD ==,得090DOA ∠=,即OA CD ⊥,所以CD ⊥面POA , 所以CD PA ⊥. ………6分取PA 中点N ,连接ON,MN .由M 为PB 中点, 得四边形MNOC 为平行四边形,所以CM ∥ON . 又在三角形POA 中3==OA OP ,N 为PA 中点,所以PA ON ⊥,所以CM PA ⊥.又C DC CM = ,所以PA ⊥面CDM . …………12分20.解:(1)19题图B………………3分(2)从甲乙两人所得成绩中各随机抽取一个,所有情况如下: (78,90) (78,70) (78,75) (78,85) (78,80) (76,90) (76,70) (76,75) (76,85) (76,80) (74,90) (74,70) (74,75) (74,85) (74,80) (90,90) (90,70) (90,75) (90,85) (90,80) (82,90) (82,70) (82,75) (82,85) (82,80)共有25种,而甲大于乙的情况有12种,.2512=∴P . ………………8分 (3)80=甲x ,80=乙x ,而32s 2=甲,50s 2=乙.22s 乙甲s < ,,∴选甲参加更合适.………………12分21.解:(1)由题设得143122=+ba① , 且2322=-a b a ②.…………2分 由①、②解得1,2==b a . 则椭圆的方程为224y x +=1.……………4分(2)显然0x =不满足题意,可设l 的方程为2y kx =+,设1122(,),(,)A x y B x y .…6分联立22221(14)1612042x y k x kx y kx ⎧+=⎪⇒+++=⎨⎪=+⎩△2223(16)4(14)120,4k k k =-+⋅>∴>. 且1212221216,1414kx x x x k k∴=+=-++.………………8分 又AOB ∠为锐角,0OA OB ∴⋅>,12120x x y y ∴+>,1212(2)(2)0x x kx kx ∴+++>.222121222212164(4)(1)2()4(1)2()40141414k k k x x k x x k k k k k -∴++++=++-+=>+++.…………10分24,k ∴<又234k >,2344k ∴<<,3(2,(,2)22k ∴∈--.……………12分 22.解:(1)由题设可知,方程/22()320f x x ax a =+-=在[]1,1-上没有实数根,∴/2/2(1)320(1)3200f a a f a a a ⎧=+-<⎪-=--<⎨⎪>⎩,解得3a >. ………4分 (2)当1a =时32()f x x x x m =+-+,∵()f x 有三个互不相同的零点, ∴32()0f x x x x m =+-+=即32m x x x =--+有三个互不相同的实数根. 令32()g x x x x =--+,则/2()321(31)(1)g x x x x x =--+=--+ ∵()g x 在(,1)-∞-和1(,)3+∞均为减函数,在1(1,)3-为增函数, ∴15()(1)1,()()327g x g g x g =-=-==极小极大 所以m 的取值范围是5(1,)27-. ………………8分 (3)∵/22()323()(),3af x x ax a x x a =+-=-+又0a >,∴当x a <-或3a x >时,/()0f x >;当3a a x -<<时,/()0f x <.∴函数()f x 的递增区间为(,)(,),3a a -∞-+∞和单调递减区间为(,)3aa -当[]3,6a ∈时, []1,2,33aa ∈-≤-, 又[]2,2x ∈-,∴{}max ()max (2),(2)f x f f =-而2(2)(2)1640f f a --=-<,∴2max ()(2)842f x f a a m =-=-+++, 又∵()1f x ≤在[]2,2-上恒成立,∴2max ()18421f x a a m ≤-+++≤即,即[]29423,6m a a a ≤--∈在上恒成立.∵2942a a --的最小值为87-, ∴87.m ≤- ………12分。
山西省高三数学四校第四次联考试题 文

2012届高三年级第四次四校联考数学(文)试题(满分150分,考试时间120分钟)命题: 长治二中 康杰中学 临汾一中 忻州一中第Ⅰ卷一、选择题:(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的)1.已知i 为虚数单位,若复数i z -=11,i z +=22,则=⋅21z zA .i -3B .i -2C .i -1D .i 22+2.已知集合B A 、,{}22<≤-=x x A ,A B A =U ,则集合B 不可能...为 A . ∅B .{}20≤≤x xC .{}20<<x xD .{}20<≤x x3.为了得到函数xy )31(3⋅=的图象,可以把函数xy )31(=的图象A .向左平移3个单位长度B .向右平移3个单位长度C .向左平移1个单位长度D .向右平移1个单位长度4.下列函数中,周期为π,且图像关于直线3π=x 对称的函数是A .)32sin(2)(π+=x x fB .)32sin(2)(π+=x x f C .)62sin(2)(π-=x x fD .)62sin(2)(π-=x x f 5.双曲线)0(13222>=-a y a x 有一个焦点与抛物线x y 82=的焦点重合,则双曲线的渐近线方程为 A .y =x 21±B .y =x 2±C .y =x 33±D .y =x 3±6.执行如图所示的程序框图输出的结果是A .3-B .2-C .2D .37.一个几何体的三视图及部分数据如图所示,侧视图为等腰三角形,俯视图为正方形,则这个几何体的体积等于 A .13B .23第6题图第7题图C.6 D.248.已知等比数列{}n a 的公比0>q 且1≠q , 又06<a ,则A .5748a a a a +<+B .5748a a a a +>+C .5748a a a a +=+D .5748||||a a a a +>+9.下列各命题中正确的命题是① “若b a ,都是奇数,则b a +是偶数”的逆否命题是“若b a +不是偶数,则b a ,都不是奇数”;② 命题“x x R x 31,2>+∈∃”的否定是“x x R x 31,2≤+∈∀” ;③ “函数ax ax x f 22sin cos )(-=的最小正周期为π” 是“1=a ”的必要不充分条件;④“平面向量a 与b 的夹角是钝角”的充分必要条件是“0<⋅” . A .②③ B .①②③ C .①②④ D .③④10.已知实数y x ,满足⎪⎩⎪⎨⎧≤+-≤≥m y x x y y 121,若目标函数y x z -=的最小值为1-,则此目标函数的最大值为A . 3B . 2C . 1D . 5 11.设曲线)(*1N n x y n ∈=+在点)1,1(处的切线与x 轴的交点横坐标为n x ,则++2201212012log log x x …20112012log x +的值为A .2011log 2012-B .1-C .2011log 12012+-D .112.对实数a 和b ,定义运算“⊗”:a ⊗b =⎩⎪⎨⎪⎧a ,a -b ≤1,b ,a -b >1.设函数f (x )=(x 2-2)⊗(x -x 2),x ∈R ,若函数y =f (x )-c 的图象与x 轴恰有两个公共点,则实数c 的取值范围是A .(-∞,-2]∪⎝ ⎛⎭⎪⎫-1,32B .⎝ ⎛⎭⎪⎫-1,-34∪⎣⎢⎡⎭⎪⎫14,+∞C .⎝ ⎛⎭⎪⎫-1,14∪⎝ ⎛⎭⎪⎫14,+∞D .(-∞,-2]∪⎝⎛⎭⎪⎫-1,-34 第Ⅱ卷本卷包括必考题和选考题两部分,第13—第21题为必考题,每个试题考生都必须作答,第22—24题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分,把正确答案填在题中横线上)13.已知向量()1,2,5,||a a b a b =⋅=-=r r r r r ||b r等于14.在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c,若22a b -=,sin C B =,则角A= 15.等差数列}{n a 中,20,873==a a ,若数列}1{1+n n a a 的前n 项和为254,则n 的值为16.已知P 、A 、B 、C 是球O 表面上的点,PA ⊥平面ABC ,AC ⊥BC ,AC =1,BCPA则球O 的表面积为三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知向量)cos ,(sin ),1,(x x m =-=,()f x a b =⋅v v且满足()12f π=.(1)求函数()y f x =的最大值及其对应的x 值;(2)若51)(=αf ,求αααtan 1sin 22sin 2--的值.18.(本小题满分12分)如图,在四棱锥P —ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为正方形,PA =AB =4,G 为PD 的中点,E 点在AB 上,平面PEC ⊥平面PDC .(1)求证:AG ∥平面PEC ;(2)求点G 到平面PEC 的距离. 19.(本小题满分12分)某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天...的数据,求出y 关于x 的线性回归方程a x b y ˆˆˆ+=; (3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?(参考公式:1221ˆni ii ni i x y nx ybx nx==-=-∑∑,x b y a ˆˆ-=)(参考数据:97731=∑=i i i y x ,434312=∑=i i x )20.(本小题满分12分)已知椭圆C 的对称中心为原点O,焦点在x 轴上,离心率为21,且过点)23,1(. (1)求椭圆C 的方程;(2) 过椭圆C 的左焦点1F 的直线l 与椭圆C 相交于B A ,两点,若AOB ∆的面积为726,求圆心在原点O 且与直线l 相切的圆的方程. 21.(本小题满分12分)已知函数1ln ()xf x x +=. (1)设a >0,若函数)(x f 在区间1(,)2a a +上存在极值,求实数a 的取值范围;(2)如果当x ≥1时,不等式2()1k kf x x -≥+恒成立,求实数k 的取值范围.请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑. 22. (本题满分10分)选修4-1:几何证明与选讲如图,ABC ∆为直角三角形,90=∠ABC ,以AB为直径的圆交AC 于点E ,点D 是BC 边的中点,连OD 交圆O 于点M .(1)求证:E D B O ,,,四点共圆;(2)求证:AB DM AC DM DE ⋅+⋅=22. 23. (本题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系中,直线l 的参数方程为⎪⎩⎪⎨⎧+-=+-=ty t x 541531(t 为参数).若以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,则曲线C 的极坐标方程为)4sin(2πθρ+=.(1)求曲线C 的直角坐标方程; (2)求直线l 被曲线C 所截得的弦长.24.(本题满分10分)选修4-5:不等式选讲函数|2||1|)(-+-=x x x f(1)画出函数)(x f y =的图象;(2)若不等式),,0)((||||||R b a a x f a b a b a ∈≠≥-++恒成立,求实数x 的范围.2012届高三年级第四次四校联考数学(文)参考答案一、选择题:1.A 2.B 3.D ⒋C 5.D 6.C 7.A 8.B 9.A 10.A 11.B 12.D 二、填空题13.5 14.030 15.16 16.9π 三、解答题17.解:(1) x x m x f cos sin )(-=⋅=,()12f π=,∴12cos2sin=-ππm ,即1=m .……………………………3分则x x x f cos sin )(-= )4sin(2π-=x ,当)(224Z k k x ∈+=-πππ,即)(432Z k k x ∈+=ππ时,2)(max =x f ……6分(2)51)(=αf ,即51cos sin =-αα ……………………………………8分 两边平方得:251)cos (sin 2=-αα,所以2524cos sin 2=αα ………………9分2524cos sin 2cos sin 1)sin (cos sin 2tan 1sin 22sin 2==--=--αααααααααα………………12分 18.(1)证明:∵CD ⊥AD ,CD ⊥PA ,∴CD ⊥平面PAD ∴CD ⊥AG , 又PD ⊥AG , ∴AG ⊥平面PCD …………3分作EF ⊥PC 于F ,因面PEC ⊥面PCD ,∴EF ⊥平面PCD ,又由(1)知AG ⊥平面PCD ∴EF ∥AG ,又AG ⊄面PEC ,EF ⊂面PEC , ∴AG ∥平面PEC . ………6分 (2)由AG ∥平面PEC 知A 、G 两点到平面PEC 的距离相等 由(1)知A 、E 、F 、G 四点共面,又AE ∥CD ∴ AE ∥平面PCD ∴ AE ∥GF ,∴ 四边形AEFG 为平行四边形,∴ AE =GF ,PA =AB =4, G 为PD 中点,, ∴FG =2 ∴ AE =FG =2……………9分∴ 1116(24)4323P AEC V -=⋅⋅⋅=, 又EF ⊥PC ,EF =AG = ∴ 1122EPCSPC EF =⋅=⋅=又 P AEC A PEC V V --=,∴11633EPC S h ⋅=, 即16=, ∴h =,∴ G 点到平面PEC .………………………12分19.解:(1)n m ,的所有取值情况有(23,25),(23,30),(23,26),(23,16),(25,30)(25,26),(25,16),(30,26),(30,16),(26,16),共有10个………2分 设“n m ,均不小于25”为事件A ,则事件A 包含的基本事件有(25,30),(25,26)(30,26),所以103)(=A P ,故事件A 的概率为103.………………6分 (2)由数据得27,12==y x ,9723=y x ,43232=x ,又97731=∑=i i i y x ,434312=∑=i i x , ∴25432434972977ˆ=--=b,3122527ˆ-=⨯-=a .所以y 关于x 的线性回归方程为325ˆ-=x y.……………………………10分 (3)当10=x 时,22ˆ=y,|22-23|2<,当8=x 时,,17ˆ=y |17-16|2< 所以得到的线性回归方程是可靠的.……………………………12分20.解: (1) 设椭圆C 的方程为)0(12222>>=+b a by a x ,由题意可得21==a c e ,又222c b a +=,所以2243a b =.……………2分 又椭圆C 经过点)23,1(,所以14349122=+a a ,解得2=a .……………4分所以1=c ,3=b ,则椭圆C 的方程为13422=+y x .……………6分 (2) 解法一:当直线x l⊥轴时,经过计算可以得到:)23,1(--A ,)23,1(-B 或)23,1(-A ,)23,1(--B ,231321||||211=⨯⨯=⋅⋅=∆OF AB S AOB ,不符合题意. ……………7分当直线l 与x 轴不垂直时,设直线l 的方程为0),1(≠+=k x k y ,由⎪⎩⎪⎨⎧=++=134)1(22y x x k y ,消去y ,得01248)43(2222=-+++k x k x k . ……………8分 显然0>∆恒成立,设),(),,(2211y x B y x A ,则2221222143124,438kk x x k k x x +-=⋅+-=+.……………9分 又2122122212214)(1)()(||x x x x k y y x x AB ⋅-+⋅+=-+-=2222224243)1(1243)124(4)43(641kk k k k k k ++=+--+⋅+=. 又圆O 的半径221||1|00|k k k k k r +=++-⨯=,所以726431||6||2122=++=⋅⋅=∆k k k r AB S AOB,……………10分 化简,得0181724=-+k k,解得1718,12221-==k k (舍去),所以221||2=+=k k r …11分故圆O 的方程为2122=+y x .…………………12分解法二:设直线l 的方程为1-=ty x ,由⎪⎩⎪⎨⎧=+-=134122y x ty x ,消去x ,得096)34(22=--+ty y t ,显然0>∆恒成立,……8分 设),(),,(2211y x B y x A ,则221221349,346ty y t t y y +-=⋅+=+,……………9分 所以222122121341124)(||t t y y y y y y ++=-+=-,所以||||21211y y O F S AOB-⋅⋅=∆726341622=++=t t .……………10分 化简,得0171824=--t t ,解得121=t ,181722-=t (舍去). 又圆O 的半径22111|100|t t t r +=++⨯-=,所以22=r .……………11分故圆O 的方程为2122=+y x .…………………12分 21.解:(1)因为x x x f ln 1)(+=,则)0(ln )(2>-='x xxx f …………………1分 当10<<x 时,0)(>'x f ;当1>x 时,0)(<'x f . 所以)(x f 在)1,0(上单调递增,在),1(+∞上单调递减. 所以)(x f 在1=x 处取得极大值.…………………3分 因为)(x f 在区间1(,)2a a +(其中0>a )上存在极值,所以⎪⎩⎪⎨⎧>+<1211a a ,解得121<<a .…………………6分(2)不等式2()1k k f x x -≥+,即k k x x x -≥++2)ln 1)(1(. 设x x x x g )ln 1)(1()(++=,则22ln )(xx x x g -='. 令x x x h ln )(2-=,则x x h 11)(-='. 因为1≥x ,所以0)(≥'x h ,则)(x h 在),1[+∞上单调递增.…………………9分 所以)(x h 得最小值为01)1(>=h ,从而0)(>'x g ,故)(x g 在),1[+∞上单调递增,所以)(x g 得最小值为2)1(=g ,所以22≤-k k ,解得21≤≤-k .…………………12分22. 解:(1)连接BE ,则EC BE ⊥ ---------1分 又D 是BC 的中点,所以BD DE = ----------------3分又OD OD OB OE ==,,所以ODB ODE ∆≅∆,所以90=∠=∠OED OBD故B O E D ,,,四点共圆. -------------5分(2) 延长DO 交圆于点H ,+⋅=+⋅=⋅=DO DM OH DO DM DH DM DE )(2 OH DM ⋅ ------------8分)21()21(2AB DM AC DM DE ⋅+⋅=∴,即AB DM AC DM DE ⋅+⋅=22--------10分23. 解:解:(1) 由)4sin(2πθρ+=得:θθρsin cos +=两边同乘以ρ得:θρθρρsin cos 2+= -------------3分∴022=--+y x y x 即 21)21()21(22=-+-y x -----------5分(2)将直线参数方程代入圆C 的方程得:0202152=+-t t ------------6分 4,5212121==+∴t t t t ------------8分 5414)(||2122121=-+=-=∴t t t t t t MN ------------10分24.解:(1)⎪⎩⎪⎨⎧≤-<<≥-=)1( 23)2(11)2( 32)(x x x x x x f分(2) 由)(x f a b a b a ≥-++ 得)(||||||x f a b a b a ≥-++又因为2||||||||||=-++≥-++a b a b a a b a b a 则有)(2x f ≥--------8分解不等式212-+-≥x x , 得2521≤≤x--------10分。
山西省临汾一中2012届高三第一次四校联考数学文

2012届高三年级第一次四校联考数 学 试 题(文)命题:忻州一中 康杰中学 临汾一中 长治二中(满分150分,考试时间为120分钟)一、选择题:(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集为R ,集合{}1|<=x x A ,B =}021|{2>-+-x x x x ,则 A .B A ⊆B .A B ⊆C .R C A B ⊆D .B C A R ⊆2.如果11abi i=++(,,a b R i ∈表示虚数单位),那么a b += A .0 B . 3- C .1 D .33.下列四个函数中,在区间(0,1)上为增函数的是A .x y 2log -=B .x y sin =C .xy )21(= D .21-=x y4.定义在R 上的函数)(x f 满足⎩⎨⎧>---≤-=0)2()1(0)1(log )(2x x f x f x x x f ,则)2(f 的值为 A . -1 B . 0 C .1 D . 2 5.某流程如右图所示,现输入如下四个函数, 则可以输出的函数是 A .2)(x x f =B .xx f 1)(=C .62ln )(-+=x x x fD .x x f sin )(=6.下列说法错误..的是A .如果命题“p ”与命题“p 或q ”都是真命题,那么命题 q 一定是真命题;B .命题“若a =0,则ab =0”的否命题是:“若a ≠0,则ab ≠0”;C .若命题p :∃x ∈R ,x 2-x +1<0,则p :∀x ∈R ,x 2-x +1≥0;D .“21sin =θ”是“ 30=θ”的充分不必要条件 7.将函数sin()3y x π=-的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再 将所得的图象向左平移3π个单位,得到的图象对应的解析式是 第5题图A .1sin2y x =B .1sin()22y x π=-C .1sin()26y x π=-D .sin(2)6y x π=-8.设0.3222,0.3,log 5a b c ===,则a 、b 、c 的大小关系是A. a b c <<B. b a c <<C. c b a <<D. b a c <<9.已知函数bx x x f +=2)(的图象在点))1(,1(f A 处的切线l 与直线3x-y+2=0平行,若数列⎭⎬⎫⎩⎨⎧)(1n f 的前n 项和为n S ,则2012S 的值为 A .20112010 B .20122011 C .20132012 D .2014201310.已知函数x x f x3log )51()(-=,若0x 是函数)(x f 的零点,且010x x <<,则)(1x f 的值为A .恒为正值 B. 等于0 C. 恒为负值 D. 不大于011.△ABC 满足32=⋅AC AB ,∠BAC=30°,设M 是△ABC 内的一点(不在边界上),定义)(M f =(x,y,z),其中x,y,z 分别表示△MBC ,△MCA,△MAB 的面积,若)(M f =(x,y,21),则yx 41+的最小值为 A .9 B .8 C .18 D .16 12.将一骰子抛掷两次,所得向上点数分别为m 和n ,则函数3213y mx nx =-+在[1,)+∞上为增函数的概率是 A .12B .56C .34D .23二、填空题(本大题共4小题,每小题5分,共20分,把正确答案填在题中横线上) 13.设函数()(1)()f x x x a =++为偶函数,则a = .14.已知向量a =(sin α,2)与向量b =(cos α,1)互相平行,则tan2α的值为_______.15.若直线1+=kx y 与圆0422=-+++my kx y x 相交于P 、Q 两点,且点P 、Q 关于直线0=+y x 对称,则不等式组1000kx y kx my y -+≥⎧⎪-≤⎨⎪≥⎩表示的平面区域的面积为__ .16. ①存在)2,0(πα∈使31cos sin =+αα②存在区间(a ,b )使x y cos =为减函数且x sin <0 ③x y tan =在其定义域内为增函数 ④)2sin(2cos x x y -+=π既有最大值又有最小值,且是偶函数以上命题错误..的为 .(注:把你认为错误的命题的序号都填上) 三、解答题(本大题共6小题,满分70分,解答应给出文字说明,证明过程或演算步骤) 17.(本小题满分10分)已知集合(){}185log 22=+-=x x x A ,{}1,0,1822≠≠==-+m m mx B x x ,{}01922=-+-=a ax x x C 满足A∩C ≠φ,B∩C=φ,求实数a 的值.18. (本题满分12分)如图,在直三棱柱111ABC A B C -中,AC =3, BC =4, AB =5,14AA =,点D 是AB 的中点。
山西省高三数学第四次四校联考 文 新人教A版

n=10s=0 DOs=s+n n=n-1LOOP UNTIL s ﹥=40 PRINT nEND高三年级第四次四校联考数学试题(文)本试卷分必考题和选考题两部分,第1题~第21题为必考题,每个试题学生都必须做答,第22题~第24题为选考题,考生根据要求做答.共150分,考试时间为120分钟.第 I 卷(选择题 共60分)一.选择题:(本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知{}1,2,3,4M ⊆,且{}{}1,21,2M=,则集合M 的个数是( )A.1B. 2C. 3D.4 2.已知i 为虚数单位,复数z 满足z (1-i )+ i=3,则复数z 的值是 ( )A.1+2iB. 1-2iC. 2-iD. 2+i3.已知12xa ⎛⎫= ⎪⎝⎭,12logb x =,2c x =,当x ∈(0,12)时,,,a b c 的大小关系是 ( )A. a b c <<B. b c a <<C. c a b <<D. b a c <<4. 下列命题中真命题的个数是①∀x ∈R ,x 4>x 2;②若p ∧q 为假命题,则p 、q 均为假命题;③命题“∀x ∈R ,x 3-x 2+1≤0”的否定是“∃x ∈R ,x 3-x 2+1>0”.A. 0B. 1C. 2D. 35. 右边程序运行结果为( ) A. 3 B. 4C. 5D. 66. 若一几何体的正视图与侧视图均为边长是1的正方形,且其体积为12,则该几何体 的俯视图可以是 ( )A B C D7.已知平面直角坐标系内的两个向量a =(1,2),b =(m ,3m -2),且平面内的任一向量c 都可以唯一的表示成c =λa +μb (λ,μ为实数),则m 的取值范围是( )A.(-∞,2)B.(2,+∞)C.(-∞,+∞)D.(-∞,2)∪(2,+∞)8. 设函数(2)2()1122xa x x f x x -≥⎧⎪=⎨⎛⎫-< ⎪⎪⎝⎭⎩在R 上为减函数,则实数a 的取值范围是( )A .(],2-∞B .13,8⎛⎤-∞ ⎥⎝⎦ C .(),2-∞ D .13,28⎛⎫⎪⎝⎭9.已知函数()f x 是R 上的偶函数且(1)(1),f x f x -=+当[]0,1x ∈时,2()f x x =,则 函数7()log y f x x =-的零点个数是( )A.3B. 4C.5D.610. 设x , y 满足约束条件2044000x y x y x y -+≥⎧⎪--≤⎪⎨≥⎪⎪≥⎩,若目标函数(0,0)z ax by a b =+>>的最大值为6,则12a b+的最小值为( ) A .1 B .3 C.2 D.411. 已知函数52)(2+-=ax x x f ,若)(x f 在区间(,2]-∞上是减函数,且对任意的 12,[1,1]x x a ∈+,总有12|()()|4f x f x -≤,则实数a 的取值范围是( )A .]3,2[B .]2,1[C .]3,1[-D .),2[+∞12.已知12,F F 分别为双曲线22221(0,0)x ya b a b-=>>的左右焦点,P 为双曲线右支上一点,满足212PF =FF ,直线1PF 与圆222x y a +=相切,则双曲线离心率e 为( )A.53B.5C. 3D. 52第Ⅱ卷(非选择题 共90分)二.填空题:(本大题共4小题,每小题5分,共20分)13. 为积极倡导“学生每天锻炼一小时”的活动,某学校举办了一次以班级为单位的广播操比赛,9位评委给高三.1班打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x )无法看清,若记分员计 算无误,则数字x 应该是 .14.△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积等于 . 15.实数[][]1,1,0,2a b ∈-∈.设函数3211()32f x x ax bx =-++的两个极值点为12,x x .现向点(),a b 所在平面区域投掷一个飞镖,则飞镖恰好落入使1211x x ≤-≥且的区域的概率为 . 16.给出下列命题: ①函数2cos()32y x π=+是奇函数;②存在实数α,使得3sin cos 2αα+=;③若,αβ是第一象限角且αβ<,则tan tan αβ<;④8x π=是函数5sin 24y x π⎛⎫=+ ⎪⎝⎭的一条对称轴方程;⑤函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象关于点,012π⎛⎫⎪⎝⎭成中心对称图形.其中正确的序号为三、解答题(本大题共6小题,共70分。
山西省高三数学第四次四校联考 文 新人教A版

2011届高三年级第四次四校联考数学试题(文)本试卷分必考题和选考题两部分,第1题~第21题为必考题,每个试题学生都必须做答,第22题~第24题为选考题,考生根据要求做答.共150分,考试时间为120分钟.第 I 卷(选择题 共60分)一.选择题:(本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 已知{}1,2,3,4M ⊆,且{}{}1,21,2M=,则集合M 的个数是( )A.1B. 2C. 3D.4 2.已知i 为虚数单位,复数z 满足z (1-i )+ i=3,则复数z 的值是 ( )A.1+2iB. 1-2iC. 2-iD. 2+i3.已知12xa ⎛⎫= ⎪⎝⎭,12logb x =,2c x =,当x ∈(0,12)时,,,a b c 的大小关系是 ( )A. a b c <<B. b c a <<C. c a b <<D. b a c <<4. 下列命题中真命题的个数是 ①∀x ∈R ,x 4>x 2;②若p ∧q 为假命题,则p 、q 均为假命题;③命题“∀x ∈R ,x 3-x 2+1≤0”的否定是“∃x ∈R ,x 3-x 2+1>0”.A. 0B. 1C. 2D. 35. 右边程序运行结果为( ) A. 3 B. 4C. 5D. 66. 若一几何体的正视图与侧视图均为边长是1的正方形,且其体积为12,则该几何体 的俯视图可以是 ( )A B C D7.已知平面直角坐标系内的两个向量a =(1,2),b =(m ,3m -2),且平面内的任一向量c 都可以唯一的表示成c =λa +μb (λ,μ为实数),则m 的取值范围是( )A.(-∞,2)B.(2,+∞)C.(-∞,+∞)D.(-∞,2)∪(2,+∞)8. 设函数(2)2()1122xa x x f x x -≥⎧⎪=⎨⎛⎫-< ⎪⎪⎝⎭⎩在R 上为减函数,则实数a 的取值范围是( )A .(],2-∞B .13,8⎛⎤-∞ ⎥⎝⎦C .(),2-∞D .13,28⎛⎫⎪⎝⎭ 9.已知函数()f x 是R 上的偶函数且(1)(1),f x f x -=+当[]0,1x ∈时,2()f x x =,则 函数7()log y f x x =-的零点个数是( )A.3B. 4C.5D.610. 设x , y 满足约束条件2044000x y x y x y -+≥⎧⎪--≤⎪⎨≥⎪⎪≥⎩,若目标函数(0,0)z ax by a b =+>>的最大值为6,则12a b+的最小值为( ) A .1 B .3 C.2 D.411. 已知函数52)(2+-=ax x x f ,若)(x f 在区间(,2]-∞上是减函数,且对任意的 12,[1,1]x x a ∈+,总有12|()()|4f x f x -≤,则实数a 的取值范围是( )A .]3,2[B .]2,1[C .]3,1[-D .),2[+∞12.已知12,F F 分别为双曲线22221(0,0)x y a b a b -=>>的左右焦点,P 为双曲线右支上一点,满足212PF =FF ,直线1PF与圆222x y a +=相切,则双曲线离心率e 为( ) A.53 B.C.D.第Ⅱ卷(非选择题 共90分)二.填空题:(本大题共4小题,每小题5分,共20分)13. 为积极倡导“学生每天锻炼一小时”的活动,某学校举办了一次以班级为单位的广播操比赛,9位评委给高三.1班打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x )无法看清,若记分员计 算无误,则数字x 应该是 .14.△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积等于 . 15.实数[][]1,1,0,2a b ∈-∈.设函数3211()32f x x ax bx =-++的两个极值点为12,x x .现向点(),a b 所在平面区域投掷一个飞镖,则飞镖恰好落入使1211x x ≤-≥且的区域的概率为 .16.给出下列命题: ①函数2cos()32y x π=+是奇函数;②存在实数α,使得3sin cos 2αα+=; ③若,αβ是第一象限角且αβ<,则tan tan αβ<;④8x π=是函数5sin 24y x π⎛⎫=+ ⎪⎝⎭的一条对称轴方程;⑤函数sin 23y x π⎛⎫=+⎪⎝⎭的图象关于点,012π⎛⎫⎪⎝⎭成中心对称图形. 其中正确的序号为三、解答题(本大题共6小题,共70分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012届高三年级第四次四校联考数学(文)试卷(满分150分,考试时间120分钟)命题:长治二中 康杰中学 忻州一中 临汾一中第Ⅰ卷一、选择题:(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的)1.已知i 为虚数单位,若复数i z -=11,i z +=22,则=⋅21z zA .i -3B .i -2C .i -1D .i 22+ 2.已知集合B A 、,{}22<≤-=x x A ,A B A = ,则集合B 不可能...为 A . ∅ B .{}20≤≤x x C .{}20<<x x D .{}20<≤x x 3.为了得到函数xy )31(3⋅=的图象,可以把函数xy )31(=的图象A .向左平移3个单位长度B .向右平移3个单位长度C .向左平移1个单位长度D .向右平移1个单位长度4.下列函数中,周期为π,且图像关于直线3π=x 对称的函数是A .)32sin(2)(π+=x x f B .)32sin(2)(π+=x x fC .)62sin(2)(π-=x x f D .)62sin(2)(π-=x x f5.双曲线)0(13222>=-a yax 有一个焦点与抛物线x y 82=的焦点重合,则双曲线的渐近线方程为A .y =x 21±B .y =x 2±C .y =x 33±D .y =x 3±6.执行如下图所示的程序框图输出的结果是A .-3B .-2C .2D .37.一个几何体的三视图及部分数据如图所示,侧视图为等腰三角形,俯视图为正方形,则这个几何体的体积等于A .13B .23C .6D .248.已知等比数列{}n a 的公比0>q 且1≠q ,又06<a ,则A .5748a a a a +<+B .5748a a a a +>+C .5748a a a a +=+D .5748||||a a a a +>+9.下列各命题中正确的命题是 ① “若b a ,都是奇数,则b a +是偶数”的逆否命题是“若b a +不是偶数,则b a ,都不是奇数”; ② 命题“x x R x 31,2>+∈∃”的否定是“x x R x 31,2≤+∈∀” ;③ “函数ax ax x f 22sin cos )(-=的最小正周期为π” 是“1=a ”的必要不充分条件; ④“平面向量a 与b 的夹角是钝角”的充分必要条件是“0<⋅b a ” . A .②③ B .①②③ C .①②④D .③④10.已知实数y x ,满足⎪⎩⎪⎨⎧≤+-≤≥m y x x y y 121,若目标函数y x z -=的最小值是-1,则此目标函数的最大值是A .1B . 2C . 3D . 511.设曲线)(*1N n x y n ∈=+在点)1,1(处的切线与x 轴的交点横坐标为n x ,则++2201212012loglogx x (20112012)logx +的值为A .2011log2012- B .1- C .2011log 12012+- D .112.对实数a 和b ,定义运算“⊗”:a ⊗b =⎩⎪⎨⎪⎧a ,a -b ≤1,b ,a -b >1.设函数f (x )=(x 2-2)⊗(x -x 2),x ∈R ,若函数y =f (x )-c 的图象与x 轴恰有两个公共点,则实数c 的取值范围是A .(-∞,-2]∪⎝⎛⎭⎫-1,32B .⎝⎛⎭⎫-1,-34∪⎣⎡⎭⎫14,+∞C .⎝⎛⎭⎫-1,14∪⎝⎛⎭⎫14,+∞D .(-∞,-2]∪⎝⎛⎭⎫-1,-34第Ⅱ卷本卷包括必考题和选考题两部分,第13—第21题为必考题,每个试题考生都必须作答,第22—24题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分,把正确答案填在题中横线上)13.已知向量()1,2,5,||a a b a b =⋅=-= ||b等于14.在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c,若22a b -=,sin C B =,则角A= 15.等差数列}{n a 中,20,873==a a ,若数列}1{1+n n a a 的前n 项和为254,则n 的值为16.已知P 、A 、B 、C 是球O 表面上的点,PA ⊥平面ABC ,AC ⊥BC ,AC =1,BC,PA,则球O 的表面积为三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知向量)cos ,(sin ),1,(x x b m a =-=,()f x a b =⋅且满足()12f π=.(1)求函数()y f x =的最大值及其对应的x 值;(2)若51)(=αf ,求αααtan 1sin 22sin 2--的值.18.(本小题满分12分)如图,在四棱锥P —ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为正方形,PA =AB =4, G 为PD 的中点,E 点在AB 上,平面PEC ⊥平面PDC . (1)求证:AG ∥平面PEC ;(2)求点G 到平面PEC 的距离.19. (本小题满分12分) 某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:n m ,n m ,(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天...的数据,求出y 关于x 的线性回归方程a x b y ˆˆˆ+=; (3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?(参考公式:1221ˆniii ni i x yn x ybx n x==-=-∑∑,x b y a ˆˆ-=)(参考数据:97731=∑=i i i y x ,434312=∑=i i x )20. (本小题满分12分) 已知椭圆C 的对称中心为原点O ,焦点在x 轴上,离心率为21,且过点)23,1(.(1)求椭圆C 的方程;(2) 过椭圆C 的左焦点1F 的直线l 与椭圆C 相交于BA ,两点,若AOB ∆的面积为726,求圆心在原点O 且与直线l 相切的圆的方程.21.(本小题满分12分)已知函数1ln ()x f x x+=.(1)设a >0,若函数)(x f 在区间1(,)2a a +上存在极值,求实数a 的取值范围;(2)如果当x ≥1时,不等式2()1k k f x x -≥+恒成立,求实数k 的取值范围.请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑. 22. (本题满分10分)选修4-1:几何证明与选讲如图,ABC ∆为直角三角形, 90=∠ABC ,以AB 为直径的圆交AC 于点E ,点D 是BC 边的中点,连OD 交圆O 于点M . (1)求证:E D B O ,,,四点共圆; (2)求证:AB DM AC DM DE ⋅+⋅=22. 23. (本题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系中,直线l 的参数方程为⎪⎩⎪⎨⎧+-=+-=t y tx 541531(t 为参数).若以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,则曲线C 的极坐标方程为)4sin(2πθρ+=.(1)求曲线C 的直角坐标方程; (2)求直线l 被曲线C 所截得的弦长. 24.(本题满分10分)选修4-5:不等式选讲 函数|2||1|)(-+-=x x x f(1)画出函数)(x f y =的图象;(2)若不等式),,0)((||||||R b a a x f a b a b a ∈≠≥-++恒成立,求实数x 的范围.2012届高三年级第四次四校联考数学(文)参考答案一、选择题:1.A 2.B 3.D ⒋C 5.D 6.C 7.A 8.B 9.A 10.C 11.B 12.D 二、填空题13.5 14.030 15.16 16.9π 三、解答题17.解:(1) x x m b a x f cos sin )(-=⋅=,()12f π=,∴12cos2sin=-ππm ,即1=m .……………………………3分则x x x f cos sin )(-= )4sin(2π-=x ,当)(224Z k k x ∈+=-πππ,即)(432Z k k x ∈+=ππ时,2)(max =x f ……6分(2)51)(=αf ,即51cos sin =-αα …………………………………………8分两边平方得:251)cos (sin 2=-αα,所以2524cos sin 2=αα ………………9分2524cos sin 2cos sin 1)sin (cos sin 2tan 1sin 22sin 2==--=--αααααααααα………………12分18.(1)证明:∵CD ⊥AD ,CD ⊥PA ,∴CD ⊥平面PAD ∴CD ⊥AG , 又PD ⊥AG , ∴AG ⊥平面PCD …………3分作EF ⊥PC 于F ,因面PEC ⊥面PCD ,∴EF ⊥平面PCD ,又由(1)知AG ⊥平面PCD ∴EF ∥AG ,又AG ⊄面PEC ,EF ⊂面PEC , ∴AG ∥平面PEC . ………6分 (2)由AG ∥平面PEC 知A 、G 两点到平面PEC 的距离相等 由(1)知A 、E 、F 、G 四点共面,又AE ∥CD ∴ AE ∥平面PCD ∴ AE ∥GF ,∴ 四边形AEFG 为平行四边形,∴ AE =GF ,PA =AB =4, G 为PD 中点,2CD , ∴FG =2 ∴ AE =FG =2……………9分∴ 1116(24)4323P A ECV -=⋅⋅⋅=, 又EF ⊥PC ,EF =AG = ∴ 1122E P C S P C EF =⋅=⋅= 又 P AEC A PEC V V --=,∴11633EPC S h ⋅=,即16=, ∴3h =,∴ G 点到平面PEC 的距离为3.………………………12分19.解:(1)n m ,的所有取值情况有(23,25),(23,30),(23,26),(23,16),(25,30)(25,26),(25,16),(30,26),(30,16),(26,16),共有10个………2分 设“n m ,均不小于25”为事件A ,则事件A 包含的基本事件有(25,30),(25,26)(30,26),所以103)(=A P ,故事件A 的概率为103.………………6分(2)由数据得27,12==y x ,9723=y x ,43232=x ,又97731=∑=i i i y x ,434312=∑=i i x , ∴25432434972977ˆ=--=b ,3122527ˆ-=⨯-=a . 所以y 关于x 的线性回归方程为325ˆ-=x y.……………………………10分(3)当10=x 时,22ˆ=y ,|22-23|2<,当8=x 时,,17ˆ=y |17-16|2< 所以得到的线性回归方程是可靠的.……………………………12分 20.解: (1) 设椭圆C 的方程为)0(12222>>=+b a by ax ,由题意可得21==ac e ,又222c b a +=,所以2243a b =.……………2分又椭圆C 经过点)23,1(,所以14349122=+aa,解得2=a .……………4分所以1=c ,3=b ,则椭圆C 的方程为13422=+yx.……………6分(2) 解法一:当直线x l ⊥轴时,经过计算可以得到:)23,1(--A ,)23,1(-B 或)23,1(-A ,)23,1(--B ,231321||||211=⨯⨯=⋅⋅=∆OF AB S AOB ,不符合题意. ……………7分 当直线l 与x 轴不垂直时,设直线l 的方程为0),1(≠+=k x k y , 由⎪⎩⎪⎨⎧=++=134)1(22y x x k y ,消去y ,得01248)43(2222=-+++k x k x k . ……………8分 显然0>∆恒成立,设),(),,(2211y x B y x A , 则2221222143124,438kk x x kkx x +-=⋅+-=+.……………9分 又2122122212214)(1)()(||x x x x k y y x x AB ⋅-+⋅+=-+-=2222224243)1(1243)124(4)43(641kk kk k kk ++=+--+⋅+=.又圆O 的半径221||1|00|kk kk k r +=++-⨯=,所以726431||6||2122=++=⋅⋅=∆kk k r AB S AOB ,……………10分化简,得0181724=-+k k ,解得1718,12221-==k k (舍去),所以221||2=+=kk r …11分故圆O 的方程为2122=+y x .…………………12分解法二:设直线l 的方程为1-=ty x ,由⎪⎩⎪⎨⎧=+-=134122y x ty x ,消去x ,得096)34(22=--+ty y t ,显然0>∆恒成立,……8分 设),(),,(2211y x B y x A ,则221221349,346ty y tt y y +-=⋅+=+,……………9分所以222122121341124)(||tt y y y y y y ++=-+=-,所以||||21211y y O F S AOB -⋅⋅=∆726341622=++=tt .……………10分化简,得0171824=--t t ,解得121=t ,181722-=t (舍去).又圆O 的半径22111|100|ttt r +=++⨯-=,所以22=r .……………11分故圆O 的方程为2122=+y x .…………………12分21.解:(1)因为xxx f ln 1)(+=,则)0(ln )(2>-='x xx x f …………………1分当10<<x 时,0)(>'x f ;当1>x 时,0)(<'x f . 所以)(x f 在)1,0(上单调递增,在),1(+∞上单调递减. 所以)(x f 在1=x 处取得极大值.…………………3分 因为)(x f 在区间1(,)2a a +(其中0>a )上存在极值,所以⎪⎩⎪⎨⎧>+<1211a a ,解得121<<a .…………………6分 (2)不等式2()1k k f x x -≥+,即k k xx x -≥++2)ln 1)(1(.设xx x x g )ln 1)(1()(++=,则22ln )(xx x x g -='. 令x x x h ln )(2-=,则xx h 11)(-='.因为1≥x ,所以0)(≥'x h ,则)(x h 在),1[+∞上单调递增.…………………9分 所以)(x h 得最小值为01)1(>=h ,从而0)(>'x g ,故)(x g 在),1[+∞上单调递增,所以)(x g 得最小值为2)1(=g ,所以22≤-k k ,解得21≤≤-k .…………………12分22. 解:(1)连接BE ,则EC BE ⊥ ----------------1分 又D 是BC 的中点,所以BD DE = ----------------3分 又OD OD OB OE ==,,所以ODB ODE ∆≅∆,所以 90=∠=∠OED OBD故B O E D ,,,四点共圆. -------------5分 (2) 延长DO 交圆于点H ,+⋅=+⋅=⋅=DO DM OH DO DM DH DM DE )(2OH DM ⋅------------8分)21()21(2AB DM AC DM DE⋅+⋅=∴,即AB DM AC DM DE ⋅+⋅=22--------10分23. 解:解:(1) 由)4sin(2πθρ+=得:θθρsin cos +=两边同乘以ρ得:θρθρρsin cos 2+= -------------3分 ∴022=--+y x y x 即 21)21()21(22=-+-y x -----------5分(2)将直线参数方程代入圆C 的方程得:0202152=+-t t ------------6分 4,5212121==+∴t t t t ------------8分5414)(||2122121=-+=-=∴t t t t t t MN ------------10分24.解:(1)⎪⎩⎪⎨⎧≤-<<≥-=)1( 23)2(1 1)2( 32)(x x x x x x f(2) 由)(x f a b a b a ≥-++ 得)(||||||x f a b a b a ≥-++又因为2||||||||||=-++≥-++a b a b a a b a b a 则有)(2x f ≥--------8分 解不等式212-+-≥x x , 得2521≤≤x--------10分。
