第三章应变状态理论-PPT课件
合集下载
岩土弹塑性力学教学课件(共13章)第3章_应变状态
§3.1 应变状态11
• 三个刚性转动分量及6个应变分量合在一起，才全 面反映了物体变形
xyz x y z xy yz zx
B
B’’ 刚性转动
B’’’
B’
变形
A 刚性平动 A`
§3.1 应变状态12
• 工程应变： ln l0
l0
变形后长度 原始长度
不适用于大变形
• 自然应变/对数应变：
在塑性变形较大时，用-曲线不能真正代表加载和变形的状态。
x y z
• ——弹性体一点的体积改变量
• 引入体积应变有助于简化公式。
• 大于零表示体积膨胀，小于零体积压缩。
• 注意：土力学中塑性体应变符号约定相反。
§3.2 主应变与应变主方向8
应变Lode参数: 为表征偏量应变张量的形式，引入应变Lode参数：
22 3 1 3
1
(1.66)
如果两种应变状态με 相等，表明它们所对应的应变莫尔圆 相似，也即偏应变张量的形式相同。
Vz y
;
zx
Vz x
Vx z
;
§3.3 应变率张量 2
小变形情况下，应变速率分量与应变分量间存在如下关系:
x
Vx x
du x dt
d dt
u x
x
u x
y
Vy y
dv y dt
d v
dt
y
y
v y
z
Vz z
z
dw dt
d w dt z
z
w z
线应变速率
j
Vj,i )
(1.56)
§3.3 主应变与应变主方向 4
由于时间度量的绝对值对塑性规律没有影响，因
第三章应变状态理论PPT课件
思考题：当形变分量完全确定时，位移分量 是否能完全确定。
22.11.2020
12
22.11.2020
同样，空间一
点的变形我们用该
点x、y、z方向上 的正应变和xy、yz、
zx方向构成的直角 的变化－切应变来
描述。
张量形式为
ij
1 ui 2 xj
uj xi
13
22.11.2020
空间的应变分量共九 个分量，是一个对称张量， 和应力张量一样，它们遵 从坐标变换规则，同样存 在着三个互相垂直的主方 向，对应的主应变值是该 张量的特征值。这些互相 垂直的主方向构成的直角 在该应变张量的变形时， 角度不变，由主平面组成 的单元体，由正方体变为 直角长方体。在主方向构 成的坐标系中，张量分量 构成对角阵，切应变分量 为零。
x
y
z
x'
l1
m1
n1
y'
l2
m2
n2
z'
l3
m3
n3
其中 li,mi,ni(i1,2,3)表示新坐标轴对老坐标轴的 方向余弦。
22.11.2020
20
位移矢量在新坐标系中的3个分量u',v',w' 分别为：
u' v'
Ue1' Ue2'
ul1 ul2
vm1 w vm2 w
nn12
w' Ue3' ul3 vm3 wn3
第三章 应变状态理论
22.11.2020
1
外力(或温度变化)作用下，物体内部各部 分之间要产生相对运动。物体的这种运动形态， 称为变形。
本章任务有两个：
1、分析一点的应变状态；
第三章应变理论课件
Venant）1797年生于法国，
1886年逝世。1825年毕业于
巴黎桥梁公路学校，后从事
工程设计工作，1837年回该
校任教，1868年当选为法国
科学院院士。在弹性力学、
塑性力学、流体力学等方面
做出了贡献。他的力作用的
局部思想被称为“圣维南原 理”。
圣维南
（A.J.Saint-Venant）
§3-5 变形协调方程
§3-3 转动张量
如图4设过点 从物体中任意取出
一微元线段 。若令点 的坐标
为
，则点 的坐标为
变形后， 变成 的位移为
。令点 的位移为
于是
图4
, 则点
§3-3 转动张量
§3-3 转动张量
其中
若令
则
表示位移矢量 的旋度，
则分别表示物体
内微元体绕相应的坐标轴的旋转分量，而
则代
表微元体的刚性转角。
§3-3 转动张量
应变协调方程的物理意义： ➢ 物体变形后每一单元体都发生形状改变，如变形不满
足一定的关系，变形后的单元体将不能重新组合成连 续体，其间将产生缝隙或出现相互嵌入现象。 ➢ 为使变形后的物体保持连续体，应变分量必须满足一 定的关系。 注：应变协调方程是变形连续的必要和充分条件！
例题
例1. 设物体变形时产生的应变分量为
在略去二阶及更高阶的微量以后简化为 线段 的正应变是
（3）
§3-2 小应变张量（几何方程）
由于位移是微小的， 方向的位移所引起的线段 的伸缩，是更高一阶微小的，略去不计。同样线段
的正应变是 （4）
求出线段 与 之间的直角改变，也就是剪应 变 ，用位移分量来表示。
§3-2 小应变张量（几何方程）
第三章-应变分析
3－4 体积应变
单元体的体积： dVdxdydz
变形后，体积： dV'(dxxdx)(dyydy)(dzzdz)
dxdy(d1z )(1 )(1 )
x
y
z
dxdy(d1z )
x
y
z
则，体积应变：
d' V d V d
x(1 d y d z) d
x
y
z
x d y d z
dV
d xd yd zx y z
Man◇ ._Ha!n.℡ɡ1rl。 ゜ eVer ㄨ 、 Give up沸 点 soon startˊ Sorry -aesar 凯 撒 Julietˋ Ａ m , 七 分 醒 ▌SakitIf- ExpectΜ elod y丶 低 声 、 saybetrayeiove 均 My、
queen哀 伤 之 后 After sad□ Yinkuimy、 zyO° Myへ Loveヽ ρuzzledPoison丶
第二种位移是弹性体形状的变化，位移发生时不仅改变 物体的绝对位置，而且改变了物体内部各个点的相对位 置，这是物体形状变化引起的位移，称为变形位移。
M（x，y，z）移动至M'（x'，y'，z'）
点的位移为MM'
z
u = x'- x = u（x，y，z）
v = y'- y = v（x，y，z）
w = z’- z = w（x，y，z）
变形后：
m'点的坐标为( x+u，y+v）
a '点的坐标为( x+dx+u+微分增量，y+v +微分增量）
b '点的坐标为 ( x+u+微分增量，y+dy+v +微分增量）
弹性力学_第三章应变.ppt
v
B"
B
u u dx x
线素AB的转角为： BB tg AB
弹性力学
第三章 应变
§3-1 变形与应变概念 §3-2 变形连续条件 §3-3 应变增量和应变速率张量 §3-4 应力应变分析的相似性与差异性
§3-1 变形与应变概念
弹性体在受外力以后，还将发生变形。物体的 变形状态，一般有两种方式来描述： 1、给出各点的位移；2、给出各体素的变形。 弹性体内任一点的位移，用此位移在x、y、z 三个坐标轴上的投影u、v、w来表示。以沿坐标轴 正方向为正，沿坐标轴负方向为负。这三个投影称 为位移分量。一般情况下，弹性体受力以后，各点 的位移并不是定值，而是坐标的函数。
变形的度量——应变
一个物体受作用力后，其内部质点不仅要发生相对位置的改 变（产生了位移），而且要产生形状的变化（产生了变形）。 物体的变形程度用应变来度量，物体在某一时刻的形态与早先 的形态（一般指初始状态或未变形的状态）之间的差别就是物 体在该时刻的应变。物体变形时，其体内各质点在各方向上都 会有应变。
AB、AD的正应变 x 、 y ：
C'
D" D '
D C
dy
u
A
A'
B'
v v dx x
v
B"
B
u u dx x
dx 0 图 2-5
x
线素AB的正应变为： u (u dx)u u x x dx x 同理，AD的正应变为： v (v dy) v v y y dy y
§3-1 变形与应变概念
刚体位移：物体内部各点位置变化，但仍保持初始状态相对 位置不变（即其体内任意两点之间距保持不变）。
弹性力学课件第三章应变理论
有限元法的实现需要借助计算机编程，利用有限 元分析软件进行建模、求解和后处理。
有限差分法
01
有限差分法是一种基于离散化的数值分析方法，通过将连续的时间或 空间离散化为有限个差分，建立差分方程进行求解。
02
在弹性力学中，有限差分法常用于求解波动问题和热传导问题等偏微 分方程。
03
有限差分法的优点在于简单直观，易于编程实现，特别适合处理规则 区域的问题。
应变分析在断裂力学中的应用对于评估材料的安全性和可靠性具有重要意义，特别是在 航空航天、石油化工和核能等领域的高强度材料中尤为重要。
流体力学中的应变分析
01
流体力学是研究流体运动规律和流体与固体相互作用的一门学科。 在流体力学中，应变分析是研究流体流动状态和流体机械性能的 基础。
02
应变分析在流体力学中主要关注流体在不同压力、温度和 剪切力等条件下的流动行为。通过测量流体的应变响应， 可以评估流体的流动特性和机械性能，为流体机械的设计 和优化提供依据。
应变理论在处理大变形和塑性变形时存在困难，需要 引入更复杂的模型和理论。
应变理论在处理多相材料和复合材料时，难以准确描 述材料的复杂行为。
应变理论的新发展
发展了高阶应变理论，以更准确地描述材料的复杂 变形行为。
引入了有限变形理论，对应变和应力进行更全面的 描述。
结合数值计算方法，如有限元法，对应变进行数值 模拟和分析。
弹性力学课件第三章应变理论
目
CONTENCT
录
• 应变理论概述 • 应变理论基础 • 应变分析方法 • 应变理论应用 • 应变理论发展前景
01
应变理论概述
应变定义与测量
应变定义
物体在外力作用下发生的形状和尺寸 的相对变化。
有限差分法
01
有限差分法是一种基于离散化的数值分析方法，通过将连续的时间或 空间离散化为有限个差分，建立差分方程进行求解。
02
在弹性力学中，有限差分法常用于求解波动问题和热传导问题等偏微 分方程。
03
有限差分法的优点在于简单直观，易于编程实现，特别适合处理规则 区域的问题。
应变分析在断裂力学中的应用对于评估材料的安全性和可靠性具有重要意义，特别是在 航空航天、石油化工和核能等领域的高强度材料中尤为重要。
流体力学中的应变分析
01
流体力学是研究流体运动规律和流体与固体相互作用的一门学科。 在流体力学中，应变分析是研究流体流动状态和流体机械性能的 基础。
02
应变分析在流体力学中主要关注流体在不同压力、温度和 剪切力等条件下的流动行为。通过测量流体的应变响应， 可以评估流体的流动特性和机械性能，为流体机械的设计 和优化提供依据。
应变理论在处理大变形和塑性变形时存在困难，需要 引入更复杂的模型和理论。
应变理论在处理多相材料和复合材料时，难以准确描 述材料的复杂行为。
应变理论的新发展
发展了高阶应变理论，以更准确地描述材料的复杂 变形行为。
引入了有限变形理论，对应变和应力进行更全面的 描述。
结合数值计算方法，如有限元法，对应变进行数值 模拟和分析。
弹性力学课件第三章应变理论
目
CONTENCT
录
• 应变理论概述 • 应变理论基础 • 应变分析方法 • 应变理论应用 • 应变理论发展前景
01
应变理论概述
应变定义与测量
应变定义
物体在外力作用下发生的形状和尺寸 的相对变化。
弹性力学应变状态
第三章 应变状态
物体变形 位移与应变的基本关系－几何方程 应变状态分析 位移的单值连续性质-变形协调方程
目录
§3.1 变形与应变概念 §3.2 主应变与主应变方向 §3.3 应变协调方程
§3.1 变形与应变概念
• 由于外部因素——载荷或温度变化 • 位移——物体内部各点空间位置发生变化 • 位移形式_位置的改变与弹性体形状的变化
是连续的。
在数学上，x'，y'，z' 必为x，y， z的单值连续函数。
§3.1 变形3
设MM‘=S为位移矢量， 位移矢量的三个分量 u，v，w为位移分量，则
U =x' （x，y，z）-x = u（x，y，z） V =y'（x，y，z）-y = v（x，y，z） W =z'（x，y，z）-z = w（x，y，z）
特别是物体位移中不影响变形的计算， 假设各点的位移仅为自身的大小和形状的 变化所确定，则这种微分线段的转动的误 差是十分微小的，不会导致微分单元体的 变形有明显的变化。
正应变 §3.1 变形7
– 微分单元体的棱边长为dx，dy，dz – M点的坐标：（x，y，z） – M点的位移分量：u（x,y,z）,v(x,y,z), w（x,y,z）
应变，由于六个应变分量对应三个位移分量，则其求解将相
对复杂。 这个问题以后作专门讨论。
几何方程给出的应变通常称为工程应变。
使用张量符号，几何方程可以表达为：
ij
1 2
ui, j u j,i
§3.1 变形11
上式表明应变分量ij 将满足二阶张量的坐 标变换关系，应变张量分量与工程应变分 量的关系可表示为
• 刚体位移：物体内部各点位置变化，但仍保持初始
物体变形 位移与应变的基本关系－几何方程 应变状态分析 位移的单值连续性质-变形协调方程
目录
§3.1 变形与应变概念 §3.2 主应变与主应变方向 §3.3 应变协调方程
§3.1 变形与应变概念
• 由于外部因素——载荷或温度变化 • 位移——物体内部各点空间位置发生变化 • 位移形式_位置的改变与弹性体形状的变化
是连续的。
在数学上，x'，y'，z' 必为x，y， z的单值连续函数。
§3.1 变形3
设MM‘=S为位移矢量， 位移矢量的三个分量 u，v，w为位移分量，则
U =x' （x，y，z）-x = u（x，y，z） V =y'（x，y，z）-y = v（x，y，z） W =z'（x，y，z）-z = w（x，y，z）
特别是物体位移中不影响变形的计算， 假设各点的位移仅为自身的大小和形状的 变化所确定，则这种微分线段的转动的误 差是十分微小的，不会导致微分单元体的 变形有明显的变化。
正应变 §3.1 变形7
– 微分单元体的棱边长为dx，dy，dz – M点的坐标：（x，y，z） – M点的位移分量：u（x,y,z）,v(x,y,z), w（x,y,z）
应变，由于六个应变分量对应三个位移分量，则其求解将相
对复杂。 这个问题以后作专门讨论。
几何方程给出的应变通常称为工程应变。
使用张量符号，几何方程可以表达为：
ij
1 2
ui, j u j,i
§3.1 变形11
上式表明应变分量ij 将满足二阶张量的坐 标变换关系，应变张量分量与工程应变分 量的关系可表示为
• 刚体位移：物体内部各点位置变化，但仍保持初始
弹性力学-第三章 应变分析
(3.9)
α xy
% dr2
% dr1
dr2
α yx
dr1
x
第三章 应变分析 §3-3
应变张量的进一步解释
由式(3.12)得 由式(3.12)得dr1和dr2间直角的减小量为 (3.12)
∆ϕ = 22ε ij nm j j = 2ε 12 = 2ε xy ∆ϕ = ε ij ni i m
上式表示剪应变是角度变化的一半 图中: 图中:
% dr 2 = dr 2 + 2dr ⋅ G ⋅ dr = (1 + 2n ⋅ G ⋅ n)dr 2
第三章 应变分析 §3-2
变形状态和应变张量
只讨论小变形问题,忽略高阶项 只讨论小变形问题 忽略高阶项 式(3.6) 为 其中
∇u ⋅ u∇
(3.7)
% dr 2 = (1 + 2n ⋅ ε ⋅ n)dr 2
ε x 1 γ ε ij = 2 yx 1 γ zx 2
εy
1 γ zy 2
对称张量 张量的剪切应变分量 ≠ 实际的剪切应变
第三章 应变分析 §3-3
应变张量的进一步解释
应变与位移的关系（几何方程） 点的位移是u(x+dx，y)、 应变与位移的关系（几何方程） A点的位移是 点的位移是 ， 、 v(x+dx，y)， ， ，
分别为Y 分别为Y和Z方向的正应变 如图, 如图, 设n为x轴向的单位基矢量即n=e1 轴向的单位基矢量即n=e n1 = 1, n2 = 0, n3 = 0 设m为y轴向的单位基矢量即m=e2 轴向的单位基矢量即m=e O m1 = 0, m2 = 1, m3 = 0
y
ε nn = εijni⋅ ε ⋅ n11 =ε ijxni n j ε = n nj = ε = ε
塑性力学_第三章应变状态
第三章 应变状态理论在外力、温度变化或其他因素作用下，物体内部各质点将产生位置的变化，即发生位移。
如果物体内各点发生位移后仍保持各质点间初始状态的相对位置，则物体实际上只发生了刚体平移和转动，这种位移称为刚体位移。
如果物体各质点发生位移后改变了各点间初始状态的相对位置，则物体同时也产生了形状的变化，其中包括体积改变和形状畸变，物体的这种变化称为物体的变形运动或简称为变形，它包括微元体的纯变形和整体运动。
应变状态理论就是研究物变形后的几何特性。
即给定物体内各点变形前后的位置，确定无限接近的任意两点之间所连矢量因物体变形所引起剧烈变化。
这是一个单纯的几何问题，并不涉及物体变形的原因，也就是说并不涉及物体抵抗变形的物理规律。
本章主要从物体变形前后的几何变化论述物体内一点的应变状态。
3.1 位移与线元长度、方向的变化1.1坐标与位移设变形前物体上各点的位置在笛卡尔坐标(Descarter coordinate)系的轴(X 、、Y、Z )上的投影为(z y x ,,)，又设物体上各点得到一位移，并在同一坐标轴上的投影为(u 、v 、w )，这些位移分量可看作是坐标(z y x ,,)的函数。
于是物体上任点的最终位置由下述坐标值决定。
即⎪⎭⎪⎬⎫+=+=+=),,(),,(),,(z y x w z z y x v y z y x u x ζηξ (3.1-1)上式中函数u 、v 、w 以及它们对坐标(z y x ,,)的偏导数假设是连续的，则式(3.1-1)确定了变量(z y x ,,)与),,(ζηξ之间的关系。
因为物体中变形前各点对应看变形后的各点，因此式(3.1-1)是单值的，所以式(3.1-1)可看成是坐标的一个变换。
如果在(3.1-1)中，假设00,y y x x ==，则由(3.1-1)式可得如下三个方程⎪⎭⎪⎬⎫+=+=+=),,(),,(),,((00000000z y x w z z y x v y z y x u x ςηξ (3.1-2)式(3.1-2)决定了一条曲线，曲线上各点 ,,21**M M ，在物体变形前为平行于z 轴的直线(00,y y x x ==)上(图3.1)。
3.应变理论
y 2
2 y
x 2
2 xy
xy
上式即为 变形协调方 程，共81个， 而独立方程 只有6个：
2 y
z 2
2 z
y 2
2 yz
yz
2 z
x 2
2 x
z 2
2 zx
zx
( zx
x y
xy
z
yz )
x
2 2 x
yz
(3.19)
Hale Waihona Puke y( xyz
yz
x
zx
y
)
2
2 y
xz
( yz
第三章 应变理论 第一节小变形理论
若边长 AB=dx,则在 x 轴方向
AB 边变形后的伸长为：
AB
AB
AB
u
u1
u
u x
dx
故 x 方向的应变为：
x
AB AB
u dx
u x
同理可得：
y
v y
; z
w z
图 3.1 单元的变形图
现在研究棱边角度的改变。
zx
tg
BB AB
w dx x dx u dx
3u j xi xk xl
(3.16)
2 ik
x jxl
1 3uk 2 x jxixl
3ui x jxk xl
(3.17)
（3.14)＋(3.15)－(3.16)－(3.17)得
2 ij 2 kl 2 lj 2 ik 0
xk xl xix j xk xi x jxl
2 x
第一个坐标系各轴的方向余弦如表 3.1 所示。
表 3.1 新旧坐标系间的方向余弦
X
2 y
x 2
2 xy
xy
上式即为 变形协调方 程，共81个， 而独立方程 只有6个：
2 y
z 2
2 z
y 2
2 yz
yz
2 z
x 2
2 x
z 2
2 zx
zx
( zx
x y
xy
z
yz )
x
2 2 x
yz
(3.19)
Hale Waihona Puke y( xyz
yz
x
zx
y
)
2
2 y
xz
( yz
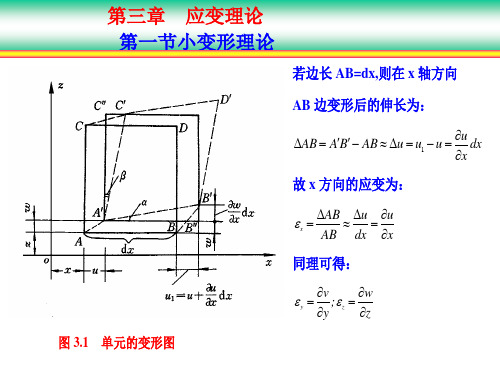
第三章 应变理论 第一节小变形理论
若边长 AB=dx,则在 x 轴方向
AB 边变形后的伸长为：
AB
AB
AB
u
u1
u
u x
dx
故 x 方向的应变为：
x
AB AB
u dx
u x
同理可得：
y
v y
; z
w z
图 3.1 单元的变形图
现在研究棱边角度的改变。
zx
tg
BB AB
w dx x dx u dx
3u j xi xk xl
(3.16)
2 ik
x jxl
1 3uk 2 x jxixl
3ui x jxk xl
(3.17)
（3.14)＋(3.15)－(3.16)－(3.17)得
2 ij 2 kl 2 lj 2 ik 0
xk xl xix j xk xi x jxl
2 x
第一个坐标系各轴的方向余弦如表 3.1 所示。
表 3.1 新旧坐标系间的方向余弦
X
高等材料力学课件第三章-应变状态
应变与变形
1 变与变形的关系
应变是描述物体形变程度的量，而变形是指物体由于受力而发生的形状改变。
2 应变分量与应力分量的关系
应变和应力是密切相关的，通过应变和应力之间的关系可以对材料的力学性质进行分析。
3 应变表面与应力表面的关系
应变表面和应力表面是描述物体应变和应力分布情况的图形，它们是密切相关的。
总结
1 本章主要内容回顾
本章我们深入学习了材料力学中的应变状态，包括应变概念、应变矩阵、平面应变状态 和空间应变状态等。
2 应变概念和应变矩阵的关系
应变概念是研究物体形变程度的基本概念，而应变矩阵是用于描述物体应变状态的重要 工具。
3 平面应变状态和空间应变状态的区别和联系
平面应变状态是指物体在平面内发生的应变情况，而空间应变状态是指物体在三维空间 内发生的应变情况。
高等材料力学课件第三章 变状态
欢迎来到本课件第三章，我们将深入探讨材料力学中的应变状态。了解应变 概念、应变矩阵、平面应变状态和空间应变状态等重要内容。
应变概念
1 应变定义
应变是描述物体在受到力 作用后形变程度的量，可 分为线性应变和非线性应 变。
2 应变率
应变率是指物体单位时间 内的形变速率，可以用来 描述物体的变形速度。
3 应变分量
应变分量是指在应变矩阵 中表示物体变形情况的各 个分量，分为正应变和剪 应变。
应变矩阵
1 应变矩阵的表示
应变矩阵是用矩阵形式表示物体各个方向上的应变分量。
2 应变矩阵的性质
应变矩阵具有可逆性、对称性和线性性等特点，这些性质在材料的力学分析中起到重要 的作用。
3 应变矩阵的运算
应变矩阵可以进行加法、减法和乘法等基本运算，这些运算可以用于分析和计算材料的 应变状态。
连续介质力学第三章(分析“应力”文档)共110张PPT
一点的应变状态可用二阶张量的形式来表示，称为 应变张量，用表示，即：
x xy xz
ij
y
yz
=
(对称)
z
x
1 2
xy
y
(对称 )
u
x
1 2
u y
v x
1 2
u z
w x
=
v y
1 2
v z
w y
(对称)
w
z
1
2 1
2
xz yz
z
◆ 几何方程：
x
u x
；
y
v y
性体变，从而出现奇异屈服面。
⑩.平衡（或运动）微分方程
◆ 平衡微分方程：
x
x
yx
y
zx
z
F
x 0
2u t2
xy
x
y
y
zy
z
F
y
0
2v t2
xz
x
yz
y
z
z
F
z 0
2w t2
ij'j Fi 0
◆ 一个客观的弹性力学问题，在物体体内任意一点的 应力分量和体力分量必定满足这组方程。
xxyssii n n xyycco o s sq q00sci on s xy
(xyq0)ctg (xyq0) tg
yxtan
左边界：据圣文南原理和平衡的原理得：
Fx 0 , Fy 0 , M0 0 ,
h
hxdy 0
h
hxydy P0
h
h x ydy M 0
h xdy 0
理论上可证明：当一点的应力状态确定时，经推导 必可求出三个实根，即为主应力，且主应力彼此正交。
x xy xz
ij
y
yz
=
(对称)
z
x
1 2
xy
y
(对称 )
u
x
1 2
u y
v x
1 2
u z
w x
=
v y
1 2
v z
w y
(对称)
w
z
1
2 1
2
xz yz
z
◆ 几何方程：
x
u x
；
y
v y
性体变，从而出现奇异屈服面。
⑩.平衡（或运动）微分方程
◆ 平衡微分方程：
x
x
yx
y
zx
z
F
x 0
2u t2
xy
x
y
y
zy
z
F
y
0
2v t2
xz
x
yz
y
z
z
F
z 0
2w t2
ij'j Fi 0
◆ 一个客观的弹性力学问题，在物体体内任意一点的 应力分量和体力分量必定满足这组方程。
xxyssii n n xyycco o s sq q00sci on s xy
(xyq0)ctg (xyq0) tg
yxtan
左边界：据圣文南原理和平衡的原理得：
Fx 0 , Fy 0 , M0 0 ,
h
hxdy 0
h
hxydy P0
h
h x ydy M 0
h xdy 0
理论上可证明：当一点的应力状态确定时，经推导 必可求出三个实根，即为主应力，且主应力彼此正交。
弹塑性力学-第3章 应变状态
第三章 应变状态理论在外力、温度变化或其他因素作用下，物体内部各质点将产生位置的变化，即发生位移。
如果物体内各点发生位移后仍保持各质点间初始状态的相对位置，则物体实际上只发生了刚体平移和转动，这种位移称为刚体位移。
如果物体各质点发生位移后改变了各点间初始状态的相对位置，则物体同时也产生了形状的变化，其中包括体积改变和形状畸变，物体的这种变化称为物体的变形运动或简称为变形，它包括微元体的纯变形和整体运动。
应变状态理论就是研究物变形后的几何特性。
即给定物体内各点变形前后的位置，确定无限接近的任意两点之间所连矢量因物体变形所引起剧烈变化。
这是一个单纯的几何问题，并不涉及物体变形的原因，也就是说并不涉及物体抵抗变形的物理规律。
本章主要从物体变形前后的几何变化论述物体内一点的应变状态。
位移与线元长度、方向的变化坐标与位移设变形前物体上各点的位置在笛卡尔坐标(Descarter coordinate)系的轴(X 、、Y、Z )上的投影为(z y x ,,)，又设物体上各点得到一位移，并在同一坐标轴上的投影为(u 、v 、w )，这些位移分量可看作是坐标(z y x ,,)的函数。
于是物体上任点的最终位置由下述坐标值决定。
即⎪⎭⎪⎬⎫+=+=+=),,(),,(),,(z y x w z z y x v y z y x u x ζηξ上式中函数u 、v 、w 以及它们对坐标(z y x ,,)的偏导数假设是连续的，则式确定了变量(z y x ,,)与),,(ζηξ之间的关系。
因为物体中变形前各点对应看变形后的各点，因此式是单值的，所以式可看成是坐标的一个变换。
如果在中，假设00,y y x x ==，则由式可得如下三个方程⎪⎭⎪⎬⎫+=+=+=),,(),,(),,((00000000z y x w z z y x v y z y x u x ςηξ式决定了一条曲线，曲线上各点Λ,,21**M M ，在物体变形前为平行于z 轴的直线(00,y y x x ==)上(图。
弹塑性力学 第03章应变状态理论
第三章 应变状态理论
在外力（或温度变化）作用下，物体内各部分之 间要产生相对运动。物体的这种运动状态，称为“变 形”。本章专门分析物体的变形，它的任务是 （1）分析一点的应变状态； （2）建立几何方程和应变协调方程。
§3-1 §3-2 §3-3 §3-4 §3-5 §3-6 §3-7
变形和应变的概念 应变与位移的关系—几何方程 相对位移张量 转动分量 主应变 应变张量不变量 体应变 应变协调方程 位移边界条件
可以证明，与物体内A点无限邻近的一点B的位移由三部分 组成。
B B2 B3 B1
A
A1
① 随同A点平移位移，如左图中的BB2所示 ② 绕A点刚性转动在B点所产生的位移，如左图中的B2B3所示 ③ 由A点邻近的微元体的变形在B点引起的位移，如左图中的 B3B1
§3-4 主应变 应变张量不变量
设在坐标系Oxyz下，某点（譬如M点）的6个应变分量为
1 2
1 2 1 2
γ xz ⎤ ⎥ γ yz ⎥ εz ⎥ ⎦
⎡ 0 ⎢ 1 + ⎢ 2 ωz 1 ⎢ ⎣− 2 ω y
− ωz 0
1 2
ωx
ωy ⎤ ⎥ 1 − 2 ωx ⎥
1 2
0 ⎥ ⎦
u ⎡∂ ∂x ⎢ ∂v ⎢ ∂x ∂w ⎢ ⎣ ∂x
∂u ∂y ∂v ∂y ∂w ∂y
∂u ∂z ∂v ∂z ∂w ∂z
2 2 2
n=(l , m , n)为该微分线段的方向余弦。
ε i′j′ = ε ij ni′i n j′j
物体内某点的6个应变分量将随着坐标系的旋转而改 变。物体受力变形后，过物体内的某一确定的点能否找到这 样一个坐标系，在这个坐标下，只有正应变分量，而所有切 应变分量都为零。也就是说，过该点能否找到这样3个互相垂 直的方向，使沿这3个方向的微分线段在物体变形后只是各自 地改变了长度，而其夹角仍保持为直角。 A F A F B F B F
在外力（或温度变化）作用下，物体内各部分之 间要产生相对运动。物体的这种运动状态，称为“变 形”。本章专门分析物体的变形，它的任务是 （1）分析一点的应变状态； （2）建立几何方程和应变协调方程。
§3-1 §3-2 §3-3 §3-4 §3-5 §3-6 §3-7
变形和应变的概念 应变与位移的关系—几何方程 相对位移张量 转动分量 主应变 应变张量不变量 体应变 应变协调方程 位移边界条件
可以证明，与物体内A点无限邻近的一点B的位移由三部分 组成。
B B2 B3 B1
A
A1
① 随同A点平移位移，如左图中的BB2所示 ② 绕A点刚性转动在B点所产生的位移，如左图中的B2B3所示 ③ 由A点邻近的微元体的变形在B点引起的位移，如左图中的 B3B1
§3-4 主应变 应变张量不变量
设在坐标系Oxyz下，某点（譬如M点）的6个应变分量为
1 2
1 2 1 2
γ xz ⎤ ⎥ γ yz ⎥ εz ⎥ ⎦
⎡ 0 ⎢ 1 + ⎢ 2 ωz 1 ⎢ ⎣− 2 ω y
− ωz 0
1 2
ωx
ωy ⎤ ⎥ 1 − 2 ωx ⎥
1 2
0 ⎥ ⎦
u ⎡∂ ∂x ⎢ ∂v ⎢ ∂x ∂w ⎢ ⎣ ∂x
∂u ∂y ∂v ∂y ∂w ∂y
∂u ∂z ∂v ∂z ∂w ∂z
2 2 2
n=(l , m , n)为该微分线段的方向余弦。
ε i′j′ = ε ij ni′i n j′j
物体内某点的6个应变分量将随着坐标系的旋转而改 变。物体受力变形后，过物体内的某一确定的点能否找到这 样一个坐标系，在这个坐标下，只有正应变分量，而所有切 应变分量都为零。也就是说，过该点能否找到这样3个互相垂 直的方向，使沿这3个方向的微分线段在物体变形后只是各自 地改变了长度，而其夹角仍保持为直角。 A F A F B F B F
弹性力学 第三章应变状态理论
w
w
1 2
xz
dx
1 2
yz
dy
z
dz
1 2
y
dx
1 2
xdy
§3-2 相对位移张量 转动分量
0
u u
v
v
1 2
z
w
w
1 2
y
1 2
z
0
1 2
x
1 2
y
dx
1 2
x
dy
dz
0
x
1 2
xy
1 2
xz
dx
1 2
xy
y
1 2
yz
dy
1 2
xz
1 2
yz
dz
x
u x
y
v y
z
w z
yz
w y
v z
zx
u z
w x
xy
v x
u y
1 2
yz
yz
,
1 2
zx
zx ,
1 2
xy
xy
ij
1 2
(ui,
j
u j,i )
§3-2 相对位移张量 转动分量
相对位移张量：
u u u
x
y
z
v v v
x
y
z
w w w
x y z
转动矢量：
u(x dx, y, z) u u dx
a:
x
v(x dx, y, z) v v dx x
u(x, y dy, z) u u dy
b:
y
b a
v(x, y dy, z) v v dy
材料力学 第三章 应变理论
ij 称为柯西应变张量或小应变张量
其实体表示形式为 1 u u 2
是二阶对称张量，只有六个独立分量。
§3-1 位移和变形
在笛卡尔坐标系中，其常用形式为
11
u1 x1
u x
x ,12
21
1 2
u1 x2
u2 x1
1 u
2
y
v x
xy
yx
22
u2 x2
v y
i
ji
ui x j
j
1
i
ui x j
j
i
可由位移梯度分量 ui 和线元正应变 计算任意方向线元
变形后的方向余弦。x j
考虑两线元间的夹角变化
t cos , t t 2 t 1 1
t
1 t t 2 t
§3-2 小应变张量（几何方程）
若变形前两线元互相垂直，即 t 0
u j xi
ei ej
E 1 u u u u 2
➢ 按照欧拉描述还可以定义描述大变形的阿尔曼西（Almansi,E)
应变张量，即
dS2 dS02 2eijdxidxj
eij
1 2
ui xj
u j xi
um xi
um xj
它也是二阶对称张量
由此可见：物体无变形（线元长度不变，仅作刚体运动） 的充分必要条件是应变张量处处为零。
令 为变形后线元间直角的减小量，则由上式可得
cos
2
cos , t
2 t 2ij it j 2t
通常定义两正交线元间的直角减小量为工程剪应变 t ，即
t 2t 2 t 2ijit j
若 , t 为坐标轴方向的单位矢量，例如 i 1, t j 1(i j)
高等材料力学课件第三章-应变状态
( yz xz xy ) 2 2 x
x x y z
yz
( yz xz xy ) 2 2 y
y x y z
xz
( yz xz xy ) 2 2 z
z x y z
xy
§3.3 应变协调7
•变形协调方程的数学意义
•使3个位移为未知函数的六个几何方程不相矛 盾。
•变形协调方程的物理意义
而且改变了物体内部各个点的相对 位置。
§3.1 变形2
M (x, y, z) M (x, y, z)
u=x'（x，y，z）－ x=u（x，y，z） v=y'（x，y，z）－ y=v（x，y，z） w=z'（x，y，z）－ z=w（x，y，z）
位移u，v，w是单值连续函数
进一步分析假定位移函 数具有连续的三阶导数
• 目录
• §3.1 变形与应变概念
• §3.2 向
主应变与主应变方
• §3.3 应变协调方程
§3.1 变形与应变概念
• 由于外部因素 ——载荷或温度变化 • 位移—— 物体内部各点空间位置发
生变化 • 位移形式 • 刚体位移：物体内部各点位置变化，
但仍保持初始状态相对位置不变。 • 变形位移：位移不仅使得位置改变，
§3.3 应变协调15
• 如果物体表面的位移已知，称为位移边界 • 位移边界用Su表示。
• 如果物体表面的位移 u, v, w,已知
• 边界条件为
uu vv ww
• 称为位移边界条件
§3.3 应变协调16
• 设物体表面为S • 位移已知边界Su • 面力已知边界Ss
则 S＝Su＋Ss
• 弹性体的整个边界，是由面力边界和位移边 界构成的。
点的应变状态、体积不变条件资料ppt课件
第三章 金属塑性变形的力学基础
应变分析
河南科技大学材料学院
位移及其分量
位移：变形体内任一 点变形前后的直线距离
位移分量：在坐标系中， 一点的位移矢量在三个坐 标轴上的投影称为该点的
位移分量。用u，v，w或ui
表示。
位移场：变形体内不同点 的位移分量不同。根据连续 性基本假设，位移或分量应是 坐标的连续函数，而且一般 都有连续的二阶偏导数。
两棱边所夹直角的变化量。
同理有： φyz, φzx
显然： yx xy ,yz zy ,xz zx
r ry
tanyx yx
应变及其分量
棱边PA在x方向的线应变：
同理：
y z
ry
ry rz rz
x
rx rx
应变及其分量
u u(x, y, z) v v(x, y, z) w w(x, y, z)
即 ui ui (x, y, z)
变形体内无限接近两点的位移分量间的关系
设M
ui M1 (x+u,y+v,z+w)
(x位,y移,z分)量：ui ui (x, y, z)
M
ui ui
M1'((xx++ddxx,+yu++d△y,uz,+yd+zd)y+v+△v,z+dz+w+△w)
l
2l
ln 2l ln 2 69%; ln l ln 1 69%
l
2l 2
点的应变状态与应变张量
任意方向上的应变
设任意点a(x,y,z)的应变分量：
应变分析
河南科技大学材料学院
位移及其分量
位移：变形体内任一 点变形前后的直线距离
位移分量：在坐标系中， 一点的位移矢量在三个坐 标轴上的投影称为该点的
位移分量。用u，v，w或ui
表示。
位移场：变形体内不同点 的位移分量不同。根据连续 性基本假设，位移或分量应是 坐标的连续函数，而且一般 都有连续的二阶偏导数。
两棱边所夹直角的变化量。
同理有： φyz, φzx
显然： yx xy ,yz zy ,xz zx
r ry
tanyx yx
应变及其分量
棱边PA在x方向的线应变：
同理：
y z
ry
ry rz rz
x
rx rx
应变及其分量
u u(x, y, z) v v(x, y, z) w w(x, y, z)
即 ui ui (x, y, z)
变形体内无限接近两点的位移分量间的关系
设M
ui M1 (x+u,y+v,z+w)
(x位,y移,z分)量：ui ui (x, y, z)
M
ui ui
M1'((xx++ddxx,+yu++d△y,uz,+yd+zd)y+v+△v,z+dz+w+△w)
l
2l
ln 2l ln 2 69%; ln l ln 1 69%
l
2l 2
点的应变状态与应变张量
任意方向上的应变
设任意点a(x,y,z)的应变分量：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
U是位移矢量，不难 其中 为那勃勒算子， e e e 1 2 3
算得 的3个分量为:
2019/3/25 17
x
y
z
w y u z v x
v z w x u y
z 称为转动分量。 y ， 这里的 称为转动矢量，而 x， 由此，可将相对位移张量分解为两个张量：
u x v x w x u y v y w y u z v z w z
x 1 2 yx 1 xz 2 1 2 1 2 1 2
如果各点的位移不 同，但各点间的相对距 离保持不变，物体发生 刚体转动等刚体移动。
2019/3/25
6
如果各点(或部分点）间的相对距离 发生变化，则物体发生了变形。这种变 形一方面表现在微线段长度的变化，称 为线应变；一方面表现在微线段间夹角 的变化，称为切应变。
2019/3/25
7
dx dx
我们从物体中取出x方向上长dx的线段PA，变形后
u PB的转角为： y
2019/3/25
y
v y
10
A
线段PA的转角是
v x
线段PB的转角是
u y
于是，直角APB的改变量为
v u xy x y
P B
2019/3/25
A
有时用张量分量 1 v u xy 2 x y
11
这样，平面上一点的 变形我们用该点x方向上 的正应变、y方向上的正 应变和xy方向构成的直角 的变化来描述，称为应变 分量，也就是所说的几何 方程。
从几何方程可见，当 物体的位移分量完全确定 时，形变分量即完全确定。
u x x v y y
xy
1 2
v u x y
第三章
应变状态理论
2019/3/25
1
外力(或温度变化)作用下，物体内部各部 分之间要产生相对运动。物体的这种运动形态， 称为变形。 本章任务有两个：
1、分析一点的应变状态；
2、建立几何方程和应变协调方程。
2019/分量－几何方程 3.2 一点的形变状态 形变张量
PA的转角为
v v dx v v x dx x
9
2019/3/25
我们从物体中取出y方向 上长dy的线段PB，变形后为 P'B'，B'点y方向的位移为
v v d y y
u u dy y
x 方向上的位移为
PB的正应变在小变形时是由y方向的 位移所引起的，因此PB正应变为：
思考题：当形变分量完全确定时，位移分量 是否能完全确定。
2019/3/25 12
同样，空间一 点的变形我们用该 点x、y、z方向上 的正应变和xy、yz、 zx方向构成的直角 的变化－切应变来 描述。 张量形式为
u 1 u j i ij 2 x x i j
1 1 z y 0 2 2 1 1 0 x z 2 2 1 1 x 0 y 2 2
xy
xz
=
y
1 2
yz
+
yz
z
2019/3/25
18
上式，等号右边第一项为对称张量，表示微 元体的纯变形，称为应变张量，第二项为反对称 张量，它表示微元体的刚体转动，即表示物体变
2019/3/25 13
空间的应变分量共九 个分量，是一个对称张量， 和应力张量一样，它们遵 从坐标变换规则，同样存 在着三个互相垂直的主方 向，对应的主应变值是该 张量的特征值。这些互相 垂直的主方向构成的直角 在该应变张量的变形时， 角度不变，由主平面组成 的单元体，由正方体变为 直角长方体。在主方向构 成的坐标系中，张量分量 构成对角阵，切应变分量 为零。
为P‘A’，P‘点的位移为(u,v)，A’点
x方向的位移为 y方向上的位移为
2019/3/25
u u dx x
v v dx x
8
dx
α
dx
PA的正应变在小变形时是由x方向的位移所 引起的，因此PA正应变为
u u d x u u x x d x x
形后微元体的方位变化。
如物体中一点M的形变分量为
x y z x y
y z
z x
则相对位移张量（非对称）可分解为应变张量与转 动张量。
2019/3/25 19
3.3 转轴时应变分量的变换
设在坐标轴oxyz下，物体内某一点的6个应 , , , , , 变分量为 x y z xy yz zx。现使坐标轴旋 转一个角度，新老坐标的关系为：
14
2019/3/25
物体除形变外，还存在转动、刚体位移： （a）均匀形变：u、v、w是线性函数，称为均匀形变； （b）刚体位移：“形变为零”时的位移，即是“与形变
无关的位移”；
（c）纯形变：形变分量不等于零，而转动分量等于零。
2019/3/25
15
3.2 一点的形变状态，形变张量
2019/3/25
16
相对位移张量 6个应变分量是通过位移分量的9个一阶偏导，即：
u x v x w x u y v y w y u z v z w z
引入
U
x y z
3.3 转轴时应变分量的变换
3.4 主形变 形变张量不变量
3.5 体应变 应变协调方程
2019/3/25
3
3.1
位移分量与应变分量 －几何方程
2019/3/25
4
在外力作用下，物 体整体发生位置和形状 的变化，一般说来各点 的位移不同。
2019/3/25
5
如果各点的位移完 全相同，物体发生刚体 平移；