2019-2020学年吉林省长春市南关区东北师大附中明珠学校七年级(上)期末数学试卷(解析版)
2019-2020学年度上学期东北师大附中初一年级因故试卷期末考试
2019-2020学年度上学期东北师大附中初一年级期末考试英语试卷共120分考试时间90分钟命题人：张巍审题人：徐婧一、听力部分（20分）I. 听句子，选择恰当的答语。
（句子读两遍，每小题1分，共5分。
）1．A．Yes, he does. B．Yes, he is. C．Yes, I am. 2．A．No, I don’t. B．That sounds good. C．You are welcome. 3．A．Thanks. B．No, I can’t. C．Yes, I do.4．A．No, I don’t like it. B．He likes thrillers. C．I like action movies. 5．A．Because it’s fun. B．He likes Chinese. C．He likes it very much. II. 听对话，选出合适的图片。
将其序号写在横线上。
其中有一幅是多余的。
（对话读两遍，每小题1分，共5分。
）6.________ 7．_________ 8．_________ 9．________ 10．_________III. 听一段对话，判断正误（正确的写．．．．．F．）。
（对话读三遍，每空1分，共5分。
）．．．．T．；错误的写( ) 11．Bob’s favorite sport is basketball.( ) 12．Bob thinks ping-pong is exciting.( ) 13．Bob often plays ping-pong at home.( ) 14．Bob has two P.E. classes in a week.( ) 15．Bob likes P.E. because his P.E. teacher Mr. Brown is funny.IV. 听短文，选择最佳答案。
（短文读三遍，每小题1分，共5分。
2019—2020学年度上学期东北师大附中初一年级期末考试初中数学
2019—2020学年度上学期东北师大附中初一年级期末考试初中数学数 学 试 卷总分：120分 考试时刻：120分钟一、选择题〔每题只有一个正确答案，每题2分，共20分〕 1．某市某日的气温是－2℃~6℃，那么该日的温差是〔 〕A ．8℃B ．6℃C ．4℃D ．－2℃2．以下各式中，是一元一次方程的是〔 〕A ．652=+y xB ．23-xC ．12=x D ．853=+x3．如下图的几何体，从上面看得到的平面图形是〔 〕A ．B ．C ．D ．4．以下不是．．同类项的是〔 〕A ．2263xy y x -与 B ．a b ab 33与- C ．012和 D ． zyx xyz 212-与 5．如图，以A 、B 、C 、D 、O 为端点的线段共有〔 〕条A ．4B ．6C ．8D ．106．如图，OC 是∠AOB 的平分线，OD 是∠AOC 的平分线，且∠COD =25，那么∠AOB 等于〔 〕A ．50 B ．75C ．100D ．120 7．假设13+a 与372-a 互为相反数，那么a 为〔 〕A ．34 B ．10C ．34-D ．10- 8．关于x 的方程2x －4=3m 和x +2=m 有相同的解, 那么m 的值是 〔 〕A ． 10B ． －8C ． －10D ． 89．线段AB ，延长AB 到C ，使BC =2AB ，M 、N 分不是AB 、BC 的中点，那么 〔 〕A ．MN =21BC B ．AN =23AB C ．BM ：BN =1：2 D ．AM =43BC 10．CCTV-2«快乐辞典»栏目中，有一期的题目如下图，两个天平都平稳，那么三个球体的重量等于〔 〕个正方体的重量．A ．2B ．3C ．4D ．5二、填空题〔每空3分，共24分〕11．木匠在木料上画线，先确定两个点的位置，依照 就能把线画得专门准确．12．下面是 〝美好家园〞 购物商场中 〝飘香〞 洗发水的价格标签,请你在横线上填出它的现价．13．关于x 的一元一次方程a x x a 32)3(-=-的解是x =3，那么a = ． 14．不大于．．．3的所有非负整数是 ．15．如下图，是一个正方体的平面展开图，当把它折成一个正方体时，与空白面相对的字应该是 ．16．如下图，将长方形ABCD 的一角沿AE 折叠，假设D BA '∠=30，那么D EA '∠= ．17．假设线段AB =8，BC =3，且A ，B ，C 三点在一条直线．．上，那么AC = ． 18．小王利用运算机设计了一个运算程序，输入和输出的数据如下表：输入 (1)2345… 输出…2152 103 174 265 …那么，当输入数据为8时，输出的数据为 ． 三、运算题〔每题3分，共18分〕19．(1))17()31()26()76(++-+++-； (2)24)3(21-⨯--；(3))65()32(22a a a a -+-； (4))32(3)32(2b a a b -+-； (5)15259432'+'； (6)3256180'-． 四、解以下一元一次方程〔每题3分，共12分〕 20．(1)x x 413243-=+； (2))15(2)2(5-=+x x ； (3)212)2(3-=-x x ； (4)y y y +-=+3323． 四、作图题〔每题3分，共6分〕21．如下图，直线l 是一条平直的公路，A ，B 是两个车站，假设要在公路l 上修建一个加油站，如何使它到车站A ，B 的距离之和最小，请在公路上表示出点P 的位置，并讲明理由.〔保留作图痕迹，并用你所学的数学知识讲明理由〕.22．有一张地图，图中有A 、B 、C 三地，但地图被墨迹污染，C 地具体位置看不清晰了，但明白C 地在A 地的北偏东30 ，在B 地的南偏东45 ，你能确定C 地的位置吗？五、解答题〔每题3分，共9分〕23．假设一个角的补角比那个角的余角的3倍大10，求那个角的度数． 24．先化简，再求值：10,151),()2(2222=-=+--+++--b a b ab a b ab a 其中． 25．如下图，C 、D 是线段AB 的三等分点，且AD =4，求AB 的长．六、列方程解以下应用题〔每题5分，共25分〕26．一个长方形的周长为28cm ，将此长方形的长减少2cm ，宽增加4cm ，就可成为一个正方形，那么原长方形的长和宽分不是多少？27．据某统计数据显示，在我国的664座都市中，按水资源分布的情形可分为三类：暂不缺水都市、一样缺水都市和严峻缺水都市．其中暂不缺水都市数比严峻缺水都市数的4倍少50座，一样缺水都市数是严峻缺水都市数的2倍．求严峻缺水都市有多少座？ 28．从甲站到乙站原需16小时．采纳〝和谐〞号动车组提速后，列车行驶速度提高了．．．176千米/时，从甲站到乙站的时刻缩短了．．．11小时，求列车提速后的速度．29．某通信运营商短信收费标准为：发送网内短信0.1元/条，发送网际短信0.15元/条．该通信运营商的用户小王某月发送以上两种短信共150条，依照收费标准共支出短信费用19元，咨询小王该月发送网内、网际短信各多少条？30．某都市按以下规定收取每月的煤气费：假如用气量不超过60m 3，按每立方米0.8元收费；假如用气量超过60 m3，那么超过部分按每立方米1.2元收费，某用户8月份交的煤气费是平均每立方米0.88元，那么该用户8月份的用气量是多少？他交的煤气费是多少元？七、解答题〔6分〕31．如图〔1〕所示，∠AOB、∠COD差不多上直角．E图〔1〕〔1〕试猜想∠AOD与∠COB在数量上是相等，互余，依旧互补的关系．请你用推理的方法讲明你的猜想是合理的．〔2〕当∠COD绕着点O旋转到图〔2〕所示位置时，你在〔1〕中的猜想还成立吗？请你证明你的结论．图〔2〕。
2019—2020学年度上学期东北师大附中初一年级期末考试初中语文
2019—2020学年度上学期东北师大附中初一年级期末考试初中语文语文试卷总分值：120分考试时刻：120分钟一、字词〔10分〕1．给加点字．．．注音。
〔4分〕抽泣．．〔〕．．〔〕迂．回〔〕迸．溅〔〕惩处踉．跄〔〕确凿．〔〕威吓．〔〕羞涩．〔〕2．依照拼音填写汉字。
〔6分〕诱huò( )nì( )爱人迹罕zhì( ) yí〔〕然自得yǒu( )黑倜tǎng( ) 多多yì( )善máo( )塞顿开繁mì( ) 喧téng( ) 不xiè( )一顾盘qiú( )卧龙二、古诗词默写〔15分〕3．上邪！我欲与君相知，□□□□□。
«上邪»4．少壮不努力，□□□□□。
«长歌行»5．大风起兮云飞扬，威加海内兮归故乡!□□□□□□□□?〔刘邦«大风歌»〕6．□□□□□，帘卷西风，□□□□□。
〔李清照«醉花阴»〕7．马作的卢飞速，□□□□□□。
〔辛弃疾«破阵子·为陈同甫赋壮词以寄之»〕8．«关雎»中，借雎鸠和鸣起兴，制造一种缠绵欢愉的气氛，联想到淑女应是君子的佳偶的句子是：□□□□，□□□□。
9．曹操的«观沧海»中，制造了一个宏大的意境，表现了作者吞吐日月的博大胸襟的诗句是：□□□□，□□□□。
10．晏殊的«浣溪沙»中着重写今日的感伤、被誉为千古奇偶的诗句是：□□□□□□□，□□□□□□□。
11．因送不而衍生出专门多千古绝唱，它们照映这中华民族的吟坛声苑，使我们的诗心为之震荡，为之深思翘首，为之惊魂动魄。
请从古代诗、词、曲中找出具有这一特点的除上文外连续的两句来，并注明作者或出处。
句子：，。
作者或题目：三、文言文阅读〔15分〕〔一〕阅读«小石潭记»，回答以下咨询题。
2019-2020学年吉林省长春市南关区东北师大附中明珠学校七年级(上)期末数学试卷(解析版)
2019-2020 学年吉林省长春市南关区东北师大附中明珠学校七年级上）期末数学试卷．选择题（共 8小题）1．﹣3 的相反数是（ ）A ．B ．﹣ 3C ．D ． 32．2018年10月 24日上午 9时港珠澳大桥正式通车，它是东亚建设的跨海大桥，连接香港大屿山、示为（ ）11A ．7.2× 101110B ．7.2×1010C．110.72×1011D．72×109333．计算﹣ a +2a的结果为（ ）33C．33A ． a 3B ．﹣a 33a3D．﹣3a 34．下列方程中为一元一次方程的是（ ）A ．2x+3＝ 0B ．2x+y ＝3C．2x +x ＝ 3D．x ﹣ ＝ 35．下列判断正确的是（ ）A ．单项式 a 的次数是 02B ．单项式﹣ 2a 2bc 的系数是 2C ．单项式﹣ xy 2z 的次数是 232D ．多项式 3xy 3+5x 2﹣8 是四次三项式正确的算式有（ ）7．下列四个图中，能用∠ 1、∠ AOB 、∠ O 三种方法表示同一个角的是澳门半岛和广东省珠海市，整个大桥造价超过 720 亿元人民币，将 72000000000 用科学记数法表6．下列四个算式： 3① ﹣2﹣3＝﹣1；② 2﹣|﹣3|＝﹣1；③ （﹣2） ＝﹣6；④ 2÷＝﹣ 6．其中，A ．0个B ．1个C ．2个D ．3个8．如图，直线AB、CD 相交于点O，OE 平分∠ BOC ，∠ FOD ＝90°，若∠ BOD ：∠BOE＝1：2，则∠AOF 的度数为（）A ．70°B ．75°C．60°D．54°二．填空题（共 6 小题）24 9．把多项式2m2﹣4m4+2m﹣1 按m 的升幂排列．10．长春市奥林匹克公园于2018 年年底建成，它的总占地面积约为528000 平方米，528000 这个数字用科学记数法表示为．11．如图，∠ AOB＝72°32′，射线OC在∠ AOB内，∠ BOC＝30° 40′，则∠ AOC＝．12．今年十一小长假期间，迟老师一家三口开着一辆轿车去长春市净月潭森林公园度假，若门票每人 a 元，进入园区的轿车每辆收费40 元，则迟老师一家开车进入净月潭森林公园园区所需费用是元（用含 a 的代数式表示）．14．如图，在三角形ABC中，AB⊥AC于点A，AB＝6，AC＝8，BC＝10，点P是线段BC上的一点，则线段AP 的最小值为．三．解答题（共 10 小题）15．计算：（ 1）（ + ﹣ ）×（﹣ 48）32 （ 2）（﹣ 5） 3×（﹣ ） +32÷（﹣ 2） 2×16．计算：1）3x+2（x ﹣ ）﹣（ x+1）2） 5（2a 2b ﹣ ab 2）﹣ （ 6a 2b ﹣ 3ab 2） 17．解下列一元一次方程：2（y ﹣ ）＝ （3y ﹣ 2） ﹣ ＝ 1﹣ ＝ 12218．先化前，再求值： 2（a 2+2a ﹣1）﹣ 3（a 2﹣ 2a ﹣3），其中 a ＝﹣ 2 19．如图，点 P 是∠AOB 的边 OB 上的一点，点 M 是∠ AOB 内部的一点，按下述要求画图，并回答问题：（ 1）过点 M 画 OA 的平行线 MN ；（2）过点 P 画OB 的垂线 PC ，交OA 于点 C ； （ 3）点 C 到直线 OB 的距离是线段 的长度．20．如图，已知点 E 、 F 在直线 AB 上，点 G 在线段 CD 上， ED 与 FG 相交于点 H ，∠ C ＝∠ EFG ，∠ BFG ＝∠ AEM ，求证： AB ∥CD ．（完成下列填空）1）4x+7＝32﹣x 2）8x ﹣ 3（ 3x+2 ）＝ 1 3） 4）证明：∵∠ BFG ＝∠ AEM（已知）且∠ AEM ＝∠ BEC（）∴∠ BEC＝∠ BFG （等量代换）∴MC ∥（）∴∠ C＝∠ FGD （）∵∠C＝∠ EFG（已知）∴∠＝∠ EFG，（等量代换）∴AB∥CD （）21．如图已知点C为AB上一点，AC＝12cm，CB＝AC，D、E分别为AC、AB的中点，求长．23．如图，直线AB、CD 相交于点O，OF 平分∠ AOE，OF⊥CD，垂足为O．（1）写出图中所有与∠ AOD 互补的角；DE 的1＝∠2．24．感知：如图① ，若AB∥CD，点P在AB、CD 内部，则∠P、∠A、∠C满足的数量关系是探究：如图② ，若AB∥CD，点P在AB、CD外部，则∠ APC 、∠A、∠C满足的数量关系是请补全以下证明过程：证明：如图③ ，过点P 作PQ ∥AB∴∠ A＝∵AB∥CD，PQ∥AB∴ ∥ CD∴∠ C＝∠∵∠ APC ＝∠﹣∠∴∠ APC ＝应（1）如图④ ，为北斗七星的位置图，如图⑤ ，将北斗七星分别标为A、B、C、D、E、G，其中B、C、D 三点在一条直线上，AB∥EF，则∠ B、∠D、∠E 满足的数量关系是线BP和EP，交于点P，使得BD平分∠ MBP，EN平分∠ DEP，若∠ MBD ＝25°，则∠ D﹣∠P延长FE 到点N，过点 B 和点E分别作射2019-2020 学年吉林省长春市南关区东北师大附中明珠学校七年级（上）期末数学试卷参考答案与试题解析．选择题（共8 小题）1．【分析】根据负数的绝对值是它的相反数是，可得答案．【解答】解：﹣ 5 的绝对值是5．故选：A．点评】本题考查了绝对值，利用了绝对值的性质是解题关键．2．【分析】根据实数的大小比较解答即可．【解答】解：由数轴可得：a< b<c<d，故选： D ．点评】此题利用数轴比较大小，在数轴上右边的点表示的数总是大于左边的点表示的数．分析】根据题目中的几何图形，可以得到它的主视图，从而可以解答本题．3．解答】解：由两个小正方体和一个圆锥组成的几何体，它的主视图是故选：B．【点评】本题考查简单组合的三视图，解答本题的关键是明确题意，画出相应的图形．4．【分析】根据单项式和多项式的有关概念逐一求解可得．【解答】解：A．﹣的系数是﹣，此选项错误；2B．x2+x﹣1 的常数项为﹣1，此选项错误；C．22ab3的次数是 4 次，此选项错误；2D ．2x﹣5x2+7 是二次三项式，此选项正确；故选： D ．【点评】本题考查多项式的知识，几个单项式的和叫做多项式，每个单项式叫做多项式的项，其中不含字母的项叫做常数项．单项式的个数就是多项式的项数，如果一个多项式含有 a 个单项式，次数是b，那么这个多项式就叫 b 次 a 项式．5．【分析】根据三棱柱的展开图的特点进行解答即可．【解答】A、是三棱锥的展开图，故选项错误；B 、是三棱柱的平面展开图，故选项正确；C 、两底有 4 个三角形，不是三棱锥的展开图，故选项错误；D 、是四棱锥的展开图，故选项错误．故选： B ．【点评】 此题主要考查了几何体展开图，熟练掌握常见立体图形的平面展开图的特征，是解决此 类问题的关键．分析】 根据等式的性质，依次分析各个选项，选出等式不一定成立的选项即可．A. 3a ＝2b+5，等式两边同时减去 5 得：3a ﹣5＝2b ，即 A 项正确，故选： C ．解答】 解： A 、图中的∠ AOB 不能用∠ O 表示，故本选项错误；B 、图中的∠ 1 和∠ AOB 不是表示同一个角，故本选项错误；C 、图中的∠ 1和∠AOB 不是表示同一个角，故本选项错误；D 、图中∠ 1、∠ AOB 、∠ O 表示同一个角，故本选项正确；故选： D ．【点评】 本题考查了角的表示方法的应用，主要考查学生的理解能力和观察图形的能力．8．【分析】 根据角平分线的定义和邻补角的性质计算即可．【解答】 解：∵∠ BOD ：∠BOE ＝1：2，OE 平分∠ BOC ， ∴∠ BOD ：∠ BOE ：∠ EOC ＝ 1：2：2， ∴∠ BOD ＝ 36°， ∴∠ AOC ＝ 36°，又∵∠ COF ＝∠ DOF ＝90°， ∴∠ AOF ＝90°﹣ 36°＝ 54°． 故选： D ．【点评】 本题考查的是对顶角、邻补角的性质以及角平分线的定义，掌握对顶角相等、邻补角之6． 解答】 解：B.3a ＝2b+5， 等式两边同时加上 1 得： 3a+1＝2b+6，即 B 项正确，C.3a ＝ 2b+5 ， 等式两边同时乘以 c 得： 3ac ＝ 2bc+5c ，即 C 项错误，D.3a ＝2b+5， 等式两边同时除以 3 得：a ＝ + ，即 D 项正确， 点评】 本题考查了等式的性质， 正确掌握等式的性质是解题的关键．7． 分析】 根据角的表示方法和图形选出即可．和等于180°是解题的关键．二．填空题（共 6 小题）9．【分析】先分清多项式的各项，然后按多项式升幂排列的定义排列．2 4 2 4【解答】解：多项式2m2﹣4m4+2m﹣1 按m 的升幂排列为﹣1+2m+2m2﹣4m4，故答案为：﹣1+2m+2m2﹣4m4．【点评】本题考查多项式，我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列，称为按这个字母的降幂或升幂排列．要注意，在排列多项式各项时，要保持其原有的符号．10．【分析】科学记数法的表示形式为a× 10n的形式，其中1≤|a|< 10，n 为整数．确定n的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值>10时，n 是正数；当原数的绝对值< 1 时，n 是负数．【解答】解：528000＝ 5.28×105，5故答案为： 5.28× 105．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a| <10，n为整数，表示时关键要正确确定a的值以及n 的值．11．【分析】根据图形进行角的计算即可【解答】解：∠ AOC＝∠ AOB﹣∠ BOC＝72° 32′﹣30°40′＝41°52′，故答案为：41° 52′．【点评】本题考查的是角的计算，掌握度、分的转化是解本题的关键．12．【分析】根据题意得：每辆车的收费与每个人门票之和列出代数式即可．【解答】解：根据题意得：（40+3a），故答案为：（40+3a）【点评】此题考查了列代数式，弄清题意是解本题的关键．13．【分析】两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．依此求解即可．【解答】解：由同位角的定义知，能与∠1 构成同位角的角有∠2、∠3 共2＝﹣ 36；点评】 本题考查了同位角、内错角、同旁内角．三线八角中的某两个角是不是同位角、内错角 或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角 的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“ 同旁内角的边构成“ U ”形．解答】 解：∵ AB ⊥ AC ，∴∠ BAC ＝90°， 当 AP ⊥BC 时， AP 的值最短， ∴AP ＝∴AP ＝ ∴线段 AP 的最小值为 ， 故答案为：点评】 本题考查了垂线段最短，三角形的面积，熟练掌握勾股定理的逆定理即可得到结论．解答题（共 10 小题）2）先算乘方，再算乘除，最后算加法；同级运算，应按从左到右的顺序进行计算．【解答】 解：（ 1）（ + ﹣ ）×（﹣ 48） ＝ ×（﹣ 48）+ ×（﹣ 48）﹣×（﹣ 48 ） ＝﹣ 40﹣ 42+462）（﹣ 5）3×（﹣ ）+32÷（﹣ 2）2×F “形，内错角的边构成“ Z “形，14 ．【分析】 根据三角形的面积公式即可得到结论．15 ．【分析】 （ 1）根据乘法分配律简便计算；＝（﹣125）×（﹣）+32÷ 4×＝75+8×＝75﹣10＝65 ．【点评】考查了有理数的混合运算，有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化．16．【分析】（1）直接去括号，进而合并同类项得出答案；（2）直接去括号，进而合并同类项得出答案．【解答】解：（1）3x+2（x﹣）﹣（x+1）＝3x+2x﹣1﹣x﹣1＝4x﹣2；2 2 2 2（2）5（2a2b﹣ab2）﹣（6a2b﹣3ab2）2 2 2 2＝10a2b﹣2ab2﹣4a2b+2ab2＝6a2b．【点评】此题主要考查了整式的加减运算，正确合并同类项是解题关键．17．【分析】（1）依次移项、合并同类项、系数化为1 可得；（2）依次去括号、移项、合并同类项、系数化为 1 可得；（3）依次去括号、移项、合并同类项、系数化为 1 可得；（4）依次去分母、去括号、移项、合并同类项、系数化为 1 可得．【解答】解：（1）4x+7＝32﹣x，4x+x＝32﹣7，5x＝﹣25，x＝﹣5；（2）8x﹣9x﹣6＝1，8x﹣9x＝1+6，﹣x＝7，x＝﹣7；（3）2y﹣3＝y﹣4，2y﹣y＝﹣4+3 ，y＝2．（4）3（5y﹣1）﹣4（2y+6）＝12，15y﹣3﹣8y﹣24＝12，15y﹣8y＝12+3+24，7y＝39，y＝．【点评】本题主要考查解一元一次方程，去分母、去括号、移项、合并同类项、系数化为仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向＝ a 形式转化．18．【分析】根据整式的运算法则即可求出答案．【解答】解：原式＝2a2+4a﹣2﹣3a2+6a+92＝﹣a +10a+7 ，当a＝﹣2 时，原式＝﹣4﹣20+7＝﹣24+7＝﹣17．【点评】本题考查整式的运算，解题的关键是熟练运用整式的运算法则，本题属于基础题型．19．【分析】（1）根据平行线的判定画图，（2）根据垂线的定义画图，3）根据点到直线的距离即可解决问题．解答】解：（1）如图所示：1，这x2）如图所示：3）点 C 到直线OB 的距离是线段PC 的长度；故答案为：PC．【点评】本题考查作图﹣复杂作图，垂线，点到直线距离，平行线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．20．【分析】根据同位角相等两直线平行，可证MC∥GF ，进而利用平行线的性质和判定证明．【解答】证明：∵∠ BFG＝∠ AEM （已知）且∠ AEM＝∠ BEC（对顶角相等）∴∠ BEC＝∠ BFG （等量代换）∴ MC ∥GF（同位角相等，两直线平行）∴∠C＝∠ FGD（两直线平行，同位角相等）∵∠ C＝∠ EFG （已知）∴∠ FGD ＝∠ EFG，（等量代换）∴AB∥CD（内错角相等，两直线平行）．故答案是：对顶角相等；GF；同位角相等，两直线平行；FGD ；内错角相等，两直线平行．【点评】考查了平行线的判定与性质，解答此题的关键是注意平行线的性质和判定定理的综合运用．21．【分析】求DE 的长度，即求出AD 和AE 的长度．因为 D 、 E 分别为AC、AB 的中点，故DE＝，又AC＝12cm，CB＝AC，可求出CB，即可求出CB，代入上述代数式，即可求出DE 的长度．【解答】解：根据题意，AC＝12cm，CB＝AC，所以CB＝8cm，所以AB＝AC+CB＝20cm，又D、 E 分别为AC、AB 的中点，所以DE＝AE﹣AD＝（AB﹣AC）＝4cm．即DE ＝4cm ．故答案为4cm．【点评】此题要求学生灵活运用线段的和、差、倍、分之间的数量关系，熟练掌握．22．【分析】先判定AB∥ CD，则∠ ABC＝∠ BCD ，再由∠ P＝∠ Q，则∠ PBC＝∠ QCB，从而得出∠ 1＝∠ 2．【解答】证明：∵∠ ABC+∠ECB＝180°，∴AB∥DE，∴∠ ABC＝∠ BCD ，∵∠P＝∠ Q，∴PB∥CQ，∴∠ PBC＝∠ BCQ，∵∠ 1＝∠ ABC﹣∠ PBC，∠ 2＝∠ BCD ﹣∠ BCQ ，∴∠ 1＝∠ 2．【点评】本题考查了平行线的判定和性质，解答此题的关键是注意平行线的性质和判定定理的综合运用．23．【分析】（1）根据邻补角的性质可知，与∠ AOD 互补的角：∠ BOD 与∠ AOC；（2）先求出∠ BOE的度数，然后根据OF平分∠ AOE求出∠ FOE，再根据OF⊥CD，可知∠ FOD＝90°，求出∠ EOD，最后得出∠ BOD＝∠ BOE﹣∠ EOD 求出答案．【解答】解：（1）与∠ AOD 互补的角：∠ BOD 与∠ AOC；（2）∵∠ AOE＝110°，∴∠ BOE＝180°﹣∠ AOE ＝180°﹣110°＝70°，∵ OF 平分∠ AOE，∴∠ FOE＝∠AOE＝，∵OF⊥ CD，∴∠ FOD ＝90°，∴∠ EOD＝∠ FOD﹣∠FOE＝90°﹣55°＝35°，∴∠ BOD＝∠ BOE﹣∠ EOD ＝70°﹣35°＝35°．【点评】本题考查了补角以及角平分线的性质．正确运用补角的定义和角平分线性质是解题的关键．24．【分析】作平行线利用平行线的性质与角平分线的性质通过角等量关系转化解题即可．【解答】解：感知：如图① ，过点P 作PQ∥AB∴∠A＝∠ APQ，∵AB∥CD，PQ∥AB∴PQ∥ CD，∴∠ C＝∠ QPC，∴∠ APQ+∠QPC＝∠ A+∠C，∠APC＝∠A+∠C．故答案为∠ P＝∠ A+∠C；探究：证明：如图③ ，过点P 作PQ ∥AB∴∠ A＝∠ APQ∵AB∥CD，PQ∥AB∴PQ∥ CD∴∠ C＝∠ CPQ∵∠ APC＝∠ APQ﹣∠ CPQ∴∠ APC＝∠ A﹣∠ C．故答案为：∠ APC＝∠ A﹣∠ C，∠APQ，PQ，∠ CPQ ，∠ APQ ，∠ CPQ ，∠ A﹣∠ C．应用：（1）如图⑤ ，过点 D 作DH ∥EF，∴∠ HDE ＝∠ E，∵AB∥EF，DH ∥EF∴ AB∥ DH ，∴∠ B+∠BDH ＝180°，即∠ BDH ＝180°﹣∠ B，∴∠ HDE +∠BDH ＝∠ E+180 °﹣∠ B，即∠ BDE+∠B﹣∠ E＝180°，故答案为∠ D+∠B﹣∠ E＝180°，（2）如图⑥ ，过点P 作PH ∥EF，∴∠ EPH＝∠ NEP，∵AB∥EF，PH∥ EF，∴AB∥PH，∴∠ MBP+∠BPH＝180°，∵BD 平分∠ MBP，∠ MBD ＝25 °，∠MBP＝2∠MBD＝2×25°＝50°，∠BPH ＝180°﹣50°＝ 130∵EN 平分∠ DEP ，∴∠ NEP ＝∠ DEN∠DEF﹣50° 由① ∠ D+∠ABD ﹣∠ DEF ＝180°， ∵∠ MBD ＝ 25°，∴∠ ABD ＝155°，BPE ＝∠ DEF ﹣50°＝∠ D ﹣25°﹣50°＝∠D ﹣75°故答案 75．的关键．∴∠ BPE ＝∠ BPH ﹣∠ EPH ＝∠ BPH ﹣∠ NEP ＝∠ BPH ﹣ ∠ DEN ＝ 130°﹣( 180° DEF ）＝∴∠ D +∠ 155°﹣∠ DEF ＝ 180°，∴∠ DEF ＝∠ D ﹣25°∴∠ ∠D ﹣∠ BPE ＝ 75°即∠D ﹣∠ P ＝ 75°， 点评】 本题考查了角平分线的性质与平行线的性质， 正确运用角平分线与平行线的性质是解题。
2019-2020学年吉林长春市七年级（上）语文期末试卷（含答案）
2019-2020学年吉林长春市七年级（上）语文期末试卷（含答案）2019-2020学年吉林长春市七年级（上）语文期末试卷温馨提示：语文试题共8页，包括三道大题，共23道小题。
全卷满分120分，考试时间为120分钟。
一、积累与运用（15分）1.给加点字注音，根据拼音写汉字。
（4分）（1）狭隘．（）（2）祷．（）告（3）汲．（）水（4）庇．（）护（5）yuān（）博（6）jué（）别（7）热chén（）（8）爱mù（）2.找出下列加点词语使用不当的一项（）。
（2分）A.那种清冷是柔和的，没有北风那样咄咄逼人．．．．。
B.昨晚，这里发生了一起骇人听闻．．．．的案件。
C.我想找一个两全齐美的办法，找不出；我想拆散一家人，分成两路，各得其所．．．．，终不愿意。
D.在利益的驱使下，一些不法厂商大肆仿冒名牌，各种“山寨名牌”如雨后春笋．．．．般不断涌现，严重扰乱了市场的正常秩序。
3.请在下面的田字格中端正地书写诗文名句。
（7分）（1），落花时节又逢君。
（杜甫《江南逢李龟年》）（2）非淡泊无以明志，。
（诸葛亮《诚子书》）（3），；星汉灿烂，若出其里。
（曹操《观沧海》）（4）古诗中，诗人往往借物抒情或借景抒情。
王湾的《次北固山下》“乡书何处达，”一句，借大雁抒发了对家人的思念之情；马致远的《天净沙·秋思》“夕阳西下，”一句，借夕阳表达了游子对家的思念；李白的《闻王昌龄左迁龙标遥有此寄》“我寄愁心与明月，”一句，借明月表达了对友人的牵挂之情。
4.学习了敬辞与谦辞后，小明同学特别感兴趣，并尝试在续写《陈太丘友致太丘书》中使用。
下面短文中画线的敬辞或谦辞使用不当的一项是（）。
（2分）弟这次到贵府拜访愚兄，感触良多。
令郎元方虽年纪尚小，却甚有见识。
弟言语不周，还请见谅。
A.贵府B.愚兄C.令郎D.见谅二、阅读（45分）（一）文言文阅读（15分）【甲】一屠晚归，担中肉尽，止有剩骨。
吉林省长春市南关区东北师大附中明珠学校2022-2023学年七年级上学期期末数学试题及解析
∴CD=AD-AC=7-6=1．
【点睛】此题主要考查学生对比较线段的长短的掌握情况，比较简单．
25．画图见解析
【分析】读图可得，从正面看有3列，每列小正方形数目分别为2，3，1；从左面看有3列，每列小正方形数目分别为3，1，2；从上面看有3行，每行小正方形数目分别为2，2，2，依此画出图形即可．
【详解】解：如图所示：
22．
【详解】解：去分母，得：
去括号得：
移项得：
合并同类项得：
解得： ．
【点睛】本题主要考查了解一元一次方程，熟练掌握解一元一次方程的基本步骤是解题的关键．
23． ，54
【分析】原式去括号合并得到最简结果，把a和b的值代入计算即可求出值．
【详解】 ，其中a＝－2，b＝3．
=
=
_________________）．
27．如图，直线 、 相交于点 ， ．
(1)若 ，求 的度数．
(2)若 平分 ，求 与 的度数．
28．【阅读理解】定义：数轴上给定不重合两点 、 ，若数轴上存在一点 ，使得点 到点 的距离等于点 到点 的距离的2倍，则称点 为点 与点 的“双倍绝对点”．请解答下列问题：
【点睛】本题主要考查含乘方的有理数混合运算，掌握运算法则和顺序是解题关键．
16．
【详解】解：
．
【点睛】本题考查的是有理数的四则混合运算，掌握“四则混合运算的运算顺序”是解本题的关键，运算顺序为：先计算括号内的减法，再计算乘除运算．
17．
【分析】先去括号，再合并同类项即可．
【详解】解：
．
【点睛】本题考查的是整式的加减运算，掌握“去括号，合并同类项的法则”是解本题的关键．
【详解】解：∵DE∥AF，
吉林省长春市南关区东北师大附中明珠学校2023-2024学年七年级上学期期末数学试题
吉林省长春市南关区东北师大附中明珠学校2023-2024学年七年级上学期期末数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，在数轴上对应的数互为相反数的两个点是（）A ．点A 和点CB ．点B 和点C C ．点A 和点BD ．点B 和点D 2．杭州第19届亚运会公众售票官方网站8日上午上线开放注册，首批上架比赛项目包括举重、克柔术、网球、花样游泳、击剑、摔跤、蹦床、高尔夫球、跳水、游泳、软式网球、攀岩等12个项目，总计预售113700张门票，数据113700用科学记数法可表示为（）A ．60.113710⨯B ．51.13710⨯C ．61.13710⨯D ．411.3710⨯3．下列四个生活中的现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要确定两棵树的位置，就能确定这一行树所在的直线；③从A 地到B 地架设电线，总是尽可能沿着线段AB 方向架设；④把弯曲的公路改直，就能缩短路程．其中可以用基本事实“两点确定一条直线”来解释的有（）A ．①②B ．①③C ．②③D ．③④4．如图，图（1）和图（2）中所有的正方形都完全相同，将图（1）的正方形放在图（2）中的某一位置，其中所组成的图形不能围成正方体的是（）A ．①B ．②C ．③D ．④5．若单项式213n ax y +与42m ax y -是同类项，则()2023m n -的值是（）A ．0B ．1C ．1-D ．20236．“盈不足问题”作为我国数学的古典问题，在2000多年前的《九章算术》一书中就有很详尽而深刻的阐述．书中记载：今有人买鸡，人出九，盈十一；人出六，不足十六．问人数、物价各几何？意思是：有若干人一起买鸡，如果每人出9文钱，就多出11文钱；A ．911x +7．如图，直线度数是（）A ．15︒B ．8．如图，将矩形ABCD 沿若∠AGE =32°，则∠GHC 等于（A ．112°B ．110°二、填空题9．比较大小：34--10．近似数4.50万精确到11．如图，一把长方形直尺沿直线断开并错位摆放，若131ADE =︒∠，则DBC ∠12．计算：6136'︒=°．13．若244x x +=，则2782x x --的值为14．如图所示，未来公园的广场背景墙上有一系列用灰砖和白砖铺成的图案，图①有块灰砖，8块白砖；图②有4块灰砖，砖，则此图案中有块白砖．三、解答题15．计算：(1)()511110.5626⎛⎫⎛⎫+----+ ⎪ ⎪⎝⎭⎝⎭；(2)1422379⎛⎫⎛⎫-⨯÷- ⎪ ⎪⎝⎭⎝⎭；(3)()()2321162332-÷-⨯-⨯+-．16．解方程：(1)4363x x -=+；(2)()()21213x x --=-+；(3)4172136x x +--=．17．先化简，再求值()(22252334a a a a -++-18．在2023年空军航空开放活动·长春航空展中，某飞机起飞5千米后的高度变化情况如下表所示，按要求解答下列问题：(1)过点A 作直线BC 的垂线，垂足为点(2)作线段AE BC ∥．且AE =(3)若点F 在线段AC 上，连结并说明此时DF EF +的长度最小的理由：20．已知线段AB ，延长AB 到AB 的长．21．已知，如图，点A ，O ，(1)求证：OC 是∠BOE 的平分线，证明：∵90COD ∠=︒，∴DOE ∠+____________90=又∵OD 平分AOE ∠，∴AOD ∠=__________．（________________∴COE ∠=__________．（________________∴OC 是∠BOE 的平分线．(2)图中COE ∠的补角是____________22．随着《某市生活垃圾分类管理条例》正式实施，某市垃圾分类工作进入强制实施阶段，某小区物业管理负责人提出了购买分类垃圾桶的方案．方案一：买A 型号分类垃圾桶，-，b，c，24．已知数轴上A，B，C三个点表示的数分别是10动点P从点A出发，以每秒2个单位长度的速度沿数轴向终点t秒．(1)b=_________，c=__________；(2)点P在数轴上表示的数为___________（用含t的代数式表示）(3)另一动点Q也从点A出发，沿数轴运动至点C后，立刻以原来的速度返回到止，①若P、Q两点同时出发，点Q的速度为每秒4个单位长度，当t=时，PQ②若点P运动到点B时，点Q再从点A出发，当7运动速度．。
吉林省长春市新区2019-2020学年第一学期七年级数学期末试卷 解析版
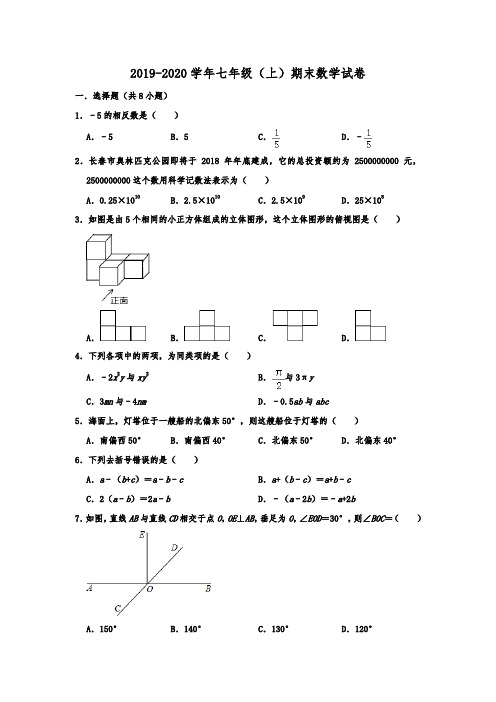
2019-2020学年七年级（上）期末数学试卷一．选择题（共8小题）1．﹣5的相反数是（）A．﹣5 B．5 C．D．﹣2．长春市奥林匹克公园即将于2018年年底建成，它的总投资额约为2500000000元，2500000000这个数用科学记数法表示为（）A．0.25×1010B．2.5×1010C．2.5×109D．25×1083．如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是（）A．B．C．D．4．下列各项中的两项，为同类项的是（）A．﹣2x2y与xy2B．与3πyC．3mn与﹣4nm D．﹣0.5ab与abc5．海面上，灯塔位于一艘船的北偏东50°，则这艘船位于灯塔的（）A．南偏西50°B．南偏西40°C．北偏东50°D．北偏东40°6．下列去括号错误的是（）A．a﹣（b+c）＝a﹣b﹣c B．a+（b﹣c）＝a+b﹣cC．2（a﹣b）＝2a﹣b D．﹣（a﹣2b）＝﹣a+2b7．如图，直线AB与直线CD相交于点O，OE⊥AB，垂足为O，∠EOD＝30°，则∠BOC＝（）A．150°B．140°C．130°D．120°8．如图，把一块含有45°的直角三角形的两个顶点放在直尺的对边上．如果∠1＝20°，那么∠2的度数是（）A．15°B．20°C．25°D．30°二．填空题（共6小题）9．两点整，时针与分针所成角的度数为．10．如图，要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为0，则x﹣2y＝．11．若单项式﹣2x3y n与4x m y5合并后的结果还是单项式，则m﹣n＝．12．如图，在一条直线上有A．B．C．D四个点，则图中共有条不同的线段．13．将多项式﹣9+x3+3xy2﹣x2y按x的降幂排列为：．14．由黑色和白色的正方形按一定规律组成的图形如图所示，从第二个图形开始，每个图形都比前一个图形多3个白色正方形，则第n个图形中有白色正方形个（用含n 的代数式表示）．三．解答题（共10小题）15．计算：﹣22+[18﹣（﹣3）×2]÷4．16．计算：20°18′+34°56′﹣12°34′．17．将直尺与三角尺按如图所示的方式叠放在一起．在图中标记的角中，写出所有与∠1互余的角．18．先化简，再求值：2x3+4x﹣3x2﹣（x﹣3x2+2x3），其中x＝﹣3．19．如图，直线EF分别与直线AB、CD交于M，N两点，∠1＝55°，∠2＝125°，求证：AB∥CD【要求写出每一步的理论依据】．20．如图，在6×6的正方形网格中，每个小正方形的边长均为1cm，点A，B，C均在格点上，画图并回答问题．（1）画射线AC，画直线AB．（2）过点C画直线AB的垂线，垂足为点D．（3）点A到直线BC的距离为cm．21．如图，OB平分∠COD，∠AOB＝90°，∠AOC＝125°，求∠DOC的度数．22．如图所示，线段AB＝12，点C是AB上一点，AC＝7，点M是AB的中点，点N是BC的中点，求线段CM和MN的长．23．感知与填空：如图①，直线AB∥CD．求证：∠B+∠D＝∠BED．阅读下面的解答过程，井填上适当的理由．解：过点E作直线EF∥CD∴∠2＝∠D（）∵AB∥CD（已知），EF∥CD，∴AB∥EF（）∴∠B＝∠1（）∵∠1+∠2＝∠BED，∴∠B+∠D＝∠BED（）应用与拓展：如图②，直线AB∥CD．若∠B＝22°，∠G＝35°，∠D＝25°，则∠E+∠F ＝度．方法与实践：如图③，直线AB∥CD．若∠E＝∠B＝60°，∠F＝80°，则∠D＝度．24．如图，相距10千米的A、B两地间有一条笔直的马路，C地位于A、B两地之间且距A 地4千米．小明同学骑自行车从A地出发沿马路以每小时5千米的速度向B地匀速运动，当到达B地后立即以原来的速度返回，到达A地停止运动．设运动时间为t（时），小明的位置为点P．（1）当t＝0.5时，求点P、C间的距离．（2）当小明距离C地1千米时，直接写出所有满足条件的t值．（3）在整个运动过程中，求点P与点A的距离（用含t的代数式表示）．参考答案与试题解析一．选择题（共8小题）1．﹣5的相反数是（）A．﹣5 B．5 C．D．﹣【分析】根据相反数的定义直接求得结果．【解答】解：﹣5的相反数是5．故选：B．2．长春市奥林匹克公园即将于2018年年底建成，它的总投资额约为2500000000元，2500000000这个数用科学记数法表示为（）A．0.25×1010B．2.5×1010C．2.5×109D．25×108【分析】利用科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：2500000000用科学记数法表示为2.5×109．故选：C．3．如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是（）A．B．C．D．【分析】从上面看到的平面图形即为该组合体的俯视图，据此求解．【解答】解：从上面看共有2行，上面一行有3个正方形，第二行中间有一个正方形，故选：C．4．下列各项中的两项，为同类项的是（）A．﹣2x2y与xy2B．与3πyC．3mn与﹣4nm D．﹣0.5ab与abc【分析】本题考查同类项的定义，所含字母相同且相同字母的指数也相同的项是同类项，同类项与字母的顺序无关，与系数无关．【解答】解：A．相同字母的指数不同，不是同类项，故本选项不合题意；B.与3πy，所含字母不同，不是同类项，故本选项不合题意；C.3mn与﹣4nm字母相同，且相同的字母的指数也相同，是同类项，故本选项符合题意；D．﹣0.5ab与abc所含字母不尽相同，不是同类项，故本选项不合题意．故选：C．5．海面上，灯塔位于一艘船的北偏东50°，则这艘船位于灯塔的（）A．南偏西50°B．南偏西40°C．北偏东50°D．北偏东40°【分析】结合题意图形可知，这艘船位于灯塔的方向与灯塔位于这艘船的方向正好相反，但度数不变．【解答】解：船位于灯塔南偏西50°．故选：A．6．下列去括号错误的是（）A．a﹣（b+c）＝a﹣b﹣c B．a+（b﹣c）＝a+b﹣cC．2（a﹣b）＝2a﹣b D．﹣（a﹣2b）＝﹣a+2b【分析】根据去括号法则对四个选项逐一进行分析，要注意括号前面的符号，以选用合适的法则．【解答】解：A、a﹣（b+c）＝a﹣b﹣c，故本选项不符合题意；B、a+（b﹣c）＝a+b﹣c，故本选项不符合题意；C、2（a﹣b）＝2a﹣2b，故本选项符合题意；D、﹣（a﹣2b）＝﹣a+2b，故本选项不符合题意；故选：C．7．如图，直线AB与直线CD相交于点O，OE⊥AB，垂足为O，∠EOD＝30°，则∠BOC＝（）A．150°B．140°C．130°D．120°【分析】根据垂直的定义可得∠BOE＝90°，然后列式计算即可求出∠BOD，再根据邻补角互补求出∠BOC即可．【解答】解：∵EO⊥AB，∴∠BOE＝90°，∵∠EOD＝30°，∴∠BOD＝90°﹣∠EOD＝90°﹣30°＝60°，∴∠BOC＝180°﹣∠BOD＝180°﹣60°＝120°，故选：D．8．如图，把一块含有45°的直角三角形的两个顶点放在直尺的对边上．如果∠1＝20°，那么∠2的度数是（）A．15°B．20°C．25°D．30°【分析】根据两直线平行，内错角相等求出∠3，再求解即可．【解答】解：∵直尺的两边平行，∠1＝20°，∴∠3＝∠1＝20°，∴∠2＝45°﹣20°＝25°．故选：C．二．填空题（共6小题）9．两点整，时针与分针所成角的度数为60°．【分析】先结合图形，确定时针和分针的位置，再进一步求其度数．【解答】解：如图：2点整，时针指向2，分针指向12，每相邻两个数字之间的夹角为30°，则其夹角为30°×2＝60°．故答案为：60°．10．如图，要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为0，则x﹣2y＝ 6 ．【分析】利用正方体及其表面展开图的特点，根据相对面上的两个数之和为0，也就是互为相反数，求出x、y的值，从而得到x﹣2y的值．【解答】解：将题图中平面展开图按虚线折叠成正方体后，可知标有数字“2”的面和标有x的面是相对面，标有数字“4”的面和标有y的面是相对面，∵相对面上两个数之和为0，∴x＝﹣2，y＝﹣4，∴x﹣2y＝﹣2﹣2×（﹣4）＝﹣2+8＝6．故答案为：6．11．若单项式﹣2x3y n与4x m y5合并后的结果还是单项式，则m﹣n＝﹣2 ．【分析】根据同类项定义可得m＝3，n＝5，然后可得答案．【解答】解：由题意得：m＝3，n＝5，则m﹣n＝3﹣5＝﹣2，故答案为：﹣2．12．如图，在一条直线上有A．B．C．D四个点，则图中共有，6 条不同的线段．【分析】根据线段的定义找出不同的线段即可．【解答】解：任取其中两点作为线段的端点，则可以得到的线段为：AB、AC、AD、BC、BD、CD六条．故答案为：6，13．将多项式﹣9+x3+3xy2﹣x2y按x的降幂排列为：x3﹣x2y+3xy2﹣9 ．【分析】按字母x的指数从大到小排列即可．【解答】解：按x的降幂排列为x3﹣x2y+3xy2﹣9，故答案为：x3﹣x2y+3xy2﹣9．14．由黑色和白色的正方形按一定规律组成的图形如图所示，从第二个图形开始，每个图形都比前一个图形多3个白色正方形，则第n个图形中有白色正方形（3n﹣1）个（用含n的代数式表示）．【分析】仔细观察图形，找到图形的个数与白色正方形的个数的通项公式，即可求解．【解答】解：观察图形发现：图①中有2个白色正方形，图②中有2+3×（2﹣1）＝5个白色正方形，图③中有2+3（3﹣1）＝8个白色正方形，图④中有2+3（4﹣1）＝11个白色正方形，…，图n中有2+3（n﹣1）＝3n﹣1个白色的正方形．故答案为：（3n﹣1）．三．解答题（共10小题）15．计算：﹣22+[18﹣（﹣3）×2]÷4．【分析】原式先计算乘方运算，再计算乘除运算，最后算加减运算即可求出值．【解答】解：原式＝﹣4+（18+6）÷4＝﹣4+6＝2．16．计算：20°18′+34°56′﹣12°34′．【分析】根据度分秒间的换算单位是60进行解答．【解答】解：20°18′+34°56′﹣12°34′＝55°14′﹣12°34′＝42°40′．17．将直尺与三角尺按如图所示的方式叠放在一起．在图中标记的角中，写出所有与∠1互余的角．【分析】考查余角的基本概念，与∠1互余的角是∠2，又因为∠2与∠4是同位角，∠4与∠3是对顶角，故可求解．【解答】解：∵直尺的两边平行，∴∠2＝∠3；∵∠3＝∠4，∠1+∠2＝90°，∴∠1的余角有：∠2，∠3，∠4．18．先化简，再求值：2x3+4x﹣3x2﹣（x﹣3x2+2x3），其中x＝﹣3．【分析】原式去括号合并得到最简结果，把x的值代入计算即可求出值．【解答】解：原式＝2x3+4x﹣3x2﹣x+3x2﹣2x3＝3x，当x＝﹣3时，原式＝﹣9．19．如图，直线EF分别与直线AB、CD交于M，N两点，∠1＝55°，∠2＝125°，求证：AB∥CD【要求写出每一步的理论依据】．【分析】根据对顶角相等可求∠CNM，再根据平行线的判定定理即可求解．【解答】证明：∵∠1＝55°（已知），∴∠CNM＝55°（对顶角相等），∵∠2＝125°（已知），∴∠CNM+∠2＝180°（等式的性质），∴AB∥CD（同旁内角互补，两直线平行）．20．如图，在6×6的正方形网格中，每个小正方形的边长均为1cm，点A，B，C均在格点上，画图并回答问题．（1）画射线AC，画直线AB．（2）过点C画直线AB的垂线，垂足为点D．（3）点A到直线BC的距离为 2 cm．【分析】（1）画射线AC，画直线AB即可；（2）过点C画直线AB的垂线，垂足为点D即可；（3）点A到直线BC的距离为2cm．【解答】解：如图所示：（1）射线AC，直线AB即为所求作的图形．（2）过点C画直线AB的垂线，垂足为点D，CD即为所求作的图形．（3）点A到直线BC的距离为2cm．21．如图，OB平分∠COD，∠AOB＝90°，∠AOC＝125°，求∠DOC的度数．【分析】根据角的和差关系求出∠BOC，再根据角平分线的定义解答即可．【解答】解：∵∠AOB＝90°，∠AOC＝125°，∴∠BOC＝∠AOC﹣∠AOB＝35°，∵OB平分∠COD，∴∠DOC＝2∠BOC＝70°．22．如图所示，线段AB＝12，点C是AB上一点，AC＝7，点M是AB的中点，点N是BC的中点，求线段CM和MN的长．【分析】由点M是AB的中点可得出AM的长度，结合CM＝AC﹣AM即可求出CM的长度，由AB、AC的长度可得出BC的长度，由N是BC的中点可得出CN的长度，结合MN＝CM+CN 即可求出MN的长度．【解答】解：∵M是AB的中点，∴AM＝AB＝×12＝6，∴CM＝AC﹣AM＝7﹣6＝1．∵AB＝12，AC＝7，∴BC＝AB﹣AC＝12﹣7＝5．∵N是BC的中点，∴CN＝BC＝×5＝2.5，∴MN＝CM+CN＝1+2.5＝3.5．23．感知与填空：如图①，直线AB∥CD．求证：∠B+∠D＝∠BED．阅读下面的解答过程，井填上适当的理由．解：过点E作直线EF∥CD∴∠2＝∠D（两直线平行，内错角相等）∵AB∥CD（已知），EF∥CD，∴AB∥EF（两直线都和第三条直线平行，那么这两条直线也互相平行）∴∠B＝∠1（两直线平行，内错角相等）∵∠1+∠2＝∠BED，∴∠B+∠D＝∠BED（等量代换）应用与拓展：如图②，直线AB∥CD．若∠B＝22°，∠G＝35°，∠D＝25°，则∠E+∠F ＝82 度．方法与实践：如图③，直线AB∥CD．若∠E＝∠B＝60°，∠F＝80°，则∠D＝20 度．【分析】感知与填空：过点E作直线EF∥CD，由两直线平行，内错角相等得出∠2＝∠D，由两直线都和第三条直线平行，那么这两条直线也互相平行得出AB∥EF，由两直线平行，内错角相等得出∠B＝∠1，由∠1+∠2＝∠BED，等量代换得出∠B+∠D＝∠BED．应用与拓展：过点G作GN∥AB，则GN∥CD，由感知与填空得∠E＝∠B+∠EGN，∠F＝∠D+∠FGN，即可得出结果．方法与实践：设AB交EF于M，∠AME＝∠FMB＝180°﹣∠F﹣∠B＝40°，由感知与填空得∠E＝∠D+∠AME，即可得出结果．【解答】解：感知与填空：过点E作直线EF∥CD，∴∠2＝∠D（两直线平行，内错角相等），∵AB∥CD（已知），EF∥CD，∴AB∥EF（两直线都和第三条直线平行，那么这两条直线也互相平行），∴∠B＝∠1（两直线平行，内错角相等），∵∠1+∠2＝∠BED，∴∠B+∠D＝∠BED（等量代换），故答案为：两直线平行，内错角相等；两直线都和第三条直线平行，那么这两条直线也互相平行；两直线平行，内错角相等；等量代换．应用与拓展：过点G作GN∥AB，则GN∥CD，如图②所示：由感知与填空得：∠E＝∠B+∠EGN，∠F＝∠D+∠FGN，∴∠E+∠F＝∠B+∠EGN+∠D+∠FGN＝∠B+∠D+∠EGF＝22°+25°+35°＝82°，故答案为：82．方法与实践：设AB交EF于M，如图③所示：∠AME＝∠FMB＝180°﹣∠F﹣∠B＝180°﹣80°﹣60°＝40°，由感知与填空得：∠E＝∠D+∠AME，∴∠D＝∠E﹣∠AME＝60°﹣40°＝20°，故答案为：20．24．如图，相距10千米的A、B两地间有一条笔直的马路，C地位于A、B两地之间且距A 地4千米．小明同学骑自行车从A地出发沿马路以每小时5千米的速度向B地匀速运动，当到达B地后立即以原来的速度返回，到达A地停止运动．设运动时间为t（时），小明的位置为点P．（1）当t＝0.5时，求点P、C间的距离．（2）当小明距离C地1千米时，直接写出所有满足条件的t值．（3）在整个运动过程中，求点P与点A的距离（用含t的代数式表示）．【分析】（1）根据题意列式计算即可；（2）根据题意，分两种情况：①当小明在C点的左边时；②当小明在C点的右边时；然后根据路程÷速度＝时间，求出小明距离C地1km 时，所有满足条件的t值是多少即可；（3）根据题意，分两种情况讨论，当小明从A地运动到B或小明从B地运动到A，然后列式计算即可．【解答】解：（1）由题意得，v＝5km/h，AC＝4km，AB＝10km，当t＝0.5时，s＝vt＝5×0.5＝2.5km，即AP＝2.5km，∴PC＝AC﹣AP＝4﹣2.5＝1.5km；（2）①当小明在C点的左边时，（4﹣1）÷5＝3÷5＝0.6；②当小明在C点的右边时，（4+1）÷5＝5÷5＝1③同法可得返回时，t＝3h或s答，当小明距离C地1km时，t的值是0.6h或1h或3h或3.4s；（3）当小明从A地运动到B的过程中，AP＝vt＝5tkm，当小明从B地运动到A的过程中，AP＝20﹣vt＝（20﹣5t）km．。
吉林省长春市东北师大附中七年级(上)期末数学试卷
24. 感知：如图①，若 AB∥CD，点 P 在 AB、CD 内部，则∠P、∠A、∠C 满足的数量关 系是______．
探究：如图②，若 AB∥CD，点 P 在 AB、CD 外部，则∠APC、∠A、∠C 满足的数量
关系是______．
请补全以下证明过程：
证明：如图③，过点 P 作 PQ∥AB
∴∠A=______
（4）5������−1-2������ + 6=1
4
3
17. 先化前，再求值：2（a2+2a-1）-3（a2-2a-3），其中 a=-2．
四、解答题（本大题共 7 小题，共 56.0 分） 18. 计算：
（1）3x+2（x-1）-（x+1）
2
（2）5（2a2b-2ab2）-2（6a2b-3ab2）
七年级（上）期末数学试卷
题号 得分
一
二
三
四
总分
一、选择题（本大题共 8 小题，共 24.0 分）
1. -5 的绝对值是（ ）
A. 5
B.
1
−5
C. −5
D.
1 5
2. 实数 a，b，c，d 在数轴上对应的点的位置如图所示，这四个数中最大的是（ ）
A. a
B. b
C. c
D. d
ቤተ መጻሕፍቲ ባይዱ
3. 如图是一个由两个小正方体和一个圆锥组成的几何体，它的主视 图是（ ）
20. 如图，已知点 E、F 在直线 AB 上，点 G 在线段 CD 上，ED 与 FG 相交于点 H，∠C=∠EFG，∠BFG=∠AEM，求证： AB∥CD．（完成下列填空） 证明：∵∠BFG=∠AEM（已知） 且∠AEM=∠BEC（______） ∴∠BEC=∠BFG（等量代换） ∴MC∥______（______） ∴∠C=∠FGD（______） ∵∠C=∠EFG（已知） ∴∠______=∠EFG，（等量代换） ∴AB∥CD（______）
2019-2020学年吉林省长春市数学七年级(上)期末考试模拟试题
2019-2020学年吉林省长春市数学七年级(上)期末考试模拟试题一、选择题1．如图，O为直线AB上一点，∠COB＝26°30′，则∠1＝( )A.153°30′B.163°30′C.173°30′D.183°30′2．如图，点C、O、B在同一条直线上，∠AOB=90°，∠AOE=∠DOB，则下列结论：①∠EOD=90°；②∠COE=∠AOD；③∠COE=∠DOB；④∠COE+∠BOD=90°．其中正确的个数是（）A.1B.2C.3D.43．如图所示的图形绕虚线旋转一周，所形成的几何体是（）A． B． C． D．4．今年某月的月历上圈出了相邻的三个数a、b、c，并求出了它们的和为39，这三个数在月历中的排布不可能是（）A. B. C. D.5．在如图所示的2019年1月的月历表中，任意框出表中竖列上的三个相邻的数，这三个数的和不可能是( )A.27B.51C.65D.726．在代数式 a+b ，37x 2，5a ，m ，0，3a b a b +-，32x y -中，单项式的个数是( ) A.6 B.5 C.4D.3 7．若A 和B 都是五次多项式，则（ ） A.A+B 一定是多项式 B.A ﹣B 一定是单项式C.A ﹣B 是次数不高于5的整式D.A+B 是次数不低于5的整式 8．在1，－2，0，53这四个数中，绝对值最大的数是（ ） A.－2 B.0 C.53 D.19．“地球停电一小时”活动的某地区烛光晚餐中，设座位有 x 排，每排坐 30 人，则有 8 人无 座位；每排坐 31 人，则空 26 个座位．则下列方程正确的是（ ）A ．30x ﹣8=31x ﹣26B ．30x + 8=31x+26C ．30x + 8=31x ﹣26D ．30x ﹣8=31x+2610．中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，将67500用科学记数法表示为（ ）A.46.7510⨯吨B.367.510⨯吨C.3 0.67510⨯吨D.4 6.7510-⨯吨11．8-的相反数是（ ）A.18B.8C.8-D.1212．已知a 、b 为有理数，ab≠0，且M=||||a b a b +，当a 、b 取不同的值时，M 的值是( ) A.±2B.±1或±2C.0或±1D.0或±2二、填空题13．如图，已知∠A 1OA 11是一个平角，且∠A 3OA 2－∠A 2OA 1=∠A 4OA 3－∠A 3OA 2=∠A 5OA 4－∠A 4OA 3=……=∠A 11OA 10－∠A 10OA 9=3°，则 ∠A 11OA 10的度数为______．14．计算：12°20＇×4=______________．15．若2x ﹣3y=﹣2，那么3﹣2x+3y 的值是_____．16．某商品的标价为200元，8折销售仍获利25%，则商品进价为_____元．17．12a m-1b 3与12-a 3b n 是同类项，则m+n=______． 18．如图，某广场用正方形地砖铺地面，第一次拼成图（1）所示的图案，需要4块地砖；第二次拼成图（2）所示的图案，需要12块地砖，第三次拼成图（3）所示的图案，需要24块地砖，第四次拼成图（4）所示的图案，需要_____块地砖…，按照这样的规律进行下去，第n 次拼成的图案共用地砖_____块．19．若a,b 是整数，且ab ＝12，|a|＜|b|，则a+b=________ .20．请写出一个关于 a 的代数式 .使 a 不论取何值，这个代数式的值总是负数.三、解答题21．如图，已知四点A ，B ，C ，D.(1)画直线AB ；(2)画射线DC ；(3)连接AC ，BD ，线段AC 与BD 相交于点E.22．如图，O 为直线AB 上一点，∠AOC ＝50°20′，OD 平分∠AOC ，∠DOE ＝90°．（1）求∠DOB 的度数；（2）请你通过计算说明OE 是否平分∠COB ．23．如图在长方形ABCD 中，AB=12cm ，BC=8cm ，点P 从A 点出发，沿A→B→C→D 路线运动，到D 点停止；点Q 从D 点出发，沿D→C→B→A 运动，到A 点停止．若点P 、点Q 同时出发，点P 的速度为每秒1cm ，点Q 的速度为每秒2cm ，用x （秒）表示运动时间．（1）求点P 和点Q 相遇时的x 值．（2）连接PQ ，当PQ 平分矩形ABCD 的面积时，求运动时间x 值．（3）若点P 、点Q 运动到6秒时同时改变速度，点P 的速度变为每秒3cm ，点Q 的速度为每秒1cm ，求在整个运动过程中，点P 、点Q 在运动路线上相距路程为20cm 时运动时间x 值．24．昨天老师带着我们班同学去深圳少年宫玩，我们一共去了 60人（包括老师），买门票共花了1240元.玩得可开心了！小明：真羡慕你们，不过听说门票还是挺贵的.小红：是的，老师票每张30元，学生票每张20元.那你能猜出我们去了几位老师，几位学生吗？ 小明：去了……根据以上的对话，你能用解方程的知识帮助小明回答小红的提问吗？25．有这样一道题：“先化简，再求值：222(324)2()x x x x x -+---,其中100x =”甲同学做题时把100x =错抄成了10x =，乙同学没抄错，但他们做出来的结果却一样，你能说明这是为什么吗？并求出这个结果.26．先化简，再求值：12(2)2(3)2x y x y ---，其中1x =-，2y =. 27．王红有5张写着以下数字的卡片，请按要求抽出卡片，完成下列各题：（1）从中取出2张卡片，使这2张卡片上数字乘积最小，最小值是 ．（2）从中取出2张卡片，使这2张卡片数字相除商最大，最大值是 ．（3）从中取出除0以外的4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使结果为24，（注：每个数字只能用一次，如：23×[1﹣（﹣2）]），请另写出一种符合要求的运算式子 ．28．计算：（1）（-71）+（+64）；（2）（-16）-（-7）；（3）()2184-⨯；（4）315()2÷-【参考答案】一、选择题1．A2．C3．B4．C5．D6．D7．C8．A9．C10．A11．B12．D二、填空题13．5°14．49°20＇15．16．12817．718．2n2+2n ．19．7，8，1320．- a2 -1(答案不唯一）三、解答题21．(1)如图见解析； (2)如图见解析；(3)如图见解析. 22．(1) 154°50′；(2)见解析23．（1）x=323；（2）4 或20；（3）4或14.524．共去了4位老师,56位学生.25．说明见解析.26．-2x-y,0.27．（1）﹣6；（2）3；（3） [3﹣（﹣2）]2﹣1=24（答案不唯一，符合题意正确即可）. 28．（1）－7；（2）－9；（3）-42；（4）-10。
2019-2020学年吉林省长春市南关区东北师大附中明珠校区七年级(上)期末数学试卷(附答案详解)
2019-2020学年吉林省长春市南关区东北师大附中明珠校区七年级（上）期末数学试卷1.单项式−35ab2的系数是()A. −35B. 35C. −3D. 32.在数轴上，表示−2的点与原点的距离是()A. −2B. 0C. 2D. 不能确定3.如图，水杯的主视图是()A.B.C.D.4.下列各式中正确的是()A. −|5|=|−5|B. |−5|=5C. |−5|=−5D. |−1.3|<05.由下面正方体的平面展开图可知，原正方体“我”字所在的面的对面的汉字是()A. 中B. 国C. 的D. 梦6.下列图形中，∠1与∠2不是互补关系的是()A. B.C. D.7.x、y、c是有理数，则下列判断错误的是()A. 若x=y，则x+2c=y+2cB. 若x=y，则a−cx=a−cyC. 若x=y，则xc =ycD. 若xc=yc，则x=y8.如图，将一副三角尺按不同的位置摆放，下列各图中，∠α与∠β互余的是()A. B.C. D.9.将多项式x2+2−3x3按字母x的降幂排列为______ ．10.2018年10月23日，世界上最长的跨海大桥一港珠澳大桥正式开通，这座海底隧道于一身，全长约55000米．其中55000用科学记数法可表示为______．11.已知∠α=60°32′，则∠α的余角是______ ．12.某商品原价为a元，因销量下滑，经营者连续两次降价，每次降价10%，问现在这种商品的价格是______ 元.13.如图，AB//CD，DB⊥BC，∠1=40°，则∠2的度数是______．14.欢欢观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知AB//CD，∠BAE=92°，∠DCE=115°，则∠E的度数是______°.15.计算：(1)−13+28−77；(2)4−4×(−3)×(−1 3 ).16.计算：(1)3a3+a2−2a3−a2；(2)(2x2−12+3x)−3(x−x2+12).17.解方程：(1)14x=2x−6；(2)x−1=13x+1；(3)4x−x=2(x−1)+5；(4)6x−18=34+x．18.先化简，再求值：(5xy−8x3)−(−12x2+4xy)，其中x=1，y=2．219.如图是由6个边长为1的相同小正方体组成的几何体，请在边长为1的网格中画出它的三视图．20.如图，延长线段AB至点D，使点B为线段AD的中点，点C在线段BD上，CD=2BC，若BC=3，求AD的长．21.如图，某花园的护栏是用一些半圆形造型的钢条围成的，半圆的直径为80厘米，且每增加一个半圆形条钢，护栏长度就增加a厘米(a>0)，设半圆形条钢的总个数为x个(x为正整数)，护栏总长度为y厘米．(1)当a=60时，用含x的代数式表示护栏总长度y(结果要求化简)；(2)用含a、x的代数式表示护栏的总长度y(结果要求化简)，并求a=50，x=41时，护栏长度y的值．22.推理填空已知：如图，AB//CD，∠1=∠2求证：∠BEF=∠EFC证明：连接BC∵AB//CD(已知)∴∠ABC=______(______)∵∠1=∠2∴∠ABC−∠1=______−∠2∴∠EBC=______∴______//______(______)∴∠BEF=∠EFC(______)23.如图，直线AB与直线MN相交，交点为O，OC⊥AB，OA平分∠MOD，若∠BON=20°，求∠COD的度数．24.数轴上任意三个点，如点A、点B、点C，如果满足：点A在点B的左侧，且AC=kBC(k>0)，我们称点C为AB的k阶好点，比如点A、B、C在数轴上表示的数分别是−2，4，2，则AC=2BC，则称点C为AB的2阶好点．(1)若点A、点B、点C表示的数分别是−2，3，8，则点C是AB的______ 阶好点；(2)若点A、点B、点C表示的数分别是−2，3，1，则点C是AB的______ 阶好点；2(3)若点D、点E表示的数分别是−5和−3，动点M从点D出发，以每秒1个单位的速度向左运动，同时，动点N从点E出发，以每秒2个单位的速度向右运动，设运动时间为t，①点M表示的数为______ ，点N表示的数为______ (用含字母t的代数式表示)；②原点为线段MN的2阶好点时，求t的值；③设MN的1阶好点为点P，3阶好点为点Q，直接写出点P、点Q到原点的距离相等时t的值．25.把两个三角尺ABC与DEF按如图所示那样拼在一起，其中点D在BC上，DM为∠CDE的平分线，DN为∠BDF的平分线，则∠MDN的度数是______ ．26.如图，点C是线段AB上的一点，点D是线段CB的中点，已知图中所有线段的长度之和为23，线段AC的长度与线段CB的长度都是正整数，则线段AC的长度是______ ．27.小明学习了《有理数》后，对运算非常感兴趣，于是定义了一种新运算“△”规则．如下：对于两个有理数m，n，m△n=|m−n|+m+n2(1)计算：1△(−2)=______ ；(2)这个运算中，交换m、n两数的位置，计算结果是否会受到影响，请结合整式的计算，说明理由．(3)若a1=|x|，a2=|x−1|，若a1△a2=3，直接写出x的值．28.如图(1)，用两个等腰直角三角形的三角板拼成正方形ABCD，含有30°角的三角板AEF的顶点A与正方形的顶点A重合，边AE与正方形的边AB在同一直线上，∠FAE=30°，∠AEF=90°，将三角形AEF绕点A逆时针旋转，旋转的速度为每秒5°.设运动时间为t秒(0≤t≤18)．(1)如图(2)，当正方形的顶点C在△AEF的内部时，AE、AF与正方形ABCD的边交于点H、G(设AE、AF足够长)；①求此时t的范围；②∠FGC与∠CHE度数的和是否变化？若不变，直接写出∠FGC与∠CHE度数和，若变化，请说明理由；∠FGC．③当t=______ 时，∠CHE=75(2)如图(3)，在整个运动过程中，过点D作DP//EF交正方形ABCD的边于点P，直接写出DP将∠ADC分成的两部分角度之比为1：2时，t的值．答案和解析1.【答案】A【知识点】单项式【解析】解：单项式−35ab2的系数是−35．故选：A．单项式中数字因数叫做单项式的系数．考查了单项式，解答此题关键是构造单项式的系数，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数关键．2.【答案】C【知识点】数轴【解析】解：如图，在数轴上，表示−2的点与原点的距离为2，故选：C．结合数轴可直接得出答案．本题主要考查数轴，解题的关键是掌握数轴的概念：规定了原点、正方向、单位长度的直线叫做数轴．3.【答案】B【知识点】简单组合体的三视图【解析】解：从正面看，圆柱体的部分看到的是长方形，再加上把手即可，故选：B．从正面看，圆柱体的部分看到的是长方形，再加上把手即可，考查简单几何体的三视图，主视图是从正面看到的图形，左视图是从左面看到的图形，俯视图是从上面看到的图形．4.【答案】B【知识点】绝对值、非负数的性质：绝对值【解析】解：A、∵−|5|≠|−5|，∴选项A不符合题意；B、∵|−5|=5，∴选项B符合题意；B、∵|−5|=5，∴选项C不符合题意；D、∵|−1.3|>0，∴选项D不符合题意．故选：B．根据有理数大小比较的方法，以及绝对值的含义和求法，逐项判断即可．此题主要考查了有理数大小比较的方法，以及绝对值的含义和求法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．5.【答案】B【知识点】正方体相对两个面上的文字【解析】解：根据正方体相对的面的特点，“我”字所在的面的对面的汉字是“国”，故选：B．正方体的展开图有11种情况，分析平面展开图的各种情况后再认真确定哪两个面是对面．本题考查了正方体侧面展开图，熟记正方体侧面展开图对面和相邻的面是解题的关键．6.【答案】C【知识点】对顶角、邻补角【解析】解：A.∠1与∠2是互补关系，故本选项不合题意；B.由平行线的性质可知∠1与∠2是互补关系，故本选项不合题意；C.由对顶角的定义可知∠1与∠2是对顶角，不一定具有互补关系，故本选项符合题意；D.∠1+∠2=180°，即∠1与∠2是互补关系，故本选项不合题意．故选：C．根据互补的两个角的和为180°判定即可．本题主要考查了补角的定义，熟记定义是解答本题的关键．7.【答案】C【知识点】等式的概念及其基本性质【解析】解：A、根据等式的性质1可得出，若x=y，则x+2c=y+2c，原变形正确，故此选项不符合题意；B、根据等式的性质1和2得出，若x=y，则a−cx=a−cy，原变形正确，故此选项不符合题意；C、由x=y得出xc =yc必须c≠0，当c=0时不成立，故本选项符合题意；D、根据等式的性质2可得出，若xc =yc，则x=y，原变形正确，故此选项不符合题意；故选：C．根据等式的性质一一判断即可．本题考查等式的性质，解题的关键是记住等式的性质：性质1、等式两边加同一个数(或式子)结果仍得等式；性质2、等式两边乘同一个数或除以一个不为零的数，结果仍得等式．8.【答案】D【知识点】余角和补角、对顶角、邻补角【解析】解：A、∠α与∠β不互余，故本选项错误；B、∠α与∠β不互余，故本选项错误；C、∠α与∠β不互余，故本选项错误；D、∠α与∠β互余，故本选项正确．故选：D．根据图形，结合互余的定义判断即可．本题考查了对余角和补角的应用，主要考查学生的观察图形的能力和理解能力．9.【答案】−3x3+x2+2【知识点】多项式【解析】解：多项式x2+2−3x3的项为x2，2，−3x3，按字母x降幂排列为−3x3+x2+2，故答案为：−3x3+x2+2．先分清多项式的各项，然后按多项式降幂排列的定义排列．本题考查了多项式，我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列，称为按这个字母的降幂或升幂排列．要注意，在排列多项式各项时，要保持其原有的符号．10.【答案】5.5×104【知识点】科学记数法-绝对值较大的数【解析】解：将55000用科学记数法表示为：5.5×104．故答案为：5.5×104．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值<1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．11.【答案】29°28′【知识点】度分秒的换算、余角和补角【解析】解：∵∠α=60°32′，∴∠α的余角是：90°−60°32′=29°28′，故答案为：29°28′．根据余角的概念进行计算即可．本题考查余角的概念和度分秒的换算．解题的关键是掌握余角和补角的定义，如果两个角的和等于90°，就说这两个角互为余角．如果两个角的和等于180°，就说这两个角互为补角．12.【答案】0.81a【知识点】列代数式【解析】解：根据题意得：设现在的商品价格为s元，则s=a×(1−10%)×(1−10%)=0.81a，故答案为：0.81a．根据题意在原价a的基础上连续两次降价列出代数式，即可求解．本题考查了列代数式，解决本题得关键是正确理解题意．13.【答案】50°【知识点】平行线的性质【解析】解：∵AB//CD，∴∠1=∠BCD=40°，∵DB⊥BC，∴∠CBD=90°，∴∠2=90°−40°=50°．故答案为50°．根据平行线性质由AB//CD得到∠1=∠BCD=40°，再根据垂直的定义得∠CBD=90°，然后利用三角形内角和定理计算∠2的度数．本题考查了平行线性质：两直线平行，同位角相等．14.【答案】23【知识点】三角形的外角性质、平行线的性质【解析】解：如图，延长DC交AE于F，∵AB//CD，∠BAE=92°，∴∠CFE=92°，又∵∠DCE=115°，∴∠E=∠DCE−∠CFE=115°−92°=23°．故答案为：23．延长DC交AE于F，依据AB//CD，∠BAE=92°，可得∠CFE=92°，再根据三角形外角性质，即可得到∠E=∠DCE−∠CFE．本题主要考查了平行线的性质，三角形外角的性质，解决问题的关键是掌握：两直线平行，同位角相等．15.【答案】解：(1)原式=−13−77+28=−90+28=−62；(2)原式=4−4×3×13=4−4=0．【知识点】有理数的混合运算【解析】(1)原式结合后，相加即可求出值；(2)原式先计算乘法运算，再计算减法运算即可求出值．此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．16.【答案】解：(1)原式=a3；(2)原式=2x2−12+3x−3x+3x2−32=5x2−2．【知识点】整式的加减【解析】(1)原式合并同类项即可得到结果；(2)原式去括号合并即可得到结果．此题考查了整式的加减，熟练掌握运算法则是解本题的关键．17.【答案】解：(1)14x=2x−6，移项得：14x−2x=−6，合并同类项得：12x=−6，解得：x=−12；(2)x−1=13x+1，移项得：x−13x=1+1，合并同类项得：23x=2，解得：x=3；(3)4x−x=2(x−1)+5，去括号得：4x−x=2x−2+5，移项得：4x−x−2x=−2+5，合并同类项得：x=3；(4)6x−18=34+x，去分母得：6x−1=6+8x，移项得：6x−8x=6+1，合并得：−2x=7，解得：x=−72．【知识点】一元一次方程的解法【解析】(1)移项，合并同类项，系数化为1即可求解；(2)移项，合并同类项，系数化为1即可求解；(3)去括号，移项，合并同类项，系数化为1即可求解；(4)去分母，移项，合并同类项，系数化为1即可求解．本题考查了解一元一次方程，熟练掌握等式的性质是解题的关键．18.【答案】解：(5xy−8x3)−(−12x2+4xy)=5xy−8x3+12x2−4xy=xy−8x3+12x2，当x=12，y=2时，原式=12×2−8×(12)3+12×(12)2=1−8×18+12×14=1−1+3=3．【知识点】整式的加减【解析】根据去括号、合并同类项化简后再代入求值即可．本题考查整式的加减，掌握去括号、合并同类项法则是正确计算的前提．19.【答案】解：如图所示：【知识点】简单几何体的三视图【解析】由几何体可得从正面看有4列，每列小正方形数目分别为1，2，1，1；从左面看有2列，每列小正方形数目分别为2，1；从上面看有4列，每行小正方形数目分别为1，2，1，1，进而得出答案．本题考查作图−三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．∴CD=6，∴BD=BC+CD=3+6=9，∵点B为线段AD的中点，∴AD=2BD=18．【知识点】两点间的距离【解析】先由CD=2BC，BC=3，求得CD=6，进而得BD，再由点B为线段AD的中点，得AD．本题主要考查了线段的和差计算，线段的中点定义，关键是弄清各线段之间的关系，正确运用线段和差和线段中点，进行解答．21.【答案】解：(1)y=80+a(x−1)，当a=60时，y=80+60(x−1)=60x+20．(2)y=80+a(x−1)，当a=50，x=41时，y=80+50(41−1)=2080．【知识点】列代数式、代数式求值【解析】本题根据每增加一个半圆形护栏长度就增加a，列出代数式，代入值即可．本题考查了根据图形规律列出代数式，能够把数值代入代数式求值的能力．22.【答案】∠DCB；两直线平行，内错角相等；∠DCB；∠FCB；BE；FC；内错角相等，两直线平行；两直线平行，内错角相等【知识点】平行线的判定与性质【解析】证明：连接BC∵AB//CD(已知)∴∠ABC=∠DCB(两直线平行，内错角相等)∵∠1=∠2∴∠ABC−∠1=∠DCB−∠2∴∠EBC=∠FCB∴BE//FC(内错角相等，两直线平行)∴∠BEF=∠EFC(两直线平行，内错角相等)两直线平行，两直线平行，内错角相等．依据两直线平行，内错角相等，可得∠ABC =∠DCB ，进而得出∠EBC =∠FCB ，依据内错角相等，两直线平行，可得BE//FC ，进而得到∠BEF =∠EFC ．本题考查了平行线的判定与性质，熟记性质与判定方法是解题的关键，难点在于作辅助线．23.【答案】解：∵∠BON =20°，∴∠AOM =20°，∵OA 平分∠MOD ，∴∠AOD =∠MOA =20°，∵OC ⊥AB ，∴∠AOC =90°，∴∠COD =90°−20°=70°．【知识点】角的平分线、垂线的相关概念及表示【解析】利用对顶角相等可得∠AOM 的度数，再利用角平分线的定义和垂线定义进行计算即可．此题主要考查了垂线，关键是掌握对顶角相等，当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线． 24.【答案】2 1 −5−t 2t −3【知识点】列代数式、数轴、一元一次方程的应用【解析】解：(1)∵AC =10，BC =5，∴AC =2BC ，∴C 为AB 的2阶好点．故答案为：2．(2)∵AC =52，BC =52∴AC =BC ，∴C 为AB 的1阶好点．故答案为：1．(3)①M 表示的数为−5−t ，N 表示的数为2t −3，故答案为：−5−t ，2t −3；∴OM =2ON ，∴|−5−t|=2|2t −3|，即5+t =−4t +6或5+t =4t −6，解得：t =15或113；③∵MN 的1阶好点为P ，∴MP =NP ，即P 为MN 中点，∴P 表示的数为−5−t+2t−32=12t −4， 又∵Q 为MN 的3阶好点，设表示的数为m ，∴QM =3QN ，|m +t +5|=3|m −2t +3|，解得m =72t −2或54t −72，即|12t −4|=|72t −2|，解得t =32或−23(舍)，|12t 一4|=|54t −72|， 解得t =307或−23， 综上所述，P 、Q 到原点距离相等时t =32或307．(1)分别计算出AC 与BC 的长度，可得结论；(2)分别计算出AC 与BC 的长度，可得结论；(3)①根据两个点的运动速度和方向可得答案；②根据2阶好点的定义列方程可解决问题，注意分情况；③先用含t 的式子表示出P 和Q ，再列方程即可．考查了一元一次方程的应用，此题比较复杂，读题是难点，所以解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解． 25.【答案】135°【知识点】角的平分线【解析】解：∵∠EDF=90°，∴∠CDE+∠BDF=90°，∵DM为∠CDE的平分线，DN为∠BDF的平分线，∴∠MDE=12∠CDE，∠FDN=12∠BDF，∴∠CDM+∠BDF=12(∠CDE+∠BDF)=12×90°=45°，∴∠MDN=180°−45°=135°，故答案为135°．根据∠EDF=90°，可得出∠CDE+∠BDF=90°，再根据DM为∠CDE的平分线，DN为∠BDF的平分线，可得出∠CDM+∠BDF=45°，从而得出∠MDN的度数．本题考查了角平分线的定义，求得∠CDE+∠BDF=90°是解题的关键．26.【答案】3【知识点】两点间的距离【解析】解：设AC=y，CD=BD=12x，则AC+CD+DB+AD+AB+CB=23，即：y+12x+12x+(12x+y)+(x+y)+x=23，得：7x+6y=46，因为线段AC的长度与线段CB的长度都是正整数，所以可知x最大为6，可知：x=6，y为小数，不符合；x=5，y为小数，不符合；x=4，y=3，符合题意；x=3，y为小数，不符合；x=2，y为小数，不符合；x=1，y为小数，不符合．故答案为：3．可以设出AC和CD的长，再根据图中所有线段的长度之和为23，即可列出等式，再根据线段AC的长度与线段CB的长度都是正整数，即可求出答案．本题考查了两点间的距离，有一定难度，根据题意列出方程式，并探讨解的合理性是关键．27.【答案】1【知识点】有理数的混合运算【解析】解：(1)1△(−2)=|1−(−2)|+1+(−2)2=3+1−22=1，故答案为：1；(2)∵m△n=|m−n|+m+n2，n△m=|n−m|+n+m2．而|m−n|=|n−m|，∴m△n=n△m，因此交换m、n两数的位置，计算结果不会受到影响；(3)∵a1△a2=3，∴|a1−a2|+a1+a22=3，∴|a1−a2|+a1+a2=6，①当a1>a2时，|a1−a2|+a1+a2=6，即a1−a2+a1+a2=6，∴a1=3，又∵a1=|x|，∴x=3或x=−3，当x=−3时，a2=|x−1|=4>a1(舍去)，②当a1<a2时，|a1−a2|+a1+a2=6，即−a1+a2+a1+a2=6，∴a2=3，又∵a2=|x−1|，∴x=4或x=−2，当x=4时，a1=|x|=4>a2(舍去)，因此x=3或x=−2．(1)根据“新定义”的运算进行计算即可；(2)求出“m△n”和“n△m”的结果，比较得出结论；(3)求出a1、a2的值，再求出x的值即可．本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．28.【答案】4【知识点】四边形综合【解析】解：(1)①当∠FAB=∠CAB=45°时，点C落在AF上，∴∠EAB=∠FAB−∠FAE=5t=45°−30°=15°，∴t=3，当点C落在AE上时，∠EAB=∠CAB=5t=45°，解得t=9，∴3<t<9．②∠FGC与∠CHE度数的和不变，理由如下：∵CD//AB，∴∠FGC=∠FAB=∠FAE+∠EAB=30°+5t，∠EHC=∠AHB=90°−∠EAB=90°−5t，∴∠FGC+∠CHE=30°+5t+90°−5t=120°．③由②得∠CHE=90°−5t，∠FGC=30°+5t，当∠CHE=75∠FGC时，90°−5t=75(30°+5t)，解得t=4，故答案为：4．(2)∵∠ADC=90°，DP将∠ADC分成的两部分角度之比为1：2，∴∠ADP=13∠ADC=30°，∠CDP=23∠ADC=60°或∠ADP=23∠ADC=60°，∠CDP=13∠ADC=30°，设DP交AE于点M，∵DP//EF，∴∠DMA=∠E=90°，∴∠ADP=90°−∠DAM，又∵∠EAB=90°−∠DAM，∴∠ADP=∠EAB=5t，当5t=30°时，t=6，当5t=60°时，t=12，∴t=6或12．(1)①分别求出点C在AF与AE上的值．②用含t代数式分别表示出∠FGC与∠CHE，再表示出∠FGC与∠CHE度数的和．∠FGC求解．③用含t代数式表示∠CHE=75(2)由DP将∠ADC分成的两部分角度之比为1：2，求出∠ADP的度数为30°或60°，然后由含t代数式分别求解．本题考查动角问题，解题关键是熟练掌握平行线的性质并注意分类讨论．。
2019-2020学年吉林省长春市新区七年级(上)期末数学试卷
2019-2020学年吉林省长春市新区七年级（上）期末数学试卷一、单项选择题（每小题3分，共24分）1．（3分）5-的相反数是( )A ．5-B ．5C ．15D ．15- 2．（3分）长春市奥林匹克公园即将于2018年年底建成，它的总投资额约为2500000000元，2500000000这个数用科学记数法表示为( )A ．100.2510⨯B ．102.510⨯C ．92.510⨯D ．82510⨯3．（3分）如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是( )A ．B ．C ．D ．4．（3分）下列各项中的两项，为同类项的是( )A ．22x y -与2xyB ．2π与3y πC ．3mn 与4nm -D ．0.5ab -与abc5．（3分）海面上，灯塔位于一艘船的北偏东50︒，则这艘船位于灯塔的( )A ．南偏西50︒B ．南偏西40︒C ．北偏东50︒D ．北偏东40︒6．（3分）下列去括号错误的是( )A ．()a b c a b c -+=--B ．()a b c a b c +-=+-C ．2()2a b a b -=-D ．(2)2a b a b --=-+7．（3分）如图，直线AB 与直线CD 相交于点O ，OE AB ⊥，垂足为O ，30EOD ∠=︒，则(BOC ∠= )A ．150︒B ．140︒C ．130︒D ．120︒8．（3分）如图， 把一块含有45︒的直角三角形的两个顶点放在直尺的对边上 ． 如果120∠=︒，那么2∠的度数是( )A ．15︒B ．20︒C ．25︒D ．30︒二、填空题（每小题3分，共18分）9．（3分）两点整，时针与分针所成角的度数为 ．10．（3分）如图，要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为0，则2x y -= ．11．（3分）若单项式32n x y -与54m x y 合并后的结果还是单项式，则m n -= ．12．（3分）如图，在一条直线上有A ．B ．C ．D 四个点，则图中共有 条不同的线段．13．（3分）将多项式32293x xy x y -++-按x 的降幂排列为： ．14．（3分）由黑色和白色的正方形按一定规律组成的图形如图所示，从第二个图形开始，每个图形都比前一个图形多3个白色正方形，则第n 个图形中有白色正方形 个（用含n 的代数式表示）．三、解答题（本大题共10小题，共78分15．（6分）计算：22[18(3)2]4-+--⨯÷．16．（6分）计算：201834561234︒'+︒'-︒'．17．（6分）将直尺与三角尺按如图所示的方式叠放在一起．在图中标记的角中，写出所有与1∠互余的角．18．（7分）先化简，再求值：3223243(32)x x x x x x +---+，其中3x =-．19．（7分）如图，直线EF 分别与直线AB 、CD 交于M ，N 两点，155∠=︒，2125∠=︒，求证：//AB CD 【要求写出每一步的理论依据】．20．（7分）如图，在66⨯的正方形网格中，每个小正方形的边长均为1cm ，点A ，B ，C 均在格点上，画图并回答问题．（1）画射线AC ，画直线AB ．（2）过点C 画直线AB 的垂线，垂足为点D ．（3）点A 到直线BC 的距离为 cm ．21．（8分）如图，OB 平分COD ∠，90AOB ∠=︒，125AOC ∠=︒，求DOC ∠的度数．22．（9分）如图所示，线段12AB =，点C 是AB 上一点，7AC =，点M 是AB 的中点，点N 是BC 的中点，求线段CM 和MN 的长．23．（10分）感知与填空：如图①，直线//AB CD ．求证：B D BED ∠+∠=∠．阅读下面的解答过程，井填上适当的理由．解：过点E 作直线//EF CD2(D ∴∠=∠ )//AB CD （已知），//EF CD ， //(AB EF ∴ )1(B ∴∠=∠ )12BED ∠+∠=∠，(B D BED ∴∠+∠=∠ )应用与拓展：如图②，直线//AB CD ．若22B ∠=︒，35G ∠=︒，25D ∠=︒，则E F ∠+∠= 度．方法与实践：如图③，直线//AB CD ．若60E B ∠=∠=︒，80F ∠=︒，则D ∠= 度．24．（12分）如图，相距10千米的A 、B 两地间有一条笔直的马路，C 地位于A 、B 两地之间且距A 地4千米．小明同学骑自行车从A 地出发沿马路以每小时5千米的速度向B 地匀速运动，当到达B 地后立即以原来的速度返回，到达A 地停止运动．设运动时间为t （时)，小明的位置为点P ．（1）当0.5t =时，求点P 、C 间的距离．（2）当小明距离C 地1千米时，直接写出所有满足条件的t 值．（3）在整个运动过程中，求点P 与点A 的距离（用含t 的代数式表示）．。
2019-2020学年吉林大学附中七年级(上)期末数学试卷(解析版)
2019-2020学年吉林大学附中七年级（上）期末数学试卷一、选择题1、20181-的相反数是（ ） A 、20181-B 、2018-C 、20181D 、2018 2、下列四个几何体中，主视图与左视图相同的几何体有（ ）A 、1个B 、2个C 、3个D 、4个3、下列合并同类项的结果正确的是（ ）A 、233a a a =+B 、2-3=a aC 、ab b a 33=+D 、2222-3-a a a =4、下列调查中，适合采用普查方法的是（ ）A 、对全市中学生使用“小影”情况的调查B 、对东风渠河水质量情况的调查C 、对旅客上飞机前的安检D 、对某类烟花爆竹燃放安全情况的调查5、如图所示，能用1,,∠∠∠O AOB 三种方法表示同一个角的图形是（ ）6、在数轴上到原点距离等于2的点所表示的数是（ ）A 、2±B 、2C 、-2D 、不能确定7、下列数中，不可能是某月相邻的三个日期之和的是（ ）A 、24B 、43C 、57D 、698、若整式b a b a m n 3212+化简的结果是单项式，则n m +的值是（ ）A 、2B 、3C 、4D 、5二、填空题9．（3分）计算：|﹣3|﹣2＝ ．10．（3分）如图是一个计算程序，若输入a 的值为﹣2，则输出的结果应为 ．11．（3分）已知∠α与∠β互余，且∠α＝35°18′，则∠β＝°′．12．（3分）如图，C岛在A岛的北偏东45°方向，在B岛的北偏西25°方向，则∠ACB ＝°．13．（3分）如图，将一副直角三角板叠在一起，使直角顶点重合于点O，则∠AOB+∠DOC ＝度．14．（3分）龙龙做事很认真，每次大扫除都会把桌椅排的很整齐!他先把每一列最前和最后的课桌摆好，然后再一次摆中间的课桌，一会儿一列课桌摆在一条线上整整齐齐的，这是因为．15．（3分）设a﹣3b＝5，则2（a﹣3b）2+3b﹣a﹣15的值是．16．（3分）如图，已知O是直线AB上一点，∠1＝20°，OD平分∠BOC，则∠2的度数是度．17．（3分）如图是一个正方体的平面展开图，正方体中相对的面上的数字或代数式互为相反数，则2x+3y的值为．18．（3分）在同一平面内，两条直线相交时最多有1个交点，三条直线相交时最多有3个交点，四条直线相交时最多有6个交点，…，那么十条直线相交时最多有个交点．三、计算题19．（1）﹣（+9）﹣12﹣（）（2）4﹣2×（﹣3）2+6÷（﹣）（3）化简：5（a2+5a）﹣（a2+7a）（4）先化简，再求值：2（a2b+ab2）﹣3（a2b﹣1）﹣2ab2﹣4，其中a＝2018，b＝．四、解答题20．小区规划一个长70m、宽30m的长方形草坪上修建三条同样宽的甬道，使其中两条与AB平行，另一条与BC平行，场地其余部分种草，甬道的宽度为xm．（1）用含x的代数式表示草坪的总面积S；（2）如果每一块草坪的面积都相等，且甬道的宽为1m，那么每块草坪的面积是多少平方米？（精确到0.1）21．用5个棱长为1的正方体组成如图所示的几何体．（1）该几何体的体积是立方单位，表面积是平方单位（包括底面积）；（2）请在方格纸中用实线画出它的三个视图．22．如图，直线AB、CD相交于点O，OE平分∠BOD（1）若∠AOC＝60°，求∠BOE的度数；（2）若OF平分∠AOD，试说明OE⊥OF．23．如图，已知AC⊥AE，BD⊥BF，∠1＝15°，∠2＝15°，AE与BF平行吗？为什么？24．如图a是长方形纸带（提示：AD∥BC），将纸带沿EF折叠成图b，再沿GF折叠成图c．（1）若∠DEF＝20°，则图b中∠EGB＝，∠CFG＝；（2）若∠DEF＝20°，则图c中∠EFC＝；（3）若∠DEF＝α，把图c中∠EFC用α表示为；（4）若继续按EF折叠成图d，按此操作，最后一次折叠后恰好完全盖住∠EFG，整个过程共折叠了9次，问图a中∠DEF的度数是．25．如图，从数轴上的原点开始，先向左移动2cm到达A点，再向左移动4cm到达B点，然后向右移动10cm到达C点．（1）用1个单位长度表示1cm，请你在题中所给的数轴上表示层A、B、C三点的位置；（2）把点C到点A的距离记为CA，则CA＝cm；（3）若点B以每秒3cm的速度向左移动，同时A、C点以每秒lcm、5cm的速度向右移动，设移动时间为t（t＞0）秒，试探究CA﹣AB的值是否会随着t的变化而改变？请说明理由．26．【问题原型】如图①，AB∥CD，点M在直线AB、CD之间，则∠M＝∠B+∠D，小明解决上述问题的过程如下：如图②，过点M作MN∥AB则∠B＝（）∵AB∥CD，（已知）MN∥AB（辅助线的做法）∴MN∥CD（）∴∠＝∠D（）∴∠B+∠D＝∠BMD请完成小明上面的过程．【问题迁移】如图③，AB∥CD，点M与直线CD分别在AB的两侧，猜想∠M、∠B、∠D之间有怎样的数量关系，并加以说明．【推广应用】（1）如图④，AB∥CD，点M在直线AB、CD之间，∠ABM的平分线与∠CDM的平分线交于点N，∠M＝96°，则∠N＝°；（2）如图⑤，AB∥CD，点M与直线CD分别在AB的两侧，∠ABM的平分线与∠CDM 的平分线交于点N，∠N＝25°，则∠M＝°；（3）如图⑥，AB∥CD，∠ABG的平分线与∠CDE的平分线交于点M，∠G＝78°，∠F＝64°，∠E＝64°，则∠M＝°．2019-2020学年吉林大学附中七年级（上）期末数学试卷参考答案与试题解析一、选择题1．【解答】解：A、﹣2＜﹣1，故A正确；B、﹣1＝﹣1，故B错误；C、﹣＞﹣1，故C错误；D、1＞﹣1，故D错误；故选：A．2．【解答】解：A、不是正方体展开图，故选项错误；B、有田字格，不是正方体展开图，故选项错误；C、不是正方体展开图，故选项错误；D、1﹣4﹣1型，是正方体展开图，故选项正确．故选：D．3．【解答】解：11700000用科学记数法表示为1.17×107，故选：B．4．【解答】解：（A）原式＝x2﹣2xy2，故A错误；（B）原式＝2a﹣3b，故B错误；（C）原式＝a2+a3，故C错误；故选：D．5．【解答】解：如图1，由M是AB的中点，N是BC的中点，得MB＝AB＝4cm，BN＝BC＝1cm，由线段的和差，得MN＝MB+BN＝4+1＝5cm；如图2，由M是AB的中点，N是BC的中点，得MB＝AB＝4cm，BN＝BC＝1cm，由线段的和差，得MN＝MB﹣BN＝4﹣1＝3cm；故选：B．6．【解答】解：如图，∵直线a∥b，∴∠3＝∠1＝60°．∵AC⊥AB，∴∠3+∠2＝90°，∴∠2＝90°﹣∠3＝90°﹣60°＝30°，故选：D．7．【解答】解：设小长方形卡片的长为a，宽为b，∴L上面的阴影＝2（n﹣a+m﹣a），L下面的阴影＝2（m﹣2b+n﹣2b），∴L总的阴影＝L上面的阴影+L下面的阴影＝2（n﹣a+m﹣a）+2（m﹣2b+n﹣2b）＝4m+4n﹣4（a+2b），又∵a+2b＝m，∴4m+4n﹣4（a+2b），＝4n．故选：B．8．【解答】解：a0＝0，a1＝﹣|a0+1|＝﹣|0+1|＝﹣1，a2＝﹣|a1+2|＝﹣|﹣1+2|＝﹣1，a3＝﹣|a2+3|═﹣|﹣1+3|＝﹣2，a4＝﹣|a3+4|═﹣|﹣2+4|＝﹣2，a5＝﹣|a4+4|＝﹣|﹣2+5|＝﹣3；a6＝﹣|a5+4|＝﹣|﹣3+6|＝﹣3；a7＝﹣|a6+7|＝﹣|﹣3+7|＝﹣4……由此可以看出，这列数是0，﹣1，﹣1，﹣2，﹣2，﹣3，﹣3，﹣4，﹣4，……2019÷2＝1009…1，故a2019＝﹣1009﹣1＝﹣1010故选：B．二、填空题9．【解答】解：|﹣3|﹣2＝3﹣2＝1．10．【解答】解：由图可得，当a＝﹣2时，（a2﹣2）×（﹣3）+4＝[（﹣2）2﹣2]×（﹣3）+4＝（4﹣2）×（﹣3）+4＝2×（﹣3）+4＝（﹣6）+4＝﹣2，故答案为：﹣2．11．【解答】解“∠β＝90°﹣∠α＝90°﹣35°18′＝54°42′．12．【解答】解：连接AB．∵C岛在A岛的北偏东45°方向，在B岛的北偏25°方向，∴∠CAB+∠ABC＝180°﹣（45°+25°）＝110°，∵三角形内角和是180°，∴∠ACB＝180°﹣（∠CAB+∠ABC）＝180°﹣110°＝70°．故答案为：70．13．【解答】解：如右图所示，∵∠AOD+∠COD＝90°，∠COD+∠BOC＝90°，∠BOD＝∠COD+∠BOC，∠AOD+∠BOD＝∠AOB，∴∠AOD+∠COD+∠COD+∠BOC＝180°，∴∠AOD+2∠COD+∠BOC＝180°，∴∠AOB+∠COD＝180°．故答案是180．14．【解答】解：根据题意，最前与最后的课桌看做两点，排成一条直线，所以应用的是直线的性质：两点确定一条直线．故答案为：两点确定一条直线．15．【解答】解：∵3b﹣a＝﹣5，∴2（a﹣3b）2+3b﹣a﹣15＝2×52﹣5﹣15＝30．16．【解答】解：如图，∵∠1＝20°，∠1+∠BOC＝180°，∴∠BOC＝160°．又∵OD平分∠BOC，∴∠2＝∠BOC＝80°；故填：80．17．【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形．“5”与“2x﹣3”是相对面，“y”与“x”是相对面，“﹣2”与“2”是相对面，∵相对的面上的数字或代数式互为相反数，∴2x﹣3+5＝0，x+y＝0，解得x＝﹣1，y＝1，∴2x+3y＝﹣2+3＝1．故答案为：1．18．【解答】解：在同一平面内，两条直线相交时最多有1个交点，三条直线最多有3＝1+2个交点，四条直线最多有6＝1+2+3个交点，…，n条直线最多有1+2+3+4+…+（n﹣1）个交点，即1+2+3+4+…+（n﹣1）＝．当n＝10时，＝45故答案为：45三、计算题19．【解答】解：（1）原式＝﹣﹣21＝﹣21＝；（2）原式＝4﹣2×9﹣12＝4﹣18﹣12＝﹣14﹣12＝﹣26；（3）原式＝5a2+25a﹣a2﹣7a＝4a2﹣18a；（4）原式＝2a2b+2ab2﹣3a2b+3﹣2ab2﹣4＝﹣a2b﹣1，当a＝2018，b＝时，原式＝﹣20182×﹣1＝﹣2018﹣1＝﹣2019；四、解答题20．【解答】解：（1）S＝70×30﹣（70x+2×30x﹣2x2）＝2x2﹣130x+2100；（2）当x＝1时，S＝2×12﹣130×1+2100＝1972m2所以每一块草坪的面积为1972÷6＝328.6m2答：每一块草坪的面积是328.6m2．21．【解答】解：（1）几何体的体积：1×1×1×5＝5（立方单位），表面积：22（平方单位）；故答案为：5，22；（2）如图所示：22．【解答】解：（1）∵直线AB、CD相交于点O，∴∠BOD＝∠AOC＝60°，又∵OE平分∠BOD，∴∠BOE＝∠BOD＝30°；（2）∵OF平分∠AOD，∴∠DOF＝∠AOD，又∵OE平分∠BOD，∴∠DOE＝∠BOD，∴∠EOF＝∠DOF+∠DOE＝（∠AOD+∠BOD）＝×180°＝90°．∴OE⊥OF．23．【解答】解：AE∥BF．理由如下：因为AC⊥AE，BD⊥BF（已知），所以∠EAC＝∠FBD＝90°（垂直的定义）．因为∠1＝∠2（已知），所以∠EAC+∠1＝∠FBD+∠2（等式的性质），即∠EAB＝∠FBG，所以AE∥BF（同位角相等，两直线平行）．24．【解答】解：（1）∵长方形的对边是平行的，∴∠BFE＝∠DEF＝20°，∴∠EGB＝∠BFE+∠DEF＝40°，∴∠FGD＝∠EGB＝40°，∴∠CFG＝180°﹣∠FGD＝140°；故答案为：40°，140°；（2）∵长方形的对边是平行的，∴∠BFE＝∠DEF＝20°，∴图a、b中的∠CFE＝180°﹣∠BFE，以下每折叠一次，减少一个∠BFE，∴图c中的∠CFE度数是120°；故答案为：120°；（3）由（2）中的规律，可得∠CFE＝180°﹣3α．故答案为：180°﹣3α；（3）设图a中∠DEF的度数是x°，由（2）中的规律，可得180﹣10x＝0．解得：x＝18．故答案为：18°．25．【解答】解：（1）如图所示：（2）CA＝4﹣（﹣2）＝4+2＝6（cm）；故答案为：6．（3）CA﹣AB的值不会随着t的变化而变化，理由如下：根据题意得：CA＝（4+5t）﹣（﹣2+t）＝6+4t，AB＝（﹣2+t）﹣（﹣6﹣3t）＝4+4t，∴CA﹣AB＝（6+4t）﹣（4+4t）＝2，∴CA﹣AB的值不会随着t的变化而变化．26．【解答】解：【问题原型】如图①，过点M作MN∥AB，则∠B＝∠BMN（两直线平行，内错角相等）∵AB∥CD，（已知）∴MN∥AB（辅助线的做法）∴MN∥CD（平行于同一条直线的两直线平行）∴∠NMD＝∠D（两直线平行，内错角相等）∴∠B+∠D＝∠BMD，故答案为：∠BMN，两直线平行，内错角相等，平行于同一条直线的两直线平行，∠NMD，两直线平行，内错角相等，【问题迁移】过点M作MN∥AB，∴∠1＝∠B，∵AB∥CD，∴MN∥AB，∴∠NMD＝∠D，∵∠NMD＝∠1+∠BMD，∴∠BMD＝∠D﹣∠B；【推广应用】如图④，由如图①的结论可得，∠ABM+∠CDM＝∠M＝96°，∠N＝∠ABN+∠CDN，∵BN，DN分别平分∠ABM，∠CDM，∴∠ABN+∠CDN＝＝（∠ABM+∠CDM）＝48°，∴∠N＝48°；如图⑤，由如图②的结论可得，∠M＝∠CDM﹣∠ABM，∵BN，DN分别平分∠ABM，∠CDM，∴∠CDN﹣∠ABN＝∠CDM﹣∠ABM＝（∠CDM﹣∠ABM）＝M＝∠N＝25°，∴∠M＝50°；如图⑥，过G，F，E分别作GN∥AB，FH∥AB，EP∥AB，∵AB∥CD，∴AB∥GN∥FH∥EP∥CD，∴∠2＝∠GFH，∠3＝∠EFH，∴∠2+∠3＝∠GFE＝64°，∴∠1+∠4＝∠BGF+∠DEF﹣∠GFE＝78°，∵AB∥GN，EP∥CD，∴∠ABG＝∠1，∠CDE＝∠4，∴∠ABG+∠CDE＝78°，∵BM，DM分别平分∠ABG，∠CDE，∴∠ABM＝∠ABG，∠CDM＝∠CDE，由如图①中的结论可得∠M＝∠ABM+∠CDM＝（∠ABG+∠CDE）＝78°＝39°，故答案为：48，50，39．。
2019-2020学年吉林省长春市七年级上册期末数学测试卷
2019-2020学年吉林省长春市七年级上册期末数学试卷题号一二三四总分得分第I卷（选择题）一、选择题（本大题共8小题，共16.0分）1.在数轴上，到原点距离是8的点表示的数是()A. 8和−8B. 0和−8C. 0和8D. −4和42.下图是正方体的表面展开图，则与“前”字相对的字是()A. 认B. 真C. 复D. 习3.将591000000用科学记数法表示应为()A. 0.591×109B. 59.1×107C. 5.91×108D. 5.91×1074.在矩形纸片ABCD中，AB=3cm，BC=4cm，现将纸片折叠压平，使A与C重合，如果设折痕为EF，那么重叠部分△AEF的面积等于()A. 738B. 758C. 7316D. 75165.如图，从一艘船上测得一个灯塔的方向是北偏西47°，那么这艘船在这个灯塔的()A. 南偏东47°B. 南偏东43°C. 南偏西47°D. 南偏西43°6.−(−a+b−1)去括号结果正确的是()A. −a+b−1B. a−b+1C. −a+b+1D. a+b+17.如图，已知直线a、b被直线c所截，下列说法不正确的是()A. ∠1与∠5是同位角B. ∠1与∠3是内错角C. ∠2与∠3是同旁内角D. ∠4是∠5的补角8.如图，A是直线l外一点，过点A作AB⊥l于点B，在直线l上取一点C，连结AC，使AC=2AB，P在线段BC上，连结AP.若AB=3，则线段AP的长不可能是()A. 4B. 5C. 2D. 5.5第II卷（非选择题）二、填空题（本大题共7小题，共21.0分）9.计算：13×(−6)=_________．10.已知多项式2x2+25x3+x−5x4−13把这个多项式按x的降幂重新排列_______________．11.计算：20°45′=________°；50.8°=________°________′；15°35′+31°45′=________．12.若x m−1y3与2xy n的和仍是单项式，则(m−n)2018的值等于______．13.如图，一副三角尺有公共的顶点O，若∠BOD=40°，则∠AOC=______．14.如图，点M是线段AB的中点，AC：CB=1：2，CM=2.则AB=______．15.如图，每个图形均由边长相等的黑、白两色正方形按规律拼接而成，照此规律，第n个图形中白色正方形比黑色正方形多________个．(用含n的代数式表示)三、计算题（本大题共2小题，共17.0分）16.计算(1)−22+3×(−1)4−9÷(−3)；(2)(12+56−712)÷(−136)17.计算：①5a−(2a−4b)；②(3a2−b2)−3(a2−2b2)四、解答题（本大题共7小题，共46.0分）18.如图，若l1//l2，l3//l4，求出图中所有与∠1互补的角．19.如图所示，火车站，码头分别位于A、B两点，直线a和b分别表示铁路与河流。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019-2020学年吉林省长春市南关区东北师大附中明珠学校七年级（上）期末数学试卷一．选择题（共8小题）1．﹣3的相反数是（）A．B．﹣3 C．D．32．2018年10月24日上午9时港珠澳大桥正式通车，它是东亚建设的跨海大桥，连接香港大屿山、澳门半岛和广东省珠海市，整个大桥造价超过720亿元人民币，将72000000000用科学记数法表示为（）A．7.2×1011B．7.2×1010C．0.72×1011D．72×1093．计算﹣a3+2a3的结果为（）A．a3B．﹣a3C．3a3D．﹣3a34．下列方程中为一元一次方程的是（）A．2x+3＝0 B．2x+y＝3 C．x2+x＝3 D．x﹣＝35．下列判断正确的是（）A．单项式a的次数是0B．单项式﹣2a2bc的系数是2C．单项式﹣xy2z的次数是2D．多项式3xy3+5x2﹣8是四次三项式6．下列四个算式：①﹣2﹣3＝﹣1；②2﹣|﹣3|＝﹣1；③（﹣2）3＝﹣6；④﹣2÷＝﹣6．其中，正确的算式有（）A．0个B．1个C．2个D．3个7．下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）A．B．C．D．8．如图，直线AB、CD相交于点O，OE平分∠BOC，∠FOD＝90°，若∠BOD：∠BOE＝1：2，则∠AOF的度数为（）A．70°B．75°C．60°D．54°二．填空题（共6小题）9．把多项式2m2﹣4m4+2m﹣1按m的升幂排列．10．长春市奥林匹克公园于2018年年底建成，它的总占地面积约为528000平方米，528000这个数字用科学记数法表示为．11．如图，∠AOB＝72°32′，射线OC在∠AOB内，∠BOC＝30°40′，则∠AOC＝．12．今年十一小长假期间，迟老师一家三口开着一辆轿车去长春市净月潭森林公园度假，若门票每人a元，进入园区的轿车每辆收费40元，则迟老师一家开车进入净月潭森林公园园区所需费用是元（用含a的代数式表示）．13．如图，能与∠1构成同位角的角有个．14．如图，在三角形ABC中，AB⊥AC于点A，AB＝6，AC＝8，BC＝10，点P是线段BC上的一点，则线段AP的最小值为．三．解答题（共10小题）15．计算：（1）（+﹣）×（﹣48）（2）（﹣5）3×（﹣）+32÷（﹣2）2×16．计算：（1）3x+2（x﹣）﹣（x+1）（2）5（2a2b﹣ab2）﹣（6a2b﹣3ab2）17．解下列一元一次方程：（1）4x+7＝32﹣x（2）8x﹣3（3x+2）＝1（3）2（y﹣）＝（3y﹣2）（4）﹣＝118．先化前，再求值：2（a2+2a﹣1）﹣3（a2﹣2a﹣3），其中a＝﹣2．19．如图，点P是∠AOB的边OB上的一点，点M是∠AOB内部的一点，按下述要求画图，并回答问题：（1）过点M画OA的平行线MN；（2）过点P画OB的垂线PC，交OA于点C；（3）点C到直线OB的距离是线段的长度．20．如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG相交于点H，∠C＝∠EFG，∠BFG＝∠AEM，求证：AB∥CD．（完成下列填空）证明：∵∠BFG＝∠AEM（已知）且∠AEM＝∠BEC（）∴∠BEC＝∠BFG（等量代换）∴MC∥（）∴∠C＝∠FGD（）∵∠C＝∠EFG（已知）∴∠＝∠EFG，（等量代换）∴AB∥CD（）21．如图已知点C为AB上一点，AC＝12cm，CB＝AC，D、E分别为AC、AB的中点，求DE的长．22．如图，已知∠ABC+∠ECB＝180°，∠P＝∠Q．求证：∠1＝∠2．23．如图，直线AB、CD相交于点O，OF平分∠AOE，OF⊥CD，垂足为O．（1）写出图中所有与∠AOD互补的角；（2）若∠AOE＝110°，求∠BOD的度数．24．感知：如图①，若AB∥CD，点P在AB、CD内部，则∠P、∠A、∠C满足的数量关系是．探究：如图②，若AB∥CD，点P在AB、CD外部，则∠APC、∠A、∠C满足的数量关系是．请补全以下证明过程：证明：如图③，过点P作PQ∥AB∴∠A＝∵AB∥CD，PQ∥AB∴∥CD∴∠C＝∠∵∠APC＝∠﹣∠∴∠APC＝应用：（1）如图④，为北斗七星的位置图，如图⑤，将北斗七星分别标为A、B、C、D、E、F、G，其中B、C、D三点在一条直线上，AB∥EF，则∠B、∠D、∠E满足的数量关系是．（2）如图⑥，在（1）问的条件下，延长AB到点M，延长FE到点N，过点B和点E分别作射线BP和EP，交于点P，使得BD平分∠MBP，EN平分∠DEP，若∠MBD＝25°，则∠D﹣∠P ＝°．2019-2020学年吉林省长春市南关区东北师大附中明珠学校七年级（上）期末数学试卷参考答案与试题解析一．选择题（共8小题）1．【分析】根据负数的绝对值是它的相反数是，可得答案．【解答】解：﹣5的绝对值是5．故选：A．【点评】本题考查了绝对值，利用了绝对值的性质是解题关键．2．【分析】根据实数的大小比较解答即可．【解答】解：由数轴可得：a＜b＜c＜d，故选：D．【点评】此题利用数轴比较大小，在数轴上右边的点表示的数总是大于左边的点表示的数．3．【分析】根据题目中的几何图形，可以得到它的主视图，从而可以解答本题．【解答】解：由两个小正方体和一个圆锥组成的几何体，它的主视图是，故选：B．【点评】本题考查简单组合的三视图，解答本题的关键是明确题意，画出相应的图形．4．【分析】根据单项式和多项式的有关概念逐一求解可得．【解答】解：A．﹣的系数是﹣，此选项错误；B．x2+x﹣1的常数项为﹣1，此选项错误；C．22ab3的次数是4次，此选项错误；D．2x﹣5x2+7是二次三项式，此选项正确；故选：D．【点评】本题考查多项式的知识，几个单项式的和叫做多项式，每个单项式叫做多项式的项，其中不含字母的项叫做常数项．单项式的个数就是多项式的项数，如果一个多项式含有a个单项式，次数是b，那么这个多项式就叫b次a项式．5．【分析】根据三棱柱的展开图的特点进行解答即可．【解答】A、是三棱锥的展开图，故选项错误；B、是三棱柱的平面展开图，故选项正确；C、两底有4个三角形，不是三棱锥的展开图，故选项错误；D、是四棱锥的展开图，故选项错误．故选：B．【点评】此题主要考查了几何体展开图，熟练掌握常见立体图形的平面展开图的特征，是解决此类问题的关键．6．【分析】根据等式的性质，依次分析各个选项，选出等式不一定成立的选项即可．【解答】解：A.3a＝2b+5，等式两边同时减去5得：3a﹣5＝2b，即A项正确，B.3a＝2b+5，等式两边同时加上1得：3a+1＝2b+6，即B项正确，C.3a＝2b+5，等式两边同时乘以c得：3ac＝2bc+5c，即C项错误，D.3a＝2b+5，等式两边同时除以3得：a＝+，即D项正确，故选：C．【点评】本题考查了等式的性质，正确掌握等式的性质是解题的关键．7．【分析】根据角的表示方法和图形选出即可．【解答】解：A、图中的∠AOB不能用∠O表示，故本选项错误；B、图中的∠1和∠AOB不是表示同一个角，故本选项错误；C、图中的∠1和∠AOB不是表示同一个角，故本选项错误；D、图中∠1、∠AOB、∠O表示同一个角，故本选项正确；故选：D．【点评】本题考查了角的表示方法的应用，主要考查学生的理解能力和观察图形的能力．8．【分析】根据角平分线的定义和邻补角的性质计算即可．【解答】解：∵∠BOD：∠BOE＝1：2，OE平分∠BOC，∴∠BOD：∠BOE：∠EOC＝1：2：2，∴∠BOD＝36°，∴∠AOC＝36°，又∵∠COF＝∠DOF＝90°，∴∠AOF＝90°﹣36°＝54°．故选：D．【点评】本题考查的是对顶角、邻补角的性质以及角平分线的定义，掌握对顶角相等、邻补角之和等于180°是解题的关键．二．填空题（共6小题）9．【分析】先分清多项式的各项，然后按多项式升幂排列的定义排列．【解答】解：多项式2m2﹣4m4+2m﹣1按m的升幂排列为﹣1+2m+2m2﹣4m4，故答案为：﹣1+2m+2m2﹣4m4．【点评】本题考查多项式，我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列，称为按这个字母的降幂或升幂排列．要注意，在排列多项式各项时，要保持其原有的符号．10．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：528000＝5.28×105，故答案为：5.28×105．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．11．【分析】根据图形进行角的计算即可【解答】解：∠AOC＝∠AOB﹣∠BOC＝72°32′﹣30°40′＝41°52′，故答案为：41°52′．【点评】本题考查的是角的计算，掌握度、分的转化是解本题的关键．12．【分析】根据题意得：每辆车的收费与每个人门票之和列出代数式即可．【解答】解：根据题意得：（40+3a），故答案为：（40+3a）【点评】此题考查了列代数式，弄清题意是解本题的关键．13．【分析】两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．依此求解即可．【解答】解：由同位角的定义知，能与∠1构成同位角的角有∠2、∠3共2个．故答案为2【点评】本题考查了同位角、内错角、同旁内角．三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．14．【分析】根据三角形的面积公式即可得到结论．【解答】解：∵AB⊥AC，∴∠BAC＝90°，当AP⊥BC时，AP的值最短，∴AP＝＝＝，∴线段AP的最小值为，故答案为：．【点评】本题考查了垂线段最短，三角形的面积，熟练掌握勾股定理的逆定理即可得到结论．三．解答题（共10小题）15．【分析】（1）根据乘法分配律简便计算；（2）先算乘方，再算乘除，最后算加法；同级运算，应按从左到右的顺序进行计算．【解答】解：（1）（+﹣）×（﹣48）＝×（﹣48）+×（﹣48）﹣×（﹣48）＝﹣40﹣42+46＝﹣36；（2）（﹣5）3×（﹣）+32÷（﹣2）2×＝（﹣125）×（﹣）+32÷4×＝75+8×＝75﹣10＝65．【点评】考查了有理数的混合运算，有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化．16．【分析】（1）直接去括号，进而合并同类项得出答案；（2）直接去括号，进而合并同类项得出答案．【解答】解：（1）3x+2（x﹣）﹣（x+1）＝3x+2x﹣1﹣x﹣1＝4x﹣2；（2）5（2a2b﹣ab2）﹣（6a2b﹣3ab2）＝10a2b﹣2ab2﹣4a2b+2ab2＝6a2b．【点评】此题主要考查了整式的加减运算，正确合并同类项是解题关键．17．【分析】（1）依次移项、合并同类项、系数化为1可得；（2）依次去括号、移项、合并同类项、系数化为1可得；（3）依次去括号、移项、合并同类项、系数化为1可得；（4）依次去分母、去括号、移项、合并同类项、系数化为1可得．【解答】解：（1）4x+7＝32﹣x，4x+x＝32﹣7，5x＝﹣25，x＝﹣5；（2）8x﹣9x﹣6＝1，8x﹣9x＝1+6，﹣x＝7，x＝﹣7；（3）2y﹣3＝y﹣4，2y﹣y＝﹣4+3，﹣y＝﹣1，y＝2．（4）3（5y﹣1）﹣4（2y+6）＝12，15y﹣3﹣8y﹣24＝12，15y﹣8y＝12+3+24，7y＝39，y＝．【点评】本题主要考查解一元一次方程，去分母、去括号、移项、合并同类项、系数化为1，这仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向x ＝a形式转化．18．【分析】根据整式的运算法则即可求出答案．【解答】解：原式＝2a2+4a﹣2﹣3a2+6a+9＝﹣a2+10a+7，当a＝﹣2时，原式＝﹣4﹣20+7＝﹣24+7＝﹣17．【点评】本题考查整式的运算，解题的关键是熟练运用整式的运算法则，本题属于基础题型．19．【分析】（1）根据平行线的判定画图，（2）根据垂线的定义画图，（3）根据点到直线的距离即可解决问题．【解答】解：（1）如图所示：（2）如图所示：（3）点C到直线OB的距离是线段PC的长度；故答案为：PC．【点评】本题考查作图﹣复杂作图，垂线，点到直线距离，平行线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．20．【分析】根据同位角相等两直线平行，可证MC∥GF，进而利用平行线的性质和判定证明．【解答】证明：∵∠BFG＝∠AEM（已知）且∠AEM＝∠BEC（对顶角相等）∴∠BEC＝∠BFG（等量代换）∴MC∥GF（同位角相等，两直线平行）∴∠C＝∠FGD（两直线平行，同位角相等）∵∠C＝∠EFG（已知）∴∠FGD＝∠EFG，（等量代换）∴AB∥CD（内错角相等，两直线平行）．故答案是：对顶角相等；GF；同位角相等，两直线平行；FGD；内错角相等，两直线平行．【点评】考查了平行线的判定与性质，解答此题的关键是注意平行线的性质和判定定理的综合运用．21．【分析】求DE的长度，即求出AD和AE的长度．因为D、E分别为AC、AB的中点，故DE ＝，又AC＝12cm，CB＝AC，可求出CB，即可求出CB，代入上述代数式，即可求出DE的长度．【解答】解：根据题意，AC＝12cm，CB＝AC，所以CB＝8cm，所以AB＝AC+CB＝20cm，又D、E分别为AC、AB的中点，所以DE＝AE﹣AD＝（AB﹣AC）＝4cm．即DE＝4cm．故答案为4cm．【点评】此题要求学生灵活运用线段的和、差、倍、分之间的数量关系，熟练掌握．22．【分析】先判定AB∥CD，则∠ABC＝∠BCD，再由∠P＝∠Q，则∠PBC＝∠QCB，从而得出【解答】证明：∵∠ABC+∠ECB＝180°，∴AB∥DE，∴∠ABC＝∠BCD，∵∠P＝∠Q，∴PB∥CQ，∴∠PBC＝∠BCQ，∵∠1＝∠ABC﹣∠PBC，∠2＝∠BCD﹣∠BCQ，∴∠1＝∠2．【点评】本题考查了平行线的判定和性质，解答此题的关键是注意平行线的性质和判定定理的综合运用．23．【分析】（1）根据邻补角的性质可知，与∠AOD互补的角：∠BOD与∠AOC；（2）先求出∠BOE的度数，然后根据OF平分∠AOE求出∠FOE，再根据OF⊥CD，可知∠FOD ＝90°，求出∠EOD，最后得出∠BOD＝∠BOE﹣∠EOD求出答案．【解答】解：（1）与∠AOD互补的角：∠BOD与∠AOC；（2）∵∠AOE＝110°，∴∠BOE＝180°﹣∠AOE＝180°﹣110°＝70°，∵OF平分∠AOE，∴∠FOE＝∠AOE＝，∵OF⊥CD，∴∠FOD＝90°，∴∠EOD＝∠FOD﹣∠FOE＝90°﹣55°＝35°，∴∠BOD＝∠BOE﹣∠EOD＝70°﹣35°＝35°．【点评】本题考查了补角以及角平分线的性质．正确运用补角的定义和角平分线性质是解题的关键．24．【分析】作平行线利用平行线的性质与角平分线的性质通过角等量关系转化解题即可．【解答】解：感知：如图①，过点P作PQ∥AB∴∠A＝∠APQ，∵AB∥CD，PQ∥AB∴∠C＝∠QPC，∴∠APQ+∠QPC＝∠A+∠C，∠APC＝∠A+∠C．故答案为∠P＝∠A+∠C；探究：证明：如图③，过点P作PQ∥AB∴∠A＝∠APQ∵AB∥CD，PQ∥AB∴PQ∥CD∴∠C＝∠CPQ∵∠APC＝∠APQ﹣∠CPQ∴∠APC＝∠A﹣∠C．故答案为：∠APC＝∠A﹣∠C，∠APQ，PQ，∠CPQ，∠APQ，∠CPQ，∠A﹣∠C．应用：（1）如图⑤，过点D作DH∥EF，∴∠HDE＝∠E，∵AB∥EF，DH∥EF∴AB∥DH，∴∠B+∠BDH＝180°，即∠BDH＝180°﹣∠B，∴∠HDE+∠BDH＝∠E+180°﹣∠B，即∠BDE+∠B﹣∠E＝180°，故答案为∠D+∠B﹣∠E＝180°，（2）如图⑥，过点P作PH∥EF，∴∠EPH＝∠NEP，∵AB∥EF，PH∥EF，∴AB∥PH，∴∠MBP+∠BPH＝180°，∵BD平分∠MBP，∠MBD＝25°，∠MBP＝2∠MBD＝2×25°＝50°，∠BPH＝180°﹣50°＝130°，∵EN平分∠DEP，∴∠NEP＝∠DEN∴∠BPE＝∠BPH﹣∠EPH＝∠BPH﹣∠NEP＝∠BPH﹣∠DEN＝130°﹣（180°﹣∠DEF）＝∠DEF﹣50°由①∠D+∠ABD﹣∠DEF＝180°，∵∠MBD＝25°，∴∠ABD＝155°，∴∠D+∠155°﹣∠DEF＝180°，∴∠DEF＝∠D﹣25°∴∠BPE＝∠DEF﹣50°＝∠D﹣25°﹣50°＝∠D﹣75°∠D﹣∠BPE＝75°即∠D﹣∠P＝75°，故答案75．【点评】本题考查了角平分线的性质与平行线的性质，正确运用角平分线与平行线的性质是解题的关键．。