吉林省长春市东北师大附中明珠学校2020-2021学年第一学期九年级第一次月考语文试题
2024-2025学年吉林省长春市南关区东北师大附中明珠学校九年级(上)期初数学试卷+答案解析

2024-2025学年吉林省长春市南关区东北师大附中明珠学校九年级(上)期初数学试卷一、选择题:本题共8小题,每小题3分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.在平面直角坐标系中,若点A坐标为,且,则点A所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限2.人体内一种细胞的直径约为,数据用科学记数法表示为()A. B. C. D.3.如图,,,,,则EF的长为()A.5B.C.D.4.已知一次函数的图象如图所示,则m、n的取值范围是()A.,B.,C.,D.,5.已知点,是反比例函数图象上的两点,若,则有()A. B. C. D.6.根据图象,可得关于x的不等式的解集是()A. B. C. D.7.如图,在▱ABCD中,F是AD上一点,CF交BD于点E,CF的延长线交BA的延长线于点G,,则下列结论错误的是()A.B.C.D.8.如图,在平面直角坐标系中,点A在反比例函数的图象上,过点A作轴,与反比例函数的图象交于点B,点C为y轴上一点,连结AC、BC,若的面积为4,则k的值为()A. B. C. D.二、填空题:本题共6小题,每小题3分,共18分。
9.若分式有意义,则实数x的取值范围是______.10.关于x的一元二次方程没有实数根是常数,则c的取值范围是______.11.若点与点关于y轴对称,则______.12.如图,线段CD两个端点的坐标分别为、,以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为,则点A的坐标为______.13.如图,已知,CD和BE相交于点O,::25,则______.14.如图,在平面直角坐标系中,矩形ABCD的边AB在x轴正半轴上,点A在点B的左侧,直线经过点和点P,且,将直线沿y轴向下平移得到,若点P落在矩形ABCD的内部不含边界,则b的取值范围是______.三、解答题:本题共10小题,共78分。
解答应写出文字说明,证明过程或演算步骤。
吉林省长春市东北师大附中明珠学校2024-2025学年九年级上学期期中化学测试卷

初三年级综合练习化学学科试卷时长: 40 分钟分值: 50分可能用到的相对原子质量: H-1, C-12, N-14, O-16, S-32, Fe-56一、选择题:每小题1分,共10分1. 被誉为“古代中国的百科全书”的《齐民要术》是世界上最早记录食品酿造的典籍。
下列酿酒过程中一定发生化学变化的是A. 粮食粉碎B. 小麦发酵C. 清液过滤D. 酒水蒸馏2. 空气是人类赖以生活的重要资源,空气的质量影响我们的健康,下列物质中没有被计入空气污染物的是A. 二氧化碳B. 二氧化氮C. 二氧化硫D. 臭氧3. 将铜片放入稀硝酸(HNO₃) 中会生成硝酸铜[ Cu(NO₃)₂]、水和--种气体化合物,则该气体可能是A. SO₂B. H₂C. NOD. CO4.化学是以实验为基础的学科,下列实验操作正确的是A.加热液体B.过液C.验证质量守恒定律D.取少虽液体试剂5. 下列事实的微观解释中,不正确的是A. 墙内开花墙外可闻到花香----分子在不断地运动B. 蔗糖放入水中溶解——蔗糖分子变小了C. 氧气和液氧都能支持燃烧——构成物质的分子相同,物质的化学性质相同D. 水壶中的水烧开沸腾后,壶盖被顶起——冰分子间的间隔增大6. 豆腐是人们喜爱的食物,营养丰富,能为人体提供所需要的多种氨基酸,其中含量最多是亮氨酸(化学式为C₆H₁₃NO₂),下列关于亮氨酸的说法错误的是A. 亮氨酸由碳元素、氢元素、氮元素和氧元素组成B. 亮氨酸中碳原子、氢原子、氮原子和氧原子的原子个数比为6:13:1:2C. 亮氨酸属于化合物D. 亮氨酸由6个碳原子、13个氢原子、1个氮原子和2个氧原子构成7. 科学思维是化学核心素养的重要组成部分。
下列说法正确的是A. 分类:双氧水、冰水共存物、澄清石灰水均属于混合物B. 比较; O₂和2O中都有O和2,则O₂和2O表示的意义完全一样C. 分析:试管加热时发生炸裂,可能是没有预热或试管底部触及灯芯D. 推理:氢原子的最外层电子数为1(少于4个)。
2020年吉林省长春市东北师大附中明珠校区九年级(上)第一次月考物理试卷

九年级(上)第一次月考物理试卷得分1.在国际单位制中,电压的单位是()A. 安培B. 伏特C. 瓦特D. 焦耳2.如图所示的物品中,通常情况下属于导体的是()A. 陶瓷B. 不锈钢锅C. 玻璃杯D. 木铲3.一个验电器的两个金属箔片因带电而张开,则这两个金属箔片一定()A. 带正电B. 带负电C. 带同种电荷D. 带异种电荷4.下列实例中与“水的比热容较大”这一特性无关的是()A. 让热水流过散热器供暖B. 用循环水冷却汽车发动机C. 沿海地区昼夜温差较小D. 夏天在房间内洒水降温5.如图所示电路中,开关能够同时控制两盏灯,且两灯发光情况互不影响的电路是()A. B.C. D.6.用电压表测灯L1两端的电压,如图所示四个电路图中,正确的是()A. B.C. D.7.下列关于四冲程内燃机的说法中正确的是()A. 热机效率越高,所做的有用功就越多B. 汽油机在吸气冲程中吸入气缸的是空气C. 一个工作循环对外做功一次D. 压缩冲程中将内能转化为机械能8.在如图所示的电路中,正确的说法是()A. 闭合S1,断开S2,L1发光,L2不发光B. 闭合S1,S2,L1,L2都发光C. S1,S2都断开,L1,L2都不发光D. 闭合S2,断开S1,L1,L2都发光9.“光控开关”在光线暗时自动闭合,光线亮时自动断开;“声控开关”在有声音时自动闭合,一段时间后,若再无声音则自动断开。
下图中能让电灯要么一直熄灭,要么一直亮,要么在光线较暗且有声音时才亮的电路是()A. B.C. D.10.如图开关由闭合到断开,电流表A1、A2的示数I1、I2的变化()A. I1变小,I2变大B. I1不变,I2变大C. I1变大,I2变小D. I1不变,I2变小11.榴莲因其果肉香甜又富有营养,被称为水果之王。
榴莲被切开后,其臭味将很快充满整个房间,这是______现象,该现象主要说明______。
12.电扇使用一段时间后,扇叶很容易粘上灰尘,这是因为扇叶转动过程中带上了______,具有______的性质,所以灰尘被吸在扇叶上。
2021学年吉林省长春市南关区东北师大附中明珠校区九年级(上)第一次月考物理试卷(附答案详解)

2020-2021学年吉林省长春市南关区东北师大附中明珠校区九年级(上)第一次月考物理试卷1.电流这一物理量的国际单位是()A. 安培B. 牛顿C. 伏特D. 瓦特2.下列物品中,通常情况下属于导体的是()A. 玻璃杯B. 不锈钢锅C. 陶瓷碗D. 干木棒3.一个验电器的两个金属箔片因带电而张开,则这两个金属箔片一定()A. 带正电B. 带负电C. 带同种电荷D. 带异种电荷4.如图所示,电源电压是6伏,电压表的示数为2.4伏,则()A. L1两端的电压是2.4伏B. L2两端的电压是2.4伏C. L2两端电压为3.6伏D. L1和L2电压的总和是2.4伏5.如图所示的电路中a、b是电表,闭合开关要使电灯发光,则()A. a、b都是电流表B. a、b都是电压表C. a是电流表,b是电压表D. a是电压表,b是电流表6.关于温度、热量和内能,下列说法正确的是()A. 0℃的物体也具有内能B. 只要物体放出热量,温度就一定降低C. 物体温度越高,含有的热量越多D. 热量总是从内能大的物体传递给内能小的物体7.将两个灯泡L1和L2接到同一电路中,闭合开关,两灯均发光,则下列说法中可以确认两灯并联的是()A. 两灯两端的电压不相等B. 两灯两端的电压相等C. 通过两灯的电流相等D. 通过两灯的电流不相等8.某种电子测温枪靠近被测者额头,闭合测温开关S1,只有热敏电阻R工作。
测温枪的显示屏显示被测者温度;在环境光线较暗看不清示数时,再闭合开关S2,显示屏补光灯泡L发光;在测温开关S1断开时,闭合开关S2,灯泡L不发光。
关于热敏电阻R与补光灯泡L在电路中的连接方式,下列的电路符合要求的是()A. B.C. D.9.如图所示,是小普同学跟爷爷学习气功的四个基本动作,由此他联想到热机的四个冲程,以下与做功冲程最相似的是()A. 鼻孔吸气B. 气沉丹田C. 排山倒海D. 打完收工10.如图所示,开关由闭合到断开,电流表A1、A2的示数I1、I2的变化()A. I1变小,I2变大B. I1不变,I2变大C. I1变大,I2变小D. I1不变,I2变小11.一节新干电池的电压为______V;我国家庭电路的电压为______V,这个电压对人体来说是______的(选填“安全”或“不安全”)。
吉林省长春市东北师大附中明珠学校2020-2021学年九年级第一次月考数学试题
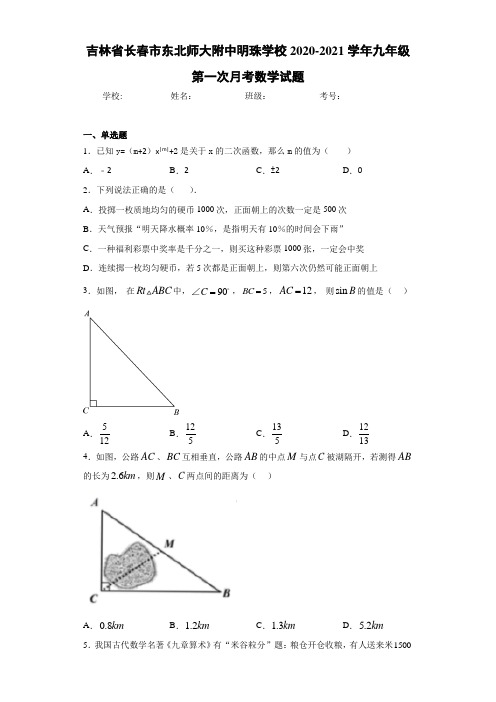
4.如图,公路 、 互相垂直,公路 的中点 与点 被湖隔开,若测得 的长为 ,则 、 两点间的距离为()
A. B. C. D.
5.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米 石,验得米内夹谷,抽样取米一把,数得 粒内夹谷 粒,则这批米内夹谷约为()
A. 石B. 石C. 石D. 石
吉林省长春市东北师大附中明珠学校2020-2021学年九年级第一次月考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2B.2C.±2D.0
22.(1)如图①,在 中,点 为边 延长线上的点,若 ,过点 作 交 延长线于点 ,若 ,求 的长.
(2)(探究)如图②,在 中,点 时边 上的点,点 是边 的中点,连结 、 交于点 , ,小明尝试探究 的值,在图②中,小明过点D作 交 于点 ,易证 ,则 ,从而得到 的值为;易证 ,则 ,从而得到 的值为;从而得到 的值为.
19.图①、图②、图③都是 的网格,每个小正方形的顶点为格点, 的顶点 、 、 均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求作图,不要求写出画法.
(1)在图①中画出 边 上的中线AD,则 .
(2)在图②中画出 ,点 、 分别在边 、 上,满足 ,且 ;
(3)在图③中画出 ,点 分别在边 、 上,使得 与 是位似图形,且点 为位似中心,位似比为 (保留作图痕迹)
(3)(应用)如图③,在 中,点 是边 上的点, 为边 延长线上的点,连结 ,延长 ,交 于点 ,若 , 且 的面积为 ,则 的面积为.
吉林省长春市东北师大附中(明珠校区)2019-2020学年九年级上第一次月考物理试题 Word解析版
2019 -2020东北师大明珠初三年级上综合测试物理试题考试时长:60 分钟 试卷分值:70 分一、单项选择题(每题 2 分,共计 20 分)1.在国际单位制中,电压的单位是( ) A.安培 B.库仑 C.伏特 D.焦耳2.如图所示的物品中,通常情况下属于导体的是 ( ) A.陶瓷盘 B.不锈钢锅 C.玻璃杯 D.木铲 第 2 题图3.如果一个验电器的两个金属箔片因带电而张开,则这两个金属箔片一定( ) A.带正电 B.带负电C.带同种电荷D.带异种电荷4.下列实例中与“水的比热容较大”这一特性无关的是 ( )A.让热水流过散热器供暖B.用循环水冷却汽车发动机C.沿海地区昼夜温差较小D.夏天在房间内洒水降温5.如图所示电路中,开关能够同时控制两盏灯,且两灯发光情况互不影响的电路是( )A B C D第 5 题图6.用电压表测灯 L1 两端的电压,如图所示四个电路图中,正确的是( )A B 第 6 题图C D 第 8 题图 7.下列关于四冲程内燃机的说法中正确的是 ( )A.热机效率越高,所做的有用功就越多B.汽油机在吸气冲程中吸入气缸的是空气C.一个工作循环对外做功一次D.压缩冲程中将内能转化为机械能8.在如图所示的电路中,正确的说法是 ( )A.闭合 S 1,断开S 2,L 1 发光,L 2 不发光B.闭合 S 1、S 2,L 1、L 2 都发光C.S 1、S 2 都断开,L 1、L 2 都不发光D.闭合 S 2,断开 S 1,L 1、L 2 都发光9.“光控开关”在光线暗时自动闭合,光线亮时自动断开;“声控开关”在有声音时自动闭合,一段时间后,若再无声音则自动断开。
下图中能让电灯实现一直熄灭、一直亮或在光线较暗且有声音时才亮三种状态的电路是 ( )A B C D第 9 题图10.如图所示,开关从闭合到断开,电流表 A 1 和A 2 的示数 I 1、I 2 的变化情况是 ( )A.I 1 变小,I 2 变大B.I 1 不变,I 2 变大C.I 1 变大,I 2 变小D.I 1 不变,I 2 变小第 10 题图 第 14 题图 第 16 题图二、填空题(每空 1 分,共计 12 分)11.榴莲因其果肉香甜又富有营养,被称为水果之王。
2023-2024学年吉林省长春市东北师大附中明珠学校九年级上学期第一次月考物理试题

2023-2024学年吉林省长春市东北师大附中明珠学校九年级上学期第一次月考物理试题1.在发生力的作用时,以下说法正确的是()A.可以没有物体,既没有施力物体也没有受力物体B.只要有受力物体就行,可以没有施力物体C.只要存在施力物体就行,有没有受力物体没关系D.一定既有受力物体也有施力物体,离开物体就谈不上力的作用,就没有力了2.下列关于惯性的说法正确的是A.高速行驶的火车不容易停下来,说明速度越大惯性越大B.跳高运动员助跑起跳是为了增大惯性C.羽毛球容易被扣杀是因为它的惯性小D.宇宙飞船在太空中运行时没有惯性3.如图所示,从图钉的构造来看,钉帽的面积做得很大是为了使用时对手指A.增大压强B.减小压强C.增大压力D.减小压力4.如图所示,甲、乙、丙三个容器底面积相同,放在水平面上,容器装有同种液体,且液面相平,则液体对容器底的压强关系是()A.p甲 = p乙 = p丙B.p甲 > p乙 > p丙C.p甲 < p乙 < p丙D.无法确定5.如图所示,某同学用弹簧秤拉着放在水平桌面上的木块匀速滑动,在木块前端离开桌面至一半移出的过程中,弹簧秤的示数和木块对桌面压强的变化情况分别是A.不变,增大B.不变,不变C.减小,不变D.增大,减小6.用水平力F将一木块压在竖直墙上保持静止(如图),下列说法中正确的是()A.水平力F与木块所受到的重力是一对平衡力B.水平力F与木块所受到的摩擦力是一对平衡力C.若水平力F增大,则木块所受到的摩擦力随着增大D.木块所受到的重力和摩擦力是一对平衡力7.小车重200N,一涵用30N的水平力推小车沿水平路面匀速前进50m的过程中,下列判断正确的是()A.重力对小车做功10000J B.人对车做功10000JC.人对车做功1500J D.小车受到的阻力是170N8.如图所示,玻璃水槽中装有一定深度的水,一正方体木块漂浮在水面上,在水槽口下方设有固定的水平金属网,现缓慢向水槽中注水,使水槽内水面上升,直到水面与水槽口相平。
吉林省长春市东北师大附中明珠学校2022-2023学年九年级下学期第一次月考数学试题
吉林省长春市东北师大附中明珠学校2022-2023学年九年级下学期第一次月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题....A .a b >B .a b -<C .|||a b <5.如图①是一种手机平板支架,图②是其侧面结构示意图.托板端的点C 处,托板AB 可绕点C 转动,支撑板CD 可绕点D CDE α∠=,则点C 到底座DE 的距离为()8sin αA .20°7.如图,Rt ABC △两个三角形,其中一个三角形是等腰三角形,其作法错误的是(A ..C .D .8.如图,点P 在函数()00x kxk y >=>,的图象上,过点P 作PQ ∥Q ,将点P 绕线段PQ 的中点M 逆时针旋转90︒得到点P ',点P '恰好落在函数()00x kxk y >=>,的图象上,连接P M '、P P ',若PMP ' 的面积等于()A .2B .4C 二、填空题9.因式分解:2ab -.10.关于x 的一元二次方程14.如图,在平面直角坐标系中,三、解答题要求:=.(1)求证:DE ADb.八年级学生知识竞赛成绩在8090x≤<这一组的数据如下:80,81,81,81,82,83,83,83,84,85,86,87c.八年级、九年级学生知识竞赛成绩的平均数、中位数、方差如下:(1)【思考尝试】以下是华华对于本问题的部分解答过程,请你补全余下的证明过程.=,连接EF,解:在边AB上截取AF CE,EP AE^动点P 从点A 出发,沿折线AB BD -以每秒1个单位长度的速度运动,连接PM ,作点A 关于直线PM 的对称点A ',设点P 的运动时间为t 秒()0t >.(1)用含t 的代数式表示线段BP 的长.(2)当点A '在ABC 内部时,求t 的取值范围.(3)连接CP ,当CP AB ⊥时,求BCP 的面积.(4)当MA AB '∥时,直接写出t 的值.24.在平面直角坐标系中,抛物线2y x bx c =-++(b 、c 是常数)经过点()1,0A -和点()3,0B ,点P 在抛物线上,且点P 的横坐标为m .(1)求b 、c 的值.(2)当PAB 的面积为8时,求m 的值.(3)当点P 在点A 的右侧时,抛物线在点P 与点A 之间的部分(包含端点)记为图象G ,设G 的最高点与最低点的纵坐标之差为h ,求h 与m 之间的函数关系式.(4)点Q 的横坐标为13m -,纵坐标为1m +,以PQ 为对角线构造矩形,且矩形的边与坐标轴平行.当抛物线在矩形内部的点的纵坐标y 随x 的增大而增大或y 随x 的增大而减小时,直接写出m 的取值范围.。
