7,3循环码要点
第9章 差错控制编码习题解答

Z4
1000
0001000
b3
Z8
1101
0010000
b4
Z13
0111
0100000
b5
Z7
1110
1000000
b6
Z14
(7)画出译码器电路如下:
b6 b5 b4 b3 b2 b1 b0
纠错电路
b6
异或运算
b5
b4
Z15
Z14
S4 4-16 Z13 S3 译 S2 码 Z7 S1 器 Z 2
a3 a2 a1a0 0000 1101 0111 1010 1110 0011 1001 0100
5
(3)由上表知汉明距离为 d0 = 4 。 (4)画出编码器电路如下:
a6 a5 a4
a3 a2 a1
a0
⎧s4 = e6 ⊕ e4 ⊕ e3
(5) S
=
EH T
→ ⎪⎪⎪⎨ss32
= e6 ⊕ e5 ⊕ e4 = e6 ⊕ e5 ⊕ e1
1
解:
(1) 检测e个随机错误,则要求d0 ≥ e +1 (2) 纠t个随机错误,则要求d0 ≥ 2t +1 (2) 纠t个,同时检测e个(e > t)随机错误,则要求d0 ≥ t + e +1 由上述公式得 : (5,1)重复码d0 = 5,故能检4位错,纠2位错, 并同时能纠1位错和检3位错.
通信原理二--循环码

实验报告
学科:通信原理(二)
题目:数字信号基带传输系统仿真
实验设备:安有matlab仿真软件的计算机
学院:光电信息与通信工程学院
系别:通信工程
学号:
姓名:
指导教师:
一、实验目的与要求
1. 学习并理解信道编码的根本目的、技术要求与基本目标等基本概念;
2. 掌握循环码、miller码的物理涵义、数学基础及检纠错原理;
3. 掌握循环码、miller码的码型特点、检纠错能力、编译码方法及基本技术;
4. 学会使用MATLAB 实现循环码及miller码的编译码及检纠错模拟与分析。
二、实验仪器与设备
1. 安装了matlab程序的计算机 1 台
三、实验原理
(一)循环码
循环码是线性分组码的一个重要子集,是目前研究得最成熟的一类码,它有许多特殊的代数性质,例如,循环码中任一许用码组经过循环移位后,所得到的码组仍然是许用码。
循环码A= a n−1+a n−2+…+a 1+a 0可以表示为如下的码多项式:
1.生成多项式g (x)
定义:若一个循环码的所有码字多项式都是一个次数最低的、非零的、首一多项式g (x)的倍式,则称g (x)为生成该码,并称g (x) 为该码的生成元或生成多项式。
可以证明生成多项式g (x)具有以下特性:
(1)g (x) 是一个常数项为1 的r=n −k 次多项式;
(2)g (x) 是x n+1 的一个因式;
(3)该循环码中其它码多项式都是g (x)的倍式。
为了保证构成的生成矩阵G的各行线性不相关,通常用g (x) 来构造生成矩阵。因此,一旦生成多项式g (x) 确定以后,该循环码的生成矩阵就可以确定。
基于C语言的RS(7,3) 编码器设计

教学院长(主任) (签字) : 年 备注: 月 日
[摘要]RS(Reed-Solomon)码是一种多进制的BCH码。既适宜纠正随机错误,更适宜纠正突发 错误,因而被广泛地用于各种通信系统及数据存储中,如深空通信、移动通信、光纤通信、 磁盘阵列、DRAM、光盘数字视频广播(DVB)等系统。 本论文重点介绍了纠错码基本理论,有限域乘法器、RS码编码原理。利用C语言实现 了RS(7,3)码的编码器和伽罗华域GF( 23 )内的乘法器的设计,并通过Matlab仿真对编码器 结果进行验证,程序输出结果与验证结果一致,表明所设计的编码器和乘法器算法能够满 足设计要求。 [关键词]Reed-Solomon码;乘法器;编码器
毕业论文(设计)题目 指导教师 晋 学历
基于 C 语言的 RS (7,3)编码器设计 研究 生 职称 讲师 所学专业 通信与信息系统
具体要求(主要内容、基本要求、主要参考资料等): 主要内容:研究纠错码的基本理论和数学基础,学习循环码,BCH 码,RS 码等几种常见 的纠错码,研究它们的编码、解码原理。重点研究 RS 编码原理及实现方法。应用 C 语 言进行 RS 编码器的软件设计,并选用 MATLAB 对编码结果进行验证。 基本要求:应用 C 语言进行有限域乘法器、RS 编码器的仿真设计,并利用 TLAB 对编码 结果进行验证,实现编码功能。 参考资料:1.王新梅, 肖国镇.纠错码——原理与方法.西安电子科技大学出版社.2002. 2.张鸣瑞,邹世开.编码理论.北京航空航天大学出版社.1990. 3.曹雪虹,张宗橙.信息论与编码.清华大学出版社.2004. 4.叶才炜,李式巨.RS 编译码的 c 语言实现.无线电工程第 33 卷第 8 期. 5.孙屹,李妍.MATLAB 通信仿真开发手册.北京:国防工业出版,2005 进度安排:2008-2009-1 学期第 8 周—第 16 周,选定毕业论文题目、进行开题。 2008-2009-2 学期第 1 周—第 4 周,查阅资料,完成相关文献翻译。 2008-2009-2 学期第 5 周—第 8 周,有限域乘法器、RS 编码器的软件设计。 2008-2009-2 学期第 8 周—第 13 周,设计结果的 Matlab 验证,撰写论文。 2008-2009-2 学期第 14 周—第 15 周,论文答辩。 指导教师(签字) : 年 院(系)意见: 月 日
9 第九章 信道编码

例:
一个码组:(000100,111111)B,能发现多少 个错误码元 ,能纠正多少个错误码元 ,能 同时发现和纠正多少个错误码元?
1)e=4 , 2)t=2, 3)t=1,e=3
6
9.3 线性分组码
1. 奇偶监督码 编码方法
把信息码元先分组,在每组最后加一位监督码 元,使该码组中1的数目为奇数或偶数
产生如下线性方程组: a2 = a4 + a5 + a6 a1 = a3 + a5 + a6 a0 = a3 + a4 + a6
纠错:
由监督关系式可构造出下面错码位置关系表:
S2 S1 S0 000 001 010 100 011 101 110 111
错码位置 无错 a0 a1 a2 a3 a4 a5 a6
⎢⎣0110001⎥⎦
译码器接收到的码组是:
y = (1001001)
则伴随式s = yH T = eH T = 0111的所对应的可纠正错误图样为:
∧
∧
∧
e = (0100000) 得到的译码结果:c = y + e = (1101001)
汉明码的监督矩阵H:可以用任意次序 的2m-1列非0的m比特二进制矢量组 成,任意两列线性无关。
g...2
⎥ ⎥ ⎥
循环码(7,4)

8.4 循环码
时间:2012年09月01日信息来源:《通信原理》精品课程网站点击:2452次我要评论(0) 【字体:大中小】
循环码是线性分组码重要的一个子类,现有的重要线性分组码都是循环码或与循环码密切相关。与其他大多数码相比,循环码的编码及译码易于用简单的具有反馈连接的移位寄存器来实现,这是它的优势所在。另外,对它的研究是建立在比较严密的数学方法基础之上,因此比较容易获得有效的译码方案。循环码在实际中应用很广。
8.4.1 循环码基本概念
一个线性()分组码,如果它的任一码字经过循环移位后(左移或右移),仍然是该码
的一个码字,则称该码为循环码。上一节中表8-3所示的(7,3)分组码就是一个循环码。为了便于观察,将(7,3)码重新排列如表8-9所示。
表8-9 循环码的循环移位
在代数编码理论中,常用多项式
(8.4-1)
来描述一个码字。表8-9中的任一码组可以表示为
(8.4-2)
这种多项式中,仅是码元位置的标记,因此我们并不关心x的取值,这种多项式称为码多项式。例如,码字(0100111)可以表示为
(8.4-3)
左移一位后为(1001110),其码字多项式为
(8.4-4)
需要注意的是,码字多项式和一般实数域或复数域的多项式有所不同,码字多项式的运算是基于模二运算的。
(1)码多项式相加,是同幂次的系数模二加,不难理解,两个相同的多项式相加,结果系数全为0。例如
(8.4-5)
(2)码多项式相乘,对相乘结果多项式作模二加运算。例如
(8.4-6)
(3)码多项式相除,除法过程中多项式相减按模二加方法进行。当被除式的幂次高于等于除式的幂次,就可以表示为一个商式和一个分式之和,即
循环码

x 2 g ( x) G ( x) xg ( x) g ( x)
1011100 G ( x) 0101110 0010111
5 循环码的生成
(1) 已知信息码,由生成矩阵G得到循环码
x k 1 g ( x ) MG T ( x ) ( mk 1 , m1 , m0 ) xg ( x ) g( x )
2016/6/24
例如: 7位的循环码组
T ( x) x6 x5 x 2 1
其码长n = 7,现给定i = 3,则
x 3 T ( x ) x 3 ( x 6 x 5 x 2 1) x9 x8 x5 x3
x5 x 3 x 2 x
但是这样编成的循环码不一定是系统码。如要编成前k位是
信息元,后r=n-k位是监督元的n位系统码,则可以采用以下方
2016/6/24 法。
1. 编码原则 在编码时,首先要根据给定的(n, k)值,从(xn + 1) 的因子中选一个(n-k)次多项式作为g(x);
由于所有码多项式T(x)都可以被g(x)整除。根据这条原
即生成多项式:g(x) = x4 + x2 + x + 1。将此g(x)代入 (0010111)
x k 1 g ( x) k 2 x g ( x) G ( x) xg ( x) g ( x)
数字通信卷积码作业答案

⎜⎝1 0 1 0 1 0 1⎟⎠ ⎜⎝1 0 1 0 1 0 1⎟⎠ ⎜⎝1 1 0 1 0 0 1⎟⎠ ⎜⎛ 0 1 1 1 1 0 0⎟⎞ → ⎜1 0 1 1 0 1 0⎟ ⎜⎝1 1 0 1 0 0 1⎟⎠
c1,i = bi + bi−4 + bi−5 , c2,i = bi−1 + bi−3 + bi−4 + bi−5 , 由此得到编码器方框图如下
图 7.9 题 7.15 编码器框图
由已知给出的生成序列可得该卷积码的生成矩阵为
⎜⎛10 01 00 01 11 11
⎟⎞
⎜00 10 01 00 01 11 11 ⎟来自百度文库
1 1
1 1
1 0
⎟⎞ ⎟
。
⎜⎝ 0 0 1 0 1 1⎟⎠
7.8 已知(7,3)循环码的生成多项式为 g(x) = x4 + x2 + x + 1 ,输入信息码元为
101,求编码后的系统码码组。 解: 输入信息码元对应的多项式为:
m(x) = x2 +1 x4m(x) = x6 + x4 r(x) = x4m(x) mod g (x) = x3 + x2 A(x) = x6 + x4 + x3 + x2 即 1011100
循环码

8.5 循环码
循环码是线性分组码中最重要的一个子类码,它的基本特点是编码电路及伴随式解码电路简单易行;循环码代数结构具有很多有用的特性,便于找到有效解码方法。因此在实际差错控制系统中所使用的线性分组码,几乎都是循环码。
下面将介绍循环码的多项式表示及其性质,同时简介几种重要的循环码,CRC、BCH和R-S 码等。
8.5.1 循环码的描述
1. 码多项式及其运算
通式表示为:
(8-69)于是称与为“同余”式,即
[模]
(8-70)如:
则[模] 即能被整除
利用这一运算原理,我们可对一个码字进行移位表示:
如:的多项式表示为:
使码组向左移2位(循环)则有
对应多项式
然后以去除得:
这一结果表明,以作除法运算(称模)后,
即与为同余
因此,(模)
应注意,利用这种同余式表示,必须加注(模),否则就不明确在什么条件下得到的
这一同余关系式。
2.循环码的构成
循环码的构成突出特点是只要是该码中的一个许用码组——码字,通过循环位
其结果则可包括全部个非全0码字,如上面介绍的(7,3)分组码,从
信码位0 0 1构成的码字(0011101)开始逐一向左(或者向右)移一位,可得其余6个码字:(0111010)、(1110100)、(1101001)、(1010011)、(0100111)、(1001110)。
若把这些码字写成码多项式,都具有同一个移位运算模式,并设(0011101)对应的码多项
式,
于是,有:
(模)
(8-71)这样,就构成了(7,3)循环码,如表8-4。从表8-4看出,循环得到的(7,3)码,仍为系
统码,信息码组均在表中码字的高位(左方)。
循 环 码

= x +1 + x6+ x4 x5·g(x) = x9 + x8+ x7+ x5
= x 2+ x + 1 + x5 x6·g(x) = x10 + x9+ x8+ x6
= x 3+ x2 + x + x6
对应码组: 0011101 0111010 1110100
1101001
1010011
0100111
1001110
• 定义循环码的生成矩阵(用生成多项式表示):
x k-1 ·g(x)
则(7, 3)循环码的生成矩阵:
G(x)= xk-2 ·g(x)
1110100
…
G= 0 1 1 1 0 1 0
g(x)
0011101
(由上式得到的G不是典型矩阵,经过线性变换后可以 化成典型矩阵。)
Qx
Rx N x
则可以写为:F(x)≡R(x) (模N(x))。 在循环码中,若A(x)是一个长为n的许用码组,则在按
模 xn 1运算下,亦是一个许用码组。
例如,
x3 A7 x x3 x6 x5 x2 1 x9 x8 x5 x3 x5 x3 x2 x 模x7 1
7,3循环码

******************
实践教学
*******************
兰州理工大学
计算机与通信学院
2014年秋季学期
计算机通信课程设计
题目:(7,3)循环码编译码软件设计
专业班级:
姓名:
学号:
指导教师:
成绩:
摘要
随着计算机通信的日益发展,传输数据的场合越来越多。串行数据的差错检验是保证数据传输正确的必要手段,而循环码是差错码中最常用的一种编码。
循环码是线性分组码中最重要的一种子类,它除了具有分组码的线性外,还具有循环性,其码字结构一般用符号(n,k)表示,其中,n是该码组中的码元数,k是信息码元位数,r=n-k是监督码元位数。循环码具有许多特殊的代数性质,这些性质有助于按照要求的纠错能力系统地构造这类码,能简化译码算法,并且目前发现的大部分线性码与循环码有密切关系。已有循环码编译码系统大多以标准逻辑器件(如中小规模TTL系列、CMOS系列)按传统数字系统设计方法设计而成,其主要缺点是逻辑规模小、功耗大、可靠性低。随着大规模、超大规模集成电路的发展,以及电子设计自动化水平的提高,这种制约正在被逐渐消除。
本文通过C 语言平台运行所编写的程序,观察了在输入信息码情况下输出对应的编码结果以及相反的译码功能。通过多组的对比验证了该(7,4)循环码的编译码程序的正确性。最后,在程序运行的过程中进步分析循环码的编译码原理,并通过比较仿真模型与理论计算的性能,证明了仿真模型的可行性。
关键词:循环码;编码;译码;程序仿真
目录
前言 (1)
1、目的及意义 (2)
2、设计原理 (3)
2.1循环码的介绍 (3)
信息论(7,4)汉明码(7,3)循环码

functionvarargout = Hamming(varargin)
% HAMMING M-file for Hamming.fig
% HAMMING, by itself, creates a new HAMMING or raises the existing % singleton*.
%
% H = HAMMING returns the handle to a new HAMMING or the handle to % the existing singleton*.
%
% HAMMING('CALLBACK',hObject,eventData,handles,...) calls the
local
% function named CALLBACK in HAMMING.M with the given input arguments. %
% HAMMING('Property','Value',...) creates a new HAMMING or raises the % existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before Hamming_OpeningFunction gets called. An % unrecognized property name or invalid value makes property application
第八章 循环码.

(1 x)(1 x 2 x 3 ) 1 x x 2 x 4 (1 x)(1 x x ) 1 x x x
3 2 3 4
(两个)
六次因式: (1 x 2 x 3 )(1 x x 3 ) 1 x x 2 x 3 x 4 x 5 x 6 (一个)
2 3 n k 1 则: xg( x) g 0 x g1 x g 2 x g n k x
x 2 g ( x) g 0 x 2 g1 x 3 g 2 x 4 g n k x n k 2 x k 1 g ( x) g 0 x k 1 g1 x k g 2 x k 1 g n k x n 1
方法:当循环码的生成多项式g(x)给定后,可以取g(x)本身加上移位 k – 1次所得到的k – 1码字作为k个基底,即:
g ( x), xg( x), , x k 1 g ( x) →构成基底
若:
g ( x) g 0 g1 x g 2 x 2 g n k x n k
1110100 1 x x 2 x 4
移一位
0111010 x x 2 x 3 x 5 x(1 x x 2 x 4 )
移两位
0011101 x 2 x 3 x 4 x 6 x 2 (1 x x 2 x 4 )
循环码的生成
循环码的生成
有了生成矩阵G,就可以由k个信息位得出整个码组: 例: A a6 a5 a4 a3 a2 a1a0 a6 a5 a4 a3 G 式中, 1000 111
0100 110 G I k Q 0010 101 0001 011
4
011
1001
8
111
0010
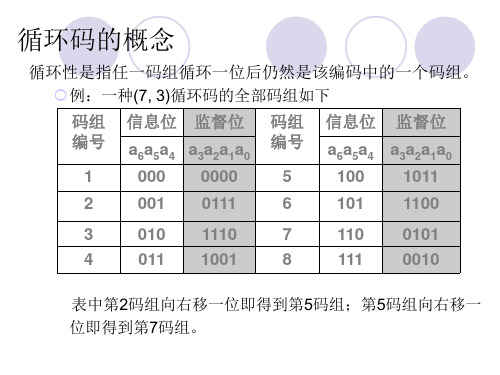
表中第2码组向右移一位即得到第5码组;第5码组向右移一 位即得到第7码组。
一般情况
若(an-1 an-2 …a0)是循环码的一个码组,则循环移位后的 码组: (an-2 an-3 … a0 an-1) (an-3 an-4 … an-1 an-2) … … (a0 an-1 …a2 a1) 仍然是该编码中的码组。 多项式表示法 一个长度为n的码组(an-1 an-2 …a0)可以表示成
循环码的概念
循环性是指任一码组循环一位后仍然是该编码中的一个码组。 例:一种(7, 3)循环码的全部码组如下 码组 编号 1 2 3 信息位 000 001 010 监督位 0000 0111 1110 a6a5a4 a3a2a1a0 码组 编号 5 6 7 信息位 100 101 110 监督位 1011 1100 0101 a6a5a4 a3a2a1a0
例: 码组编
号 1
信息位 A 6 a5 a4 000
监督位 a3 a2 a1 a
现代通信原理教程10章部分习题解答

10.1 已知码集合中有8个码组为(000000)、(001110)、(010101)、(011011)、(100011)、(101101)、(110110)、(111000),求该码集合的最小码距。 解 因为该码集合中包含全零码组(000000),所以对于线性分组码,最小码距等于除全零码外的码组的最小重量,即3min =d 。
10.2 上题给出的码集合若用于检错,能检出几位错码?若用于纠错,能纠正几位错码?若同时用于检错与纠错,问纠错、检错的能力如何?
解 只用于检错时,由条件:最小码距1min +≥e d ,求出2=e ,即能检出2位错码。
只用于纠错时,由12min +≥t d ,可得1=t ,既能纠正1位错码。 同时用于检错与纠错,且3min =d 时,无法满足下列条件
⎩⎨⎧>++≥t
e e t d 1m i n
故该码不能同时用于检错与纠错。 10.4 已知(7,3)码的生成矩阵为
⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡=001110101001111001110G
列出所有许用码组,并求监督矩阵。
解 分别将信息段(000)、(001)、(010)、(011)、(100)、(101)、(110)和(111)代入式A =m G ,得到许用码组如下 0000000 0011101 0100111 0111010 1001110 1010011 1101001 1110100
生成矩阵G 为典型阵,有
⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡=110101111110Q 所以
⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡==011110111101T
信息论(7,4)汉明码(7,3)循环码

functionvarargout = Hamming(varargin)
% HAMMING M-file for Hamming.fig
% HAMMING, by itself, creates a new HAMMING or raises the existing % singleton*.
%
% H = HAMMING returns the handle to a new HAMMING or the handle to % the existing singleton*.
%
% HAMMING('CALLBACK',hObject,eventData,handles,...) calls the
local
% function named CALLBACK in HAMMING.M with the given input arguments. %
% HAMMING('Property','Value',...) creates a new HAMMING or raises the % existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before Hamming_OpeningFunction gets called. An % unrecognized property name or invalid value makes property application
循环码(7,3)码

,对应的码组为1110010 ,它与
直接对码组进行循环左移的结果相同。 码多项式之间可以进行代数运算,在二元码中遵循模 2运算的规 则。根据线性码的封闭性,任意两码字经模运算后仍为本码组中的码 字。
1.1.4、生成多项式
(n,k)循环码码组集合中(全“0”码除外)幂次最低的多项式 (n-k)阶称为生成多项式 g ( x ) 。它是能整除 x + 1 且常数项为1的 多项式,具有唯一性。集合中其他码多项式,都是按模( x + 1 )运 算下 g ( x ) 的倍式,即可以由多项式 g ( x ) 产生循环码的全部码组。 假设信息码多项式为 m ( x ) ,则对应的循环码多项式为
(1.1.12)
对式(1.1.12)作线性变换,整理成典型形式的生成矩阵
(1.1.13)
若信息码元与式(1.1.13)相乘,得到的就是系统循环码。
如前所述,在(n,k)循环码中,由于 g(x)能除尽,因此 x n + 1 可分解成 g(x)和其他因式的乘积,记为
《信息论与编码》课程设计报告 -8-
x n + 1 = g ( x ) h( x )
3号
0100111
0111010 4号
0011101 2号
1001110 5号
图1.1-1(7,3)循环码中的循环圈
可见除全零码组外,不论循环右移或左移,移多少位,其结果均 在该循环码组的集合中(全零码组自己构成独立的循环圈) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
******************
实践教学
*******************
兰州理工大学
计算机与通信学院
2014年秋季学期
计算机通信课程设计
题目:(7,3)循环码编译码软件设计
专业班级:
姓名:
学号:
指导教师:
成绩:
摘要
随着计算机通信的日益发展,传输数据的场合越来越多。串行数据的差错检验是保证数据传输正确的必要手段,而循环码是差错码中最常用的一种编码。
循环码是线性分组码中最重要的一种子类,它除了具有分组码的线性外,还具有循环性,其码字结构一般用符号(n,k)表示,其中,n是该码组中的码元数,k是信息码元位数,r=n-k是监督码元位数。循环码具有许多特殊的代数性质,这些性质有助于按照要求的纠错能力系统地构造这类码,能简化译码算法,并且目前发现的大部分线性码与循环码有密切关系。已有循环码编译码系统大多以标准逻辑器件(如中小规模TTL系列、CMOS系列)按传统数字系统设计方法设计而成,其主要缺点是逻辑规模小、功耗大、可靠性低。随着大规模、超大规模集成电路的发展,以及电子设计自动化水平的提高,这种制约正在被逐渐消除。
本文通过C 语言平台运行所编写的程序,观察了在输入信息码情况下输出对应的编码结果以及相反的译码功能。通过多组的对比验证了该(7,4)循环码的编译码程序的正确性。最后,在程序运行的过程中进步分析循环码的编译码原理,并通过比较仿真模型与理论计算的性能,证明了仿真模型的可行性。
关键词:循环码;编码;译码;程序仿真
目录
前言 (1)
1、目的及意义 (2)
2、设计原理 (3)
2.1循环码的介绍 (3)
2.1.1循环码的定义 (3)
2.1.2循环码的特点 (3)
2.1.3循环码的多项式表示 (4)
2.1.4(n,k)循环码的生成多项式 (4)
2.1.5循环码的生成矩阵和一致校验矩阵 (6)
2.2循环码编码原理 (8)
2.2.1多项式除法电路 (8)
2.3循环码译码原理 (9)
3、设计结果及分析 (11)
3.1程序运行结果 (11)
3.2运行结果理论分析 (14)
3.3软件可行性分析 (15)
4、总结 (16)
附录 (17)
参考文献 (22)
前言
数字信号在传输过程中,由于受到干扰的影响,码元波形将变坏。接收端收到后可能发生错误判决。由乘性干扰引起的码间串扰,可以采用均衡的办法纠错,而加性干扰的影响则需要用其他方法解决,在设计数字通信系统时,应该首先从合理选择调至制度,解调方法一级发送功率等方面考虑,使加性干扰不足以影响达到误码率的要求。在仍不能妈祖要求是,就要考虑才用差错控制技术。
现代通信的发展趋势为数字化,随着现代通信技术的不断开发,差错控制技术已日趋成熟,在各个领域都得到了广泛的应用和认同。本文就(7,4)循环码的编码与译码原理进行C 语言的编程及运行仿真。
现代社会发展要求通信系统功能越来越强,可靠性越来越高,构成也越来越复杂,这就要借助于功能强大的计算机辅助分析设计技术和工具才能实现。现代计算机科学技术快速发展,已经研发出了新一代的可视化的仿真软件。这些能强大的仿真软件,使得通信系统仿真的设计和分析过程变得相对直观和便捷,由此也使得通信系统仿真技术得到了更快的发展。本文使用的是功能强大的C 语言软件。
C 语言是一种使用简便的,特别适用于科学研究和工程计算的高级语言,与其他计算机语言相比,它的特点是简洁和智能化,具有极高的编程和调试效率。通过使用C 工具箱函数对数字调制进行仿真,更能直观彻底的掌握循环码的编码与译码原理。有助于我们的学习和研究,加深对知识的理解和运用。C 的便利性还体现在它的仿真结果还可以存放到的工作空间里做事后处理。方便我们修改参数对不同情况下的输出结果进行对比。
1、目的及意义
在实际的通信系统中,由于信道传输特性不理想以及加噪声的影响,接收到的信息中不可避免的会发生错误,影响通信系统的传输可靠性。随着数字通信技术的发展,各种业务对系统误码率的要求逐渐提高,差错控制编码技术是提高数字通信可靠性的有效方法之一。
循环码的编码与译码电路比较简单,纠错能力也较强,是应用比较广泛的差错控制编码方法之一。
通过完成本课题的设计,拟达到以下目的:
1、学习循环码编、译码的基本原理,并重点掌握(7,3)循环码的编码与译码;
2、查找并分析选择一个合理的生成多项式;
3、用C语言分别编程实现(7,3)循环码的编码与译码部分;
4、输入任意的数字信息序列,仿真并分析(7,3)循环码的编码结果;
5、分别在无差错和部分差错的情况下仿真并分析(7,3)循环码的译码结果;
6、分析软件的可行性。
2、设计原理
2.1循环码的介绍
循环码是线性分组码中一个重要的分支。它的检、纠错能力较强,编码和译码设备并不复杂,而且性能较好,不仅能纠随机错误,也能纠突发错误。
循环码是目前研究得最成熟的一类码,并且有严密的代数理论基础,故有许多特殊的代数性质,这些性质有助于按所要求的纠错能力系统地构造这类码,且易于实现,所以循环码受到人们的高度重视。
2.1.1循环码的定义
循环码是一种线性代数分组码,记为(n,k )码,其中n 为码长,k 为信息码元数。
2.1.2循环码的特点
若()0121c c c c n n --是一个码字,则它的循环移位()1032---n n n c c c c 也是一个码字。
循环码是线性分组码的一种,所以它具有线性分组码的一般特性,此外还具有循环性。循环码的编码和解码设备都不太复杂,且检(纠)错能力强。它不但可以检测随机的错误,还可以检错突发的错误。(n,k )循环码可以检测长为n-k 或更短的任何突发错误,包括首尾相接突发错误。
循环码是一种无权码,循环码编排的特点是相邻两个数码之间符合卡诺图中的邻接条件,即相邻两个数码之间只有一位码元不同,码元就是组成数码的单元。符合这个特点的有多种方案,但循环码只能是表中的那种。循环码的优点是没有瞬时错误,因为在数码变换过程中,在速度上会有快有慢,中间经过其它一些数码形式,称它们为瞬时错误。这在某些数字系统中是不允许的,为此希望相邻两个数码之间仅有一位码元不同,即满足邻接条件,这样就不会产生瞬时错误。循环码就是这样一种编码,它可以在卡诺图中依次循环得到。循环码又称格雷码( Grey Code )。
