《实际问题与二次函数(1)最大面积问题》课件
合集下载
实际问题与二次函数(1)
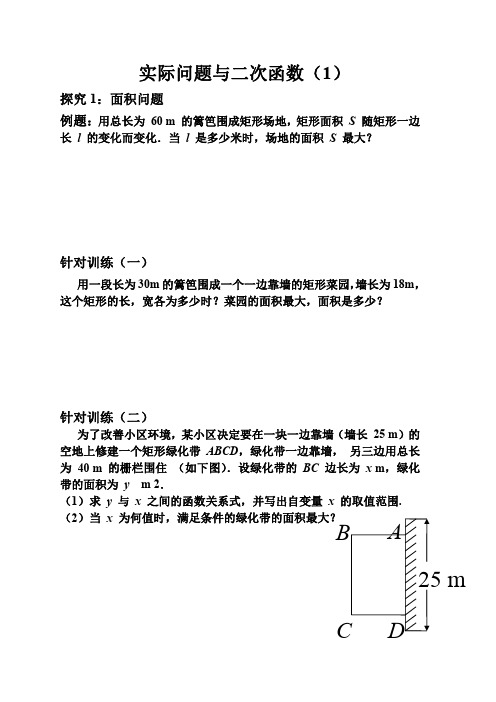
D
C B A
25m
实际问题与二次函数（1）
探究1：面积问题
例题：用总长为60m 的篱笆围成矩形场地，矩形面积S 随矩形一边长l 的变化而变化．当l 是多少米时，场地的面积S 最大？针对训练（一）
用一段长为30m 的篱笆围成一个一边靠墙的矩形菜园，墙长为18m ，这个矩形的长，宽各为多少时？菜园的面积最大，面积是多少？针对训练（二）
为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m ）的空地上修建一个矩形绿化带ABCD ，绿化带一边靠墙，另三边用总长为40m 的栅栏围住（如下图）．设绿化带的BC 边长为x m ，绿化带的面积为y m 2．
（1）求y 与x 之间的函数关系式，并写出自变量x 的取值范围.
（2）当x 为何值时，满足条件的绿化带的面积最大？
探究（二）利润问题
例题：已知某商品的进价为每件40元。
现在的售价是每件60元，每星期可卖出300件。
市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件；如何定价才能使利润最大？
针对训练（一）
商场销售一批衬衫，每天可售出20件，每件盈利40元，为了扩大销售，减少库存，决定采取适当的降价措施，经调查发现，如果一件衬衫每降价1元，每天可多售出2件。
每件降价多少元时，商场每天的盈利达到最大？盈利最大是多少元？
针对训练（二）
某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅行团每增加一人,每人的单价就降低10元.你能帮助分析一下,当旅行团的人数是多少时,旅行社可以获得最大营业额？。
22.3实际问题与二次函数第1课时几何图形的最大面积课件人教版数学九年级上册
试一试 求自变量的取值范围.
解得 21≤x＜30
变问题2 当21≤x＜30时，S的值随x的增大，是如何变化的？当x取何值时，
式S取得最大值？
y
450
训 当21≤x＜30时，S随x的增大而减小;
练
当x＝21时，S取得最大值，
此时S＝－2×(21－15)2＋450＝378m2.
注意：实际问题中求解二次函数最值问 题时，需要结合自变量的取值范围，不 一定都是在顶点处取得最值.
堂
y
练
习
200
∵0＜20＜25
∴当x＝20时，绿化带的面积取 得最大值，最大值为200m2.
O
20 25
x
课 5. 某广告公司设计一幅周长为12m的矩形广告牌，广告设计费用 堂 每平方米1000元，设矩形的一边长为x(m)，面积为S(m2). 练 (1)写出S与x之间的关系式，并写出自变量x的取值范围； 习 解：设矩形一边长为xm，则另一边长为(6－x)m.
∴S＝x(6－x)＝－x2＋6x,(0＜x＜6)
课 (2)请你设计一个方案，使获得的设计费最多，并求出这个费用.
堂 解：把 S＝x(6－x)＝－x2＋6x (0＜x＜6)化为顶点式得
练
习
S＝－(x－3)2＋9 (0＜x＜6)
∵0＜3＜6
∴当x＝3时，即矩形的一边长为3m时，矩形面积最大，为9m2.
矩形菜园的面积S＝
x(60－2x)＝－2x2＋60.x
想一想 如何求解自变量x的取值范围？墙长32m对此题有什么作用？
0＜60－2x≤32，即14≤x＜30.
变 解：设垂直于墙的边长为xm，则平行于墙的边长为(60－2x)m. 式 ∴矩形菜园的面积 S＝x(60－2x)＝－2x2＋60x. y
22.3实际问题与二次函数 第1课时 最大面积问题(精品原创)
基础扫描
3. 二次函数y=2(x+3)2-5的对称轴是
坐标是
。当x=
时，y的最 值是
，顶点 。 ，顶点 值，是 。
4. 二次函数y=-3(x-4)2+7的对称轴是 坐标是 。当x= 时，函数有最 5.二次函数y=2x2-4x+1的对称轴是 坐标是 .当x= 时，函数有最
，顶点 值，是 。
基础扫描
最大，最大面积是多少？ 问题3 可否试设与墙平行的一边为x米？ 如何表示另一边？ 60-x x 2 x
x 解：设矩形面积为Sm2,与墙平行的一边为x米，则 60 x 1 2 S x x 30 x 2 2 问题4 如何求解自变量x的取值范围？ 0 ＜ x ≤18. 问题5 如何求最值？ 由于x=30不在0 ＜ x ≤18 范围内，因此只能利用函数的增减
A
B
D C
6、如图，在矩形ABCD中，AB=6cm，BC=12cm，点P从A开始向 B以1cm/s的速度移动，点Q从B开始向C以2cm/s的速度移动。 如果P、Q分别从A、B同时出发，设△PBQ的面积为S(cm2)，移 动时间为t(s)。 动点问题：三要素（范围、方向与速度） (1)求S与t的函数关系； (2)当移动时间为多少时，△PBQ的面积最大？ 最大面积是多少？
3、如图，点E，F，G，H分别位于正方形ABCD 的四条边上．四边形EFGH也是正方形．当点E 位于何处时，正方形EFGH的面积最小？
利用勾股定理
4.如图,直线y=-2x+6交x轴于点A,交y轴于点B, 点P为线段AB上一动点(不与点A,B重合), 过点P分别作OA和OB的垂线,垂足为C,D.
（1）求点P在何处时,矩形OCPD 的面积为4? （2）求点P在何处时,矩形OCPD 的面积最大?
初中人教版数学课件-223实际问题与二次函数(1)最大面积问题
（3）能围出比45 m2更大的花圃吗？若能，求出最大 的面积；若不能，请说明理由．
解:(1)由题意，得S=x(24－3x)=－3x2+24x ，14 x 8 3
(2)由S=-3x2+24x=45，即x2－8x＋45=0.解得 x1=5,x2=3（不合题意，舍去）. ∴AB的长为5m.
自变量x的取值范围； （2）当x为何值时，满足条件的绿
xm
化带的面积最大． 解：（1）由题意得：
自变量x的取值范围是0＜x≤25 .
(2)
y 1 x2 20x 1 (x 20)2 200.
2
2
x
倘若墙AD的
长为10m呢？
y (m2) 200
O 20 25 x (m)
综合运用
如图，点E，F，G，H分别位于 D
22.3 实际问题与二次函数 （第1课时）
利用抛物线的最值解决几何图形的最大面积问题。
• 学习目标： 能够表示实际问题中变量之间的二次函数 关系，会运用二次函数的顶点坐标求出实 际问题的最大值（或最小值）．
• 学习重点： 探究利用二次函数的最大值（或最小值） 解决实际问题的方法．
回顾旧知
如何求出二次函数 y = ax2 + bx + c 的最小（大）值？
S a2 4 1 x(a x) a2 2x(a x) 2x2 2ax a2
∴当x= 22a a 时，正方形EFGH的面积最小
42
此时点E为AB的中点.
拓展
2013淄博中考压轴题：矩形纸片ABCD中，AB=5， AD=4. （1）如图1，四边形MNEF是在矩形纸片 ABCD中裁剪出的一个正方形．你能否在该矩形中 裁剪出一个面积最大的正方形，最大面积是多少？ 说明理由；
解:(1)由题意，得S=x(24－3x)=－3x2+24x ，14 x 8 3
(2)由S=-3x2+24x=45，即x2－8x＋45=0.解得 x1=5,x2=3（不合题意，舍去）. ∴AB的长为5m.
自变量x的取值范围； （2）当x为何值时，满足条件的绿
xm
化带的面积最大． 解：（1）由题意得：
自变量x的取值范围是0＜x≤25 .
(2)
y 1 x2 20x 1 (x 20)2 200.
2
2
x
倘若墙AD的
长为10m呢？
y (m2) 200
O 20 25 x (m)
综合运用
如图，点E，F，G，H分别位于 D
22.3 实际问题与二次函数 （第1课时）
利用抛物线的最值解决几何图形的最大面积问题。
• 学习目标： 能够表示实际问题中变量之间的二次函数 关系，会运用二次函数的顶点坐标求出实 际问题的最大值（或最小值）．
• 学习重点： 探究利用二次函数的最大值（或最小值） 解决实际问题的方法．
回顾旧知
如何求出二次函数 y = ax2 + bx + c 的最小（大）值？
S a2 4 1 x(a x) a2 2x(a x) 2x2 2ax a2
∴当x= 22a a 时，正方形EFGH的面积最小
42
此时点E为AB的中点.
拓展
2013淄博中考压轴题：矩形纸片ABCD中，AB=5， AD=4. （1）如图1，四边形MNEF是在矩形纸片 ABCD中裁剪出的一个正方形．你能否在该矩形中 裁剪出一个面积最大的正方形，最大面积是多少？ 说明理由；
人教版数学九年级上册实际问题与二次函数课件
对称轴：x=2；
3
对称轴：x=− ；
2
顶点坐标：(2，－9)；
顶点坐标：( − ，
最小值：－9；
3
2
最大值：
25
4
.
25
4
)；
新知探究
问题：从地面竖直向上抛出一小球，小球的高度 h(单位：m)与小球的运
动时间 t(单位：s)之间的关系式是h= 30t － 5t 2 (0≤t≤6)．小球的运动时间
是多少时，小球最高？小球运动中的最大高度是多少？
是多少？(铝合金型材宽度不计)
解：设矩形窗框的宽为x m，则高为
这里应有x＞0，
6−3
＞0，
2
6−3
m.
2
故0＜x＜2.
矩形窗框的透光面积y与x之间的函数关系式是：
=∙
6−3
2
x
例题探究
当 =
− 时，二次函数
2
值 =
4−2
．
4
y = ax 2 ＋ bx ＋ c 有最小(大)
h/m
=
−
2
=
30
−
2×(−5)
ℎ=
4−2
4
−302
4×(−5)
=
= 3，
40
= 45．
20
O
h= 30t － 5t 2 (0≤t≤6)
1
2 3
4
5 6 t/s
小球运动的时间是 3s 时，小球最高. 小球运动中的最大高度是 45 m．
墙长18m，这个矩形的长、宽
各为多少时，菜园的面积最大， 问题3 可否试设与墙平行的一边为x米？
则如何表示另一边？
最大面积是多少？
22.3 实际问题与二次函数 第1课时 几何图形面积问题
22.3 实际问题与二次函数 第1课时 几何图形面积问题
R·九年级上册
新课导入
问题:从地面竖直向上抛出一小球，小球的高度h(单位：m)与小球的运动时间t(单位：s)之间的关系式是h＝30t－5t2 (0≤t≤6). 小球运动的时间是多少时，小球最高？何图形相关的实际问题. (2)会用二次函数的图象和性质解决实际问题.
课堂小结
2.图形面积最值问题： 由图形面积公式直接计算列出关系式，再利用二次函数的性质分析、解决问题.
1.运动问题： （1）运动中的距离、时间、速度问题，这类问题多根据运动规律中的公式求解； （2）物体的运动路线（轨迹）问题，解决这类问题的思想方法是建立合适的平面直角坐标系，根据已知数据求出运动轨迹（抛物线）的解析式，再利用二次函数的性质分析、解决问题.
推进新课
问题:从地面竖直向上抛出一小球,小球的高度h(单位：m)与小球的运动时间t(单位：s)之间的关系式是h＝30t－5t2 (0≤t≤6). 小球运动的时间是多少时,小球最高？小球运动中的最大高度是多少？
分析： ①由a=-5可得，图象的开口向下； ②结合自变量t的取值范围0≤t≤6，画函数图象的草图如图； ③根据题意，结合图象可知，小球在抛物线的顶点时为最大高度。
课后作业
1.从课后习题中选取； 2.完成练习册本课时的习题。
解：设矩形的长为x m,面积为y m2,则矩形的宽为 m.
∴0<x≤18.
综合应用
3.如图，点E、F、G、H分别位于正方形ABCD的四条边上，四边形EFGH也是正方形，当点E位于何处时，正方形EFGH的面积最小？
解：令AB长为1，设DH=x，正方形EFGH的面 积为y，则DG=1-x. 即当E位于AB中点时，正方形EFGH面积最小.
R·九年级上册
新课导入
问题:从地面竖直向上抛出一小球，小球的高度h(单位：m)与小球的运动时间t(单位：s)之间的关系式是h＝30t－5t2 (0≤t≤6). 小球运动的时间是多少时，小球最高？何图形相关的实际问题. (2)会用二次函数的图象和性质解决实际问题.
课堂小结
2.图形面积最值问题： 由图形面积公式直接计算列出关系式，再利用二次函数的性质分析、解决问题.
1.运动问题： （1）运动中的距离、时间、速度问题，这类问题多根据运动规律中的公式求解； （2）物体的运动路线（轨迹）问题，解决这类问题的思想方法是建立合适的平面直角坐标系，根据已知数据求出运动轨迹（抛物线）的解析式，再利用二次函数的性质分析、解决问题.
推进新课
问题:从地面竖直向上抛出一小球,小球的高度h(单位：m)与小球的运动时间t(单位：s)之间的关系式是h＝30t－5t2 (0≤t≤6). 小球运动的时间是多少时,小球最高？小球运动中的最大高度是多少？
分析： ①由a=-5可得，图象的开口向下； ②结合自变量t的取值范围0≤t≤6，画函数图象的草图如图； ③根据题意，结合图象可知，小球在抛物线的顶点时为最大高度。
课后作业
1.从课后习题中选取； 2.完成练习册本课时的习题。
解：设矩形的长为x m,面积为y m2,则矩形的宽为 m.
∴0<x≤18.
综合应用
3.如图，点E、F、G、H分别位于正方形ABCD的四条边上，四边形EFGH也是正方形，当点E位于何处时，正方形EFGH的面积最小？
解：令AB长为1，设DH=x，正方形EFGH的面 积为y，则DG=1-x. 即当E位于AB中点时，正方形EFGH面积最小.
精编课件人教版九年级数学上册第22章二次函数22.3实际问题与二次函数(共12张PPT)(第1课时)
… 2分
2
∴当x为30cm时，菱形风筝面积最大，最大面积是450 cm .
课堂小结
将一 来定 的会 你感 激 现 在 拼 命 的 自 己
牛刀小试
变式1：现要用60米长的篱笆围成一个矩形 场地（一边靠墙且墙长40米）。应怎样围 才能使矩形的面积s最大？最大是多少？
变式2现要用60米长的篱笆围成一个矩形 场地（一边靠墙且墙长28米）。应怎样围才 能使矩形的面积s最大？最大是多少？
（1）列出二次函数的解析式，并根 据自变量的实际意义，确定自变量的 取值范围； （2）在自变量的取值范围内，运用 公式法或通过配方求出二次函数的 最大值或最小值。
参考答案及评分标准
解：（1）S=
（2）∵S= -
-
1 2 x 30 x ，a= 2
30
1 x 2
2
30 x
1 2
… 2分
＜0,
∴S有最大值
b ∴当x= 2a
= —
S的最大值为
4ac b 2 4a
1 2 ( ) 2 2
30 … 2分
30
4 (
1 ) 2
450
临沂太平中学
牛雅琪
视频
问题
排球运动员从地面竖直向上抛出排球，排球的高 度 h（单位：m）与排球的运动时间 t（单位：s）之间 的关系式是h= 20t - 5t 2 （0≤t≤4）．排球的运动时间 是多少时，排球最高？排球运动中的最大高度是多少 ？ h
0 4
t
探究1
用总长为 60 m 的篱笆围成矩形场地，矩形面积 S 随矩形一边长 l 的变化而变化．当 l是多少米时，场地 的面积 S 最大？
A B D C
二次函数应用几何图形的最大面积问题课件
对未来学习的思考和展望
深入学习二次函数和几何图形的基础知识，掌握更多解 决实际问题的技巧和方法。
拓展学习领域，了解更多与数学相关的学科知识，如线 性代数、微积分等，为解决更复杂的问题提供支持。
关注数学在实际生活中的应用，了解数学与其他学科的 交叉点，培养跨学科解决问题的能力。
THANKS
的最大面积。
03
几何图形面积的最大值问 题
几何图形面积最大值的求解方法
03
代数法
几何法
参数法
通过代数运算和不等式性质，求出几何图 形面积的最大值。
利用几何图形的性质和特点，通过作图和 观察，求出面积最大值。
引入参数表示几何图形，通过参数的变化 和约束条件，求出面积的最大值。
面积最大值在二次函数中的应用
二次函数应用几何图形的最 大面积问题课件
目录
• 二次函数与几何图形的关系 • 二次函数的最值问题 • 几何图形面积的最大值问题 • 实际应用案例分析 • 总结与思考
01
二次函数与几何图形的关 系
二次函数图像的几何意义
01
二次函数图像是抛物线，其 顶点是函数的极值点。
02
二次函数图像的对称轴是x=h ，顶点的纵坐标是k。
二次函数与几何图形面积最大值问题 紧密相关，通过合理设定函数参数， 可以找到几何图形面积的最大值。
在解决实际问题时，需要综合考虑多 种因素，如几何图形的形状、大小和 位置等，以及二次函数的参数和约束 条件。
二次函数开口方向和顶点位置对几何 图形面积的影响是关键，需要根据实 际情况调整函数表达式，以获得最佳 效果。
01
总结词
02
详细描述
矩形面积最大化
在给定长和宽的条件下，利用二次函数求矩形的最大面积。通过设定 长和宽为二次函数的形式，并利用求导数的方法找到面积的最大值。
秋九年级上学期数学22.3 实际问题与二次函数(第1课时 几何图形的最大面积问题)-课件
可画出图 象找顶 点
思考4 x为何值时面积取得最大值？
变式2 如图，用一段长为60m的篱笆围成一个一边靠墙的矩形菜 园，墙长22 m，这个矩形的长、宽各为多少时，菜园的面积最大， 最大面积是多少？
思考1 仿照变式1设未知数、列函数解析式. 设垂直于墙的边长为x m，则
思考2 若设与墙平行的一边为x m，则另一边如何表示？
(1)写出S与x之间的解析式，并写出自变量x的取值范围； （2）请你设计一个方案，使获得的设计费最多，并求出这个费用.
这时设计费最多，为16×1 000=1 6000（元）.
数阅
学读
使使
人人
精充
细实
；；
博会
物谈
使使
人人
深敏
沉捷
；；
You made my day!
伦 理 使 人 庄 重 ； 逻 辑 与 修 辞 使 人 善 辩 。
例2 解：
课堂小结
解题关键
几何图形 最大面积
问题
注意
依据常见 几何图 形的面 积公式 建立函 数关系 式 最值有时 不在顶 点处， 此时要 利用函 数的6厘米
B. 12厘米 C. 24厘米 D. 36厘米
3
A
C
Q
AP
B
3. 某广告公司设计一幅周长为16 m的矩形广告牌，广告设计费用每平方米1 000元， 设矩形的一边长为x(m),面积为S(m2).
设矩形面积为S m2,与墙平行的一边为x m，则
思考3 当x=30时，S是否取得最大值？ 不是
注意
实际问题中求解二次函数最值问题时，函数的最值要考虑自变量的取 值范围： （1）当自变量的取值包含顶点时，函数的最值在函数的顶点处取得； （2）当自变量的取值不包含顶点时，函数的最值一般在端点处取得，此 时要考虑函数的增减性.
思考4 x为何值时面积取得最大值？
变式2 如图，用一段长为60m的篱笆围成一个一边靠墙的矩形菜 园，墙长22 m，这个矩形的长、宽各为多少时，菜园的面积最大， 最大面积是多少？
思考1 仿照变式1设未知数、列函数解析式. 设垂直于墙的边长为x m，则
思考2 若设与墙平行的一边为x m，则另一边如何表示？
(1)写出S与x之间的解析式，并写出自变量x的取值范围； （2）请你设计一个方案，使获得的设计费最多，并求出这个费用.
这时设计费最多，为16×1 000=1 6000（元）.
数阅
学读
使使
人人
精充
细实
；；
博会
物谈
使使
人人
深敏
沉捷
；；
You made my day!
伦 理 使 人 庄 重 ； 逻 辑 与 修 辞 使 人 善 辩 。
例2 解：
课堂小结
解题关键
几何图形 最大面积
问题
注意
依据常见 几何图 形的面 积公式 建立函 数关系 式 最值有时 不在顶 点处， 此时要 利用函 数的6厘米
B. 12厘米 C. 24厘米 D. 36厘米
3
A
C
Q
AP
B
3. 某广告公司设计一幅周长为16 m的矩形广告牌，广告设计费用每平方米1 000元， 设矩形的一边长为x(m),面积为S(m2).
设矩形面积为S m2,与墙平行的一边为x m，则
思考3 当x=30时，S是否取得最大值？ 不是
注意
实际问题中求解二次函数最值问题时，函数的最值要考虑自变量的取 值范围： （1）当自变量的取值包含顶点时，函数的最值在函数的顶点处取得； （2）当自变量的取值不包含顶点时，函数的最值一般在端点处取得，此 时要考虑函数的增减性.
《实际问题与二次函数》二次函数PPT课件(第1课时)
1 (x 20)2 200 2
∵0＜x＜25，
∴当x=20时，满足条件的绿化带面积ymax=200.
课堂检测
拓广探索题
某广告公司设计一幅周长为12m的矩形广告牌，广告 设计费用每平方米1000元，设矩形的一边长为x(m), 面积为S(m2). (1)写出S与x之间的关系式，并写出自变量x的取值范 围；
解：令AB长为1，设DH=x，正方形EFGH的面
积为y，则DG=1-x.
∴
y
12
4
1 2
x(1
x)
当x= 1 时，y有最小值
2
1 2
2
.
x
1 2
2
1 2
(0
x 1).
即当E位于AB中点时，正方形EFGH面积最小.
课堂检测
2. 某小区在一块一边靠墙(墙长25m)的空地上修建一个矩形 绿化带ABCD，绿化带一边靠墙， 另三边用总长为40m的栅 栏围住．设绿化带的边长BC为xm，绿化带的面积为ym²． (1)求y与x之间的函数关系式，并写出自变量的取值范围.
链接中考 （2）求矩形菜园ABCD面积的最大值．
解：设AD=xm，
∴S=
1 2
x（100﹣x）=﹣12（x﹣50）2+1250，
当a≥50时，则x=50时，S的最大值为1250；
当0＜a＜50时，则当0＜x≤a时，S随x的增大而增大； 当x=a时，S的最大值为50a﹣1 a2，
2
综上所述，当a≥50时，S的最大值为1250；
高？小球运动中的最大高度是多少？
h/m
可以看出，这个函数的图象是一条抛
4
物线的一部分，这条抛物线的顶点是这个 0
函数的图象的最高点.也就是说，当t取顶
∵0＜x＜25，
∴当x=20时，满足条件的绿化带面积ymax=200.
课堂检测
拓广探索题
某广告公司设计一幅周长为12m的矩形广告牌，广告 设计费用每平方米1000元，设矩形的一边长为x(m), 面积为S(m2). (1)写出S与x之间的关系式，并写出自变量x的取值范 围；
解：令AB长为1，设DH=x，正方形EFGH的面
积为y，则DG=1-x.
∴
y
12
4
1 2
x(1
x)
当x= 1 时，y有最小值
2
1 2
2
.
x
1 2
2
1 2
(0
x 1).
即当E位于AB中点时，正方形EFGH面积最小.
课堂检测
2. 某小区在一块一边靠墙(墙长25m)的空地上修建一个矩形 绿化带ABCD，绿化带一边靠墙， 另三边用总长为40m的栅 栏围住．设绿化带的边长BC为xm，绿化带的面积为ym²． (1)求y与x之间的函数关系式，并写出自变量的取值范围.
链接中考 （2）求矩形菜园ABCD面积的最大值．
解：设AD=xm，
∴S=
1 2
x（100﹣x）=﹣12（x﹣50）2+1250，
当a≥50时，则x=50时，S的最大值为1250；
当0＜a＜50时，则当0＜x≤a时，S随x的增大而增大； 当x=a时，S的最大值为50a﹣1 a2，
2
综上所述，当a≥50时，S的最大值为1250；
高？小球运动中的最大高度是多少？
h/m
可以看出，这个函数的图象是一条抛
4
物线的一部分，这条抛物线的顶点是这个 0
函数的图象的最高点.也就是说，当t取顶
22.3实际问题与二次函数(面积问题)公开课优质课课件.pptx
1.二次函数y=2x2-6x+4当x=_____时，y有最 _____值为_______
2最.二__次__函_值数为y=_-__12_x_2_+_2x-1当x=_____时，y有
（1）配方法求最值（2）公式法求最值
当x=-
b 2a
时，y有最大（小）值
4ac-b2 4a
探究
九年级的小勇同学家是开养鸡场的，现要用 60米长的篱笆围成一个矩形的养鸡场地。
长为（30- l）m，场地的面积: S=l(30-l)
即S=-l2+30l （0<l
s
可以看出，这个<函3数0的) 图象是一条
抛物线的一部分，这条抛物线的顶
200
点是函数图象的最高点，也就是说
，当l取顶点的横坐标时，这个函数 100 有最大值.
因此，当l = − b = − 30 = 15时 2a 2 (−1)
解：由题意，得：s = x 60 − x
2
即
s = − 1 x2 + 30x 2
又由题意，得：
解得：
a = − 1 0 ,这个二次函数的对称轴是：x=30
2
∴当x ≤ 30时，s随x的增大而增大。
∴当与墙平行的一边长为28米，另一边长为16米时，围 成的矩形面积最大，其最大值是448米2。
（1）列出二次函数的解析式，并根 据自变量的实际意义，确定自变量的 取值范围； （2）在自变量的取值范围内，运用 公式法或通过配方求出二次函数的最 大值或最小值。
问题1：
（1）若矩形的一边长为10米，它的面积s 是多少？ （2）若矩形的一边长分别为15米、20米、 30米，它的面积s分别是多少？
思考：
1.在这个问题中，x只能取10，15， 20，30这几个值才能围成矩形吗？ 如果不是，还可以取哪些值？
2最.二__次__函_值数为y=_-__12_x_2_+_2x-1当x=_____时，y有
（1）配方法求最值（2）公式法求最值
当x=-
b 2a
时，y有最大（小）值
4ac-b2 4a
探究
九年级的小勇同学家是开养鸡场的，现要用 60米长的篱笆围成一个矩形的养鸡场地。
长为（30- l）m，场地的面积: S=l(30-l)
即S=-l2+30l （0<l
s
可以看出，这个<函3数0的) 图象是一条
抛物线的一部分，这条抛物线的顶
200
点是函数图象的最高点，也就是说
，当l取顶点的横坐标时，这个函数 100 有最大值.
因此，当l = − b = − 30 = 15时 2a 2 (−1)
解：由题意，得：s = x 60 − x
2
即
s = − 1 x2 + 30x 2
又由题意，得：
解得：
a = − 1 0 ,这个二次函数的对称轴是：x=30
2
∴当x ≤ 30时，s随x的增大而增大。
∴当与墙平行的一边长为28米，另一边长为16米时，围 成的矩形面积最大，其最大值是448米2。
（1）列出二次函数的解析式，并根 据自变量的实际意义，确定自变量的 取值范围； （2）在自变量的取值范围内，运用 公式法或通过配方求出二次函数的最 大值或最小值。
问题1：
（1）若矩形的一边长为10米，它的面积s 是多少？ （2）若矩形的一边长分别为15米、20米、 30米，它的面积s分别是多少？
思考：
1.在这个问题中，x只能取10，15， 20，30这几个值才能围成矩形吗？ 如果不是，还可以取哪些值？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由于抛物线 y = ax 2 + bx + c 的顶点是最低（高）点，
当
b x 2a
时，二次函数 y = ax 2 + bx + c 有最小（大）值
4ac b 2 y ． 4a
探究问题
用总长为 60 m 的篱笆围成矩形场地，矩形面积 S 随矩形一边长 l 的变化而变化．当 l 是多少米时，场地 的面积 S 最大？ 解： S l (30 l ) ， l 2 整理后得 S l 30l（0＜l＜30）． 思考：(1)你是 b 30 ∴ 当l 15 时， 如何确定自变量 2a 2 （1） l的取值范围的？ 2 4ac b 225 ． S 有最大值为 (2)当矩形面积 4a 当 l 是 15 m 时，场地的面积 S 最大． 最大时，又是哪 种特殊的四边形？
22.3 实际问题与二次函数 （第1课时）
利用抛物线的最值解决几何图形的最大面积问题。
学习目标： 能够表示实际问题中变量之间的二次函数关系， 会运用二次函数的顶点坐标求出实际问题的最 大值（或最小值）． 学习重点： 探究利用二次函数的最大值（或最小值）解决 实际问题的方法．
回顾旧知
如何求出二次函数 y = ax 2 + bx + c 的最小（大）值？
拓展
分别用定长为l的线段围成矩形和圆，哪种图形 2 x x x _______ __________ __， 2 2
l - 2x 解：设矩形的长为 x，则宽为______ ，面积为S。 2
∵S
x
l l2 02 l l 当x - 2 时，矩形有最大面积 4 . -2 4 4 16 l ∵圆周长l 2R， 半径R ，其面积为S R 2 2 l2 l2 l2 l2 2 . ∵ ， 圆的面积最大 . 4 4 4 16
1．由于抛物线 y = ax 2 + bx + c 的顶点是最低（高） 点，当 b x 2a 时，二次函数 y = ax 2 + bx + c 有最小（大） 值 4ac b 2 y ． 4a 2．列出二次函数的解析式，并根据自变量的实际 意义，确定自变量的取值范围. 3．在自变量的取值范围内，求出二次函数的最大 值或最小值.
1 S a 2 4 x(a x) a 2 2 x(a x) 2 x 2 2ax a 2 2
G
C
F
3
B
a 为常数a，则由题意易知 △AEH≌△BFE≌△CGF≌△DHG，故有 DH=AE=x，AH=a－x，∴正方形EFGH的面积S是 ∴当x=
2a a 4 2
变式： 为了改善小区环境，某小区决定要在一块一 边靠墙（墙长25m）的空地上修建一个矩形绿化带 ABCD，绿化带一边靠墙，另三边用总长为40m的栅 栏围住（如图）．若设绿化带的BC边长为xm，绿化 带的面积为ym2． （1）求y与x之间的函数关系式，并写出 自变量x的取值范围； （2）当x为何值时，满足条件的绿 化带的面积最大． 解：（1）由题意得：
达标训练
用长为8米的铝合金条制成如图形状的矩 形窗框，使窗户的透光面积最大，那么窗 户的最大透光面积是 平方米．
2.如图，英华学校准备围成一个 中间隔有一道篱笆的长方形花圃， 现有长为24m的篱笆，一面靠墙 x （墙长为10 m），设花圃宽AB 为x（m），面积为S(m2)． （1）求S与x的函数关系式； 2的花圃，AB的长是多少； （2）如果要围成面积为45 14 m x 8 3 （3）能围出比45 m2更大的花圃吗？若能，求出最大 的面积；若不能，请说明理由．
解:(1)由题意，得S=x(24－3x)=－3x2+24x ，
(2)由S=-3x2+24x=45，即x2－8x＋45=0.解得 x1=5,x2=3（不合题意，舍去）. ∴AB的长为5m.
xm
自变量x的取值范围是0＜x≤25 .
(2)
1 2 1 y x 20 x ( x 20) 2 200 . 2 2
x
y (m2)
倘若墙AD的 长为10m呢？
200
O
20
25
x (m)
综合运用
如图，点E，F，G，H分别位于 D 正方形ABCD的四条边上.四边形 H EFGH也是正方形.当点E位于何 处时，正方形EFGH的面积最小？ 1 （课本P52页第7题） 2 A x E 解:设AE=x，正方形ABCD的边长
时，正方形EFGH的面积最小 此时点E为AB的中点.
拓展
2013淄博中考压轴题：矩形纸片ABCD中，AB=5， AD=4. （1）如图1，四边形MNEF是在矩形纸片 ABCD中裁剪出的一个正方形．你能否在该矩形中 裁剪出一个面积最大的正方形，最大面积是多少？ 说明理由；
4-x
x 4-x
总结归纳