静水压强及其特性共43页文档
静水压强及其特性

(2)物理学中的大气压是标准大气压,水力 学中的大气压是工程大气压。 (3)液体的势能不仅有位置势能,还有压力 势能。 (4)测压管高度(压强水头),它不等于测 p 压管水头 z 。 (5)要注意区分压力中心 D 、受压面形心 C 和压强分布图的形心 O 的概念。
(6)要注意区分 P AP b 中 AP 是压强分布图 的面积, P pc A 中 A 是受压面的面积。
z1 p1
z2
p2
或
z
p
C
•
在重力作用下连通的 同种静止液体中: ① 压强随位置高程线性 变化; ② 等压面是水平面,与 质量力垂直; ③ z
p
是常数。
3. 绝对压强、相对压强、真空
•
压强 p基准点不同,可将压强分为: 以完全真空为零点,记 为 p 其值总为正值
(1)绝对压强
以当地大气压为 (2)相对压强 零点,记为 p 两者的关系为: p p p a
水利工程中,自由面上的气体压强等于 大气压强,则液体内任一点的相对压强为
p ( pa h) pa h
(3)真空压强 相对相 对压强为负 值时,其绝 对值称为真 空压强
压强
A
A点相 对压强
L e 3
H
L
e
(2) 任意平面上的静水总压力的计算 适用条件:受压面为任意平面。
a. 总压力的大小
P pc A hc A
b. 总压力的作用点
IC y D yC yC A
例题3:如图所示矩形平板闸门AB宽 b=3m, 门重 G=9800N,α=60°,h1 =1m,h2=1.73m。试
2 3 1 1.73 he 2 1.154m 3 2 1 1.73
静水压强特征

静水压强特征静水压强是描述在静止状态下水对物体施加的压力的一个物理量。
它是由水的密度、重力加速度和水的高度决定的。
静水压强对于我们理解和应用于许多日常生活和工程问题中的水压力非常重要。
我们来解释一下静水压强的概念。
在静止的水体中,每一点都受到来自上方水柱的压力作用。
这种压力是由于水的重力引起的。
根据物理学的原理,静水压强可以用公式P = ρgh 来表示,其中 P 是压强,ρ 是水的密度,g 是重力加速度,h 是水的高度。
静水压强的特征主要有以下几点:1. 与水的密度有关:静水压强与水的密度成正比。
密度越大,压强也就越大。
这意味着在相同高度和重力加速度下,不同密度的水对物体施加的压力是不同的。
2. 与重力加速度有关:静水压强与重力加速度成正比。
重力加速度是地球上的常数,约等于9.8 m/s²。
因此,在相同高度和水的密度下,重力加速度越大,静水压强也就越大。
3. 与水的高度有关:静水压强与水的高度成正比。
高度越大,压强也就越大。
这是因为在相同密度和重力加速度下,水柱的高度越大,上方的水重力对下方物体施加的压力就越大。
静水压强的特征使得它在许多方面都发挥着重要的作用。
首先,静水压强是我们理解和应用于液体力学和水压力学中的基础概念之一。
静水压强的计算和分析可以帮助我们了解液体在静止状态下的行为,例如在水池、水塔和水管中的液位变化。
静水压强还与水压力相关。
在日常生活和工程实践中,我们经常需要测量和控制水的压力。
例如,我们需要确保水管中的压力适当,以便供水系统正常运行;在水坝和堤坝工程中,我们需要了解水对结构物的压力,以确保工程的安全性。
静水压强还与液压技术密切相关。
液压技术是利用液体的传力性质来进行能量传递和控制的一种技术。
在液压系统中,静水压强的大小决定了液体对工作部件施加的力和压力。
通过控制液体的静水压强,我们可以实现各种工程和机械设备的运动和控制。
静水压强是描述水对物体施加的压力的一个重要物理量。
静水压强特征

静水压强特征静水压强是指在静止的液体中,由于液体的重力而产生的压力。
本文将从静水压强的定义、计算公式、影响因素以及应用等方面进行探讨。
一、静水压强的定义静水压强是指液体在静止状态下由于液体自身重力而产生的压力。
液体的重力作用于其表面上的单位面积上,从而产生了压力。
静水压强与液体的密度、重力加速度以及液体所在的深度有关。
二、静水压强的计算公式静水压强的计算公式可以用以下公式表示:P = ρgh其中,P表示静水压强,ρ表示液体的密度,g表示重力加速度,h 表示液体所在的深度。
三、影响静水压强的因素1. 液体的密度:液体的密度越大,静水压强也就越大。
2. 重力加速度:重力加速度越大,静水压强也就越大。
3. 液体所在的深度:液体所在的深度越大,静水压强也就越大。
四、静水压强的应用1. 水压力的应用:水压力是静水压强的一种应用,常见的例子包括水压机、液压系统等。
水压机利用液体传递压力的性质,通过增大液体的压强来实现对物体的压缩、挤压等操作。
2. 水下施工:在水下施工中,人们需要考虑到水的压力对施工造成的影响。
根据水的深度和压强,合理地选择施工材料和方法,确保施工的安全和稳定。
3. 水下探测:在水下探测中,静水压强是一个重要的考虑因素。
通过测量水的压强,可以间接地推断出水下的深度和水的密度,从而帮助人们进行水下地质勘探、海洋调查等工作。
4. 水下运输:在水下运输中,考虑到水的压力对物体的影响,需要合理地设计和制造船只、潜艇等水下交通工具,确保其在不同深度下的安全运行。
静水压强是液体在静止状态下由于液体自身重力而产生的压力。
其计算公式为P = ρgh,受到液体的密度、重力加速度以及液体所在的深度的影响。
静水压强的应用广泛,涉及到水压力的应用、水下施工、水下探测以及水下运输等领域。
对于理解和应用静水压强,有助于我们深入了解液体力学的基本原理,并在实际生活和工作中进行相应的应用。
静水压强及其特性-精选文档

2.静水压强的特性
特性1静水压强的方向垂直并且指向受压 面;
N
AP
Ⅰ
τ
B
NP
Ⅱ Pn
特性2:静止液体内任一点沿各方 向上静水压强的大小都相等。
• 或静压强的大小与作用面的方位无关
pnpxpypz
等压面
液体中由压强相等的各点所构成的 面(可以是平面或曲面)称为等压面, 静止液体的自由表面就是等压面。
H
L
L/3
P
h
h
H
H
eL
H
h
h H
h
(Hh)
H
• 2.静水压力的计算
(1)用压强分布图求矩形平面上的静水总压力 适用条件:受压面为矩形平面。
例题2 图示为复式比压计,各点的高度
如图所示,已知油的密度为ρ油=800kg/m3, 水银的密度为水的密度13.6倍,求A,B两点
的压强差。
解:
油0.89.87.84KNm3 水银 1.369.813.238KNm3
由等压面原理可知, 1-2.3-4.和5-6为等 压面,则
p1p2pA0.5油 p3p4p2水银 0.2油0.5
1. 重力作用下静水压强的基本方程式
p p 0 h
上式表明:静止液体内任一点的静水压强
由两部分组成,一部分是液体表面压强p0 ,它
将等值地传递到液体内每一点;另一部分是高
度为h的液柱产生的压强γh 。该式还表明,静 水压强p沿水深呈线性分布。对于连通器,水深
相同的点组成的面是等压面;当自由表面是水 平面时,等压面也是水平面。
如果连通的静止液体区域包括多种液体,则须在 它们的分界面处作过渡。
静水压强及其特性

0
pzAz pnAz 3 ZzAz 0
35
p x Ax
pnAx
1 3
XxAx
0
p y Ay
pnAy
1 3 YyAy
0
1
pzAz pnAz 3 ZzAz 0
when : Ax , Ay , Az 0 V A Point
18
2.1 静水压强及其特性
2.1.1 静水压强 2.1.2 静水压强的两个性质
1. 静水压强与受压面垂直并指向受压面 2. 任一点静水压强大小和受压面方向无关
19
2. 任一点静水压强大小和受压面方向无关
pc
h
pc
c
c
pc
图2.1.5 静水压强方向示意
20
p1
A
p2
p1 = p2
图2.1.6 平板转折处的静水压强
2 水静力学
1
水静力学的任务 研究液体平衡的规律及其应用
液体平衡
• 绝对静止 • 相对静止
2
• 绝对静止 液体相对地球没有运动,液体处于静止状态
3
• 相对静止 液体相对于地球处于运动,但液体相对于运
动着的容器之间却是静止的、无相对运动的。 直线等加速度行驶车厢中的容器所盛液体。
4
水静力学特点 液体内部不存在内摩擦力 实际液体与理想液体无区别
21
证明 任一点静水压强大小与受压面方向无关
22
pz
pn
?
py
px
图2.1.7 任一点各方向静水压强示意
如能证明,任意点三个方向的静 压强都等于任意方向的静水压强, 则就证明了这个性质。
水力学——水静力学
第一章 水静力学考点一 静水压强及其特性1、静水压强的定义:静止液体作用在受压面每单位面积上的压力称为静水压强。
2、静水压强的特性:(1)静水压强垂直于作用面,并指向作用面的内部; (2)静止液体中任一点处各个方向的静水压强大小相等。
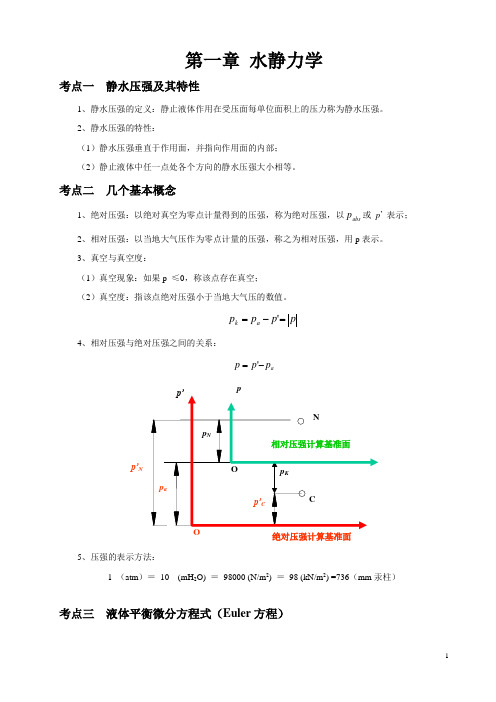
考点二 几个基本概念1、绝对压强:以绝对真空为零点计量得到的压强,称为绝对压强,以abs p 或 p ’ 表示;2、相对压强:以当地大气压作为零点计量的压强,称之为相对压强,用p 表示。
3、真空与真空度:(1)真空现象:如果p ≤0,称该点存在真空; (2)真空度:指该点绝对压强小于当地大气压的数值。
p p p p a k =-='4、相对压强与绝对压强之间的关系:a p p p -='5、压强的表示方法:1 (atm )= 10 (mH 2O) = 98000 (N/m 2) = 98 (kN/m 2) =736(mm 汞柱)考点三 液体平衡微分方程式(Euler 方程)绝对压强计算基准面p’Np1、微分方程:液体平衡微分方程式,是表征液体处于平衡状态时作用于液体上的各种力之间的关系式。
2、综合表达式——压强差公式 :)=z Z y Y x X z zpy y p x x p p d d d (d d d d ++=∂∂+∂∂+∂∂ρ )=z Z y Y x X p d d d (d ++ρ 3、积分结果 :若存在一个与坐标有关的力势函数U (x ,y ,z ),使对坐标的偏导数等于单位质量力在坐标投影,即⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂=∂∂=∂∂=z U Z y U Y x UX 可得U z Z y Y x X z zUy y U x x U p d d d d (d d d d ρρ=++=∂∂+∂∂+∂∂)=U p d d ρ=积分上式得到: C U p +ρ= 或者 )(00U U p p -+ρ= 式中, 为自由液面上的压强和力势函数。
考点四 等压面1、定义:静止液体中压强相等的点所组成的面称为等压面。
静水压强的两个特性

静水压强的两个特性
静水压力,也称作静水头,是指将水从一定高度引入容器中所产生的压力,是
直接决定水在管道中的流速和流动特性的重要因素之一。
静水压强的特性是它可以产生各种流量。
它在气体管网中的应用是显而易见的,在固定的气压下,只要改变水压,就可以改变管网中流体的流量。
此外,静水压强还有助于控制和调节气体管线中流体的流动。
在管道中有一个阀门可以控制水的分流,从而调节气体的流速。
静水压强的另一个特点是它的线性可调性。
它的可调范围在整个压力阶层上都
是可调的,并且可以按照指示的要求改变压力。
另外,压力的改变不会影响到水的质量,因此可以在不改变水容量的情况下调整水压。
最后,静水压强可以提供最明确和精确的压力控制方案。
很多行业甚至涉及到
比较复杂的管道,可以利用静水压力来控制管道内各段的压力,而且可以比较准确地把控管道内流体的流量。
总之,静水压强具有改变流量、线性可调性、精准控制水压等特点,是众多行
业提升自身效率、优化压力控制方案的重要手段。
只要正确的利用静水压强的特性,就能以有效的方式改善行业的运营效率。
静水压强及其特性共45页

56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。 60、迢迢新秋夕,亭亭月将ห้องสมุดไป่ตู้。
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
静水压强分布图实例

水下地形地貌研究
静水压强分布图可以反映水下地形地貌的特征,通过分析压力分布和变化规律, 揭示水下地形的起伏、坡度、河床深度等信息。
静水压强分布图还可以用于研究水下地貌的形成和演化过程,通过模拟不同时间 点的压力分布,分析水流动力和地质作用对地貌的影响。
静水压强分布图在环境监测中的应用
静水压强分布图在环境监测中具有广 泛的应用价值,如监测水库、湖泊、 河流等水域的水位变化,评估水利工 程对周边环境的影响等。
VS
预警系统:基于静水压强分布图的监 测数据,可以建立预警系统,及时发 现异常情况,为防洪抗旱等应急响应 提供支持。
THANKS FOR WATCHING
静水压强分布图实例
目录
• 静水压强概述 • 静水压强分布图的绘制 • 静水压强分布图实例解析 • 静水压强分布图的应用 • 静水压强分布图的未来发展
01 静水压强概述
静水压强的定义
01
静水压强是指在静止液体中,由 重力产生的压力分布。
02
静水压强的大小与液体深度和液 体的密度有关。
静水压强的特性
误差分析
误差来源分析
分析测量过程中可能产生的误差来源,如测量设备的精度、环境因素的影响等。
误差评估
对测量误差进行评估,并采取适当的措施减小误差对结果的影响。
03 静水压强分布图实例解析
河流静水压强分布图
总结词
河流的静水压强分布图呈现了河流中不同位置的静水压强情况。
详细描述
河流的静水压强分布图是根据实测数据绘制而成,展示了河流中不同位置的静水压强值。这种分布图对于了解河 流的水力学特性、预测水流运动规律以及设计水利工程具有重要意义。
静水压强的特征

静水压强的特征
静水压强的特征
1. 定义
静水压强是指水体静止时产生的压强,也可以理解为水分子自身重力对单位面积的压力。
2. 形成的原理
静水压强是由于重力作用下,水分子受到下方水体的压力而产生的。
当水深增加时,上面的水体会对下方施加更大的压力,从而产生更高的静水压强。
3. 特征特点
静水压强具有以下特征:
•与水深成正比:静水压强与水深成正比关系,水深越大,静水压强越大。
•与液体密度成正比:静水压强与液体的密度成正比关系,密度越大,静水压强越大。
•与重力加速度成正比:静水压强与重力加速度成正比关系,重力加速度越大,静水压强越大。
4. 应用
静水压强有很多重要的应用,例如:
•水压力计:在实验室和工业中常用水压力计来测量静水压强,以便做进一步的研究和应用。
•水坝设计:在设计水坝时,需要考虑到静水压强对水坝的压力影响,以保证水坝的结构安全。
•水下探测器:在海洋勘探等领域,利用静水压强可以测量水深和进行海底地形的勘测等。
5. 总结
静水压强是水分子受到重力作用下产生的压力,其特征包括与水深、液体密度和重力加速度成正比。
静水压强在实验、工业和海洋勘探等领域有着重要的应用价值。
静水力学

pA pB ( m )△h △z
作用于平面壁上的静水总压力
静水压强分布图
1、相对压强分布图绘制原则 (1)用有向线段(或箭头)长度代表该点静水压强的大小。 (2)用箭头的放向表示静水压强的方向,必须垂直并指向受压
面。
2、相对压强分布图绘制方法 选择上下两点,计算压强大小,定性绘出两点的箭杆长度,连接 箭杆尾端,标注两点压强大小,图形中间以箭头填充。
水静力学
主要内容
静水压强及其基本特性 静水压强的基本规律
压强的单位及量测 作用于平面壁上的静水总压力 作用于曲面壁上的静水总压力
静水压强及其基本特性
一 静水压强
静水压力 把静止液体作用在与之接触的表面上的压力称为静水 压力。用大写字母P表示,受压面面积用A表示。
• 静水压强
绕一点取微小面积ΔA,极限值
等压面
在静止液体中,凡是静水压强相等的那些点组成的 面,称为等压面。 (1)在连通的同种的静止液体中,水平面必定是等 压面。 (2)静止液体的自由液面是一个水平面。 (3)两种液体的分界面是水平面。 成立条件:静止、连通及均质液体
压强的测量及计算
1、测压管
测压管就是一端开口的 玻璃管,管中液注高度就 反映了所测点的相对压强 p,p h h为测压管内液
2 a
绝
真
真
真
压强的三种表示方法:
压强
如图,表明了 绝对压强、相 对压强和真空 值之间的关系。
A 0 B A点相对压强 B点真空压强 相对压强基准
A点绝对压强
B点绝对压强
绝对压强基准
0
大气压
例1:
已知静止水体 中B点的绝对压强 pB=78kN/m2 , 求 A点的压强,A、B 两点的压差和B点 的真空度。
二章水静力学ppt课件

P0
hA
即为测压管高度。
这种测量压强的管子叫测压管。
h
在容器内有 pA = p0 h
A
在右管中有 pA = pa hA
ZA
因此 p0 h = pa hA
hA
=
pA
pa
=
p
所以:测压管高度hA表示A点的的相对压强(计算压强)
第二章 水静力学
若 P0<Pa
则:位于测压管中的水位高
度将低于容器内液面高度。
1、方法
由 pabs = p0 h压强与水深成线性关系。
因而,在任一平面的作用面上,其压强分布为一
直线。只要算出作用面最上和最下两个点的压强后
,即可定出整个压强的分布线。
2、原则 ⑴、每一点处的压强垂直于该点处的作用面。 ⑵、静水压强的大小随着距自由面的深度而增加
另外:对实际工程有用的是相对压强的图示。如欲
• Dy
•
p z
Pn
=
Ds
•
p n
Z D Pn Px A Py C
O B Pz X
Y
第二章 水静力学
四面体的体积D V为
Z D Pn Px A Py
D
V=
1
6
Dx
•
Dy
•Dz
C
O B Pz X
Y
总质量力在三个坐标方向的投影为
Fx
=1 6
•
Dx • Dy
• Dz X
Fy
=
1 6
•
Dx • Dy
• Dz Y
z ω
oA x
x
A
•
2x
y 2 y 2r
第二章 水静力学
第2章 水静力学

第二章 水静力学目的要求:掌握静水压强的有关概念;作用在平面、曲面上静水总压力的计算方法。
难点:压力体的绘制 全部内容均为重点水静力学研究液体平衡时的规律及其实际应用,静止时0=τ,只有p 存在。
§2-1 静水压强及其特性 一、定义P ∆—面积ω∆上的静水压力 (N )平均静水压强ω∆∆=Ppa 点的静水压强)(/lim 20a P m N d dpP p ωωω=∆∆=→∆二、静水压强的特性1、第一特性:静水压强的方向垂直指向被作用面。
2、第二特性:作用于同一点上各方向的静水压强大小相等。
yzp⊿⊿⊿zxxpp ynpxzynACBnzyxpppp,,,,则⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∆∆∆∆∆∆∆spyxpzxpzypnzyx212121⎪⎪⎪⎩⎪⎪⎪⎨⎧∆∆∆∆∆∆∆∆∆zyxZzyxYzyxX616161ρρρ沿x方向力的平衡方程:61),cos(21=∆∆∆+∆-∆∆zyxXxnspzypnxρ612121=∆∆∆+∆∆-∆∆zyxXzypzypnxρ1=∆+-xXppρ取微分四面体无限缩至o 点的极限表面力质量力C pz C z p dz gdz dp =+→'+-=→-=-=γγγρ或 γγ2211p z p z +=+——重力作用下水静力学的基本方程。
对于液面点与液体内任意点h p p pz p h z γγγ+=→+=++00——水静力学基本方程的常用表达式说明:(1)当 2121z z p p >< ,位置较低点压强恒大于位置较高点压强。
液面压强0p 由γh 产生的压强(3) p 随h 作线性增大。
(4)常用a a p h p p ,γ+=为大气压强, 取p a =1个工程大气压=98kN/m 2。
(5)h p p ∆+=γ12二、等压面1、定义:在同一种连续的静止液体中压强相等的点组成的面2、等压面方程:0=dp 0=++Zdz Ydy Xdx3、特性:(1)平衡液体中等压面即是等势面。
静水压强及其特性重力作用下静水压强的分布规律

2.几何意义
单位重量流体所具有的能量也可以用液柱高度 来表示,并称为水头。
式中:
z 具有长度单位,如图所示,z 是流体质点离基准面
水静力学的主要内容
§2-1 静水压强及其特性 §2-2重力作用下静水压强的分布规律 §2-3压强的计算基准和量度单位 §2-4测量压强的仪器 §2-5静水压强分布图 §2-6 作用在平面上的静水总压力 §2-7 作用在曲面上的静水总压力 §2-8液体平衡微分方程 §2-9重力和惯性力同时作用下液体的相对平衡
相对压强为什么是负值? 什么位置处相对压强为零?
pk pa p 98 59.8 38.2kN / m2
§2.4测量压强的仪器
1. 测压管 2. U型管测压计 3. 差压计 4. 微压计
1、测压管
如图可测水中大于大气压的相对压强
pa
p0
h
A
测压管
p gh;
2、 U 形管测压计 当被测流体压强较大时,常采用图所示的U形管测压计在
的高度,所以z的几何意义表示为单位重量流体的位置高
度或位置水头。
p g
也是长度单位,它的几何意义表示为单位重
量流体的压强水头。位置水头和压强水头之和称为静水
头。所以该式也表示在重力作用下静止流体中各点的静
水头都相等。 在实际工程中,常需计算有自由液面的静
止液体中任意一点的静压强。
z
p0
pA
g
A Z
强相等,即任一水平面都是等压面。
水力学静水压力

z
hd—z —曲面AB所托的液体的体积,
称为压力体,其体积用V表示
。
Pz V
作用在曲面上静水总压力的垂直分力Pz 等于其压力体的重量。
2、压力体的绘制和 Pz 的方向 (1)压力体是由曲面本身、过曲面边缘的铅直面、自由液面
(或自由液面的延长面)包围而成的体积。 (2)压力体不一定由实际水体构成,故分为实压力体和虚压力体。
dP hd (d 很小,近似认为各点压强相等)
y sind
P dP y sind sin yd sinyc
hc pc
其静水总压力的大小等于形心点的
压强乘以受压面的面积。
2、方向:垂直指向被作用面。 3、作用点:用合力矩定理
PyD
ydP
y2 sind
sin
y 2 d
(3) Pz 的作用线通过压力体的体积形心
四、静水总压力
大小:P Px2 Pz2
方向: tg Pz
Px
作用点:通过 Px 、Pz的交点K,过K点沿P的方向延长交曲面
得D点,对于圆弧面,P的延长线通过圆心。
p --单位压能
z+
p
-- 单位势能
§2-5 压强的单位及液柱式测压计
一、压强的单位
1、用应力单位表示 2、用大气压表示 3、用液柱高度表示
N / m2 或Pa 1个工程大气压=98KPa=9800Pa
1个工程大气压=9800Pa=10m水柱=735mm水银柱
二、液柱式测压计
1、测压管 pA hA
则称该点存在真空。
真空度 p p p p
K
a
abs
(该点绝对压强小于当地大气压强的数值)
第一章 水静力学
实际工程中, 作用于平衡液 体上的质量力 常常只有重力 ,即所谓静止 液体。
18
重力作用下 X=0,Y=0,Z=-g ,代入平衡微分方 程式
dp ( f x dx f y dy f z dz) dz 积分得 p
z
g
C
而自由面上
p0 p z z0 , g g
pk pa p
'
29
例1-2:一封闭水箱(见图),自由面上气体压强 为85kN/m2,求液面下淹没深度h为1m处点C的绝
对静水压强、相对静水压强和真空度。
解:C点绝对静水压强为
p' p0 gh 85 9.8 1 94.8kPa
C点的相对静水压强为
p p' pa 94.8 98 3 .2kPa 相对压强为负值,说明 C 点存在
27
地球表面大气所产生的压强为大气压强。海拔高程不同,大气压强也有差异。我国法 定计量单位中,把98223.4 Pa称为一个标准大气压。
水利工程中,自由面上的气体压强等于当地大气压强,故静止液体内任意点的相对压 强为
p ( pa gh) pa gh
28
三、真空及真空度
绝对压强总是正值,相对压强可能为正也可能为负。 相对压强为负值时,则称该点存在真空。 真空度是指该点绝对压强小于当地大气压强的数值。
作用下沿等压面移动。
F ( f xi f y j f z k )dm ds (d xi d y j d z k )
静水压强的两个特征

静水压强的两个特征
静水压强有以下两个特征:
1. 静水压强的方向垂直并且指向受压面:当液体静止时,其对受压面施加的压力是垂直于受压面的,并且指向液体内部。
这是因为液体分子间的碰撞和相互作用使得液体内部的压力向外传递,并最终在受压面上产生一个垂直的压力。
2. 静止液体内任一点沿各方向上的静水压强大小都相等:在静止液体内,无论观察的位置在液体中的哪个点,沿各个方向上的静水压强大小均相等。
这是因为液体是一个连续介质,液体分子之间的相互作用使得压力在整个液体内部均匀传递,导致沿任何方向上的静水压强都保持相等。
换句话说,液体的压力是各向同性的。
20120308水力学第一章第二部分

四、压力体
压力体是所研究的曲面(淹没在静止液体中的部分)到自 由液面或自由液面的延长面间投影所包围的一块空间体积。 其计算式
V p hdAz
A
是一个纯数学体积计算式。作用在曲面上的垂直分力的大 小等于压力体内液体的重量,并且与压力体内是否充满液 体无关。
1. 压力体的种类
压力体仅表示 Ahd Az 的积分结果(体积),与该体积内是否有液体存在无关。
LD ( L
h1 ) e 14.71m sin 60
用解析法求解:
P h b dL h b
h1 h2
dh 1 1 1 2 b(h2 h12 ) Lb(h1 h2 ) sin 2 sin 2
结论:
液体作用于平面上总压力的计算: 1. 解析法 首先确定淹没在流体中物体的形心位置以及惯性矩,然后由解析 法计算公式确定总压力的大小及方向。
解:当不计门重时,T至少需克服闸门与门之间的摩擦力,故T=P·f为此, 需求出P。 用图解法求P及其作用点。 如图画出其压力分布图,则 P=A·b=1/2 (γ h1+γ h2) ·L·b =2964KN
作用点距闸门底部的斜距
e
P距平面的斜距
L(2h1 h2 ) 2.79m ( h1=10,h2=10+6sinα) 3(h1 h2 )
外包线亦为曲线。
静水总压力的大小:
其中b为矩形受压面的宽度; Ω为静水压强分布图形的面积;
FP b
静水总压力的方向:垂直并指向受压面
静水总压力的作用点(压力中心或压心):通过压强分布体的重心 (或在矩形平面的纵对称轴上,且应通过压强分布图的形心点)
P
H H
