超静定梁的影响线绘制机动法.ppt

合集下载

结构力学-机动法作静定梁的影响线

C
C1 VC
第19讲机动法作静定梁的影响线
例：利用机动法作
下图所示梁上B 截面的弯矩、B 左右
剪力影响线。
第19讲机动法作静定梁的影响线
VB左
例：利用机动法作
下图所示梁上B 截面的弯矩、B 左右
剪力影响线。
VB左
VB右 VB右
练习：习题10-1
静定结构在拆除相应的 ‘一个约束’后，具有一个自由度，结构变为机构；拆除相应约束后，仍未静定的部分无虚位移。
第19讲机动法作静定梁的影响线
Structural Mechanics
结构力学
机动法作静定梁的影响线
第19讲机动法作静定梁的影响线
一、问题引入
以下用静力法简支梁的反力影响线的步骤 P=1
（1）反力取向上为正。
过程麻烦！！！ x
x
（2）选择坐标如图：
P=1
l
M B 0 M A 0
A
RA
B
第19讲机动法作静定梁的影响线
１、优点： 1）不用计算竖标就能画出影响线的轮廓 2）用静力法所做出的影响线形状也可用机动法快速校核。
２、理论依据：以虚位移原理为理论基础
第19讲机动法作静定梁的影响线约束反力影响线
第19讲机动法作静定梁的影响线
机动法绘制约束反力影响线原理
刚体体系的虚功原理
教学方法：一去一加，去掉与量值相应的约束, 带以正向的约束力，课件配以动画演示
第19讲机动法作静定梁的影响线
机动法步骤（P267）
1）一去一加：去掉与量值相应的约束, 带以正向的约束力约束反力影响量——去支承链杆，并代以正向的约束力Z。
剪力影响量——去掉限制发生错动的约束，将刚结点改为滑动端，并代以一对正向的约束力Z。

结构力学影响线4

哈工大土木工程学院
19/ 81
第五章移动荷载作用下结构计算
FP=1 x
FP=1
<状态1>
P ( x)<状态2>
ILFBy
由刚体虚功方程
FBy B 1 P ( x) 0
FBy
FBy
P B
1
1
B
P(x)
B
FBy 与P (x)的变化规律
一致，故可用其位移图
1
比拟影响线。当B＝1
时，位移图与影响线形
(2) 简支梁弯矩影响线：变铰，沿力偶方向微小转动
A
FP=1 MC MC
B
C
C 1 P
ab
ILMC
l
哈工大土木工程学院
9 / 81
第五章移动荷载作用下结构计算
(3) 简支梁剪力影响线：变错动机构（剪力铰）
A
FP=1 FQC
B
C FQC
P
C 1
b
l
a l
ILFQC
哈工大土木工程学院
10 / 81
设单位荷载作用位置 x ，由力法可求支座B的
约束反力FBy。
FP=1
A x
EI
B
l
解除FBy对应的约束，并以FBy代之，取它作为力法的基本结构。
FP=1
A
B
由B 点的位移条件建立力法方程： FBy
11FBy ( x) 1P ( x) 0
哈工大土木工程学院
14 / 81
第五章移动荷载作用下结构计算
除在基本部分发生虚位移外，还影响到附属部分；若在附属部分形成机构，则虚位移图仅涉及到附属部分。
规律：先从欲求影响量值截面所在跨画起，然后利用

结构力学第八章影响线

与其他截面上的弯矩无关。
(4) 绘制规定不同 MC的影响线中的正弯矩画在基线的上方，负弯矩画在基线的下方，标明正负号。
★第三节
结点荷载作用下梁的影响线
(1)支座反力FRA和FRB的影响线
(2)MC的影响线 C点正好是结点。
(3) MD的影响线 (4) FQCE的影响线力，以FQCE表示。 MD的影响线如图8-5c所示。在结点荷载作用下，主梁在C、E两点之间
3.弯矩影响线作法由此得简支梁作弯矩影响线简易作法：先作一基线，在基线对
应所作弯矩影响线截面处作一竖线，其值为ab/l，连接A、B两
端，即为此截面弯矩的影响线，如图8-2e所示。弯矩影响系数其量纲为L，单位为m
3.弯矩影响线作法【例8-1】试用静力法绘制图8-3所示外伸梁的FAy、FBy、FQC、 MC 、FQD、MD的影响线。【解】(1)绘制反力FAy、FBy的影响线。取A点为坐标原点，横坐标x向右为正。当荷载F＝1作用于梁上任一点x时，分别求得反力FAy、FBy的影响线方程为
这就是FRB的影响线方程。由此方程知，FRB的影响线是一条
直线。在A点，x=0，FRA=0。在B点，x=1，FRB=1。利用这两个竖距便可以画出FRB的影响线，如图8-2b所示。
(2) 支座反力FRA影响线作法将FP=1放在任意位置，距A点为x。由平衡条件解得这就是FRA的影响线方程。由此方程知，FRA的影响线也是一
1.支座反力的影响线 (1) 支座反力FRB影响线作法如图8-2a所示简支梁，将FP=1放将FP=1放在任意位置，距A点为x。
在任意位置，距A点为x。
(2) 支座反力FRA影响线作法
(1) 支座反力FRB影响线作法如图8-2a所示简支梁，将FP=1放在任意位置，距A点为x。由平

多跨静定梁的影响线利用影响线求量值连续梁影响线形.ppt

FP=1距A支座的距离为x，并假设反力方向以向上为正，
由平衡方程ΣMB=0，得
FA l 1 (l x) 0
lx FA l
(0 x l)
上式称为反力FA的影响线方程，它是x的一次式，即FA的影响线是一段直线。为此，可定出以下两点：
当x=0时， FA=1 当x=l时， FA=0 即可绘出反力FA的影响线，如图 (b)所示。绘影响线图形时，通常规定
MC=FB·b， FSC =-FB 当F=1在截面C以右部分移动时，取截面C以左部分为隔离体，由平衡条件得
MC=FA·a， FSC =FA 由此可知，MC和FSC的影响线方程和简支梁相应截面的相同。因而与作反力影响线一样，只需将相应简支梁截面C的弯矩和剪力影响线的左、右两直线向两伸臂部分延长，即可
FSC+FB=0
FSC=-FB
由此可知，在AC段内，FSC的影响线与反力FB的影响线相同，但正负号相反。因此，可先把FB影响线画在基线下面，再取其中的AC部分。C点的纵距由比例关系可知为。该段称为FSC影响线的左直线，如图4-4(c)所示。
当 F=1 在 CB 段移动时 (a<x≤l) ，可取 AC 段为隔离体，由 ΣFy=0，得
MK=-x (0≤x≤d) FSK=+1
由此可作出MK和FSK的影响线，如图4-6(b)、(c)所示。
(a) D
A
l1
x F=1 B
KE
d
l
l2
(b) (c)
(d)
(e)
l1 l
图4-6
d MK影响线
1
FSK 影响线
1 FRSB影响线
l2 FSLB影响线 l 1

10.5 用机动法作静定梁的影响线

C1
FP =1
P
B
MC C MC
a
All Rights Reserved 重庆大学土木工程学院®
b)
1
ab 竖向位移 P图 l C B
A
2）使铰C左右两刚片沿MC的正方向发生相对转角 Z 1 的虚位移，如图所示。须注意的是，这里应理解为是一个可能的微小的单位转角，而不是 1rad。 3）列写虚位移方程为（假设 P向上为正）
All Rights Reserved
B
B 1
C
B
重庆大学土木工程学院®
3）列写虚位移方程（假设 p 向上为正）
A C F QC Z 1 P 0 FP =1 B A
Z =1
FQ C C
C2
P
Fp =1 B
a P b P FQC l P Z 1
A1
Z =1 a P A 当取时的荷载作用点的竖向位移图（ B P MC C MC 图）即为F 影响线，如图所示。由三
x A FP =1 K B E F C D
2m
6m
2m 2m
8m
2m
8m
2m
第一类，属于附属部分的某量值。撤去相应约束后，体系 D F C 1m A B E 2 K 只能在附属部分发生虚位移，基本部分仍不能动。因此， M M 3m 2 1 位移图只限于附属部分。 4
K K
3 m K1 2 1 2m
K 第二类，属于基本部分的某量值。先作基本部分某量值的 1 4 位移图，再向两侧作直线延伸，在延伸范围内（仅限于所 3 K 4 支承的附属范围内），遇全铰处转折，遇支座处为零，其间连以直线。
1 E (B 右 E向上平移至B 1右 E1 ) 1 C E FQB 右

用机动法绘制静定梁的影响线

2）使该量值的作用点（面）沿该量值的正方向发生单位虚
位移，绘出静定梁的虚位移图，即为该量值的影响线。
3）标明正负号。在基线以上的图形取正号，在基线以下的
图形取负号。
目录
影响线\用机动法绘制静定梁的影响线
【例18.2】试用机动法绘制下面图ａ所示简支梁横截面C上的
弯矩MC和剪力FSC的影响线。
【解】 1)绘弯矩MC的影响线。将与MC相对应的转动约束去掉，即在横截面C处改刚接为铰接，并以一对大小为MC的力偶代替转动约束的作用。然后使MC的作用面沿MC的正方向发生单位虚位移δ
=1，δ=+ 是C点左右两截面的
x F=1
A
aC
b
l
(a)
1
A y
＋
MC (b)
B
B
相对转角，如图b所示。
影响线\用机动法绘制静定梁的影响线
x F=1
A
B
aC
b
l
(a)
b
a ab/l
A
C
B
(c)MC的影响线
所得的虚位移图即表示MC的影响线。如图c中实线所示，根据几何关系求得C点的竖标为ab/l。
建筑力学
影响线\用机动法绘制静定梁的影响线
用机动法绘制静定梁的影响线
1. 基本原理用静力法可以绘出任何结构在单位荷载作用下的影响线。但当结构型式比较复杂时，用静力法就比较繁琐，此时用机动法绘制影响线就比较简单。机动法绘制结构的影响线是以刚体虚功原理为依据，把绘制内力或支座反力影响线的静力问题转化为绘制刚体位移图的几何问题。下面以绘制简支梁支座反力影响线为例，说明应用机动法绘制结构影响线的基本原理。
目录
影响线\用机动法绘制静定梁的影响线

chap12超静定结构的影响线

日期：2020/1/1 15:35 Copyright © 2003-2020年1月版权所有：上海理工大学城建学院土木工程系第 12/52 页
上海理工大学结构力学教程
0
2
4
6
8
10
12
Mmax
0
210 －100 120 －100 210
0
Mmin
0
60 －260 －30 －260 60
0
260
260
0
12
100 3 4 5 360 7
100 8 9 10 11 12
60
60
120
210
210
弯矩图包络图（kN.m)
将设计时不需要考虑的弯矩图，在弯矩图包络图用虚线表示。

lAB 6EI
(2M
B

M
A
)

lBC 6EI
(2M
B

M
C
)
杆端弯矩使梁下侧

P1

x(l x) 6EIl
(M
A
(2l

x)

M
B
(l

x))
受拉为正。
日期：2020/1/1 15:35 Copyright © 2003-2020年1月版权所有：上海理工大学城建学院土木工程系第 5/52 页
上海理工大学结构力学教程
§12-2 x
A
连续梁的最不利荷载布置及内力包络图
P=1
B
C
D
E
K
F
MK.I.L
MKma↓x↓↓↓↓↓↓
↓↓↓↓↓↓↓
↓↓↓↓↓↓↓

超静定影响线

6m
6m
6m

2.依次作出每一跨分布活载作用时的弯矩图（每跨4等分）
96
66
36
6 18 24 第1跨布活载 12 6
63 111 132

2.依次作出每一跨分布活载作用时的弯矩图（每跨4等分）
96 66 36
6
第1跨布活载 63 111 132 36 18 第2跨布活载 63 108 36 6 第3跨布活载 6 12 18 24 66 54 72 18 24 12 6
1 0.3125 11/8
2a
2a
a
从上述作法可见，其过程与静定结构影响线的作法并没有不同，只是计算麻烦，需用力法求解

例2 静力法作连续梁支座处弯矩影响线。
x P=1
1 L L
2 L
思路：按影响线的定义，作出P=1在不同位置x处的M1表达式。 1）P=1在第一跨移动，取如下基本体系

力法基本体系
6m
6m
6m

弯矩影响线轮廓
B 1 2 C 3 1 跨截面
2 跨截面 3 跨截面
支座B 支座C

说明：
要使1跨某截面取最大值，只需把第1跨和第3跨布满活载；要使1跨某截面取最小值，只需把第2跨布满活载；
1. 由1跨截面弯矩影响线可知：
2. 由支座B截面弯矩影响线可知：
要使截面B的弯矩最大，只需第3跨布满活载；
A
B K C D E
F

三、影响线的应用：连续梁的内力包络图
1．基本原理连续梁的设计必须以该梁在恒载（自重等）及活载（人群、货物等）作用下每一截面上可能出现的内力最大值及最
小值作为设计依据。
其中恒载作用下的内力是确定的；活载作用下的内力随分布的不同有不同的值。下面以连续梁为例说明活载分布的最不利情形的特点

04-讲义：10.2 静力法作静定梁的影响线

第二节静力法作静定梁的影响线绘制影响线的基本方法有两种：静力法和机动法。

静力法作影响线的基本步骤包括：（1）选定坐标系，将单位集中荷载1F =放在任意x 位置；（2）根据平衡条件写出所求量值与荷载位置x 的函数关系式（称为影响线方程）；（3）根据影响线方程直接绘出该量值的影响线图形。

本节主要讨论利用静力法作单跨静定梁、多跨静定梁的支座反力及截面内力的影响线。

一、简支梁的影响线作如图10-4(a)所示简支梁支座反力A F 、B F 及截面C 的弯矩C M 、剪力SC F 的影响线。

取A 为坐标原点，向右为x 轴正向。

假设1F =作用在简支梁上任意x 位置（l x ≤≤0），根据梁的平衡条件0AM=∑和0B M =∑，可得到支座反力A F 、B F （向上取为正向）与x 的函数关系：l x l x F l x l F B A ≤≤⎪⎪⎭⎪⎪⎬⎫=-=0 （10-2）式（10-2）就是A F 、B F 的影响线方程。

由此可知：A F 、B F 与荷载位置x 呈一次函数关系，所以A F 、B F 的影响线为直线图形。

因此只需定出两点即可绘出支座反力A F 、B F 的影响线，分别如图10-4(b)及图10-4(c)所示。

作弯矩C M 影响线时，仍以结点A 为坐标原点，x 表示单位集中荷载1F =作用点位置，以使梁截面的下边缘纤维受拉的弯矩为正。

当1F =在截面C 左侧梁段AC 上移动时，为了计算方便，取截面C 以右部分作为隔离体，由截面法可得：b F M B C .=（a x ≤≤0）（10-3a ）由于AC 范围内B F 影响线为一条直线，且b 为常数，因此C M 影响线在AC 范围内也为直线，而且竖标等于B F 影响线相应竖标乘以b 。

当1F =在截面C 右侧梁段CB 上移动时，取截面C 以左部分作为隔离体，由截面法可得：a F M A C .=（l x a ≤≤）（10-3b ）同时，由于在CB 范围内A F 影响线为一条直线，且a 为常数，因此C M 影响线在CB 范围内也为直线，而且竖标等于A F 影响线相应竖标乘以a 。

连续梁的影响线和内力包络图

KK X K KF 0
得
XK
KF KK
(a)
式中： δKK ——由于XK＝1 的作用，基本结构上截面
K沿X的方向所引起的虚位移，如图c所示，其值与荷载F=1的位置无关，为一
正值常数；
δFK——由于荷载F＝1的作用，基本结构上截面K沿XK的方向所引起的位移，如图d所示，其值随F=1的位置移动而变化。
X K FK （c）
由此可见，由 δKK ＝1而产生的梁的虚竖向位移图就代表XK的影响线，如图e所示。因两者的符号相反，故在影响线中，应取梁轴线上方的图形为正，下方的为负。
目录
影响线\连续梁的影响线和内力包络图
综上所述，由机动法绘制超静定梁的某量值XK影响线的步骤如下：
1）去掉与XK相应的约束，并用XK代替其作用。 2）使所得基本结构沿XK的正向产生单位虚位移，由此得到的梁的虚竖向位移图即代表XK的影响线。 3）在梁轴线上方的图形标注正号，下方的标注负号。
建筑力学
影响线\连续梁的影响线和内力包络图
连续梁的影响线和内力包络图
1.1 连续梁的影响线
连续梁属于超静定梁，欲求影响线方程，必须先解超静定结构，并且反力、内力的影响线都为曲线，绘制较繁琐。
土木工程中通常遇到的多跨连续梁在活载作用下的计算，大多是可动均布荷载的情况（如楼面人群荷载）。此时，只需知道影响线的轮廓，就可确定最不利荷载位置，因此，对于活载作用下的连续梁，通常采用机动法绘制影响线的轮廓。
目录
影响线\连续梁的影响线和内力包络图
设有一n次超静定梁，如图a 所示，现绘制某指定量值XK（例如MK）的影响线。
为此，可先去掉与XK相应的约束，并以XK代替其作用，如图 b所示，把这个（n－1）次超静定结构作为基本结构

结构力学-第4章影响线

简要介绍某大桥的工程背景，包括桥梁类型、跨度、设计荷载等。
影响线和包络图在该桥设计中的应用
详细阐述影响线和包络图在该桥设计中的应用过程，包括影响线和包络图的绘制、最不利位置的确定、最大内力的计算等。
设计结果分析与评价
对该桥的设计结果进行分析和评价，包括结构安全性、经济性等方面的评估。同时，可以与其他设计方案进行对比分析，以进一步验证影响线和包络图在工程设计中的有效性和优越性。
通过绘制建筑结构的包络图，可以找到结构在地震作用下的最大变形和位移，为结构的刚度设计和稳定性分析提供依据。
影响线和包络图在建筑结构优化设计中的作用
利用影响线和包络图，可以对建筑结构进行优化设计，如调整结构布置、改变构件截面等，以提高结构的抗震性能和经济效益。
工程案例分析：某大桥设计过程剖析
工程背景介绍
结构优化设计
根据影响线的形状和分布，对结构进行优化设计，以改善结构的受力性能。
80%
工程实例分析
结合具体工程实例，利用影响线理论进行结构分析和设计，验证理论的正确性和实用性。
03
超静定结构影响线绘制与应用
超静定梁影响线绘制实例
实例一
实例三
一次超静定梁的影响线绘制。通过选取基本体系和基本未知量，利用力法方程求解多余未知力，并绘制影响线。
影响线用于确定桥梁结构在移动荷载作用下的最不利位置
通过绘制桥梁结构的影响线，可以确定移动荷载在桥梁上的最不利位置，从而进行结构分析和设计。
包络图用于确定桥梁结构的最大内力
通过绘制桥梁结构的包络图，可以找到桥梁在移动荷载作用下的最大内力，为桥梁的强度设计和稳定性分析提供依据。
影响线和包络图在桥梁优化设计中的作用
影响线在结构优化中的应用

结构力学专题四(机动法做影响线)

A
x
FP=1
k
B
c
l
a
b
小结：
用机动法做影响线的最大优点是能直接给出影响线的形状，从中看出影响线的特征点（零点、折点），对一些只要求形状而不要求纵距数值的影响线来说（包括超静定结构），机动法有许多优点。
机动法的步骤：１、去掉约束，代之以反力或内力；２、沿所求量值的正方向做单位虚位移图；该图即为
第四章影响线
§4-6 机动法做影响线
目的：不经计算直接得到影响线的形状（包括超静定结构），可用来对静力法的结果进行校核。
理论基础：虚功原理
单位虚位移法
方法特点：把做影响线的静力计算问题转化为作位移图的几何问题。
一、单跨梁影响线１、反力（YB）影响线 2、内力（MK）影响线 3、内力（FQK）影响线
三、联合法例3 ：作图示连续梁C支座反力影响线和B支座弯矩影响线。
x FP =1
A
B
C
D
小结：
1）撤除与x1相应的约束，使原结构成为n-1次超静定结构。
2）使体系产生沿x1的正方向产生位移，作结构在x1=1作用下的挠度图，该图即为δP1(x)图。x1影响线形状与δP1(x)图形相同，只是正负号相反。
一、静力法
例1：作图示梁B支座反力影响线。
x F＝1
A
B
EI
L
x1
x2 2 L3
(3L
x)
x
F＝1
x1
1
x1影响线
二、机动法
例2 ：作YC、MA、Mk、FQk、MC、FQC左、FQC右影响线。
A
FP=1
B
Ck D
E
１、用机动法可以迅速得到影响线大致形状；２、连续梁影响线形状是曲线；

10(超)静定结构的影响线

§9-5 超静定力的影响线1、影响线的特征与求解方法1）影响线的特征静定结构——反力、内力影响线均为直线；位移影响线为曲线。

超静定结构——各量值的影响线均为曲线。

2）影响线的求作方法静力法——利用静力平衡条件求影响线方程，进而绘制影响线。

但对超静定力的影响线须解超静定问题，复杂、少用。

机动法——利用影响线与移动载荷作用点位移（挠度）图的比拟关系，快速绘制影响线轮廓。

简便、实用。

2、机动法求作超静定力影响线以图9-14连续梁（超静定梁）M K的影响线为例，说明用机动法求作超静定力影响线的方法。

1）取基本结构（超静定、几何不变体系）图b——去掉与XK 相应的约束，代之以(暴露出)约束反力XK ；A B C D EF P=1K（a）原结构A B C D EF P=1X K(M K)(下拉为正)(b)基本结构图9-14§9-5 超静定力的影响线2）建立力法典型方程k kk kp X δδ+=1()kp k pk kk kkX x δδδδ∴=-=-⋅()()pk kp x x δδ=ABCD EF P =1K ABCD E F P =1X K (M K )(下拉为正)(b)基本结构§9-5 超静定力的影响线K 截面相对转角为0式中δkk ——常数,不随X 而变化。

δpk ——载荷F P =1位置参数X 的函数，即δPK =δPK (x)，其位移图如图9-14c 所示。

互等定理图9-14ABCDEX K (M K )(下拉为正)θB(c)挠度图⏹写成更明确的形式：()()1pk kkk x x X δδ=-ABCD EK+图9-15X k (M k )的影响线结论:X k 与δpk 成正比;挠度图即为影响线轮廓线图9-14ABCDEX K (M K )(下拉为正)θB(c)作用挠度图1kM=§9-5 超静定力的影响线X k 向上为正δpk 以向下为正(与p=1同向)X k 与δpk 反向3、求做超静定力影响线的步骤⏹1）撤去与所求约束力（或量值）相应的约束，代之以反力X K ；●2）使体系沿X K 正方向发生位移，作出移动载荷作用点的挠度δPK =δPK (x)（位移）图即为影响线X K (x)的形状；●3）将δPK 图除以常数δKK 使可确定影响线的具体数值；●4）横坐标以上图形为正号，横坐标以下图形为负号。

超静定梁的影响线绘制(机动法)

x (l − x) l
杆端弯矩使梁下侧受拉为正。
δ P 1例题2-11 M A ( 2 l − x ) + M B ( l + x )) δ 11 = AB ( 2 M B + M A ) + BC ( 2 M B + M C ) = ( 求图示连续梁支座弯矩M 的影响线。 B 6 EI 6 EI 6 EIl
(6 − x1 ) x3 (12 − x3 ) y ( x3 ) = 486
返回
0.x )
l
l
x1
P=1
B
x2
P=1
C
x2
P=1
D
6m MB=1
6m
0.25
6m
1 6 3.25 [(2 − 0.5) + (2 − 0.25)]= δ 11 = 6 EI EI 2 x1 (6 − x1 ) (6 − x1 ) x1 [− 0.5(12 − x1 ) + ( x1 + 6)]÷δ11 = AB: y ( x1 ) = 6× 6 EI 78 x2 ( 6 − x2 ) ( 6 − x2 ) x2 [(12 − x2 ) − 0.25( x2 + 6)]÷δ11 = (8.4 − x2 ) BC: y ( x2 ) = 6× 6 EI 93.6 x3 (6 − x3 ) (6 − x1 ) x3 (12 − x3 ) [− 0.25(12 − x3 )]÷δ11 = y ( x3 ) = CD: 6× 6 EI 486
0.346m
0.389m
0.497m
0.520m
A
0.123m
B
0.281m
C
D
0.151m

第十六章影响线

第十六章
影响线和内力包络图
• 第一节影响线的一般概念第二节 • 用静力法作简支梁的影响线利用影响线求反力和内力最不利荷载位置简支梁的内力包络图连续梁的内力包络图小结返回
• 第三节 • • • •
第四节
第五节
第六节
• 第一节
影响线的一般概念
一、活荷载定义：大小、方向不变，作用位置、时间改变的荷载。分类：1）移动荷载—大小和方向不变，但作用位置可移动。 2）暂时荷载—时有时无，可按一定方式任意布置。二、量值（以S表示）反力、内力（M,Q,N）及位移、变形等力学量的统称。三、影响线定义：在竖向单位移动荷载P=1作用下，表示结构的某一量值S 变化规律的函数图形，称为该量值的影响线。本章介绍：绘制单跨静定梁影响线的基本方法（静力法）；量值最不利荷载位置的确定以及简支梁和连续梁的内力包络图。
•
S
max
=
n
∑
Pi y
i
返回
下一张上一张
小结
• • • • • • • • • • • • •
例9-2 某公路桥承受公路桥设计规范中汽 —15级车队荷载如图所示，试求截面C最大弯矩。
返回下一张上一张小结
• 解:在汽—15级车队荷载中，排列密集且数值较大的为重车后轮 • 压力130KN，可将它设为临界荷载Pk。 • 1）车队向左行驶时，把PK=130KN置于梁的C截面上（即影响 • 线的顶点），相应的整个荷载队位置，如图所示。 • 车队行驶中相应截面C弯矩MC为
• •
三、静定梁影响线： 1. 外伸梁影响线 2. 悬臂梁影响线
返回
下一张上一张
小结
•
3. 多跨静定梁影响线

影响线的绘制

用机动法作图示静定多跨梁m3m3m2m2m2m2m影响线2m3m3m2m2m2m2m12121316影响线的应用在移动荷载作用下要确定反力和内力的最大值以作为结构设计的依据显然要确定该量值的最大值必须先确定产生这个最大值的荷载位置
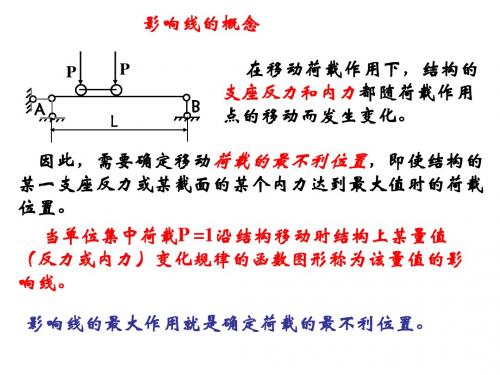
影响线的概念
P A L P B
在移动荷载作用下，结构的支座反力和内力都随荷载作用点的移动而发生变化。
a MC = R A×a = L－x L
RB
( a≤x≤L )
MC影响线：
ab L ＋ A C B ab 提问：纵坐标的物理意义？ L
当P=1作用在AC段时用截面法取C截面以右为对象
b x MC =RB ×b = L
( 0≤x≤a )
注意：在作影响线时，假定P = 1是没有单位的量，因此，反力RA、RB和剪力影响线的纵坐标也都没有单位；弯矩影响线的纵坐标的单位是[长度]。但是，当利用影响线研究实际荷载作用的影响时，要将影响线的纵坐标乘以实际荷载，这时再将荷载的单位计入，便可得到该量值的实际单位。
1、撤去与所求量值X相应的约束，代以对应的约束力。 2、使体系沿X的正方向发生位移δX，得到位移图。该位移图即为影响线的形状。 3、令δX = 1，确定影响线的纵坐标。 4、确定正负号：基线以上取正号，以下取负号。
四、机动法作简支梁的影响线 1、作RB影响线 x A P=1 A RB影响线: ＋ 1 A －1 P=1 B MC影响线: δZ B RB x A a
（二）伸臂梁的影响线
E L1 x A P=1 a L C B b L2 F
L＋L1 L
E
1 ＋ A
RA影响线
F － L2 B L＋L2 L L 1 ＋ B
1、支座反力影响线 L－ x ∑MB= 0 得 RA=

用机动法作静定梁的影响线

RA·δx+P·δP=0 以P=1代入式(16-1)，得
(16-1)
(16-2)
用机动法作静定梁的影响线
δx和δP都是微小的，但是它们的比值却是有限的。
Hale Waihona Puke 当P=1移动时，δP随着x变化，是荷载位置参数x的函数。
而δx则与x无关，是一个常数，可以任意给定，为了分析
简便，取δx=1，则式(16-2)可变为
用机动法作静定梁的影响线
当绘制AC部分的支座A 的约束反力RA的影响线时，可确定影响线在AC段与对应的单跨外伸梁的影响线相同，在 CD 段只需确定C点和D点的竖标，就可绘出其影响线，C点竖标已由AC段得出，D点竖标可求出为零，最后绘出RA的影响线如图16-6(c)所示。
图16-6
工程力学
用机动法作静定梁的影响线
1.3
机动法作多跨静定梁的影响线
作多跨静定梁影响线，需要分清它的基本部分和附属部分及这些部分之间的相互约束关系，再利用单跨静定梁已知的影响线进行分析。当P=1在基本部分的梁段上移动时，量值的影响线与相应单跨静定梁相同，其附属部分梁段上的量值影响线为零。当P=1在附属部分的梁段上移动时，量值的影响线与相应单跨静定梁相同。位于附属部分的任何量值的影响线只限于附属部分局部，可按相应单跨梁的影响线作出，而该影响线在基本部分范围的竖标都为零。
(1)解除与所求量值相对应的约束，代之以正值的约束反力。 (2)使机构沿所求量值的正方向发生虚拟单位位移，即位移图。 (3)在位移图上标纵坐标及正负号，就得到该量值的影响线。
用机动法作静定梁的影响线
1.2
机动法作简支梁的影响线
1. 弯矩的影响线
如图16-5(a)所示，如果要作C截面弯矩影响线，则去掉相应的转动约束，把C点变成可动铰，并以一对力偶MC代替转动作用，如图16-5(b)所示，使AC、CB沿MC正向发生相对单位转角1，得到图16-5(c)所示的位移图，即为MC的影响线。由δx=α+β=1，可求出A点的值为a，再根据比例关系可求得 C点的值为。