力学2动力学II-非惯性系概要
《大学物理上教学课件》6.非惯性系

反,大小等于物体质量乘以非惯性系的加速度。
实验验证的必要性
03
通过实验验证可以帮助我们理解非惯性系中的物理现象,加深
对相对论和牛顿运动定律的理解。
实验验证的方法和步骤
准备实验器材
准备必要的实验器材,如滑轮、砝码、 弹簧秤等。
进行实验操作
按照实验方案进行操作,记录实验数 据。
设计实验方案
根据非惯性系中的物理现象,设计合 理的实验方案,包括实验目的、操作 步骤、数据记录等。
牛顿第二定律
总结词
在非惯性系中,牛顿第二定律的形式发生变化,需要加上一 个假想的惯性力来保持等价性。
详细描述
在非惯性系中,牛顿第二定律的形式会发生变化。为了保持 等价性,需要在方程中加上一个假想的惯性力。这个惯性力 的大小等于物体质量与非惯性系相对于惯性系的加速度的乘 积,方向与非惯性系加速度方向相反。
VS
详细描述
科里奥利力的大小计算公式为 F=2m×v×ω,其中 m 是物体的质量,v 是物体的速度,ω 是旋转参考系的角速度。
科里奥利力的应用实例
总结词
科里奥利力在气象学、地球物理学等领域有 广泛的应用。
详细描述
在气象学中,科里奥利力对气体的流动和天 气系统的形成有重要影响,例如旋风和龙卷 风的形成就与科里奥利力有关。在地球物理 学中,科里奥利力是解释地球自转和地球上 水循环的重要因素之一。
THANKS.
参考系变换的方法和步骤
确定变换关系
根据相对性原理和伽利略变换,确定 两个惯性参考系之间的变换关系。
转换物理量
将一个惯性参考系中的物理量(如速 度、加速度、力等)按照变换关系转
换到另一个惯性参考系中。
求解问题
在新的惯性参考系中,应用物理规律 求解问题。
第二章 非惯性系中的质点动力学

M1-28
积分可得
mgR(cos jmax 1 1) m 2 R 2 sin 2 jmax 0 2
因 sin 2 jmax 1 cos2 jmax 上式变为
mgR(cos jmax 1) 1 m 2 R 2 (1 cos 2 jmax ) 0 2
z
或
2 R cos2 jmax 2 g cos jmax 2 g 2 R 0
2. 当加速度 ae 2 g tan 时,牵连惯性力 FIe 2mg tan ,应用 相对运动动能定理,有
m v 2 0 ( F cos )l (mg sin )l Ie 2 r
整理后得
y' m
FN FIe
mg θ ae x'
m 2 vr (mg sin )l 2
力大小为 FIe m 2 R sin j ,方向如图。 经过微小角度dj 时,此惯性力作功为
z
W FIe R cos jdj m 2 R sin j cos jRdj
相对运动的动能定理,得
R
0 0 mgR(1 cos j max )
jmax
0
Байду номын сангаас
j
mg
FIe
m 2 R 2 sin j cos j dj
vr 质点相对动参考系速度
M1-20
上式两端点乘相对位移
dr
dvr m dr F dr FIe dr FIC dr dt
dr 注意到vr , 且科氏惯性力垂直于vr , 有FIC dr 0, 则 dt mvr dvr F dr FIe dr
非惯性系 惯性力

地球自转和公转产生的惯性力,使得地球上的物体受到向心力的作用, 从而解释了地球形状为椭球体的原因以及昼夜交替和四季变化的现象。
03
解释潮汐现象
月球和太阳对地球的引力作用,使得地球表面的水体产生潮汐现象。通
过引入惯性力的概念,可以解释潮汐的成因以及潮汐对地球自转速度的
影响。
分析微观粒子行为
分类
非惯性系可分为加速平动参考系和转动参考系两类。加速平动参考系中的物体 受到与加速度方向相反的惯性力作用;转动参考系中的物体则受到与转动角速 度相关的科里奥利力和向心力作用。
牛顿运动定律在非惯性系中适用性
牛顿运动定律在惯性系中成立,但在非惯性系中不再适用。 在非惯性系中,为了描述物体的真实运动状态,需要引入虚 拟的惯性力。
4. 分析实验数据,比较物体在惯性系 和非惯性系中的运动状态。
数据采集和处理方法
数据采集:使用高精度测量设备记录物 体在平台旋转过程中的位置、速度和加 速度等参数。
3. 通过统计分析方法,对实验结果的可 靠性和准确性进行评估。
2. 使用数值分析方法对物体在惯性系和 非惯性系中的运动状态进行模拟和比较 。
01
为解决工程实际问题提供理论支持。
02
研究内容
非惯性系的定义和分类。
03
研究目的和内容
1
惯性力的概念、性质及其在非惯性系中的作用。
2
非惯性系下物体的运动方程和动力学特性分析。
3
非惯性系在实际工程中的应用案例研究。
02
非惯性系基本概念
非惯性系定义及分类
定义
非惯性系是指不满足牛顿第一定律的参考系,即在其中观察到的物体运动状态 不遵循惯性定律。
洛伦兹变换是相对论中描述不同惯性参考系之间物理量转换的基本规则,适用于高速运动的物体。在 洛伦兹变换下,时间和空间是相对的,会随着参考系的改变而改变。洛伦兹变换考虑了光速不变原理 ,是更精确的描述方式。
第二章非惯性系中的质点动力学

x'
y
O
x
非惯性系中的质点动力学基本方程
mar F FIe FIC 或质点相对运动动力学基本方程
在非惯性系内,上式写成微分方程形式
m
d
2
r
dt 2
F
FIe
FIC
非惯性系中的质点运动微分方程
质点相对运动微分方程
其中 r表 示质点M在非惯性系中的矢径
d 2r dt 2
解:
以上抛点为坐标原点,选取固定于地球的非惯 性参考系为 Oxyz
其中 z轴 铅直向上, 近似通过地球中心。
x轴水平向东, y轴水平向北。
表现重力
P F FIe mg
其中 F为地球引力
科氏惯性力
FIC maC 2m vr
vr xi yj zk
FIC
的矢量积可展开为
i j k
例2- 4 已知:一平板与水平面成θ角,板上有一质量为m 的小球,
如图所示,若不计摩擦等阻力。
求:平板以多大加速度向右平移时,小球能保持相对静止。 若平板又以这个加速度的两倍向右平移时,小球应沿 板向上运动。球沿板走了l 距离后,小球的相对速度是 多少?
a
解: (1)在平板上固结一动参考系 Oxy
md2来自rdt 2mg
F1
F2
FIe
FIC
(a)
将上式投影到 x轴 上得 mx mx 2
令 vr x
dvr dvr dx 2x
dt dx dt
z'
O
y' F1
F2
B
mg
FIC
FIeA x'
注意
dx dt
vr
lxy理论力学(II) 非惯性系中的质点动力学

小球相对非惯性基的运动已知
FT
xC l0 vt yC 0
xC yC 0
x : 0 mg cos FT m 2 (l0 vt)
Fe
FC
y : 0 mg sin m(l0 vt) 2mv
G
Fωe
15
刚体动力学/非惯性基下刚体动力学/平面平动/解
18
例2–4 一平板与水面成角, 板上有一质量为 m 的小球, 如图示. 若不计摩擦等阻力, 问平板以多大的加速度向右平移时, 小球能保 持相对静止? 若平板又以这个速度的两倍向右平移时, 小球沿板向
上运动. 问小球沿板走了l 距离后, 小球的相对速度是多少?
解: (1) 令板向右平移, 则无科氏惯 性力.
1
C
转aω动e C向心牵连O2 r加C 速a度ωeC 小球C牵连惯性力 F e
切向牵连惯性力
(l0 vt) 2 FαemaCe mdefaFαeCαe
方向已知
Fωe
Fαe m(l0 vt)
法向牵连惯性力
Fωe方向已m知aωe C
Fωe ml 2
(3)当质点相对动参考系静止时,有ar=0,vr=0,又FIC=0,则
F FIe 0
上式称为质点相对静止的平衡方程,即当质点在非惯性参考 系中保持相对静止时,作用在质点上的力与质点的牵连惯性 力相互平衡。
(4)当质点相对于动参考系作等速直线运动时,有ar=0,则
F FIe FIC 0
方向已知
x 0
aωe C
Fe
x
aαeC
Fωe
13
刚体动力学/非 惯性基下刚体动力学/平面平动/解
动力学2:非惯性系

Fc v(qv) ω(B) v(qv)
上
Fc
上
ɺ a = a'+ω ×r +ω ×(ω ×r ) + 2ω ×v'.
关键:掌握“绝对、牵连 质点作一般的“相对” 运动 a’≠0 和相对”加速度之间的关 v = v'+ω ×r. 系,从而正确计入惯性力。
aρ = lim aϕ = lim ∆vρ ∆t ∆vϕ ∆t
∆t →0
2’
= −ω2r, = 2ωv'.
径 加 度 ω(r+v’∆t) 向 速 科 加 度 氏 速
∆t →0
ac = 2ω ×v'.
牵连运动改变了相对速度v’方向,因而产生了横 向加速度ωv’;同时,相对运动又改变了牵连速 度的量值(r变为r+v’∆t),故又产生了横向加速度 ωv’,因而科氏加速度为2ωv’.
位置
ds =v dt
R + µt(v0 +ωR) s = ln −ωRt. µ R R
练习:p516(9.6) 质量为m的质点在光滑的水平桌面上运动, 练习 桌子绕通过原点的竖直轴以匀角速转动。求质点的运动方程。 解1:以地面为参考系(惯性系),质点在桌面内受力 为零,所以 d2x d2 y
dt
2
由于ω=7.29x10-5弧度/秒,很小: 简化 ω
2 2
GMm mω Rcos φ P≈ [1− ] 2 R2 GMm/ R GMm = − mω2Rcos2 φ, R2 2 θ ≈ ω Rsin 2φ / 2g.
• 重量是引力与惯性离心力的合力; • 重量大小小于真正的引力大小; • 重量指向偏离引力指向。
力学2动力学II-非惯性系讲解

设有一质量为m的质点,在真实的外力F 的作 用下相对于某一惯性系S产生加速度 a ,
则根据牛顿第二定律,有:
F ma
假 沿设直线另运有动一。参在考S系参S考相系对中于,惯质性点系的S加以速加度速是度aa。0
则: a a a0
aAB aAC aCB
将此式代入上一式可得:
e
er
方向描述:er :径向方向
e :极角增加方向
O
位矢 r rer
速度
v
dr dt
d( rer dt
)
dr dt
er
r der dt
dr dt
er
r
d
dt
e
vr er
v e
r
P
X
e
r
der
d er
der der e der er d d
vr : v :
dt
参阅专业《力学》书
本地加速度
牵连横向 加速度
牵连向心 加速度
科里奥利 加速度
a a d r ( r ) 2 v
dt
a绝 a相 a牵
牵连加速度
f惯性力 ma牵
m
d
dt
r
[m
(
r
)]
2m(v )
欧拉力
对匀速转动的S'系:
非惯性系中的牛顿第二定律:
虚拟力
F ma F真实力 R
惯性力不是物体间的真实的相互作用,是一种假想的 力。它既无施力者, 也无反作用力, 不满足牛顿第三定律。
力学的发展历程

力学的发展历程力学是物理学的一个重要分支,研究物体的运动和相互作用规律。
它的发展历程可以追溯到古代,经历了数千年的演变和进步。
以下是力学的发展历程的详细描述。
1. 古代力学古代力学的起源可以追溯到公元前4世纪的古希腊。
古希腊的哲学家亚里士多德提出了一套关于物体运动的理论,他认为物体的运动是由其固有属性所决定的。
这种观点在古代长期占主导地位,直到17世纪被新的理论所取代。
2. 牛顿力学的建立17世纪末,英国科学家艾萨克·牛顿提出了经典力学的三大定律,奠定了现代力学的基础。
牛顿的第一定律(惯性定律)指出,物体在没有外力作用时将保持静止或者匀速直线运动。
第二定律(运动定律)描述了物体的加速度与受力之间的关系。
第三定律(作用与反作用定律)说明了物体之间的相互作用。
3. 动力学的发展随着牛顿力学的建立,人们开始研究物体的运动轨迹和受力情况。
这导致了动力学的发展。
动力学研究物体在受到外力作用时的运动规律,包括速度、加速度和力的关系。
动力学的发展使人们能够更准确地描述物体的运动和相互作用。
4. 非惯性系力学的发展牛顿力学只适合于惯性系,即不受外力影响的参考系。
但在实际情况下,不少物体都处于非惯性系中,受到惯性力的影响。
为了解决这个问题,19世纪末,法国科学家亨利·庞加莱提出了非惯性系力学的理论。
他引入了惯性力的概念,使得牛顿力学能够适合于非惯性系。
5. 相对论力学的浮现20世纪初,爱因斯坦提出了相对论理论,对牛顿力学进行了革命性的改进。
相对论力学认为,时间和空间是相对的,而不是绝对的。
它描述了高速运动物体的运动规律,并解释了质能关系和引力的本质。
相对论力学在宏观和微观尺度上都具有重要意义。
6. 量子力学的兴起20世纪初,量子力学的浮现彻底改变了人们对物质和能量的理解。
量子力学是一种描述微观世界的理论,它研究微观粒子的运动和相互作用。
量子力学的发展使人们能够解释原子和份子的结构、光的特性以及粒子的波粒二象性等现象。
非惯性系

m F惯 S′
Sω3Fra bibliotek理学院 物理系 陈强
r r FC m以速度 v 相对圆盘运动, 以速度 相对圆盘运动, S中:m受合力为零⇔匀速直线运动 受合力为零⇔ 中 受合力为零 匀速直线运动. S'中:m沿曲线 运动, 沿曲线l 中 沿曲线 运动, r 等价于受到了一个与 v 垂直且 指向右侧的惯性力. 右侧的惯性力 指向右侧的惯性力
则牛顿定律在S ′中从形式上恢复了! 形式上恢复了 恢复了! 则牛顿定律在 2. 匀速转动参考系中的惯性力 匀速转动参考系中的惯性力 要恢复牛顿定律形式,可证需两种惯性力: 要恢复牛顿定律形式,可证需两种惯性力 惯性离心力 + 科里奥利力 r r r r r FC = 2mv × ω F惯 = − man (与m的速度有关 的速度有关) 与 的速度有关
2
理学院 物理系 陈强
§2-2. 力学中常见的力
r F惯 : 如图,小球 相对圆盘静止 如图,小球m相对圆盘静止
S中: 小球匀速圆周运动 中 ⇒弹簧拉长 ⇒ m受到向心力 受到向心力 静止, ⇒ S'中: 小球静止, 中 小球静止 ⇒弹簧拉力和一个 (虚设 惯性 虚设)惯性 虚设 惯性离心力) 力平衡 (惯性离心力) r r F惯 = − man
S v m F惯 O ω S′
由此可以解释: 北半球 北半球+南北向 由此可以解释:(北半球 南北向 ) • 河流冲刷右岸较严重, 河流冲刷右岸较严重, • 单向行使的铁轨右轨磨损较多, 单向行使的铁轨右轨磨损较多, • 远程炮弹发生横向偏离, 远程炮弹发生横向偏离, • 信风 北→南)形成气旋 信风(北 形成气旋, 形成气旋 • 傅科摆的运动等等。 傅科摆的运动等等。
惯性力! 惯性力
非惯性系下的动力学

非惯性系下的动力学引言:在物理学中,我们经常研究物体在惯性系下的运动规律,即不受外力作用时的运动状态。
然而,现实生活中存在许多非惯性系,例如地球的自转和公交车的加速等。
在这些非惯性系下,物体的运动会受到额外的力的影响,因此我们需要研究非惯性系下的动力学。
一、非惯性系的定义和特点非惯性系是指相对于惯性系而言,具有加速度的参考系。
在非惯性系中,物体的运动受到惯性力的影响,这是由于参考系的加速度导致的。
惯性力的大小和方向与物体的质量和加速度有关。
二、离心力的作用在非惯性系下,离心力是一种常见的惯性力。
当物体在旋转的参考系中运动时,会受到离心力的作用。
离心力的大小与物体的质量、角速度和距离旋转中心的距离有关。
离心力的方向指向旋转中心的外侧,是一种向心加速度的结果。
三、科里奥利力的效应科里奥利力是另一种非惯性系下的力。
当物体在旋转的参考系中有径向速度时,会受到科里奥利力的作用。
科里奥利力的方向垂直于物体的速度和旋转轴,并且与速度的大小和旋转角速度有关。
科里奥利力会使物体偏离其惯性轨迹,导致物体的运动轨迹呈现出曲线形状。
四、福科力的存在福科力是一种在非惯性系下的惯性力。
当物体在加速的参考系中运动时,会受到福科力的作用。
福科力的大小与物体的质量、加速度和参考系的加速度有关。
福科力的方向与参考系的加速度相反,并且与物体的质量和加速度成正比。
五、应用举例:地球自转和人体感受地球的自转是一个非惯性系,因此我们可以观察到一些非惯性系下的动力学效应。
例如,地球的自转导致了地球上的离心力,使得物体在赤道上的重力稍微减小。
此外,地球的自转也会导致科里奥利力的作用,使得气流和海洋流的运动呈现出特定的曲线形状。
在人体感受方面,非惯性系下的动力学效应也起到一定的作用。
例如,当乘坐公交车或电梯加速或减速时,我们会感受到身体向前或向后倾斜的力。
这是由于福科力的作用,使得我们的身体相对于参考系有一个相对的加速度。
结论:非惯性系下的动力学是物理学中一个重要的研究领域。
2-2 力学相对性原理 非惯性参考系
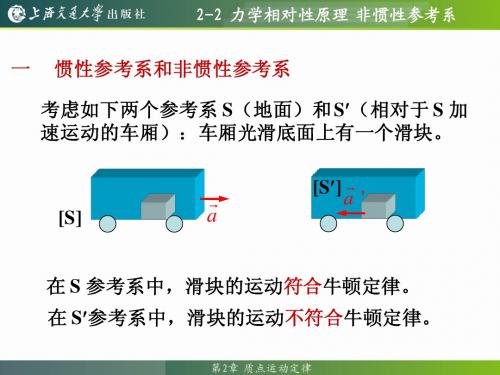
两 y 个 相 [S] 对 平 动 参 考 o 系
y′ u [S] r R o′ r′
.P (x, y, z )
(x,y,z ) x′ x
r r R
v v u
第11章 静电场 第2章 质点运动定律
a a
du dt
2-2 力学相对性原理 非惯性参考系 11-1 电荷
若质点 m 在 S 系中满足牛顿第二定律: m a F
力与参考系无关
则在 S ' 系中: F ' m a '
F ' F m a0 m a '
牛顿第二定律在非惯性系不成立!
第11章 静电场 第2章 质点运动定律
2-2 力学相对性原理 非惯性参考系 11-1 电荷
S′一定也是惯性系
一切相对于惯性系作匀速直线运动的参照系都是惯 性参照系。
第11章 静电场 第2章 质点运动定律
2-2 力学相对性原理 非惯性参考系 11-1 电荷
换句话说:牛顿定律在所有惯性系中均成立 且具有相同的形式。 力学相对性原理! 又可表述为:不可能通过惯性系内部进行任何形式的 力学实验来确定该惯性系相对于其它惯性 系的速度。
g
2-2 力学相对性原理 非惯性参考系 11-1 电荷
dy
x
2
dx
g
y 0dy x 0 x2
dx
g
2 2
y
x
2g
所以金属丝要弯抛物线的形状!
第11章 静电场 第2章 质点运动定律
2-2 力学相对性原理 非惯性参考系 11-1 电荷
参考视频
三种相互作用 惯性力
非惯性系中的动力学

在非惯性系中由于牛顿运动定律不成立, 不能直接用 牛顿运动定律处理力学问题。若仍希望能用牛顿运动定律 处理这些问题, 则必须在非惯性系中引入一种作用于物体 上的惯性力。惯性力不同于前面所说的力,因为惯性力既 没有施力物体,也不存在它的反作用力。
小车作加速运动a≠0时,单摆偏 转了一个角度,拉小球的弹簧被 拉伸,其状态不符合牛顿定律, 引入了惯性力后,就能把牛顿运 动定律应用于非惯性系。
a cos
g
sin
(m2 m1)sin m2 m1 sin2
g
m2g
二、转动参照系中的离心惯性力
m
FT
m
F*
观 察 者2
一光滑的圆盘以匀角速ω绕其铅直轴转动,将一质
量为m的小球用长为r的细线栓在轴上,并使小球在圆
盘上与圆盘一起以匀角速ω绕铅直轴转动。
如果在O则系对内于的观观察测者者1:1测F量T 到 m细a线对m小球2r的拉力为FT
§3.5 非惯性中的动力学
一、 直线加速参考系中的惯性力 二、 离心惯性力 *三、 科里奥利力
§3.5 非惯性中的动力学
一、 直线加速参考系中的惯性力
问题:如图,一单摆悬挂在小车的天花板上,另一个小
球用弹簧拉着,现均以小车为参考系来研究小球的运动
a =0
a 0
小车作匀速直线运动,即a = 0 时,单摆、小球均处于 静止状态符合牛顿定律。
小车作加速直线运动,即a≠0时,单摆偏转了一个角度,拉 小球的弹簧被拉伸,其状态不符合牛顿定律,为什么?
inertia force 1.avi
如图:O系为基本参考系,O 系为动参考系
设 O系相对O系以加速度 a 作直线加速运动,
z
质点在空间运动, 某时刻位于P点
非惯性系

清北学堂物理集训导学资料系列之在非惯性系中的惯性力首先让我们了解一下什么是惯性系,什么是非惯性系?惯性系:牛顿第一定律只在一类特殊的参照系中成立,此参照系称为惯性参照系。
相对某一惯性系作匀速运动的参照系必定也是惯性系,非惯性系:牛顿第一定律不成立的参照系称为非惯性参照系,非惯性系相对惯性系必作变速运动。
地球是较好的惯性系,太阳是精度更高的惯性系。
用牛顿定律时,选用的参照系应该是惯性系。
在非惯性系中,为了能得到形式上与牛顿第二定律一致的动力学方程,引入惯性力的概念,引入的惯性力必须满足式中是质点受到的真实合力,是质点相对非惯性系的加速度。
真实力与参照系的选取无关,惯性力是虚构的力,不是真实力。
惯性力不是自然界中物质间的相互作用,因此不属于牛顿第三定律涉及的范围之内,它没有施力物体,不存在与之对应的反作用力.非惯性系中的惯性力在物理竞赛中考察考生用牛顿定律解决实际问题的能力。
也是一个难点。
考生经常容易出错的地方。
一平动加速系统中的惯性力 例一设平动非惯性系相对于惯性系的加速度为。
质点相对于惯性系加速度求质点相对于平动非惯性系的加速度,惯性力。
解:由相对运动知识可知,质点相对于平动非惯性系的加速度质点受到的真实力对惯性系有对非惯性系得 平动非惯性系中,惯性力由非惯性系相对惯性系的加速度及质点的质量确定,与质点的位置及质点相对于非惯性系速度无关。
二匀速转动系中的惯性力例二如图1,圆盘以角速度绕竖直轴匀速转动,在圆盘上用长为r 的细线把质量为m 的点系于盘心且质点相对圆盘静止,即随盘一起作匀速圆周运动,求质点的惯性力。
解:以惯性系观察,质点在线拉力作用下做匀速圆周运动,符合牛顿第二定律.以圆盘为参照系观察,质点受力拉到作用而保持静止,不符合牛顿定律.要在这种非惯性系中保持牛顿第二定律形式不变,在质点静止于此参照系的情况下,引入惯性力为转轴向质点所引矢量,与转轴垂直,由于这个惯性力的方向沿半径背离圆心,通常称为惯性离心力.由此得出:若质点静于匀速转动的非惯性参照系中,则作用于此质点的惯F Ga m F F ′=+K K K 惯F K a ′K0a K a K )(0a a a KK G −+=′a m F KK =a m F F ′=+KK K 惯)(0a m a m F F K K K K −+=+惯0a m F KK −=惯ωF K F K 0=′=+a m F F K K K 惯rm T F KKK 2ω=−=惯r Kwt 图1真实(半律来奥利即指使得由于而双不进的小来观运动向后动定定律参照加速m 的在非相对常说系中运动相对方向析图例四定在不可-2Kg v 0=4张力 实力与惯性离惯性离心力半径),必须指出的来分析质点的利力是以地球指向相对速度得北半球河流于右轨所受压双线铁路的左进一步讨论了三、用实验在一列以加小球,放在光观测,小球保动定律,相对后运动,而小定律不再成立不过,车厢律写为照系是非惯性速度相对惯的物体都受到非惯性里也可对于地面出现说受到了离心中出现的惯性例三如图动,才能保持解:可取B 对地面有加速向水平向右,图可知f=ma=mg ∴ 四(第17届预在桌面上的圆可伸长的柔软g 的小物块。
非惯性系动力学简析

Mach认为惯性是物体与其他宇宙间万物相互作用的结果。 物体的惯性力与惯性质量成正比,而万有引力与引力质量成正比, 实验表明惯性质量与引力质量相同,万有引力与惯性力间便有了相互取代 的基础。水面之所以弯曲,可认为水并没有旋转,而是天地万物相对于水 旋转,对水产生作用,使得水面弯曲。惯性系或空间的建立离不开物质。 在自由下降的升降机内, 观察者可以认为,自己在地球的引力场中向下加速,升降机内小球所受重 力与平移惯性力抵消,可以浮在空中匀速漂移; 观察者也可以认为,不存在地球引力场,升降机处于静止状态,小球因受 力为零而浮空匀速漂移。 由此,观察者无法通过对小球运动状态的力学观测来区分,究竟是车厢系 静止在无引力场区域,还是加速在某个引力场区域。 由此可提炼出等效原理,促使爱因斯坦广义相对论的建立。
非惯性系动力学简析
——星河陨冰
牛顿约定,只要在某参考系中测得物体所受的合外力、质量和加速度满 足牛顿第二定律,该系便是一个惯性系。
向量叉乘运算符合以上要求。
你想要配一些插图么?
如果说仅仅通过分析运动合成而得到的以上公式,还是给人一些 困惑的感觉, 那么我们便从位移矢量的合成关系以及位移矢量的变化率讲起。
Now we are ready to derive it once more!
平移惯性力 Coriolis 力
惯性பைடு நூலகம்心力
向量,其实是个很简单的概 念............
还需要我配插图么? 不,你不想............
惯性的本质
引自《力学》P62~P65
运动学中A和B之间的运动是相对的。A认为B相对于A做加速运动,而B认为 A相对于B做加速运动,这是同一种运动的两种等价表述,具有对称性。 而在牛顿定律中,惯性是每个物体相对于惯性系具有的重要的动力学属性。 物体不受其他物质作用时,惯性使得物体相对于惯性系保持静止或匀速直 线运动状态。力迫使物体改变这种状态时,惯性表现出抗拒作用。惯性越 大,相同大小的力产生的加速度越小。 将惯性量化为惯性质量m,并进行度量,也是在惯性系中实现的。惯性在 非惯性系中的表现和度量,是通过非惯性系与惯性系之间的运动关联,引 申和转移过去的。
非惯性系讲解

a
弹簧K1
弹 体 引 信
击针
击针座
ma
惯性力的应用
(2)炮弹引爆
a. 引爆原理
a
K1 击针 击针座
弹 体 引 信
ma
惯性力的应用
(2)炮弹引爆
a. 引爆原理
a
K1
弹 体 引 信
b. 保险装置
击针 击针座
ma
K2 离心子
惯性力的应用(2)炮弹来自爆a. 引爆原理解 取电梯为参考系。已知这个非惯性系以 a=0.5m/s2的加速度对地面参考系运动,与之相应 的惯性力
惯性力的应用
即
于是
N G F惯 0 N G F惯 m( g a ) 618 N
由此可见,磅秤上的读数(根据牛顿第三定律, 它读的是人对秤的正压力,而正压力和N是一对大小 相等的相互作用)不等于物体所受的重力G。当加速 上升时, N>G ;加速下降时, N<G 。前一种情况叫做 “超重”,后一种情况叫做“失重”。尤其在电梯 以重力加速度下降时,失重严重,磅秤上的读数将 为 0。
非惯性系
2. 惯性力
在平动加速系中,对牛顿第二定律进行推广。 S------惯性系
----- 非惯性系 S ----S 系相对S系的 a0
加速度
a0
a 和 a 分别表示一质量为
m的质点在S系和 系中的加速度 S
惯性力
据加速度的变换关系有 在S系中,牛顿定律成立 在 S 系中
非惯性系
3. 惯性力的应用
(1)加速度计
a.结构 B — 指针 K — 平衡弹簧 C — 表盘 o — 支点
m
o K
B
2-2 非惯性系 惯性力

2 fc m r
2 此时 a r s
第2章 质点动力学
* 2–2 非惯性系 惯性力
5
重力W实际上应是F引和ƒ*c的合力
W F引 f 惯
W F 引 m R cos
2 2
2 7.3 105 rad / s 地球自转角速度很小 24 3600
T
N
* fk
径向:惯性离心力,牵引张力平衡;
v相
fc
*
横向:必需有一力与槽的侧向推力N 平衡,这个力即为科里奥利力
fk 2mu相
*
第2章 质点动力学
非惯性系惯性力一圆盘绕铅直轴以角速转动盘心有一光滑小孔沿半径方向有一光滑槽槽中有一小球被穿过小孔的细线所控制使其只能沿槽做匀速运动现小球沿槽以从圆盘上观察则小球仅有径向匀速运动即小球处于平衡态径向
* 2–2 非惯性系 惯性力
1
1.在变速直线运动参考系中的惯性力 非惯性系
定义:对某一特定物体惯性定律成立的参考系叫做 惯性参考系.相对惯性系作加速运动的参考系为非惯 性参考系 .
第2章 质点动力学
* 2–2 非惯性系 惯性力
3
例 动力摆可用来测定车辆的加速度. 一根质量不 计的细棒一端固定在车厢的顶部, 另一端系一小球, 当 列车以加速度 a 行驶时, 细杆偏离竖直线成 角. 试求 加速度 a 与摆角 间的关系 . 解 以车厢为参考系(非惯性系)小球处于平衡状态. 分量式
第2章 质点动力学
* 2–2 非惯性系 惯性力
2
惯性力— 惯性在非惯性系中 的表现.
mas
N
P
m
a
'
平动非惯性系中惯性力
第2章 非惯性系与惯性力

y
v0
x
h
O
a0
1 2 y y0 h gt F F惯 m a 2
t
2h g
真实力:
Fx 0 , F y m g
惯性力: ( F ) m a 0 惯 x
0 ma0 ma x , ( F惯 ) y 0 mg 0 ma y
宇航员将水果摆放 在立圆的圆周上, 不受力,维持图形 不变 在飞船中可验证惯性定律
霍金体验零重力飞行 飞船中验证了惯性定律
(真正验证惯性定律的参考系恰恰是相对牛顿 惯性系的加速系,认识上的飞跃)
2. 潮 汐 现 象
涨潮
和
退潮
利用平移惯性力可解释潮汐现象
解释: 在地球上分析:海水除了受太阳(月亮)的引力 外,还需考虑地球是个非惯性系的惯性力。 在质量较大的运动空间中,由于太阳(月球)引力强 度不同(存在引力梯度)从而质点的‘合力’不同,整 个质点系就会发生形变。 以太阳引力变化为例图示定性说明, 假设平移惯性力 强度处处相等。
讨论
科氏力:
f c 2 m
1、科里奥利力的特征 1)与相对速度成正比, 只有在转动参考系中运动时才出现; 2)与转动角速度一次方成正比, 当角速度较小时,科氏力比惯性离心力更重要; 3)科氏力方向垂直于相对速度, 因此该力不会改变相对速度的大小; 4)科氏力在地球上的表现:
作用静止物体的合力? 向心力? 向心力与离心力是否是 作用力与反作用力?
科里奥利力简单推导
下面以特例推导,然后给出一般表达式。
如图,质点m在转动参考系(设为S'系)中沿一光滑凹槽运 动,速度为 光滑凹槽 在惯性系(地面)S: m ·
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
加速平动参考系中惯性力的形式:
设有一质量为m的质点,在真实的外力F 的作 用下相对于某一惯性系S产生加速度 a , 则根据牛顿第二定律,有:
F ma
假设另有一参考系S相对于惯性系S以加速度a0 沿直线运动。在S参考系中,质点的加速度是a 。
则:
a a a0
a AB a AC aCB
将上式代入(1)得
( M m ) sin a2 g 2 M m sin
m对地:
a a1 a2
圆周运动及角量描述
1)圆周运动:曲率半径r恒定,即径向速度为零。只需变量 描述。 角位矢: θ 角速度: lim
t 0
角位移:
d (rad/s) t dt
R ma0
这样在S系中就可以在形式上应用牛顿第二定律了。 非惯性系中的牛顿第二定律: 虚拟力
F ma F 真实力 R
惯性力不是物体间的真实的相互作用,是一种假想的 力。它既无施力者, 也无反作用力, 不满足牛顿第三定律。
例1、一光滑的劈,质量为 M ,斜面倾角为 ,并位于 光滑的水平面上,另一质量为 m 的小块物体,沿劈的斜 面无摩擦地滑下, 求劈和滑块对地的加速度。 动画 解:研究对象:m 、M m a2 设 M 对地的加速度 a1 a1 m 对M的加速度 a 2 M 以劈为参照系,建立坐标如图。
0
t
•匀变速运动:β为恒量
0 t
1 2 0 0t t 2
平面极坐标
O为极点,OX极轴,OP为极径r, 为极角 质点的位置由(r , ) 完全确定了。 方向描述: er :径向方向
e
er
P
r
e
位矢 速度
:极角增加方向
Oቤተ መጻሕፍቲ ባይዱ
r rer
der dr d( rer ) dr v er r dt dt dt dt dr d er r e vr er v e dt dt
为质点径向速度大小, 反应位矢大小的变化
e r
d
X
der
er
der der e der er d d
der d e dt dt
vr : v :
为质点横向速度大小, 反应位矢方位的变化
v vr er v e
加速度矢量
de
d
d e a (vrer ve ) dt de dvr der dv er vr e v dt dt dt dt
r
径向位移变 化引起的径 向加速度
横向角速度 引起的向心 加速度
角加速度对 应的横向 线加速度
径向速度和角速 度耦合引入的横 向线加速度
②物体相对非惯性系有相对运动 如图:在一个以ω转动的水平转盘上, 一物体相对转动圆 盘径向方向做 直线运动, v 求动参考系中物体受到的惯性力? Z (Z’) 在动参考系中 在静参考系中
将此式代入上一式可得:
F m ( a a0 ) ma ma0
上式可改写为 :
若假想在S系中观察时,除了真实的外力 F 外,质点还受到另外一个力 ma0 的作用 , 这 个力便称为惯性力。记为:
F m (aa0 ) ma ma0 F F ma0 ma
y,
受力分析:如图
N1
x
,
a2
R1
y N2
R2
a1
mg
Mg
' N1
x
y,
N1
y N2
R2
x
,
a2
R1
a1
x
mg
Mg
' N1
运动方程:
,
m对M
ma ( 1 ) x : mg sin R cos 2 1 对m: , y : mg cos N1 R1 sin 0 ( 2 ) ' Ma1 0 ( 3 ) x : N sin R 1 2 对M: ' M对M y : N 2 N1 cos Mg 0(4)
v ver
u牵 v绝 v相 v ver re v r
据速度变换
0
dv d dr d d a er v e e r e r er dt dt dt dt dt d aer r e r 2 er 2v e dt d a a r ( r ) 2 v 参阅专业《力学》书 dt
e
d v r dt dv dr d d2 r 2 dt dt dt dt
de d d er er d t dt dt
2 d2r dr d d 2 dr d d 2 er e e r 2 e r( ) er dt dt dt dt dt dt dt d2r d22 d2 dr d [ 2 r( ) ]er (r 2 2 )e dt dt dt dt dt
2
O
P
方向: 与角位移成右手螺旋关系,规定为轴向
d d O 角加速度: lim 2 (rad/s2) t0 t dt dt 方向取决于ω, 加速转动, , 方向一致 减速转动, , 方向相反
•匀速圆周运动:ω为恒量
0
X
O
d dt d dt 0 t
力学III – 非惯性系
Mechanics III - Non Inertial Reference Frames
华中科技大学物理学院 姜巍 2012年3月7日
第 2节
非惯性系中的力学方程
怎么办?
a0 m
a0
惯性力
没问题!
F 0
a球 0
惯性力 R ma0
(将动力学问题化作静力学问题处理 达朗贝尔原理)
R1 R1
R2
' 将 N1
N 1 , R1 ma1 , R2 Ma1 代入(2)(3)
m对M:
N1 mg cos ma1 sin N1 sin Ma1
m sin cos a1 g M对地 2 M m sin
