多相流模拟介绍多相流动模式
FLUENT多相流模型

FLUENT多相流模型分类1、气液或液液流动气泡流动:连续流体中存在离散的气泡或液泡液滴流动:连续相为气相,其它相为液滴栓塞(泡状)流动:在连续流体中存在尺寸较大的气泡分层自由流动:由明显的分界面隔开的非混合流体流动。
2、气固两相流动粒子负载流动:连续气体流动中有离散的固体粒子气力输运:流动模式依赖,如固体载荷、雷诺数和例子属性等。
最典型的模式有沙子的流动,泥浆流,填充床以及各相同性流流化床:有一个盛有粒子的竖直圆筒构成,气体从一个分散器进入筒内,从床底不断冲入的气体使得颗粒得以悬浮。
3、液固两相流动泥浆流:流体中的大量颗粒流动。
颗粒的sto kes数通常小于1。
大于1是成为流化了的液固流动。
水力运输:在连续流体中密布着固体颗粒沉降运动:在有一定高度的盛有液体的容器内,初始时刻均匀散布着颗粒物质,随后,流体会出现分层。
4、三相流以上各种情况的组合多相流动系统的实例气泡流:抽吸、通风、空气泵、气穴、蒸发、浮选、洗刷。
液滴流:抽吸、喷雾、燃烧室、低温泵、干燥机、蒸发、气冷、洗刷。
栓塞流:管道或容器中有大尺度气泡的流动分层流:分离器中的晃动、核反应装置沸腾和冷凝粒子负载流:旋风分离器、空气分类器、洗尘器、环境尘埃流动气力输运:水泥、谷粒和金属粉末的输运流化床:流化床反应器、循环流化床泥浆流:泥浆输运、矿物处理水力输运:矿物处理、生物医学、物理化学中的流体系统沉降流动:矿物处理。
多相流模型的选择原则1、基本原则1)对于体积分数小于10%的气泡、液滴和粒子负载流动,采用离散相模型。
2)对于离散相混合物或者单独的离散相体积率超出10%的气泡、液滴和粒子负载流动,采用混合模型或欧拉模型。
3)对于栓塞流、泡状流,采用VOF模型4)对于分层/自由面流动,采用VOF模型5)对于气动输运,均匀流动采用混合模型,粒子流采用欧拉模型。
流体力学中的多相流模型与仿真

流体力学中的多相流模型与仿真在流体力学领域中,多相流模型和仿真技术在研究和应用中发挥着重要的作用。
多相流模型是描述多个不同物理相互作用的数学模型,而仿真技术则是利用计算机来模拟和预测多相流体的行为。
本文将探讨多相流模型和仿真技术在流体力学中的应用和发展。
一、多相流模型多相流模型是流体力学中研究多相流体行为的重要工具。
多相流是指在同一空间中存在着两种或多种物质相的流动状态。
常见的多相流包括气固流动、气液流动和固液流动等。
1. 气固流动模型气固流动模型是研究气体和颗粒物质相互作用的模型。
这种流动模型在煤矿爆炸、粉尘扬尘、颗粒输送等领域有着广泛的应用。
常用的气固流动模型有Euler-Euler模型和Euler-Lagrange模型。
2. 气液流动模型气液流动模型是研究气体和液体相互作用的模型。
气液两相流动在石油、化工、环保等行业中具有重要的应用价值。
常用的气液流动模型有两流体模型、体积力平衡模型和界面平衡模型等。
3. 固液流动模型固液流动模型是研究固体颗粒和液体相互作用的模型。
这种流动模型在颗粒床反应器、混凝土输送等领域有着广泛的应用。
常用的固液流动模型有物理模型、经验模型和计算流体动力学模型等。
二、多相流仿真技术多相流仿真技术是利用计算机来模拟和预测多相流体行为的方法。
仿真技术可以通过数值计算的方式,将多相流动的数学模型转化为离散的数值计算模型,并通过迭代求解来获得流体的相关参数。
1. 传统的数值模拟方法传统的数值模拟方法基于有限差分法、有限元法等数值计算方法,通过网格划分和离散化,将流体力学方程数值化求解。
这种方法在处理简单的流动问题时有效,但对于复杂的多相流问题,计算效率较低。
2. 基于粒子的仿真方法基于粒子的仿真方法是通过跟踪流体颗粒的运动轨迹,模拟多相流体的流动行为。
这种方法可以精确地模拟颗粒与流体之间的相互作用,并考虑颗粒的密度、粒径等特性。
常用的基于粒子的仿真方法有离散元法和分子动力学方法等。
Fluent多相流模型选择与设定

1.多相流动模式我们可以根据下面的原则对多相流分成四类:•气-液或者液-液两相流:o 气泡流动:连续流体中的气泡或者液泡。
o 液滴流动:连续气体中的离散流体液滴。
o 活塞流动: 在连续流体中的大的气泡o 分层自由面流动:由明显的分界面隔开的非混合流体流动。
•气-固两相流:o 充满粒子的流动:连续气体流动中有离散的固体粒子。
o 气动输运:流动模式依赖诸如固体载荷、雷诺数和粒子属性等因素。
最典型的模式有沙子的流动,泥浆流,填充床,以及各向同性流。
o 流化床:由一个盛有粒子的竖直圆筒构成,气体从一个分散器导入筒内。
从床底不断充入的气体使得颗粒得以悬浮。
改变气体的流量,就会有气泡不断的出现并穿过整个容器,从而使得颗粒在床内得到充分混合。
•液-固两相流o 泥浆流:流体中的颗粒输运。
液-固两相流的基本特征不同于液体中固体颗粒的流动。
在泥浆流中,Stokes 数通常小于1。
当Stokes数大于1 时,流动成为流化(fluidization)了的液-固流动。
o 水力运输: 在连续流体中密布着固体颗粒o 沉降运动: 在有一定高度的成有液体的容器内,初始时刻均匀散布着颗粒物质。
随后,流体将会分层,在容器底部因为颗粒的不断沉降并堆积形成了淤积层,在顶部出现了澄清层,里面没有颗粒物质,在中间则是沉降层,那里的粒子仍然在沉降。
在澄清层和沉降层中间,是一个清晰可辨的交界面。
•三相流(上面各种情况的组合)各流动模式对应的例子如下:•气泡流例子:抽吸,通风,空气泵,气穴,蒸发,浮选,洗刷•液滴流例子:抽吸,喷雾,燃烧室,低温泵,干燥机,蒸发,气冷,刷洗•活塞流例子:管道或容器内有大尺度气泡的流动•分层自由面流动例子:分离器中的晃动,核反应装置中的沸腾和冷凝•粒子负载流动例子:旋风分离器,空气分类器,洗尘器,环境尘埃流动•风力输运例子:水泥、谷粒和金属粉末的输运•流化床例子:流化床反应器,循环流化床•泥浆流例子: 泥浆输运,矿物处理•水力输运例子:矿物处理,生物医学及物理化学中的流体系统•沉降例子:矿物处理2. 多相流模型FLUENT中描述两相流的两种方法:欧拉一欧拉法和欧拉一拉格朗日法,后面分别简称欧拉法和拉格朗日法。
多相流动的基础知识和数值模拟方法

多相流动的基础知识和数值模拟方法多相流动是指在同一空间中存在两种及以上物质的流动现象。
在工程领域中,多相流动具有广泛应用,如化工反应器中的气液流动、石油勘探中的油水混合流动等。
本文将介绍多相流动的基础知识,并探讨一些常用的数值模拟方法。
一、多相流动的分类多相流动可以根据不同的分类标准进行分类,常见的分类方法包括:1.根据组分:固液流动、气液流动、固气流动等;2.根据速度:稳定流动、不稳定流动、湍流等;3.根据形态:离散相、连续相、两相界面等。
二、多相流动的基础知识1.多相流动的基本方程多相流动的基本方程包括连续性方程、动量方程和能量方程。
在连续性方程中,考虑到多相流动中各相的质量守恒关系;在动量方程中,引入各相之间的相互作用力和速度差等因素;在能量方程中,考虑到各相之间的相变、传热等现象。
2.多相流动的相互作用多相流动中的不同相之间存在相互作用力,如液固两相之间的颗粒间碰撞力、气液两相之间的表面张力等。
这些相互作用力对多相流动的行为和特性具有重要影响。
3.多相流动的模型为了更好地描述多相流动的行为,研究者们提出了多种多相流动模型,如两流体模型、Eulerian-Eulerian模型和Eulerian-Lagrangian模型等。
不同的模型适用于不同的多相流动情况,选择合适的模型对于准确描述多相流动至关重要。
三、多相流动的数值模拟方法数值模拟是研究多相流动的重要手段之一,常用的数值模拟方法包括:1.有限体积法有限体积法是常用的求解多相流动的数值方法之一,它将流动域划分为网格单元,通过离散化各个方程,利用差分格式求解模拟区域内的物理量。
2.多尺度方法多尺度方法考虑到多相流动中存在不同尺度的现象和作用力,通过将流动域划分为不同的区域进行求解,以更好地描述多相流动的行为。
常见的多尺度方法有多尺度网格方法和多尺度时间方法。
3.相场方法相场方法是一种常用的描述多相流动界面的方法,它通过引入相场函数来表示相界面,并利用Cahn-Hilliard方程等对相场函数进行求解,从而获得界面位置和形状等信息。
Fluent多相流模型选择与设定

1.多相流动模式我们可以根据下面的原则对多相流分成四类:•气-液或者液-液两相流:o 气泡流动:连续流体中的气泡或者液泡。
o 液滴流动:连续气体中的离散流体液滴。
o 活塞流动: 在连续流体中的大的气泡o 分层自由面流动:由明显的分界面隔开的非混合流体流动。
•气-固两相流:o 充满粒子的流动:连续气体流动中有离散的固体粒子。
o 气动输运:流动模式依赖诸如固体载荷、雷诺数和粒子属性等因素。
最典型的模式有沙子的流动,泥浆流,填充床,以及各向同性流。
o 流化床:由一个盛有粒子的竖直圆筒构成,气体从一个分散器导入筒内。
从床底不断充入的气体使得颗粒得以悬浮。
改变气体的流量,就会有气泡不断的出现并穿过整个容器,从而使得颗粒在床内得到充分混合。
•液-固两相流o 泥浆流:流体中的颗粒输运。
液-固两相流的基本特征不同于液体中固体颗粒的流动。
在泥浆流中,Stokes 数通常小于1。
当Stokes数大于1 时,流动成为流化(fluidization)了的液-固流动。
o 水力运输: 在连续流体中密布着固体颗粒o 沉降运动: 在有一定高度的成有液体的容器内,初始时刻均匀散布着颗粒物质。
随后,流体将会分层,在容器底部因为颗粒的不断沉降并堆积形成了淤积层,在顶部出现了澄清层,里面没有颗粒物质,在中间则是沉降层,那里的粒子仍然在沉降。
在澄清层和沉降层中间,是一个清晰可辨的交界面。
•三相流 (上面各种情况的组合)各流动模式对应的例子如下:•气泡流例子:抽吸,通风,空气泵,气穴,蒸发,浮选,洗刷•液滴流例子:抽吸,喷雾,燃烧室,低温泵,干燥机,蒸发,气冷,刷洗•活塞流例子:管道或容器内有大尺度气泡的流动•分层自由面流动例子:分离器中的晃动,核反应装置中的沸腾和冷凝•粒子负载流动例子:旋风分离器,空气分类器,洗尘器,环境尘埃流动•风力输运例子:水泥、谷粒和金属粉末的输运•流化床例子:流化床反应器,循环流化床•泥浆流例子: 泥浆输运,矿物处理•水力输运例子:矿物处理,生物医学及物理化学中的流体系统•沉降例子:矿物处理2. 多相流模型FLUENT中描述两相流的两种方法:欧拉一欧拉法和欧拉一拉格朗日法,后面分别简称欧拉法和拉格朗日法。
多相流动动力学的数值模拟与分析

多相流动动力学的数值模拟与分析多相流动是指在流体中同时存在两种或两种以上的物质,这些物质可以是气体、液体或固体。
由于多相流动的复杂性,数值模拟成为研究多相流动的有效手段之一。
数值模拟可以通过计算机模拟多相流动的各种特性,如相互作用、相变、物理效应等,以更深入地理解多相流动动力学行为。
本文将介绍多相流动动力学的数值模拟与分析方法和应用,包括模型、算法以及重要应用领域。
多相流动动力学模型在数值模拟中,多相流动动力学模型是处理多相流动问题的基础。
多相流动模型可以大致分为两类:欧拉-欧拉模型和欧拉-拉格朗日模型。
欧拉-欧拉模型使用两个或多个连续性方程对每个相的物质守恒和动量守恒进行建模。
这些方程用于描述不同相之间的相互作用,包括不同相之间的质量和能量传递。
欧拉-欧拉模型被广泛应用于处理多孔介质中的多相流,如油藏、地下水系统等。
欧拉-拉格朗日模型则使用一个欧拉方程对流体整体进行建模,用于描述流体的运动和相互作用。
该模型建立在欧拉方程的基础上,使用另一种拉格朗日方程来描述固体颗粒运动。
欧拉-拉格朗日模型通常用于研究一个或多个固体颗粒在流体中的运动,例如颗粒悬浮在液体中的情况。
多相流动动力学算法在多相流动动力学数值模拟中,有多种算法可供选择。
以下是几种常用的多相流动动力学算法:Lattice-Boltzmann方法:Lattice-Boltzmann方法是Lattice-Gas方法的一种改进。
该算法将连续性方程转化为离散空间和时间的微分方程,从而简化了计算过程。
Lattice-Boltzmann方法已经被广泛应用于湍流数值模拟、多孔流动和多相流动等领域。
有限元法:有限元法通过将流场划分为多个小区域来离散化流 field。
这种方法对任意复杂的几何形状和流动条件都有一个准确的数值解,已被广泛用于数值模拟和工程设计中。
元胞自动机方法:元胞自动机方法是一种离散事件方法,通过定义哪些工作单元(mesh cell)可以容纳颗粒,颗粒在各个时间步长内向相邻工作单元的移动,来模拟多相流动的行为。
多相流模型
多相流模型
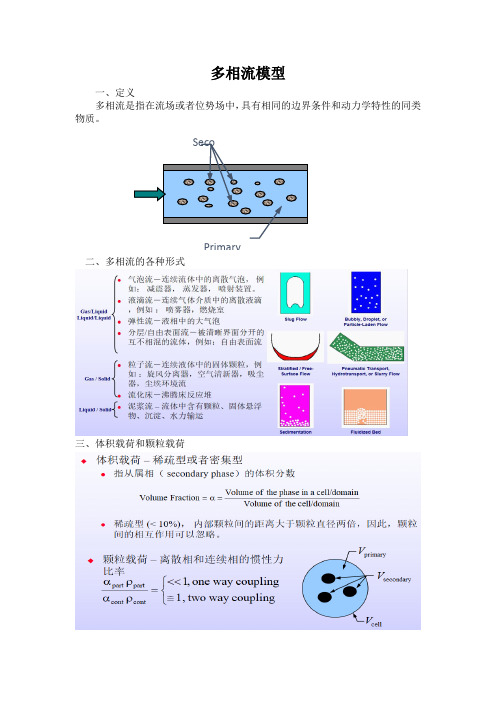
一、定义
多相流是指在流场或者位势场中,具有相同的边界条件和动力学特性的同类物质。
二、多相流的各种形式
三、体积载荷和颗粒载荷
Primary Seco
ndary
四、离散相模型
1、拉格朗日计算方法下粒子/液滴/气泡的轨迹、粒子可以与连续相交换热,质量和动量。
每条轨迹都是由一组初始条件相同的颗粒形成。
粒子与粒子间的相互作用可以忽略。
可以使用随机轨道方法或者粒子云模型来建立湍流扩散模型。
2、子模型。
离散相的加热/冷却。
流体液滴的汽化和蒸发。
燃烧粒子的挥发和燃烧。
喷雾模型中液滴的破碎聚合。
侵蚀/沉积
五、混合模型方程
六、欧拉多相模型方程。
Fluent多相流模型选择与设定(优选.)

1.多相流动模式我们可以根据下面的原则对多相流分成四类:•气-液或者液-液两相流:o 气泡流动:连续流体中的气泡或者液泡。
o 液滴流动:连续气体中的离散流体液滴。
o 活塞流动: 在连续流体中的大的气泡o 分层自由面流动:由明显的分界面隔开的非混合流体流动。
•气-固两相流:o 充满粒子的流动:连续气体流动中有离散的固体粒子。
o 气动输运:流动模式依赖诸如固体载荷、雷诺数和粒子属性等因素。
最典型的模式有沙子的流动,泥浆流,填充床,以及各向同性流。
o 流化床:由一个盛有粒子的竖直圆筒构成,气体从一个分散器导入筒内。
从床底不断充入的气体使得颗粒得以悬浮。
改变气体的流量,就会有气泡不断的出现并穿过整个容器,从而使得颗粒在床内得到充分混合。
•液-固两相流o 泥浆流:流体中的颗粒输运。
液-固两相流的基本特征不同于液体中固体颗粒的流动。
在泥浆流中,Stokes 数通常小于1。
当Stokes数大于1 时,流动成为流化(fluidization)了的液-固流动。
o 水力运输: 在连续流体中密布着固体颗粒o 沉降运动: 在有一定高度的成有液体的容器内,初始时刻均匀散布着颗粒物质。
随后,流体将会分层,在容器底部因为颗粒的不断沉降并堆积形成了淤积层,在顶部出现了澄清层,里面没有颗粒物质,在中间则是沉降层,那里的粒子仍然在沉降。
在澄清层和沉降层中间,是一个清晰可辨的交界面。
•三相流(上面各种情况的组合)各流动模式对应的例子如下:•气泡流例子:抽吸,通风,空气泵,气穴,蒸发,浮选,洗刷•液滴流例子:抽吸,喷雾,燃烧室,低温泵,干燥机,蒸发,气冷,刷洗•活塞流例子:管道或容器内有大尺度气泡的流动•分层自由面流动例子:分离器中的晃动,核反应装置中的沸腾和冷凝•粒子负载流动例子:旋风分离器,空气分类器,洗尘器,环境尘埃流动•风力输运例子:水泥、谷粒和金属粉末的输运•流化床例子:流化床反应器,循环流化床•泥浆流例子: 泥浆输运,矿物处理•水力输运例子:矿物处理,生物医学及物理化学中的流体系统•沉降例子:矿物处理2. 多相流模型FLUENT中描述两相流的两种方法:欧拉一欧拉法和欧拉一拉格朗日法,后面分别简称欧拉法和拉格朗日法。
Fluent多相流模型选择及设定

1.多相流动模式我们可以根据下面的原则对多相流分成四类:•气-液或者液-液两相流:o 气泡流动:连续流体中的气泡或者液泡。
o 液滴流动:连续气体中的离散流体液滴。
o 活塞流动: 在连续流体中的大的气泡o 分层自由面流动:由明显的分界面隔开的非混合流体流动。
•气-固两相流:o 充满粒子的流动:连续气体流动中有离散的固体粒子。
o 气动输运:流动模式依赖诸如固体载荷、雷诺数和粒子属性等因素。
最典型的模式有沙子的流动,泥浆流,填充床,以及各向同性流。
o 流化床:由一个盛有粒子的竖直圆筒构成,气体从一个分散器导入筒内。
从床底不断充入的气体使得颗粒得以悬浮。
改变气体的流量,就会有气泡不断的出现并穿过整个容器,从而使得颗粒在床内得到充分混合。
•液-固两相流o 泥浆流:流体中的颗粒输运。
液-固两相流的基本特征不同于液体中固体颗粒的流动。
在泥浆流中,Stokes 数通常小于1。
当Stokes数大于1 时,流动成为流化(fluidization)了的液-固流动。
o 水力运输: 在连续流体中密布着固体颗粒o 沉降运动: 在有一定高度的成有液体的容器内,初始时刻均匀散布着颗粒物质。
随后,流体将会分层,在容器底部因为颗粒的不断沉降并堆积形成了淤积层,在顶部出现了澄清层,里面没有颗粒物质,在中间则是沉降层,那里的粒子仍然在沉降。
在澄清层和沉降层中间,是一个清晰可辨的交界面。
•三相流 (上面各种情况的组合)各流动模式对应的例子如下:•气泡流例子:抽吸,通风,空气泵,气穴,蒸发,浮选,洗刷•液滴流例子:抽吸,喷雾,燃烧室,低温泵,干燥机,蒸发,气冷,刷洗•活塞流例子:管道或容器内有大尺度气泡的流动•分层自由面流动例子:分离器中的晃动,核反应装置中的沸腾和冷凝•粒子负载流动例子:旋风分离器,空气分类器,洗尘器,环境尘埃流动•风力输运例子:水泥、谷粒和金属粉末的输运•流化床例子:流化床反应器,循环流化床•泥浆流例子: 泥浆输运,矿物处理•水力输运例子:矿物处理,生物医学及物理化学中的流体系统•沉降例子:矿物处理2. 多相流模型FLUENT中描述两相流的两种方法:欧拉一欧拉法和欧拉一拉格朗日法,后面分别简称欧拉法和拉格朗日法。
多相流动的模拟与控制

多相流动的模拟与控制随着技术的不断进步,现代工业不断涌现出各种复杂的多相流动系统,这些系统广泛应用于能源、生物医学等诸多领域。
多相流动系统是指在流动过程中同时存在液体、气体、固体或者两个不同的液体之间的相互作用。
由于其存在多种相互作用,使用传统流体动力学模型难以描述和预测多相流动系统的行为。
为了更好地控制和设计这些多相流动系统,研究人员借鉴计算机领域的虚拟现实技术,基于现有的计算流体力学技术,开发了多相流动的模拟与控制技术。
多相流动的数学模型多相流动系统的数学模型是通过描述液体、气体、固体之间的相互作用和相互运动来实现的。
多相流动系统的主要物理参数包括物体大小和形状、流体性质、流动速度、压力、温度和密度等。
基于液-气和液-液的多相流模型,现有的多相流动数学模型主要有两种,分别为欧拉模型和拉格朗日模型。
欧拉模型:欧拉模型是一种连续介质模型,它假设物质是连续的并且具有自己的基本属性。
该模型通过应用牛顿第二定律,来描述物质的运动状态,该定律反映的是物质加速度与作用力之间的关系。
这种模型的优点是适用范围广和计算效率高,因此在工业应用中应用广泛。
然而,欧拉模型忽略了单个粒子的行为,不能精确地描述复杂的多相流动系统。
拉格朗日模型:拉格朗日模型是一种离散介质模型,它以悬浮颗粒的行为为基础,描述了在流体中运动的颗粒的运动轨迹和相互作用。
在拉格朗日模型中,微小的颗粒单独被跟踪,并通过求解牛顿第二定律来计算其运动所受到的力。
该模型的优点是能够准确地预测颗粒间的相互作用、运动和沉降,但由于需要追踪每个颗粒的运动轨迹,所以计算量非常大。
多相流动的仿真技术在多相流动仿真技术中,计算流体力学(CFD)是应用最广泛的数值模拟方法之一。
CFD是利用计算机模拟、解析流体的运动状态、压力分布、速度分布、涡量和湍流等流场现象的计算方法。
在多相流动仿真中,CFD技术模拟不同流体的相互作用过程,同时考虑多相流动系统内的速度,流量和压力等参数。
多相流的数值模拟和实验研究

多相流的数值模拟和实验研究多相流是指由两种或两种以上不同物质组成的两相或多相混合物所表现出来的流动现象。
对多相流的研究具有重要的理论和实际意义,它对于理解自然界的物理现象和化学过程,以及各种工业生产过程的优化和控制有着重要的意义。
由于多相流的复杂性,传统的实验和经验研究方法很难对其进行全面而准确的理论分析和实验研究,因此,数值模拟技术成为多相流研究的重要手段。
一、多相流的数学及物理模型多相流的模型是描述多相流动行为、相间传质、相间传热及相间反应过程的数学模型。
对于粒子数量较少的多相流应用连续介质模型,人们将不同相之间人为的断裂为一个个离散的颗粒,在一段时间内它们遵循阻力、碰撞、转移等物理规律分别运动。
在三维颗粒动力学(Discrete Element Method,DEM)模拟中,将某物质视作一堆颗粒的集合,部分颗粒之间具有碰撞和摩擦等相互作用。
相较于欧拉模型,DEM直接模拟颗粒的运动,颗粒运动的规律和特性可直接反映在输出的数据中。
对于粒子数量较多的多相流,例如颗粒流和气固两相流,需要采用欧拉模型。
欧拉模型将多相流看作为运动的连续介质,通过对流动状态中各相界面的移动和膨胀收缩来描绘多相流的运动及相间耦合反馈关系。
其中最重要的问题是对各相之间的相互作用关系、相互传递关系、相互转移关系进行描述和计算。
其中最经典的方法是用Navier-Stokes方程和质量守恒方程来描述多相流的欧拉模型,但是由于微观尺度的混沌运动和相互作用关系的复杂性,欧拉模型仅能模拟在能量和数量分布方面相对均一的现象。
二、多相流的数值模拟多相流的数值模拟将多相流视为连续介质,通过数值解法在离散化的时间和空间网格上对多相流动的各项参数进行计算,从而通过计算机模拟的方法来模拟多相流的运动行为。
数值模拟的过程通常包括以下几个方面的内容:建立数学模型、数值解法、模型验证和优化等。
1.建立数学模型多相流动的数学模型是研究多相流动过程的基础,在多相流动的数值模拟中,合适的模型对于准确得到各相的体积分数、速度以及温度等参数具有重要意义。
多相流动的物理模型与计算模拟

多相流动的物理模型与计算模拟随着科技的不断进步,能够为人们提供更多的便利和创造更多的价值。
在很多领域,科技的进步都离不开计算模拟,尤其是在多相流动的研究方面。
所谓多相流动,是指两个或两个以上的相互作用并占据同一场空间的流体系统。
在化工、石油、制药、食品等工业领域,多相流动是非常常见且重要的现象。
对多相流动的研究和模拟可以提高工业生产效率,降低成本,同时还有助于环保和安全生产。
以下我们将探讨多相流动的物理模型和计算模拟。
一、物理模型在对多相流动进行计算模拟时,需要建立相应的物理模型。
物理模型是描述多相流动系统运动规律和物理状态变化的一组方程,通常包括质量守恒、动量守恒和能量守恒方程等。
这些方程可以描述多相流动中液体、气体、固体颗粒等相互作用的物理过程和特性。
在物理模型中,还需要对多相流动的物理现象进行描述,如气泡的运动、颗粒的运动、界面的扩散等。
为了更好地描述多相流动的物理现象,还需要考虑相互作用力和相变过程等复杂的物理现象,以提高对多相流动系统的模拟精度。
二、计算模拟在多相流动领域中,计算模拟是一种非常重要的研究手段。
计算模拟可以通过建立物理模型和数值计算方法等,对多相流动系统的相互作用、流动过程、物质传递等不同方面进行模拟分析。
目前,多相流动的计算模拟方法主要分为两类,分别是欧拉-拉格朗日方法和欧拉-欧拉方法。
欧拉-拉格朗日方法在模拟中将液体和颗粒等物质视为不同的物理实体,用两个不同的速度场描述其运动情况,通过追踪颗粒的位置、速度、力等变量来计算弥散现象和碰撞结果;而欧拉-欧拉方法则将多相流体看作一个单一的流体,对其宏观流动状态进行描述,基于均质模型进行多相流动的模拟。
总的来说,欧拉-拉格朗日方法适用于小颗粒浓度和高相变率的情况,可以考虑颗粒形变、表面张力、相变、分散相排斥等复杂的物理现象;而欧拉-欧拉方法适用于高颗粒浓度和低相变率的情况,通常不考虑颗粒形变和表面张力,但可以模拟大规模颗粒流。
多相流动的流动机理及其数值模拟

多相流动的流动机理及其数值模拟多相流动是指在同一空间内流动的不同相的流动现象。
其中的不同相可以是气体、液体、固体颗粒、液-气界面等。
多相流动广泛应用于化工、能源、环保、航空等领域。
多相流的流动机理及其数值模拟一直是该领域中一个重要研究方向。
多相流动的流动机理是多方面的,它包括相互作用、相接触、相之间的质量传递和能量传递等方面。
相互作用包括相对速度的差异、颗粒之间的碰撞与弹性变形等。
相接触涉及到各种相之间的跨界面传递物理量的问题,包括物质的质量、能量和动量。
相互质量传递是指流动中不同相之间的物质交换过程,它们之间的质量传递会导致质量浓度的变化。
相互能量传递指的是热传递,它是在多相流中恒定的热量。
多相流动的流动机理十分复杂,需要综合考虑不同领域的基础理论。
多相流动的数值模拟是该领域研究的重要方法。
它可以通过计算机模拟来分析不同相之间的相互作用。
数值模拟使用的模型包括欧拉-拉格朗日计算、欧拉-欧拉计算等。
其中,欧拉-拉格朗日计算是最常用的一种方法。
在欧拉-拉格朗日计算中,液相和气相都可以用不同的欧拉方程求解。
尽管这种方法可以解决许多多相流动问题,但在处理涉及到多相互作用和相互传质的问题时,往往需要使用更为复杂的方法。
多相流动的数值模拟依赖于用于解决流体动力学方程组的计算流体力学(CFD)方法。
CFD能够数值求解流体动力学问题,所以该方法可以广泛应用于多相流动。
使用CFD方法可以将连续介质区域分成许多小单元,并利用有限差分或有限元法对模型进行分析。
在各相中,不同的流动方程和相互作用模型被考虑在内,以一种迭代的方式求解完整的流动方程。
初级的模拟将考虑流体中颗粒物质的运动方程,如果涉及到多种物质,那么就需要处理多组物质的连续性及其之间的相互作用。
此外,由于其非线性,一般情况下,需要使用特殊的计算方法或算法来解决问题。
大多数多相流动的CFD算法包括基于干涉法的粒子跟踪技术、基于雷诺平均NS方程的Euler-Euler方法、基于DSL-wall能量平衡技术的针像法以及基于蒙特卡罗方法来模拟气体流动和颗粒流化的离散元素法。
多相流动的理论及模拟方法研究

多相流动的理论及模拟方法研究随着科技的不断发展,多相流动的研究已经变得越来越重要。
多相流动是指两种或两种以上物质同时流经同一管道或同一过程的流动状态,比如气体和液体的混合物、气体和固体的混合物等。
多相流动的研究不仅对环境与工业的安全具有重要作用,也对生产和制造过程的优化和高效化具有重要的应用价值。
因此,多相流动的理论及模拟方法研究备受研究者的关注。
一、多相流动的分类多相流动的分类主要有三种:气液两相流、气固两相流和液固两相流。
气液两相流是指气体和液体在同一介质中同时流动。
气固两相流是指气体和固体在同一介质中同时流动。
液固两相流是指液体和固体在同一介质中同时流动。
二、多相流动的复杂性多相流动具有复杂性,其原因是物质的形态复杂多样,流场也因此变得非常复杂,并且由于多相流体物质间存在诸多相互作用,因此也需要考虑多种因素的影响。
多相流动中的流体物质通常存在相互作用力,如表面张力、粘滞力,流体物质间的阻力、剪切力等。
同时,不同相之间也会发生相互作用,如颗粒的堆积、沉积、振动等。
由于多相流动的复杂性,当前多相流动的研究面临着很多挑战。
三、多相流动的理论研究多相流动的理论研究主要涉及多相介质的流动过程和现象,它通过建立数学模型来解析和描述多相流动中的规律和特性。
目前,多相流动的研究主要集中在两个方面:多相流动规律的研究以及数值计算模拟的研究。
在多相流动规律研究方面,主要研究多相介质中各种物质之间的相互作用规律、相变规律、热传递规律、质量传递规律等。
例如:多相介质中各相的浓度分布规律、表面张力、视黏度等物理量的变化规律、各相之间的相互作用,以及这些规律对多相流动中流体的运动规律的影响。
在数值计算模拟方面,多相流动的基本方程组和物理模型实现了数值解析和计算机模拟。
计算机模拟可以帮助我们更深入并且更全面地了解多相介质中的物质运动规律,提高多相流动的分析和预测能力。
其中,最常用的方法是Euler- Euler方法和Euler-Lagrange方法。
多相流动的数值模拟

多相流动的数值模拟引言在石油、化工、冶金等领域,多相流动是一类十分重要的现象。
它对于流体力学、化学反应等方面的研究都有着重要的意义。
在实验室内研究多相流动往往受到条件的限制,因此人们常常借助数值模拟的方法来探究多相流动的规律。
随着高性能计算技术的进步,多相流动的数值模拟得到了显著的发展。
概述多相流动是指两种以上物质同时存在于同一空间内、流动行为相互影响的现象。
其中流体中两相之间相对运动存在的现象称为相互作用。
两相之间的相互作用表现为牛顿第三定律:相互作用力相等,方向相反。
多相流动的计算方法目前主要有多介质方法、连续介质方法等。
多介质方法:将流体划分为两个或以上相分离的单相流,依据一个对象在单相流中的位置,判定该对象处于哪个相中,并且根据两相之间物质交换规律,计算两个相之间的相互作用和传质传热情况。
多介质方法的优点是可以明确地区分出多种物质,但是在相界面上,流体速度及物理量的梯度会达到无穷大,时间步长受到的限制较大。
连续介质方法:将两个相或多个相混合在一起作为一个流体进行数值模拟。
连续介质方法将相互作用作为成分间的扩散流。
连续介质方法的优点是计算机容易处理,且时间步长相对较大。
缺点是得到的结果是平均化的量,难以表达相之间的详细信息。
多相流动的数值模拟方法主要有欧拉法、拉格朗日法和欧拉-拉格朗日方法。
欧拉法:与连续介质方法相似,欧拉法以物质点的质量为基础来进行计算。
以两相为例,沿任何一条雷诺迹线,可以得到该点处气相和液相的不同体积分数。
欧拉法的优点是可以精确的描述流体的宏观特征,计算快速简单,缺点是欧拉法忽略了颗粒之间的相互作用。
拉格朗日法:是以颗粒为基础,采用颗粒运动方程和颗粒轨迹计算颗粒的定位和速度。
拉格朗日法的优点是可以精确的描述颗粒间的相互作用,计算精度高。
缺点是需要像物理颗粒模型这样的复杂的计算,计算量很大。
欧拉-Lagrange方法:欧拉-Lagrange方法采用欧拉法描述流体的运动,采用Lagrange法描述颗粒间的相互作用。
矿石选矿中多相流动的模拟研究

矿石选矿中多相流动的模拟研究在矿石选矿的复杂工艺中,多相流动的模拟研究具有极其重要的意义。
它就像是一位默默工作的幕后英雄,为选矿流程的优化和效率的提升提供着关键的支持。
要理解多相流动在矿石选矿中的作用,首先得清楚什么是多相流动。
简单来说,在选矿过程中,涉及到的不仅仅是矿石颗粒这一固相,还有水、空气等液相和气相。
这些不同相态的物质相互作用、共同流动,形成了复杂的多相流动体系。
想象一下,矿石颗粒在水流中翻滚、碰撞,而空气可能会以气泡的形式存在,影响着颗粒的运动轨迹。
这种多相流动的情况十分复杂,难以直接通过肉眼观察和简单的实验来完全掌握其规律。
这时候,模拟研究就派上了大用场。
通过建立数学模型和运用计算机模拟技术,我们能够在虚拟的环境中重现选矿过程中的多相流动现象。
在进行模拟研究时,需要考虑众多的因素。
矿石颗粒的大小、形状、密度等特性会对流动产生影响。
较小的颗粒可能更容易被水流带走,而较大且密度高的颗粒则可能沉淀得更快。
同时,流体的性质,如流速、粘度等也是关键因素。
流速快的水流能够带动更多的矿石颗粒,但也可能导致一些细小的有用颗粒被过度冲走。
另外,选矿设备的几何形状和内部结构也不容忽视。
不同的设备设计会导致流体流动的路径和速度分布发生变化,从而影响选矿效果。
模拟研究的方法多种多样。
常见的有基于欧拉欧拉方法的模型,它将不同相视为相互渗透的连续介质,通过求解一系列的方程来描述多相流动。
还有基于欧拉拉格朗日方法的模型,将颗粒视为离散的个体,追踪它们在流体中的运动轨迹。
这些模拟方法各有优缺点,需要根据具体的研究问题和条件来选择合适的方法。
通过模拟研究,我们能够获得很多有价值的信息。
比如,可以了解在不同条件下矿石颗粒在选矿设备中的分布情况,从而优化设备的结构和操作参数。
我们可以预测不同粒度的矿石颗粒在选矿流程中的分离效果,为提高选矿品位和回收率提供依据。
而且,模拟研究还能够帮助我们降低实验成本和缩短研发周期。
在实际的选矿实验中,每次改变条件都需要耗费大量的人力、物力和时间。
多相流动的物理模型与数值模拟研究

多相流动的物理模型与数值模拟研究多相流动是指在同一空间内同时存在多种物质或相,这些物质之间会发生相互作用和传递,常见的涉及气体、液体和固体等颗粒相。
多相流动广泛应用于化工、环保、材料学等领域。
不同领域对于多相流动的研究重点不同,但有一些基本的物理模型和数值模拟方法可以共用。
气液两相流润滑机理在机械加工过程中,由于摩擦和冲击等作用,使润滑油被带入摩擦接触区,形成气液两相流,同时也发生很多细小的气泡,从而对润滑起到促进、稳定、减少磨损、冷却和清洗等重要作用。
当摩擦运动变化时,气液两相流的分布、密度、体积分数等属性也会随之发生变化,这就需要建立相应的数学模型追踪其变化。
目前普遍采用的方法为欧拉-拉格朗日(Euler-Lagrange)方法,即在欧拉网格上求解连续相的运动,对离散相采取拉格朗日求解。
相互作用力模型主要采用物理学界知名的乔伊斯——格里芬模型(Joyce-Griffin model),该模型对液体相和气泡相的相互作用力有一个完整的描述。
液液两相流分离机制在一些化工、生物医学等领域,液液两相流也是常见的现象。
例如,胶体分离技术、乳化液体的生产、血液分离等等,这些都是液液两相流的具体应用。
其实液液两相流的数值模拟相比于气液两种流已经相对成熟,主要是采用欧拉-欧拉两相流模型,在该模型里面液体相之间的相互作用通常采用基于格子布朗运动的布朗动力学(Brownian Dynamics)方法的随机游走方法求解。
液-液界面的张力计算通常采用连续介质力学的方法(continuum mechanical method),或者是分子动力学模拟(molecular dynamic simulation),或者是耦合上述两种方法,应用tensor Green 的方法,进一步优化数值模拟精度,减小时空误差和数值离散化误差。
凝聚相多相流动的模型及数值模拟除了气液两相流和液液两相流外,凝聚态相的多相流动同样是非常重要的。
例如,混凝土加工过程会产生混凝土石料相和水泥胶浆相之间的多相流动;金属加工过程中,金属熔融会形成液相,但还会同时固化出固态晶体相。
多相流模型——精选推荐

(5.381)
式中, τd
ρd dd2 为颗粒响应时间(也称为松弛时间或弛相速度为常数以及Stokes阻力条件下,颗粒相对于连 续相的速度按指数规律衰减,经过时间τd后衰减为初始值的e−1;τs为系统响应时间,为 系统特征长度Ls与特征速度Vs之比,即 τs
β αd ρd αc ρc
(5.378)
分散相与连续相物质密度比:
γ ρd ρc
(5.379)
式中, αd和αc分别为分散相和连续相的体积分数, ρd和ρc分别为分散相和连续相的物质密 度。
115
沈阳航空工业学院
由颗粒含量率β和物质密度比γ可估算分散相颗粒之间的平均距离:[41]
L π 1 κ dd 6 κ
弹状流
气泡流、含液滴气流、带粉气流
气力输送、液力输送、泥浆流
分层流、有自由表面流
沉降
流化床
图5.13 多相流流型
根据所依赖的数学方法和物理原理不同,多相流的理论模型分为三大类:(1)经典的 连续介质力学方法;(2)建立在统计分子动力学基础上的分子动力学模拟方法;(3)介观层 次上的模拟方法,即格子 - Boltzmann 方法。目前多在工程中应用的多相流连续介质力学
(2) 体积分数方程
a. 体积分数方程 通过求解一相或多相体积分数的连续性方程,可以追踪各相之间的界面。第 q 相体 积分数的连续性方程为
流体力学中的多相流模拟及应用

流体力学中的多相流模拟及应用流体力学是研究流体运动规律和作用的一个重要分支学科。
多相流模拟是流体力学中的一个重要研究内容,也是近年来越来越受到关注的热门领域之一。
回顾历史,20世纪50年代初,美国科学家艾萨克•普鲁克(Isaac Prigogine)首次提出了多相流的概念,随后国内外学者在此基础上进行了大量的研究工作。
本文将简要介绍多相流的概念、研究方法及其应用场景。
一、多相流的概念多相流是指在同一空间内同时存在多种流体或气体,它们之间相互作用产生各种相变(如凝固、气化、沉降以及相互转化等)现象的流动状态。
多相流包括两相、三相、四相以及更多的相。
其中最常见的是两相流,指的是同时存在两种不同的流体,如气液、液液、气固等。
例如汽车轮胎在行驶时,胎面与路面之间会产生两相流,其中气体是一相,胎面与路面接触的水和空气是另一相,两者相互作用形成一个流体体系。
二、多相流研究方法多相流的研究方法主要可以分为两类:实验研究和数值模拟。
实验研究是通过实际实验器材对实际流动进行观察和分析,从而揭示实际过程的规律性和特性。
数值模拟则是通过建立数学模型、采用计算机仿真技术,对多相流动进行模拟,以此研究多相流动的规律和特性。
基于数值模拟的多相流动研究方法又可分为欧拉方法和拉格朗日方法两大类。
欧拉方法是以流场为研究对象,分析不同位置流体属性的变化规律,把多相流动转化为流场数值模拟问题来研究。
而拉格朗日方法是以流体微观粒子为研究对象,通过对微观粒子的运动轨迹进行分析,揭示多相流动中各种相之间的相互作用。
实际上,两种研究方法并不是完全独立的,而是相互补充、相互依赖的。
三、多相流的应用场景多相流的研究在工程领域中有着广泛的应用。
下面我们列举出多种多相流模拟的应用场景。
1.多相流在化学工程中的应用化学反应过程涉及到多相流动,多相流动不均匀性会严重影响化工反应的效果。
比如,列管反应器中的快速催化反应的过程,常常涉及多种流体、气体与液体组分的同时存在,气液两相流相互作用的现象效应和反应时间都会对反应结果产生很大的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多相流算例多相流模拟介绍在自然界和工程问题中会遇到大量的多相流动。
物质一般具有气态、液态和固态三相,但是多相流系统中相的概念具有更为广泛的意义。
在多项流动中,所谓的“相”可以定义为具有相同类别的物质,该类物质在所处的流动中具有特定的惯性响应并与流场相互作用。
多相流动模式根据多相流系统中相的概念,按照下面的原则对多相流分成如下几类:•气-液或者液-液两相流:o气泡流动:连续流体中的气泡或者液泡。
o液滴流动:连续气体中的离散流体液滴。
o活塞流动: 在连续流体中的大的气泡o分层自由面流动:由明显的分界面隔开的非混合流体流动。
•气-固两相流:o充满粒子的流动:连续气体流动中有离散的固体粒子。
o气动输运:流动模式依赖诸如固体载荷、雷诺数和粒子属性等因素。
最典型的模式有沙子的流动,泥浆流,填充床,以及各向同性流。
o流化床:由一个盛有粒子的竖直圆筒构成,气体从一个分散器导入筒内。
从床底不断充入的气体使得颗粒得以悬浮。
改变气体的流量,就会有气泡不断的出现并穿过整个容器,从而使得颗粒在床内得到充分混合。
•液-固两相流o泥浆流:流体中的颗粒输运。
液-固两相流的基本特征不同于液体中固体颗粒的流动。
在泥浆流中,Stokes数通常小于1。
当Stokes数大于1时,流动成为流化(fluidization)了的液-固流动。
o水力运输: 在连续流体中密布着固体颗粒o沉降运动: 在有一定高度的成有液体的容器内,初始时刻均匀散布着颗粒物质。
随后,流体将会分层,在容器底部因为颗粒的不断沉降并堆积形成了淤积层,在顶部出现了澄清层,里面没有颗粒物质,在中间则是沉降层,那里的粒子仍然在沉降。
在澄清层和沉降层中间,是一个清晰可辨的交界面。
•三相流(上面各种情况的组合)多相系统的例子各流动模式对应的例子如下:•气泡流例子:抽吸,通风,空气泵,气穴,蒸发,浮选,洗刷•液滴流例子:抽吸,喷雾,燃烧室,低温泵,干燥机,蒸发,气冷,刷洗•活塞流例子:管道或容器内有大尺度气泡的流动•分层自由面流动例子:分离器中的晃动,核反应装置中的沸腾和冷凝•粒子负载流动例子:旋风分离器,空气分类器,洗尘器,环境尘埃流动•风力输运例子:水泥、谷粒和金属粉末的输运•流化床例子:流化床反应器,循环流化床•泥浆流例子:泥浆输运,矿物处理•水力输运例子:矿物处理,生物医学及物理化学中的流体系统•沉降例子:矿物处理多相建模方法计算流体力学的进展为深入了解多相流动提供了基础。
目前有两种数值计算的方法处理多相流:欧拉-拉格朗日方法和欧拉-欧拉方法。
欧拉-拉格朗日方法在Fluent中的拉格朗日离散相模型遵循欧拉-拉格朗日方法。
流体相被处理为连续相,直接求解时均纳维-斯托克斯方程,而离散相是通过计算流场中大量的粒子,气泡或是液滴的运动得到的。
离散相和流体相之间可以有动量、质量和能量的交换。
该模型的一个基本假设是,作为离散的第二相的体积比率应很低,即便如此,较大的质量加载率仍能满足。
粒子或液滴运行轨迹的计算是独立的,它们被安排在流相计算的指定的间隙完成。
这样的处理能较好的符合喷雾干燥,煤和液体燃料燃烧,和一些粒子负载流动,但是不适用于流-流混合物,流化床和其他第二相体积率不容忽略的情形。
欧拉-欧拉方法在欧拉-欧拉方法中,不同的相被处理成互相贯穿的连续介质。
由于一种相所占的体积无法再被其他相占有,故此引入相体积率(phasic volume fraction)的概念。
体积率是时间和空间的连续函数,各相的体积率之和等于1。
从各相的守恒方程可以推导出一组方程,这些方程对于所有的相都具有类似的形式。
从实验得到的数据可以建立一些特定的关系,从而能使上述方程封闭,另外,对于小颗粒流(granular flows),则可以通过应用分子运动论的理论使方程封闭。
在FLUENT中, 共有三种欧拉-欧拉多相流模型,分别为:流体体积模型(VOF),混合物模型,以及欧拉模型。
VOF模型所谓VOF模型,是一种在固定的欧拉网格下的表面跟踪方法。
当需要得到一种或多种互不相融流体间的交界面时,可以采用这种模型。
在VOF模型中,不同的流体组分共用着一套动量方程,计算时在全流场的每个计算单元内,都记录下各流体组分所占有的体积率。
VOF模型的应用例子包括分层流,自由面流动,灌注,晃动,液体中大气泡的流动,水坝决堤时的水流,对喷射衰竭(jet breakup)(表面张力)的预测,以及求得任意液-气分界面的稳态或瞬时分界面。
混合物模型混和物模型可用于两相流或多相流(流体或颗粒)。
因为在欧拉模型中,各相被处理为互相贯通的连续体,混和物模型求解的是混合物的动量方程,并通过相对速度来描述离散相。
混合物模型的应用包括低负载的粒子负载流,气泡流,沉降,以及旋风分离器。
混合物模型也可用于没有离散相相对速度的均匀多相流。
欧拉模型欧拉模型是Fluent中最复杂的多相流模型。
它建立了一套包含有n个的动量方程和连续方程来求解每一相。
压力项和各界面交换系数是耦合在一起的。
耦合的方式则依赖于所含相的情况,颗粒流(流-固)的处理与非颗粒流(流-流)是不同的。
对于颗粒流,可应用分子运动理论来求得流动特性。
不同相之间的动量交换也依赖于混合物的类别。
通过FLUENT的客户自定义函数(user-defined functions),你可以自己定义动量交换的计算方式。
欧拉模型的应用包括气泡柱,上浮,颗粒悬浮,以及流化床。
多相流模型的选择基本原则通常,你一旦决定了采用何种模式最能符合实际的流动,那么就可以根据以下的原则来挑选最佳的模型。
更为具体的指导,包括如何选择含有气泡,液滴和粒子的流动模型可以参见FLUENT中文帮助。
•对于体积率小于10%的气泡、液滴和粒子负载流动,采用离散相模型。
•对于离散相混合物或者单独的离散相体积率超出10%的气泡、液滴和粒子负载流动,采用混合物模型或者欧拉模型。
具体采用何种模型。
•对于活塞流,采用VOF模型。
•对于分层/自由面流动,采用VOF模型。
•对于气动输运,如果是均匀流动,则采用混合物模型;如果是粒子流,则采用欧拉模型。
•对于流化床,采用欧拉模型模拟粒子流。
•对于泥浆流和水力输运,采用混合物模型或欧拉模型。
•对于沉降,采用欧拉模型。
•对于更加一般的,同时包含若干种多相流模式的情况,应根据最感兴趣的流动特征,选择合适的流动模型。
此时由于模型只是对部分流动特征做了较好模拟,其精度必然低于只包含单个模式的流动。
DPM模型概述DPM模型可以用来模拟流场中的离散相,它的特点是使用方便,模拟思路清晰,计算中可以对颗粒运动轨迹进行跟踪,结果直观;其缺点是,计算结果无法得到离散相各种场图,为结果分析造成很大不便。
FLUENT提供了如下的离散相模型选项:1. 使用Lagrangian 坐标下的公式计算颗粒的轨迹。
这些公式涉及了稳态及非稳态条件下离散相的惯性力、曳力和重力。
2. 连续相中的漩涡对于离散相扩散产生的扰动进行预测。
3. 离散相的加热与冷却。
4. 液滴的蒸发和沸腾。
5. 提供对颗粒燃烧的模拟,可以通过对挥发份析出和焦炭燃烧来模拟煤粉的燃烧。
6. 可以选择是否进行连续相与离散相的耦合计算。
7. 液滴的破碎与合并。
这些模型时的FLUENT 可以用来对许多种离散相的问题进行模拟,包括颗粒的分离与分级,喷雾干燥,烟雾的扩散,液体中气泡的搅浑,液体燃料和煤的燃烧。
当需要在FLUENT 的模型中加入离散相时,可以通过定义颗粒的初始位置、速度、粒径、温度等参数实现,具体的操作过程在“Discrete Phase Model”面板中完成。
以上的参数再加上颗粒的物理属性,就可以作为计算颗粒轨迹和颗粒热、质传递的初始化条件。
下面就使用DPM 模型的基本步骤归纳如下,仅供参考(一)对于稳态问题,可采用以下步骤求解:1. 求解连续向流动;2. 添加离散相;3. 如果需要的话可以求解耦合流动;4. 对计算结果进行后处理(二)对于非稳态问题,可通过以下步骤求解;1. 添加离散相;2. 初始化流场;3. 设定时间步长。
对于非耦合问题,FLUENT 会在每个时间步长的最后更新离散相的位置;对于耦合问题,在每次相间耦合计算中离散相的位置都回更新。
2 应用DPM模型需要注意的一些问题在Fluent中应用DPM模型进行计算时,需要注意DPM 模型忽略了两相流中颗粒之间的相互作用,以及颗粒相对连续相流动产生的影响。
这就决定了两相流中颗粒相的体积分数不能太高,通常情况下这一体积分数要小于10%~20%。
但是,这并不意味着在应用DPM 模型时颗粒相的质量分数也要小于10%~20%,实际上,我们可以使用DPM 模型来模拟离散相质量分数等于或超过连续相质量分数的流动。
如果颗粒是以喷射的形式进入连续相的,而且流场中有明确的入口和出口,这种情况下可以使用稳态的DPM 模型来计算;如果颗粒相在连续相中处于一种无限期的悬浮状态,这种情况下稳态的Lagrangian 模型就不再适用了,对于这样的工况可以考虑使用非稳态的DPM 模型来进行求解。
换句话说,对于搅拌器、混和器、流化床这一类容器如果应用DPM 模型来模拟其流场,应该在非稳态的前提下进行。
一旦应用DPM 模型来对流动进行模拟后,Fluent 中的某些功能将不能再被使用。
具体如下:1. 周期性的边界条件;2. 可调的时间步长;3. 使用非预混燃烧模型时,颗粒不能参加反应;4. 当使用动网格或变形网格时,颗粒喷射的表面便不能随网格一起运动;5. 如果使用了复合参考系,在参考系下颗粒轨道失去了原有的意义,同理,相间耦合计算也失去了意义。
解决这个问题的方法就是采用绝对速度来对颗粒进行跟踪而不是采用相对速度,这一方法可以通过在文本窗口输入以下命令实现:define/models/dpm/tracking/track-in- absolute-frame。
需要注意的是,计算结果会与符合参考系下壁面的位置有很大关系。
颗粒的跟踪是在哪个参考坐标系下进行的,颗粒的入射速度就要在哪个参考坐标系下定义的。
默认情况下,颗粒速度是基于当地坐标系定义的,如果你激活了track-in-absolute-frame(方法如前所述),颗粒速度就基于绝对坐标系来定义。
3 DPM模型的简便用法所谓的简便用法,就是不用考虑细节,甚至不必知道模型设置面板中每一项的意义所在,而只给出相应参数的设定来进行求解。
我们不提倡这样的做法,不敢保证一次建模、一次计算就能得到满意的结果,所以,需要使用者的慢慢调试!对于稳态的工况,为了确保计算结果的收敛,可以暂时先不在流场中添加离散相,而仅仅进行连续相的迭代,一直迭代到连续相收敛再加入离散相。
当然,也可在计算得到收敛趋势时加入离散相。
本节只讨论DPM 模型面板的设定。
下面说明DPM简便用法的操作步骤:1. 通过Define→Models→Discrete Phase 来打开DPM 模型的控制面板,如图1所示;2. 选中interaction with Continuous Phase;3. 将Number of Continuous Phase Iterations per DPM Iteration置为20;4. 选中Specify Length Scale,将Length Scale置为0.01,注意Length Scale后面的单位是m;5. 粗略估计颗粒的行程,然后用该行程除以Length Scale,得到的值就是Max. Number Of Steps 要输入的值。
