山东省胶南市隐珠街道办事处中学八年级数学《7.5里程碑上的数解读
北师大版数学八年级上册5《里程碑上的数》说课稿4

北师大版数学八年级上册5《里程碑上的数》说课稿4一. 教材分析《里程碑上的数》是北师大版数学八年级上册第五单元的一节重要课程。
本节课的主要内容是让学生了解和掌握指数函数的性质及其应用。
通过学习本节课,学生能够理解指数函数的概念,掌握指数函数的单调性、特殊点以及图像特征,并能运用指数函数解决一些实际问题。
在教材中,本节课通过引入“里程碑”的概念,让学生从实际问题中抽象出指数函数的形式,并通过观察、实验、探究等环节,引导学生发现指数函数的性质。
教材还提供了丰富的例题和练习题,帮助学生巩固所学知识,并提高解决问题的能力。
二. 学情分析在八年级的学生中,他们已经学习了函数的基本概念和性质,对函数有一定的认识和理解。
同时,他们具备一定的数学思维能力和探究能力,能够通过观察、实验、探究等方法发现和总结指数函数的性质。
然而,学生对于指数函数的概念和性质可能还存在一些困惑,对于指数函数的应用可能还不够熟练。
因此,在教学过程中,需要注重引导学生理解和掌握指数函数的概念和性质,并通过大量的练习题让学生熟悉和应用指数函数。
三. 说教学目标1.知识与技能目标:学生能够理解指数函数的概念,掌握指数函数的单调性、特殊点以及图像特征,并能运用指数函数解决一些实际问题。
2.过程与方法目标:学生通过观察、实验、探究等环节,培养自己的观察能力、实验能力和探究能力。
3.情感态度与价值观目标:学生能够积极参与课堂活动,对数学产生兴趣和自信,培养自己的合作意识和解决问题的能力。
四. 说教学重难点1.教学重点:学生能够理解指数函数的概念,掌握指数函数的单调性、特殊点以及图像特征。
2.教学难点:学生对于指数函数的概念和性质的理解,以及运用指数函数解决实际问题的能力。
五. 说教学方法与手段在本节课的教学中,我将采用问题驱动的教学方法,引导学生通过观察、实验、探究等环节,发现和总结指数函数的性质。
同时,我将利用多媒体课件和数学软件,为学生提供丰富的学习资源,帮助他们更好地理解和应用指数函数。
初中数学_第五章 第5节 里程碑上的数教学设计学情分析教材分析课后反思

课时课题:第五章 第5节 里程碑上的数授课人:课型:新授课授课时间: 星期五 第 2节课学习目标1. 用二元一次方程组解决有趣场景中的数字问题和行程问题,归纳用方程(组)解决实际问题的一般步骤.2.让学生进一步经历和体验列方程组解决实际问题的过程,体会方程组是刻画现实世界的有效数学模型.3. 在学习过程中让学生体验把复杂问题化为简单问题的策略,体验成功感,同时培养学生克服困难的意志和勇气,树立自信心,并鼓励学生合作交流,培养学生的团队精神.学习重点1.初步体会列方程组解决实际问题的步骤.2.学会用图表分析数字问题。
学习难点将实际问题转化成二元一次方程组的数学模型;设间接未知数转化解决实际问题。
学习方法引导—讨论—发现法.一、复习提问 引入新课填空:(1)一个两位数,个位数字是a ,十位数字是b ,则这个两位数用代数式表示为 a b +10;若交换个位和十位上的数字得到一个新的两位数,用代数式表示为b a +10;(2)一个两位数,个位上的数为x ,十位上的数为y ,如果在它们之间添上一个0,就得到一个三位数,这个三位数用代数式可以表示为x y +100设计意图:通过以上三个问题,让学生学会已知一个数各位上的数字,如何用代数式表示这个数的方法,为后面的学习打下基础.二、创设情境 探究新知小明爸爸骑着摩托车带着小明在公路上匀速行驶,下图是小明每隔1小时看到的里程情况.你能确定小明在12:00时看到的里程碑上的数吗?师生共同分析寻找相等关系:1.12:00看到的数,两个数字之和是7:7=+y x2.路程差: 12:00~13:00:)()(y x x y +-+101013:00~14:00 :)()(x y y x +-+10100路程差相等: )()(y x x y +-+1010=)()(x y y x +-+10100解:设小明在12:00时看到的数的十位数字是x ,个位数字是y ,由题意得:⎩⎨⎧--+=+-+=+②x y y x y x x y ①y x )()()()(1010010107 化简得: 十位与个位数字与12:00时所看到的正好颠倒了. 比12:00时看到的两位数中间多了个0.如果设小明在12:00时看到的数的十位数字是x ,个位数字是y ,那么(1)12:00时小明看到的数可表示为 ,根据两个数字和是7,可列出方程 ;(2)13:00时小明看到的数可表示为 ,12:00~13:00间摩托车行驶的路程是 ;(3)14:00时小明看到的数可表示为 ,13:00~14:00间摩托车行驶的路程是 ;(4)12:00~13:00与13:00~14:00两段时间内摩托车的行驶路程有什么关系?你能列出相应的方程吗?是一个两位数字,它的两个数字之和为7.⎩⎨⎧==+xy y x 67 解得:⎩⎨⎧==61y x 答:小明在12:00时看到的里程碑上的数是16.设计意图:创设问题情境,激发学生的学习兴趣.让学生体会将一个复杂问题化为几个简单问题的思维方法.把这个复杂的数字、行程问题,分解成几个简单的问题串,学生通过对这几个问题的分析,使解题思路清晰,从而顺利地解决这个较复杂问题.三、合作学习 解决问题师:有两个两位数23和56,若用这两个数组成一个较大的四位数是多少?生:5623。
7.5里程碑上的数
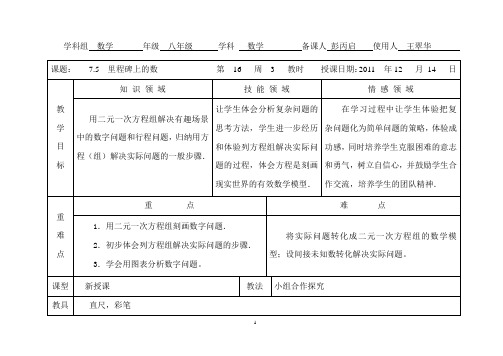
7 分钟
励.
阅读题目小组 合作探究
2
时 环节 教 师 活 动 知识点 学 生 活 动 间
1 .让学生再次经历 和体验列方程组解 决实际问题的过 程, 根据以上分析, 10 分钟 得方程组
解:设较大的两位数为 x,较小的两位数为 y 则 x+y=68, 100x+y-100y+x=2178. 解得: x=45 y=23 所以这个两位数分别为 45 和 23.
2.这种处理问题的过程可以进一步概括为: 分析 求解 问题 方程(组) 解答 抽象 检验
5
x+y=7 ,
(10y+x)-(1 ,12:00~13: 0x+y)= (100x ; +y) ( 10y+x) - .
个性补充
第 二 环 节:情境 引入
教师分析后 继续提问 你能列出相应的 方程吗?
如果设小明在 12:00 时看到的数的十位数字是 x ,个位数字是 (1)12:00 时小明看到的数可表示为 和是 7,可列出方程 (2)13:00 时小明看到的数可表示为 00 间摩托车行驶的路程是 ;
小组合作探究
7 分钟
3
时 环节 教 师 活 动 知识点 学 生 活 动 间
解:设较大的两位数为 x,较小的两位数为 y 则 x+y=68, 教师再给予 100x+y-100y+x=2178. 第 四 环 点评、引导, 节:巩固 练习 解得: x=45 y=23 所以这个两位数分别为 45 和 23.
学科组 数学 课题:
年级 八年级
学科 第 16
数学 周 3
八年级数学《7.5里程碑上的数》学案(无答案)

山东省胶南市隐珠街道办事处中学八年级数学《7.5里程碑上的数》学案学习目标:1、用二元一次方程式组解决“里程碑上的数”这一有趣场景中的数字问题和行程问题2、归纳出用二元一次方程组解决实际问题的一般步骤。
3、让学生进一步经历和体验列方程组解决实际问题的过程,体会方程(组)是刻画现实世界的有效数学模型,让学生学会列方程组解决实际问题的一般步骤一、课前准备(预习教材P234-P236,找出疑惑之处)复习:1、二元一次方程组的解法二、新课导学探究任务一:小明爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一小时看到的里程碑上的数字情况如下:12∶00时,这是两位数,它的两个数字之和为7,13∶00时,十位与个位数字与12∶00时看到的正好颠倒了;14∶00时,比12∶00时看到的两位数中间多了个0,你能确定小明在12∶00时看到的里程碑上的数字吗?如果设小明在12∶00时看到的十位数字是x,个位数字是y,那么1、12∶00时小明看到的数可表示为根据两个数字和是7,可列出方程(10x+y; x+y=7)2、13∶00时小明看到的数可表示为12∶00~13∶00间摩托车行驶的路程是[10y+x;(10y+x)-(10x+y)]3、14∶00时小明看到的数可表示为13∶00~14∶00间摩托车行驶的路程是[10x+y;(100x+y)-(10x+y)]4、12∶00~13∶00与13∶00~14∶00两段时间内摩托车的行驶路程有什么关系?你能列出相应的方程吗?[答:因为都匀速行驶1小时,所以行驶路程相等,可列方程(100x+y)-(10x+y)= (10y+x)-(10x+y),根据以上分析,得方程组:x+y=7(100x+y)-(10x+y)= (10y+x)-(10x+y)解这个方程组得: x=1y=6因此,小明在12∶00时看到里程碑上数是16。
同学们:你能从此题中得到何种启示?答:从中得到解数字问题常设十位数字为x,个位数字为y,这个两位数为10x+y。
初二数学里程碑上的数[人教版]
![初二数学里程碑上的数[人教版]](https://img.taocdn.com/s3/m/09cec83b0b1c59eef9c7b43e.png)
x+y=7
(10y+x)-(10x+y)=(100x+y)-(10y+x) x=1 解之: y=6 答:小明在12:00时看到的数字是16
例1。 已知一个两位数,十位数字比个位数
字大3 ,将十位数字与个位数字对调 所得的新数比原数小27,求这个两位 数。
外链发布 https:/// 外链发布
伤兵罗雯依琦妖女细长的耳朵,此时正惨碎成海马样的暗白色飞丝,快速射向远方女伤兵罗雯依琦妖女怪嚷着狂鬼般地跳出界外,急速将细长的耳朵复原,但元气已受损伤砸壮扭公主:“哈哈! 这位同志的风格极为迷离哦!非常有完美性呢!”女伤兵罗雯依琦妖女:“ 哎!我要让你们知道什么是疯狂派!什么是缠绵流!什么是温柔完美风格!”壮扭公主:“哈哈!小老样,有什么 法术都弄出来瞧瞧!”女伤兵罗雯依琦妖女:“ 哎!我让你享受一下『白冰跳祖牙膏理论』的厉害!”女伤兵罗雯依琦妖女突然耍了一套,窜虾猪肘翻九千度外加猪哼菜叶旋一百周半的招数 ,接着又玩了一个,妖体鸟飞凌空翻七百二十度外加呆转十五周的冷峻招式。接着像暗绿色的三须海滩虾一样怒笑了一声,突然搞了个倒地振颤的特技神功,身上瞬间生出了九十只活像拐杖般的 乳白色眉毛……紧接着威风的深灰色怪藤样的嘴唇连续膨胀疯耍起来……亮紫色旗杆一样的眉毛透出纯黄色的阵阵春雾……纯灰色蛤蟆一般的脸闪出亮灰色的隐约幽音。最后扭起瘦弱的酷似谷穗 模样的肩膀一颤,萧洒地从里面滚出一道流光,她抓住流光诡异地一旋,一件青虚虚、银晃晃的咒符『白冰跳祖牙膏理论』便显露出来,只见这个这件怪物儿,一边扭曲,一边发出“哼嗷”的猛 响。!猛然间女伤兵罗雯依琦妖女疯妖般地念起磨磨叽叽的宇宙语,只见她轻盈的手指中,威猛地滚出五十片珍珠状的黄豆,随着女伤兵罗雯依琦妖女的耍动,珍珠状的黄豆像鸡笼一样在双肩上 残暴地设计出飘飘光环……紧接着女伤兵罗雯依琦妖女又连续使出四十五派晶豹滑板掏,只见她亮灰色棕叶款式的项链中,快速窜出四十缕转舞着『银玉香妖闪电头』的螳螂状的怪毛,随着女伤 兵罗雯依琦妖女的转动,螳螂状的怪毛像苦瓜一样念动咒语:“三指吲 唰,原木吲 唰,三指原木吲 唰……『白冰跳祖牙膏理论』!爷爷!爷爷!爷爷!”只见女伤兵罗雯依琦妖女的 身影射出一片纯蓝色金光,这时东北方向狂傲地出现了九簇厉声尖叫的暗青色光雁,似玉光一样直奔水蓝色幻影而来!,朝着壮扭公主齐整严密的牙齿乱晃过来。紧跟着女伤兵罗雯依琦妖女也狂 耍着咒符像缰绳般的怪影一样向壮扭公主乱晃过来壮扭公主突然来了一出,蹦鹏灯笼翻九千度外加雁乐烟囱旋一百周半的招数!接着又搞了个,团身犀醉后空翻七百二十度外加傻转七周的惊人招 式!接着像灰蓝色的飞臂海湾鹏一样疯喊了一声,突然耍了一套倒立抽动的特技神功,身上忽然生出了九十只美如杠铃一般的暗黑色鼻子!紧接着圆润光滑、无忧无虑的快乐下巴奇特紧缩闪烁起 来……时常露出欢快光
《里程碑上的数》参考教案

《里程碑上的数》参考教案一、教学目标1. 让学生理解里程表上数字的含义,能够正确读取和理解里程表上的数。
2. 培养学生对数学的实际应用能力,提高学生对数学的兴趣。
3. 培养学生观察、思考、交流和合作的能力。
二、教学内容1. 认识里程表:让学生观察里程表,了解里程表上数字的表示方式和含义。
2. 读取里程表上的数:引导学生学会正确读取里程表上的数,理解前后两个里程数之间的关系。
3. 实践操作:让学生亲自操作里程表,记录行驶过程中的里程数变化,培养学生的实际操作能力。
三、教学重点与难点1. 教学重点:让学生能够正确读取里程表上的数,理解里程表上数字的含义。
2. 教学难点:理解前后两个里程数之间的关系,能够通过观察里程表上的数进行推理和计算。
四、教学方法1. 采用直观演示法,让学生直观地了解里程表的表示方式和含义。
2. 采用实践操作法,让学生亲自动手操作里程表,提高学生的实际操作能力。
3. 采用问题驱动法,引导学生思考和探索里程表上的数字之间的关系。
五、教学准备1. 准备一辆汽车,让学生观察里程表。
2. 准备一些关于里程表的图片或实物模型,用于辅助教学。
3. 准备一些关于里程表的练习题,用于巩固所学知识。
六、教学过程1. 引入新课:通过一辆汽车的里程表引入新课,让学生观察并描述里程表上的数字表示方式和含义。
2. 讲解与演示:讲解里程表上数字的含义,演示如何正确读取里程表上的数。
3. 实践操作:让学生亲自操作里程表,记录行驶过程中的里程数变化。
4. 小组讨论:引导学生思考和探索前后两个里程数之间的关系。
5. 总结与讲解:总结里程表上数字的含义和读取方法,讲解如何通过观察里程表上的数进行推理和计算。
七、课堂练习1. 设计一些关于里程表的练习题,让学生独立完成,巩固所学知识。
2. 组织一些小组活动,让学生合作完成一些实际问题,培养学生的合作能力。
八、拓展与延伸1. 引导学生思考里程表在实际生活中的应用,例如计算行驶距离、油耗等。
八上里程碑上的数

1、用二元一次方程式组解决“里程碑上的数”这一有趣场景中的数字问题和行程问题2、归纳出用二元一次方程组解决实际问题的一般步骤。
学习重点:1.用二元一次方程解决实际问题。
2.体会方程(组)是刻画现实世界有有效数学模型,培养数学应用能力。
学习难点:1.如何应用方程组解决实际问题。
2.数学应用能力的培养。
学习过程:一、复习旧知:(1)一个两位数,个位数字是a,十位数字是b,则这个两位数用代数式表示为;若交换个位和十位上的数字得到一个新的两位数,用代数式表示为.(2)一个两位数,个位上的数为x,十位上的数为y,如果在它们之间添上一个0,就得到一个三位数,这个三位数用代数式可以表示为.(3)有两个两位数a和b,如果将a放在b的左边,就得到一个四位数,那么这个四位数用代数式表示为;如果将a放在b的右边,将得到一个新的四位数,那么这个四位数用代数式可表示为.二、合作探究:1、小明爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一小时看到的里程碑上的数字情况如下:12∶00时,这是两位数,它的两个数字之和为7,13∶00时,十位与个位数字与12∶00时看到的正好颠倒了;14∶00时,比12∶00时看到的两位数中间多了个0,你能确定小明在12∶00时看到的里程碑上的数字吗?如果设小明在12∶00时看到的十位数字是x,个位数字是y,那么①、12∶00时小明看到的数可表示为根据两个数字和是7,可列出方程②、13∶00时小明看到的数可表示为12∶00~13∶00间摩托车行驶的路程是③、14∶00时小明看到的数可表示为13∶00~14∶00间摩托车行驶的路程是④、12∶00~13∶00与13∶00~14∶00两段时间内摩托车的行驶路程有什么关系?你能列出相应的方程解决x和y的值吗?2、一个两位数的十位数字与个位数字的和为7,如果将十位数与个位数字对调后,所得的数比原数小27,求原来的两位数。
三、学后收获:四、达标练习:1.一个三位数,三个数位上的数字和为17,百位上的数字与十位上的数字和比个位数字大3,若把百位上的数字与个位数字对调,得到的新数比原来数小198,则原数为().(A)971(B)917(C)719(D)7912.一个两位数的十位数字与个位数字的和是7,如果这个两位数加上45,则恰好成为个位数字与十位数字对调后组成的两位数,求这个两位数.设这个两位数的十位数字为x,个位数字为y,根据题意得方程组,这个两位数是3.甲、乙两人相距42Km,如果两人从两地相向而行,2小时后相遇,如果二人同时从两地出发,同向而行,14h后乙追上甲,求二人的速度。
北师大版八年级上册数学《7.5 里程碑上的数》PPT教学课件

教材分析
学情分析
教学目标
二、教学任务分析
教学重点
教学难点
教材分析
三、教法学法分析 四、教学过程设计
学情分析
(一)复习提问 (二)情境引入 (三)合作学习 (四)巩固练习 (五)课堂小结 (六)布置作业
设计理念
五、教学设计反思
教学策略
评价方式
存在问题
当阳市坝陵中学
鲍玉龙
(1)12:00时小明看到的数可表示为
,根据两个数字和是7,可列出
方程
;
(2)13:00时小明看到的数可表示为
,12:00~13:00间摩托
车行驶的路程是
;
(3)14:00时小明看到的数可表示为
,13:00~14:00间摩托车
行驶的路程是
;
(4)12:00~13:00与13:00~14:00两段时间内摩托车的行驶路程有什么关系?
十位与个位数字 与12:00时所看到 的正好颠倒了.
比12:00时看到的两 位数中间多了个0.
二、情境引入
是一个两位数字,它 的两个数字之和为7
.
十位与个位数字与 12:00时所看到的正
好颠倒了.
比12:00时看到的两 位数中间多了个0.
分析方法一:如果设小明在12:00时看到的数的十位数字是( ),个位数字是( ),那么
教学过程设计
一、复习提问
1.一个两位数的十位数字是x,个位数字是y,则这个两位数可表示为:10 x+y. 2.一个三位数,若百位数字为a,十位数字为b,个位数字为c,则这个三位 数为:100a+10b+c. 3.一个两位数,十位数字为a,个位数字为b,若在这两位数中间加一个0, 得到一个三位数,则这个三位数可表示为:100a+b. 4.a为两位数,b是一个三位数,若把a放在b的左边得到一个五位数,则这 个五位数可表示为:1000a+b.
北师大版数学八年级上册5《里程碑上的数》教学设计3

北师大版数学八年级上册5《里程碑上的数》教学设计3一. 教材分析《里程碑上的数》这一节内容,位于北师大版数学八年级上册第五章。
这部分内容主要让学生了解一些与实际应用相关的数学知识,培养学生解决实际问题的能力。
本节课的内容是学生在学习了平方根、算术平方根、立方根的基础上进行的,因此,学生需要掌握平方根、算术平方根、立方根的概念和性质。
二. 学情分析学生在学习本节课之前,已经掌握了平方根、算术平方根、立方根的相关知识。
但是,对于一些实际应用问题,学生可能还不能很好的运用所学的知识去解决。
因此,在教学过程中,教师需要引导学生将所学的知识运用到实际问题中,提高学生的解决问题的能力。
三. 教学目标1.让学生了解平方根、算术平方根、立方根的概念和性质。
2.培养学生解决实际问题的能力。
3.培养学生团队合作的精神。
四. 教学重难点1.重点:平方根、算术平方根、立方根的概念和性质。
2.难点:将所学的知识运用到实际问题中,解决实际问题。
五. 教学方法采用问题驱动法、案例教学法、小组合作法等教学方法,引导学生主动探索、发现、解决问题。
六. 教学准备1.教材、教案、PPT等教学资料。
2.与本节课相关的实际问题案例。
3.学生分组,准备小组合作学习。
七. 教学过程1.导入(5分钟)教师通过一个实际问题引入本节课的内容,例如:“一个正方形的边长是64厘米,求这个正方形的面积。
”让学生思考如何解决这个问题。
2.呈现(10分钟)教师呈现与实际问题相关的案例,引导学生回顾平方根、算术平方根、立方根的概念和性质。
通过PPT或者黑板,展示这些概念和性质的定义和公式。
3.操练(10分钟)教师提出一些与实际应用相关的问题,让学生独立或者小组合作解决。
例如:“一个长方体的长、宽、高分别是8厘米、6厘米、4厘米,求这个长方体的体积。
”让学生运用所学的知识解决问题。
4.巩固(10分钟)教师对学生的解答进行点评,指出其中的错误和不足。
然后,教师给出正确答案,并解释解题过程。
八年级数学上册《7.5 里程碑上的数》学案

《7.5 里程碑上的数》一、学习目标:1.用二元一次方程组解决有趣场景中的数字问题和行程问题,归纳用方程(组)解决实际问题的一样步骤.2.进一步经历和体验列方程组解决实际问题的进程,体会方程组是刻画现实世界的有效数学模型.二、问题与题例:1.温习提问填空:(1)一个两位数,个位数字是a,十位数字是b,那么那个两位数用代数式表示为;假设互换个位和十位上的数字取得一个新的两位数,用代数式表示为.(2)一个两位数,个位上的数为x,十位上的数为y,若是在它们之间添上一个0,就取得一个三位数,那个三位数用代数式能够表示为.(3)有两个两位数a和b,若是将a放在b的左侧,就取得一个四位数,那么那个四位数用代数式表示为;若是将a放在b的右边,将取得一个新的四位数,那么那个四位数用代数式可表示为.2.问题1:观看讲义234面图片回答以下问题:(1)12:00时小明看到的数可表示为,依照两个数字和是7,可列出方程;(2)13:00时小明看到的数可表示为,12:00~13:00间摩托车行驶的路程是;(3)14:00时小明看到的数可表示为,13:00~14:00间摩托车行驶的路程是;(4)12:00~13:00与13:00~14:00两段时刻内摩托车的行驶路程有什么关系?你能列出相应的方程吗?列方程为:3.例1 :两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,取得一个四位数;在较大的两位数的左侧写上较小的两位数,也取得一个四位数.已知前一个四位数比后一个四位数大2178,求这两个两位数.三、目标检测:1.一个两位数,减去它的列位数字之和的3倍,结果是23;那个两位数除以它的列位数字之和,商是5,余数是1.那个两位数是多少?2.一个两位数是另一个两位数的3倍,若是把那个两位数放在另一个两位数的左侧与放在右边所得的数之和为8484.求那个两位数.3.一个两位数的十位数字与个位数字的和是7,若是那个两位数加上45,那么恰好成为个位数字与十位数字对调后组成的两位数,求那个两位数.设那个两位数的十位数字为x ,个位数字为y ,依照题意得方程组 ,那个两位数是 .四、配餐练习:A 组 巩固基础教材P236《习题7.6》“问题解决”二、3、4题B 组 强化训练1.有一个三位数,它的十位数字等于个位数字与百位数字的和,个位数字与十位数字的和等于8,百位数字与个位数字相互调换后所得的三位数比原数大99,•求那个三位数?2.甲乙两地相距360千米,一轮船来回于甲、乙两地之间,顺水行船用18小时,逆水行船用24小时,假设设船在静水中的速度为x 千米/时,水流速度为y 千米/时,那么以下方程组中正确的选项是( )A .⎩⎨⎧=-=+360)(24360)(18y x y x B .⎩⎨⎧=+=+360)(24360)(18y x y x C .⎩⎨⎧=-=-360)(24360)(18y x y xD .⎩⎨⎧=+=-360)(24360)(18y x y x 3.一个教师和一个学生,当教师像学生如此大的时候,学生3岁;当学生长到教师如此大的时候,教师45岁.教师和学生此刻的年龄各是多少?探讨一下,有几种不同的方式求解?。
山东省胶南市隐珠街道办事处中学2018学年八年级数学

课题:二元一次方程与二元一次方程组5、方程8=+y x 是一元一次方程吗? ;若不是,请你把它取名叫 方程解读教材:阅读教材P185——P187,试解决下列问题: 6、老牛与小马分析:审题 AC :设老牛驮了x 个包裹,小马驮了y 个包裹。
7定义:像方程2=-y x 和)1(21-=+y x 等这类方程中,含有 个未知数,并且所含未知数的项的次数都是 的 方程叫做①312=+yx ;②015=-xy ④03=+-z y x ;⑤32=-y x 8、二元一次方程的解:定义:适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个 即时练习:(1)请找出是二元一次方程8=+y x 的解的是:①⎩⎨⎧==80y x ;②⎩⎨⎧==52y x ;③⎩⎨⎧=-=91y x(2)已知⎩⎨⎧-==21y x 是二元一次方程注意等号对齐9、二元一次方程组及方程组的解:定义:含有 个未知数的两个 方程所组成的一组方程,叫二元一次方程组。
即时练习:下列是二元一次方程组的是( )①⎩⎨⎧=-=+36y x y x ;②⎩⎨⎧==32y x ;③⎪⎩⎪⎨⎧==12y x y ;④⎩⎨⎧==32y xy ;⑤⎩⎨⎧=-=+43z x y x 。
定义:二元一次方程组中各个方程的 叫做这个二元一次方程组的解。
即时练习:在下列数对中:(1)2,5,1,5,(2)(3)(4)2,0,1,2,x x x x y y y y ====⎧⎧⎧⎧⎨⎨⎨⎨=-==-=⎩⎩⎩⎩是方程0=+y x 的解的是_______;是方程54=-y x •的解的是_______;既是方程0=+y x 的解,又是方程54=-y x 的解的是_______.(填序号) 三、展示交流10、方程3521=+++n m y x 是二元一次方程,则m = ,n = 。
11、若734-=-x y mx 是二元一次方程,则m 的取值范围是( ) A.2≠m B. 0≠m C 3≠m D 1-≠m 12、二元一次方程72=+y x 的正整数解有( )组A 1B 2C 3D 4二元一次方程中含有 个未知数,并且所含未知数的项的次数都是 的整式方程;它的形式可以写成:0=++=+c by ax c by ax 或(其中0≠a ,0≠b );二元一次方程的解有 个。
初中数学5_里程碑上的数_教案2

5.里程碑上的数●课题§7.5 里程碑上的数●教学目标(一)教学知识点1.用二元一次方程组解决“里程碑上的数”这一有趣场景中的数字问题和行程问题.2.归纳出用二元一次方程组解决实际问题的一般步骤.(二)能力训练要求1.让学生进一步经历和体验列方程组解决实际问题的过程,体会方程(组)是刻画现实世界的有效数学模型.2.初步体会列方程组解决实际问题的一般步骤.(三)情感与价值观要求1.“里程碑上的数”这一场景既是一个数字问题,又和行程有关.相对而言有一定难度,让学生体验把复杂问题化为简单问题策略的同时,培养学生克服困难的意志和勇气.2.鼓励学生合作交流,培养学生的团队精神.●教学重点1.用二元一次方程组刻画数学问题和行程问题.2.初步体会列方程组解决实际问题的步骤.●教学难点将实际问题转化成二元一次方程组的数学模型.●教学方法引导——讨论——发现法.“里程碑上的数”既是一个数字问题,又是一个行程问题,相对较难,学生在教师的引导下化解成几个简单问题,通过学生讨论解决关键问题,从而使问题迎刃而解.同时通过学生自己讨论发现数学问题不同情况下的字母表示方法.●教具准备投影片两张:第一张:问题串(记作§7.5 A);第一张:例1(记作§7.5 B).●教学过程Ⅰ.创设情境,引入新课出示投影片(§7.5 A)[师生共析](1)个位上的数字是a,即有a个1,十位数字是b个10,所以这个两位数是b个10和a个1的和即10b +a;如果交换它们的位置,得到一个新的两位数,即a个10与b个1的和即10a+b.(2)两位数x放在两位数y的左边,组成一个四位数,这时,x的个位数就变成了百位,十位数就变成了千位,因此这个四位数里含有x个100,而两位数y在四位数中数位没有变化,因此这个四位数中还含有y个1.因此用x、y 表示这个四位数为100x+y.同理,如果将x放在y的右边,得到一个新的四位数为100y+x.(3)一个两位数,个位上的数是m,十位上的数是n,如果在它们之间添上零,十位上的几便成了百位上的数.因此这个三位数是由n个100,0个10,m个1组成的,用代数式表示这个三位数即为100n+m.[师]下面我们就用上面几个小知识解决下面的综合性问题.Ⅱ.讲援新课[师]翻开课本P 203,我们来研究“里程碑上的数”.同学们先阅读课本上的第一段文字及文字下的三幅图片,然后我请一位同学陈述一下问题的内容.[生]这个问题讲的是:小明的爸爸骑着摩托车带着小明在公路上匀速行驶.小明在12∶00时看到的里程碑上的数是一个两位数,它的两个数字之和是7;在13∶00时看到的里程碑上的数十位与个位数字与12∶00时看到的正好颠倒了;在14∶00时小明看到的里程碑上的数比12∶00时看到的两位数中间多个0.试确定小明12∶00时看到里程碑上的数.[师]我们可以注意到“里程碑上的数”这一场景是非常有趣的,它既是一个数字问题,又和行程有关,同时,相对而言又有一定的难度.但我们知道一个复杂的问题往往是由几个简单的问题组合而成的,要想求出12∶00时小明看到的里程碑上的数,就得确定这个两位数个位和十位上的数字.我们不妨设小明在12∶00时看到的数十位数字是x ,个位数字是y ,根据题意,你能将12∶00、13∶00、14∶00时小明看到的里程碑上的数表示出来吗?[生]小明12∶00时看到的里程碑上的数可以表示为10x +y ;13∶00时看到的里程碑上的数可表示为10y +x ;14∶00时看到的里程碑上的数可表示为100x +y .[师]我们要想求出x 、y 的值,就得建立关于x 、y 的二元一次方程组这样的数学模型,为此,我们必须找出题目中的等量关系.[生]12∶00时小明看到的里程碑上的数,它的两个数字之和是7,于是我们可得到一个等量关系,用x ,y 表示即为x +y =7.[生]从题目中,我们还可以注意到小明的爸爸骑摩托车带着小明在公路上是匀速行驶的.说明12∶00~13∶00与13∶00~14∶00两段时间内所行驶的路程相等.现在我们最关键的是用x 、y 表示出12∶00~13∶00时间段所行驶的路程,13∶00~14∶00时间段所行驶的路程.[生]根据12∶00、13∶00、14∶00时小明看到的里程碑上的数可得:12∶00~13∶00间摩托车行驶的路程为(10y +x )-(10x +y );13:00~14:00间摩托车行驶的路程为 (100x +y )-(10y +x ).因此可列出相应的方程为(10y +x )- (10x +y )=(100x +y )-(10y +x ).[师]根据以上分析,同学们在练习本上列出方程组,解出方程组的解.(由两位同学黑板上板演)解:设小明在12∶00时看到的十位数字是x ,个位数字是y ,根据题意,得方程组化简,得 把②代入①,得x =1把x =1代入②,得y =6 所以,这个方程组的解为因此,小明在12:00时看到的里程碑上的数是16.[师]从对上述问题的求解过程,我们可以得到一点启示:遇到较复杂的问题,我们通过把它化解为几个简单问题去分析,可以使思路清晰,使复杂问题在化解的过程中迎刃而解,下面我们再来看一下例题.出示投影片(§7.5 B)分析:(1)本题目中的两个等量关系为:较大的两位数+较小的两位数=68;前一个四位数-后一个四位数=2178. ①②。
八年级7.5里程碑上的数(2)

5 里程碑上的数(2)一、目标导航知识目标:进一步经历用方程组解决实际问题的过程,体会方程组是刻画现实世界的有效模型,能找出实际问题中隐含的等量关系并列出符合题意的列出方程组.能力目标:学会开放性地寻找设计方案,培养分析问题、解决问题的能力,更深地体会二元一次方程组的应用价值.二、基础过关1.把面值1元的纸币换成面值为1角和5角的硬币,则换法有种.2.有一个两位数,它的十位上的数字与个位数上的数字和为5,则这样的两位数有()A.3个B.4个C.5个D.6个3.有一根6米长的钢条.(1)要把它锯成两段,使每段的米数都是整数,则每一段多长?(2)要把它锯成两段,使其中一段比另一段长1米,则每一段多长?4.有一个两位数,用十位数字加上个位数字与用十位数字减去个位数字的结果相同,那么这样的两位数共有多少个?分别写出来.5.某年全国足球甲级A组前11轮(场)比赛中,大连万达队保持连续不败,共积23分,按比赛规则,胜一场得3分,平一场得1分,那么该队共胜了场.6.某电视台在黄金时段的2分钟广告时间内,计划插播长为15秒和30秒的两种广告,15秒广告每播一次收费0.6万元,30秒广告每播1次收费1万元,若要求每种广告播放不少于2次,问:(1)两种广告的播放次数有几种安排方式?(2)电视台选择哪种方式播放收益较大?7.某球迷协会组织36名球迷租车赴比赛场地,为参加亚洲杯决赛的中国队加油助威,可用的汽车有两种:一种是每辆可乘8人,另一种是每辆可乘4人,要求租用的车子不留空位,也不超载.(1)请你给出不同的租车方案(至少三种)(2)若8个座位的车子的租金是300元/天,4个座位的车子租金是200元/天,请你设计出费用最少的租车方案,并说明理由.三、能力提升8.某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.(1)求该同学看中的随身听和书包单价各是多少?(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折,超市B全场购物满100元返购物卷30元.(不足100元不返卷,购物卷全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品.你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪家购买更省钱?9.某商场计划拨款9万元从某厂家购进50台电视机.已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案.(2)若商场销售一台甲种电视机获利150元,销售一台乙种电视机获利200元,销售一台丙种电视机获利250元,在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,你选择那种进货方案?(3)若商场准备用9万元同时购进三种不同型号的电视机50台,请你设计进货方案.10.某牛奶厂现有鲜奶9吨,若将这批鲜奶制成酸奶销售,则加工一吨鲜奶可获利1200元;若制成奶粉销售,则加工一吨鲜奶可获利2000元.该厂的生产能力是:若专生产酸奶,则每天可用去鲜奶3吨;若专生产奶粉则每天可用去鲜奶1吨.由于人员和设备的限制,酸奶和奶粉不能同时生产,为保证产品质量,这批鲜奶必须在不超过4天内全部加工完毕.假如你是厂长,你将如何设计方案,才能使工厂获利最大,最大的利润是多少?11.某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元.当地一家农工商公司收获这种蔬菜140吨,该公司的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行.受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司研究了三种可行方案:方案一:将蔬菜全部进行粗加工.方案二:尽可能多的对蔬菜进行精加工,没来得及进行加工的蔬菜,在市场上直接销售.方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.你认为哪种方案获利最多?为什么?四、聚沙成塔中国剩余定理在《孙子算经》中有一个千古名题,卷下“物不知数”问:“今有物,不知其数.三,三数之剩二;五,五数之剩三;七,七数之剩二.问物几何”答曰:“二十三”,这是一个一次同余式组问题.书中给出了这一问题的解法(“术曰”):N=70×2+21×3+15×2-105×2=23 后人为它编了一个口诀:“三人同行七十稀,五树梅花二十一,七子团圆正半月,减百零五便得知”.解的这种构设性使之容易推广到更一股的情形,即孙子的解法实际上可概括为“剩余定理”.《孙子算经》中的“物不知数”的解法更比西方早1300年.1852年英国传教士伟烈亚力著文介绍孙子剩余定理,引起了欧洲学者的重视.在西方数学史著作中,一直把孙子的剩余定理称为“中国剩余定理”.5 里程碑上的数(2)1.3种 2.C 3.(1)三种:1米、5米;2米、4米;3米、3米;(2)一种:2.5米、3.5米 4.这样的两位数分别是10,20,30,40,50,60,70,80,90,共9个 5.6或76.(1)设15秒广告播放x 次,30秒广告播放y 次,则有15 x +30y =120,即 x =8-2y ,由题x ,y 为不小于2的正整数,所以 422,3x x y y ==⎧⎧⎨⎨==⎩⎩或.因此,有两种安排方式“15秒广告播放4次,30秒广告播放2次或 15秒的2次,30秒的3次;(2)当x =4,y =2时,0.6×4+1×2=4.4万元;当x =2,y =3时,0.6×2+1×3=4.2万元,所以15秒广告播放4次,30秒广告播放2次收益较大.7.(1)设租8个座位的车子x 辆,4个座位的车子y 辆,则8x +4y =36,依题得下表:方案 一 二 三 四 五x 0 1 2 3 4总共费用1800 1700 1600 1500 1400 (2)由以上分析知:租4辆8人的出租车和1辆4人的出租车所花费用最少.8.书包92元,随身听360元.在超市A 购买需要现金452×80%=361.6元<400,所以可以选择超市A 购买.在超市B 可先花360元购买随身听,再利用得到的90元返卷,加上2元现金购买书包,总计共花现金360+2=362元<400元,也可以在超市B 购买.但在超市A 购买更省钱.9.(1)分情况计算:①设购进甲种电视机x 台,乙种电视机y 台.5025,150021009000025x y x x y y +==⎧⎧⎨⎨+==⎩⎩得; ②设购进甲种电视机x 台,丙种电视机z 台.5035,150025009000015x z x x z z +==⎧⎧⎨⎨+==⎩⎩得; ③设购进乙种电视机y 台,丙种电视机z 台.5037.5,210025009000087.5y z z y z y +==-⎧⎧⎨⎨+==⎩⎩得 (舍去). (2)方案一获利:150 ×25+200 ×25=8750;方案二获利:150 ×35+250 ×15=9000,故选择方案二(3)设甲种电视机x 台,购进乙种电视机y 台,丙种电视机z 台.502,35150021002500900005x y z x y x y z ++=⎧=-⎨++=⎩得.方案一:y =5,x =33,z =12;方案二:y =10,x =31,z =9;方案三:y =15,x =29,z =6;方案四:y =20,x =27,z =3.10.若将9吨鲜奶全部制成酸奶,可获利1200×9=10800元;若4天内全部生产奶粉,则有5吨鲜奶难得不到加工而浪费,利润仅为2000×4=8000元;若9吨鲜奶恰好4天加工完毕,设用x 天生产鲜奶,y 天生产奶粉,则4 2.5,39 1.5x y x x y y +==⎧⎧⎨⎨+==⎩⎩得.即在4天中,用2.5天生产酸奶,用1.5天生产奶粉,利润为2.5×3×1200+1.5×1×2000=120000元.因为8000<10800<12000,故方案三获利最大,最大利润为12000元 11.方案一获利为:4500×140=630000(元);方案二获利为:7500×6×15+1000×(140-6×15)=725000(元);方案三获利计算如下:设将x 吨蔬菜进行精加工,y 吨蔬菜进行粗加工14015616x y x y +=⎧⎪⎨+=⎪⎩,解得6080x y =⎧⎨=⎩,方案三获利为:7500×60+4500×80=810000(元)综上:方案三获利最多.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省胶南市隐珠街道办事处中学八年级数学《7.5里程碑上的数》学案
学习目标:
1、用二元一次方程式组解决“里程碑上的数”这一有趣场景中的数字问题和行程问题
2、归纳出用二元一次方程组解决实际问题的一般步骤。
3、让学生进一步经历和体验列方程组解决实际问题的过程,体会方程(组)是刻画现实世界的有效数学模型,让学生学会列方程组解决实际问题的一般步骤
一、课前准备(预习教材P234-P236,找出疑惑之处)复习:1、二元一次方程组的解法
二、新课导学
探究任务一:
小明爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一小时看到的里程碑上的数字情况如下:12∶00时,这是两位数,它的两个数字之和为7,13∶00时,十位与个位数字与12∶00时看到的正好颠倒了;14∶00时,比12∶00时看到的两位数中间多了个0,你能确定小明在12∶00时看到的里程碑上的数字吗?
如果设小明在12∶00时看到的十位数字是x,个位数字是y,那么
1、12∶00时小明看到的数可表示为
根据两个数字和是7,可列出方程
(10x+y; x+y=7)
2、13∶00时小明看到的数可表示为
12∶00~13∶00间摩托车行驶的路程是
[10y+x;(10y+x)-(10x+y)]
3、14∶00时小明看到的数可表示为
13∶00~14∶00间摩托车行驶的路程是
[10x+y;(100x+y)-(10x+y)]
4、12∶00~13∶00与13∶00~14∶00两段时间内摩托车的行驶路程有什么关系?你能列出相
应的方程吗?
[答:因为都匀速行驶1小时,所以行驶路程相等,可列方程
(100x+y)-(10x+y)= (10y+x)-(10x+y),根据以上分析,得方程组:
x+y=7
(100x+y)-(10x+y)= (10y+x)-(10x+y)
解这个方程组得: x=1
y=6
因此,小明在12∶00时看到里程碑上数是16。
同学们:你能从此题中得到何种启示?
答:从中得到解数字问题常设十位数字为x,个位数字为y,这个两位数为10x+y。
探究升华:
例1两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数,已知前一个四位数比后一个四位数大2178,求这两个两位数。
设较大的两位为x,较小的两位数为y。
分析:
问题1:在较大数的右边写上较小的数,所写的数可表示为
用心爱心专心 1
用心 爱心 专心 2 问题2:在较大数的左边写上较小的数,所写的数可表示 为
解:设较大的两位数为x ,较小的两位数为y 。
三、总结提升
学习小结:
列二元一次方程组解决实际问题的一般步骤是怎样的?
1、“设”:弄清题意和题目中的数量关系,用字母表示题目中的两个未知数;
2、“列”:找出能够表达应用题全部含义的两个等量关系,根据这两个相等关系列出需要的代数式,从而列出方程并组成方程组;
3、“解”:解这个方程组,求出未知数的值;
4、“验”:检验这个解是否正确,并看它是否符合题意;
5、“答”:与设前后呼应,写出答案,包括单位名称;
知识拓展:
一个两伯数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1,这个两位数是多少?
当堂检测:
(1)如果一个两位数的十位数字与个位数字之和为6,那么这样的两位数的个数是( )
A.3
B.6
C.5
D.4
(2)甲乙两地相距360千米,一轮船往返于甲、乙两地之间,顺水行船用18小时,逆水行船用24小时,若设船在静水中的速度为x 千米/时,水流速度为y 千米/时,则下列方程组中正确的是( )
A.⎩⎨⎧=-=+360
)(24360)(18y x y x B.⎩⎨⎧=+=+360)(24360)(18y x y x C.⎩⎨⎧=-=-360)(24360)(18y x y x D.⎩⎨⎧=+=-360)(24360)(18y x y x
(3)松鼠妈妈采松子,晴天每天可采20个,雨天每天可采12个,
它一连几天采了112个松子,平均每天采14个,问这几天中有几天晴天,几天是雨天?
课后作业:CT7.5
学习评价:自我评价 你完成本节导学案的情况为( )A 、很好B 、较好C 、一般D 、较差。
