四川大学信号与系统考研真题+答案11年
2010年信号与系统A卷答案

四川大学期末考试试题(闭卷)A 卷答案(2009——2010学年第二学期)1 True or False Question (10 points)(1)[]sin(3/4)x n n = is aperiodic(非周期的) .( T )(2) The Fourier transform of an aperiodic discrete-time signal is periodic (T ) and continuous.(T ) (3) An LTI system with frequency function j t H j e 0()ωω= has linear phase(线性相位). (T)(4) e st is the eigenfunction(特征函数) of LTI systems.(F)(5) The continuous-time Fourier transform of a real-even signal is a real-even function. (T ) (6) The discrete-time Fourier transform of a real-even signal is an imaginary-odd function. ( F) (7) If the ROC (收敛域)of the Laplace transform X (s ) includes the unit circle of s -plane (s 平面),then ==()()s j X j X s ωω.(F)(8) If x (t ) is real and if X (s ) has a pole (极点)at s = s 0 , then X (s ) also has a pole at the point0-s s =. ( F)(9) A discrete-time LTI system is stable if and only if the ROC of its system function H (z ) includesthe unit circle of z -plane. (T )2 Blank Filling (20 points)(1) (1)*()t t δδ--=(1)t δ-.(2 points)(2) I f12[]{1,2,3},[]{1,2,3,4}x n x n ==↑↑, and 12[][][]y n x n x n =*, then the maximumlength of y [n ] is 6 . (2 points)(3) If the spectrum-density (谱密度)function of an aperiodic continues-time signal x (t ) is1()1X j j ωω=+, then the magnitude (幅度)of frequency response is (相位)of frequency response is arctg ω-. (3 points)(4) Expansion in the time domain corresponding to compressing (Compressing,Expansion )in the frequency domain. (2 points)(5) If ()()Fx t X j ω←−→, then 0()cos Fx t t ω←−→00[()][()]2X j X j ωωωω-++. (2 points)(6) If ()()F x t X j ω←−→, then the inverse Furious transform (傅里叶反变换) of 0[()]X j ωω- is 0()j tx t eω. (2 points)(7) Consider an LTI system with unit impulse response [][],||1n h n a u n a =<. The frequency response of the system is 11jweα--. The system is a lowpass (highpass, lowpass or bandpass)filter. (4 points)(8) Suppose 1()x t and 2()x t are band limited to 1ω, 2ω respectively, that is11()0,||X j ωωω=≥, 22()0,||X j ωωω=≥. Under the sampling theorem, the minimumsampling frequency (最小采样频率)is or 12122()2()2s s f ωωωωωπ+==+ .(3 points)3. Calculation(70 points)3.1 (15 points) Let x (t ) be the input to an LTI system with unit impulse response h (t ), whereand 2()()()()tx t eu t h t u t -==.Calculating the output of the system y (t ) by use of convolution integral equation (卷积公式), but not Fourier T ransform or Laplace T ransform. 解:2()()()()()t t y t x h t d e u u t d τττττττ--∞-∞=-=-⎰⎰当0t <时 ()0y t =当0t ≥时 2201()(1)2t ty t ed eττ--==-⎰3.2 (15 points) Suppose we are given the following information about a signal x (t ):a. x (t ) is real and odd.b. x (t ) is periodic (周期)with period T = 2 and has Fourier coefficients k a .c. 0k a = for ||1k > .d.22|()|1x t dt =⎰Specify two different signals that satisfy these conditions. 解:因x (t ) 为实、奇函数,因此可得. k k a a -=-且00a =, 又因当||1k >时0k a = ,因此不为零的傅里叶级数为11-a a 与 根据parseval 方程2201|()|||T k k x t dt a T+∞=-∞=∑⎰22221101|()|||||2x t dt a a -=+⎰,222101|()|2||2x t dt a =⎰,211||4a =所以,112a j = 或112a j =-,与此对应的112a j -=-或112a j -=111()sin()22j tj tx t jejet πππ-=-+=-211()sin()22j tj tx t jejet πππ-=-=3.3 (15 points) Consider a continuous-time ideal lowpass filter S whose frequencyresponse is()10c cHj ,,ωωωωω⎧<⎪=⎨>⎪⎩The input to this filter is a signal ()0sin tx t tωπ=, and the output of the filter is ()y t .Please answer the following questions:a. Calculate ()X j ω.解:0||1()||0X j ωωωωω<⎧=⎨≥⎩b. When 0c ωω<,determine ()y t .0sin ()ty t t ωπ= c. When 0c ωω>,determine ()y t .sin ()c ty t tωπ=d. In the case b or c, which will result in distortion(失真) in output ?C3.4 (15 points) The input x (t ) and output y (t ) of a causal (因果)LTI system are related through the block-diagram representation (方框图表示) shown in Fig. 1a. Determine the system function H (s ) and its ROC.b. Determine a differential equation (微分方程) relating y (t) and x (t ).c. Is the system stable (稳定)? 解:a.221()()()()Z s X s Z s Z s s s=-+,246()2()()()Y s Z s Z s Z s ss=+-消去中间变量Z(s) 可得22246()()21s s Y s X s s s +-=+-,故22246()21s s H s s s +-=+-因极点为1-±R e ()2s >- b. 微分方程为:2222()()()()2()246()d y t dy t d x t dx t y t x t dtdtdtdt+-=+-C. 因收敛域不包含ωj 故系统不稳定。
四川大学信号与系统考研真题+答案07年

¥
x(t) = [Re ct(t) · cosp t]* å d (t - n)
n = -¥
x(t) « c( jkp ) = 1 {[sin c 1 w * 1 [d (w - p ) + d (w + p )]}
2p
22
¥
·2p å d (w - 2p k )
k =-¥
¥
å x(t) = c( jkp )e jkp t
k =-¥
6,己知奇信号 FT 的正频率部份有 x( jw) = 1 ,求 x(t) jw
解:因为
ò ò x( jw) =
¥
x(t)[coswt - j sin wt]dt = - j
¥ x(t) sin wtdt = - j 1
-¥
-¥
w
3
由此可知, x(t) 是实奇信号,故有
x ( jw ) w > 0 = x * ( jw ) w < 0
s =1 = - e -tu (t )
x(t) = (3e-t - e-t )u (t)
4,求 x(n) = -n, n £ 1的 ZT
解:先识别信号,可草画其波形
…… …
2
10
n
-2 -1 0 1 -1
从图可见,信号 x(n) 可表示为 x(n) = -d (n -1) - nu(-n)
则有
-d (n -1) « -z-1 , z > 0
1,已知 x(n) = n + 2, -2 £ n £ 3, 求 x(2n -1) 的波形。
X(n) 2 01
···
-2 -1 0
X(n-1)
34
34
00 12
奥本海姆《信号与系统》配套题库【名校考研真题】(周期信号的傅里叶级数表示)

【答案】4
【解析】因是周期信号,其角频率
2π T
π
,则: a0
2 T
2 f (t)dt 2
0
T
2 dt 2,k 0
0
2
ak T
2 f (t) cos(kt)dt 2
0
T
2
cos(kπt)dt
sin(kπt)
2
0, k
1, 2,
0
kπ 0
所以:
ak 2 4
k
3 . x t 是 一 连 续 时 间 周 期信 号 , 其 基 波 频率 为 1 , 傅 里 叶 系 数 为 ak , 现 已 知
y(t) x(1 t ) x(t 1,) 问 y(t) 的基本频率 2 与 1 是什么关系?______; y(t) 的傅里叶级数
系数 bk 与 ak 的关系是什么?______。[华南理工大学 2007 研]
t0 T
1
bk T
T
t0 T x 1 t
x
t 1
e jkt dt
1 T
T
x 1t
t0 T
e jktdt 1 T
T x t 1 e jktdt
t0 T
1 T
T x 1 t ejktd 1 t 1
t0 T
T
T
x
t0 T
t 1
e jkt d
t 1
ak ak
2.一连续时间
LTI
系统的频率响应
H ( j)
1, 0,
≥250 ,当输入基波周期 T= π ,
其余
7
傅立叶级数系数为 ak 的周期信号 x t 时,发现输出 y(t) x(t) 。ak 需满足什么条件?( )
川大信号与系统习题集及答案

(1)
2 - j2 = 2 2e
(2)
(1 + j) = 1 + 2 j - 1 =
2
p j 2e 2
(3)
j = -1+ j
e
p j 2
j 3p 4
2e
2 -j4 = e 2
p
j2 tan è 3ø 3 + j4 5e (4) = = e æ -4 ö 3 - j4 j tan -1 ç ÷ è 3 ø 5e
r[ k + 2] + 2 r[ k ] = f [ k + 2] + 2 f [ k + 1] + f [ k ]
PDF created with pdfFactory Pro trial version
习
2.1 已知系统微分方程为
题
二(解)
d2 d d r ( t ) + 3 r ( t ) + 2 r( t ) = f ( t ) + f (t ) 2 d t d t dt
( t ³ 0)
其中:
æ1 3ö ÷ l2 = -ç - j ç2 ÷ 2 è ø ì 1 ïC1 = - j ï 2 í ï 1 C2 = + j ï î 2
-j 3 =e 3 2 j 3 =e 3 2
æ1 3ö ÷ l1 = -ç + j ç2 ÷ 2 è ø
ìæ 1 æ æ1 3ö 3ö 3ö ÷C ç 1 ÷C ç ÷ ïç ç 2 + j 2 ÷ 1 + ç 2 + j 2 ÷ 2 = 1´ ç 2 + j 2 ÷ ïè ø è ø è ø 24 3 14 24 3 14 24 3 ï14 同乘 同乘 同乘 í ï æ ö æ ö ï- ç 1 + j 3 ÷C1 - ç 1 - j 3 ÷C2 = -2 ç ÷ ç ï è2 2 ø 2 ÷ è2 ø î
四川大学电子信息学院2018年硕士拟录取(学硕)
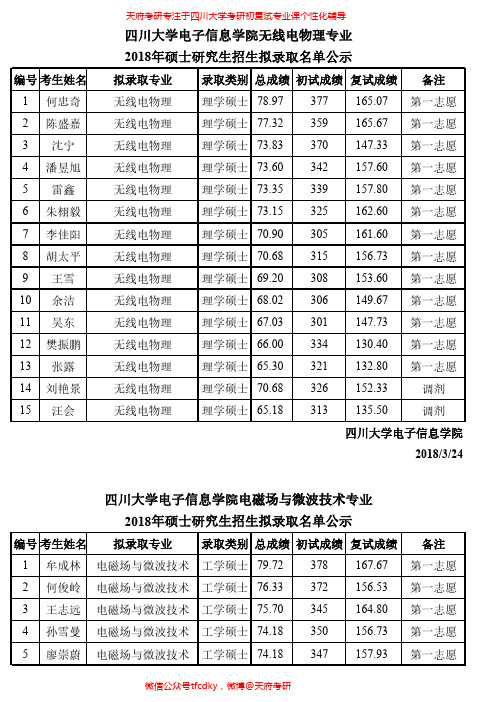
四川大学电子信息学院无线电物理专业
2018年硕士研究生招生拟录取名单公示
四川大学电子信息学院
2018/3/24
四川大学电子信息学院电磁场与微波技术专业
2018年硕士研究生招生拟录取名单公示
四川大学电子信息学院
2018/3/24
四川大学电子信息学院电路与系统专业
2018年硕士研究生招生拟录取名单公示
四川大学电子信息学院
2018/3/24
四川大学电子信息学院模式识别与智能系统专业
2018年硕士研究生招生拟录取名单公示
四川大学电子信息学院
2018/3/24
四川大学电子信息学院通信与信息系统专业
2018年硕士研究生拟录取名单公示
四川大学电子信息学院
2018/3/24
四川大学电子信息学院信号与信息处理专业
2018年工学硕士研究生招生拟录取名单公示
四川大学电子信息学院
2018/3/24
四川大学电子信息学院光学专业
2018年硕士研究生招生拟录取名单公示
四川大学电子信息学院
2018/3/24
四川大学电子信息学院光学工程(学硕)专业
2018年硕士研究生招生拟录取名单公示
四川大学电子信息学院
2018/3/24
四川大学电子信息学院物理电子学专业
2018年硕士研究生招生拟录取名单公示
四川大学电子信息学院
2018/3/24。
2014年信号与系统A卷-供学生用含答案

四川大学期末考试试题(A卷)(2013——2014 学年第二学期)课程号:303123040课序号:课程名称:信号与系统任课教师:任小梅邓丽华余勤王忠罗伟钟俊蒲明刘亚梅成绩:注:1试题字迹务必清晰,书写工整。
本题5 页,本页为第 1 页2 题间不留空,一般应题卷分开教务处试题编号:学号: 姓名6、 一个周期为N 的离散时间信号,其傅里叶级数表示式是一个N +1项的有限级数。
( F )7、 一个非因果稳定的离散信号,其z 变换收敛域包含z =∞。
( F )8、 一个因果的连续时间系统的系统函数X (s ),若其极点都在虚轴以左,那么该系统一定稳定。
( T )9、 一个稳定的连续系统,其系统函数为2()(1)(2)s e H s s s =++,收敛域为Re{}1s >-,那么该系统是因果的。
( F )10、 单位冲激响应为6()th t e-=的系统是非因果稳定的。
( T )二、单项选择题:(共10小题,每题1.5分,共15分)1、 三个连续时间系统S 1、S 2和S 3,它们对于输入jt e 的响应分别是:312(1), , sin()S S S jt jt jt j t jt e te e e e t -−−→−−→−−→以下说法正确的是:( C )A .都是非线性系统B .S 1是非线性系统C .S 1、S 2是线性系统D .S 2和S 3是非线性系统 2、 已知x (t ) ,为求x (3-2t ) 则下列运算正确的是( D )A .x (-2t ) 左移3B .x (-2t ) 右移3C .x (-2t ) 左移3/2D .x (-2t ) 右移3/2 3、 已知信号1()x t 和2()x t 分别如右图所示,且12()()()y t x t x t =*,则(1)y =( C )。
A .1B .2C .4D .0 4、 下列各式正确的是( B )。
A.1(2)()2δδt t -=-B.1(2)()2δδt t -=C .(2)()δδt t -=-D. (2)()δδt t -=5、 系统的幅频特性|H (j ω)|和相频特性如右图所示,则下列信号通过该系统时,不产生失真的是( B ) 。
郑君里《信号与系统》(第3版)(下册)配套题库【名校考研真题+课后习题+章节题库+模拟试题】

目 录第一部分 名校考研真题第7章 离散时间系统的时域分析第8章 z变换、离散时间系统的z域分析第9章 离散傅里叶变换以及其他离散正交变换第10章 模拟与数字滤波器第11章 反馈系统第12章 系统的状态变量分析第二部分 课后习题第7章 离散时间系统的时域分析第8章 z变换、离散时间系统的z域分析第9章 离散傅里叶变换以及其他离散正交变换第10章 模拟与数字滤波器第11章 反馈系统第12章 系统的状态变量分析第三部分 章节题库第7章 离散时间系统的时域分析第8章 z变换、离散时间系统的z域分析第9章 离散傅里叶变换以及其他离散正交变换第10章 模拟与数字滤波器第11章 反馈系统第12章 系统的状态变量分析第四部分 模拟试题第一部分 名校考研真题 说明:本部分从指定郑君里主编的《信号与系统》(第3版)为考研参考书目的名校历年考研真题中挑选最具代表性的部分,并对其进行了详细的解答。
所选考研真题既注重对基础知识的掌握,让学员具有扎实的专业基础;又对一些重难点部分(包括教材中未涉及到的知识点)进行详细阐释,以使学员不遗漏任何一个重要知识点。
第7章 离散时间系统的时域分析一、填空题1.周期分别为3和5的两个离散序列的卷积和的周期性为______。
[北京航空航天大学2007研]【答案】7【解析】对于线性卷积,若一个周期为M,另一个周期为N,则卷积后周期为M+N-1,所以。
2.某线性时不变(L TI)离散时间系统,若该系统的单位阶跃响应为则该系统的单位脉冲响应为______。
[北京交通大学研]【答案】【解析】本题考查离散时间系统的单位脉冲响应。
用表示单位阶跃响应,由于利用线性和时不变特性可得二、判断题一个离散时间信号实际上就是一组序列值的结合{x(n)}。
( )[南京大学2010研]【答案】√【解析】离散时间函数,只有在某些离散时给出函数值,只是在某些离散瞬时给出函数值。
因此,它是时间不连续的“序列”的。
三、选择题1.信号的周期是( )。
四川大学信号与系统考研真题+答案09年

5,CLTI 系统是因果的之充分必要条件是 h(t) º 0,t < 0. 。
6,周期信号 x(t) 的周期 T=4, x(0.5t) 的 FS 系数 ak = k, k = 0, ±1, ±2. 则 x(t) 的平均
2
å 功率= k = k 2 = 1+1+ 4 + 4 = 10w
。
k =-2
7, x(n) ZT 为 x(z),1 < z < 3, 则 nx(n) 的 ZT 为 -z dX (z) ,1 < z < 3. 。 dz
关,与 h(t), h(n) 的函数形式无关。
ò 5,x(t) 满足 ¥ x(t)e4 t dt < ¥ ,其 LT 有且仅有两个极点 0 和-2,则s = -3 位于 ROC -¥ 内,判断此说法的正确性,并说明理由。 解:由题给条件,可得 x(s) = k s(s + 2)
① e4t 在正时域是增长的,如 x(t) 是正时域信号,则 x(t) 必以 e-atu(t), a > 4 隨
24 28
32 ,k=8 k
X (s) = 1 - 1 e-4s = 1- e-4s ,s > 0.
1 - e-8k s 1 - e-8k s
1 - e-8k s
2,因果信号的 LT X (s) 仅有两个极点 3 和 0,在无限远处有一个二阶零点, x(1) = -1 ,
求 x(t) 。
解:由题给条件,可得 x ( s ) = k
- j 4p n
[ j cos(2p )e 5 - j cos(2p )e 5 ]
j 2p n
- j 2p n
x(n) = - j[e 5 - e 5 ] +
信号与系统西南交通大学2011年全日制硕士研究生入学考试试卷

西南交通大学2011年全日制硕士研究生入学考试试卷(信号与系统一)一、(30分)选择题(10题)1、已知()t u 的拉氏变换为s1,则()()[]2--t u t u 的拉氏变换为()。
(A )211sess -- (B )211sess -(C )se ss 211--(D )se ss 211-2、下列输入—输出关系的系统中,( )是因果LTI 系统。
(A )()()t nx t y =(B )()()()01=+-n x n y n y (C )()()()221+=++n x n y n y(D )()()()12-=+-n x n y n y3、已知某线性非时变系统的单位冲激响应()()t u e t h t25-=,则其系统函数()=ωj H ()。
(A )25+ωj(B )ωj 5(C )22+ωj(D )ωj 24、周期信号()()2Tt f t f ±-=,(T 为周期),则其傅里叶级数展开式的结构特点为()。
(A )只有正弦项(B )只有余弦项 (C )只含偶次谐波(D )只含奇次谐波5、已知()()ωj F t f ↔,则()42+t f 的傅里叶变换为()。
(A )ωω2221j e j F ⎪⎭⎫ ⎝⎛ (B )2221ωωj e j F ⎪⎭⎫ ⎝⎛ (C )ωω222j e j F ⎪⎭⎫ ⎝⎛(D )()22ωωjej F6、某因果系统的系统函数()()()221--=z z z z H ,此系统属于( )。
(A )只渐进稳定的 (B )临界稳定的 (C )不稳定的 (D )不可物理实现的 7、信号()()65sin 2cos π++=t t t y 的Nyquist 采样间隔为()秒。
(A )π2(B )π(C )π4(D )18、已知()()ωj F t f ↔,()t f 的频带宽度为为m ω,则信号()3-t f 的奈奎斯特间隔等于( )。
四川大学信号与系统考研真题+答案08

川大08硕题解一,填空题(每小题3分,共21分)1,信号sin 3()t x t t ππ=的总能量E =2231Re ()326siin t dt ct d t πωωπππ∞∞-∞-∞==⎰⎰焦。
1()3sin (3)Re ()(3;)63p x t c t ct A t ωππ=↔== 2,5cos 2sin22ttππ-的周期T =411212222544;;5;225TT T T T T ππππ=→==→==是有理数。
故5cos 2sin 22t t ππ-是周期信号。
其周期T 是1,2T T 的最小公倍数,即为4。
3,CLTI 系统的输入输出满足1()()ty t e x d τττ-+-∞=⎰该系统的冲激响应()h t =11()()()()tt y t e x d e x t u t τττ-+--∞==*⎰这由图可知,是一个时变系统,时变系统的冲激响应是二元函数(,)h t τ,己超出范围。
4,DLTI 系统是稳定系统的必要充分条件是1),l i m ()0x t y n →∞=;2),()H z 的所有极点1,1,2,3,i r i <= 3),()n h n ∞=<∞∑4),()j H e ω存在。
5,周期信号的周期T =7,傅利(什么形式的)叶级数系数为1(1)kk a =--,则(3)x t-的第三次谐波分量的平均功率等于认为是基本形式的叶级数系数2122k p a W ==。
6,己知()x t 的FT 0100(){elsex j ωω=≠<则()()(0.5)y t x t x t =*-的理想抽样频率为(0.5)x t -比()x t 的时间展宽一倍,其频谱压缩一倍,即有100ω∆=(()x t 的200ω∆=);()y j ω则是{}{}()()(0.5)()(0.5)y t x t x t FT x t FT x t =*-↔∙-,结果的频谱宽度由窄的100ω∆=25(50;)H H f ωπ==决定,故得抽样频率502s H f f π≥=7,()x n 的ZT 为(),2x z z <;则()x n -的ZT 为111()()()();2nn n n x n zx n X z Z Z ∞∞'--'=-∞=-∞'-==<∑∑ 二,判断题(每小题4分,共20分)1,设()(21)x t t δ=-⨯标出。
(NEW)四川大学《951信号与系统》历年考研真题汇编

5 假设实信号x[n]和其ZT变换X(z)满足下列四个条件: (1)X(z)是有理函数;
(2)
;
(3)X(z)在原点有二阶零点; (4)X(z)仅有两个极点1和-2。 求满足条件的所有x[n]。
6 已知
计算x(t)的傅里叶变换。
五、(本题共12分)一因果连续LTI系统,满足以下条件: (1)系统函数H(s)为有理函数,H(s)仅有两个极点3和1; (2)H(-2)=0,H(∞)=2; (3)输入x(t)=e-t时,系统零状态响应为0。 求:
2010年四川大学951信号与系统考 研真题
2011年四川大学951信号与系统考 研真题
2012年四川大学951信号与系统考 研真题
2014年四川大学951信号与系统考 研真题
2015年四川大学951信号与系统考 研真题
2016年四川大学951信号与系统考 研真题
8 周期信号x(t)(基波频率为ω0)的指数形式傅里叶级数系数为 ak,设x(t)的傅里叶变换存在,则x(2t-1)的傅里叶变换为 ______。
9 已知x1[n]=u[n/3],x2[n]=u[n+3]-u[n-4],x[n]=x1[n]*x2[n],则 x[3]=______。
10 已知离散线性时不变系统的单位冲激响应
B.cos(5πn/3) C.cos(7πn/4) D.cos(11πn/5)
5 已知一持续时间有限的实信号x(t),0≤t≤T;当x(t)输入单位冲 激响应h(t)=x(T-t)的线性时不变系统时,其输出y(t)在T时刻 的值即y(T)等于信号x(t)的能量。
6 已知信号x(t)的最高频率为fm,运用图1的采样函数p(t)对 x(t)采样,则当采样频率大于2fm时,信号x(t)能根据采样值序列无 失真恢复出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11答案解析-,填空题(每小题3分,共27分) 1,信号33cos()sin()75t tππ-的最小周期为 70 . 2,323(5)(36)t t dt δ---+=⎰33223311(5)[3(2)(5)(2)33t t dt t t dt δδ-----=--=-⎰⎰ 。
3,实信号x(t)的FT 为()()R jI ωω+则1()()()x t x t X t =--FT 为 j2I(ω) 。
(x 1(t)是实奇函数)4,已知连续时间周期信号x(t)(周期为T)的FS 系数k a ,其谱线间隔由 2Tπ或决定,当周期增大时其谱线间隔减小 。
5,55(55)[()(1)()(1)()]5tt t e u t t e u t d e u t u t dt δ----*--=-=* 6,DLTI 系统的单位阶跃响应是()()s n nu n =则其单位脉冲响应()h n =u(n-1)。
7,巳知(),22x t t t =-<<的FT ()x j ω,则()j t x j e d ωωω∞-∞⎰2πx(t) 。
.8,连续时间周期信号的FS 表示信号可分解成 各? 个不同的谐波关系复措数信号之和.9,0()(1)(3)kk x t t k δ∞==--∑的LT 为 361,01kskse e σ--->- 。
. 二,简答题(每小题4分,共24分)1,已知周期信号()cos(150)x t t π=通过-LTI 系统,能输出下列哪些频率(50Hz, 75Hz, 130Hz,140Hz,150Hz, 225Hz,)的信号?一定会输出吗?为什么?解:从题给,输入信号的频率75Hz ,输出信号中只可能有75Hz ,的简谐信号。
因为LTI系统具有频谱成份不增加性。
2, 连续时间周期信号的FT 是否具有周期性和离散性?写出其FS 与FT 的关系。
解:1),因连续周期信号()f t 可表为11()()(),()()T f t f t t f t f t δ=*其中为的一个周期它的FT 为/21/222()[()][()]T j tT k f t f t edt k TTωππδω∞--=-∞↔∙-∑⎰故不具有周期性(不是周期重复)。
但具有离散性。
2),同一个连续周期信号的FT()F j ω与FS 的关系为001()[()]2j n tn n f t F j eωωωωπ∞==-∞=∙∑可见FT 仅是FS 的幅度中的一个因子。
3,有一因果信号()x t 在0t +=时刻为一有限值,其LT 在有限S 平面仅有两个零点,请问在有限S 平面内有多少极点?(要求写出理由)解:因为题给()x t 在0t +=时刻为一有限值,即是()x t 中没有()()t t δδ(n )及其,可推定其LT 的()x s 没有整式项,即分子中s 的最高方次低于分母中s 的最高方次。
故在有限S 平面内至少有三个极点。
4,()x n 的ZTX(z)共有两个极点,分别为1212;13p j p j =-=+且()(2)()n x n u n *--绝对可和,请问x(n)为左边信号、右边信号、双边信号中的哪一种?(要求写出理由) 解:由题给()x z 的极点,可推知ROC 有下三种情况(),()X z z x n ⇒为正时域因果(右)信号;(()X z x n <为正、负时域信号(),()X z z x n ⇒为负时域左信号;由()(2)()n x n u n *--绝对可和,即存在ZT ,而 ()(2)()()[(2)()]n n x n u n x z ZT u n *--↔∙-- 而 2[(2)()],22n ZT u n z z --↔<+ 故 ()[(2)()]n x z ZT u n ∙--的公共ROC 为2z <。
则()x z 为(),()X z z x n <为负时域(左)信号;5,信号sin10cos300tt tπ的能量和功率是多少?(要求有一定步骤) 解:因信号sin10cos300t t t π是能量型信号(10sin1010cos300,,1010p t t t A t πππ∙==),其能量E ,根据Parseval Theorem 有221110()Re ()2220E F j d ct d ωωωωπππ∞∞-∞-∞===⎰⎰0P =(能量型信号的平圴功率为零)6,下列式子中,哪些式子所表示的系统同时具有时不变性、线性性、因果性和稳定性? 1),()(1)ty t x d ττ-∞=-⎰2),()3()()y t y t x t '+-=3),y(n)=()nm x m =-∞∑ 4),()2(1)3()y n x n x n =-+三,完成下列运算或变换(每小题6分,共42分)1,己知(25)x t -+如图一所示,请画出()()x t x t '和的波形图。
2,已知x1(t)和x2(t)如下图a,c 所示。
其中1()()()y t x t h t =*如下图b 所示。
求2()()x t h t *3,已知信号x(t)的FT (),22X j ωωω=-<<。
求x(t)=?解:按IFT 有 11()1()22j t j tt e d j t e d ωωδωδωωππ∞∞-∞-∞'=∙→-=∙⎰⎰ ();(2,2)Re ()42Re ()sin 24j t ct ct c t ωδωωωωπ'↔-∈-→∙↔2()sin 2[()]x t c t j t δπ'=*-2[sin 2]d jc t dt π=- 4,设信号()sin()3tx t π=,计算其FS 。
()[Re ()sin ](3)33n t x t ct t t n πδ∞=∞=*-∑13(){3sin [()()]}223322()33[sin ()sin ()]22n n x j c j n j c n c n ππωωπδωδωπππδωπππππ∞=-∞∞=-∞=∙*---+∙-=--++∑∑21()()32x n x j πωπ=∙232()()3j n t n x t x n e ππ∞=-∞=∑ 5,求信号3()(1),11tx t et t -=--<<的LT 。
解:3,11t e t --<<及1,11tt --<<都是能量信号,可用LT 的卷积性质133(3)11111,11()3tt st s e t F s e e dt e s ----+---<<↔==-+=⎰22111(1)(1)2()(1)(1)1()(2)s st t t u t tu t t u t F s e e s---<<→++-+--↔=-+ 121()()()2x s F s F s jπ=∙*6,已知3512211(), 3., 3.38333833z z x z z z z z z z --=<<→<<----3121(), 3.3833z x z z z z --=<<--求信号x(n).解:55113, 3.13833()(3)3z z z z z z z =<<--+- 即求1()x z =54111133, 3.113()(3)()(3)33n n z z z z z z z z z -=<<+-+-围线积分,由于分子是单项式,将其作位移考虑,减少运算复杂度。
用留数法则有113(),313()(3)3n F z z z z z =<<+-1111Re [)()]()33103nz s z F z =-+=--左移4位得 411111()()()()1038103n n f n u n +-=--=-31Re [3)()](3)10n z s z F z =-=左移4位得 281()(3)(1)10nf n u n =-- X(n)=12()()f n f n +7,-带限信号x(t)的最高角频率200/rad s π求x(3t)+x(0.5t)、x 2(2t)的米样周期T 以便通过理想低通滤波器可完全恢复出来。
解: (3)(0.5)x t x t +→其中(3)x t 时间压缩3倍,频谱扩展, 最高角频600πrad;(0.5)x t时间扩展, 频谱压缩2倍。
其线性运算结果的最高角频600πrad,如x(t)是低频带限信号,则抽样周期1()600600Ts ππ≤=秒 相应2111(2)(2)(2)()()()22222xt x t x t F j x j x j ωωωπ=∙↔=∙* 由比例和线性卷积可得2(2)x t 的最高角频仍为200πrad, 则抽样周期1()200200T s ππ≤=秒四, (本题共3小题,,共19分)有一因果DLTI 系统,其系统函数H(z)仅有两个极点p 1=-0.5,p 2=0.8,仅有一个零点z 1=2,且13()3n h n ∞==∑。
求:1),系统函数H(z)和单位脉冲响应h(n) 2),判断系统稳定性3),起始条件y(-1)=15,y(-2)=3.5,输入x(n)=u(n)-u(n-2)的全响。
解:1),由题给条件可得H(z)为 (2)()(0.5)(0.8)z H z kz z -=--10.5(2)Re [(0.5)](0.5)(0.8)n z z s z kz z z -=----10(0.5)()n k u n = 10.8(2)Re [(0.8)](0.5)(0.8)n z z s z kz z z -=----5(0.8)()n k u n =()[10(0.5)5(0.8)]()n n h n k k u n =+ 2),稳定。
因为极点均在单位园内。
3),12()(0.5)(0.8)()()(1)(()(2)()(1))n nx f y n c c y n h n h n u n u n n n δδ=+=+---=+-五, (本题共3小题,,共20分)有一因果cLTI 系统满足如下方程2()()4()()2()tt y t y t x e d x t τττ--∞'+=+⎰ 求:1), 系统函数H(s)2),画出系统零—极点图和系统方框图 3),输入()(2)t x t e u t -=-时的零状态响应 解:1),在2()()tt x e d τττ--∞⎰中,用,,t t t t d dt τττ'''=-=-=222()()()(),22tt t t x s x t t e dt x t t e dt x t e s σ∞''-∞-∞''''-=-=*↔>-⎰⎰ 得由题给方程,设()();()()y t y s x t x s ↔↔则得 123(4)()[2]()()22s s y s x s x s s s -+=+=--23()(2)(4)s H s s s -=-+2),zero :32z =Poles :124;2p p =-= 3),2(1)2(1)22()(2)11s sts te e x t e u t e dt es s -+-∞--+-=-↔==++⎰2223()(2)(4)(1)s f s y s e e s s s --=-++2Re [(2)()]st f s s s y s e =-= 4Re [(4)()]st f s s s y s e =-+=1Re [(1)()]st f s s s y s e =-+=六, (本题共3小题,,共18分)已知某系统如下图所示,其牛()()()x t u t u t ττ=+--的频谱为();X j ω00()()k p j k ωωδωω∞=-∞=-∑求:1),图中A 点处的时域表达式(或画出A 点处的时域波形)6分 2),当0ω满足何条件时,可在图B 的B 点处得刭y(t)=x(t )? 3),求满足2)(y(t)=x(t))的g(t)。
