2014.1.28小五第8次立体图形综合
(完整版)立体图形计数

1.下图中,共有多少个小正方体?A.3B.4C.5D.6来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:C2.下图中,共有多少个小正方体?A.3B.4C.5D.6来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D3.下图中,共有多少个小正方体?A.6B.7C.8D.9来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:B4.下图中,共有多少个小正方体?A.5B.6C.7D.8来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D5.下图中,共有多少个小正方体?A.9B.8C.7D.6来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:A6.下图中,共有多少个小正方体?A.7B.8C.9D.10来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D7.下图中,共有多少个小正方体?A.10B.11C.12D.13来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D8.下图中,共有多少个小正方体?A.21B.22C.23D.24来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D9.下图中,共有多少个小正方体?A.15B.16C.17D.18来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:B10.下图中,共有多少个小正方体?A.10B.11C.12D.13来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:A首页上一页1234下一页尾页11.下图中,共有多少个小正方体?A.11B.12C.13D.14来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D12.下图中,共有多少个小正方体?A.15B.16C.17D.18来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:C13.下面的大正方体是由几个小正方体组成的?A.4B.6C.8D.10来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:C14.下面的大正方体是由几个小正方体组成的?A.19B.22C.25D.27来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D15.下面的大正方体是由几个小正方体组成的?A.68B.64C.60D.56来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:B16.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.1B.2C.3D.4来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:B17.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.5B.6C.7D.8来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:A18.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.4B.5C.6D.7来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D19.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.14B.15C.16D.17来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:B20.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.14B.15C.16D.17来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:A首页上一页1234下一页尾页21.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.17B.16C.15D.14来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:C22.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.3B.4C.5D.6来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:C23.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.14B.15C.16D.17来源:2014·乐乐课堂·练习难度:中等类型:选择题答案:C24.如果要把下面的立体图形补全成为一个完整的大正方体,那至少需要再添加几个小正方体呢?A.16B.17C.18D.19来源:2014·乐乐课堂·练习难度:中等类型:选择题答案:B25.如图所示,将大正方体中的红色部分挖穿,那得挖走多少个小正方体呢?A.1B.2C.3D.4来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:B26.如图所示,将大正方体中的红色部分挖穿,那得挖走多少个小正方体呢?A.1B.2C.3D.4来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:C27.如图所示,将大正方体中的红色部分挖穿,那得挖走多少个小正方体呢?A.1B.2C.3D.4来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D28.如图所示,将大正方体中的红色部分挖穿,那得挖走多少个小正方体呢?A.3B.6C.9D.12来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:C29.如图所示,将大正方体中的红色部分挖穿,那得挖走多少个小正方体呢?A.2B.4C.6D.8来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:C30.如图所示,将大正方体中的红色部分挖穿,那得挖走多少个小正方体呢?A.16B.12C.8D.4来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:B首页上一页1234下一页尾页31.如图所示,将立体图形中的红色部分挖穿,那得挖走多少个小正方体呢?A.3B.4C.5D.6来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:A32.如图所示,将立体图形中的红色部分挖穿,那得挖走多少个小正方体呢?A.1B.2C.3D.4来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D33.如图所示,将立体图形中的红色部分挖穿,那得挖走多少个小正方体呢?A.1B.3C.4D.5来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D34.如图所示,将立体图形中的红色部分挖穿,那得挖走多少个小正方体呢?A.2B.3C.4D.6来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D35.如图所示,将立体图形中的红色部分挖穿,那得挖走多少个小正方体呢?A.2B.4C.6D.8来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D36.如图所示,将立体图形中的红色部分挖穿,那得挖走多少个小正方体呢?A.2B.5C.8D.10来源:2014·乐乐课堂·练习难度:简单类型:选择题答案:D首页上一页1234下一页尾页。
【高考数学专题复习】第八章 立体几何初步测试(解析版)

第八章 立体几何初步测试一.单选题(每题5分,共12题,共60分)1.在四面体ABCD 中,3AB BD AD CD ====,4AC BC ==,用平行于AB ,CD 的平面截此四面体,得到截面四边形EFGH ,则四边形EFGH 面积的最大值为( )A .43B .94 C .92 D .3【答案】B【解析】设截面分别与棱,,,AD BD BC AC 交于点,,,E F G H .由直线//AB 平面EFGH , 且平面ABC I 平面EFGH GH =,平面ABD ⋂平面EFGH EF =得//GH AB ,//EF AB ,所以//GH EF ,同理可证//EH FG ,所以四边形EFGH 为平行四边形,又3AB BD AD CD ====,4AC BC ==,可证得AB CD ⊥,四边形EFGH 为矩形.设:::BF BD BG BC FG CD x ===,01x <<,则3FG x =,()31HG x =-,于是2199(1)9,0124EFGH S FG HG x x x x ⎛⎫=⋅=-=--+<< ⎪⎝⎭ 当12x =时,四边形EFGH 的面积有最大值94.故选:B.2.如图,四边形ABCD 是边长为1的正方形,MD ⊥ABCD ,NB ⊥ABCD .且MD =NB =1.则下列结论中:①MC ⊥AN②DB ∥平面AMN③平面CMN ⊥平面AMN④平面DCM ∥平面ABN所有假命题的个数是( )A .0B .1C .2D .3【答案】B【解析】由题画出该几何体外接的正方体.对①,因为//MC EB ,AN EB ⊥,故MC ⊥AN 成立.故①正确.对②,因为//,DB MN MN ⊂平面AMN,故DB ∥平面AMN 成立.故②正确.对③,连接AC 易得A MNC -为正四面体.故平面CMN ⊥平面AMN 不成立.故③错误.对④,正方体中平面DCM 与平面ABN 分别为前后两面,故④正确.故选:B3.已知互相垂直的平面αβ,交于直线l.若直线m ,n 满足m ∥α,n ⊥β,则A .m ∥lB .m ∥nC .n ⊥lD .m ⊥n【答案】C【解析】由题意知,l l αββ⋂=∴⊂,,n n l β⊥∴⊥Q .故选C .4.设,αβ是两个不同的平面,l 是一条直线,以下命题正确的是( )A .若,l ααβ⊥⊥,则l β⊂B .若//,//l ααβ,则l β⊂C .若,//l ααβ⊥,则l β⊥D .若//,l ααβ⊥,则l β⊥【答案】C【解析】对于A 、B 、D 均可能出现//l β,而对于C 是正确的.5.已知正四棱柱中,,则CD 与平面所成角的正弦值等于( )A .B .C .D .【答案】A【解析】设 ,面积为6.在Rt ABC V 中,90ABC ∠=o ,P 为V ABC 所在平面外一点,PA ⊥平面ABC ,则四面体P ABC -中直角三角形的个数为( )A .4B .3C .2D .1【答案】A【解析】由题意,知PA ⊥平面ABC 可得PAC PAB ∆∆,都是直角三角形,且PA BC ⊥,又90ABC ∠=o ,所以V ABC 是直角三角形,且BC ⊥平面PAB ,所以BC PB ⊥,即PBC △为直角三角形.故四面体P ABC -中共有4个直角三角形.7.已知直线//l α,直线a α⊂,则l 与α必定( )A .平行B .异面C .相交D .无公共点 【答案】D【解析】已知直线//l α,所以直线l 与平面α无公共点,又由a α⊂,所以直线l 与平面a 无公共点,故选D .8.如图,各棱长均为a 的正三棱柱111ABC A B C -,M 、N 分别为线段1A B 、1B C 上的动点,且MN //平面11ACC A ,则这样的MN 有 ( )A .1条B .2条C .3条D .无数条【答案】D 【解析】由题意得112A B CB a==.在11,BA CB 上分别取,M N ,使1BM B N =,过,M N 作11,MM AB NN BC ⊥⊥,垂足分别为11,M N ,则1111,MM AA NN BB P P ,故11111,BM B N BN BM BA BA B C BC==.由于111B N BM BA B C =,故11BM BN BA BC=,从而11M N AC P ,可得11M N P 平面11ACC A .又1MM P 平面11ACC A ,可得平面11MM N N P 平面11ACC A .由于MN ⊂平面11MM N N ,所以//MN 平面11ACC A ,从而满足条件的MN 有无数条.选D .9.正方体1111ABCD A B C D -中,直线AD 与平面11A BC 所成角正弦值为( )A .12B .32C .33D .63【答案】C【解析】如图所示,正方体1111ABCD A B C D -中,直线AD 与11B C 平行,则直线AD 与平面11A BC 所成角正弦值即为11B C 与平面11A BC 所成角正弦值.因为11A BC ∆为等边三角形,则1B 在平面11A BC 即为11A BC ∆的中心,则11B C O ∠为11B C 与平面11A BC 所成角.可设正方体边长为1,显然36=2=BO ⨯,因此2163=1()=3B O -,则1111103sin B B C O B C ∠==,故答案选C.10. 如图所示,在正方体ABCD —A 1B 1C 1D 1中,若E 是A 1C 1的中点,则直线CE 垂直于( )A .ACB .BDC .A 1D D .A 1D 1【答案】B 【解析】以A 为原点,1AB AD AA ,,所在直线分别为x y z ,,轴建立空间直角坐标系,设正方体棱长为1,则()000A ,,,()110C ,,,()100B ,,,()010D ,,, ()1001A ,,,11122E ⎛⎫ ⎪⎝⎭,, 11122CE ⎛⎫∴=-- ⎪⎝⎭u u u v ,, ()110AC =u u u v ,,,()110BD =-u u u v ,,,()1011A D =-u u u u v ,,,()1001AA =-u u u v ,,110022CE BD ∴=-+=u u u v u u u v n 则CE BD ⊥u u u v u u u v 即CE BD ⊥故选B11.已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )A .26B 3C .23D .22【答案】A【解析】根据题意作出图形:设球心为O ,过ABC 三点的小圆的圆心为O 1,则OO 1⊥平面ABC ,延长CO 1交球于点D ,则SD ⊥平面ABC .∵CO 1=2333=,∴116133OO =-=, ∴高SD=2OO 1=263,∵△ABC 是边长为1的正三角形,∴S △ABC =34, ∴132623436S ABC V -=⨯⨯=三棱锥.12.已知正方体1111ABCD A B C D -的棱长为2,P 是底面ABCD 上的动点,1PA PC ≥,则满足条件的点P 构成的图形的面积等于( )A .12B .4πC .44π- D .72【答案】A【解析】如图,以,AB AD 为,x y 轴在平面ABCD 内建立平面直角坐标系,设(,)P x y ,由1PA PC ≥得22222(2)(2)2x y x y +-+-+30x y +-≥,设直线:30l x y +-=与正方形ABCD 的边交于点,M N ,则P 点在CMN ∆内部(含边界),易知(1,2)M ,(2,1)N ,∴1CM CN ==,111122CMN S ∆=⨯⨯=. 故选A .二.填空题(每题5分,共20分)13.已知在直角梯形ABCD 中,AB AD ⊥,CD AD ⊥,224AB AD CD ===,将直角梯形ABCD 沿AC 折叠,使平面BAC ⊥平面DAC ,则三棱锥D ABC -外接球的体积为__________. 【答案】323π 【解析】结合题意画出折叠后得到的三棱锥D ABC -如图所示,由条件可得在底面ACB ∆中,90,22ACB AC BC ∠=︒==。
小升初立体图形专题练习
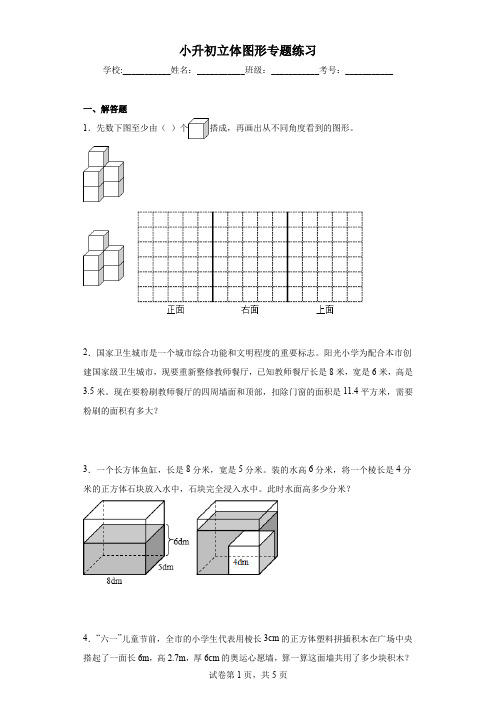
【分析】三面被涂色的小正方体,就是顶点处的小正方体;两面被涂色的小正方体,就是棱上的小正方体;一面被涂色的小正方体就是面上中间部分的小正方体。
【详解】长方体有8个顶点,所以三面被涂色的小正方体有8个。
长方体有12条棱,其中每条长上有3个小正方体,宽上有2个小正方体,高上有1个小正方体,所以两面被涂色的小正方体有:(3+2+1)×4=24(个)。
3.一个长方体鱼缸,长是8分米,宽是5分米。装的水高6分米,将一个棱长是4分米的正方体石块放入水中,石块完全浸入水中。此时水面高多少分米?
4.“六一”儿童节前,全市的小学生代表用棱长3cm的正方体塑料拼插积木在广场中央搭起了一面长6m,高2.7m,厚6cm的奥运心愿墙,算一算这面墙共用了多少块积木?
【详解】蚊帐的侧面积:
3.14×1.2×1.5÷2
=3.14×0.9
=2.826(平方米)
蚊帐的底面积:
3.14×(1.2÷2)2
=3.14×0.36
=1.1304(平方米)
至少需要:
2.826+1.1304≈4(平方米)
答:做这样一顶蚊帐至少需要4平方米的薄纱。
【点睛】本题考查圆柱表面积公式的灵活运用,关键是从图中分析出图形是由哪些面组成,根据这些面的面积公式列式计算即可。
【点睛】本题考查涂色的正方体个数,弄清三面、两面和一面被涂色的小正方体分别在长方体的什么位置是解答此题的关键。
7.64立方分米
【分析】根据题意,折成的长方体容器的长、宽、高分别为(12-2×2)分米、(8-2×2)分米、2分米,又因长方体的体积=长×宽×高,将数据代入公式即可求出这个容器的容积。
【详解】(12-2×2)×(8-2×2)×2
8.王师傅剪下一张长方形铁片中的涂色部分(如下图所示,单位:分米),正好做成一个圆柱。求做成的圆柱的底面积是多少?做完这个圆柱,这张长方形剩余的废料(空白部分)是多少平方分米?(损耗考虑不计)
小学数学精讲(9)几何(三) 立体图形

小学数学精讲(9)几何(三) 立体图形一、知识地图⎧⇒⎧⎪⎪⎧⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎩⎪⎪⎪⇒⎩⎪⎪⇒⎨⎪⎧⎪⎨⎪⎩⎪⎪⎪⎪⎪⎩3“一个思想”不规则化为规则阳光照面求图形体积表面积“三个方法”看变化规律整体切片“一个模式”整体思考最短路线与展开图形状以点定线,以线定面n 边小正方形染色规律染色问题欧拉公式 二、基础知识万丈高楼平地起。
我们可以这样说:把平面图形从平面拎到空间,让平面图形在空间上产生高度就形成了这一讲我们要研究的立体图形。
在现阶段,我们主要研究的立体图形有以下几种:立体图形 表面积体积26S a =正方体 3V a =正方体2S ab bc ac =++长方体() V abc =长方体2222S rh r ππ=+=+圆柱侧面积个底面积 2V r h π=圆柱22S l r ππ=++圆锥n侧面积底面积=360 注:l 是母线,即从顶点到底面圆上的线段长。
213V r h π=圆锥体24S r π=球体343V r π=球体特别的:关于球体还有这样一个结论:如果一个球体的直径与一个圆柱的直径与高都相等,那么:球体的体积等于以球大圆为底球的直径为高的圆柱体积的三分之二; 球体的表面积等于以球大圆为底球的直径为高的圆柱的侧面积;球体的体积还等于以球大圆为底,球的半径为高的圆锥的体积的4倍。
这个图就是有名的阿基米德圆柱容球。
二、求立体图形的表面积和体积规则立体图形的表面积和体积我们可以直接应用公式进行计算。
不规则的立体图形的表面积和体积,一方面,我们可以应用和平面图形相同思考的方法来考虑把它转化为规则的立体图形进行计算;而另一方面,我们更注重的是观察图形从规则变为不规则的变化过程,通常这个过程我们需要以图形整体考虑为出发点。
这也就是我们求解此类问题常用方法的思想基础:、 方法一:阳光照面阳光照面法从图形整体考虑出发,观察图形表面积特点。
方法二:与时俱进图形的变化,是从整体的变到不变的过程,找到变化的规律,注意图形的变化过程,观察求解,与时俱进,就是解决问题的秘籍宝典。
人教A版数学必修第2册单元测试第八章 立体几何初步(原卷版)

第八章 立体几何初步 综合测试(原卷版)考试时间120分钟,满分150分.一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知三棱柱有a 个顶点,b 条棱,则a -b =( ) A .-3 B .3 C .4D .-42.在正方体ABCD -A 1B 1C 1D 1的所有面对角线中,所在直线与直线A 1B 互为异面直线且所成角为60°的面对角线的条数为( )A .2B .4C .6D .83.已知某圆柱的内切球半径为92,则该圆柱的侧面积为( )A .49π2B .49πC .81π2D .81π4.空间四点A ,B ,C ,D 共面而不共线,那么这四点中( ) A .必有三点共线 B .必有三点不共线 C .至少有三点共线D .不可能有三点共线5.设α,β为两个不同的平面,则α∥β的一个充分条件可以是( ) A .α内有无数条直线与β平行 B .α,β垂直于同一条直线 C .α,β平行于同一条直线D .α,β垂直于同一个平面6.E ,F ,G 分别是空间四边形ABCD 的棱BC ,CD ,DA 的中点,则此四面体中与过E ,F ,G 的截面平行的棱的条数是( )A .0B .1C .2D .37.如图,P为平行四边形ABCD所在平面外一点,过BC的平面与平面P AD交于EF,E在线段PD上且异于P、D,则四边形EFBC是()A.空间四边形B.矩形C.梯形D.平行四边形8.(2022·新高考Ⅰ卷)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为(7≈2.65)() A.1.0×109 m3B.1.2×109 m3C.1.4×109 m3D.1.6×109 m3二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得2分,有选错的得0分)9.以下关于空间几何体特征性质的描述,错误的是()A.以直角三角形一边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体是圆锥B.有两个面互相平行,其余各面都是四边形的几何体是棱柱C.有一个面是多边形,其余各面都是三角形的几何体是棱锥D.两底面互相平行,其余各面都是梯形,侧棱延长线交于一点的几何体是棱台10.如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,一定正确的为()A.AC⊥BD B.AC∥截面PQMNC.AC=BD D.异面直线PM与BD所成的角为45°11.如图,在平行六面体ABCD-A1B1C1D1中,点M,P,Q分别为棱AB,CD,BC 的中点,若平行六面体的各棱长均相等,则下列说法正确的是()A.A1M∥D1P B.A1M∥B1QC.A1M∥平面DCC1D1D.A1M∥平面D1PQB112.如图,在棱长均相等的正四棱锥P-ABCD中,M、N分别为侧棱P A、PB的中点,O是底面四边形ABCD对角线的交点,下列结论正确的有()A.PC∥平面OMN B.平面PCD∥平面OMNC.OM⊥P A D.PD⊥平面OMN三、填空题(本大题共4小题,每小题5分,共20分)13.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是____.14.将长为3,宽为2的长方形,绕其一边旋转成的几何体的表面积为____.15.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为___厘米.16.我国有着丰富悠久的“印章文化”,古时候的印章一般用贵重的金属或玉石制成,本是官员或私人签署文件时代表身份的信物,后因其独特的文化内涵,也被作为装饰物来使用.图1是明清时期的一个金属印章摆件,除去顶部的环以后可以看作是一个正四棱柱和一个正四棱锥组成的几何体,如图2.已知正四棱柱和正四棱锥的高相等,且底面边长均为2,若该几何体的所有顶点都在同一个球的表面上,则这个球的表面积为____.四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)如图,圆锥底面半径为1,高为3.(1)求圆锥内接圆柱(一底面在圆锥底面上,另一底面切于圆锥侧面)侧面积的最大值;(2)圆锥内接圆柱的表面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.18.(本小题满分12分)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.19.(本小题满分12分)如图所示,在四棱锥P-ABCD中,侧面P AD⊥底面ABCD,侧棱P A⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.(1)若CD∥平面PBO,试指出点O的位置;(2)求证:平面P AB⊥平面PCD.20.(本小题满分12分)(2020·江苏卷)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.(1)求证:EF∥平面AB1C1;(2)求证:平面AB1C⊥平面ABB1.21.(本小题满分12分)(2021·全国乙卷)如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.(1)求BC;(2)求二面角A-PM-B的正弦值.22.(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,AB=2A1A=4,以AB,BC为邻边作平行四边形ABCD,连接A1D,DC1.(1)求证:DC1∥平面A1ABB1;(2)若二面角A1-DC-A为45°.①求证:平面A1C1D⊥平面A1AD;②求直线AB1与平面A1AD所成角的正切值.。
(精选试题附答案)高中数学第八章立体几何初步基础知识点归纳总结

(名师选题)(精选试题附答案)高中数学第八章立体几何初步基础知识点归纳总结单选题1、如图已知正方体ABCD−A1B1C1D1,M,N分别是A1D,D1B的中点,则()A.直线A1D与直线D1B垂直,直线MN//平面ABCDB.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1C.直线A1D与直线D1B相交,直线MN//平面ABCDD.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1答案:A分析:由正方体间的垂直、平行关系,可证MN//AB,A1D⊥平面ABD1,即可得出结论.连AD1,在正方体ABCD−A1B1C1D1中,M是A1D的中点,所以M为AD1中点,又N是D1B的中点,所以MN//AB,MN⊄平面ABCD,AB⊂平面ABCD,所以MN//平面ABCD.因为AB不垂直BD,所以MN不垂直BD则MN不垂直平面BDD1B1,所以选项B,D不正确;在正方体ABCD−A1B1C1D1中,AD1⊥A1D,AB⊥平面AA1D1D,所以AB⊥A1D,AD1∩AB=A,所以A1D⊥平面ABD1,D1B⊂平面ABD1,所以A1D⊥D1B,且直线A1D,D1B是异面直线,所以选项C错误,选项A正确.故选:A.小提示:关键点点睛:熟练掌握正方体中的垂直、平行关系是解题的关键,如两条棱平行或垂直,同一个面对角线互相垂直,正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.2、如图,点N为正方形ABCD的中心,ΔECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线答案:B解析:利用垂直关系,再结合勾股定理进而解决问题.如图所示,作EO⊥CD于O,连接ON,过M作MF⊥OD于F.连BF,∵平面CDE⊥平面ABCD.EO⊥CD,EO⊂平面CDE,∴EO⊥平面ABCD,MF⊥平面ABCD,∴ΔMFB与ΔEON均为直角三角形.设正方形边长为2,易知EO=√3,ON=1EN=2,MF=√32,BF=52,∴BM=√7.∴BM≠EN,故选B.小提示:本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.3、如图,已知正方体的棱长为a,沿图1中对角面将它分割成两个部分,拼成如图2的四棱柱,则该四棱柱的全面积为()A.(8+2√2)a2B.(2+4√2)a2C.(4+2√2)a2D.(6−4√2)a2答案:C分析:拼成的几何体比原正方体的表面增加了两个截面,减少了原来两个正方形面,据此变化,进行求解. 由题意,拼成的几何体比原正方体的表面增加了两个截面,减少了原来两个正方形面,由于截面为矩形,长为√2a,宽为a,所以面积为√2a2,所以拼成的几何体的表面积为4a2+2√2a2=(4+2√2)a2.故选:C.4、下列说法正确的是()A.有两个面平行,其余各面都是平行四边形的几何体叫棱柱B.过空间内不同的三点,有且只有一个平面C.棱锥的所有侧面都是三角形D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台答案:C分析:根据定义逐项分析即可对A:根据棱柱的定义知,有两个面平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行的几何体是棱柱,所以A错误,反例如图:对B:若这三点共线,则可以确定无数个平面,故B错误;对C:棱锥的底面为多边形,其余各面都是有一个公共顶点的三角形,故C正确;对D:只有用平行于底面的平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台,故D错误,故选:C.5、圆台的上、下底面的面积分别是π,4π,侧面积是6π,则这个圆台的体积是()A.2√33πB.2√3πC.7√36πD.7√33π答案:D分析:求出圆台的高,再利用圆台的体积公式进行计算.设圆台的上、下底面的半径分别为r,R,母线长为l,高为h.,由圆台的上、下底面的面积分别是π,4π,得{πr2=π,πR2=4π,所以r=1,R=2,由圆台侧面积公式可得π×(2+1)l=6π,所以l=2,所以ℎ=√22−(2−1)2=√3,所以该圆台的体积V=13πℎ(R2+r2+Rr)=13π×√3×(4+1+2)=7√33π.故选:D.6、已知正四面体P−ABC内接于球O,点E是底面三角形ABC一边AB的中点,过点E作球O的截面,若存在半径为√3的截面圆,则正四面体P−ABC棱长的取值范围是()A.[√2,√3]B.[√3,√6]C.[2√2,2√3]D.[2√3,2√6]答案:C分析:根据条件设正四面体的棱长为a,用棱长a表示出其外接球的半径R=√64a,过E点作外接球O的截面,只有当OE⊥截面圆所在的平面时,截面圆的面积最小,此时此时截面圆的半径为r=12a,最大截面圆为过球心的大圆,半径为R=√64a,根据题意则12a≤√3≤√64a,从而可得出答案.如图,在正四面体P−ABC中,设顶点P在底面的射影为O1,则球心O在PO1上,O1在CE上,且|PO1|=23|CE|,连接OE、OC,设正四面体的棱长为a,则|CE|=√32a,|PO1|=23|CE|=√33a则正四面体的高PO1=√PC2−O1C2=(√33=√63a,设外接球半径为R,在Rt△OO1C中,OC2=OO12+O1C2,即R2=(√63a−R)2+(√33a)2,解得R=√64a,∴在Rt△OO1E中,OE=√OO12+O1E2=(√612(√36=√24a,过E点作外接球O的截面,只有当OE⊥截面圆所在的平面时,截面圆的面积最小,此时截面圆的半径为r=√R2−OE2=√(√64a)2−(√24a)2=12a,最大截面圆为过球心的大圆,半径为R=√64a,由题设存在半径为√3的截面圆,∴12a≤√3≤√64a,解得2√2≤a≤2√3,故选:C.小提示:关键点睛:本题考查正四棱锥的外接球的截面圆的半径范围问题,解答本题的关键是用正四棱锥棱长a表示出其外接球的半径R=√64a,得出过E点的球的截面圆的半径的范围,从而得解,属于中档题.7、如图,“蘑菇”形状的几何体是由半个球体和一个圆柱体组成,球的半径为2,圆柱的底面半径为1,高为3,则该几何体的表面积为()A .18πB .20πC .22π3D .26π答案:A分析:由题意可知该几何体的体积是由半球的表面积加上圆柱的侧面积,再加上圆的面积即可解:由题意得,球的半径R =2,圆柱的底面半径r =1,高ℎ=3,则该几何体的表面积为S =2πR 2+πR 2+2πrℎ=8π+4π+2π×1×3=18π故选:A.8、已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的体积为( )A .√3πB .√33C .√33πD .√3答案:C分析:求出圆锥的底面半径和圆锥的母线长与高,再计算圆锥的体积.解:设圆锥的底面半径为r ,圆锥的母线长为l ,由πl =2πr ,得l =2r ,又S =πr 2+πr ⋅2r =3πr 2=3π,所以r 2=1,解得r =1;所以圆锥的高为ℎ=√l 2−r 2=√22−12=√3,所以圆锥的体积为V=13πr2ℎ=13π×12×√3=√33π.故选:C.9、过半径为4的球O表面上一点M作球O的截面,若OM与该截面所成的角是30°,则O到该截面的距离是()A.4B.2√3C.2D.1答案:C分析:作出球的截面图,根据几何性质计算,可得答案.作出球的截面图如图:设A为截面圆的圆心,O为球心,则OA⊥截面,AM在截面内,即有OA⊥AM,故∠OMA=30∘,所以OA=4×12=2 ,即O到该截面的距离是2,故选:C10、设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题中的真命题为()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊥α,则m∥nC.若m∥α,m∥β,则α∥βD.若m⊥α,α⊥β,则m∥β答案:B分析:在正方体中取直线和平面可排除ACD,由线面垂直的性质可得B正确.在正方体ABCD−EFGH中,记底面ABCD为α,EF为m,EH为n,显然A不正确;记底面ABCD为α,EF为m,平面CDHG为β,故排除C;记底面ABCD为α,BF为m,平面ABFE为β,可排除D;由线面垂直的性质可知B正确.故选:B填空题11、达•芬奇认为:和音乐一样,数学和几何“包含了宇宙的一切”,从年轻时起,他就本能地把这些主题运用在作品中,布达佩斯的伊帕姆维泽蒂博物馆收藏的达•芬奇方砖,在正六边形上画了具有视觉效果的正方体图案(如图1),把三片这样的达•芬奇方砖形成图2的组合,这个组合表达了图3所示的几何体.若图3中每个正方体的边长为1,则点F到直线QC的距离是__________.答案:√2分析:根据题意,求得△FQC的三条边长,在三角形FQC中求边QC边上的高线即可.根据题意,延长QN,BA交于点M,连接QF,FC,如下所示:在△QFC中,容易知:QF=√QN2+NF2=√12+(√2)2=√3;同理FC=√12+(√5)2=√6,QC=√QM2+MC2=√22+(√5)2=3,满足QF2+FC2=QC2,设点F到直线QC的距离为d,由等面积法可知:QF×FC=QC×d,解得d=√3×√6=√2,即点F到直线QC的距离是√2.3所以答案是:√2.12、我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱ABC−A1B1C1,其中AC⊥BC,若AA1=AB=1,当“阳马”即四棱锥B−A1ACC1,体积最大时,“堑堵”即三棱柱ABC−A1B1C1的表面积为_______.答案:3+2√22分析:依据均值定理去求四棱锥B−A1ACC1取体积最大值时AB的长度,再去求三棱柱ABC−A1B1C1的表面积即可.四棱锥B−A1ACC1的体积是三棱柱体积的23,V ABC−A1B1C1=12AC⋅BC⋅AA1=12AC⋅BC≤14(AC2+BC2)=14AB2=14,当且仅当AB=BC=√22时,取等号.所以三棱柱ABC−A1B1C1的表面积为S=2×12×√22×√22+(√22+√22+1)×1=3+2√22.所以答案是:3+2√2213、空间给定不共面的A,B,C,D四个点,其中任意两点间的距离都不相同,考虑具有如下性质的平面α:A,B,C,D中有三个点到的距离相同,另一个点到α的距离是前三个点到α的距离的2倍,这样的平面α的个数是___________个答案:32分析:按照四个点的位置不同分类讨论,即可求解首先取3个点相等,不相等的那个点由4种取法;然后分3分个点到平面α的距离相等,有以下两种可能性:(1)全同侧,这样的平面有2个;(2)不同侧,必然2个点在一侧,另一个点在一侧,1个点的取法有3种,并且平面过三角形两个点边上的中位线,考虑不相等的点与单侧点是否同侧有两种可能,每种情况下都唯一确定一个平面,故共有6个,所有这两种情况共有8个,综上满足条件的这样的平面共有4×8=32个,所以答案是:3214、如图所示,有边长为2的正方体ABCD−A1B1C1D1,P为正方体表面的一个动点.若三棱锥A−PBC的体积为12,则|PD1|的取值范围是____________.答案:[54,3√174]分析:根据三棱锥A−PBC的体积求出点P到平面ABC的距离ℎ,由此确定点P的轨迹,结合图形即可得出答案. 设点P到平面ABC的距离为ℎ,则V P−ABC=13S△ABC⋅ℎ=23ℎ=12,所以ℎ=34,如图在AA1上取点E,使得AE=34,过点E作平面EFGH∕∕平面ABCD,F,G,H分别在BB1,CC1,DD1上,故点P在四边形EFGH的边上,则当点P在点H的位置时,|PD1|最小,为54,当点P在点F的位置时,|PD1|最大,为√4+4+2516=3√174,所以|PD1|的取值范围是[54,3√174].所以答案是:[54,3√174].15、已知角α和角β的两边分别平行且一组边方向相同,另一组边的方向相反,若α=45°,则β=________.答案:135°分析:首先根据题意将图画出,然后根据α=45°,AB∥CD,可得∠BCD=180°−α,进而得出结论. 解:如图,由题意知α=45°,AB∥CD,∴∠BCD=180°−α=135°,即β=135°.所以答案是:135°.小提示:本题考查了平行线的性质,结合图会使问题变得简单,属于基础题.解答题16、在正方体ABCD−A1B1C1D1中,E为BB1的中点.求证:BC1//平面AD1E.答案:证明见解析.分析:如图,根据正方体的结构特征可得AD1//BC1,利用线面平行的判定定理即可证明.如图,E为BB1的中点,连接AE,AD1,ED1,BC1,在正方体ABCD−A1B1C1D1中,AB=D1C1且AB//D1C1,∴四边形ABC1D1是平行四边形,∴AD1//BC1,又∵AD1⊂平面AD1E,BC1⊄平面AD1E,∴BC1//平面AD1E.17、如图,在正方体ABCD−A1B1C1D1中.(1)求异面直线A1B和CC1所成的角的余弦值;(2)求证:直线A1B//平面DCC1D1.答案:(1)√22(2)证明见解析分析:(1)根据已知CC1//BB1,可将异面直线A1B和CC1所成的角转化为直线A1B和BB1所成的角,再根据题目的边长关系,即可完成求解;(2)可通过连接D1C,证明四边形A1BCD1为平行四边形,从而得到A1B//D1C,再利用线面平行的判定定理即可完成证明.(1)因为CC1//BB1,所以∠A1BB1就是异面直线A1B和CC1所成的角.又因为ABCD−A1B1C1D1为正方体,所以异.面直线A1B和CC1所成的角为45o,所以异面直线A1B和CC1所成的角的余弦值为√22(2)连接D1C,因为A1D1//BC且A1D1=BC,所以四边形A1BCD1为平行四边形,所以A1B//D1C;A1B⊄平面DCC1D1,D1C⊂平面DCC1D1;所以直线A1B//平面DCC1D1.即得证.18、如图,在四棱锥P−ABCD中,AB//CD,且∠BAP=∠CDP=90°.(1)证明:直线AB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90,且四棱锥P−ABCD的体积为83,求该四棱锥的侧面积.答案:(1)证明见解析(2)6+2√3分析:(1)由线面垂直的判定定理证明线面垂直;(2)在平面PAD内作PE⊥AD,垂足为点E.证明PE⊥平面ABCD.设AB=x,则AD=√2x,PE=√22x.由棱锥体积求得x后可得各面面积.即可得侧面积.(1)证明:因为AB//CD,且∠BAP=∠CDP=90,所以AB⊥AP且AB⊥DP.又AP∩DP=P,AP,DP⊂平面PAD,所以直线AB⊥平面PAD.(2)解:在平面PAD内作PE⊥AD,垂足为点E.由(1)知AB⊥平面PAD,故AB⊥PE.又AB∩AD=A,AB,AD⊂平面ABCD,所以PE⊥平面ABCD.设AB=x,则AD=√2x,PE=√22x.故四棱锥P−ABCD的体积V P−ABCD=13AB⋅AD⋅PE=13x3.由题设得13x3=83,故x=2.从而PA=PD=AB=DC=2,AD=BC=2√2,PB=PC=2√2.所以四棱锥P−ABCD的侧面积为12PA⋅PD+12PA⋅AB+12PD⋅DC+12BC2⋅sin60°=6+2√3.19、如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;(2)当E为AB的中点时,求点E到面ACD1的距离.答案:(1)证明见解析;(2)13.分析:(1)证明AE⊥A1D、A1D⊥AD1,由线面垂直的判定定理可证明A1D⊥平面AD1E,即证;(2)由勾股定理求出△ACD1各个边长,设点E到平面ACD1的距离为ℎ,由V E−ACD1=V D1−ACE即可求解.(1)因为AE⊥平面ADD1A1,A1D⊂平面ADD1A1,所以AE⊥A1D,因为四边形ADD1A1是矩形,AD=AA1,所以四边形ADD1A1是正方形,所以A1D⊥AD1,又AD1⊂平面AD1E,AE⊂平面AD1E,AD1∩AE=A,所以A1D⊥平面AD1E,又因为D1E⊂平面AD1E,所以D1E⊥A1D.(2)因为AD=AA1=1,AB=2,E为AB的中点,所以AD1=√2,AC=CD1=√5,CE=√2,AE=1,所以S△ACD1=12×√2×√5−(√22)2=32,S△ACE=12×1×1=12,设点E到平面ACD1的距离为ℎ,由V E−ACD1=V D1−ACE可得:13⋅S△ACD1⋅ℎ=13⋅S△ACE⋅DD1,即13×32ℎ=13×12×1,解得:ℎ=13,所以点E到面ACD1的距离为13.。
立体图形的展开图(有答案)汇总

01
02
03
空间性
立体图形存在于三维空间 中,具有长、宽、面围 成的封闭空间。
组合性
立体图形可以由多个简单 的基本图形组合而成。
立体图形的重要性
实际应用
立体图形在建筑、机械、 电子等领域有广泛应用。
数学研究
立体图形是数学中几何学 的重要研究对象,对于理 解空间结构和性质具有重 要意义。
优化材料
根据立体图形的结构和展开图的特 点,选择合适的材料,如金属、塑 料等,以降低成本和提高加工效率。
考虑加工工艺
在绘制展开图时需要考虑加工工艺 的可行性,如折弯、切割、焊接等, 以保证加工的准确性和效率。
04 立体图形展开图的实例分 析
正方体展开图的实例分析
正方体的展开图是一个六面体,其中 三个面是正方形,另外三个面是长方 形。
01
选择合适的CAD软件,如AutoCAD、SolidWorks等。
02
在软件中创建立体图形的三维模型,然后通过软件的展开功能
生成展开图。
CAD软件可以快速生成准确的展开图,并可以方便地进行修改
03
和优化。
立体图形展开图的优化技巧
简化图形
在保证功能的前提下,尽量简化 展开图的形状和结构,减少材料
的使用和加工难度。
教育价值
立体图形的教学有助于培 养学生的空间想象能力和 逻辑思维能力。
02 常见立体图形的展开图
正方体的展开图
1-4-1型
2-3-1型
三个面相连构成底面,上方有两个面 相互垂直。
三个面相连构成底面,上方有两个面 相互垂直且不相邻。
1-3-2型
四个面相连构成底面,上方有一个面 与底面相邻。
长方体的展开图
青岛版(五年制)数学五年级下册《第八单元 总复习2

课后作业 课本: 第125页第3题
返回
谢谢观看!
【班主任工作职责】
在对学生的教育管理中,班主任工作是尤为重要的。因此,加强班主任的考核是相当重要的。主 要从以下几个方面进行考核。
一、重视学生的思想工作:认真组织好晨会、班队的活动;经常对学生进行教育,与学生进行沟 通。
二、班级管理:严格按班主任“一日常规管理”的操作流程工作。
从图中观察可以看出,长有2条,宽有2条,高有4条。
彩带的长度 = 70×2+Байду номын сангаас0×2+30×4+90 = 140+100+120+90 = 450(cm)
答:这条彩带的长度是450cm。
返回
3、如果一个长方体的棱长总和是40分米,长是5分米,宽 是3分米,高是多少?
长方体的棱长总和=(长+宽+高)×4 (40-5×4-3×4)÷4 =(40-32)÷4 = 2(dm)
队员”的评选工作。
底面是一个圆,侧面展开是扇形,只有一条高。
返回
课堂练习
1. 想一想,将下列平面图形以一条边为轴旋转一周,会形成什么样的空 间图形,用线连一连。
返回
2、 一个长方体包装盒长70cm,宽50cm,高30cm,现在用 一条彩带捆扎这个包装盒(如图所示)。如果接头处的彩带 长90cm,求这条彩带的长度.
长方体
立 正方体
体
图
圆柱
形
圆锥
返回
长方体:
长方体有6个面、12条棱和8个顶点;
6个面都是长方形(特殊情况下有两
h
个相对的面是正方形),相对的面 b 完全相同,相对4条棱的长度相等。
返回
正方体:
立体图形的认识北京课改版数学六年级下册PPT课件

(1)长方体六个面一定是长方形。
特殊情况有两个相
对的面是正方形的(
× 八)五折
(2)圆柱和圆锥的侧面展开都是长方形。圆锥的侧面展 ( × )
开是一个扇形
(3)正方体棱长总和是48厘米,它的每条棱长是4厘米(。 √ )
8倍
(4)正方体的棱长扩大2倍,它的体积就扩大6倍。 ( × )
(5)圆柱体的体积等于圆锥体的3倍。
可能是平行四边 形,底是圆柱底 面圆的周长,高 是圆柱的高。
当底面圆的周长 和高相等时,侧 面展开图可能是 正方形。
立体图形的认识
请把下面图形从正面、上面、左面看到的图形画出来。 八五折
正面
上面
左面
立体图形的认识
一个立体图形从上面看是:
从左面看是:
要搭成这样的立体图形,至少要用( 5个 )个小立方体, 最多可以有( 7个 )个小立方体
要从长方体、正方体的特征出发, 从而确定小棒和连接器的数量。
连接器相当 于顶点。
长方体和正方体各有12条棱,要准备24根小棒。
长方体和正方体各有8个顶点,要准备16个连接器。
立体图形的认识
有28根小棒,有16个连接器(如右图)。小棒的长度如下:长6 厘米的有4根,长5厘米的有14根,长4厘米的有10根。用这些小八棒五做折 一个长方体框架(这个长方体有一组相对的面是正方形),再做一 个正方体框架。 (2)小棒的长度是怎样确定的?你还能提出什么问题?
(2)在蓄水池的底面和四周抹上水泥,抹水泥的面积有多大? 10×4 +(4×2+2×10)×2= 96(平方米) 答:抹水泥的面积是96平方米。
(3)蓄水池最多能蓄水多少立方米? 10×2×4 = 80(立方米) 答:最多能蓄水80立方米。
五年级数学下册教材课件-第8单元探索乐园整理与评价-冀教版(共59张PPT)精选全文完整版

3
1
1
1
P95~98知识与技能
1.填空。 在 中,当a( )时, 等于1; 当a( )时, 没意义; 当a( )时, 是真分数; 当a( )时, 是假分数;
最多可以装60个。如下图所示。
每排放5个,一层可放15个,2.08米高,可以放4层,共60个。
7.有一批有线数字电视机顶盒,外形尺寸是34厘米×25厘米×8厘米。(1)请你设计一个能装20个有线数字电视机顶盒的包装箱。
34×2=68(厘米)
25×2=50(厘米)
8×5=40(厘米)
做长68厘米、宽50厘米、高40厘米的纸箱能装20个。
(2+1)×2=6(种)
2.聪聪、红红、亮亮和丫丫4人进行跳棋比赛。比赛实行单循环制,每2人都要赛一局。(1)一共比赛几局?(2)最后一局,聪聪赢了丫丫。前几局,红红、丫丫和亮亮赢的局数相同。他们各赢了几局? 聪聪赢了 局; 亮亮赢了 局; 红红赢了 局; 丫丫赢了 局。
2分米=20厘米
16×20=320(立方厘米)
15.胜利小学新挖一个长方体沙坑,沙坑的长是4米,宽是2米,深是0.4米。需要多少立方米的黄沙才能填满?每立方米黄沙重1.4吨,这些黄沙重多少吨?
4×2×0.4=3.2(立方米)
1.4×3.2=4.48(吨)
16.一个长方体鱼缸的长是6分米,宽是4分米,高是3分米。(玻璃厚度不计)(1)做这个鱼缸至少需要多少平方分米玻璃?
41
50
3
5
1
40
1
3
25
9
20
1
4
1
5.在下面的圈里填上>或<。 〇 〇 〇 〇
2
《第八章立体几何初步》综合检测卷

《第八章 立体几何初步》综合检测卷(时间:120分钟,满分:150分)一、选择题:1.空间中有三条线段AB ,BC ,CD ,且∠ABC =∠BCD ,那么直线AB 与CD 的位置关系是( )A.平行B.异面C.相交或平行D.平行或异面或相交均有可能2.一个水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC =45°,AB =AD =1,DC ⊥BC ,则这个平面图形的面积为( )A.14+24B.2+22C.14+22D.12+ 2 3.对两条不相交的空间直线a 与b ,必存在平面α,使得( )A.a ⊂α,b ⊂αB.a ⊂α,b ∥αC.a ⊥α,b ⊥αD.a ⊂α,b ⊥α4.正方体的表面积与其外接球的表面积的比为( )A.3∶πB.2∶πC.1∶2πD.1∶3π5.如图在长方体ABCD -A 1B 1C 1D 1中,棱锥A 1ABCD 的体积与长方体的体积的比为( ) A.12 B.16 C.13 D.156.在正方体ABCD -A 1B 1C 1D 1中,点Q 是棱DD 1上的动点,则过A ,Q ,B 1三点的截面图形是( )A.等边三角形B.矩形C.等腰梯形D.以上都有可能 7.给出下列命题:①过平面外一直线有且仅有一个平面和这个平面平行;②如果一个平面经过另一个平面的斜线,那么这两个平面不可能垂直;③若直角三角形ABC 在平面α内的射影仍是直角三角形,则平面ABC ∥平面α.其中正确命题的个数为( )A.0B.1C.2D.38.如图,在三棱锥D -ABC 中,若AB =CB ,AD =CD ,E 是AC 的中点,则下列结论中正确的是( )A.平面ABC ⊥平面ABDB.平面ABD ⊥平面BDCC.平面ABC ⊥平面BDE ,且平面ADC ⊥平面BDED.平面ABC ⊥平面ADC ,且平面ADC ⊥平面BDE9.若空间中四条两两不同的直线l 1,l 2,l 3,l 4,满足l 1⊥l 2,l 2⊥l 3,l 3⊥l 4,则下列结论一定正确的是( )A.l 1⊥l 4B.l 1∥l 4C.l 1与l 4既不垂直也不平行D.l 1与l 4的位置关系不确定10.在等腰Rt △A ′BC 中,A ′B =BC =1,M 为A ′C 的中点,沿BM把它折成二面角,折后A 与C 的距离为1,则二面角C -BM -A 的大小为( )A.30°B.60°C.90°D.120°11.如图,已知六棱锥P -ABCDEF 的底面是正六边形,P A ⊥平面ABC ,P A =2AB ,则下列结论正确的是( )A.PB ⊥ADB.平面P AB ⊥平面PBCC.直线BC ∥平面P AED.直线PD 与平面ABC 所成的角为45°12.已知四棱锥S -ABCD 的所有顶点都在同一球面上,底面ABCD 是正方形且和球心O 在同一平面内,当此四棱锥体积取得最大值时,其表面积等于4+43,则球O 的体积等于( )A.423πB.823πC.1623π D .3223π 二、填空题:本题共4小题,每小题5分.13.如果用半径R =23的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高是 .14.已知a ,b 表示不同的直线,α,β,γ表示不重合的平面.①若α∩β=a ,b ⊂α,a ⊥b ,则α⊥β;②若a ⊂α,a 垂直于β内任意一条直线,则α⊥β;③若α⊥β,α∩β=a ,α∩γ=b ,则a ⊥b ;④若a ⊥α,b ⊥β,a ∥b ,则α∥β.上述命题中,正确命题的序号是 W.15.已知直二面角α-l -β,A ∈α,AC ⊥l ,C 为垂足,B ∈β,BD ⊥l ,D 为垂足.若AB =2,AC =BD =1,则D 到平面ABC 的距离为 .16.如图,在棱长均相等的正四棱锥P -ABCD 中,O 为底面正方形的中心,M ,N 分别为侧棱P A ,PB 的中点,有下列结论:①PC ∥平面OMN ;②平面PCD ∥平面OMN ;③OM ⊥P A ;④直线PD 与直线MN 所成角的大小为90°.其中正确结论的序号是 W.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.(1)求证:BD⊥PC;(2)若平面PBC与平面P AD的交线为l,求证:BC∥l.18.(本小题满分12分)如图,在三棱锥P-ABC中,AB⊥平面P AC,∠APC=90°,E是AB的中点,M是CE的中点,N在PB上,且PB=4PN.(1)求证:平面PCE⊥平面P AB;(2)求证:MN∥平面P AC.19.(本小题满分12分)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.(1)证明:BC1∥平面A1CD;(2)设AA1=AC=CB=2,AB=22,求三棱锥C-A1DE的体积.20.(本小题满分12分)如图,在四棱锥P-ABCD中,侧面P AD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,E为AD 的中点,过A,D,N的平面交PC于点M.求证:(1)EN∥平面PDC;(2)BC⊥平面PEB;(3)平面PBC⊥平面ADMN.21.(本小题满分12分)如图(1),在直角梯形ABCD 中,AD ∥BC ,∠BAD =90°,AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点,将△ABE 沿BE 折起到图(2)中△A 1BE 的位置,得到四棱锥A 1BCDE .(1)求证:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1BCDE 的体积为362,求a 的值.22.(本小题满分12分)如图,在三棱柱ABC -A 1B 1C 1中,侧棱AA 1⊥底面ABC ,M 为棱AC 的中点.AB =BC ,AC =2,AA 1= 2.(1)求证:B 1C ∥平面A 1BM ;(2)求证:AC 1⊥平面A 1BM ;(3)在棱BB 1上是否存在点N ,使得平面AC 1N ⊥平面AA 1C 1C ?如果存在,求此时BN BB 1的值;如果不存在,请说明理由.。
高考数学总复习 中档题目强化练 立体几何专题精讲课件 理 新人教A版

9
10
又AD綊A1D1,∴BE綊A1D1,∴四边形A1D1EB是平行四边形. ∴D1E∥A1B.
∵D1E⊄平面A1BD,A1B⊂平面A1BD, ∴D1E∥平面A1BD.
第十四页,共29页。
A组 专项基础训练
1
2
3
4
5
6
7
8
9 10
10. 在正方体 ABCD-A′B′C′D′中, 棱 AB,BB′,B′C′,C′D′的中点 分别是 E,F,G,H,如图所示. (1)求证:AD′∥平面 EFG; (2)求证:A′C⊥平面 EFG; (3)判断点 A,D′,H,F 是否共面?并说明理由.
(1)证明 在 Rt△ABD 中,AB=AD=1,BD
= 2, 又∵BC= 2,CD=2,
∴∠DBC=90°,即BD⊥BC.
又BD⊥BB1,B1B∩BC=B,
∴BD⊥平面B1BCC1. (2)解 DC 的中点即为 E 点,
连接D1E,BE,∵DE∥AB,DE=AB,
第十三页,共29页。
9
10
A组 专项基础训练
( D)
解析 对于选项 A,当 A∈l1时,结论不成立;对于选项 B、C,
当l2 ⊂α时,结论不成立.
第二十页,共29页。
B组 专项能力(nénglì)提升
1
2
3
4
5
2.已知直线 l⊥平面 α,直线 m⊂平面 β,有下面四个命题:
①α∥β⇒l⊥m; ②α⊥β⇒l∥m;③l∥m⇒α⊥β; ④l⊥m⇒α∥β.
D.α⊥γ,β⊥γ,m⊥α
解析 如图①知 A 错;如图②知 C 错; 如图③在正方体中,两侧面α与β相交于l,都与底面γ垂直,γ
内的直线m⊥α,但m与β不垂直,故D错; 由 n⊥α,n⊥β,得 α∥β.又 m⊥α,则 m⊥β,故 B 正确.
吉美版小学五年级下册综合实践活动 第八课图形的翻转、旋转与拉伸

第八课 图形的翻转、旋转与拉伸
CONTENTS
翻转效果的实现 旋转效果的实现 拉伸效果的实现 综合案例:翻转、旋转与拉伸的绘图应用
1 翻转效果的实现
PA R T
翻转效果的实现
横向翻转
纵向翻转
自定义翻转
翻转效果的实现
横向翻转
横向翻转是指将图形沿着水平中心线进行翻转,可以使用图形 绘制软件中的翻转工具实现。在Adobe Illustrator中,可以通过 选择图形并右键点击选择“转换”-“翻转水平”来实现。在 PowerPoint中,可以选择图形并点击“格式”选项卡中的“翻转形 状”按钮来实现横向翻转。
4
PA R T
综合案例:翻转、旋转与 拉伸的绘图应用
综合案例:翻转、旋转与拉伸的绘图应用
翻转
旋转
拉伸
综合案例:翻转、旋转与拉伸的绘图应用
翻转
翻转是指将图形沿着某个轴线进行镜像对称,实现图形的左右 或上下翻转。在计算机绘图中,可以通过改变图形的坐标或者 像素值来实现翻转效果。常见的翻转操作有水平翻转和垂直翻 转,可以应用在图片编辑、图形变换等场景中。
2 旋转效果的实现
PA R T
旋转效果实现
旋转基本概念
旋转算法
旋转效果的实现步 骤
旋转效果的实现
旋转基本概念
旋转是计算机图形处理中常用的一种变换效果,通过改变图形 元素的角度来实现图像的旋转。旋转可以使图形在平面内绕指 定的旋转中心点旋转一定的角度。旋转角度可以是正值,表示 顺时针旋转;也可以是负值,表示逆时针旋转。旋转效果可以 为图形增添动感和活力,广泛应用于多媒体设计、游戏开发等 领域。
翻转效果的实现
纵向翻转
纵向翻转是指将图形沿着垂直中心线进行翻转,同样可以使用 图形绘制软件中的翻转工具实现。在Adobe Illustrator中,可以 通过选择图形并右键点击选择“转换”-“翻转垂直”来实现。在 PowerPoint中,可以选择图形并点击“格式”选项卡中的“翻转形 状”按钮来实现纵向翻转。
五年级下册数学教案-第八单元图形王国-苏教版

五年级下册数学教案-第八单元图形王国-苏教版一、教学目标1. 让学生掌握平面图形的基本特征和性质,能够识别和运用各种平面图形。
2. 培养学生的空间想象能力和逻辑思维能力,提高他们解决实际问题的能力。
3. 培养学生合作学习的精神,增强他们的团队协作能力。
二、教学内容1. 平面图形的基本特征和性质2. 平面图形的识别和运用3. 平面图形在实际生活中的应用三、教学重点与难点1. 教学重点:平面图形的基本特征和性质,平面图形的识别和运用。
2. 教学难点:平面图形在实际生活中的应用,培养学生的空间想象能力和逻辑思维能力。
四、教具与学具准备1. 教具:平面图形模型,平面图形卡片,多媒体设备。
2. 学具:平面图形练习册,彩笔,剪刀,胶水。
五、教学过程1. 导入:通过生活中的实例,引发学生对平面图形的思考,激发他们的学习兴趣。
2. 新课导入:讲解平面图形的基本特征和性质,让学生了解和掌握各种平面图形。
3. 实践操作:让学生通过观察、实验、讨论等方式,深入了解平面图形的性质和运用。
4. 小组讨论:分组讨论平面图形在实际生活中的应用,培养学生的合作学习能力和解决问题的能力。
5. 总结讲解:对学生的讨论进行总结和讲解,强化他们对平面图形的理解和运用。
6. 课堂练习:让学生进行平面图形的练习,巩固他们的学习成果。
六、板书设计1. 五年级下册数学教案-第八单元图形王国2. 目录:教学目标、教学内容、教学重点与难点、教具与学具准备、教学过程、板书设计、作业设计、课后反思3. 正文:根据教学过程,逐步展示平面图形的基本特征和性质,以及平面图形的识别和运用。
七、作业设计1. 让学生完成平面图形的练习册,巩固他们的学习成果。
2. 让学生观察生活中的平面图形,记录下来并进行分析。
八、课后反思1. 教师应反思教学过程中的不足,找出问题所在,并寻求改进的方法。
2. 教师应关注学生的学习情况,及时给予指导和帮助,提高他们的学习效果。
3. 教师应不断更新教学观念,改进教学方法,提高教学水平。
五年级下第8次图形 内角和
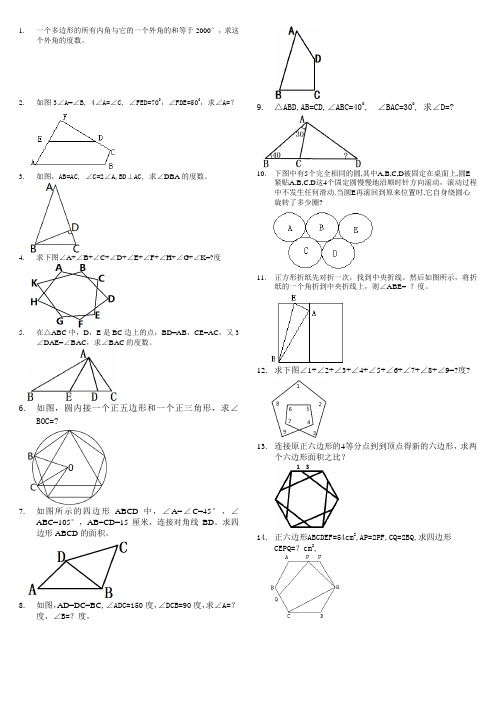
1.一个多边形的所有内角与它的一个外角的和等于2000°,求这
个外角的度数。
2.如图3∠A=∠B, 4∠A=∠C, ∠FED=700,∠FDE=500,求∠A=?
3.如图,AB=AC, ∠C=2∠A,BD⊥AC,求∠DBA的度数。
4.求下图∠A+∠B+∠C+∠D+∠E+∠F+∠H+∠G+∠K=?度
5.在△ABC中,D,E是BC边上的点,BD=AB,CE=AC,又3
∠DAE=∠BAC,求∠BAC的度数。
6.如图,圆内接一个正五边形和一个正三角形,求∠
BOC=?
7.如图所示的四边形ABCD中,∠A=∠C=45°,∠
ABC=105°,AB=CD=15厘米,连接对角线BD。
求四边形ABCD的面积。
8.如图,AD=DC=BC,∠ADC=150度,∠DCB=90度,求∠A=?
度,∠B=?度,9.△ABD,AB=CD,∠ABC=400, ∠BAC=300, 求∠D=?
10.下图中有5个完全相同的圆,其中A,B,C,D被固定在桌面上,圆E
紧贴A,B,C,D这4个固定圆慢慢地沿顺时针方向滚动,滚动过程中不发生任何滑动.当圆E再滚回到原来位置时,它自身绕圆心
旋转了多少圈?
11.正方形折纸先对折一次,找到中央折线。
然后如图所示,将折
纸的一个角折到中央折线上,则∠ABE= ?度。
12.求下图∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9=?度?
13.连接原正六边形的4等分点到到顶点得新的六边形,求两
个六边形面积之比?
14.正六边形ABCDEF=54cm2,AP=2PF,CQ=2BQ,求四边形
CEPQ=?cm2,。
2014-2018年理科数学五年真题分类 第八章 立体几何

5.(2017•浙江,3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2) 是( )
A.
B.
C.
D.
2.A 观擦图形图可知,俯视图为
,故答案为 A.
3.(2018 浙江,3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3) 是( )
A.2 B.4 C.6 D.8
3.C 根据三视图可得几何体为一个直四棱柱,高为 2,底面为直角梯形,上下底分别为 1,2,
梯形的高为
A. +1
B. +3
C. +1 D. +3
5. A 由几何的三视图可知,该几何体是圆锥的一半和一个三棱锥组成, 圆锥的底面圆的半径为 1,三棱锥的底面是底边长 2 的等腰直角三角形,圆锥的高和棱锥的
高相等均为 3,故该几何体的体积为 × ×π×12×3+ × × × ×3= +1,故选 A.
6.(2016·全国Ⅲ,9)如图,网格纸上小正方形的边长为 1,粗实线画出的是某多面体的三视图, 则该多面体的表面积为( )
,∴sin
,
cos
,∴sin∠GEM=sin(∠EGM+∠EMG)=sin∠EGMcos∠EMG+cos∠EGMsin∠
EMG= ,∴EN=
= =20cm.∴玻璃棒 l 没入水中部分的长度为 20cm.
考点 2 空间几何体的表面积和体积
1.(2018 全国Ⅲ,10)设A , B , C , D是同一个半径为 4 的球的球面上四点, △ ABC为 等边三角形且其面积为9 3,则三棱锥D−ABC体积的最大值为( ) A.12 3 B.18 3 C.24 3 D.54 3 1.B 如图所示,
黑龙江鹤岗市2024年数学(高考)统编版真题(评估卷)模拟试卷

黑龙江鹤岗市2024年数学(高考)统编版真题(评估卷)模拟试卷一、单项选择题(本题包含8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题已知,为虚数单位,则()A.B.C.D.第(2)题几何中常用表示的测度,当为曲线、平面图形和空间几何体时,分别对应其长度、面积和体积.在中,,,,为内部一动点(含边界),在空间中,到点的距离为的点的轨迹为,则等于()A.B.C.D.第(3)题抽样统计某位学生8次的数学成绩分别为,则该学生这8次成绩的分位数为()A.85B.85.5C.87D.88.5第(4)题已知复数,则的实部是()A.2B.0C.D.第(5)题已知奇函数在上的最大值为,则()A.或3B.或2C.3D.2第(6)题在三棱锥中,已知△ABC是边长为8的等边三角形,平面ABC,,则AB与平面PBC所成角的正弦值为()A.B.C.D.第(7)题蹴鞠,又名“蹴球”“蹴圆”等,“蹴”有用脚蹴、踢的含义,“鞠”最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的踢足球活动.如图所示,已知某“鞠”的表面上有四个点,,,满足,,则该“鞠”的表面积为()A.B.C.D.第(8)题已知集合,,则等于()A.B.C.D.二、多项选择题(本题包含3小题,每小题6分,共18分。
在每小题给出的四个选项中,至少有两个选项正确。
全部选对的得6分,选对但不全的得3分,有选错或不答的得0分) (共3题)第(1)题已知平面上的线段及点,任取上一点,称线段长度的最小值为点到线段的距离,记作.已知线段,,点为平面上一点,且满足,若点的轨迹为曲线,,是第一象限内曲线上两点,点且,,则( )A .曲线关于轴对称B .点的坐标为C.点的坐标为D .的面积为第(2)题在中,角所对的边分别为,则能确定为钝角的是( )A .B .均为锐角,且C .均为锐角,且D .第(3)题已知抛物线C :的准线为,直线与C 相交于A 、B 两点,M 为AB 的中点,则( )A.当时,以AB 为直径的圆与相交B .当时,以AB 为直径的圆经过原点OC .当时,点M 到的距离的最小值为2D .当时,点M 到的距离无最小值三、填空(本题包含3个小题,每小题5分,共15分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体图形综合基本知识点:
2.各类图形的形成方式以及内在联系
典型例题:
例1:如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?
例2:如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.
例3:如右图,一个正方体形状的木块,棱长l米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么,这60块长方体表面积的和是多少平方米?
例4:有一个棱长为10cm的正方体,从它的上方截去一个棱长为10cm,4cm,3cm的长方体,求它的表面积减少了百分之几?
例5:从长为20厘米,宽为12厘米的长方形硬纸板的四角去掉边长4厘米的正方形.然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?
例6:有大、中、小3个正方形水池.它们的内边长分别是6米、3米、2米.把两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米.如果将这两堆碎石都沉没在大水池的水里,大水池的水面升高了多少厘米?
例7:下图所示为一个棱长6厘米的正方体,从正方体的底面向内挖去一个最大的圆锥体,求剩下的体积是原正方体的百分之几?(保留一位小数).
例8:从一个底面半径为3厘米,高为4厘米的圆柱中,挖去一个以圆柱上底面为底,下底面圆心为顶点的圆锥,得到一个如下图的几何体.求这个几何体的体积.
例题9: 要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?
例10:有A 、B 两个容器,如下页图,先将A 容器注满水,然后倒入B 容器,求B 容器的水深.(单位:厘米)
例11:如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)
11
10.511.5
例12:有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?
例13:如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14=
)
例14:一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? (π 3.14=)
例15:一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是_______ 立方厘米.(π取3.14
)
(单位:厘米)
例16:如图,ABC 是直角三角形,AB 、AC 的长分别是3和4.将ABC ∆绕AC 旋转一周,求ABC ∆扫出的立体图形的体积.(π 3.14=)
C
B A
4
3
例题17:小玲有两种不同形状的纸板.一种是正方形的,一种是长方形的(如下图).正方形纸板的总数与长方形纸板的总数之比是1:2.她用这些纸板做成一些竖式和横式的无盖纸盒,正好将纸板用完.在小玲所做的纸盒中,坚式纸盒的总数与横式纸盒的总数之比是多少?
课后练习:
1、一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大2
cm.(π取3.14)
2008cm,则这个圆柱体木棒的侧面积是________2
2、张大爷去年用长2米宽1米的长方形苇席围成容积最大的圆柱形粮囤.今年改用长3米宽2米的长方形苇席围成容积最大的圆柱形的粮囤.问:今年粮囤的容积是去年粮囤容积的多少倍?
3、有30个边长为1m的正方体,在地面摆成如图所示的形式,然后把露出的表面涂成红色,问涂成红色的表面积是多少?
4、如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水
升.
5、如右图,一个正方体形状的木块,棱长l米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么,这60块长方体表面积的?
和是多少平方米
6、右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)。
