递推最小二乘辨识概要
递推最小二乘法原理

递推最小二乘法原理递推最小二乘法(Recursive Least Squares, 简称RLS)是一种经典的参数估计方法,广泛应用于信号处理、通信系统、自适应滤波等领域。
它通过不断迭代更新参数,逐步逼近最优解,具有快速收敛、适应性强的特点。
本文将从最小二乘法出发,介绍递推最小二乘法的原理及其应用。
最小二乘法(Least Squares)是一种常见的参数估计方法,用于寻找一组参数,使得模型预测值与观测值之间的误差平方和最小。
对于线性模型,最小二乘法可以通过求解正规方程或者利用矩阵运算的方式得到最优参数。
然而,在实际应用中,数据通常是逐步到来的,因此需要一种能够动态更新参数的方法,于是递推最小二乘法应运而生。
递推最小二乘法的基本原理是利用递推的方式不断更新参数,以逼近最优解。
在每一时刻,根据当前的观测数据和先前的参数估计,通过递推公式计算出新的参数估计值,从而实现参数的动态更新。
这样的方法不仅能够适应数据的动态变化,还能够实现快速的收敛,适用于实时系统和非平稳环境下的参数估计。
递推最小二乘法的核心思想是利用指数加权的方式对历史数据进行处理,赋予近期数据更大的权重,从而更好地适应数据的变化。
通过引入遗忘因子(Forgetting Factor),可以控制历史数据对参数估计的影响程度,使得算法更具灵活性和适应性。
同时,递推最小二乘法还可以结合正交分解等技术,进一步提高计算效率和数值稳定性。
在实际应用中,递推最小二乘法被广泛应用于自适应滤波、信道均衡、系统辨识等领域。
例如,在自适应滤波中,递推最小二乘法可以根据接收信号的实际情况,动态调整滤波器的参数,实现信号的实时去噪和增强。
在通信系统中,递推最小二乘法可以用于自适应调制解调器的设计,提高系统的抗干扰能力和适应性。
此外,递推最小二乘法还被广泛应用于雷达跟踪、无线定位等领域,发挥着重要作用。
总之,递推最小二乘法作为一种经典的参数估计方法,具有快速收敛、适应性强的特点,在信号处理、通信系统、自适应滤波等领域有着重要的应用。
遗忘因子递推最小二乘法辨识rc电路

遗忘因子递推最小二乘法辨识rc电路遗忘因子递推最小二乘法(Recursive Least Squares,简称RLS)是一种用于参数辨识的方法,主要针对线性时变系统的辨识问题。
在本文中,我们将探讨如何使用RLS方法辨识RC电路。
首先,我们需要了解什么是RC电路。
RC电路由一个电阻和一个电容组成,其工作原理是通过电阻阻碍电流的流动,而电容则储存电荷。
RC电路可以用于滤波器、积分器等应用中。
在辨识RC电路时,我们可以将其视为一个一阶系统,其传递函数可以表示为:H(s) = 1 / (RCs + 1)其中,s是频率,RC是电阻和电容的乘积。
我们的目标是辨识出RC的值。
接下来,我们将介绍如何使用RLS方法辨识RC电路的参数。
首先,我们需要采集一些输入-输出数据对。
我们可以通过施加不同的输入信号,并记录输出信号来获取这些数据对。
这些输入信号可以是脉冲信号、阶跃信号或正弦信号等。
设输入信号为u(t),输出信号为y(t),则我们可以得到如下的离散模型:y(k) = wT(k) · x(k)其中,y(k)是第k个采样点的输出,w(k)是待辨识的参数向量,x(k)是输入-输出数据对构成的特征向量。
在训练过程中,我们需要定义一个递归的更新规则来更新参数向量w(k)。
这里,我们引入遗忘因子λ,用于控制历史数据对参数的影响程度。
遗忘因子的取值范围为0到1之间,较大的值表示较快的遗忘,较小的值表示较慢的遗忘。
参数向量的更新公式如下:w(k) = w(k-1) + P(k-1) · x(k) · e(k)其中,P(k-1)是协方差矩阵,它与遗忘因子有关,可以通过递推方式得到:P(k) = 1/λ · (P(k-1) - P(k-1) · x(k) · x(k)T · P(k-1) / (λ + x(k)T · P(k-1) · x(k)))e(k)是输出误差,可以通过以下方式计算:e(k) = y(k) - wT(k-1) · x(k)以上就是使用遗忘因子递推最小二乘法辨识RC电路的基本原理和公式。
递推最小二乘法_协方差矩阵_概述说明以及解释

递推最小二乘法协方差矩阵概述说明以及解释1. 引言1.1 概述在统计学和计量经济学中,递推最小二乘法(Recursive Least Squares,简称RLS)是一种常用的参数估计方法。
它通过不断更新样本数据进行参数的估计,并且可以适用于非静态数据场景。
协方差矩阵是统计分析中重要的概念,它描述了变量之间的线性关系强度和方向,并且在许多领域具有广泛应用。
1.2 文章结构本文首先介绍递推最小二乘法的定义和原理,在此基础上详细解释算法的步骤以及其应用领域。
接着,我们将引入协方差矩阵的概念并介绍其计算方法,同时探讨了它在实际问题中所起到的作用和应用场景。
最后,我们将对递推最小二乘法与协方差矩阵之间的关系进行解释,并通过实例分析来说明它们如何相互影响。
1.3 目的本文旨在全面介绍递推最小二乘法和协方差矩阵,并深入探讨它们之间的联系。
通过对这两个概念及其应用的理解,我们可以更好地理解参数估计方法和变量间关系的描述与分析。
此外,我们还将展望相关领域未来可能的研究方向,以促进学术和实践的进一步发展。
2. 递推最小二乘法2.1 定义和原理:递推最小二乘法是一种用于估计线性模型参数的方法。
它可以通过历史数据的不断更新来逐步拟合模型,以使得估计值与观测值之间的误差达到最小化。
该方法可以被形式化地描述为以下步骤:1. 初始化模型参数的初始值。
2. 从历史数据中选择一个样本,并使用当前参数估计出该样本对应的输出值。
3. 计算该样本的预测误差。
4. 根据预测误差对参数进行调整,使得预测误差尽量减小。
5. 重复步骤2至4,直到所有样本都被处理过一遍,或者满足终止条件。
递推最小二乘法是基于最小二乘原理,即将真实观测值与模型预测值之间的差异平方求和并最小化这个目标函数。
通过迭代地更新参数,递推最小二乘法可以逐渐优化模型,并获得更准确的参数估计。
2.2 算法步骤:具体而言,在每次迭代中,递推最小二乘法按照以下步骤进行操作:1. 根据历史数据选择一个样本,并根据当前的参数估计出预测值。
递推阻尼最小二乘法辨识算法公式的详细推导与说明

控制理论与控制工程学位课程《系统辨识》考试报告递推阻尼最小二乘法公式详细推导专业:控制理论与控制工程班级:2011双控(研)学生姓名:江南学号:20110201016任课教师:蔡启仲老师2012年06月29 日摘要在参数辨识中,递推最小二乘法是用得最多的一种算法。
但是,最小二乘法存在一些缺点,如随着协方差矩阵的减小,易产生参数爆发现象;参数向量和协方差矩阵的处置选择不当会使得辨识过程在参数收敛之前结束;在存在随机噪声的情况下,参数易产生漂移,出现不稳定等。
为了防止参数爆发现象,Levenberg 提出在参数优化算法中增加一个阻尼项,以增加算法的稳定性。
本文在一般的最小二乘法中增加了阻尼因子,构成了阻尼最小二乘法。
又根据实时控制的要求,详细推到了递推阻尼最小二乘公式,实现在线辨识。
关键字:系统辨识,最小二乘法,递推算法正文1.题目的基本要求已知单入单出系统的差分方程以及噪声,在应用最小二乘法进行辨识的时候,在性能指标中加入阻尼因子,详细推导阻尼最小二乘法的递推公式。
2.输入辨识信号和系统噪声的产生方法和理论依据 2.1系统辩识信号输入选择准则(1)输入信号的功率或副度不宜过大,以免使系统工作在非线性区,但也不应过小,以致信噪比太小,直接影响辩识精度;(2)输入信号对系统的“净扰动”要小,即应使正负向扰动机会几乎均等; (3)工程上要便于实现,成本低。
2.2白噪声及其产生方法 (1) 白噪声过程(2)白噪声是一种均值为0、谱密度为非0常数的平稳随机过程。
(3)白噪声过程定义:如果随机过程()t ω的均值为0,自相关函数为()()2R t t ωσδ= (2.2.1)式中()t δ 为狄拉克(Dirac) 分布函数,即(){(),00,01t t t dt δδ∞∞=≠∞==⎰-且t (2.2.2)则称该随机过程为白燥声过程。
2.3白噪声序列 (1) 定义 如果随机序列{()}w t 均值为0,并且是两两不相关的,对应的自相关函数为()2,0,1,2w l R l l σδ==±± 式中{1,00,0l l l δ=≠=则称这种随机序列{()}w t 为白噪声序列。
递推的最小二乘法

式中
….(2)
W (N ) 0 W ( N 1) ................ ( N 1) 0
.
0 ,其中 为很大的正实数(比如1010) .
(N ) ( N 1) ........... T ( N 1)
( N , ) ( N 1, ) ........... e ( N 1, )
T ( N 1) y( N ) y( N 1) ... y( N n 1) u( N ) u( N 1) ... u( N n 1)
1、递推的最小二乘法基本思想:
• 本次(新)的估计值
(k )
=上次(老)的估计值
(k 1)
+修正项
•
可以观察随着时间的推移,新的输入、输出信息不断增加的情况下,参数估计的变化情况,特别适用于 在线实时辨识。
设原先得到的参数估计用 WLS ( N ) 表示,则
WLS ( N ) ( T ( N )W ( N ) ( N )) 1 T ( N )W ( N )Y ( N )
从
WLS ( N )
到
WLS ( N 1)
的递推公式过程(略P191)
递推公式:
T ★ ① WLS ( N 1) WLS ( N ) L( N 1) y ( N 1) ( N 1) WLS ( N ) ② L( N 1) P( N 1) ( N 1) ( N 1)
几种最小二乘法递推算法的小结

几种最小二乘法递推算法的小结最小二乘法是一种常见的参数估计方法,广泛应用于各个领域的数学和统计模型的拟合问题。
在实际应用中,我们常常需要递推地计算最小二乘法的结果,以便能够在实时数据到来的情况下,快速地更新参数估计值。
以下是几种常见的最小二乘法递推算法的小结。
1. 递推最小二乘法(Recursive least squares, RLS)递推最小二乘法是一种在线参数估计方法,可以在每次新数据到来时,快速地更新参数估计值。
RLS算法利用递推的方式,将历史数据和新数据的信息结合起来,从而得到最新的参数估计值。
该算法基于递归迭代过程,迭代公式中的权重矩阵可以由历史数据的协方差矩阵递推得到。
递推最小二乘法具有良好的收敛性和较低的计算复杂度。
2.递推最小二乘法的变种算法(RLS的变种算法)递推最小二乘法的变种算法是对传统的RLS算法进行改进和优化的方法。
其中,经典的改进算法有递归正交最小二乘法(Recursive orthogonal least squares, ROLS)和递推快速QR分解法(Recursive fast QR factorization, RFQR)。
ROLS算法通过引入正交化处理,解决了经典RLS算法中信号相关性较高时,参数估计不稳定的问题。
RFQR算法则通过对历史数据进行快速QR分解的方法,进一步提高了算法的计算速度,并降低了计算复杂度。
3. 渐进最小二乘法(Asymptotic least squares, ALS)渐进最小二乘法是一种常见的在线参数估计算法,用于解决参数估计问题的收敛速度较慢的情况。
ALS算法通过估计参数的渐进协方差矩阵,然后利用资料增益矩阵计算最新的参数估计值。
由于ALS算法不需要存储和计算全部历史数据的相关矩阵,因此可以在实时数据到来的情况下,快速地进行参数估计。
4. 数据辅助递推最小二乘法(Data-augmented recursive least squares, DARLS)数据辅助递推最小二乘法是一种常见的递推最小二乘法的改进算法,适用于当历史数据缺失或者不完整时。
递推最小二乘估计

当C=I 时, [A+BD]-1 = A-1 -A-1B[I +DA-1B]-1DA-1
理论。 • 高斯仅用1小时就算出了谷神星的
轨道形状,并进行了预测
•1794年,高斯提出了最小二乘的思想。
1:引言
最小二乘法(Least Square)Gauss 1795年提出 在预测卫星和彗星运动的轨道时,需要处理由望远镜获得的观测数 据,以估计天体运动的六个参数。
Gauss在《天体运动理论》一书中写道:“未知量的最大概值是这 样的数值,它使各实测值与计算值之差的平方乘以度量其精度的数 值后,所得的和值达到最小。” ——著名的最小二乘思想 在系统辨识中,LS已成功应用于系统参数估计。 在自校正控制中,LS是应用最广泛的算法之一。
2:原理
2:原理
2:原理
2:原理
2:原理
3:特点
3:特点
(1):无需存储全部数据,取得一组观测数据便 可估计一次参数,而且都能在一个采样周期中完 成,所需计算量小,占用的存储空间小。
(2):具有一定的实时处理能力
谢谢
递推最小二乘估计(RLS)
董博南
一:最小二乘法回顾
二:递推最小二乘估计
一:最小二乘法回顾
1:引言 2:原理
3:特点
1:引言
• 1801年初,天文学家皮亚齐发现了谷神星。
•1801年末,天文爱好者奥博斯,在高斯预 言的时间里,再次发现谷神星。 •1802年又成功地预测了智神星的轨道。
递推最小二乘法原理

递推最小二乘法原理递推最小二乘法(Recursive Least Squares, 简称RLS)是一种经典的自适应滤波算法,它在信号处理、通信系统、控制系统等领域得到了广泛的应用。
本文将介绍递推最小二乘法的原理及其在实际应用中的一些特点。
首先,让我们来了解一下最小二乘法。
最小二乘法是一种数学优化方法,用于寻找一组参数,使得给定的模型与观测数据之间的误差平方和最小。
在线性回归问题中,最小二乘法可以用来拟合一个线性模型,以最小化观测数据与模型预测值之间的差异。
最小二乘法的基本思想是通过最小化误差的平方和来寻找最优的参数。
递推最小二乘法是最小二乘法的一种变种,它的特点在于可以实时地更新参数估计,适用于需要动态调整的系统。
在实际应用中,由于系统参数可能随时间变化,传统的最小二乘法在每次参数更新时都需要重新计算整个数据集,计算复杂度较高,不适合实时性要求高的场景。
而递推最小二乘法则可以通过递推的方式,实时地更新参数估计,适用于动态环境下的参数估计问题。
递推最小二乘法的原理可以用数学公式来描述。
假设我们有一个线性模型,\[y_k = \theta^T x_k + e_k\]其中\(y_k\)是观测数据,\(x_k\)是输入向量,\(\theta\)是待估计的参数,\(e_k\)是噪声。
我们的目标是通过观测数据\(y_k\)和输入向量\(x_k\)来估计参数\(\theta\)。
递推最小二乘法的核心思想是通过递推的方式,实时地更新参数\(\theta\)的估计值。
具体来说,我们可以通过以下递推公式来更新参数\(\theta\)的估计值,\[\theta_k =\theta_{k-1} + \frac{P_{k-1}x_k}{1 + x_k^T P_{k-1} x_k}(y_k x_k^T \theta_{k-1})\]其中\(\theta_k\)是第\(k\)次的参数估计值,\(\theta_{k-1}\)是第\(k-1\)次的参数估计值,\(P_{k-1}\)是第\(k-1\)次的参数估计误差的协方差矩阵。
递归最小二乘法辨识参数

递归最小二乘法辨识参数递归最小二乘法(Recursive Least Squares, RLS)是一种参数辨识方法,它使用递归算法来求解最小二乘法中的参数。
在许多领域中,例如系统辨识、自适应控制、信号处理等,递归最小二乘法都是一个广泛使用的方法。
递归最小二乘法的基本思想是:通过递归迭代来更新参数估计值,使其逼近最优解。
在递归过程中,每一次迭代时,都会通过当前的测量值来更新参数的估计值,同时保留历史测量值的影响,从而获得更精确的估计值。
具体地说,在递归过程中,首先需要定义一个初始参数向量,然后通过观测数据序列来递归更新参数向量。
假设有一个如下所示的线性关系:y(k) = Φ(k) * θ + v(k)其中,y(k)是被观测到的输出值,Φ(k)是与该输出值相关的输入向量,θ是待辨识的参数向量,v(k)是误差项。
递归最小二乘法的目标就是通过观测数据来估计θ的值。
在递归最小二乘法中,首先需要定义一个初始的参数向量θ0,然后通过数据序列递归地更新θ的值。
每一次迭代时,都会用最新的观测数据来更新参数向量,使得估计值更接近真实值。
具体来说,每次观测到新的数据之后,都会根据当前参数估计值和新的观测值来计算估计误差,并更新参数向量。
具体的迭代步骤如下:1.从数据序列中读取观测值y(k)和输入向量Φ(k);2.计算估计值y(k)hat和估计误差e(k):y(k)hat = Φ(k) * θ(k-1)e(k) = y(k) - y(k)hat3.计算卡尔曼增益K(k)和参数估计值θ(k):K(k) = P(k-1) * Φ(k) / (λ + Φ(k)' * P(k-1) * Φ(k))θ(k) = θ(k-1) + K(k) * e(k)其中,P(k-1)是先前迭代步骤中的误差协方差矩阵,λ是一个小的正数,用于确保逆矩阵的存在性。
需要注意的是,递归最小二乘法的计算量相对较大,因此通常需要对算法进行优化,以提高计算效率和精度。
最小二乘参数辨识方法及原理

N N N N R i t i2 R i t i t i i 1 i 1 i 1 a i 1 ˆ 2 N N 2 N ti ti i 1 i 1 N N N N Ri t i Ri t i i 1 i 1 b i 1 ˆ 2 N N 2 N ti ti i 1 i 1
i 1
i
Ri |2
最小 测量误差的平方和最小
2.1 利用最小二乘法求模型参数
根据最小二乘的准则有
J min v i2
i 1 N
[ Ri ( a bt i )] 2
i 1
N
根据求极值的方法,对上式求导
N J 2 ( R i a bt i ) 0 a i 1 ˆ aa N J 2 ( R i a bt i )t i 0 b b bˆ i 1
n
y ( k ) a i y ( k i ) bi u ( k i )
i 1 i 1
2.2 一般最小二乘法原理及算法
v (k ) u (k ) G (z ) y (k ) z (k )
图 3.4 SISO 系统的“黑箱”结构
若考虑被辨识系统或观测信息中含有噪声
T
a1 a n b1 bn
V m v (1)
v ( 2) v ( m )
T
Z m H m V m
2.2 一般最小二乘法原理及算法
最小二乘的思想就是寻找一个 的估计值 ˆ ,使得各次测量
ˆ 的 Z i (i 1, m ) 与由估计 ˆ 确定的量测估计 Z i H iˆ 之差的平方
递推最小二乘法

递推最小二乘法递推最小二乘法是一种避免精度损失的迭代计算方法,在最小二乘法的基础上加以改进,主要用于拟合复杂的数据,解决拟合时出现精度下降问题。
一、什么是递推最小二乘法递推最小二乘法是一种迭代计算方法,利用多项式曲线拟合曲线数据,对于某个曲线,只需要实施最小二乘法的迭代计算,而不需要考虑精度的损失。
递推最小二乘法的主要工作是根据给定的拟合曲线,把它拟合到数据集中,从而使数据集距离拟合曲线最小。
二、递推最小二乘法的原理递推最小二乘法的核心原理是,利用多项式拟合曲线,按照“最小二乘法”的原理,以当前拟合曲线为参照,不断进行前进和后退,以达到拟合曲线将数据集中的数据最佳拟合的目的。
这个最佳拟合目标就是实现拟合曲线与数据集之间的最小误差,其中,最小误差就是拟合曲线与实际数据集之间的最小差值。
递推最小二乘法的实现方式主要有两种,一种是基于递推的方式,另一种是基于函数的方式。
前者大致的实现方法是:先计算出多项式拟合曲线的每一个系数,然后再利用这些系数计算出多项式拟合曲线的最终拟合曲线,最后比较拟合曲线与实际数据集之间的实际差异,根据差异再调整系数,不断循环,直到最后拟合曲线与实际数据集之间的实际差异达到预期值为止。
函数的实现方式也很类似,只是在计算过程中,会使用函数的方式,将拟合曲线的系数表示为函数的形式,然后再比较拟合曲线与实际数据集之间的实际差异,根据差异再调整函数系数,最后实现拟合曲线与实际数据集之间的最小差异。
三、应用递推最小二乘法在实际应用中可以用来拟合复杂的数据曲线,以求得更好的拟合效果,解决拟合时出现精度下降问题。
它具有计算量小、运算简单、拟合结果较好的优点,因此在实际应用中得到了广泛的使用,比如在众多植物物种的遗传分析中,用递推最小二乘法来拟合植物的遗传规律,以获得更准确的估计结果;在探测地球大气层时,也可以用最小二乘法来拟合大气层中的湿度数据,以获取更加准确的湿度数据;在搜索引擎中,对查询结果也可以用最小二乘法拟合出来,以获得更准确的查询结果等等。
递推最小二乘法

递推最小二乘法递推最小二乘法是用于拟合函数的一种最广泛和有效的方法。
递推最小二乘法(RecursiveLeastSquares,RLS)是针对给定样本进行线性拟合的一种机器学习算法,它在求解具有最小均方差的最优参数时用于模型的更新。
递推最小二乘法以更新参数的方式估计参数,从而将当前参数和新数据结合起来。
它可以用来求解给定样本具有最小平均方差的最优参数表达式,以解决传统最小二乘法的计算开销大的问题。
递推最小二乘法的基本原理是求解通过要拟合的数据图形的几何图案的最小二乘参数,并逐渐拟合出数据图形的最小二乘参数。
它使用一种迭代计算的方法,用新的样本点替换旧的样本点,以不断更新拟合函数参数。
该方法有利于跟踪变化快的参数。
递推最小二乘法的思想很简单:从给定的样本中求出最小二乘拟合参数,并以迭代和递推的方式求解最优拟合参数,不断地更新最小二乘拟合参数,以达到拟合数据的最优状态。
此外,递推最小二乘法也可以利用状态空间表示来改进拟合性能,尤其是在模型存在时滞性和高阶非线性性质时,能更好地拟合函数从而获得更详细的函数图形。
在应用递推最小二乘法时,我们需要注意它存在的一些局限性。
首先,它要求拟合的模型必须是线性的,这意味着参数的变化关系必须是线性的。
其次,它的迭代方式容易出现收敛速度慢的问题。
在实际应用中,一般用共轭梯度法或牛顿法加速收敛速度。
最后,它只能处理维度为n的数据,而不能处理大规模的数据。
因此,在实际应用中,在使用递推最小二乘法之前,需要结合其他方法,以减少数据维度,从而提高计算效率。
总之,递推最小二乘法是一种应用广泛、计算量小、拟合效果好的数据拟合算法,它主要用于模型参数在时间上有变化,并且有高阶非线性特性时,拟合函数参数的更新。
由于这种算法的收敛速度慢,因此,在实际应用中,一般要结合其他方法或技术进行优化,以进一步提高拟合的准确性和稳定性。
递推最小二乘估计及模型阶次辨识
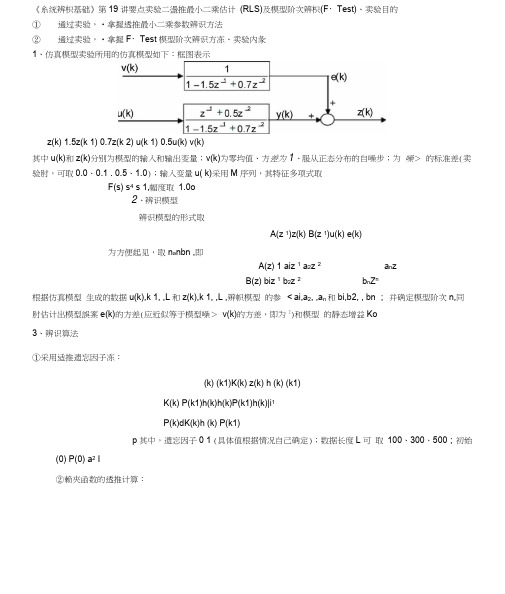
《糸统辨枳基础》第19讲要点卖验二盪推最小二乘估计(RLS)及模型阶次辨枳(F・Test)、卖验目的①通过卖验,•拿握透推最小二乘参数辨识方法②通过卖验,•拿握F・Test模型阶次辨识方冻、卖验内彖1、仿真模型卖验所用的仿真模型如下:框图表示z(k) 1.5z(k 1) 0.7z(k 2) u(k 1) 0.5u(k) v(k)其中u(k)和z(k)分别为模型的输入和输出变量;v(k)为零均值、方差为1、服从正态分布的自噪步;为噪>的标准差(卖验肘,可取0.0、0.1 . 0.5、1.0);输入变量u( k)采用M序列,其特征多项式取F(s) s4 s 1,幅度取1.0o2、辨识模型辨识模型的形式取A(z 1)z(k) B(z 1)u(k) e(k)为方便起见,取n a nbn ,即A(z) 1 aiz 1 a2z 2a n zB(z) biz 1 b2z 2b n Z n根据仿真模型生成的数据u(k),k 1, ,L和z(k),k 1, ,L ,辨帜模型的参<ai,a2, ,a n和bi,b2, , bn ;并确定模型阶次n,同肘估计出模型誤案e(k)的方差(应近似等于模型噪>v(k)的方差,即为2)和模型的静态增益Ko3、辨识算法①采用适推遗忘因子冻:(k) (k1)K(k) z(k) h (k) (k1)K(k) P(k1)h(k)h(k)P(k1)h(k)|i1P(k)dK(k)h (k) P(k1)p其中,遗忘因子0 1 (具体值根据情况自己确定);数据长度L可取100、300、500;初始(0) P(0) a2 I②赖夾函数的透推计算:J(k)|iJ(k1)z(k)h(k) (k1)2h (k) P(k1)h(k) |44、 F-Test 走阶法统计量tJ(n 1)2t(n,n J J(n)J(n"L2n2~F(2,L2n 2)其中,J ()为相应阶次下的赖夾函数值,L 为所用的数据长度,n 为模型的估计阶次。
递推最小二乘辨识讲解

(2)每增加一次观测量,都必须重新计算φ,()T -1。
(3)如果出现φ列相关,既不满秩的情况, T 为病态矩阵,则不能得到最 小二乘估计值。 *递推最小二乘参数辨识,就是当被辨识的系统在运行时,每取得一次新的观
测数据后,就在前一次估计结果的基础上,利用新引入的观测数据对前次 估计的结果,根据递推算法进行修正,从而递推地得出新的参数估计值。 这样,随着新的观测数据的逐次引入,一次接一次的进行参数计算,直到 参数估计值达到满意的精确程度为止。
P(k -1)(k -1) (k -1)
P
(k
)
I
-
1
(k
- 1) P
(k
-1)
(k
-1)
P
(k
-1)
其中的计算顺序为先计算P(k),然后再计算 θˆ(k) .
(7) (8)
有时,为计算方便并便于理解,上述RLS估计算法又可表示 为
常规最小二乘辨识的递推算法
主要内容
1.思想及原理 2.实例与MATLAB仿真 3.应用
1.递推最小二乘法的思想及原理
1.1递推最小二乘法的引入 *最小二乘法的缺陷 (1)数据量越多,系统参数估计的精度就越高,为了获得满意的辨识结果,
矩阵的阶数 T 常常取得相当大。这样矩阵求逆的计算量很大,存储量
1.2递推算法的思想 * 递推辨识算法的思想可以概括成
新的参数估计值=旧的参数估计值+修正项 即新的递推参数估计值是在旧的递推估计值的基础上而成,
这就是递推的概念. 递推算法不仅可减少计算量和存储量,而且能实现在线
实时辨识. * 递推算法是依时间顺序,每获得一次新的观测数据就修
正一次参数估计值,随着时间的推移,便能获得满意的辨 识结果. RLS法即为成批型LS算法的递推化,即将成批型LS算法
递推阻尼最小二乘法辨识算法公式的详细推导与说明

控制理论与控制工程学位课程《系统辨识》考试报告递推阻尼最小二乘法公式详细推导专业:控制理论与控制工程班级:2011双控(研)学生姓名:江南学号:20110201016任课教师:蔡启仲老师2012年06月29 日摘要在参数辨识中,递推最小二乘法是用得最多的一种算法。
但是,最小二乘法存在一些缺点,如随着协方差矩阵的减小,易产生参数爆发现象;参数向量和协方差矩阵的处置选择不当会使得辨识过程在参数收敛之前结束;在存在随机噪声的情况下,参数易产生漂移,出现不稳定等。
为了防止参数爆发现象,Levenberg 提出在参数优化算法中增加一个阻尼项,以增加算法的稳定性。
本文在一般的最小二乘法中增加了阻尼因子,构成了阻尼最小二乘法。
又根据实时控制的要求,详细推到了递推阻尼最小二乘公式,实现在线辨识。
关键字:系统辨识,最小二乘法,递推算法正文1.题目的基本要求已知单入单出系统的差分方程以及噪声,在应用最小二乘法进行辨识的时候,在性能指标中加入阻尼因子,详细推导阻尼最小二乘法的递推公式。
2.输入辨识信号和系统噪声的产生方法和理论依据 2.1系统辩识信号输入选择准则(1)输入信号的功率或副度不宜过大,以免使系统工作在非线性区,但也不应过小,以致信噪比太小,直接影响辩识精度;(2)输入信号对系统的“净扰动”要小,即应使正负向扰动机会几乎均等; (3)工程上要便于实现,成本低。
2.2白噪声及其产生方法 (1) 白噪声过程(2)白噪声是一种均值为0、谱密度为非0常数的平稳随机过程。
(3)白噪声过程定义:如果随机过程()t ω的均值为0,自相关函数为()()2R t t ωσδ= (2.2.1)式中()t δ 为狄拉克(Dirac) 分布函数,即(){(),00,01t t t dt δδ∞∞=≠∞==⎰-且t (2.2.2)则称该随机过程为白燥声过程。
2.3白噪声序列 (1) 定义 如果随机序列{()}w t 均值为0,并且是两两不相关的,对应的自相关函数为()2,0,1,2w l R l l σδ==±± 式中{1,00,0l l l δ=≠=则称这种随机序列{()}w t 为白噪声序列。
递推最小二乘辨识

ˆ (1) 选取 (0)各元素为零或较小的参数,P(0)=I,其中为 充分大的实数(105~1010);
(2) 先将大于所需辨识的参数个数的L组数据,利用成批 型的LS法求取参数估计值LS和协方差阵P(L),并将这 些量作为递推估计的初值.
y N 1 原 有 信 息 ˆ
N
N 1
ˆ (k ) (ΦΦ )1 ΦY θ k k k k
Yk=[y(1), y(2), ..., y(k)]T=[Yk y(k)]T 1
仔细考察上述LS法,可以知道,该算法进行递推化的关键是算法中的矩 阵求逆的递推计算问题. 因此,下面先讨论该逆矩阵的递推计算.
P(k ) (ΦΦk )-1 k
首先,假定在第k-1次递推中,我们已计算好参数估计值 在第k次递推时,我们已获得新的观测数据向量(k-1)和 y(k),则记 Φ k-1=[(0), (1), ..., (k-2)]T Φ k=[(0), (1), ..., (k-1)]T=[φ (k-1)T φ (k-1)]T Yk-1=[y(1), y(2), ..., y(k-1)]T
1.2递推算法的思想 * 递推辨识算法的思想可以概括成 新的参数估计值=旧的参数估计值+修正项 即新的递推参数估计值是在旧的递推估计值的基础上而成, 这就是递推的概念. 递推算法不仅可减少计算量和存储量,而且能实现在线 实时辨识. * 递推算法是依时间顺序,每获得一次新的观测数据就修 正一次参数估计值,随着时间的推移,便能获得满意的辨 识结果. RLS法即为成批型LS算法的递推化,即将成批型LS算法 化成依时间顺序递推计算即可。 该工作是1950年由Plackett完成的。
将Φ k展开,故有
(2)
P (k ) ([Φ-1 (k -1)][Φ-1 (k -1)] )-1 k k
递推最小二乘法相关辨识方法

z ( k ) + a1 z ( k − 1) + LL + ana z ( k − na ) = b1u ( k − 1) + LL +bnb u ( k − nb ) + e ( k )
l 则系统可表示为
A ( z −1 ) z ( k ) = B ( z −1 ) u ( k ) + A ( z −1 )
l 为了减少计算量,减少数据在计算机中占用的 内存,并实时辨识出系统动态特性,我们常利用最 小二乘法的递推形式。其基本思想可以概括成 ) ) 新的估计值θ ( k ) =旧的估计值θ ( k − 1) +修正项 下面我们来推导递推最小二乘算法的原理。 首先,将最小二乘一次完成算法写为
) −1 T T T θ LS = ( H L H L ) H L zL = P ( L ) H L zL
l 把P(k)写成
利用矩阵反演公式 可得
P (k ) = P
T −1
−1
( k − 1) + h ( k ) h ( k )
T
−1 T −1 −1
−1
( A + CC )
= A − A C ( I + C A C ) C T A −1
−1
−1
T P ( k ) = P ( k − 1) − P ( k − 1) h ( k ) hT ( k ) P ( k − 1) h ( k ) P ( k − 1) h ( k ) + 1
l 设一个时不变SISO线性离散动态系统的数学模 型为 A ( z −1 ) z ( k ) = B ( z −1 ) u ( k ) + e ( k ) 假设模型的阶次已经设定,且一般有na ≥ nb 。将模型 写成最小二乘形式
递推最小二乘辨识

实验4 递推最小二乘法的实现实验报告哈尔滨工业大学航天学院控制科学与工程系专业:自动化班级:1040101姓名:日期:2013 年10 月23 日1.实验题目: 递推最小二乘法的实现 2.实验目的:(n a y k -()(n b u k n ξ+-+,,n a ,0,n b b 为待辨识的未知参数,(k ξ为系统的输出,为系统的输入。
分别测出n N +个输出、(3),(),(1),(2),()y y n N u u u n N ++,则可写出矩阵形式,有0()(1)(1)(1)((1)(2)(2)(2)((1)()()()(n n y n y u n u n a y n y u n u n b y n N y N u n N u N n b ξξξ⎢⎥--+⎤⎡⎤⎡⎢⎥⎢⎥⎢⎢⎥-+-+⎢⎥⎢+⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥-+--+⎣⎦⎣⎢⎥⎢⎥⎣⎦(2)101)(1),,()()n n a n a b y n N n N b ξξθξξ⎡⎤⎢⎥++⎤⎡⎤⎢⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦,()(1)(1)(1)(1)(2)(2)(2)1)()()()y n y u n u n y u n u N y N u n N u N -+⎤⎥+-+⎥⎥⎥+--+⎦y θξ=Φ+ (维输出向量;ξ为N 维噪声向量;θ为21n +维参数向量;Φ测量矩阵。
为了尽量减小噪声ξ对θ估值的影响,应取2N n >+()T θ=ΦΦ为了实现实时控制,必须采用递推算法,这种辨识方法主要用于在线辨设已获得的观测数据长度为N ,将式N N Y θ=ΦN θ表示θ的最小二乘估计,则(TN Nθ=ΦΦ(T N N P =ΦΦT N N N P θ=Φ如果再获得一组新的观测值(u n N +11TN ψθ++=+(1),n N ++](1)(1)(1)y N u n N u N -++++)合并,并写成分块矩阵形式,可得T 111N N N N N Y y ξθξψ+++⎡⎤Φ⎡⎤⎤⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(9)于是,类似地可得到新的参数估值1T T1T T T 1111N NN N N N N N N Y y θψψψ-+++++⎧⎫⎡⎤⎡⎤⎡⎤ΦΦΦ⎡⎪⎪⎢⎥⎢⎥⎢⎥⎪⎪⎢⎥=⎨⎬⎢⎥⎢⎥⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎪⎪⎩⎭ )T1T 1111N N N N N T N N N N Y P y Y y ψψ+++++⎡⎤Φ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦Φ+)T T 111T 11N NN N N N N ψψψψ++-++⎪⎢⎥⎢⎥⎪⎬⎢⎥⎢⎥⎪⎢⎥⎢⎥⎣⎦⎣⎦⎪⎭+ )1T 11N N ψ-++ 与P 的递推关系式出发,导,最终可求得递推最小二乘法辨识公式:()T1111N N N N N N K y θθψθ++++=+- ()1T 11111N N N N N N K P P ψψψ-++++=+ ()1T T 11111N N N N N N N N P P P P ψψψψ-++++=-+ 为了进行递推计算,需要给出N P 和N θ的初值0P 和0θ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N 1
输 出 信 息
PN
递推最小二乘 参数估计算法
PN 1
开始 产生输入数据u和 输出数据z
初始化P(0)、θ(0)、w和ε
计算P(k),θ(k)和K(k)
(k 1) (k )
P(k 1) P(k )
否
max
i
ˆ (k ) ˆ ( k 1) i i ˆ ( k 1) i
D. 数据饱和
在辨识递推计算过程中,协方差矩阵P(k)随着递推的进程将衰减 很快,此时算法的增益矩阵K(k)也急剧衰减,使得新数据失去对参 数估计值的修正能力. 这种现象称为数据饱和. 因此需要考虑修正方案,以保持新数据对参数估计值的一定的 修正能力,使得能得到更准确的参数估计值,或能适应对慢时 变参数的辨识.
P(k ) [ P -1 (k -1) (k -1) (k -1)]-1
(3)
由式(3)和矩阵反演公式(4),可得P(k)的如下递推计算式
P (k ) P (k - 1) - P (k - 1) (k - 1)[1 (k - 1) P (k - 1) (k - 1)] 1 (k - 1) P (k - 1) P (k - 1) (k - 1) (k - 1) I P ( k - 1) 1 (k - 1) P (k - 1) (k - 1) (5)
选择如下的辨识模型进行递推最小二乘参数辨识。
z(k ) a1 z(k 1) a2 z(k 2) b1u(k 1) b2u(k 2) V (k )
Matlab 程序: %最小二乘的递推算法 %Z(k+2)=1.5*Z(k+1)-0.7*Z(k)+u(k+1)+0.5*u(k)+v(k) %======================================== clear clc %==========400 个产生M 序列作为输入=============== x=[0 1 0 1 1 0 1 1 1]; %initial value n=403; %n 为脉冲数目 M=[]; %存放M 序列 for i=1:n temp=xor(x(4),x(9)); M(i)=x(9); for j=9:-1:2 x(j)=x(j-1); end x(1)=temp; end %===========产生均值为0,方差为1 的高斯白噪声========= v=randn(1,400); %==============产生观测序列z=================
其中K(k)称为增益向量;令
ቤተ መጻሕፍቲ ባይዱ
ˆ (k -1), 表示基于 ˆ (k ) (k -1)θ y k-1时刻的历史数据对y(k)的预报值。 上述算法的计算顺序为
先计算K(k-1),
ˆ (k )和P(k-1). 然后再分别计算 θ
综上所述,RLS法的基本计算步骤可总结如下: 1. 确定被辨识系统模型的结构,以及多项式A(z-1)和B(z-1)的 阶次; ˆ(0),P(0); 2. 设定递推参数初值 3. 采样获取新的观测数据 y(k)和u(k),并组成观测数据向量 (k-1); 4. 用式(7)~(8)或(9)~(11)所示的RLS法计算当前参数递推估 ˆ(k ); 计值 5. 采样次数k加1,然后转回到第3步骤继续循环.
*下面讨论无加权因素时的一般LS法的递推算法的推导. 即将成批型算法化等效变换成如下所示的随时间演变递推 算法. 时不变SISO系统数学模型:A(z-1)y(k)=B(z-1)u(k)+e(k)
A( z ) 1 ai z
1 i 1
na
i
B( z ) bi z
1 i 1
ˆ(0)各元素为零或较小的参数,P(0)=I,其中为 (1) 选取 充分大的实数(105~1010);
(2) 先将大于所需辨识的参数个数的 L组数据 ,利用成批 型的LS法求取参数估计值LS和协方差阵P(L),并将这 些量作为递推估计的初值.
y N 1 原 有 信 息 ˆ
N
N 1
1 ˆ θ(k ) (Φk Φk ) Φk Yk
T Yk=[y(1), y(2), ..., y(k)]T=[Yk y ( k )] 1
仔细考察上述LS法,可以知道,该算法进行递推化的关键是算法中的矩 阵求逆的递推计算问题. 因此,下面先讨论该逆矩阵的递推计算.
-1 P(k ) (Φ Φ ) k k
ˆ (k ) . 其中的计算顺序为先计算P(k),然后再计算 θ
有时,为计算方便并便于理解,上述RLS估计算法又可表示 为
ˆ (k ) θ ˆ (k - 1) K (k )[ y (k ) - (k - 1)θ ˆ (k - 1)] θ P (k ) [ I - K (k ) (k - 1)]P (k - 1) P (k - 1) (k - 1) K (k ) 1 (k - 1) P (k - 1) (k - 1) (9) (10) (11)
1.2递推算法的思想 * 递推辨识算法的思想可以概括成 新的参数估计值=旧的参数估计值+修正项 即新的递推参数估计值是在旧的递推估计值的基础上而成, 这就是递推的概念. 递推算法不仅可减少计算量和存储量,而且能实现在线 实时辨识. * 递推算法是依时间顺序,每获得一次新的观测数据就修 正一次参数估计值,随着时间的推移,便能获得满意的辨 识结果. RLS法即为成批型LS算法的递推化,即将成批型LS算法 化成依时间顺序递推计算即可。 该工作是1950年由Plackett完成的。
nb
i
已知系统的输入u(k)和输出y(k),求参数ai,bi的估计值。 可以得到向量形式的线性方程组: Y=+e Y=[y(1), y(2), ..., y(L)]T =[(0), (1), ..., (L-1)]T,
(k - 1) [ y (k - 1), , y (k - na ) u (k - 1), , u (k - nb )]
2.递推最小二乘法实例与仿真
例:采用递推最小二乘估计辨识模型参数
z(k ) 1.5z(k 1) 0.7 z(k 2) u(k 1) 0.5u(k 2) V (k )
式中,V (k ) 是服从正态分布的白噪声 N (0,1) 。输入信号采 用 4 阶 M 序列,其幅值为 1。
ˆ (k -1) P(k ) (k -1)[ y(k ) - (k -1)θ ˆ (k -1)] θ
(6)
利用公式P(k)=[P-1(k-1)+(k-1)T(k-1)]-1
将式(5)和(6)整理可得如下RLS估计算法表示
ˆ (k ) θ ˆ (k - 1) P (k ) (k - 1)[ y (k ) - (k - 1)θ ˆ (k - 1)] θ P (k - 1) (k - 1) (k - 1) P (k ) I P (k - 1) 1 (k - 1) P (k - 1) (k - 1) (7) (8)
常规最小二乘辨识的递推算法
主要内容
1.思想及原理 2.实例与MATLAB仿真 3.应用
1.递推最小二乘法的思想及原理
1.1递推最小二乘法的引入 *最小二乘法的缺陷 (1)数据量越多,系统参数估计的精度就越高,为了获得满意的辨识结果, T 矩阵的阶数 常常取得相当大。这样矩阵求逆的计算量很大,存储量 也很大。 T (2)每增加一次观测量,都必须重新计算φ,( )-1。 T 为病态矩阵,则不能得到最 (3)如果出现φ列相关,既不满秩的情况, 小二乘估计值。 *递推最小二乘参数辨识,就是当被辨识的系统在运行时,每取得一次新的观 测数据后,就在前一次估计结果的基础上,利用新引入的观测数据对前次 估计的结果,根据递推算法进行修正,从而递推地得出新的参数估计值。 这样,随着新的观测数据的逐次引入,一次接一次的进行参数计算,直到 参数估计值达到满意的精确程度为止。
(2)
将Φ k展开,故有
-1 P (k ) ([Φ ( k 1 )][ Φ ( k 1 )] ) k -1 k -1
-1 [Φ Φ ( k 1 ) ( k 1 )] k -1 k -1
[ P -1 (k -1) (k -1) (k -1)]-1
首先,假定在第k-1次递推中,我们已计算好参数估计值 在第k次递推时,我们已获得新的观测数据向量(k-1)和 y(k),则记 Φ k-1=[(0), (1), ..., (k-2)]T Φ k=[(0), (1), ..., (k-1)]T=[φ (k-1)T φ (k-1)]T Yk-1=[y(1), y(2), ..., y(k-1)]T
否
是
kL
是
结束
B. LS法和RLS法的比较
LS法和RLS法的比较 LS法是一次完成算法,适于离线辩识,要记忆全部测量数据, 程序长; RLS法是递推算法,适于在线辩识和时变过程, 需要记忆的 数据少,程序简单; RLS法用粗糙初值时,如若N(即样本数少)较小时,估计精度 不如LS法.
C. 信号充分丰富与系统充分激励
对于所有学习系统与自适应系统,信号充分丰富(系统充分 激励)是非常重要的. 若系统没有充分激励,则学习系统与自适应系统就不能 一致收敛. 不一致收敛则意味着所建模型存在未建模动态或模 型误差较大,这对模型的应用带来巨大隐患. 如对自适应控制,未建模动态可能导致系统崩溃. 为保证学习系统与自适应系统一致收敛,则所产生的系 统的学习样本数据(系统输入输出信号)应具有尽可能多 的模态,其频带要足够宽,而且其信号强度不能以指数律 衰减.这样才能保证系统具有充分激励,所测取的信号数 据是充分丰富的,相关性矩阵P(k)不为病态.
(3)
为便于逆矩阵递推算式的推导,下面引入如下矩阵反演公 式(设A和C为可逆方阵) (A+BCD)-1=A-1-A-1B(C-1+DA-1B)-1DA-1 (4) 该公式可以证明如下:由于 (A+BCD)[A-1-A-1B(C-1+DA-1B)-1DA-1] =I-B(C-1+DA-1B)-1DA-1+BCDA-1 -BCDA-1B(C-1+DA-1B)-1DA-1 =I-B[I-C(C-1+DA-1B)+CDA-1B](C-1+DA-1B)-1DA-1 =I 因此,矩阵反演公式(4)成立.
