刚体的简单运动
合集下载
第7章刚体的简单运动
2 =0.2 × (-2)=-0.4 m/s aM= r
B
vM
M
aM
r A
aMn
O
aMn = r = 0.2×12= 0.2 m/s2
2
vA
B
vM
M
aM
r
vA = vM = 0.2m/s aA = aM = - 0.4m/s
2
aMn
O
aA
A
vA
作业： 7－ 1，4 ，6 ，7
d d 2 2 dt dt
0 t 0 t 匀变速运动: 2 2 2 1 2 0 0 0 t t 2
二.解题步骤及注意问题
1.解题步骤:
①弄清题意,明确已知条件和所求的问题。 ②选好坐标系：直角坐标法，自然法。 ③根据已知条件进行微分，或积分运算。 对常见的特殊运动， ④用初始条件定积分常数。 可直接应用公式计算。 ２．注意问题： ①几何关系和运动方向。 ②求轨迹方程时要消去参数“t”。 ③坐标系（参考系）的选择。
第七章
刚体的简单运动
刚体运动的分类：
1、平行移动；
2、定轴转动；
3、平面运动；
4、定点运动；
5、一般运动。
§7-１刚体的平行移动(平动）
1 定义 刚体内任一直线在运动过程中始终平行于
初始位置，称为平动。
★
2
速度和加速度
rA rB BA
d rA d rB d BA dt dt dt
三.例题 [例1]列车在R=300m的曲线上匀变速行驶。轨道上曲线部分长
l=200m，当列车开始走上曲线时的速度v0=30km/h，而将要离开
曲线轨道时的速度是v1＝48km/h。 求列车走上曲线与将要离开曲线时的加速度？
B
vM
M
aM
r A
aMn
O
aMn = r = 0.2×12= 0.2 m/s2
2
vA
B
vM
M
aM
r
vA = vM = 0.2m/s aA = aM = - 0.4m/s
2
aMn
O
aA
A
vA
作业： 7－ 1，4 ，6 ，7
d d 2 2 dt dt
0 t 0 t 匀变速运动: 2 2 2 1 2 0 0 0 t t 2
二.解题步骤及注意问题
1.解题步骤:
①弄清题意,明确已知条件和所求的问题。 ②选好坐标系：直角坐标法，自然法。 ③根据已知条件进行微分，或积分运算。 对常见的特殊运动， ④用初始条件定积分常数。 可直接应用公式计算。 ２．注意问题： ①几何关系和运动方向。 ②求轨迹方程时要消去参数“t”。 ③坐标系（参考系）的选择。
第七章
刚体的简单运动
刚体运动的分类：
1、平行移动；
2、定轴转动；
3、平面运动；
4、定点运动；
5、一般运动。
§7-１刚体的平行移动(平动）
1 定义 刚体内任一直线在运动过程中始终平行于
初始位置，称为平动。
★
2
速度和加速度
rA rB BA
d rA d rB d BA dt dt dt
三.例题 [例1]列车在R=300m的曲线上匀变速行驶。轨道上曲线部分长
l=200m，当列车开始走上曲线时的速度v0=30km/h，而将要离开
曲线轨道时的速度是v1＝48km/h。 求列车走上曲线与将要离开曲线时的加速度？
刚体的简单运动
5
运动学
例 题 7- 1
第七章 刚体的简单运动
O1 l A O
（+）
O2 l M B
荡木用两条等长的钢索 平行吊起，如图所示。钢索 长为长 l ，度单位为 m 。当荡 木摆动时钢索的摆动规律 π t，其中 t 为 为 ϕ = ϕ 0 sin 4 时间，单位为s；转角φ0的单 位 为 rad ， 试 求 当 t=0 和 t=2 s 时，荡木的中点M的速度和加 速度。
这里ϕ 0和ω 0是t = 0 时转角和角速度。
13
运动学
第七章 刚体的简单运动
§7-3 转动刚体内各点的速度和加速度
当刚体作定轴转动时，刚体内每一点都作圆 周运动，圆心在转轴上，圆心所在平面与转 轴垂直，半径R等于该点到轴线的距离。 用自然法， 点在 Δ t时间内，走过的弧长为 Δs=Δϕ R 速度
d 2 rB d2 d 2 rA aB = = 2 ( rA + rAB ) = = aA 2 2 dt dt dt
4
运动学
第七章 刚体的简单运动
由于点A和点B是刚体上的任意两点，因此可以 得出如下结论 平移刚体在任一瞬时速度,加速度都一样， 加速度都一样 各点的运动轨迹 形状相同。 即:平移刚体的运动可以简化为一个点的运动。
π s = ϕ 0 l sin t 4
ds π π = lϕ 0 cos t dt 4 4
将上式对时间求导，得A点的速度
v=
7
运动学
例 题 7- 1
O1 O2
第七章 刚体的简单运动
再求一次导，得A点的切向加速度
φ l
A O
（+）
l M B
π dv π2 at = =− lϕ 0 sin t dt 16 4
运动学
例 题 7- 1
第七章 刚体的简单运动
O1 l A O
（+）
O2 l M B
荡木用两条等长的钢索 平行吊起，如图所示。钢索 长为长 l ，度单位为 m 。当荡 木摆动时钢索的摆动规律 π t，其中 t 为 为 ϕ = ϕ 0 sin 4 时间，单位为s；转角φ0的单 位 为 rad ， 试 求 当 t=0 和 t=2 s 时，荡木的中点M的速度和加 速度。
这里ϕ 0和ω 0是t = 0 时转角和角速度。
13
运动学
第七章 刚体的简单运动
§7-3 转动刚体内各点的速度和加速度
当刚体作定轴转动时，刚体内每一点都作圆 周运动，圆心在转轴上，圆心所在平面与转 轴垂直，半径R等于该点到轴线的距离。 用自然法， 点在 Δ t时间内，走过的弧长为 Δs=Δϕ R 速度
d 2 rB d2 d 2 rA aB = = 2 ( rA + rAB ) = = aA 2 2 dt dt dt
4
运动学
第七章 刚体的简单运动
由于点A和点B是刚体上的任意两点，因此可以 得出如下结论 平移刚体在任一瞬时速度,加速度都一样， 加速度都一样 各点的运动轨迹 形状相同。 即:平移刚体的运动可以简化为一个点的运动。
π s = ϕ 0 l sin t 4
ds π π = lϕ 0 cos t dt 4 4
将上式对时间求导，得A点的速度
v=
7
运动学
例 题 7- 1
O1 O2
第七章 刚体的简单运动
再求一次导，得A点的切向加速度
φ l
A O
（+）
l M B
π dv π2 at = =− lϕ 0 sin t dt 16 4
第7章 刚体的简单运动
s R （逆时针为正）
自然法
2．点的速度
s R
v ds R d R
dt dt
v 指向为刚体转动的方向或与 ω 的转动方向一致。
刚体绕定轴转动 （逆时针为正）
刚体绕定轴转动
2．点的加速度
s R （逆时针为正）
切向加速度
a
dv dt
R d
dt
R
aτ 指向沿轨迹的切线与α 的转
动方向一致。
点M的全加速度大小。
解： M点的速度为
vM
vM
vA
dx dt
10t
m/s
M点的加速度为
aMt aMt
aMn
vM2 R
aA 200t 2
d2x dt 2 m/s2
10
m/s2
aM
aMt
2
aMn
2
10
1 400t 4
m/s2
三、轮系的传动比
刚体绕定轴转动
齿轮系
带轮系
刚体绕定轴转动
同一瞬时荡木上各点的速度、加速 度相等 vM vA aM aA
点A绕圆心O1，作半径为 l 的圆弧 运动
自然法： 假设弧坐标s向右为正，
s
l
l0
sin
4
t
刚体的平行移动
运动方程：
s
l
l0
sin
4
t
任一瞬时t， v ds l0 cos t
dt 4 4
， 0 sin t 4aΒιβλιοθήκη dv dt2l0 16
解： d 1681t 2 rad/s dt 162t rad/s2 4 0 时，即 16 81t2 0 时，解得 t 9 s 此时刚体改变转向。容易算得：在此之前，ω>0，刚体 逆时针转动；在此之后，ω<0，刚体顺时针转动。
自然法
2．点的速度
s R
v ds R d R
dt dt
v 指向为刚体转动的方向或与 ω 的转动方向一致。
刚体绕定轴转动 （逆时针为正）
刚体绕定轴转动
2．点的加速度
s R （逆时针为正）
切向加速度
a
dv dt
R d
dt
R
aτ 指向沿轨迹的切线与α 的转
动方向一致。
点M的全加速度大小。
解： M点的速度为
vM
vM
vA
dx dt
10t
m/s
M点的加速度为
aMt aMt
aMn
vM2 R
aA 200t 2
d2x dt 2 m/s2
10
m/s2
aM
aMt
2
aMn
2
10
1 400t 4
m/s2
三、轮系的传动比
刚体绕定轴转动
齿轮系
带轮系
刚体绕定轴转动
同一瞬时荡木上各点的速度、加速 度相等 vM vA aM aA
点A绕圆心O1，作半径为 l 的圆弧 运动
自然法： 假设弧坐标s向右为正，
s
l
l0
sin
4
t
刚体的平行移动
运动方程：
s
l
l0
sin
4
t
任一瞬时t， v ds l0 cos t
dt 4 4
， 0 sin t 4aΒιβλιοθήκη dv dt2l0 16
解： d 1681t 2 rad/s dt 162t rad/s2 4 0 时，即 16 81t2 0 时，解得 t 9 s 此时刚体改变转向。容易算得：在此之前，ω>0，刚体 逆时针转动；在此之后，ω<0，刚体顺时针转动。
大学物理刚体部分知识点总结
一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。
2.刚体平行移动。
·刚体内任一直线段在运动过程中，始终与它的最初位置平行，此种运动称为刚体平行移动，或平移。
·刚体作平移时，刚体内各点的轨迹形状完全相同，各点的轨迹可能是直线，也可能是曲线。
·刚体作平移时，在同一瞬时刚体内各点的速度和加速度大小、方向都相同。
3.刚体绕定轴转动。
•刚体运动时，其中有两点保持不动，此运动称为刚体绕定轴转动，或转动。
•刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。
•角速度ω表示刚体转动快慢程度和转向，是代数量，。
角速度也可以用矢量表示，。
•角加速度表示角速度对时间的变化率，是代数量，，当α与ω同号时，刚体作匀加速转动；当α与ω异号时，刚体作匀减速转动。
角加速度也可以用矢量表示，。
•绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系：。
速度、加速度的代数值为。
•传动比。
二．转动定律转动惯量转动定律力矩相同，若转动惯量不同，产生的角加速度不同与牛顿定律比较：转动惯量刚体绕给定轴的转动惯量J 等于刚体中每个质元的质量与该质元到转轴距离的平方的乘积之总和。
定义式质量不连续分布质量连续分布物理意义转动惯量是描述刚体在转动中的惯性大小的物理量。
它与刚体的形状、质量分布以及转轴的位置有关。
计算转动惯量的三个要素:(1)总质量； (2)质量分布； (3)转轴的位置 (1) J 与刚体的总质量有关 几种典型的匀质刚体的转动惯量平行轴定理和转动惯量的可加性 1） 平行轴定理设刚体相对于通过质心轴线的转动惯量为Ic ，相对于与之平行的另一轴的转动惯量为I ，则可以证明I 与Ic 之间有下列关系 2c I I md =+ 2）转动惯量的可加性对同一转轴而言，物体各部分转动惯量之和 等于整个物体的转动惯量。
2c I I md =+三 角动量 角动量守恒定律1．质点的角动量（Angular Momentum ）——描述转动特征的物理量 1）概念一质量为m 的质点，以速度v运动，相对于坐标原点O 的位置矢量为r ，定义质点对坐标原点O 的角动量为该质点的位置矢量与动量的矢量积，即v m r P r L⨯=⨯= 角动量是矢量，大小为 L=rmv sin α式中α为质点动量与质点位置矢量的夹角。
刚体的简单运动—转动刚体内各点的速度和加速度(理论力学)
二、角加速度 与an ，at的关系
设角加速度如图所示
A MO
O
切向加速度 at dv d (R) R d R (+)
dt dt
dt
R
an
v
at
即：转动刚体内任一点的切向加速度(又称转动加 速度)的大小，等于刚体的角加速度与该点到轴线
M
B
垂直距离的乘积。
它的方向由角加速度的符号决定，当是正值时，它沿圆周的切线，
[例]半径R=0.2m的圆轮绕定轴O的转动方程 t 2 4t ，单位为弧度。 求t=1s时，轮缘上任一点M的速度和加速度。如在此轮缘上绕一柔软而不
可伸长的绳子并在绳端悬一物体A，求当t=1s时，物体A的速度和加速度。 解：圆轮在任一瞬时的角速度和角加速度为
d 2t 4
dt
d2 2
• ①滑轮3s内的转数； • ②重物B在3s内的行程；
• ③重物B在ｔ＝3s时的速度；
• ④滑轮边上C点在初瞬时的加速度；
• ⑤滑轮边上C点在ｔ＝3s时的加速度。
解：① 因为绳子不可以伸长，所以有
C aA 1m/s2
aCt 1 2 rad/s2
R 0.5
（ ）常数
vC
vA
1.5m /s， 0 vC
4.5m /s2
a (at )2 (an )2 12 4.52 4.61 m/s2
C
C
C
tan aCt 1 0.222， 12.5
aCn 4.5
⑤ t=3s 时，
at a
1m/s2，a n
R 2
2
0.5 9
40.5m/s2
a 12 40.52 40.51m/s2，tan 1 0.0247， 1.41 C
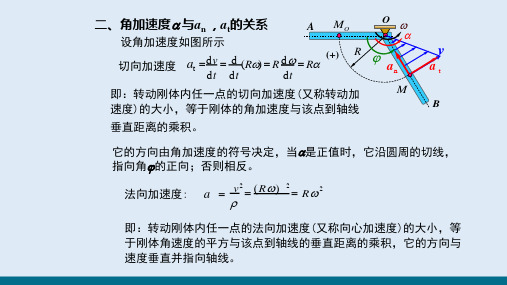
设角加速度如图所示
A MO
O
切向加速度 at dv d (R) R d R (+)
dt dt
dt
R
an
v
at
即：转动刚体内任一点的切向加速度(又称转动加 速度)的大小，等于刚体的角加速度与该点到轴线
M
B
垂直距离的乘积。
它的方向由角加速度的符号决定，当是正值时，它沿圆周的切线，
[例]半径R=0.2m的圆轮绕定轴O的转动方程 t 2 4t ，单位为弧度。 求t=1s时，轮缘上任一点M的速度和加速度。如在此轮缘上绕一柔软而不
可伸长的绳子并在绳端悬一物体A，求当t=1s时，物体A的速度和加速度。 解：圆轮在任一瞬时的角速度和角加速度为
d 2t 4
dt
d2 2
• ①滑轮3s内的转数； • ②重物B在3s内的行程；
• ③重物B在ｔ＝3s时的速度；
• ④滑轮边上C点在初瞬时的加速度；
• ⑤滑轮边上C点在ｔ＝3s时的加速度。
解：① 因为绳子不可以伸长，所以有
C aA 1m/s2
aCt 1 2 rad/s2
R 0.5
（ ）常数
vC
vA
1.5m /s， 0 vC
4.5m /s2
a (at )2 (an )2 12 4.52 4.61 m/s2
C
C
C
tan aCt 1 0.222， 12.5
aCn 4.5
⑤ t=3s 时，
at a
1m/s2，a n
R 2
2
0.5 9
40.5m/s2
a 12 40.52 40.51m/s2，tan 1 0.0247， 1.41 C
第七章：刚体的简单运动
ϕ = f (t) 角速度 ω = d ϕ
dt
M0
rr
ϕ
O
M
角速度表示刚体转动的快慢和方向，单位为弧度/ 秒（rad/s），是代数量。
角加速度
α
=
dω
dt
=
d 2ϕ
dt 2
角加速度表示角速度变化的快慢，单位为弧度/秒2
（rad/s2），是代数量。
§7-2 刚体绕定轴的转动
ω与α同号，转动加速
α ω
vr A = vr B
rrA
vrB
O
rrB B B1 B2
y
x
vr A = vr B
继续求导，则
dvrA = dvrB dt dt ar A = ar B
§７-１刚体的平行移动
z
A rrA
vrA A1 arvrAB
A2
O
rrB B arBB1 B2
y
x
当刚体平行移动时，其上各点的轨迹形状相同、在 每一瞬时，各点的速度和加速度相同。
角速度矢量
ωr
⎧⎪大 ⎪⎪⎨作
小 用
ωr
线
= 沿
ω
轴
= 线
dϕ
dt 滑动
矢
量
⎪
⎪
⎪⎩指 向 右 手 螺 旋 规 则
ωr = ωkr
角加速度矢量
αr
=
dωr
=
dω
r k
=
α
r k
dt dt
2 绕定轴转动刚体上M点的速度和加速度
vv = ωv × rv 速度
⎪⎧大小： ωv ⋅ rv sinθ = ωv R = vv
ω2 α2 +ω4
av
dt
M0
rr
ϕ
O
M
角速度表示刚体转动的快慢和方向，单位为弧度/ 秒（rad/s），是代数量。
角加速度
α
=
dω
dt
=
d 2ϕ
dt 2
角加速度表示角速度变化的快慢，单位为弧度/秒2
（rad/s2），是代数量。
§7-2 刚体绕定轴的转动
ω与α同号，转动加速
α ω
vr A = vr B
rrA
vrB
O
rrB B B1 B2
y
x
vr A = vr B
继续求导，则
dvrA = dvrB dt dt ar A = ar B
§７-１刚体的平行移动
z
A rrA
vrA A1 arvrAB
A2
O
rrB B arBB1 B2
y
x
当刚体平行移动时，其上各点的轨迹形状相同、在 每一瞬时，各点的速度和加速度相同。
角速度矢量
ωr
⎧⎪大 ⎪⎪⎨作
小 用
ωr
线
= 沿
ω
轴
= 线
dϕ
dt 滑动
矢
量
⎪
⎪
⎪⎩指 向 右 手 螺 旋 规 则
ωr = ωkr
角加速度矢量
αr
=
dωr
=
dω
r k
=
α
r k
dt dt
2 绕定轴转动刚体上M点的速度和加速度
vv = ωv × rv 速度
⎪⎧大小： ωv ⋅ rv sinθ = ωv R = vv
ω2 α2 +ω4
av
07 刚体的简单运动Hxj
角位移
Δ d lim * lim Δt 0 Δt 0 Δt dt
说明： 角速度单位是rad/s,工程单位n rpm(r/min或转/分) 换算关系为:
2n n 0.105n rad/s 60 30
3、 角加速度 设当t 时刻为 , t +△t 时刻为+△ (1) 平均角加速度
R
0.4m/s
a
M t t 1
R
t 1
d 2 R 2 dt
t 1
d 2 t 2 4t R dt 2
t 1
v
0.4m / s 2
a
M n t 1
R
2 t 1
0.2 2 0.8m / s
2
2
A
aA
全加速度大小及方向
a a 2 a 2 0.4 2 0.82 0.894m/s2 t n t 1 t 1 2 t 1 arctan 2 arctan t 1 4
§7-1 刚体的平行移动
一、概念 刚体运动时，如果在刚体内任取一直线段，在运动过程中 该直线段始终与其最初位置平行，这种运动称为平行移动 (translation),简称平移或平动。
河南理工大学力学系
理论力学
第七章 刚体的简单运动
二、刚体平行移动的性质 设刚体作平行移动，如图。在刚 体内任取两点A和B，设其矢径分别为 rA和rB，则两条矢端曲线就是两点的轨 迹。由图中几何关系可知
1、 转动方程 Ⅰ和Ⅱ夹角 ---转角（位 置角）,单位为弧度(rad)
• 定轴转动方程 对着z轴正向看
t
7 2
• 的正、负规定 逆为正 顺为负
第七章 刚体的简单运动
答案： ① (b) ； ② (a)
§7-４ 轮系的传动比
１、齿轮传动
① 啮合条件
Rω1 = vA = vB = R2ω2 1
② 传动比
ω1 R2 z2 i12 = ± = ± = ± ω2 R z1 1
２、带轮传动
rω1 = vA = v′ = v′ = vB = r2ω2 1 A B
ω1 r2 i12 = = ω2 r 1
M点切向加速度 M点法向加速度
r r r at = α × r
r r r r r r an = ω×v = ω×(ω× r )
减速箱的齿轮Ⅰ、Ⅱ、Ⅲ和Ⅳ的 转轴在同一水平线上。各齿轮的齿数分别 为z1 = 36、z2= 112、z3 = 32 和 z4 = 128。 主动轮Ⅰ的转速n1 = 1450 r/min，求从动 轮Ⅳ的转速 n4 。 Ⅱ
例7-1 图示机构O1A = O2B = a，O1O2 = AB =
2R，半圆轮半径为R 。试问图示瞬时，轮上M点 的速度为 ① ；M点的轨迹曲率半径为 ② 。 M ① (a) Rω (b) a ω R A B (c) a ω sin 60° O ω
60 °
O1
O2
②
(a) a
(b) R
(c) a+R
( )
r r r dvB dvA r aB = = = aA dt dt
刚体平移→点的运动 →
§7-2 刚体绕定轴的转动
1、定义
刚体上(或其扩展部分)两点保持不动，则这种运动称 为刚体绕定ቤተ መጻሕፍቲ ባይዱ转动，简称刚体的转动。 转轴 ：两点连线 转角： 单位:弧度(rad)
2、运动方程
= f (t )
3、角速度和角加速度
第六章刚体的简单运动
6.2 刚体的定轴转动
2.匀变速转动
刚体角加速度不变的转动，称为匀变速转动。
0 t
1 2 j j 0 0 t t 2
2 (j j0 )
2 2 0
其中ω0和j0分别是t =0时的角速度和转角。
6.2 刚体的定轴转动
一、转动刚体内各点的速度 以固定点O´为弧坐标s 的原点，按j角的正向规 定弧坐标s的正向，于是
rA rB BA
当刚体平移时，线段AB的长度 和方向都不改变。 因此只要把 点B的轨迹沿BA方向平行移动一段距离BA，就能与点A的 轨迹完全重合。 刚体平移时，其上各点的轨迹不一定是直线，也可能 是曲线，但是它们的形状是完全相同的。
6.1
速度、加速度
刚体的平移
rA rB BA
上式对时间t求导数，得 drA drB d BA dt dt dt 而
6.2 刚体的定轴转动
设轮Ⅰ是主动轮，轮Ⅱ是从动轮。 1 传动比： i12 2 1 n1 1 j1 R2 z 2 i12 2 n2 2 j 2 R1 z1 不仅适用于圆柱齿轮传动，也适用于轴成任意角度的圆 锥齿轮传动、摩擦传动等。 有时为了区分轮系中各轮的转向。对各轮都规定统 一的转动正向，这时各轮的角速度可取代数值，从而转 动比也取代数值： 1 R2 z2 i12 2 R1 z1 正号表示两轮转向相同，负号表示转向相反。
j f (t )
这个方程称为刚体绕定轴转动的转动方程。
6.2 刚体的定轴转动
二、角速度 转角j 对时间的一阶导数，称为刚体的瞬时角速度， 用ω表示，即
dj dt
角速度表示刚体转动的快慢和方向。
单位一般用rad/s（弧度/秒）。
哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案
解
设轮缘上任 1 点 M 的全加速度为 a，切向加速度 a t = rα ，法向加速度 a n = ω r ，如图
2
7-11b 所示。
tan θ =
把
α=
dω ， θ = 60° 代入上式，得 dt
at α = 2 an ω
dω tan 60° = dt2
ω
分离变量后，两边积分：
∫ω
得
ω
0
dω
ω
2
=∫
⎤ ⎡ ⎥ ⎢ sin ω t 0 θ = tan −1 ⎢ ⎥ ⎢ h − cos ω 0 t ⎥ ⎥ ⎢ ⎦ ⎣r
故
50 π ⋅ 600 100π r ω1 = rad/s ⋅ = 100 − 5t 30 10 − 0.5t d dω 5 000 π d ⎛ 1 000π ⎞ α2 = 2 = ⎜ ⎟= dt dt ⎝ 100 − 5t ⎠ (100 − 5π )2
故得
h1 =
h4 = 2 mm 6
图 7-7
7-8 如图 7-8 所示，纸盘由厚度为 a 的纸条卷成，令纸盘的中心不动，而以等速 v 拉纸条。求 纸盘的角加速度（以半径 r 的函数表示） 。 解 纸盘作定轴转动，当纸盘转过 2π rad 时半径减小 a。设纸盘转过 dθ 角时半径增加 dr ，则
dθ =
y
B
t aB
α j
O
vA x
ω
(a) 图 7-12
aC
(b)
i 45° A n
C
t aC
解
由图 7-12b 得出
84
理论力学（第七版）课后题答案 哈工大.高等教育出版社
v A = 0.2 j m/s ， v A = ω × Ri ， ω × 0.1i = 0.200 j ， ω = 2k ，
06刚体的简单运动
结论:
刚体平动的问题可归结为点的运动问题来处理。
2
例题
刚体的基本运动
例 题 1
荡木用两条等长的钢索
O1 φ O2
平行吊起，如图所示。钢索
l
l
A M
长为l，长度单位为m。当荡
B
木摆动时钢索的摆动规律
O
（+）
为 0 sin转角φ0 的单 位为rad，试求当t=0和t=2 s时，
表示摆对铅直线的偏角， φ0为最大偏角；T 表示摆的 周期。已知摆的重心C到轴 O的距离为l，试求在初瞬
C1
时和经过平衡位置(φ=0)时
重心的速度和加速度。
14
例题
刚体的基本运动
解：
和角加速度
d dt
2
例 题 3
将转动方程对时间求导，得摆的角速度
2π T
2
O φ
φ0 l C0 C C1
B
O
降落，初速v0=4 m/s，求当物体落下
距离s =2 m时轮缘上一点 M 的速度 和加速度。
17
s
A
例题
刚体的基本运动
解:
M
例 题 4
根据 v2 – v02 = 2as，得M点的速度
v 2as v0 5.96 m / s
2
R
O
v
M点的切向加速度 M点的法向加速度
B
at
dv dt
不动直线称为转轴（轴线、轴）
不在转轴上的点作圆周运动
6
2.运动方程(转动方程)
=f（t）
转角的正负由右手螺旋法则确定。 即从Oz轴正端俯视，自固定平面N0至动 平面N，若是逆时针转动，则角为正 值，反之，则角为负值。 单位：弧度（rad）
第7章 刚体的简单运动
第七章 刚体的简单运动在工程实际中，最常见的刚体运动有两种基本运动形式：平动和转动。
一些较为复杂的刚体运动，如车轮在直线轨道上的滚动等，都可以归结为这两种基本运动的组合。
因此，平动和转动是分析一般刚体运动的基础。
§7-1 刚体的平行移动平动是刚体最简单的一种运动。
例如，车刀的刀架，摆式输送机的料槽，以及沿直线轨道行驶的列车的车厢等，都是平动的实例。
这些刚体的运动具有一个共同的特点：运动时，刚体上任一直线始终与原来位置保持平行。
刚体的这种运动称为平行移动，简称为平动。
刚体作平动时，刚体上的点可以是直线运动(刀架)，也可以是曲线运动(送料槽)。
现在就一般情形，研究刚体内各点的运动轨迹，速度和加速度。
刚体作平动在刚体上任取一线段AB 。
该刚体的运动可由AB 在空间的位置确定。
为研究刚体内各点的运动，可以O 为参考点，向A 、B 两点分别引矢径r A 和r B ，则点A 和B 的运动方程分别为r A =r A (t), r B =r B (t)AB B A r r r += (*)由于刚体作平动，在运动中矢量AB 的大小和方向都不改变，所以AB 为一常矢量。
这说明：点A 和B 不仅运动轨迹形状相同，而且运动规律也相同。
如上面的各例中，刀架上各点的轨迹是相互平行的直线；料槽上各点的轨迹都是半径等于AC 的圆弧。
将式(*)对时间t 取一阶和二阶导数，同时注意到常矢量AB 的导数等于零，于是有B A v v =B A a a =这说明：刚体内任意两点的速度、加速度相等。
综合以上分析，可得如下结论：(1) 刚体平动时，其上各点的轨迹形状相同；(2) 同一瞬时各点的速度彼此相等，各点的加速度也彼此相等。
因此，在研究刚体平动时，只要知道刚体上某一点的运动，就能知道所有点的运动。
所以，刚体的运动可归结为点的运动。
§7-2 刚体绕定轴的转动定轴转动是工程中常见的一种运动，如电动机的转子，机床中的胶带轮、齿轮以及飞轮等的运动，都是定轴转动的实例。
(完整版)6刚体的简单运动
an
v2
1 R 2
R
R 2
方向：与速度垂直并指向轴线
4 速度与加速度分布图
1、定轴转动刚体上各点的速度和加速度的大小均与该点到转轴 的垂直距离成正比。
2、在任一瞬时，刚体上所有各点的加速度a与该点轨迹半径的 夹角θ都具有相同值而与该点位置无关。
v R
a at2 an2 R 2 4
tan at an 2
0 t
d (0 t)dt
0
0t
1 t 2
2
0
0t
1 2
t 2
计算机硬盘驱动器的马达以匀变速转动，启动后为了能
尽快达到最大工作转速，要求在3秒内转速从0增加到
3000r/min，求马达的角加速度及转过的转数。
解： 马达的初始角速度 0 0
3秒后
n
30
3000 100
30
rad
s
0 t
d
dt
——表征刚体转动的快慢和转向； 是代数量，单位为：rad/s
3)角加速度
d
dt
d 2
dt 2
——表征角速度随时间变化的快慢; 是代数量，单位：rad/s2
两种特殊情形
1）匀速转动
d 常数
dt
d dt
0 t
0 t
2）匀变速转动
d =常数
dt
d dt
0 dt
简化：刚体上任取一条直线A1A//z轴。 由于A1A作平动，取A代表直线运动。 即：刚体转动简化为与转轴垂直的平面
图形的运动；平面上各个点的运动代表了对应 的整个刚体的点的运动规律。
3、转动刚体的转动方程、角位移、角速度和角加速度
f ( t ) 转动方程
刚体的简单运动
定轴转动刚体在空间占有的位置，可以用它的转角 来描述。在转动过程中，转角 是[ 时间 t ]的单值连续函数。这个函数称为刚体的
[ 转动方程 ]。
定轴转动刚体的运动特征量，除转角 以外，还有角速度 ω 和角加速度ε，它们分别是转角 对时间的[ 一阶导数和二阶导数 ]。
刚体的简单运动
§7-1 刚体的平行移动 1 定义 刚体内任一直线在运动过程中始终平行 于最初位置.
2 运动方程
3 速度和加速度分布 恒矢量
结论:
当刚体平行移动时，其上各点的轨迹形状相同;在每 一瞬时，各点的速度相同，加速度也相同。 因此，研究刚体的平移，可以归结为研究刚体内任 一点的运动。 刚体 点
②
传动比
２、带轮传动
§7-5 以矢量表示角速度和角加速度.以矢积表示 点的速度和加速度
1 角速度矢量和角加速度矢量 角速度矢量
角加速度矢量
2 绕定轴转动刚体上M点的速度和加速度
在工程实际中，并不是所有研究对象的运动都可以 简化为一个几何点的运动来加以讨论的。很多情况 下，必须考虑物体的尺寸、形状。这时，可把物体 简化成另一种力学模型——[ 刚体 ]。刚体是一个其 内任意两点之间的[ 距离 ]永远保持不变的物体。
§7-2 刚体绕定轴的转动 1 定义 ：刚体上(或其扩展部分)两点保持不动， 称为定轴转动 转轴 ： 两点连线 转角： 2 运动方程
3.角速度和角加速度
角速度
§7-3 转动刚体内各点的速度和加速度
1 点的运动方程
7-４
轮系的传动比
１、齿轮传动 ① 啮合条件
无论刚体的运动形式多么复杂，都可以看成是刚体
的[ 平行移动 ]和刚体的[ 定轴转动 ]的迭加。这两种
简单的刚体运动形式，称为刚的基本运动。
运动学(刚体简单运动)
刚体的简单运动刚体的定轴转动三定轴转动刚体上点的加速度刚体定轴转动时各点均作圆周运动由自然法知转动刚体内一点的切向加速度大小等于刚体的角加速度与该点到轴线的垂直距离的乘积方向沿圆周的切线方向指向由角加速度决定
刚体的简单运动
§1 刚体的平行移动 §2 刚体的定轴转动 结论与讨论
习题
刚体的平行移动
刚体的简单运动
一、刚体平动的定义
在刚体上任取一条直线，若在运动过程中这 条直线始终与其初始的空间位置平行，则该 运动称为刚体的平行移动，简称平动。
刚体的平行移动
刚体的简单运动
二、刚体平动的运动分析
rA rB rBA rA rB rBA v A vB a A aB
刚体平移可归结为刚体内任一点（通常是质心）的运动。
2 O1 950 99.48rad/s 60
O
2
Z1 20 O1 99.48 39.79rad/s Z2 50
vC O2 AO2 0.25 39.79 9.95m/s
刚体的定轴转动
刚体的简单运动
例三 曲柄滑杆机构中,滑杆上有一圆弧滑道,其半径R=100mm, 圆心O1在导杆BC上.曲柄OA=100mm，以等角速度 4 rad 绕 s O轴转动.求导杆BC的运动规律以及当曲柄与水平线间的交角为 30时,导杆BC的速度和加速度。
刚体的简单运动
例六 图示一减速箱，由四个齿轮组成，其齿数分别为Z1＝10， Z2＝60 ， Z3＝12 ， Z4＝70 。（1）求减速箱的总传动比i13（2） 如果n1=3000rpm，求n3 。
n1 n1 n2 Z 2 Z 3 i13 i12 i23 34.8 n3 n2 n3 Z1 Z 2
刚体的简单运动
§1 刚体的平行移动 §2 刚体的定轴转动 结论与讨论
习题
刚体的平行移动
刚体的简单运动
一、刚体平动的定义
在刚体上任取一条直线，若在运动过程中这 条直线始终与其初始的空间位置平行，则该 运动称为刚体的平行移动，简称平动。
刚体的平行移动
刚体的简单运动
二、刚体平动的运动分析
rA rB rBA rA rB rBA v A vB a A aB
刚体平移可归结为刚体内任一点（通常是质心）的运动。
2 O1 950 99.48rad/s 60
O
2
Z1 20 O1 99.48 39.79rad/s Z2 50
vC O2 AO2 0.25 39.79 9.95m/s
刚体的定轴转动
刚体的简单运动
例三 曲柄滑杆机构中,滑杆上有一圆弧滑道,其半径R=100mm, 圆心O1在导杆BC上.曲柄OA=100mm，以等角速度 4 rad 绕 s O轴转动.求导杆BC的运动规律以及当曲柄与水平线间的交角为 30时,导杆BC的速度和加速度。
刚体的简单运动
例六 图示一减速箱，由四个齿轮组成，其齿数分别为Z1＝10， Z2＝60 ， Z3＝12 ， Z4＝70 。（1）求减速箱的总传动比i13（2） 如果n1=3000rpm，求n3 。
n1 n1 n2 Z 2 Z 3 i13 i12 i23 34.8 n3 n2 n3 Z1 Z 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A 图6-6
a
C
(3).如图6-7所示机构中， M为AB上的点。且 O1 A O2 B r,
AM BM。若O1A按 t 的规律绕 O1 轴转动， O1O2 AB l 。 则M点的轨迹是（ ）B
M A.半径为 r 圆 B.半径为 l 圆 1 C.半径为 l 圆 2 D.与AB 平行的直线 A O1
vA ＝0.86m/s 答案：
r
A
r
图6-9
4、如图6-10,摆式运输机构中,摆杆O1 A O2 B r 10cm,
O1O2 AB, 已知 O1 A 与 O2 B 成 60角时,铰接在摆
杆上的平板CD 的端点D 的加速度大小。
答案：
0.5 2rad / s, 0.5 3rad / s
d dt
故
a r
an
即
a a an
§4 .轮系的传动比
v r11 r22
传动比：
ω1 r1
ω2 r2Leabharlann 1 r2 i12 2 r1
ω1 r1
v
r2 ω2
2n 转速 n 转/分， rpm； 角速度 (1 s ) 60
概念题 1)转动刚体的角加速度为正时，则刚体 （1）越转越快 （2）越转越慢 （3）不一定
O2 图6-7
（4）半径为 R 的飞轮,绕垂直与图面的O轴转动。图示瞬时， a A 的大小、方向均为已知，则 轮缘上A点加速度 此时 A点速度大小为（ C ） A. B. C. D.
Ra A Ra A sin Ra A cos Ra A cos
A
O
a
图6-8
3、平板 A放置在两个半径为 r 25cm的圆筒上,如图6-9所示。 2 a 0 . 5 cm s 在某瞬时,平板具有向右的匀加速度 A ,在同一瞬 2 时的圆筒周边上一点的加速度 a 3m s ,假设平板 A与圆 筒之间无滑动,试求该瞬时平板A 的速度 A 。
o
s
R M
方向：沿圆周切线指向转动的一方.
切向加速度: 法向加速度: 全加速度:
R a s R
an v2
( R ) 2
R 2
a t an an
a an a
2 a an a2 R 4 2
矢量表示法
o R v M A
4
t
将
t0
代入以上三式，得：
M 4 cm / s , 方向水平向 右
同样
a
M
n 2 2 ， 方向铅直向上 a a 4 cm / s M 0 ， M
将 t 2 s 代入式（1）、（2）、（3），得此瞬时
M 0
a
n
M
0
am a
M
2
方向垂直于AO1斜向右上方
t
代入（1）式，得 积分： 得：
0 d
150
150
t2
t dt
t 2 0
450
t5
转数：N 1 t 3 1 3003 3 104 rad / s 2 900 900
【思考题】
1. 是非题 (1)某瞬时,刚质上有两点的轨迹相同,则刚体做平动。 （
刚体的平动可归结为 刚体内一点的运动.
rB
§2 .刚体绕定轴的转动 转动 : 刚体在运动过程中,其中只有一条直线保持不动, 则这种运动 称为刚体绕定轴的转动,简称转动. 这条不动的直线,称为刚体的转轴,简称轴. z 转角: π 转动方程: (t ) 角速度:
2 d d 角加速度: 2 dt dt 逆时针为正。
）
(2)如果刚体上任一点的轨迹都是圆曲线,则刚体一定作 定轴转动。 （ ）
2.选择题 (1).某瞬时，刚体上任意两点A、B的速度分别用 v A
vB
表示，则(
A )
A、当刚体平动时，必有 A B。
B、当 A B 时，刚体必作平动。 C、当物体作平动时，必有 A B 的方向 B , 但 A 与 可能不同 。 A 与 B 的方向必然相同，但有可 D、当物体作平动时， 能 A B
d dt
匀速转动：为常量
0 t
匀加速转动：角加速度为常量
0 t
1 0 0 t t 2 2 2 2 0 2
§3 .转动刚体内各点的速度和加速度
s R
v
速度:
R R vs
因为半圆盘作平动，所以其角速度
ab 。0
例6-3 转子启动时的角加速度与时间成正比增大,经过5分钟 转子的转速达到18000r/min,试问转子在这段时间内转了多少 转？
【解】设比例系数为k，则
kt
即
d kt dt
积分 0 d k 0tdt 1 2 kt 得 2 2 当 t 5 60 300s 时， 18000 600 rad / s 60 2 600 故 , k 2 rad / s 2 2 t 300 75
2）平动刚体上点的轨迹不可能为空间曲线 3）某瞬时平动刚体上各点的速度大小相等而方向可以不同
例6-1 如图6－1所示，在连续印刷机的生产过程中，纸张需 以匀速 v代入印刷机，设r表示纸筒在任一瞬时的半径，b表 示纸的厚度，试导出纸筒角加速度的表达式。 【解】注意到纸的速度不变，因此 , r 常数
b
r
(1) 图6-1
两边求导得：
故角加速度：
d dr d r 0 dt dt dt
d dr dr 2 dt r dt r dt
由于每转一周，半径减小b,而当角速度时，半径变化 b dr d 2
dr b d b 故： dt 2 dt 2
o R
a
r
A
r
M
M点：
v R OM r sin
据线性代数
r
dr 代入： r dt
（转动刚体上点的速度矢积表示法）
又
dr dt
角速度矢量与角加速度矢量共线
d 2r d d dr a 2 r r r dt dt dt dt
(2)
将(2)式代入(1)式得:
b 2 2r 3
例6-2 如图6-4所示,半径为R的半圆盘在A、B处与 曲柄O1A 和O2B铰接。已知 O1A= O2B= l = 4cm,O1O2=AB,曲柄O1A的 转动律 ＝4 sin t ,其中t为时间，单位以s计。试求当t=0和 4 t=2s时，半圆盘上M点的速度和加速度，以及半圆盘的角速 度 ab 。 O2 O1
(2). 如图6-6所示平面机构中，O1A=O2B= r, O1O2 =AB, O1A以 匀角速度 绕垂直于图面的O1轴转动，图示瞬时，C点的速度 为：( D )
A.
Vc 0
B. Vc r 2 a 2 水平向右 C. Vc r 0 铅直向上 D. Vc r 0 水平向右 O1 B O2
刚体的简单运动
§1 . 刚体的平行移动(平动) 刚体的平动 : 刚体在运动过程中,其上任一条直线始终与它的最 初位置平行。 简称平动或移动.
vA
A A1 A2
rA
B
vB aA
aB B1 B2
r A rB BA
平面平行四连杆机构
vA vB
a A aB
o 刚体平动时,其上各点的轨迹形状相同;在同一瞬 时,各点的速度、加速度也分别相同.
B O R M 图6-2 a nA
A
a A
【解】因为半圆盘做平动，故其上各点的运动轨迹相同， 且速度，加速度相等。则存在：
4 cos t M A l
4 a
n M
（1）
a
n
A
2 4 2 cos 2 l
2
4
t
（2） （3）
a M＝a A＝l － sin
C
aD
D B
A
O1
图6-10
O2