第57讲(理)
第57讲_附有质量保证条款的销售,主要责任人和代理人,附有客户额外购买选择权的销售

【例题·教材11-32】甲公司与乙公司签订合同,向其销售一台特种设备,并商定了该设备的具体规格和销售价格,甲公司负责按照约定的规格设计该设备,并按双方商定的销售价格向乙公司开具发票。
该特种设备的设计和制造高度相关。
为履行该合同,甲公司与其供应商丙公司签订合同,委托丙公司按照其设计方案制造该设备,并安排丙公司直接向乙公司交付设备。
丙公司将设备交付给乙公司后,甲公司按与丙公司约定的价格向丙公司支付制造设备的对价;丙公司负责设备质量问题,甲公司负责设备由于设计原因引致的问题。
甲公司在该交易中的身份为主要责任人还是代理人?【解析】是主要责任人理由:甲公司向乙公司提供的特定商品是其设计的专用设备。
虽然甲公司将设备的制造工作分包给丙公司进行,但是,甲公司认为该设备的设计和制造高度相关,不能明确区分,应当作为单项履约义务。
由于甲公司负责该合同的整体管理,如果在设备制造过程中发现需要对设备规格作出任何调整,甲公司需要负责制定相关的修订方案,通知丙公司进行相关调整,并确保任何调整均符合修订后的规格要求。
甲公司主导了丙公司的制造服务,并通过必需的重大整合服务,将其整合作为向乙公司转让的组合产出(专用设备)的一部分,在该专用设备转让给客户前控制了该专用设备。
因此,甲公司在该交易中的身份为主要责任人。
二、需要考虑的相关事实和情况实务中,企业在判断其在向客户转让特定商品之前是否已经拥有对该商品的控制权时,不应仅局限于合同的法律形式,而应当综合考虑所有相关事实和情况进行判断,这些事实和情况包括但不仅限于:1.转让商品的主要责任是企业还是第三方。
2.该商品的存货风险在商品转让前后由企业还是第三方承担。
3.所交易商品的价格由企业还是第三方决定。
需要强调的是,企业在判断其是主要责任人还是代理人时,应当以该企业在特定商品转让给客户之前是否能够控制该商品为原则。
【举例】甲旅行社与A航空公司协商以折扣价格购买一定数量的机票,并且无论其能否转售,都必须对这些机票进行支付。
高中物理竞赛讲义(超级完整版)(1)

最新高中物理竞赛讲义(完整版)目录最新高中物理竞赛讲义(完整版) (1)第0部分绪言 (5)一、高中物理奥赛概况 (5)二、知识体系 (5)第一部分力&物体的平衡 (6)第一讲力的处理 (6)第二讲物体的平衡 (8)第三讲习题课 (9)第四讲摩擦角及其它 (13)第二部分牛顿运动定律 (15)第一讲牛顿三定律 (16)第二讲牛顿定律的应用 (16)第二讲配套例题选讲 (24)第三部分运动学 (24)第一讲基本知识介绍 (24)第二讲运动的合成与分解、相对运动 (26)第四部分曲线运动万有引力 (28)第一讲基本知识介绍 (28)第二讲重要模型与专题 (30)第三讲典型例题解析 (38)第五部分动量和能量 (38)第一讲基本知识介绍 (38)第二讲重要模型与专题 (40)第三讲典型例题解析 (53)第六部分振动和波 (53)第一讲基本知识介绍 (53)第二讲重要模型与专题 (57)第三讲典型例题解析 (66)第七部分热学 (66)一、分子动理论 (66)二、热现象和基本热力学定律 (68)三、理想气体 (70)四、相变 (77)五、固体和液体 (80)第八部分静电场 (81)第一讲基本知识介绍 (81)第二讲重要模型与专题 (84)第九部分稳恒电流 (95)第一讲基本知识介绍 (95)第二讲重要模型和专题 (98)第十部分磁场 (107)第一讲基本知识介绍 (107)第二讲典型例题解析 (111)第十一部分电磁感应 (117)第一讲、基本定律 (117)第二讲感生电动势 (120)第三讲自感、互感及其它 (124)第十二部分量子论 (127)第一节黑体辐射 (127)第二节光电效应 (130)第三节波粒二象性 (136)第四节测不准关系 (140)第0部分绪言一、高中物理奥赛概况1、国际(International Physics Olympiad 简称IPhO)① 1967年第一届,(波兰)华沙,只有五国参加。
专题2-6运动学图像和追及相遇问题【练】-2023-2024学年高一物理同步讲(004)
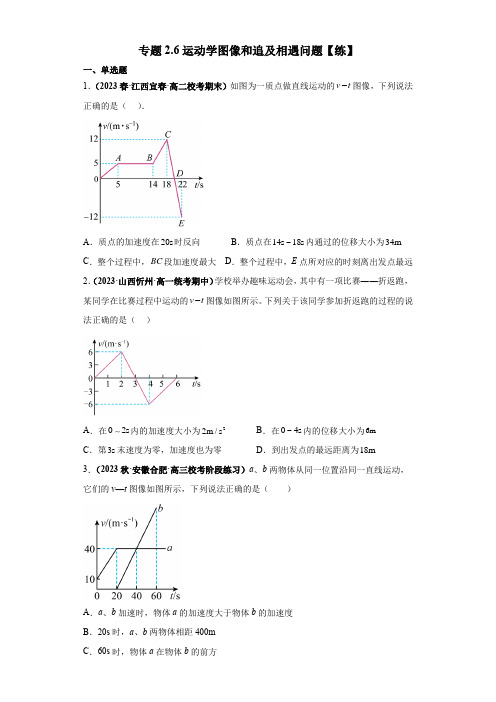
专题2.6运动学图像和追及相遇问题【练】一、单选题1.(2023春·江西宜春·高二校考期末)如图为一质点做直线运动的v t-图像,下列说法正确的是().~内通过的位移大小为34m A.质点的加速度在20s时反向B.质点在14s18sC.整个过程中,BC段加速度最大D.整个过程中,E点所对应的时刻离出发点最远2.(2023·山西忻州·高一统考期中)学校举办趣味运动会,其中有一项比赛――折返跑,-图像如图所示。
下列关于该同学参加折返跑的过程的说某同学在比赛过程中运动的v t法正确的是()A.在02s内的加速度大小为2~内的位移大小为6m2m/s B.在04sC.第3s末速度为零,加速度也为零D.到出发点的最远距离为18m 3.(2023秋·安徽合肥·高三校考阶段练习)a、b两物体从同一位置沿同一直线运动,它们的v—t图像如图所示,下列说法正确的是()A.a、b加速时,物体a的加速度大于物体b的加速度B.20s时,a、b两物体相距400mC.60s时,物体a在物体b的前方D .40s 时,a 、b 两物体速度相等,相距200m 4.(2023秋·广东河源·高三统考期末)正在行驶的某无人驾驶汽车发现正前方6m 处的斑马线上有行人,立即启动刹车程序。
已知汽车从发现行人到停下来的速度—时间()v t -图像如图所示,则可判定该汽车( )A .停在斑马线前0.5m 的地方B .停在斑马线前1.0m 的地方C .恰好在斑马线前停止D .已越过斑马线0.5m5.(2023秋·湖南永州·高三永州市第一中学校考阶段练习)高铁改变生活,地铁改变城市!地铁站距短需要频繁启停,为缩短区间的运行时间需要较大的启动加速度。
0=t 时刻,一列高铁和一列地铁沿各自所在的长直轨道由静止启动,0240s ~内的v t -图像如图所示。
下列说法正确的是( )A .甲是地铁的v t -图像,乙是高铁的v t -图像B .地铁和高铁加速过程的加速度大小之比为53:C .地铁和高铁加速过程的平均速度大小之比为31:D .0240s ~内,地铁和高铁的位移大小之比为58:6.(2023春·云南红河·高一开远市第一中学校校考期中)如图所示为A 、B 两物体在同一直线坐标系中运动的x t -图像,则下列关于物体运动的说法正确的是( )A .A 物体在7s 末速度方向改变B .两物体在第5s 末相遇C .A 物体在27s 时间内位移为4mD .05s 内两物体的平均速度不相同7.(2023秋·浙江嘉兴·高一统考期末)如图甲所示为甲物体做直线运动的x t -图像,如图乙所示为乙物体做直线运动的v t -图像。
2.1.2 有理数-七年级数学上册同步教学辅导讲义(华师大版)
2.1.2有理数同步讲义基础知识按整数、分数的关系分类:按正数、负数与0的关系分类:例题例、在下列空格里打“√”,表示该数属于哪种类型的数:类型数有理数正整数负整数正分数负分数非负数+3﹣11 30.5﹣6【答案】见解析【分析】依据有理数的分类,按整数、分数的关系分类可得:有理数包含正整数、0、负整数,正分数、负分数;按正数、负数与0的关系分类可得:有理数包含正整数、正分数、0、负整数、负分数.【详解】解:+3属于有理数,正整数,非负数;﹣113属于有理数,负分数;0属于有理数,非负数;0.5属于有理数,正分数,非负数;﹣6属于有理数,负整数.类型有理数正整数负整数正分数负分数非负数【点睛】本题考查了有理数的分类,解题的关键是熟练掌握它们之间的区别,注意0是整数,但不是正数. 练习1.下列四个选项中的数,不是分数的是( )A .80%B C .213D .2272.在下列各数中,负分数有( )1-, 3.141559-,2,13-,13,0,12,5%-,34A .1个B .2个C .3个D .4个3.零一定是( ) A .整数B .负数C .正数D .奇数4.下列语句中正确的有 ( )① 所有整数都是正数;② 所有正数都是整数;③ 自然数都是正数;④ 分数是有理数;⑤ 在有理数中除了正数就是负数. A .1 个B .2 个C .3 个D .4 个5.下列各数中,属于正有理数的是( ) A .-0.1B .0C .-1D .26.在下列各数中,正数的个数有______个.( ) -6,0.1234,152-,0.3,0,19,15A .2B .3C .4D .57.下列各数中,既不是正数又不是负数的是( ) A .2B .1C .3-D .08.下列说法正确的是( )A .正数和负数统称为有理数B .正整数包括自然数和零C .零是最小的整数D .非负数包括零和正数9.在4-, 3.5-,0,4π,54%,1,23-中,负数有_______个,分数有_______个. 10.下列各数:﹣1,2π,1.01001…(每两个1之间依次多一个0),0,227,3.14,其中有理数有_____个.11.把下列各数分别填在相应的大括号里.13,3.1415,﹣31,﹣21%,13,0,﹣0.216,﹣2020整数:{ …}; 正整数:{ …}; 负分数:{ …}; 负整数:{ …}.12.将下列各数填入适当的括号内: 9-,227,0.314-,2020,0,338-,π-,66. (1)整数集合{______…}; (2)负分数集合{______…}; (3)非负整数集合{______…}.13.在数-23,5,23,0,4,35,5.2中,是整数的_____;非正数集合____14.有理数1.7,-17,0,257-,-0.001,92-,2003和-1中,负数有____________个,其中负整数有____________个,负分数有____________个. 15.把下列各数填在相应的集合内.15,12-,0.81,3-,8%;31-.,171,0,3.14 负数集合:{ } 分数集合:{ } 非负整数集合:{ } 16.把下列各数填入它所在的集合里:-2,7,23-,0,2 015,0.618,3.14,-1.732,-5,+3①正数集合:{___________________________________…} ②负数集合:{___________________________________…} ③整数集合:{___________________________________…}④非正数集合:{_________________________________…}⑤非负整数集合:{_______________________________…}⑥有理数集合:{_________________________________…}练习参考答案1.B 【分析】根据有理数包括分数和整数,无理数一定不是分数判断即可. 【详解】故选:B . 【点睛】本题考查实数的分类,解题的关键是掌握无理数一定不是分数. 2.C 【分析】根据负分数的意义,可得答案. 【详解】解:负分数有: 3.141559-,13-,5%-,共3个,故选:C . 【点睛】本题考查了有理数,熟记有理数的分类是解题关键. 3.A 【分析】0是介于-1和1之间的整数,既不是正数也不是负数,0可以被2整除,所以0是一个特殊的偶数. 【详解】0是介于-1和1之间的整数,既不是正数也不是负数,0可以被2整除,所以0是一个特殊的偶数,只有A 选项符合. 故选:A . 【点睛】本题考查了零的相关知识,熟记并理解是解决本题的关键. 4.A 【分析】根据有理数的分类及相关概念可直接进行排除选项.解:①所有整数都是正数,错误,比如-1;②所有正数都是整数,错误,比如0.5;③自然数都是正数,错误,比如0;④分数是有理数,正确;⑤在有理数中除了正数就是负数,错误,还有零;∴正确的有一个;故选A.【点睛】本题主要考查有理数的分类,熟练掌握有理数的分类是解题的关键.5.D【分析】根据正有理数的定义即可得出答案.【详解】解:A. -0.1为负有理数,此选项不符合题意;B. 0即不是正数也不是负数,此选项不符合题意;C. -1为负有理数,此选项不符合题意;D. 2为正有理数,此选项符合题意.故选D.【点睛】本题考查了正有理数的定义,正确理解正有理数的概念是解答本题的关键.6.C【分析】根据大于0的数是正数可得结果.【详解】解:在-6,0.1234,152,0.3,0,19,15中,正数有:0.1234,0.3,19,15共4个,故选C.【点睛】本题考查了正数的定义,熟记概念是解题的关键,要注意0既不是正数也不是负数.7.D【分析】根据正数与负数的定义即可求出答案.解:0既不是正数又不是负数, 故选:D . 【点睛】本题考查正数与负数,解题的关键是正确理解正数与负数,本题属于基础题型. 8.D 【分析】按照有理数的分类进行选择. 【详解】解:A 、正数、负数和零统称为有理数;故本选项错误; B 、零既不是正整数,也不是负整数;故本选项错误; C 、零是最小是自然数,负整数比零小;故本选项错误; D 、非负数包括零和正数;故本选项正确; 故选:D . 【点睛】本题考查了有理数的分类、正数和负数;注意0是整数,但不是最小的整数. 9.2 2 【分析】根据负数及分数的定义进行解答即可. 【详解】解:4-, 3.5-,0,4π,54%,1,23-中, 负数有:4-,23-,共2个, 分数有: 3.5-,54%,共2个, 故答案为:2,2. 【点睛】本题考查的是有理数的概念,解答此题时要注意0既不是正数也不是负数,但0是有理数. 10.4. 【分析】根据有理数的定义逐一判断即可. 【详解】解:在所列实数中,有理数有﹣1、0、227、3.14,故答案为:4.【点睛】本题考查了有理数,掌握有理数的概念是解题的关键.11.13,﹣31,0,﹣2020;13;﹣21%,﹣0.216;﹣31,﹣2020【分析】依题意,根据整数、正整数、负分数、负整数的定义把有关的数填入相应的集合即可.【详解】由题知:整数:{13,﹣31,0,﹣2020…};正整数:{13…};负分数:{﹣21%,﹣0.216…};负整数:{﹣31,﹣2020…}.故填:13,﹣31,0,﹣2020;13;﹣21%,﹣0.216;﹣31,﹣2020.【点睛】本题考查对数的分类,难点在熟练的理解数分类之间依据;12.(1)9-,2020,0,66;(2)30.314,38--;(3)2020,0,66.【分析】根据整数、负分数、非负整数的意义,逐个进行判断即可.【详解】解:(1)整数有:9-,2020,0,66,故答案为:9-,2020,0,66;(2)负分数有:3 0.314,38--,故答案为:3 0.314,38--;(3)非负整数有:2020,0,66,故答案为:2020,0,66.【点睛】本题考查整数集合,负分数集合,非负整数集合,掌握有理数的分类是解题关键.13.-23,5,0,4,-23,0【分析】整数和分数统称为有理数,整数包含正整数、0、负整数;比0大的数是正数,非正数即0与负数,据此解题.【详解】解:在数-23,5,23,0,4,35,5.2中,整数的有:-23,5,0,4;非正数的有:-23,0,故答案为:-23,5,0,4;-23,0.【点睛】本题考查有理数的分类、带“非”字的有理数等知识,是重要考点,难度较易,掌握相关知识是解题关键.14.5 2 3【分析】根据负数的定义(以前学过的0以外的数叫做正数,在正数前面加负号“-”,叫做负数)以及负整数、负分数的定义,求解即可求得答案.【详解】解:负数为:-17,257-,-0.001,92-,-1共5个;负整数有:-17,-1,共2个;负分数有:257-,-0.001,92-,共3个.故答案为:5,2,3.【点睛】此题考查了有理数的分类,注意掌握负数,负整数,负分数的定义.15.12-,3-,31-.;12-,0.81,8%,31-.,3.14;15,171,0【分析】根据负数、分数及非负整数的定义即可分别判断.【详解】15,12-,0.81,3-,8%;31-.,171,0,3.14负数集合:{12-,3-,31-.…}分数集合:{12-,0.81,8%,31-.,3.14…}非负整数集合:{15,171,0…}.【点睛】此题主要考查有理数的分类,解题的关键是熟知有理数的性质及分类方法.16.①正数集合:{7,2 015,0.618,3.14,+3…};②负数集合:{-2,23-,-1.732,-5,…};③整数集合:{-2,7,0,2 015,-5,+3…};④非正数集合:{-2,23-,0,-1.732,-5,…};⑤非负整数集合:{7,0,2 015,+3…};⑥有理数集合:{-2,7,2 3-,0,2 015,0.618,3.14,-1.732,-5,+3…}【分析】根据有理数的分类即可得出答案.【详解】解:①正数集合:{7,2 015,0.618,3.14,+3…}②负数集合:{-2,23-,-1.732,-5,…}③整数集合:{-2,7,0,2 015,-5,+3…}④非正数集合:{-2,23-,0,-1.732,-5,…}⑤非负整数集合:{7,0,2 015,+3…}⑥有理数集合:{-2,7,23-,0,2 015,0.618,3.14,-1.732,-5,+3…}【点睛】本题考查了有理数的分类,解题的关键是熟练掌握它们之间的区别,注意0是整数,但不是正数.。
第05讲 有理数混合计算(6种题型)(解析版)

第05讲有理数混合计算(6种题型)考点考向一.有理数的混合运算(1)有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.(2)进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.【规律方法】有理数混合运算的四种运算技巧1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算.2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解.3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算.4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.二.计算器—基础知识(1)计算器的面板是由键盘和显示器组成.(2)开机键和关机键各是AC/ON,OFF,在使用计算器时要按AC/ON键,停止使用时要按OFF键.(3)显示器是用来显示计算时输入的数据和计算结果的装置.键上的功能是第一功能,直接输入,下面对应的是第二功能,需要切换成才能使用.(4)开方运算按用到乘方运算键x2的第二功能键”和的第二功能键“”.(5)对于开平方运算的按键顺序是:2ndfx2被开方数ENTE.(6)对于开立方运算的按键顺序是:32ndf∧被开方数ENTE.(7)部分标准型具备数字存储功能,它包括四个按键:MRC、M﹣、M+、MU.键入数字后,按M+将数字读入内存,此后无论进行多少步运算,只要按一次MRC即可读取先前存储的数字,按下M﹣则把该数字从内存中删除,或者按二次MRC.注意:由于计算器的类型不一样操作方式也不尽相同,可以参考说明书进行操作.三.计算器—有理数计算器包括标准型和科学型两种,其中科学型使用方法如下:(1)键入数字时,按下相应的数字键,如果按错可用(DEL )键消去一次数值,再重新输入正确的数字.(2)直接输入数字后,按下对应的功能键,进行第一功能相应的计算.(3)按下(﹣)键可输入负数,即先输入(﹣)号再输入数值.(4)开方运算按用到乘方运算键x 2的第二功能键”和的第二功能键“”.(5)对于开平方运算的按键顺序是:2ndfx 2被开方数ENTE 或直接按键,再输入数字后按“=”即可. (6)对于开立方运算的按键顺序是:32ndf ∧被开方数ENTE 或直接按x 3,再输入数字后按“=”即可注意:由于计算器的类型不一样操作方式也不尽相同,可以参考说明书进行操作.题型一:有理数四则混合运算一、解答题1.(2022·江苏南京·七年级期末)计算: (1)111()236+−×(-18); (2)-24-(-2)3÷83×(-3)2. 【答案】(1)-12(2)11【分析】(1)利用乘法分配律进行去括号,再进行加减计算即可;(2)先计算乘方,再计算乘除,最后进行加减计算即可.(1)解:原式=()()()111181818236⨯−+⨯−−⨯− =963−−+=12−(2)原式=()316898−−−⨯⨯ =1627−+=11【点睛】此题考查了有理数的运算,掌握先计算乘方再计算乘除,最后计算加减的运算顺序,以及适当运用乘法分配律是解题的关键.2.(2022·江苏·七年级专题练习)在1到100这100个数中,任找10个不同的数,使其倒数之和等于1.现已有2个数,为2和6,再写出另外的8个数即可.考点精讲【答案】这10个数可以是:2、6、10、12、20、30、42、56、72、90(答案不唯一)【分析】有理数的混合运算,此题要使得10个数相加和为1,可以先构造出来为1的时候,再进行计算.【详解】解:∵11111111112233491010=−+−+−+⋅⋅⋅+−+ =(112−)+(1231−)+(1341−)+…+(11910−)110+ 1111111111261220304256729010=+++++++++ ∴这10个数可以是:2、6、10、12、20、30、42、56、72、90(答案不唯一).【点睛】本题考查了有理数的综合运算,构造出1是本题的关键. (1)()()75364−⨯−−÷;(2)()2411237⎡⎤−−⨯−−⎣⎦. 【答案】(1)-26;(2)0【分析】(1)先计算有理数乘除法,再计算有理数加减法来求解;(2)先计算乘方,再计算中括号里面的,然后根据有理数乘除法的计算法则,乘方法则进行计算,最后计算加减法求解.(1)解:()()75364−⨯−−÷()359=−−−359=−+26=−(2)解:()2411237⎡⎤−−⨯−−⎣⎦ ()411297=−−⨯− ()1177=−−⨯− 11=−+0=【点睛】本题主要考查有理数的混合运算,理解有理数混合运算法则是解答关键. (1)()1347154620512⎛⎫−−+−⨯−⨯ ⎪⎝⎭; (2)5371205616815⎛⎫⨯−+− ⎪⎝⎭;(3)(﹣18)÷124×49÷(﹣16); (4)113()(10.2)(3)245÷−+−÷⨯−; (5)221283113(1)(1)(1)()32521463÷−−⨯−−−++−⨯. 【答案】(1)6(2)111−(3)29(4)4−(5)7936− 【分析】(1)根据乘法分配律拆开括号,进行运算即可;(2)根据乘法分配律拆开括号,进行运算即可;(3)把除法转化为乘法,再进行运算即可;(4)先计算括号内,把除法转化为乘法,再进行运算即可;(5)先把乘方进行计算,把除法转化为乘法,再进行运算即可.(1)原式=()134760620512⎛⎫−−+−⨯− ⎪⎝⎭134760606060620512=⨯+⨯−⨯+⨯ 1094835=+−+6=;(2)原式=3551221201201206815−⨯+⨯−⨯ 700765176=−+−111=−;(3)原式441189916=⨯⨯⨯ 29=; (4)原式()()115413253⎛⎫=⨯−+−⨯⨯− ⎪⎝⎭()12133⎛⎫=−+−⨯− ⎪⎝⎭2233=−−⨯ 22=−−4=−;(5)原式275875132721469⎛⎫=−⨯+⨯−−+⨯ ⎪⎝⎭ 5225123363=−+−+ 5252123633⎛⎫=−−++ ⎪⎝⎭115136=−+ 7936=−. 【点睛】本题考查了有理数的混合运算,掌握有理数的运算法则是解题的关键.5.(2022·江苏·七年级专题练习)计算:()81999−⨯−÷− ⎪⎝⎭. 解法1:原式()44881999⎛⎫⎛⎫=−⨯−÷− ⎪ ⎪⎝⎭⎝⎭① ()88109⎛⎫=−⨯÷− ⎪⎝⎭②0=③解法2:原式()44981998⎛⎫=−⨯−⨯− ⎪⎝⎭① 1236=−+②1362=−③步开始出现错误的;(填写序号即可)(2)请给出正确解答.【答案】(1)①;③(2)解答过程见详解【分析】(1)根据有理数运算法则判断即可;(2)按照运算法则,先进行乘除运算,再进行加减运算即可.(1)解:解法1,步骤①中“先算加减后算乘除”不符合有理数混合运算法则,故步骤①错误; 解法2,11363622−+≠−,步骤③不符合有理数加法法则,故步骤③错误. 故答案为:①;③.(2)解:原式()44981998⎛⎫=−⨯−⨯− ⎪⎝⎭1236=−+ 1235=− 【点睛】本题主要考查了有理数的混合运算,解题关键在于熟练掌握有理数混合运算的运算法则.3×4+3+4+1=20.(1)①计算:(﹣5)⊕3= ,3⊕(﹣5)= ;②说明“⊕”运算具有交换律;(2)①计算:(﹣3)⊕(4⊕2)= ,[(﹣3)⊕4]⊕2= ;②由计算结果可得“⊕”运算 结合律(填“具有”或“不具有”). 【答案】(1)①﹣16,﹣16;②见解析;(2)①-32,-27;②不具有【分析】(1)①根据新定义的运算法则,代入数值即可计算出所求式子的值;②根据a ⊕b 1ab a b =+++,可以写出b ⊕a 1ab a b =+++,然后即可说明;(2)①根据a ⊕b =ab +a +b +1,可以计算出所求式子的值;②根据①中的结果可以得到“⊕”运算是否具有结合律.【详解】解:(1)①∵a ⊕b 1ab a b =+++,∴(﹣5)⊕3=(﹣5)×3+(﹣5)+3+1=(﹣15)+(﹣5)+3+1=﹣16;3⊕(﹣5)=3×(﹣5)+3+(﹣5)+1=﹣15+3+(﹣5)+1=﹣16;故答案为:﹣16,﹣16;②∵a ⊕b 1ab a b =+++,b ⊕a 1ab a b =+++,∴a ⊕b =b ⊕a ,∴“⊕”运算具有交换律;(2)①(﹣3)⊕(4⊕2)()3=−⊕(4×2+4+2+1)()3=−⊕(8+4+2+1)()3=−⊕15,()()3153151=−⨯+−++,()453151=−+−++,32=−;[(﹣3)⊕4]⊕2()()34341⎡⎤=−⨯+−++⎣⎦⊕2=()12341⎡⎤−+−++⎣⎦⊕2()10=−⊕2()()1021021=−⨯+−++,()201021=−+−++,27=−;故答案为:﹣32,﹣27;②由计算结果可得“⊕”运算不具有结合律,故答案为:不具有.【点睛】题目主要考查有理数的四则混合运算与定义的新运算的结合,理解题中新运算的方法是解题关键.7.(2021·江苏南通·七年级期中)“分类讨论”是一种重要数学思想方法,请运用分类讨论的数学思想解决下面的问题:(1)已知3a =,1=b ,且a b <,求a b +的值;(2)已知a ,b 是有理数,当0ab ≠时,求a ab b +的值. 【答案】(1)-2或-4;(2)±2或0 【分析】(1)根据3a =,1=b ,可得3,1a b =±=±,然后根据a b <进行分类讨论即可; (2)分四种情况进行讨论:①若0a >,0b >;②若0a <,0b <;③若0a >,0b <;④若0a <,0b >,从而确定a a b b+的值. 【详解】解:(1)因为3a =,1b =,且a b <, 所以3a =−,1b =或3a =−,1b =−.则()312a b +=−+=−或()()314a b +=−+−=−,即a b +的值为-2或-4;(2)已知a ,b 是有理数,当0ab ≠时,可分为四种情况:①若0a >,0b >,112a a b b b a a b ++==+=; ②若0a <,0b <,()112a b a b a ba b +=+=−+−=−−−; ③若0a >,0b <,()110a b a b a b a b+=+=+−=−; ④若0a <,0b >,()110a b a b a b a b +=+=−+=−. 所以,a a b b+的值为±2或0. 【点睛】本题考查了绝对值的意义,分类讨论的思想,能不重不漏的分类,会确定字母的取值范围和字母的是关键.一、单选题1.(2022·江苏·七年级专题练习)一台机器有大、小齿轮用同一传送带连接,若大小齿轮的齿数分别为36和12个,大齿轮每分钟2.5×103转,则小齿轮10小时转( ) A .1.5×106转B .5×105转C .4.5×106转D .15×106转【答案】C【分析】利用大小齿轮转动的总的齿数相同,列出算式,计算出结果即可.【详解】解:小齿轮10小时转60×2.5×103×10×(36÷12)=4.5×106转. 故选:C .【点睛】本题考查了有理数四则混合运算的实际应用,根据题意列出算式是本题的关键.2.(2022·江苏·七年级专题练习)小王、小李两人分别从A 、B 两地同时相向而行,且小王到B 地后不停留而是马上继续前行.当小王走出60千米时,小李恰好走完了A 、B 两地之间距离的14,此时两人相距24千米,则A 、B 两地之间距离为 _____千米. 【答案】48或112【分析】根据题意分当两人相遇前相距24千米时,当两人相遇后相距24千米时两种情况求出A 、B 之间的距离即可.【详解】解:根据题意得:当两人相遇前相距24千米时,(60+24)÷(114−) =8434÷=844 3⨯=112(千米);当两人相遇后相距24千米时,(60﹣24)÷(114−)=363 4÷=364 3⨯=48(千米),则A、B之间的距离为48或112千米.故答案为:48或112.【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.注意分类思想的应用.有______张名片被送出.【答案】90【分析】用一个人要送出的卡片数乘以人数,即可得出结果.【详解】解:由题意得(10﹣1)×10=9×10=90(张)故答案为:90.【点睛】本题主要考查了有理数四则混合运算的应用,根据题意列出算式,是解题的关键.把一个运算符号写错了(“+”错写成“-”或“-”错写成“+”),结果算成了-17,则原式从左往右数,第______个运算符号写错了.【答案】6【分析】先确定哪一个数的符号出了错,再确定这个符号是第几个.【详解】∵1-3+5-7+9-11+13-15+17=9,∴-17小于9,∴一定是把+错写成减号了,∴这个数为[9-(-17)]÷2=13,∴是第六个符号写错了,故答案为:6.【点睛】本题考查了有理数的混合运算,大小的比较,熟练进行计算是解题的关键.三、解答题5.(2022·江苏·七年级专题练习)笑笑超市对顾客实行优惠购物,优惠规定如下:(1)如果一次性购物在500元以内,按标价给予九折优惠;(2)如果一次性购物超过500元,其中500元部分给予九折优惠,超过500元部分给予八折优惠.A.王叔叔在该超市购买了一台标价750元的吸尘器,他应付多少元?B.李阿姨先后两次去该超市购物,分别付款216和486元,如果李阿姨一次性购买,只需要付款多少元?【答案】王叔叔应付650元;李阿姨一次性购买,只需要付款678元【分析】A.根据题意,可以列出算式500×90%+(750﹣500)×80%,然后计算即可得到王叔叔应付的钱数;B.先判断486元的实际付款与原价500的商品打折后的钱数的大小关系,然后即可计算出李阿姨一次性购买,只需要付款的钱数.【详解】解:A.由题意可得,500×90%+(750﹣500)×80%=450+250×80%=450+200=650(元),答:王叔叔应付650元;B.∵500×90%=450<486,∴李阿姨第二次购物的商品原价大于500元,∴李阿姨购买的商品的原价为:216÷90%+[500+(486﹣500×90%)÷80%]=240+[500+(486﹣450)÷0.8]=240+(500+36÷0.8)=240+(500+45)=240+545=785(元),如果一次购买785元的商品实际付款为:500×90%+(785﹣500)×80%=450+285×0.8=450+228=678(元),答:李阿姨一次性购买,只需要付款678元.【点睛】本题考查有理数的混合运算,解答本题的关键是明确题意,列出相应的算式.6.(2022·江苏·七年级专题练习)观察下列两个等式:2112133−=⨯+,5225133−=⨯+.给出定义如下:使等式a﹣b=ab+1成立的对有理数a,b为“共生有理数对”,记为(a,b).如:数对(2,13),(5,23)都有“共生有理数对”.(1)数对(﹣2,1),(3,12)中是“共生有理数对”的是;(2)请再写出另外一对符合条件的“共生有理数对”(不能与题目中已有的重复).(3)小丁说:“若(a,b)是‘共生有理数对’,则(﹣b,﹣a)一定是‘共生有理数对’.”小丁说的正确吗?如果正确,请验证他的说法;如果不正确,请举出反例.【答案】(1)(3,12)(2)(﹣2,3)(答案不唯一)(3)小丁说法是正确的【分析】(1)根据“共生有理数对”的定义进行验证即可;(2)对于有理数对,只要满足新定义即可;(3)用新定义验证即可.(1)∵﹣2﹣1=﹣3,﹣2×1+1=﹣1,∴﹣2﹣1≠﹣2×1+1.∴(﹣2,1)不是“共生有理数对”.∵3﹣15=22,3×12+1=52,∴3﹣12=3×12+1.∴(3,12)是“共生有理数对”,故答案为:(3,12);(2)∵﹣2﹣3=﹣5,﹣2×3+1=﹣6+1=﹣5,∴(﹣2,3)是“共生有理数对”,故答案为:(﹣2,3)(答案不唯一);(3)若(a,b)是‘共生有理数对’,则a﹣b=ab+1,﹣b﹣(﹣a)=a﹣b=ab+1,∴(﹣b,﹣a)是‘共生有理数对’,∴小丁说法是正确的.【点睛】本题考查了有理数的混合运算,能够看懂定义并会运用定义解决问题是解题的关键.7.(2021·江苏苏州·七年级期中)如表是苏州市地铁收费标准:分段乘坐里程(公里)单程票票价1 0<里程≤6 2元2 6<里程≤11 3元3 11<里程≤16 4元4 16<里程≤23 5元5 23<里程≤30 6元6 里程20公里以上,每9公里分段加1元备注:普通乘客刷卡乘车可享受单程票票价9.5折优惠(1)求小明的妈妈刷卡乘车一个月的地铁交通费;(2)地铁公司有三种计次月票可供选择,A月票60元/20次,B月票85元/30次,C月票130元/50次.月票仅限当月使用,每次不限里程,月底清零,小明的妈妈每月用于上下班的地铁交通费最少是多少元?请说明理由.【答案】(1)167.2元;(2)交通费最少是130元,理由见解析.【分析】(1)根据题意和表格中的数据,可得出小明的妈妈每次单程票票价为4元,依据乘车时间及一天两次和普通乘客单程票价的折扣,可以计算出小明的妈妈刷卡乘车一个月的地铁交通费;(2)根据题意,利用分类讨论的方法,分别求出购买各种月票的较低费用,然后比较大小即可得出结论.【详解】解:(1)由表格可知,小明的妈妈每次单程票票价为4元,故小明的妈妈刷卡乘车一个月的地铁交通费为:4×2×22×0.95=167.2(元),即小明的妈妈刷卡乘车一个月的地铁交通费是167.2元;(2)小明的妈妈每月用于上下班的地铁交通费最少是130元,理由:∵小明妈妈一个月需要坐地铁22244⨯=(次),⨯+⨯⨯=(元),∴当选择A月票时较低的费用为:602440.95135.2+−⨯⨯=(元),当选择B月票时较低的费用为:85443040.95138.2当选择C月票时的费用为130元;<<,∵130135.2138.2∴小明的妈妈每月用于上下班的地铁交通费最少是130元.【点睛】题目主要考查有理数的混合运算的应用,理解题意,列出相应式子,同时进行分类讨论是解题关键.8.(2021·江苏苏州·七年级期中)为庆祝建党一百周年,电影公司举行“学党史,悟初心”有奖观影活动.公司拟从5种观影代金券中挑选3种作为奖品,奖品总价值不超过1000元.5种观影代金券分别是:A券499元/张,B券399元/张,C券299元/张,D券99元/张,E券19元/张.活动设一等奖1名,二等奖5名,三等奖10名.试确定三个等级奖品的名称,并简要说明理由.【答案】一等奖为C券,二等奖为D券,三等奖为E券,理由见详解【分析】根据题意,分情况计算出各个情况的总价值,找出符合题意的情况,然后再观察奖券的价值,即可得到三个等级奖品的名称.【详解】解:一等奖为C券,二等奖为D券,三等奖为E券,理由:①当一等奖为C券,二等奖为D券,三等奖为E券时,总的价值为:⨯+⨯+⨯=(元),29919951910984<,∵9841000∴当一等奖为C券,二等奖为D券,三等奖为E券时,符合题意;②当一等奖为A券,二等奖为D券,三等奖为E券时,总的价值为:⨯+⨯+⨯>(元),(不符合题意);499199519101000③当一等奖为B券,二等奖为D券,三等奖为E券时,总的价值为:⨯+⨯+⨯>(元),(不符合题意);399199519101000④当一等奖为A券,二等奖为B券,三等奖为C券时,总的价值为:49913995299101000⨯+⨯+⨯>(元),(不符合题意);综上可得,只有情况①符合题意,∴一等奖为C券,二等奖为D券,三等奖为E券.【点睛】题目主要考查有理数的四则运算的应用,理解题意,分情况计算是解题关键.9.(2022·江苏·七年级)泰州市海陵路正在进行旧城改造工程,为加强宣传力度,市政府决定派一辆宣传车宣传相关政策,如果车上的GPS系统设定以“万象城”为原点,1公里为单位长度,向南为正方向,下表是宣传车停靠点的位置,根据表中的数据回答下列列问题;宣传车出发点宣传点1 宣传点2 宣传点3 宣传点4 回出发点显示位置-9 -4 +5 -1 -3.5 -9(1)如果宣传车在上午8:00从出发点出发,以每小时8公里的速度向南行驶,在8点45分时,车上GPS显示的数字是多少?(2)如果宣传车在上午8:00从出发点出发,以每小时8公里的速度行驶,在每个宣传点宣传政策的时间是45分钟,那么回到出发点的时间是下午几点?【答案】(1)-3 ;(2)下午2:30【分析】(1)计算得出45分钟行驶的路程,即可求解;(2)先计算出每次所走路程之和,再除以速度,后加上在每个宣传点宣传政策所需的时间,即可求解.【详解】解:(1)车上GPS显示的数字是:45893 60⨯−=−;(2)根据题意得:()9445511 3.5 3.598 3.5−++−−+++−++−+÷=(小时),∴453.54 6.560+⨯=(小时),∴上午8:00从出发点出发,回到出发点的时间是下午2:30.【点睛】本题考查了有理数的混合运算、正数和负数和绝对值的概念,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.题型三:程序流程图与有理数计算一、单选题1.(2022·江苏扬州·七年级期末)如图,在这个数运算程序中,若开始输入的正整数n为奇数,都计算3n+1;若n为偶数,都除以2.若n=21时,经过1次上述运算输出的数是64;经过2次上述运算输出的数是32;经过3次上述运算输出的数是16;…;经过2022次上述运算输出的数是().A.1 B.2 C.3 D.4【答案】B【分析】分别求出部分输出结果,发现第1次输出结果到第4次输出结果只出现一次,从第5次输出结果开始,每3次结果循环一次,则经过2022次上述运算输出的数与第6次输出的结果相同,由此可求解.【详解】解:当n=21时,经过1次运算输出的数是64,经过2次运算输出的数是32,经过3次运算输出的数是16,经过4次运算输出的数是8,经过5次运算输出的数是4,经过6次运算输出的数是2,经过7次运算输出的数是1,经过8次运算输出的数是4,经过9次运算输出的数是2,……∴第1次输出结果到第4次输出结果只出现一次,从第5次输出结果开始,每3次结果循环一次,∵(2022﹣4)÷3=672……2,∴经过2022次上述运算输出的数与第6次输出的结果相同,故选:B.【点睛】本题考查数字的变化规律,通过运算找到输出结果的循环规律是解题的关键.二、填空题2.(2022·江苏淮安·七年级期末)如图是一个数值运算程序,当输入的值为﹣2时,则输出的的值为_____.【答案】-18【分析】把x=﹣2代入运算程序求值即可得最后结果.【详解】解:把x=﹣2代入得,(﹣2)2×(﹣5)+2=4×(﹣5)+2=﹣20+2=﹣18,故答案为:﹣18.【点睛】本题考查了代数式求值,有理数的混合运算,掌握运算程序的意义,读懂题意是解题关键.3.(2022·江苏·七年级专题练习)如图,是一个“数值转换机”的示意图.若x =﹣5,y =3,则输出结果为 _____.【答案】13【分析】根据题意可得,把5x =−,3y =代入()2012x y +进行计算即可解答. 【详解】解:当5x =−,3y =时, ()()2200111532613222x y ⎡⎤+=−+=⨯=⎣⎦. 故答案为:13.【点睛】本题考查了有理数的混合运算,准确熟练地进行计算是解题的关键.4.(2022·江苏宿迁·七年级期末)如图,是一个运算程序的示意图,若开始输入x 的值为25,则第2022次输出的结果为_____.【答案】1【分析】由题意利用程序图进行运算,可以发现从第一次开始输出的结果以5,1为循环节循环,由此可得结论. 【详解】解:由题意得: 第一次输入25,输出结果为:5; 第二次输入5,输出结果为:1; 第三次输入1,输出结果为:5; 第四次输入5,输出结果为:1; 第五次输入1,输出结果为:5; 第六次输入5,输出结果为:1;∴从第一次开始输出的结果以5,1为循环节循环, ∵2022÷2=1011, ∴第2022次输出的结果为:1. 故答案为:1.【点睛】本题主要考查了求代数式的值,有理数的混合运算,本题是操作型题目,理解并正确操作程序是解题的关键.5.(2022·江苏泰州·七年级期末)在如图所示的数值转换器中,如果输入的x 、y 满足()21202x y −++=,那么输出的结果为__________.【答案】0.5【分析】根据(2−x )2+|y +12|=0,可以得到x 、y 的值,然后将x 的值代入,求出最后可以输出的x 的值即可.【详解】解:∵()21202x y −++=, ∴2-x =0,y +12=0, 解得x =2,y =-12,∴(-0.5)x =(-0.5)×2=-1<-12, 当x =-1时,(-0.5)x =(-0.5)×(-1)=0.5>-12, 故答案为:0.5.【点睛】本题考查有理数的混合运算、非负数的性质,解答本题的关键是求出最后的x 的值. 内的运算后,把结果输入下一个方框继续进行运算),输出结果为_____.【答案】2021【分析】把1921代入程序中计算,判断即可得到结果.【详解】解:把1921代入得:(1921-1840+50)×(-1)=-131<1000, 把-131代入得:(-131-1840+50)×(-1)=1921>1000, 则输出结果为1921+100=2021. 故答案为:2021.【点睛】本题考查了有理数的混合运算,弄清程序中的运算过程是解本题的关键. 三、解答题7.(2022·江苏·七年级专题练习)如图所示,某数学活动小组编制了一道有理数混合运算题,即输入一个有理数,按照自左向右的顺序运算,可得计算结果,其中“●”表示一个有理数.(1)若●表示2,输入数为3−,求计算结果;(2)若计算结果为8,且输入的数字是4,则●表示的数是几?(3)若输入数为a ,●表示的数为b ,当计算结果为0时,请求出a 与b 之间的数量关系. 【答案】(1)3 (2)-17 (3)21b a =−−【分析】(1)根据题意代入相应的值运算即可;(2)设●表示的数为x ,根据题意得出相应的方程求解即可;(3)根据输入数为a ,●表示的数为b ,当计算结果为0时,求出a ,b 之间的关系. (1)解:∵●表示2,输入数为3−∴(3)(4)2(1)2122123−⨯−÷+−−=÷−−=; (2)解:设●表示的数为x ,根据题意得:4(4)2(1)8x ⨯−÷+−−=, ∴17x =−;(3)解:∵输入数为a ,●表示的数为b ,当计算结果为0时, ∴4(1)02ab −+−−=, 整理得21b a =−−.【点睛】本题主要考查有理数的混合运算,解答的关键理解清楚题意,并掌握相应的运算法则.题型四:算“24”点一、填空题 1.(2022·江苏·七年级专题练习)将这四个数3、4、﹣6、10(每个数用且只用一次)进行加、减、乘、除运算,使其结果等于24,请你写出两个符合条件的算式_________________________.(可以用括号)【答案】3×(4﹣6+10)=24;10﹣4﹣(﹣6×3)=24(答案不唯一) 【分析】根据有理数的运算法则和运算顺序,写出算式即可.【详解】解:①3×(4﹣6+10)=24;②10﹣4﹣(﹣6×3)=24;③4﹣(﹣6)÷3×10=24等.故答案为:3×(4﹣6+10)=24;10﹣4﹣(﹣6×3)=24(答案不唯一).【点睛】本题主要考查了有理数的混合运算,熟练的掌握有理数的运算法则和运算顺序是解题的关键.2.(2022·江苏·七年级专题练习)小明和同学们玩扑克牌游戏.游戏规则是:从一副扑克牌(去掉“大王”“小王”)中任意抽取四张,根据牌面上的数字进行混合运算(每张牌上的数字只能用一次),使得运算结果等于24.小明抽到的牌如图所示,请帮小明列出一个结果等于24的算式 _____.【答案】(5-3+2)×6(答案不唯一)【分析】根据有理数的加、减、乘、除、乘方运算法则,进行计算即可解答. 【详解】解:由题意得: (5-3+2)×6=24, 故答案为:(5-3+2)×6(答案不唯一).【点睛】本题考查了有理数的混合运算,熟练掌握有理数的加、减、乘、除、乘方运算法则是解题的关键.3.(2021·江苏镇江·七年级期末)将四个数2,﹣3,4,﹣5进行有理数的加、减、乘、除、乘方运算,列一个算式_____(每个数都要用,且只能用一次,写出一个即可),使得运算结果等于24.【答案】2×[4﹣(﹣3)﹣(﹣5)]=24(答案不唯一). 【分析】根据有理数的运算法则求解. 【详解】解:2×[4﹣(﹣3)﹣(﹣5)] =2×(4+3+5) =2×12 =24,故答案为:2×[4﹣(﹣3)﹣(﹣5)]=24(答案不唯一).【点睛】本题考查有理数的四则混合运算,熟练掌握有理数的运算法则是解题关键. 二、解答题4.(2021·江苏扬州·七年级阶段练习)有一种“24”点游戏,其游戏规则是:任取一副扑克牌,我们约定A 为1,J 、Q 、K 分别为11、12、13,并规定方块、红桃牌为正,黑桃、梅花牌为负.任取4张牌,将这4张牌的牌面所表示的数进行加、减、乘、除运算(使用括号).每个数用且只用一次,使其结果等于24.如:抽出4张牌黑桃4、梅花2、方块4、红桃3,可做运算:(4)(2)4324−÷−⨯⨯=.(1)若抽出黑桃3,梅花1,方块5,红桃3,请写出1种算式,并写出计算过程,验证结果为24.(2)若抽出黑桃3、梅花K 、方块8、红桃Q ,请写出2种不同的算式,并写出计算过程,验证结果为24(3)若抽出黑桃4、梅花7、方块2、红桃3,请设计1种含“乘方”的混合运算的算式,并写出计算过程,验证结果为24.【答案】(1)()()()315324−⨯−⨯+=;(2)()()38131224−⨯⨯−+=;(){}12313824⎡⎤⨯−−−−=⎣⎦;(3)()()324724⎡⎤⨯−−−=⎣⎦【分析】(1)根据所给的数是-3、-1、5、3,应用有理数混合运算的运算方法,凑成24即可;(2)根据所给的数是-3、-13、8、12,应用有理数混合运算的运算方法,凑成24即可; (3)根据所给的数是-4、-7、2、3,应用有理数混合运算的运算方法,凑成24即可. 【详解】(1)()()()31533824−⨯−⨯+=⨯=; (2)()()()38131224124−⨯⨯−+=−⨯−=; (){}()1231381210812224⎡⎤⨯−−−−=⨯−=⨯=⎣⎦;(3)()()32478324⎡⎤⨯−−−=⨯=⎣⎦.【点睛】本题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.5.(2022·江苏·七年级专题练习)小刚与小明在玩数字游戏,现有5张写着不同数字的卡片(如图),小刚请小明按要求抽出卡片,完成下列各问题:(1)从中取出2张卡片,使这2张卡片上的数字乘积最大,如何抽取?最大值是多少? (2)从中取出2张卡片,使这2张卡片上的数字相除的商最小,如何抽取?最小值是多少? (3)从中取出4张卡片,用学过的运算方法,使结果为24,如何抽取?写出运算式子(一种即可).【答案】(1)15;(2)-5;(3)答案不唯一,如[-(+3)+(-5)]×[(-1)2-(+4)]=24. 【分析】(1)抽取两个数字,使得之积最大即可; (2)抽取两个数字,使得之商最小即可;(3)抽取两个数字,利用“24”点游戏规则列出算式即可. 【详解】解:(1)根据题意得,-(+3)×(-5)=15. 则抽取卡片上的数字分别为-(+3)和-5这2张,积的值最大,最大值为 15; (2)根据题意得:-5÷(-1)2 则抽取卡片上的数字分别为-5和(-1)2这2张,商的值最小,最小值为-5; (3) [-(+3)+(-5)]×[(-1)2-(+4)]=24(答案不唯一).【点睛】本题考查的知识点是有理数的混合运算,掌握有理数混合运算的运算顺序是解此题的关键.一、单选题 1.(2021·江苏·七年级专题练习)在我国远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,类似现在我们熟悉的“进位制”.如图所示是远古时期一位母亲记录孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满五进一,根据图示可知,孩子已经出生的天数是( )A .27B .42C .55D .210【答案】B【分析】由题可知,孩子出生的天数的五进制数为132,化为十进制数即可. 【详解】解:根据题意得:孩子出生的天数的五进制数为132, 化为十进制数为:132=1×52+3×51+2×50=42. 故选:B .【点睛】本题主要考查了进位制,解题的关键是会将五进制转化成十进制. 二、填空题2.(2021·江苏南京·七年级期中)对于有理数x ,y ,若x +y ,x ﹣y ,xy ,xy这四个数中恰有三个数相等,则x +y 2=__________________. 【答案】12或32【分析】此题可以先根据分母y 不为0,确定x +y 与x ﹣y 不相等,再分类讨论即可. 【详解】解:因为xy有意义,所以y 不为0, 故x +y 和x ﹣y 不相等,分两种情况: ①x +y =xy =x y, 解得y =﹣1,x =12;②x ﹣y =xy =x y, 解得y =﹣1,x =﹣12,所以x +y 2=213(1)22+−=或211(1)22−+−=.故答案为:12或32.【点睛】本题主要考查了有理数的混合运算,解答本题的关键是分类讨论思想的运用. 3.(2022·江苏·七年级专题练习)淇淇在计算:2022311(1)(2)623⎛⎫−−−+÷− ⎪⎝⎭时,步骤如下:。
吴军·阅读与写作50讲(合集)

后来美国全方位研究了苏联基础科学研究领域领先的原因,发现在沙皇俄国 时代,俄国在人文艺术领域的教育水平和成就极高。我们知道那时俄国有托 尔斯泰这样的文豪,有柴可夫斯基这样的艺术家。 于是美国人得出了一个结论,人文和艺术的素养,可以激发科学技术上的创 造力,于是之后美国就加强了人文教育。今天它的科技原创力在世界上首屈 一指,也许就与此有关。 而且,这件事还有后续,到了 20 世纪末,美国又重新审视了俄罗斯的科研 水平,发现它已经是世界二流了。研究认为,这和苏联时代重理轻文,理科 和工科分校的教育模式有很大的关系。 当然,人文和艺术素养的培养涉及到很多方面,但经典文学的阅读,肯定是 必不可少的一环,也是适用面最广的一环。 需要提醒你的是,阅读和写作,是一种能力而不是一些知识,所以,我的方 法论只是教给了你一些工具,它还需要大量的实践。所以,这门课有一个特 色,每一讲后面,我会布置阅读材料。 当然,如果你现在比较忙,没时间全读也没有关系,可以在接下来的一年, 甚至更长的时间里慢慢读完其中的一些书。 而且,很多时候,我还会请你就当天的学习内容,写一篇两三百字的小文章。 我会抽时间评点作业。不用担心自己写得不够好,坚持练习就会有进步。 种下一棵树最好的时间是十年前,其次是现在。阅读和写作能力的培养也是 如此。 期待你加入这课,在未来的人生中,也能抓住这一张能力王牌。
更多PDF合集+微信 1107308023
21 如何写好一篇报告?........................................................ 153 22 小结:美国的大语文教育给我们什么启发?................159 23 《春江花月夜》| 如何从传世之作参悟渺小人生?... 165 24 《九三年》| 如何理解复杂的人性?............................174 25 英伦情诗 | 爱要怎么说出口?......................................180 26 《俄狄浦斯王》| 如何理解人生的底色?....................189 27 罗曼·罗兰 | 年轻时为什么需要理想主义?..............195 28 《十日谈》| 精读和泛读各自有什么意义?................200 29 《李尔王》| 什么样的作品能穿越时空?....................206 30《红楼梦》| 曹雪芹到底是在讲谁的故事?..................213 31《诗经》| 为什么是理工男恋爱宝典?..........................219 32 《简·爱》| 为什么是现代女性必读书?....................224 33 《牡丹亭》| 什么是中国人的浪漫情怀?....................231 34 《傲慢与偏见》| 奥斯汀为什么长盛不衰?................238 35 《呼啸山庄》| 如何理解文学里的黑色话题?........... 245 36 川端康成 | 如何更深地理解日本美学?......................251 37 《浮士德》| 如何理解德国的崛起?............................257 38 普希金 | 怎么理解俄罗斯文化里的精英责任?......... 264 39 托尔斯泰 | 怎么理解贵族的自我救赎?......................270 40 马克·吐温 | 怎么理解高速发展产生的社会问题?. 277 41 海明威 | 人在物质满足后有什么困惑?......................283 42 鲁迅 | 怎么理解文学与社会变革?..............................289
第05讲 有理数的乘除(解析版)新七年级数学暑假精品课(北师大版)

第05讲有理数的乘除1.理解有理数乘法、除法法则;理解倒数概念2.能利用乘法则进行简单的有理数的乘运算;3.能掌握乘法的运算定律和运算技巧,熟练计算;4.通过将除法转化成乘法,初步培养学生数学的归一思想知识点1:乘法法则(1)两数相乘,同号得正,异号得负,并把绝对值相乘。
(2)任何数同0相乘,都得0。
(3)多个不为0的数相乘,负因数的个数是偶数时,积为正数;负因数的个数是奇数时,积为负数,即先确定符号,再把绝对值相乘,绝对值的积就是积的绝对值。
(4)多个数相乘,若其中有因数0,则积等于0;反之,若积为0,则至少有一个因数是0。
知识点2:除法法则(1)除以一个(不等于0)的数,等于乘这个数的倒数。
(2)两个数相除,同号得正,异号得负,并把绝对值相除。
(3)0除以任何一个不等于0的数,都得0。
知识点3:倒数(1)定义:的两个数互为倒数。
(2)性质:负数的倒数还是负数,正数的倒数是正数。
注意:①0没有倒数;②倒数等于它本身的数为.知识点4:乘法运算定律(1)乘法交换律:两数相乘,交换因数的位置,积相等。
即a×b=ba(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。
即a×b×c=﹙a×b﹚×c=a×﹙b×c﹚。
(3)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,在把积相加即a×﹙b+c﹚=a×b+a×c。
考点1:有理数乘除法法则辨析例1(2022秋•射洪市期末)如果三个非零有理数的积为正数,则下列结论:①这三个数同号;②若其中一个数是正数,则另外两个数同号;③若其中一个数是负数,则另外两个数同号;④若其中一个数是负数,则另外两个数异号.其中必定成立的有()A.1个B.2个C.3个D.4个【答案】B【解答】解:∵若这三个数同为负数,符号相同,但它们的积为负数,∴①的结论不正确;∵若其中一个数是正数,另外两个数同号,则它们的积为正数,∴②的结论正确;∵若三个数中,其中一个数是负数,另外两个数异号,则它们的积为正数,∴③的结论不正确;∵若其中一个数是负数,另外两个数异号,则它们的积为正数,∴④的结论正确;∴②④,故选:B.【变式1-1】(2022秋•抚远市期末)若a+b>0,且ab<0,则以下正确的选项为()A.a,b都是正数B.a,b异号,正数的绝对值大C.a,b都是负数D.a,b异号,负数的绝对值大【答案】B【解答】解:∵ab<0,∴a,b异号,∵a+b>0,∴正数的绝对值大,故选:B.【变式1-2】(2022秋•碑林区校级期末)下列叙述正确的是()A.互为相反数的两数的乘积为1B.所有的有理数都能用数轴上的点表示C.绝对值等于本身的数是0D.n个有理数相乘,负因数的个数为奇数个时,积为负【答案】B【解答】解:A、互为相反数的两个数和为0,故A错误.B、实数和数轴一一对应,故所有的有理数都能用数轴上的点表示.故B正确.C、绝对值等于本身的是0和正数,故C错误.D、n个有理数相乘,负因数的个数为奇数个时,积为负,但0除外,故D错误、故选:B.【变式1-3】(2022秋•武冈市期中)两个有理数的积为负数,和为正数,那么这两个有理数()A.符号相反,且正数的绝对值较大B.符号相反,绝对值相等C.符号相反,且负数的绝对值较大D.符号相同【答案】A【解答】解:∵两个有理数的积为负数,说明两数异号,和为正数,说明这两个数中正数绝对值大于负数的绝对值.∴A选项正确,故选:A.【变式1-4】(2022秋•鹿城区校级期中)若两个数的商是正数,则下列选项中一定成立的是()A.这两数的和为正数B.这两数的差为正数C.这两数的积为正数D.这两数的和、差、积的正负都不能确定【答案】C【解答】解:A.当两个数都为负数时,这两个数的商是正数,这两个数的和为负数,故A选项不符合题意;B.当两个数都为负数时,这两个数的商是正数,这两个数的差可能为负数,故B选项不符合题意;C.若两个数的商是正数,则这个两数为同号,这两个数的积为正数,故C选项符合题意;D.若两个数的商是正数,这两数的和、差、积的正负都能确定正负,故D选项不符合题意.故选:C.考点2:倒数的概念及运用例2.(2023•西和县二模)4的倒数是()A.4B.C.D.﹣4【答案】B【解答】解:4的倒数是.故选:B.【变式2-1】(2022秋•大丰区期末)若m,n互为倒数,则|mn﹣2|=1.【答案】1.【解答】解:∵m,n互为倒数,∴mn=1,∴|mn﹣2|=|1﹣2|=|﹣1|=1,故答案为:1.【变式2-2】(2022秋•江夏区期中)若a、b互为倒数,则(﹣ab)2022=1.【答案】1.【解答】解:∵a和b互为倒数,∴ab=1,∴(﹣ab)2022=(﹣1)2022=1,故答案为:1.【变式2-3】(2023•九江一模)若m、n互为相反数,p、q互为倒数,则−2023m+−2023n 的值是3.【答案】3.【解答】解:∵m、n互为相反数,p、q互为倒数,∴m+n=0,pq=1,∴−2023m+−2023n=﹣2023(m+n)+=0+3=3.故答案为:3.考点3:有理数乘除法简单运算例3.(2023•龙川县校级开学)计算:.【答案】﹣.【解答】解:原式=(﹣)×(﹣)×(﹣)=﹣.【变式3-1】(2022秋•松江区期末)计算:4.【答案】8.【解答】解:原式=××=8.【变式3-2】(2022秋•綦江区校级月考)计算:(1)(﹣8)×(﹣6)×(﹣1.25)×;(2)(﹣81)÷(﹣2)×÷(﹣8).【答案】(1)﹣20;(2)﹣2.【解答】解:(1)(﹣8)×(﹣6)×(﹣1.25)×=﹣8×1.25×6×=﹣10×2=﹣20;(2)(﹣81)÷(﹣2)×÷(﹣8)=(﹣81)×(﹣)××(﹣)=﹣81×××=﹣2.【变式3-3】(2022秋•市中区校级月考)计算:(1)﹣56×(﹣)÷(﹣1).(2)(﹣12)÷(﹣4)×.【答案】(1)﹣15;(2).【解答】解:(1)﹣56×(﹣)÷(﹣1)=﹣56×(﹣)×(﹣)=﹣15;(2)(﹣12)÷(﹣4)×=3×=.考点4:有理数乘法运算定律的运用例4.(2022秋•朝阳区校级月考)用简便方法计算:①;②.【答案】①﹣2;②﹣2398.【解答】解:①原式=(﹣)×(﹣36)﹣×(﹣36)+×(﹣36)=3+1﹣6=﹣2.②原式=(﹣100+)×24=﹣100×24+×24=﹣2400+2=﹣2398.【变式4-1】(2022秋•济南期中)(﹣+)×(﹣24).【答案】见试题解答内容【解答】解:原式=×(﹣24)﹣×(﹣24)+×(﹣24)=﹣12+4﹣8=﹣16.【变式4-2】(2022秋•泰州月考)用简便方法计算:(1);(2)(﹣99)×999.【答案】(1)﹣159;(2)﹣98901.【解答】解:(1)原式=(20﹣)×(﹣8)=20×(﹣8)﹣×(﹣8)=﹣160+=﹣159;(2)原式=(1﹣100)×999=999﹣100×999=999﹣99900=﹣98901.【变式4-3】(2021春•徐汇区校级期中)计算:24×(﹣99).【答案】﹣2399.【解答】解:原式=﹣24×=﹣24×(100﹣)=﹣24×100+24×=﹣2400+=﹣2399.考点5:有理数乘除法与绝对值的综合例5.(2022秋•乳山市期中)已知|a|=6,|b|=4,且ab<0,求a+b的值.【答案】2或﹣2.【解答】解:∵|a|=6,|b|=4,且ab<0,∴a=6,b=﹣4或a=﹣6,b=4,∴a+b的值为2或﹣2.【变式5-1】(2022秋•朝阳区校级月考)已知|x|=5,|y|=3,若xy>0,求|x﹣y|的值.【答案】2.【解答】解:∵|x|=5,|y|=3,∴x=±5,y=±3,∵xy>0,∴①x=5,y=3,则|x﹣y|=|5﹣3|=2,②x=﹣5,y=﹣3,则|x﹣y|=|﹣5﹣(﹣3)|=2,∴|x﹣y|的值为2.【变式5-2】(2021秋•万州区期末)对于有理数x,y,若<0,则++的值是()A.﹣3B.﹣1C.1D.3【答案】B【解答】解:∵<0,∴x,y异号.∴xy<0,∴==﹣1,当x>0时,y<0,则==﹣1,==1,∴原式=﹣1+(﹣1)+1=﹣1.当x<0时,y>0,则则==1,==﹣1.∴原式=﹣1+1﹣1=﹣1.故选:B.【变式5-3】(2022秋•姜堰区期中)若|x|=2,|y|=3,且<0,则2x﹣y=.【答案】±7.【解答】解:因为|x|=2,|y|=3,所以x=±2,y=±3,又<0,所以当x=2,y=﹣3时,2x﹣y=7;当x=﹣2,y=3时,2x﹣y=﹣7.则2x﹣y=±7,故答案为:±7.考点6:有理数乘除法中的规律计算例6.(2022秋•石楼县期末)请你先认真阅读材料:计算解:原式的倒数是(﹣+)÷()=(﹣+)×(﹣30)=×(﹣30)﹣×(﹣30)+×(﹣30)﹣×(﹣30)=﹣20﹣(﹣3)+(﹣5)﹣(﹣12)=﹣20+3﹣5+12=﹣10故原式等于﹣再根据你对所提供材料的理解,选择合适的方法计算:.【答案】见试题解答内容【解答】解:原式的倒数是:(﹣+﹣)÷(﹣)=(﹣+﹣)×(﹣42)=﹣(×42﹣×42+×42﹣×42)=﹣(7﹣9+28﹣12)=﹣14,故原式=﹣.【变式6】(2022秋•越城区期中)阅读下题解答:计算:.分析:利用倒数的意义,先求出原式的倒数,再得原式的值.解:×(﹣24)=﹣16+18﹣21=﹣19.所以原式=﹣.根据阅读材料提供的方法,完成下面的计算:.【答案】见试题解答内容【解答】解:根据题意得:[﹣++(﹣)2×(﹣6)]÷(﹣)=[﹣++×(﹣6)]×(﹣42)=﹣21+14﹣30+112=75,则原式=.【变式6-2】(2021秋•平罗县期末)计算:.【答案】﹣18.【解答】解:==﹣×36﹣×36+×36=﹣27﹣6+15=﹣18.1.(2022•张家界)﹣2022的倒数是()A.2022B.﹣C.﹣2022D.【答案】B【解答】解:﹣2022的倒数是:﹣.故选:B.2.(2022•包头)若a,b互为相反数,c的倒数是4,则3a+3b﹣4c的值为()A.﹣8B.﹣5C.﹣1D.16【答案】C【解答】解:∵a,b互为相反数,c的倒数是4,∴a+b=0,c=,∴3a+3b﹣4c=3(a+b)﹣4c=0﹣4×=﹣1.故选:C.3.(2022•台州)计算﹣2×(﹣3)的结果是()A.6B.﹣6C.5D.﹣5【答案】A【解答】解:﹣2×(﹣3)=+(2×3)=6.故选:A.4.(2020•台湾)已知a=(﹣12)×(﹣23)×(﹣34)×(﹣45),b=(﹣123)×(﹣234)×(﹣345),判断下列叙述何者正确?()A.a,b皆为正数B.a,b皆为负数C.a为正数,b为负数D.a为负数,b为正数【答案】见试题解答内容【解答】解:∵a=(﹣12)×(﹣23)×(﹣34)×(﹣45)中共有4个负数相乘,∴a为正数,∵b=(﹣123)×(﹣234)×(﹣345)中共有3个负数相乘,∴b为负数,∴a为正数,b为负数,故选:C.5.(2020•山西)计算(﹣6)÷(﹣)的结果是()A.﹣18B.2C.18D.﹣2【答案】C【解答】解:(﹣6)÷(﹣)=(﹣6)×(﹣3)=18.故选:C.1.(2023•荆门一模)下列说法中,正确的是()A.2与﹣2互为倒数B.2与互为相反数C.0的相反数是0D.2的绝对值是﹣2【答案】C【解答】解:A.2与﹣2互为相反数,故选项A不正确B.2与互为倒数,故选项B不正确;C.0的相反数是0,故选项C正确;D.2的绝对值是2,故选项D不正确.故选:C.2.(2022秋•抚远市期末)若a+b>0,且ab<0,则以下正确的选项为()A.a,b都是正数B.a,b异号,正数的绝对值大C.a,b都是负数D.a,b异号,负数的绝对值大【答案】B【解答】解:∵ab<0,∴a,b异号,∵a+b>0,∴正数的绝对值大,故选:B.3.(2022秋•路北区期末)若a,b在数轴上的位置如图所示,则下列结论正确的是()A.a<﹣b B.﹣a<b C.a+b>0D.ab>0【答案】A【解答】解:由题意可得:a<0<b,且|a|>|b|,A、a<﹣b,正确,故此选项符合题意;B、﹣a>b,原结论错误,故此选项不符合题意;C、a+b<0,原结论错误,故此选项不符合题意;D、ab<0,原结论错误,故此选项不符合题意;故选:A.4.(2022秋•碑林区校级期末)下列叙述正确的是()A.互为相反数的两数的乘积为1B.所有的有理数都能用数轴上的点表示C.绝对值等于本身的数是0D.n个有理数相乘,负因数的个数为奇数个时,积为负【答案】B【解答】解:A、互为相反数的两个数和为0,故A错误.B、实数和数轴一一对应,故所有的有理数都能用数轴上的点表示.故B正确.C、绝对值等于本身的是0和正数,故C错误.D、n个有理数相乘,负因数的个数为奇数个时,积为负,但0除外,故D错误、故选:B.5.(2022•小店区校级模拟)(﹣9)×(﹣)的结果是()A.﹣3B.3C.27D.﹣27【答案】B【解答】解:(﹣9)×(﹣)=3.故选:B.6.(2022秋•防城区期中)已知|a|=2,|b|=3,且a•b<0,则a+b的值为()A.5或﹣5B.1或﹣1C.3或﹣2D.5或1【答案】B【解答】解:∵|a|=2,|b|=3,且ab<0,∴a=2,b=﹣3或a=﹣2,b=3,∴a+b=2+(﹣3)=﹣1或a+b=﹣2+3=1.故选:B.7.(2022秋•武冈市期中)两个有理数的积为负数,和为正数,那么这两个有理数()A.符号相反,且正数的绝对值较大B.符号相反,绝对值相等C.符号相反,且负数的绝对值较大D.符号相同【答案】A【解答】解:∵两个有理数的积为负数,说明两数异号,和为正数,说明这两个数中正数绝对值大于负数的绝对值.∴A选项正确,故选:A8.(2022春•南岗区校级月考)计算﹣6××|﹣|×1的值为()A.1B.36C.﹣1D.0【答案】C【解答】解:原式=﹣6×××=﹣6×××=﹣1故选:C.9.(2021秋•青龙县期末)有理数a,b在数轴上对应点的位置如图所示,则正确的式子是()A.a>0B.b<0C.ab>0D.ab<0【答案】D【解答】解:由数轴可知,a<0,b>0,ab<0,∴只有D选项正确,故选:D.10.(2022秋•隆安县期中)下列算式中,积为负数的是()A.0×(﹣5)B.4×(﹣0.2)×(﹣10)C.(﹣1.5)×(﹣2)D.(﹣3)×(﹣)×(﹣)【答案】D【解答】解:A:0×(﹣5)=0,故A错;B:4×(﹣0.2)×(﹣10)=8,故B错;C:(﹣1.5)×(﹣2)=3,故C错;D:(﹣3)×(﹣)×(﹣)=﹣.故D正确.故选:D.11.(2022秋•天河区校级期中)若|a|=3,|b|=4,a<b,且ab<0,则a与b的值是()A.a=3,b=4B.a=3,b=﹣4C.a=﹣3,b=4D.a=﹣3,b=﹣4【答案】C【解答】解:∵|a|=3,|b|=4,∴a=±3,b=±4,∵ab<0,a<b,∴a=﹣3,b=4,故选:C.12.(2022秋•江津区期中)若a、b互为倒数,则(ab﹣2)2022=1.【答案】1.【解答】解:∵a,b互为倒数,∴ab=1,则原式=(1﹣2)2022=1.故答案为:1.13.(2022•宽城县一模)若a、b互为相反数,则a+(b﹣2)的值为﹣2;若a、b互为倒数,则﹣2022ab=﹣2022.【答案】﹣2;﹣2022.【解答】解:∵a、b互为相反数,∴a+b=0,∴a+(b﹣2)=a+b﹣2=0﹣2=﹣2;∵a、b互为倒数,∴ab=1,∴﹣2022ab=﹣2022.故答案为:﹣2;﹣2022.14.(2022春•龙凤区期中)a、b、c为有理数,且abc<0,则++=1或﹣3.【答案】见试题解答内容【解答】解:∵abc<0,∴a、b、c有1个或3个数为负数,当有1个是负数,两个是正数时,++=1+1+(﹣1)=1,当3个负数时,++=﹣1﹣1﹣1=﹣3,综上所述,++=1或﹣3.故答案为:1或﹣3.15.(2021秋•常熟市校级月考)已知|x|=4,|y|=7,且<0,则x+y=﹣3或3.【答案】见试题解答内容【解答】解:∵|x|=4,|y|=7,且<0,∴x=4,y=﹣7;x=﹣4,y=7,则x +y =﹣3或3.故答案为:﹣3或3.16.(2022秋•宁远县校级月考)求值:(1)×(﹣16)×(﹣)×(﹣1);(2)(﹣)×(﹣)×(﹣2)×(﹣).【答案】(1)﹣4;(2).【解答】解:(1)×(﹣16)×(﹣)×(﹣1)=﹣=﹣4;(2)(﹣)×(﹣)×(﹣2)×(﹣)==.17.(2021春•虹口区校级期中)计算:.【答案】1.【解答】解:原式====1.18.(2021秋•洪泽区校级月考)计算:(1)﹣3÷(﹣)÷(﹣);(2)(﹣12)÷(﹣4)÷(﹣1);(3)(﹣)×(﹣)÷0.25;(4)(﹣2)÷(﹣5)×(﹣3).【答案】(1)﹣;(2)﹣;(3);(4)﹣.【解答】解:(1)原式=﹣3×(﹣)×(﹣)=﹣;(2)原式=(﹣12)×(﹣)×(﹣)=﹣;(3)原式=(﹣)×(﹣)×4=;(4)原式=(﹣)×(﹣)×(﹣)=﹣19.(2022秋•南安市校级期中)﹣24×(﹣+﹣)【答案】见试题解答内容【解答】解:﹣24×(﹣+﹣),=﹣×(﹣24)+×(﹣24)﹣×(﹣24),=20﹣9+2,=22﹣9,=13.20.(2022秋•宿豫区期中)用简便方法计算:.【答案】.【解答】解:=====.21.(2022秋•惠城区月考)计算:.【答案】﹣3300.【解答】解:45×(﹣25)××(﹣)÷×(﹣1)=﹣(45×25×××4×)=﹣(××45××25×4)=﹣3300.22.(2022秋•铜山区校级月考)已知|x|=3,|y|=6.若xy<0,求x+y的值.【答案】﹣3或3.【解答】解:∵|x|=3,|y|=6,∴x=±3,y=±6,∵xy<0,①x=3,y=﹣6,x+y=3+(﹣6)=﹣3,②x=﹣3,y=6,x+y=﹣3+6=3,∴x+y=﹣3或3.23.(2022秋•高安市期中)请利用绝对值的性质,解决下面问题:(1)已知a,b是有理数,当a>0时,则=1;当b<0时,则=﹣1.(2)已知a,b,c是有理数,a+b+c=0,abc<0,求的值.(3)已知a,b,c是有理数,当abc≠0时,求的值.【答案】(1)1,﹣1;(2)﹣1;(3)3或﹣3或1或﹣1.【解答】解:(1)∵a>0,|a|=a,∴=1;∵b<0,∴|b|=﹣b,∴==﹣1.故答案为:1,﹣1;(2)∵a+b+c=0,abc<0,∴三个数中必需有两个正数,一个负数,可设a>0,b>0,c<0∴a=﹣(b+c),b=﹣(a+c),c=﹣(a+b),∴原式=++=﹣1﹣1+1=﹣1;(3)①三个数同时大于0时,原式=1+1+1=3;②三个数同时小于0时,原式=﹣1﹣1﹣1=﹣3;③一个数大于0,两个数小于0时,原式=1﹣1﹣1=﹣1;④两个数大于0,一个数小于0时,原式=1+1﹣1=1.综上所述,代数式的值为:3或﹣3或1或﹣1。
高考物理一轮复习第57讲光电效应电子的跃迁

第57讲解 │ 要点探究
2.氢原子自发辐射由高能级向低能级跃迁 (1)当一群氢原子由某个能级向低能级跃迁时,可能产生的谱 nn-1 线条数为 条. 2 (2)当单个氢原子处于某个能级向低能级跃迁时,最多可能产 生(n-1)个频率的光子.
第57讲解 │ 要点探究
例 3 [2009· 全国卷Ⅰ] 氦氖激光器能产生三种波长的 激光,其中两种波长分别为 λ1=0.6328 μm,λ2=3.39 μm.已 知波长为 λ1 的激光是氖原子在能级间隔为 ΔE1=1.96 eV 的 两个能级之间跃迁产生的. 用 ΔE2 表示产生波长为 λ2 的激光 所对应的跃迁的能级间隔,则 ΔE2 的近似值为( ) A.10.50 eV B.0.98 eV C D.0.36 eV [ .0.53 eV
第57讲解 │ 考点整合
三、玻尔理论 1.三条假说 不连续 的能量状态中,在这 (1)定态:原子只能处于一系列________ 些状态中原子是稳定的, 电子虽然绕核运动, 但不向外辐射能量, 定态 这些状态叫做________ ; (2)跃迁:原子从一种定态跃迁到另一种定态时,它辐射 (或 E初-E终 ; 吸收)一定的能量,即:ΔE=________ 不同轨道 (3)轨道量子化: 原子的不同能量状态跟电子沿 ________绕核 运动相对应.原子的定态是不连续的,因此电子的可能轨道也是 不连续 ________的.
第57讲解 │ 要点探究
[点评] 从图象可以看出三种光照射金属时的截止电压的关 系,根据截止电压的关系可以确定三种光的频率大小关系.再 根据光电效应的规律确定光电子的最大初动能.下列变式题是 求解最大初动能的问题.
第57讲解 │ 要点探究
[2010· 广州模拟] 频率为 ν 的光照射某金属时,产 生光电子的最大初动能为 Eνh 为普朗克常量)( ) A.Ehν B.2Ekm C.Ehν D.Ehν
任之堂中药讲记

任之堂中药讲记引子治病关键是调理气机的升降 1第1讲总论——理顺理法方药脉 4◎医理——升降 4◎治法——升清阳、降浊阴 5◎常用方——顺性养真汤8◎三大典型脉10第2讲心与小肠用药16◎通心阳的心三药17◎通脉三药治头项21◎降小肠浊的通肠六药22◎多用途的丹参槟榔饮34◎一味三七治跌仆伤奇效40◎治疗痤疮、面斑的痤斑四药41◎肉桂粥45第3讲肺与大肠用药46◎肺三药46◎鼻三药48◎咳嗽喑哑二药56◎扁桃体三药57◎取象走势用麻黄与桂枝59◎从象的角度认识竹茹62◎痔疮三组药68◎中空三药70第4讲脾与胃用药73◎升降出入四药74◎黄连、干寒热搭配治脾胃病75◎脾胃三药76◎胃胀三药78◎金果榄79◎一味冰片治胃胀神效83◎生、大枣调和阴阳84◎开胃三药88◎口臭三组药89◎脾三药90第5讲肝与胆用药93◎肝三药94◎气病总司乃香附,情志不遂郁三药98◎口苦三药100◎眼痒二药103◎眼花二药104..◎白睛溢血用桑叶与生麻黄105◎降压合剂一105◎降压合剂二106◎一味穿破石善通肝胆经109◎肝郁热四药112◎养筋五药——养筋汤115◎脂肪肝六组药118第6讲肾与膀胱用药124◎腰湿四药124◎腰椎间盘突出三药126◎一味马钱子治骨痹132◎耳鸣八药134◎肾三药136◎藏精六药137◎遗精三药138◎前列腺三药138第7讲专病专方专药141◎土大黄桔梗汤治瘢痕141◎头面美容——五白散143◎活用逍遥散治头痛144◎牙痛方145◎蒲公英治眼148◎槐花树皮治面瘫149◎乌梅消息肉150◎芦根、白茅根、根治发热151◎猪十三宝153◎预防感冒的叶生汤155◎脚踝扭伤方158第8讲小儿常用药159◎小柴胡颗粒159◎午时茶冲剂159◎王氏保赤丸159◎小儿发热三根汤160◎小儿食积发热用二丑粉160◎一味鸡矢藤消积160◎小儿疳积一二三四161◎小儿常用咳嗽方161◎小儿食积感冒方162第9讲中医的宝贝163◎第一宝——药164◎第二宝——方168◎第三宝——法171◎第四宝——理173..第10讲四方山采药识药记176◎单方单药有奇效176◎蒲黄177◎枇杷叶178◎肺为水之上源的理法178◎丝瓜络180第11讲牛头山采药识药记181◎理顺药草思路181◎商陆与入地金牛181◎菟丝子与艾叶182◎土茯苓、仙鹤草与夜交藤183◎五倍子与威灵仙184◎菖蒲185◎络石藤186◎凤尾草和车前子187◎上山采药要注意些什么188◎麻骨梢根治牙痛189◎南瓜子治前列腺增生190◎八里麻治疗跌打损伤190◎橘叶治乳腺增生191◎银杏叶与白果192◎韭菜子、花生与核桃192◎薄荷与夏枯草193第12讲太白山采药识药记195◎无意得山珍195◎草医郎中的头痛酒方196◎草医郎中的耳鸣酒方197◎单味木贼草治孕妇咳嗽199◎晚期食管癌验方200后记202在线试读部分章节"引子治病关键是调理气机的升降有一次来了一位终南山的老道长,这位老道长100多岁,身着古朴,胡须飘冉,他不单精通道家养生之术,更善于用中医中药来帮人疗疾治病,是一个典型的传统道医。
2.2有理数的减法(课件)七年级数学上册(浙教版2024)

∵(-7)+16=9,∴9-(-7)=16,
∵16=9+7,∴9-(-7)=9+7。
9 - (-7) = 16
减变加
加上-7的相反数
-7变成它的相反数7
9 + 7 = 16
02
知识精讲
【做一做】1.填空:
(-10)
(1)∵12+________=2,
-10
(-12)
∴2-12=________=2+________;
B.-5+4-7-2
【分析】(-5)-(-4)+(-7)-(+2)
=(-5)+(+4)+(-7)+(-2)
=-5+4-7-2。
C.5+4-7-2
D.-5+4+7-2
03
典例精析
例2、计算:(-0.75)-(-0.5)+(+0.75)+(-8.5)
解:(1)原式=-0.75+0.5+0.75+(-8.5)
(2)∵________+(-9)=-8,
1
∴(-8)-(-9)=________=(-8)+________。
1
9
02
知识精讲
2.通过对比上面两个算式的转化,你有什么发现?
减法是加法的逆运算,减去一个数,等于加上这个数的相反数。
02
知识精讲
一般地,有理数的减法有如下法则:
减去一个数,等于加上这个数的相反数,
0+52=
52
(2)10.25-(-5.75)=
10.25+5.75=
16
七年级数学上册第二章有理数及其运算2.6有理数的加减混合运算教学讲义全国公开课一等奖百校联赛微课赛课

四、强化训练
计算: (1) 1 ( 3) 1
4 42
(2)
9 4
1 4
1 2
(3) 11.5 (4.5) 3
(4)
1 7
( 2 ) ( 2) 35 5
6/7
本课结束
7/7
2
3
= 977 23
= 57 23
= 15 14 66
=1
6 4/7
三、归纳小结
知识关键点:有理数加减混合运算, 能够依据运算次序从左往右依次计算, 其中每两个数间运算依据加法或减法法 则进行.
方法技能:转化思想——将减法转化 为加法.
易错提醒:减法转化为加法时运算符 号和性质符号要同时改变.
5/7
-3
7
0
5
与同伴做一做 这个游戏.
她抽到卡片结果是多少? 小彬抽到4张卡片一次为:
- —23
—12
4
-5
获胜是谁? 3/7
二、新课讲解
例 计算:
(1)
( 3) 1 4 5 55
解:原式=
24 55
= 2 ( 4) 55
= 6 5
(2) (5) ( 1) 7 7
2
3
解:原式= (5) 1 7 7
第二章 有理数及其运算
6 有理数加减混合运算(一)
讲课人:XXXX
1/7
一、新课引入
请按以下规则做游戏:
(1)每人每次抽取4张卡片.假如 抽到白色卡片,那么加上卡片上 数字;假如抽到红色卡片,那么减 去卡片上数字.
(2)比较两人所抽4张卡片计算结果, 结果大为胜者.2/7一、新源自引入小丽抽到4张卡片一次为:
英语四级阅读模拟训练附答案和精讲 第57篇-地理与人

英语四级阅读模拟训练附答案和精讲第57篇:地理与人A subject which seems to have been insufficiently studied by doctors and psychologists is the influence ofgeography and climate on the psychological and physical health of mankind.There seems no doubt that the general character of the landscape, the relative length of day and night, and the climate must all play a big part in determining what kind of people we are.It is true that a few studies have been made. Where all the inhabitants of a particular area enjoy exceptionally good or bad health, scientists have identified .contributory factors such as the presence or absence of substances like iodine, fluoride, calcium, or iron in the water supply, or perhaps types of land thatprovide breeding places for pests like mosquitoes or rats.Moreover, we can all generalize about types of people we have met. Those living in countries .with long dark winters are apt to be less talkative and less vivacious than inhabitants of countries where the climateis more equable(稳定的). And where the olive and the orange grow, there the inhabitants arecheerful, talkative, and spontaneous.But these commonplace generalizations are inadequate: the influence: of climate and geography should be studied in depth. Do all mountain dwellers live to a ripe old age? Does the drinking of wine, rather than beer, result in a sunny and open temperament? Is the strength and height of one of the Kenyan tribes due to their habitual drinking of the blood of cows?We are not yet sure of the answers to such .questions, but let us hope that something of benefit to mankind may eventually result from such studies.练习题:Choose correct answers to the question:1.The author's purpose of writing this passage is to______.A.alert readers to the scarcity of natural resourcesB.call for more research on the influence of geographical environmentC.introduce different elements in character cultivationD.draw more attention to the health condition of mankind2.It can be inferred that proper amounts of iodine, fluoride and calcium can_____.A.benefit people’s physical healthB. influence the quality of water supplyC.help provide breeding places for pests.D. strengthen a person's character3.How does the author evaluate the generalizations of people's types in Para. 3?A.Such generalizations help us judge the different characters of people we meetB.Such generalizations are not inclusive enough to draw a convincing conclusion.C.Such generalizations prove that nature plays an important role in determining social habits.D.Such generalizations show that there are mainly two different types of people on the planet.4.According to the passage, research into the influence of climate and geography should ____.A. focus on unknown aspectsB. be pursued on a larger scaleC. be carried out among remote tribesD. go ahead in depth5.What do we know about the generalizations of people’s type?A.People who like drinking wine tend to be optimistic.B.People who live in mountain areas tend to have a long life.C.People who live in areas with stable climate tend to be talkative and lively.D.People who like drinking cow blood tend to be strong and tall.1.[B] 主旨大意题。
小学数学---合理安排(二)

第57讲合理安排【专题简析】小朋友,你知道“统筹方法”吗?我国著名的数学家华罗庚爷爷曾积极推广、普及这种数学思考方法。
这一讲,我们就来学习日常生活中最简单的“最优化”问题——合理安排时间。
要在较短的时间内完成必须做的几件事,就要合理地安排时间,首先要理清要做几件事,做事的顺序是怎样的,然后制定工作程序,如果某几件事不可以同时进行的话,那么,按时间从少到多的顺序排列,可以使等待的时间最短,完成的时间最少。
【例题1】小明早上起床,烧开水用10分钟,吃早饭用7分钟,洗碗筷用1分钟,整理书包用2分钟,冲牛奶用1分钟,请你安排一下,用尽可能短的时间做完全部的事情。
思路导航:由题意可知,小明起床要做4件事。
烧开水时可以吃早饭,洗碗筷,整理书包,最后冲牛奶,这样可以得到完成这些事的工作程序:烧开水10分钟(同时吃早饭、洗碗筷、整理书包)+冲牛奶1分钟。
一共用11分钟。
解:10+1=11(分钟)答:小明要花11分钟才能尽快做完全部事情。
练习11.星期天妈妈出差,小雨只能自己做饭吃。
烧水2分钟,淘米3分钟,电饭锅烧饭30分钟,把妈妈烧好的几个菜用微波炉热一下花8分钟,冲一碗汤2分钟,请问小雨最快过多长时间就可以吃了?2.星期天老师来小丽家家访,妈妈让小丽给老师烧水泡咖啡,小丽要做的事:打开饮水机开关5秒,烧开水5分钟,洗咖啡杯1分钟,拿咖啡2分钟,加入糖2分钟,最快过多长时间可以让老师喝上咖啡?3.小红早晨起床后,必须做完以下事情:叠被子3分钟、刷牙洗脸8分钟、读英语20分钟,吃饭10分钟,收碗筷5分钟,听MP3(带外放功能)里的小故事20分钟。
请你帮她合理安排时间,用最少的时间完成以上事情。
【例题2】在平底锅上煎鸡蛋,每次同时放2个,煎鸡蛋的时候,煎每一面要3分钟,现在要煎3个鸡蛋,至少一共要多少时间?思路导航:先同时煎两个鸡蛋的第一面,然后煎其中一个鸡蛋的第二面,同时煎第三个鸡蛋的第一面,最后同时煎剩下两个鸡蛋的第二面。
第7讲-认识无理数、算术平方根(教案)

此外,学生在小组讨论中的表现让我深感欣慰。他们能够提出自己的观点,并与其他同学进行交流。这说明学生们在课堂上逐渐形成了良好的思考习惯和合作精神。然而,我也发现有些学生在讨论中过于依赖同学,缺乏独立思考。因此,我计划在接下来的教学中,加强培养学生的独立思考能力,让他们在讨论中发挥自己的优势。
3.重点难点解析:在讲授过程中,我会特别强调无理数的性质和算术平方根的概念这两个重点。对于难点部分,)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与无理数、算术平方根相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如测量圆的周长和直径,计算圆周率π的近似值。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解无理数的基本概念。无理数是不能表示为两个整数比的数,如圆周率π、√2等。无理数在数学和科学领域具有重要地位,它们帮助我们更准确地描述自然界和解决实际问题。
2.案例分析:接下来,我们来看一个具体的案例。以圆周率π为例,探讨其在计算圆的周长和面积中的应用,了解无理数如何帮助我们更精确地解决问题。
2.无理数的性质:讨论无理数的运算规律,如加减乘除等;
3.算术平方根的定义:引入算术平方根的概念,解释其含义;
4.求算术平方根的方法:掌握求算术平方根的估算方法及计算方法;
5.无理数与算术平方根的关系:探讨无理数与算术平方根之间的联系,如√2是2的算术平方根,它是一个无理数。
2024高考物理一轮复习第70讲用油膜法估测油酸分子的大小(练习)(学生版+解析)

第70讲用油膜法估测油酸分子的大小(模拟精练+真题演练)1.(2024·福建宁德·福建省宁德第一中学校考一模)在估测油酸分子大小的实验中,具体操作如下:①取油酸1.0mL注入2500mL的容量瓶内,然后向瓶中加入酒精,直到液面达到2500mL的刻度为止,摇动瓶使油酸在酒精中充分溶解,形成油酸酒精溶液;①用滴管吸取制得的溶液逐滴滴入量筒,记录滴入的滴数,直到达到1.0mL为止,恰好共滴了100滴;①在边长约40cm的浅水盘内注入约2cm深的水,将细爽身粉均匀地撒在水面上,再用滴管吸取油酸的酒精溶液,轻轻地向水面滴一滴溶液,酒精挥发后,油酸在水面上尽可能地散开,形成一层油膜,膜上没有爽身粉,可以清楚地看出油膜轮廓;①待油膜形状稳定后,将事先准备好的玻璃板放在浅盘上,在玻璃板上绘出油膜的形状;①将画有油酸膜形状的玻璃板放在边长为1.0cm的方格纸上。
(1)利用上述具体操作中的有关数据可知一滴油酸酒精溶液含纯油酸体积为m3,求得的油酸分子直径为m(此空保留一位有效数字)。
(2)于老师在该实验中最终得到的油酸分子的直径和大多数同学的比较,数据偏大。
出现这种结果的原因,可能是。
A.计算油酸膜面积时,错将所有不完整的方格作为完整的方格处理B.水面上爽身粉撒的较多,油酸膜没有充分展开C.求每滴溶液体积时,1mL的溶液的滴数多记了10滴2.(2023·黑龙江哈尔滨·哈尔滨三中校考模拟预测)如图在“油膜法估测分子直径”的实验中,我们可以通过宏观量的测量间接计算微观量。
(1)某同学实验中先配制一定浓度的油酸酒精溶液,接着又进行了下列操作,操作的合理顺序是 (填字母代号)。
A .将一滴油酸酒精溶液滴到水面上,在水面上自由地扩展为形状稳定的油酸薄膜B .将画有油酸薄膜轮廓的玻璃板放在坐标纸上并计算油酸薄膜的面积C . 将玻璃板盖到浅水盘上,用彩笔将油酸薄膜的轮廓画在玻璃板上D . 向浅盘中倒入约2cm 深的水,将痱子粉均匀地撒在水面上以上(2)实验中,若测量并计算出一滴油酸酒精溶液中纯油酸的体积为1132.510m -⨯,测量并计算出油膜的面积为224.010m -⨯,则油酸分子的直径为 m 。
ISA95[1].00.03-2016.pdf(57--72翻译)
![ISA95[1].00.03-2016.pdf(57--72翻译)](https://img.taocdn.com/s3/m/0466922b82c4bb4cf7ec4afe04a1b0717fd5b3b0.png)
7.4 维护定义管理维护定义管理应理解为为定义、管理、维持完成维护任务的信息和必须的操作说明等活动的集合。
维护定义管理可能包括:a)管理文件,例如维护操作指南,卖方文件,CAD图纸,数据库记录、分析工具等。
b)获得并管理一套维护说明。
c)设法改变维护说明。
这可能包括通过一个适当的审批程序、版本定义管理、修改跟踪和定义的安全控制来改变线路的能力。
d)为其它应用程序、设备、人员或活动提供维护定义。
e)以四级职责管理维护定义信息的交换,这一级别具体是由商业运作所要求的。
f)在工序和维修分析的基础上优化维修定义。
g)生成并维持与生产设备无关的维护定义,例如关于维护设备和它们的确认的维护。
h)管理与维护相关联的KPI定义。
i)管理与安全和环境规程相关的维护定义。
维护定义管理包括维护定义分布的管理。
有些维护定义适用于一级和二级设备。
这种情况下,这些信息的下载应该和其它制造过程职责相配合以减小对产品的影响。
这些信息可能是维护命令和规程的一部分,当下载开始作为维护执行管理活动的一部分是。
注:维护定义管理一般涉及了工序安全管理的各个方面,包括“种类替换”部分互换性,如果公司允许并在工序安全管理规程范围之内。
7.5维护资源管理维护资源管理应该被定义为管理维护控制范围之内使用的资源的状况的活动的集合。
被管理的资源可能包括维护设备,维护工具,人员(有一定的技能),记录和管理中使用的材料和能源。
资源状况一般包括设备健康状况,性能,位置(如果适当),可用性和使用预期。
维护资源管理可能包括:a)关于的维护人员的管理信息,包括资格信息,如第一和第二部分员工模型中定义的资历状况和资格测试成绩。
b)关于维护和设备性能测试中使用的设备的维护信息,这在第一部分设备模型中定义过。
c)补给的维护信息,这在第一部分材料模型中定义为消耗材料。
d)所有在第三级别维护活动中使用和将被使用的资源可用状况,健康和状态,分配的维护信息。
e)协调和监视合同工。
数学竞赛教案:第57讲 排列与组合

第 讲 排列与组合本节主要有:排列组合公式及应用;处理排列组合问题的常用方法:如插空法、捆绑法等;可重复排列及圆排列公式等基本内容. A 类例题例1四个不同的小球放入编号1、2、3、4、的四个盒中,则恰有一个空盒的放法有____种。
分析 排列组合中诸如把教师医生分到各所学校;把不同的小球放入盒中等问题都可以归类为分组问题,分组问题解题的原则是:“分组先分堆”.解 把4个球分成“2、1、1”三堆,有22111224A C C C 种分法,把三堆球分别放入四个盒子的任三个中,有34A 种放法,由乘法原理,恰有一个空盒的放法共有22111224A C C C ·34A =144种.说明:本题也可以分类讨论求解,若1号盒空,2号盒放二个球,3、4号盒各放一个球有2224A C ⋅=12种放法;同理,若1号盒空,3号盒放2个球,2、4号盒各放一个球也是12种放法;1号盒空,4号盒放2个球,2、3号盒各放一个球同样是12种放法。
所以,1号盒空共有12×3 = 36种放法。
故满足题设的总放法种数为4×36 = 144种。
例2 6名同学排成一排。
(1)其中甲、乙两个必须排在一起的不同排法有______种.(1997年全国高考题)(2)甲乙两人不能相邻的排法有______种.分析 排列组合中,处理“在与不在”、“邻与不邻”、“接与不接”等问题时,常常利用捆绑法或插空法.解⑴把甲、乙两人看作1人,这样6个人可看成5个人,共有55A 种排法,甲、乙两人有2种顺序,故共有55A ·24022=A 种. ⑵ 先排其他4名同学,有44A 种,再把甲乙两人插入到4名同学的5个空挡中有25A 种,所以共有44A ·25A =480种. 情景再现1.3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士,不同的分配方式共有 ( )A .90种B .180种C .270种D .540种 (1998年全国高考题)2.某校从5名优秀学生干部中选出4人分别参加“资源”、“生态”和“环保”三个夏令营,要求每一个夏令营活动至少有选出的一人参加,且每人只参加一个夏令营活动,则不同的参加方案有( )种A .90B .180C .270D .540 B 类例题例3 在正方体的8个顶点,12条棱的中点,6个面的中心及正方体的中心共27个点中,共线的三点组的个数是A 57B 49C 43D 37(1998年全国数学联赛)分析 正方体中,共线三点组的两个端点可能有三种情形:①两端点都是顶点;②两端点都是面的中心;③两端点都是棱的中点,除此之外没有别的情形.解 两端点都是顶点的共线组有2828=C 个,两端点都是面的中心的共线组有3个,两端点都是棱的中点的共线组有182312=⨯个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10页
高考总复习( 高考总复习(文、理)
考点陪练 1.已知随机变量 ξ 服从正态分布 N(3,σ2),则 P(ξ<3)=( A. 1 5 B. 1 4 )
1 C. 3
1 D. 2
解析:由正态分布图象知,µ=3 为该图象的对称轴,P(ξ<3) 1 =P(ξ>3)= . 2
解题准备:简单的随机抽样、系统抽样、分层抽样的共同特点是 每个个体被抽到的可能性相等.这是我们所研究的所有抽样的最大特征 . 【典例1】 某批零件共160个,其中一级品有48个,二级品64个
,三级品32个,等外品16个.从中抽取一个容量为20的样本,请说明分 别用简单随机抽样、系统抽样和分层抽样法抽取时总体中的每个个体被 抽到的概率均相同.
答案:D
第11页
高考总复习( 高考总复习(文、理)
2.设两个正态分布N(µ1,σ12)(σ1>0)和N(µ2,σ22)(σ2>0)的密度函数 图象如图所示,则有( )
A.µ1<µ2,σ1<σ2 C.µ1>µ2,σ1<σ2
第12页
B.µ1<µ2,σ1>σ2 D.µ1>µ2,σ1>σ2
高考总复习( 高考总复习(文、理)
解析:∵µ是平均数,σ12是方差,µ是密度函数图象的对称轴的位 置,因此图象越瘦高,数据越集中,σ2越小. 答案:A
第13页
高考总复习( 高考总复习(文、理)
3.系统抽样又称为等距抽样,为从 N=nk 个个体中抽取 n 个 N 个体为样本, 先确定抽样间隔, 即抽样距 k= , 从第一段的 1,2, …, n k 个号码中随机抽取一个入样号码 i0,则 i0,i 0+k,…,i 0+(n- 1)k 号码均入样构成样本,所以每个个体的入样概率( A.是相等的 C.与 i0 有关 B.是不相等的 D.与编号有关 )
数 µ、σ(σ>0)是参数,分别表示总体的平均数与标准差,那么这个 总体分布叫做正态分布,常记作 N(µ,σ2),它的图象称为正态曲 线.
第8页
高考总复习( 高考总复习(文、理)
4.正态曲线的性质 (1)曲线在x轴上方,并且关于直线x=µ对称. (2)曲线在x=µ时处于最高点,由这一点向左、右两边延伸时,曲 线逐渐降低. (3)曲线的对称轴位置由µ确定;曲线的形状由σ确定,σ越大,曲线 越“矮胖”;反之,曲线越“高瘦”.
第25页
高考总复习( 高考总复习(文、理)
类型二
总体分布的估计
解题准备:解决总体分布估计问题的一般程序如下: (1)先确定分组的组数(最大数据与最小数据之差除组距得组 数);
频数 ; (2)分别计算各组的频数及频率频率= 总数
(3)画出频率分布直方图,并作出相应的估计.
第26页
高考总复习( 高考总复习(文、理)
第20页
高考总复习( 高考总复习(文、理)
20 1 (3)分层抽样法:按比例 = ,分别在一级品、二级品、三 160 8 1 1 1 级品、等外品中抽取 48× =6 个,64× =8 个,32× =4 个, 8 8 8 1 6 8 4 2 16× =2 个,每个个体被抽到的概率分别为 , , , ,都 8 48 64 32 16 1 是 ;总之,无论采取哪种抽样,总体中每个个体被抽到的概率都 8 1 是 . 8
【典例2】 92 88 76 69 75 96 87 68 64 63 87 89 83 74 69 79 80 63
已知某中学一个班60名同学的数学测试成绩如下: 91 81 49 71 64 65 68 94 85 80 52 97 90 74 66 78 47 95 35 62 76 69 98 43 58 81 77 73 58 78 88 65 86 53 84 72 72 64 91 49 60 61
第五十七讲 统计
第1页
高考总复习( 高考总复习(文、理)
第2页
高考总复习( 高考总复习(文、理)
回归课本 1.抽样方法 (1)总体:所要考察的对象的全体叫做总体,其中每一个要考察的 对象称为个体.总体与个体之间的关系类似集合与元素之间的关系. (2)样本:从总体中抽取一部分叫做总体的一个样本,样本中个体 的数目称为样本的容量.样本和总体之间的关系类似于子集和集合之间 的关系. (3)简单随机抽样:设一个总体的个体数为N,如果通过逐个抽取的 方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,就 称这样的抽样为简单随机抽样,常用方法有抽签法和随机数表法两种.
答案:B
第15页
高考总复习( 高考总复习(文、理)
5.统计某校400名学生的语文会考成绩,得到样本频率分布直方 图如图所示,规定不低于60分为及格,不低于80分为优秀,则及格率与 优秀人数分别是( )
A.80%,80 C.60%,80
B.80%,60 D.60%,60
第16页
高考总复习( 高考总复习(文、理)
第21页
高考总复习( 高考总复习(文、理)
[点评]
虽然三种抽样的方式、方法不同,但最终每个个体被抽取
是等可能的,这正说明了三种抽样方法的科学性和可行性.要根据不同 的研究对象和不同的要求,采取不同的抽样方法.
第22页
高考总复习( 高考总复习(文、理)
探究1:某公司有职工160人,其中业务人员112人,管理人员16人 ,后勤服务人员32人,为了了解职工的生活状况,要从中抽取一个容量 为20的样本,进行调查研究. (1)用哪种抽样方法较为合适?为什么? (2)写出抽样过程; (3)指出总体中每个个体被抽取的概率.
第23页
高考总复习( 高考总复习(文、理)
解析:(1)采用分层抽样方法进行抽样较为合适.因为业务人员、 管理人员、后勤服务人员三类人员的生活状况有明显差异. (2)∵112∶16∶32=7∶1∶2,按这个抽样比抽取20人,则业务人 员、管理人员、后勤服务人员应依次抽取14人、2人、4人.对160个职 工按业务人员、管理人员、后勤服务人员的顺序编号:1,2,3,…, 112,113,…,128,129,…,160. ①用系统抽样方法抽取14个业务人员.在1~112号中,随机取出 一 个 号 码 , 比 如 是 5 号 , 则 每 隔 8 个 取 一 个 , 可 得 到 14 个 号 码 : 5,13,21,29,37,45,53,61,69,77,85,93,101,109.
第19页
高考总复习( 高考总复习(文、理)
[解析]
(1)简单随机抽样法:可采取抽签法,将 160 个零件
按 1~160 编号,相应地制作 1~160 号的 160 个签,从中随机抽 20 1 20 个,显然每个个体被抽到的概率为 = . 160 8 (2)系统抽样法:将 160 个零件从 1 至 160 编上号,按编号顺 序分成 20 组, 每组 8 个. 先在第 1 组用抽签法抽得 k 号(1≤k≤8), 则在其余组中分别抽取第 k+8n(n=1,2,3,4,……,19)号,此时每 1 个个体被抽到的概率为 . 8
答案:A
第14页
高考总复习( 高考总复习(文、理)
4.设有一正态总体,它的概率密度曲线是函数 f(x)的图象, (x-10) 2 1 且 f(x)= e- ,则这个正态总体的期望与标准差分别是 8 8π ( ) A.10 与 8 C.8 与 10 B.10 与 2 D.2 与 10
1 -(x-µ)2 1 -(x-10)2 解析:由 f(x)= e 2σ2 = e 8 ,可得 σ=2,µ=10. 2πσ 8π
第24页
高考总复习( 高考总复习(文、理)
②用抽签法对管理人员抽取 2 人,比如得到号码:118,120. ③用抽签法对后勤服务人员抽取 4 人,比如得到号码: 130,142,143,159. 这样抽样后就得到了一个容量为 20 的样本. 即下面的号码所 对应的职工: 5,13,21,29,37,45,53,61,69,77,85,93,101,109,118,120,130,142,14 3,159. 20 1 (3)总体中每个个体被抽取的概率是 P= = . 160 8
第28页
高考总复习( 高考总复习(文、理)
[80,90) [90,100)
13 9
13 60 3 20
(2)直方图如图
第29页
高考总复习( 高考总复习(文、理)
9 3 (3)由频率分布表可知,不及格的概率为 = =15%.又由于 60 20 38 38 11 80 分以下的概率为 ,因此,本班数学的优秀概率为 1- = 60 60 30 ≈37%.
(1)列出频率分布表; (2)画出频率分布直方图; (3)估计不及格和优秀(80分以上)的概率分别是多少?
第27页
高考总复习( 高考总复习(文、理)
[解析]
(1)频率分布表如下:
个数累计 频数 1 4 4 16 13 频率 1 60 1 15 1 15 4 15 13 60
成绩区间 [30,40) [40,50) [50,60) [60,70) [70,80)
第9页
高考总复习( 高考总复习(文、理)
5.标准正态总体 当 µ=0, σ=1 时, 正态总体称为标准正态总体, 记作 N(0,1). 由 此制作的标准正态分布表中,相应于 x0 的值 φ(x 0)是指总体取值小 于 x0 的概率,即 φ(x0)=P(x<x 0). 一般正态总体 N(µ,σ2)取值小于 x 的概率也可以通过标准正
解 析 : 由 图 可 知 及 格 率 为 0.025×10 + 0.035×10 + 0.01×10 + 0.01×10=0.8,优秀人数为(0.01×10+0.01×10)×400=80,
答案:A
第17页
高考总复习( 高考总复习(ቤተ መጻሕፍቲ ባይዱ、理)
