静定拱
结构力学的拱的受力与挠度分析解析

结构力学的拱的受力与挠度分析解析结构力学是一个研究物体在外力作用下的力学性质的学科,拱是一种重要的结构形式。
在本文中,我们将探讨拱的受力与挠度的分析解析。
一、拱的基本概念和受力特点拱是由一定数量的弧形构件组成的结构体系,具有以下几个基本概念和受力特点:1. 拱脚:拱脚指的是拱的两个支点或固定端。
2. 拱顶:拱顶是拱的上部中点,也是受力最大的位置。
3. 拱轴线:拱轴线是拱的中心线,通过拱顶、拱脚和拱的几何形状。
4. 受力特点:拱的受力特点是主要由轴力和弯矩组成,其中轴力负责承受垂直于拱轴线的力,而弯矩则负责承受沿拱轴线的力。
二、受力分析解析对于一个静定拱,其受力分析可以通过以下几个步骤来实现:1. 选择合适的坐标系:根据拱的几何形状和受力情况,选择合适的坐标系,通常选择拱轴线作为x轴,垂直于拱轴线的方向作为y轴。
2. 建立平衡方程:根据受力平衡条件,建立拱在x和y方向上的平衡方程,考虑到拱的对称性,通常只需要考虑一半的力学模型。
3. 解析受力分布:通过求解平衡方程,可以得到拱轴线上的轴力和弯矩的分布情况,这对于进一步分析拱结构的受力特点非常重要。
4. 弹性分析:对于非静定的拱结构,需要进行弹性分析,考虑拱的材料性质和几何形状等因素,通过弹性力学理论,可以计算出拱的挠度和变形情况。
三、挠度分析解析拱的挠度分析是结构力学中一个重要的问题,可以通过以下几个方法进行解析:1. 弦索法:弦索法是一种常用的解析方法,根据拱的轴线、支点位置和受力条件,假设拱为一根从支点悬挂的弦或悬链。
通过求解拉力分布和挠度方程,可以得到拱的挠度情况。
2. 力学方程法:利用弯曲方程和力学平衡条件建立拱的挠度方程,再通过求解微分方程,可以得到拱的挠度函数和挠度分布。
3. 有限差分法:有限差分法是一种数值解法,将拱的轴线划分为若干个小段,通过差分近似的方式离散挠度方程,再通过迭代计算,得到拱的挠度分布。
这些方法并非穷尽拱的受力与挠度分析解析的所有途径,但是对于常见拱结构而言,它们是非常有效的工具。
9静定拱

FNC
左 0左 FQD FQD Cos D FH Sin D
左
105 0.832 82.5 0.555 41.6kN
左 0左 FND FQD Sin D FH Cos D
A
105
0
MD A 0 FVA D FQD
0左
105 0.555 82.5 0.832 127kN
13
(2) 求dy 4 f 4 4 tg D 2 ( L 2 x) 2 (12 2 3) 0.667 dx L 12
4 4 yD 2 (12 3) 3 3m 12
D 3342'
Cos D 0.832 Sin D 0.555
第六章 静定拱
§6-1 概述
§6-2
三铰拱的计算
§7-3
三铰拱的合理拱轴线
1
1.拱的特征及其应用
(1)拱的特征: a.在竖向荷载作用下会产生水平反力(推力)。 b.杆轴线通常是曲线的。
FP
FP
曲梁
三铰拱
在竖向荷载作用下, 水平反力等于零, 曲梁结构(不是拱)。
在竖向荷载作用下, 会产生水平反力, 因此它是拱结构。
2
赵州桥
3
丫髻沙大桥
4
雁滩黄河大桥
5
大跨度体育馆
6
砌体拱顶
7
农业大棚
8
三铰拱的计算
为了便于理解, 与相应的简支梁作对比。 (1)支座反力计算 a.竖向反力 FPi bi 0 得 M 0 F F B VA VA L FPi ai 0 得 M 0 F F A VB VB L b.水平反力 取左半跨为隔离体:
第3章静定结构受力分析三铰拱

FN FQ0 sin FH cos
FQ FQ0 cos FH sin
(2)
M M 0 FH y
概念:
上式即为用相应简支梁的内力 表示的拱的内力式。当将上式 用作拱的内力计算公式时,可 以叫做公式法。
3.拱的内力图特征和制作
分析
由式2可知,在竖向荷载作用 下静定拱内力与相应简支梁
例1 图(a)所示三铰拱的拱轴 为半圆形。计算截面K1、K2的 内力。
FP=10kN
R=4m
(a)
解 1)求支座反力
竖 MA 0
向 FBy
1 [q R 2R
R 2
FP (R
R cos )] 11.33kN()
反 MB 0
力 FAy
1 [q R 2R
力与前规定相同;弯矩以使 拱的下侧受拉为正;
以图示三铰刚架为例说明拱的内 力计算的一般方法。
FH F Ay
FH
F By FN0
解:
截开指定截面K,取左侧为隔 离体,见下页图(c)(d),截 面上的内力均按规定的正方 向示出 。
M FN
FH
FQ
FAy
(c)
M0 0
FQ0
(d)
在轴力和剪力的两个正交方 向上建立投影方程,并建立 关于截面形心的力矩方程, 即得:
内力及拱水平反力有关。其
中拱水平反力对应确定的荷
载是一常数。此外,拱轴力
和剪力还与所计算截面外法
线与x轴的夹角a有关。
结论
拱轴上内力有以下3个特点:
1
不管是在均布荷载下还是在集 中荷载下,拱的三个内力图都 是曲线图形。
静定拱结构的变形公式推导

静定拱结构的变形公式推导好的,以下是为您生成的关于“静定拱结构的变形公式推导”的文章:咱先来说说啥是静定拱结构。
想象一下,有一个弯弯的桥,那个桥的形状就有点像静定拱结构。
比如说,咱经常在公园里看到的那种拱形的石桥。
这静定拱结构啊,它在受到各种力的作用时,会发生变形。
那咱就得搞清楚这个变形是咋来的,就得推导一下相关的公式。
比如说,有这么一个简单的静定拱结构,它就像一个被微微压弯的弓。
咱先假设这个拱受到一个竖直向下的集中力 P 。
这时候,拱的各个部分都会产生内力和变形。
那怎么推导这个变形公式呢?咱先得分析一下这个结构的受力情况。
就像解一道复杂的数学题一样,得一步步来。
咱把这个拱分成很多小段,每一小段都受到不同的力。
然后呢,通过一些力学的原理和方法,比如平衡方程、几何关系啥的,来逐步推导。
我记得有一次,我在一个建筑工地观察那些工人们搭建一个小型的拱结构。
他们非常仔细地测量每一个部件的尺寸,计算受力情况。
我就凑过去问一个老师傅:“师傅,这拱结构的变形咋算啊?”老师傅笑着说:“小伙子,这可复杂着呢,得一点点分析。
”他边说边比划着,给我讲了一些基本的概念和方法。
咱接着说这变形公式的推导。
通过对每个小段的分析,咱可以得到一些关于内力和变形的关系式。
然后把这些关系式整合起来,经过一番复杂的计算和推导,最终就能得到静定拱结构的变形公式。
这公式可重要啦,有了它,工程师们就能准确地预测拱结构在受力时的变形情况,从而保证结构的安全性和稳定性。
比如说,在设计一个大型的桥梁时,如果变形太大,那可就危险啦。
总之,静定拱结构的变形公式推导虽然有点复杂,但只要咱耐心分析,一步步来,就能搞明白其中的奥秘。
就像解决一个难题,只要不放弃,总有办法找到答案的。
李廉锟《结构力学》(上册)笔记和课后习题(含考研真题)详解(静定拱)【圣才出品】

第4章 静定拱4.1 复习笔记【知识框架】【重点难点归纳】一、拱的基本概念1.拱的定义拱是指轴线(截面形心的连线)为曲线并且在竖向荷载作用下会产生水平反力的结构。
2.拱的分类(1)按铰点数①三铰拱;②两铰拱;③无铰拱。
拱的定义 按铰点数:三铰拱、两铰拱、无铰拱 拱的分类 按铰趾位置:平拱、斜拱拱的基本概念 拱的特点拱式结构消除推力对支撑结构影响的方法拱各部分的名称:拱轴线、拱趾、拱的跨度、起拱线、拱顶、拱高等 反力个数 支座反力的计算 计算方法 计算公式三铰拱的计算 反力值影响因素内力的计算:弯矩、剪力、轴力斜拱支座反力计算三铰拱的合理拱轴线 合理拱轴线的定义拱轴线的计算方法 静定拱图4-1-1(2)按铰趾位置①平拱平拱是指两拱趾在同一水平线上的拱。
②斜拱斜拱是指不在同一水平线上的拱。
3.拱的特点(1)优点①与梁相比,拱在竖向荷载作用下会产生水平反力。
推力的存在与否是区别拱与梁的主要标志。
②由于推力的存在,拱的弯矩常比跨度、荷载相同的梁的弯矩小得多,使得拱截面上的应力分布较为均匀。
③主要承受压力,可利用抗拉性能较差而抗压较强的材料如砖、石、混凝土等来建造,更能发挥材料的作用。
(2)缺点拱支座要承受水平推力,因而要求比梁具有更坚固的地基或支承结构(墙、柱、墩、台等)。
4.拱式结构拱式结构是指在竖向荷载作用下会产生水平反力的结构,也称为推力结构。
如三铰刚架、拱式桁架等。
5.消除推力对支撑结构影响的方法在拱的两支座间设置拉杆来代替支座承受水平推力,使其成为带拉杆的拱(图4-1-2(a))。
为了使拱下获得较大的净空,有时也将拉杆做成折线形的(图4-1-2(b))。
图4-1-26.拱的各部分名称(1)拱轴线拱轴线是指拱身各横截面形心的连线。
(2)拱趾拱趾是指拱的两端支座的位置。
(3)拱的跨度l拱的跨度是指两拱趾间的水平距离。
(4)起拱线起拱线是指两拱趾的连线称为起拱线。
(5)拱顶拱顶是指拱轴上距起拱线最远的一点。
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第4章静定拱【圣才出品】

李廉锟《结构⼒学》笔记和课后习题(含考研真题)详解-第4章静定拱【圣才出品】第4章 静定拱4.1 复习笔记【知识框架】【重点难点归纳】⼀、拱的基本概念及特点 ★★表4-1-1 拱的基本概念及特点表4-1-2 有拉杆和⽆拉杆三铰拱的区别与联系⼆、三铰拱的计算 ★★★★★1.⽀座反⼒的计算(见表4-1-3)表4-1-3 ⽀座反⼒的计算2.内⼒的计算(见表4-1-4)表4-1-4 三铰拱的内⼒计算三、三铰拱的合理拱轴线(见表4-1-5) ★★★表4-1-5 三铰拱的合理拱轴线4.2 课后习题详解复习思考题1.拱的受⼒情况和内⼒计算与梁和刚架有何异同?答:(1)拱与梁的受⼒情况和内⼒计算的区别①约束反⼒⽅⾯,拱在竖向荷载作⽤下会产⽣⽔平反⼒(推⼒),⽽梁在竖向荷载作⽤下不会产⽣⽔平反⼒(推⼒);②内⼒分布⽅⾯,由于⽔平推⼒的存在,拱的弯矩常⽐跨度、荷载相同的梁的弯矩⼩得多,使得拱截⾯上的应⼒分布较为均匀;③内⼒分析⽅法⽅⾯,若只有竖向荷载时,梁只需进⾏简单的整体分析即可求解,⽽拱由于⽔平⼒的存在,需要整体分析与局部分析相结合。
(2)拱与刚架的受⼒情况和内⼒计算的异同①内⼒分析⽅法⽅⾯,拱与刚架的受⼒情况和内⼒计算的特点和所应⽤⽅法基本⼀致,例如三铰刚架也属于拱式结构;②拱的轴线是曲线,刚架杆的轴线是直线,在应⽤平衡条件计算内⼒时,拱仍然取投2.在⾮竖向荷载作⽤下怎样计算三铰拱的反⼒和内⼒?能否使⽤式(4-1)和(4-2)?答:(1)对于三铰拱承受⾮竖向荷载的情况,可将⾮竖向荷载分解为⽔平荷载和竖向荷载。
(2)仍然可以应⽤式(4-1)和(4-2),将⽔平反⼒加上⾮竖向荷载⽔平⽅向上的分量⼀起代⼊公式中进⾏求解。
(4-1)o AV AV o BV BV o c H F F F F M F f ??=??=?=cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F =-??=-?=+3.什么是合理拱轴线?试绘出图4-2-1各荷载作⽤下三铰拱的合理拱轴线形状。
3f静定拱
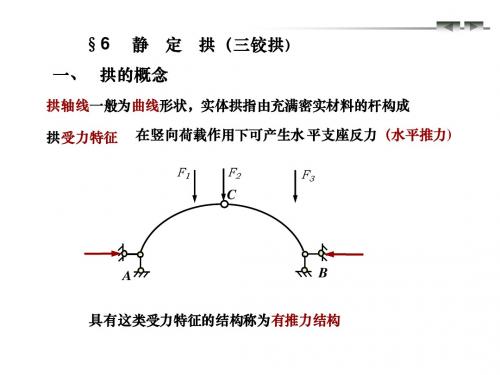
H=6
A
VA 4m 4m 4m 4m
B H=6
VB =5
=7 1) 反力
(ΣM
(ΣM
B
=0
)
)
4( 4 ) + 8( 12 ) − V A ( 16 ) = 0 V A + VB − 1 ⋅ ( 8 ) − 4 = 0
2) 内力 沿跨度分成若干等份, 沿跨度分成若干等份, 算出控制截面内力值
2.三铰拱内力 三铰拱内力 三铰拱 拱的任一截面上一般有三个内力( ),内力计算的基本 拱的任一截面上一般有三个内力(M, FQ, FN),内力计算的基本 方法仍是截面法。与直杆件不同的是拱轴为曲线时, 方法仍是截面法。与直杆件不同的是拱轴为曲线时,截面法线角 度不断改变,截面上内力( 的方向也相应改变。 度不断改变,截面上内力(FQ , FN)的方向也相应改变。
静定拱 小结
沿跨度分成若干等份, 沿跨度分成若干等份, 算出控制截面内力值
E截面 x = 4m 截面, 截面
C -0.5
-0.5 1.5 2.0 1.5 2.0
M = M 0 − Hy 1 = 7( 4 ) − 4 2 − 6( 3 ) = 2 2
Q = Q 0 cos ϕ − H sin ϕ
= 3( 0 .894 ) − 6( 0 .447 ) = 0
M = M 0 − Hy
(截面一侧竖向外力之矩) 截面一侧竖向外力之矩)
拱为合理轴线时,M=0
M0 ∴ y = H
( 可见,合理拱轴线 y与代梁截面M成正比 ) 可见,合理拱轴线 与代梁截面
上式求导两次
d2y q d M =± = ±q ) ∴ 2 (note: 2 dx H dx
结构力学第5章静定拱的内力计算

A
FA
图5-3-2(a)
同理,截取隔离体如图5-3-2(b)
FP G FN2 e2 2` D2 FQ2 A
F2
FA
图5-3-2(b)
容易看出:
图5-3-2两隔离体上截面1、2上 合力F1、F2与各自的三个内力分量 的等效关系。
AG和GB(注意GB过C铰)直线分别 是拱AD和DB段上合内力的作用线,又 叫压力线。
例5-3-1试设计一个三铰拱的轴线。
其拱上作用荷载与拱的三个铰相对位 置已定,如图(a)示
(a)
2 m 2 m 4 m
2m
2m
解
1)求支座反力
因拱的两个底铰不在一条直线上,须 先建立关于同一个铰的两个约束力的 平衡方程,联立求解,即:
先考虑支座B的约束力。以A点为 矩心,建立拱整体的力矩平衡方 程:
(a)
解 1)求支座反力
竖向反力
0 1 R FBy [q R FP ( R R cos )] 11.33kN () 2R 2
A
M
M
FAy
B
0
1 R [q R FP ( R R cos )] 1.33kN () 2R 2
结构力学
结构力学教研室
青岛理工大学工管系
第五章 静定拱的内力分析
§5.1
概 述
什么叫拱?
一般指杆的轴线为曲线形状,并且 在竖向荷载作用下会产生水平支座 反力的结构。
静定拱分类:
三铰拱 带拉杆三铰拱
静定拱的各部名称见图5-1-1。
拱 轴
( 底 铰 )
f(拱 高)
(a)三铰拱
(b)带拉杆三铰拱
结构力学6静定拱平面桁架

§3-5 静定平面桁架
12. 例4:求EF、ED、CD与DG杆内力
§3-5 静定平面桁架
§3-5 静定平面桁架
§3-5 静定平面桁架
13. 截面法和结点法联合应用 例1:求平面桁架a、b杆的内力
§3-5 静定平面桁架
§3-5 静定平面桁架
§3-5 静定平面桁架
例2:求平面桁架HC杆的内力
§3-4 静定拱
三铰拱的内力计算
三铰拱的内力值不仅与荷载及三个铰的位置有关,而 且与各铰间拱轴线的形状有关。
§3-4 静定拱
7. 例题1:试作下面三铰拱的内力图,拱轴线为抛
物线,其方程为
。
§3-4 静定拱
§3-4 静定拱
§3-4 静定拱
§3-4 静定拱
8. 斜拱的计算原理。
§3-4 静定拱
§3-4 静定拱
6. 三铰拱的数解法
三铰拱的反力只 与荷载及三个铰的位 置有关,而与各拱间 的拱轴线性状无关。 当荷载及拱跨l不变时
,H将与f成反比,f越
大即拱越陡时H越小; f越小即拱越平坦时H 越大。
§3-4 静定拱
三铰拱的内力计算
§3-4 静定拱
三铰拱的内力计算
拱内任一截面的 弯矩M等于相应 简支梁对应截面 的弯矩M0减去推 力引起的弯矩 Hy。由于推力 的存在,拱的弯 矩比梁要小。
3. 桁架的优点 各杆只承受轴力,截面上的应力是均匀分布的
,可同时达到容许值,材料能够得到充分利用。 因而与梁相比,用料更省,能跨越更大的跨度。
§3-5 静定平面桁架
4. 平面桁架内杆件的分类:弦杆和腹杆
§3-5 静定平面桁架
5. 平面桁架的分类 外形:平行弦桁架(a)、折弦桁架(b)与三角形桁架(c) 水平推力:无推力桁架或梁式桁架(a、b、c)和推力桁架或拱
结构力学第4章 静定拱结构

一、工程中的拱结构轴线为曲线、仅在竖向荷载下能产生水平反力(推力)的结构称为拱。
图4-1所示为拱结构的工程实例。
图4-1工程中的拱结构二、拱式结构的特征及其应用1、定义:通常杆轴线为曲线,在竖向荷载作用下,支座产生水平反力的结构。
2、特点:(1)弯矩比相应简支梁小,水平推力存在的原因。
(2)用料省、自重轻、跨度大。
(3)可用抗压性能强的砖石材料。
(4)构造复杂,施工费用高。
3、拱的种类:图4-2拱的种类4、拱各部分的名称:一、支座反力的计算C拱顶铰BA拱肋跨度拱趾铰(a) 等高三铰拱C高差hAB(b) 不等高三铰拱严格的来说,实体三铰拱支座反力的计算与一般三铰刚架结构反力计算相同。
本书介绍的是等代梁解法。
图4-4实体三铰拱第二节实体三铰拱的数解法图4-5等代粱ll 1l 2a 3b 3b 2b 1a 2a 1F P1F P2F P3F P1F P2F P3F A yF B yF A yF B yF B xF A x 00A CBAB C(b)(a )f0CH M F =HB A F F F ==x x 0Ay Ay F F =0ByBy FF =二、拱内截面内力的计算图4-6拱内截面内力1、拱的内力计算原理仍然是截面法。
2、拱通常受压力,所以计算拱时,规定轴力以受压为正。
对于竖向荷载作用三铰拱,其内力计算有简捷公式。
(c)CB A00F B yF A yF P3F P2F P1B F B xAF A x F A yF B y(a )C F P3F P2F P1a 1a 2b 1b 2b 3a 3lϕK F A y F A xF P1KM K F NKF QKx KK ϕy KxyK K(b)yF MM H 0-=ϕϕsin cos H 0Q Q F F F -=ϕϕcos sin H 0Q N F F F --=A0AyFQ F 0M (b) 代梁受力F Ax =F H F Ayx A y k F y FxyϕM(a) 截面k 坐标方向力图4-7拱内截面内力需要指出的是,非竖向荷载作用不等高三铰拱等情形,上述公式是不适用的。
静定拱结构(力学)

03
静定拱结构的分析方法
解析法
解析法是通过数学公式和定理来求解静定拱结构 的内力和变形的方法。
这种方法基于力学的基本原理和数学工具,能够 得到精确的解答。
解析法适用于简单形状和边界条件的静定拱结构, 但不适用于复杂结构和非线性问题。
有限元法
有限元法是一种数值计算方法, 通过将连续的结构离散化为有 限个小的单元,来求解结构的
02
静定拱结构的力学原理
力的平衡原理
总结词
静定拱结构在力的平衡原理下保持稳定,各部分受力相互抵消,不产生额外的 力矩或力。
详细描述
静定拱结构通过合理的设计,使得作用在结构上的外力(如重力、风载、雪载 等)在内部各部分之间相互抵消,没有产生额外的力矩或力,从而保持结构的 稳定。
力的分布原理
总结词
THANKS
感谢观看
静定拱结构(力学)
目录
• 静定拱结构概述 • 静定拱结构的力学原理 • 静定拱结构的分析方法 • 静定拱结构的优化设计 • 静定拱结构的稳定性分析 • 静定拱结构的案例分析
01
静定拱结构概述
定特定受力 特性的拱形结构,其受力状态仅 由其自身刚度和所受外力决定, 不依赖于其他结构部分。
静定拱结构能够将外力均匀地传递到结构的各个部分,以减小局部应力集中。
详细描述
静定拱结构的设计能够确保外力在结构中均匀分布,避免应力集中现象,从而减 小结构损坏的风险。这种力的分布原理有助于提高结构的承载能力和稳定性。
弹性力学基础
总结词
静定拱结构在弹性力学基础上进行分析和设计,考虑结构的 变形和应力分布。
优化变量
设计过程中需要优化的参数,如拱的形状、尺寸、材料等。
优化设计的数学模型
第4章:静定拱-结构力学课件

M FN
载及A 三三个x铰铰拱y的的位内f 置力有不关但,与B而荷 FH FH
FH且与拱轴l线1 的形状l有2x 关。
FAV
F1
FS
FAV 由于推力的l 存在,拱F的BV FAV0 弯矩比相应简支梁的弯矩要
FS0 M0
等小代。梁 F1 A
KC
F2
M=[FAV x– F1 (x-a1)] – FH y =M0 – FH y
F1
C
F2
结论:F1
A
f
B FBH三载铰及F拱 三H 的 个反 铰力 的只 位与 置荷 有
FAH
l1
FAV
等代梁
A
F1
l2 l
C
a1
b1
FAV0
a2
FBV
关关,。F与AV拱F轴1 线形状M无c0
F2
荷水载平与 推跨 力F度 与AV0一 矢定 高时 成, 反
B ∑Μ比。C=0
b2 FBV0 FH=1/ f [ FAV l1 – F1 (l1- a1 )]
FBV=FBV0 FAV=FAV0 FAH=FBH =F H
MC0= FAV0 l1 – F1 (l1- a1 )
FH= MC0 / f
2.内力的计算:
基本法—截面法
注: 拱的内力正负号的规定:
剪力以绕隔离体顺时针转动为正;
轴力以压力为正;
弯矩以使拱的下侧受拉为正。
y F1 K C
F2
F1
分析:本题为F非N +d竖FN向
荷载,我们可由假定拱
圆
F轴进N 处行于受R无力弯分矩析状,态建入立手平,
衡方程求出合理拱轴线。
M=0 → dM=FQ=0 因此横截面只有轴力FN ,FN+dFN. ∑MO=0 → FNR-(FN +d FN )R=0 → d FN=0 → FN=常数。 沿s-s轴投影方程:2FN sin(d/2)-qRd =0, sin(d/2)=d/2
6-4a:静定拱

可见合理拱轴为抛物线方程。
注:
1.拱的合理轴线是与荷载一一对应的,即:不同 的荷载对应有不同的合理拱轴。 2.在矢高不确定的情况下,一个荷载对应的合理 拱轴不是一条,而是一组。 3.若用压力线作为三铰拱轴线,则任一截面弯矩 都为零,故压力线为合理拱轴。 4.在工程实际中,同一结构往往受到各种荷载作 用,因此根据某一固定荷载确定的合理拱轴并不 能保证在各种荷载作用下均处于无弯矩状态。在 设计中,通常是以主要荷载作用下的合理拱轴作 为拱的轴线。
例3-2 求三铰拱在均布荷载作用下的合理拱轴。 q C FH A FVA l /2 q A f B FH l /2 FVB
M0 = qx(l − x)/ 2
x 代梁
ql / 2
解:
M0 y= FH 1 M = qx (l − x ) 2 0 M C 1 1 2 ql 2 FH = = × ql = f f 8 8f 8f 1 4f y = 2 × qx (l − x ) = 2 x (l − x ) ql 2 l
§ 4-3 三铰拱的合理拱轴
1、三铰拱的合理轴线 在固定荷载作用下使拱处于无弯距状态的轴线。 在固定荷载作用下使拱处于无弯距状态的轴线。 求解公式:在竖向荷载作用下, 求解公式:在竖向荷载作用下,三铰拱的合理轴线使拱 的各截面处于无弯距状态,即由( 第一式, 的各截面处于无弯距状态,即由(4-2)第一式,得:
斜拱的反力计算
A
P1
C
P2
B
F
f h
/ R
F
/ AV
/ R
F
= F
0 BV
0 AV
F
/ R
/ BV
= F
0 C
F = M
/h
结构力学(拱结构)

三铰拱的内力计算
表4-1:三铰拱各截面内力计算表
内力计算时,常通过 公式、列表完成
15
合理拱轴
五、 合理拱轴的概念
1、合理拱轴的概念
定义:在给定荷载作用下,拱各截面只承受轴力, 而弯矩、剪力均为零,这样的拱轴称为合理拱轴。
?
2、合理拱轴的确定
写出任一截面的弯矩表达式,令其等于零即可确 定合理拱轴。
VA0
0 2x、 荷 载 与 跨 度 一 定 M C VAl1 P1 (l 1 a 1 ) V 0 时,水平推力与矢高 MC (4-2) 等代梁计算简图 H 成反比。 f
0 B
作为结构。
7
三铰拱的内力计算
a1
a2 b1 P1 b2 P2 f
2、弯矩计算
M K [VA x K P1 (x K a1 )] H y K
q= 1kN/m
y
4f (l x)x 2 l
P=4kN 3 4 5 C 4m
x
2
6
1
H =6kN A 0
7
B H =6kN
8
VA =7kN
8×2=16m VB =5kN
解: 1、计算支座反力
0 VA VA
1 8 12 4 4 7kN 16 1 8 4 4 12 0 VB VB 5kN 16
拱结构的组成
2、拱结构的组成
3
拱结构的种类
3、拱结构的种类 静定拱
超静定拱
三铰拱
两铰拱 超静定拱
静定拱
无铰拱
高差h
静定拱
带拉杆的三铰拱
斜拱
4
拱结构的特点
4、拱结构的特点
1、弯矩比相应等代梁小;
结构力学第0708次课静定拱结构
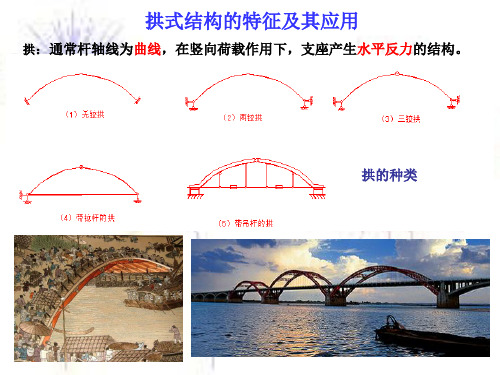
(FQ
dFQ
)
ds 2
c
os
d 2
dM
0
d 0
cos d 1
2
sin d d
22
dFN FQ d 0 FN d dFQ qds 0 FQ ds dM 0
当拱轴微合理轴线时, M 0
故 dM 0 FQ 0
从而 FN 常数 从而 FN 常数
q
dFQ 0
(a) y
A
q
C f
B
l
(b) A
q B
M0 由式 y
FH
简支梁的弯矩方程为
M x q xl x
2
拱的推力为
x
FH
M
C
ql 2
f 8f
所以拱的合理轴线方程为
yx
q 2
xl
x
8f ql 2
4f l2
xl x
y0
q
qd
在填土重量作用下,三铰平拱 的合理轴线是一悬链线。
qj
C
xx
A
f
x0
B
l
127.0 41.6
67.5
71.4
41.6
79.9 21.4
13.1
0.273m
82.5
0.5
86.2
2.4
0.7 0.0
5.6
99.1
0.0
7.5
118.4 1.8
5.6
141.52.9
0.0
M 图(单位kN.m)
F Q图(单位kN)
F N图(单位kN)
合理拱轴的概念
(1)定义:在给定荷载作用下,拱各截面只承受轴力,而弯 矩、剪力均为零,这样的拱轴称为合理拱轴。
《结构力学》第四章静定拱

实例演示
通过实例演示内力图的 绘制过程,帮助读者掌
握绘制技巧。
04 静定拱的位移计算
位移计算基本概念
位移的定义
位移是指在外力作用下,结构物 某一点或某一截面位置的变化。
静定拱的位移
静定拱在荷载作用下的位移包括 拱顶竖向位移、拱脚水平位移和
转角位移等。
位移计算的意义
位移计算是结构力学中的重要内 容,对于评估结构的安全性、稳 定性和使用功能具有重要意义。
虚功原理在位移计算中的应用
虚功原理的基本概念
01
虚功原理是结构力学中的一个基本原理,它建立了外
力功与结构内部应变能之间的关系。
虚功原理在静定拱位移计算中的应用
02 通过构建静力可能位移和虚力状态,利用虚功原理可
以求解静定拱在各种荷载作用下的位移。
虚功原理的适用条件
03
虚功原理适用于线弹性结构,即结构在受力过程中满
解题思路
同样需要构建静力可能位移和虚力 状态,利用虚功原理求解位移。
解题步骤
详细列出解题步骤,并解释每一步 的意义和计算方法。
05 静定拱的稳定性分析
稳定性分析基本概念
稳定性
结构在受到外部扰动后,能够恢复原有平衡状态的能力。
临界荷载
使结构失去稳定或发生破坏的最小荷载。
稳定性分析
研究结构在荷载作用下是否会发生失稳或破坏,以及如何提高结 构的稳定性。
通过截取拱的任意截面,利用静 力平衡条件求解截面上的内力。
叠加法
将复杂的拱结构分解为若干简单结 构,分别计算内力后再进行叠加。
力法
通过引入多余未知力,建立力法方 程求解拱的内力。
典型例题解析
圆弧拱内力计算
01
静定结构的内力—三铰拱(建筑力学)
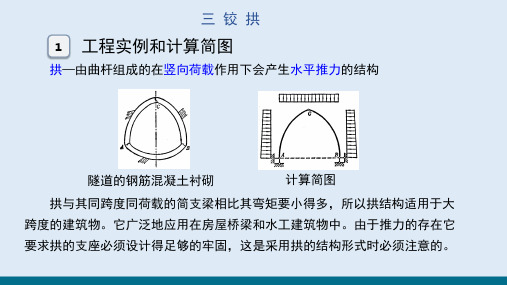
愈大)。
三铰拱
(2)截面内力的计算
① 截面内力的正负规定
轴力以压力为正;剪力以有使截面产生顺时针转动的趋势者为正;弯矩
以拱内侧纤维受拉者为正。
② 任意截面的内力计算
设K截面形心的坐标分别为xK、yK,K截面的法线与x轴
的夹角为φK,且左半拱的φK为正值,右半拱的φK为负值。
取三铰拱的K截面以左
部分为隔离体,得
FNE FQ0E sin E Fx cosE 134kN
三铰拱
4 三铰拱的合理拱轴线
若拱的所有截面上的弯矩都为零,这样的拱轴线为合理拱轴线。
三铰拱在竖向荷载作用下任意截面上的弯矩为
MK
M
0 K
Fx yK
由 M M 0 Fx y 0 得
M0
合理拱轴线方程为: y
Fx
M 0——代梁在该竖向荷载作用下的弯矩方程
三铰拱
C B
C
C
A
B
A
B
l
有拉杆的三铰拱
两铰拱
(c)
(a)
梁式结构在竖向荷载作用下是不会产生推力的。
C
A B
B
A
B
曲梁
三铰拱
2 三铰拱的组成
拱顶
拱轴线
f 矢高
拱趾
拱趾
l 跨度
拱顶:拱的最高点
拱趾:支座处
跨度:两支座之间的水平距离,用l表示
矢高:拱顶到两拱趾间联线的竖向距离,用f 表示 高跨比 f/l 是拱的一个重要的几何参数 工程实际中,高跨比在1/10 ~ 1之间,变化的范围很大
Fx
M
0 C
f
ql 2 f
8 ql 2 8f
合理拱轴的方程为
【毕业论文】静定拱的受力分析
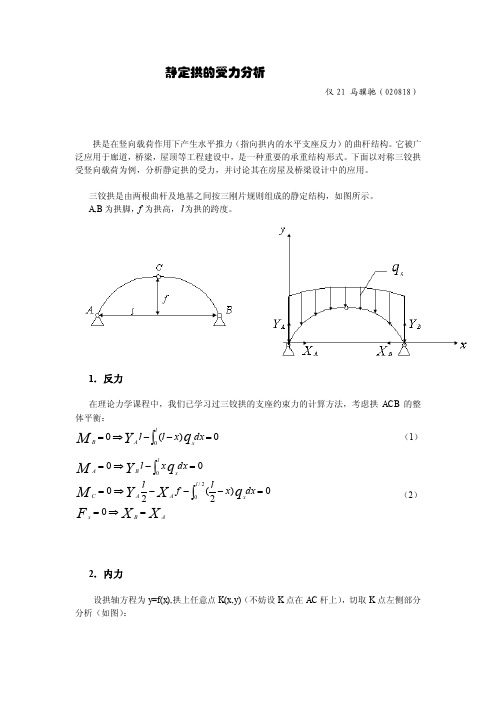
静定拱的受力分析仪21 马骥驰(020818)拱是在竖向载荷作用下产生水平推力(指向拱内的水平支座反力)的曲杆结构。
它被广泛应用于廊道,桥梁,屋顶等工程建设中,是一种重要的承重结构形式。
下面以对称三铰拱受竖向载荷为例,分析静定拱的受力,并讨论其在房屋及桥梁设计中的应用。
三铰拱是由两根曲杆及地基之间按三刚片规则组成的静定结构,如图所示。
A,B 为拱脚, 为拱高, 为拱的跨度。
1.反力在理论力学课程中,我们已学习过三铰拱的支座约束力的计算方法,考虑拱ACB 的整体平衡:0)(00=--⇒=⎰dx x l l l xA B q Y M (1) X X F q X Y M q Y M AB x l x A AC lx B A dx x l f l dx x l =⇒==---⇒==-⇒=⎰⎰00)2(20002/00 (2)2.内力设拱轴方程为y=f(x),拱上任意点K(x,y)(不妨设K 点在AC 杆上),切取K 点左侧部分分析(如图):f ldt t x x y dx dx xt A A k A x x A n N A x x A q Y X M Y q X N F Y q XN F ⎰⎰⎰-+-==-++⇒==--+⇒=000)(0sin )(sin 00sin )(cos 0ϕϕϕϕττ 其中ϕ值可由dx dy =ϕtan 计算。
3.拱与梁的比较拱与梁最基本的区别是:在竖向载荷作用下,水平推力的有无。
为了便于比较梁与拱的受力特性,我们考虑具有相同跨度,受相同载荷的梁的受力,分析方法与拱类似。
反力:000)(000=-⇒==--⇒=⎰⎰dx x l dx x l l l x B A l xA B q N M q N M内力:x dt t x N q M A xt k --=⎰00)( 比较可得,N Y N Y B B A A ==,拱在K 点的弯矩:y X M M A k k -=0由此可见,由于拱有水平推力X A 的存在,拱的弯矩比同跨度同载荷梁的弯矩要小得多,这使拱成为一个以受压为主或近似单纯受压的结构,这样就可以充分利用抗拉强度低,抗压强度高的廉价建筑材料(如砖,石,混凝土等)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§4-2 三铰拱的数值解
与代梁相比较有:
FVA
FV0A
FVB
FV0B
FH
M
0 C
f
y
FHA
A
FV0A
可见:
F
F
C
K
A
x
x
l/ 2
FVAF1 F2
K
a1 a2
C
a3
F
f B
l/ 2
F3
FHB FVB
B
FV0B
三铰拱的竖向支座反力就等于代梁的反力;
水平推力就等于代梁C 截面的弯矩除以矢高;
F HF H
AA
xx
FVFAVA
ff BB
FH FH
F VBF VB
最终弯矩图,可以看出, 它是由代梁的弯矩图M 0减
去一个与拱轴线相似的抛 AA 物 线 图 形 后 剩 下 的 图 形 FV0FAV0A FH•y , 即右下图阴影部份. 可见拱的弯矩是很小的,
B
A
B
有拉杆的三铰拱
两铰拱
(c)
梁式结构在竖向荷载作用下是不会产生推力的。
C
B
A
B
曲梁
§4-1 概 述
三铰拱各部分名称
拱顶
拱轴线
f 矢高
拱趾
拱趾
l 跨度
拱顶:拱的最高点。
拱趾: 支座处。 跨度:两支座之间的水平距离, 用l表示。 矢高:拱顶到两拱趾间联线的竖向距离,用f表示。 高跨比f/l是拱的一个重要的几何参数。工程实际 中,高跨比在l~1/10之间,变化的范围很大。
三铰拱任意截面K上的内力MK、FSK和FNK的计 算公式:
MK
M
0 K
FH y
FSK FS0K cos FH sin
FNK FS0K sin FH cos
拱的弯矩要比同跨度同荷载的简支梁的弯矩小 很多,当跨度比较大时采用拱比用梁要更为经济合 理。
§4-2 三铰拱的数值解
例4-1 试求图示三铰拱截面D的内力。 设拱轴线
105 kN5.25 m 100 kN2.25 m82.5 kN3.938 m
1.365 kN m
§4-2 三铰拱的数值解
注意:内力微分关系不适用于拱(拱轴线为曲线)。
作拱的内力图时需计算若干个截面的内力值然后
连线成图。 在本例的情况至少
qq yy FF
CC
要计算9个截面的内力 值然后连线成图才能获 得满意的效果。
为抛物线,当坐标原点选在左支座时,它的轴线方程式
为
y
4f l2
xl x ,已知D截面的坐标为: xD=5.25m
q=20 kN/m
。
Y F = 100 kN
解:(1) 代入数据后
C
拱轴线方程为:
y 1 x(12 x) 9
FH= 82.5 kN
D y=3.983 m A
X
FVA =105 kN 3m
§4-1 概 述
拱与其同跨度同荷载的简支梁相比其弯矩要小 得多,所以拱结构适用于大跨度的建筑物。它广泛 地应用房屋桥梁和水工建筑物中。由于推力的存在 它要求拱的支座必须设计得足够的牢固,这是采用 拱的结构形式时必须注意的。
§4-2 三铰拱的数值解
一、三铰拱的反力和内力计算。
1.支座反力 计算(与三铰刚 架反力的求法类 似)。
代梁:同跨度、 同荷载的简支梁,其 反力、内力记为
FV0A、FV0B、M 、0 FS0
y
F
F
F
C
K f
A
x
FHA
x
B
FHB
l/ 2
l/ 2
FVA
FVB
三铰拱
F1 F2
A
FV0A
a1
K C
a2
a3
F3
B
FV0B
代梁
§4-2 三铰拱的数值解
考虑整体平衡
由∑X=0,得 FHA FHB FH
y
F
F
C
F
FS0D 105 kN 100 kN 5 kN
FSD FS0D cosD FH sin D 5 kN0.9864 82.5 kN0.1644 8.631kN
FND FS0D sin D FH cos0
5 kN0.164482.5 kN0.9864 82.2 kN
MD
M
0 D
FH y
由∑MA=0
F1a1 F2a2 F3a3 FVBl 0 FHA
得
FVB
1 l
F1a1
F2a2
F3a3
K
A
x
x
l/ 2 FVA
由∑MB=0,得
FVA
1 l
F1
l
a1
F2 l
a2
F3 l
a3
f B
l/ 2
考虑C 铰左侧部分平衡
FHB FVB
由∑MC=0,得
FH
1 f
FyA
l 2
F1
l 2
拱的矢高对水平推力影响很大(矢高愈小即拱的 形状愈扁平推力愈大)。
§4-2 三铰拱的数值解
讨论:当拱的矢高 f=0 时,情况如何?
2.内力计算
(1)截面的内力假定: 轴力以压力为正, 剪力以有使截面产生顺时针转动的趋势者为正, 弯矩以拱内侧纤维受拉者为正。
§4-2 三铰拱的数值解
(2)内力计算
y
f=4m B
FH= 82.5 kN F = 115 kN
VB
当x =5.25m 时,y =3.938m
5.25m 12m
y tan 2 6 x
9
故 tanD 0.1667 ,因而 sin D 0.1644 ,cosD 0.9864
§4-2 三铰拱的数值解
(2) 求支座反力,结果为: FVA 105 kN , FVB 115 kN (3) 求内力 由水平推力 FH 82.5 kN 得
结构 力学
STRUCTURE MECHANICS
第四章 静定拱
§4-1 §4-2 §4-3
概述 三铰拱的数值解 三铰拱的合理拱轴线
§4-1 概 述
拱式结构的特点:杆 轴 线 为 曲 线 , 在 竖 向 荷 载 作用下会产生水平反力(称为推力)。
拱式结构又称为推力结构。
§4-1 概 述
C
C
A B
F
F
F
C
K截面形心的坐标为 x、y,截面切线的倾斜 角 为 θ 。 且 左 半 拱 的 为 FHA 正值,右半拱的θ为负 值。
考虑截面左侧部份平衡,由 FH
K f
A
x
B
x
l/ 2 FVA F2
F1 K
l/ 2
MK FN K y
F SK
FHB FVB
由∑MK=0可得
FVA
M K FVA x F1x b1 F2x b2 FH y
FVA
F2 MK
F1 K
FNK
ξ
y
FVB
FSK FS0K cos FH sin
FH
F SK
由 0
η FVA
FNK FVA F1 F2 sin FH cos 0 F1 F2
F3
与代梁相比较
A
FV0A
a1
K C
B
FV0B
FNK FS0K sin FH cos
a2 a3
§4-2 三铰拱的数值解
与代梁相比较
A
MK
M
0 K
FH y
FV0A
拱的弯矩等于相应截面代梁
的弯矩再减去推力引起的弯矩。
F1
a1 a2
F2 K C
a3
F3
B
FV0B
§4-2 三铰拱的数值解
y
F
F
F
C
K f
由 0
A x
FHA
x
B
FHB
l/ 2
l/ 2
FVA F1 F2 cos FH sin FSK 0
与代梁相比较
