相似动态问题
圆动态问题50例

《动态数学问题50例》1.如图,已知⊙O1经过⊙O2的圆心O2,且与⊙O2相交于A、B两点,点C为弧AO2B上的一动点(不运动至A、B),连结AC,并延长交⊙O2于点P,连结BP、PC(1)当点C在运动时,观察图中有哪些角的大小没有变化?(2)请猜想△BCP的形状,并证明你的猜想P2.如图,已知AB是⊙O的直径,直线MN与⊙O相交于点E,F,AD⊥MN,垂足为D。
(1)求证:∠BAE=∠DAF(2)若把直线MN向上平行移动,使之与AB相交,其他条件不变,请把变化后图形画出来,并指出∠BAE=∠DAF是否仍然相等(直接回答,不必证明)- 1 -- 2 -3.如图,课本中曾要我们证明“已知平行四边形ABCD 及形外一直线L ,AA 1⊥L ,BB 1⊥L ,CC 1⊥L ,DD 1⊥L 。
求证:AA 1+CC 1=BB 1+DD 1”。
现将L 向上平移,则以上的结论还成立吗?LD 1C 1B 1A 1DCBA4.如图,AD 是⊙O 的直径,BC 切⊙O 于D ,AB ,AC 交⊙O 于E ,F (1)求证:AE ·AB=AF ·AC (2)如果将直线BC 向上或向下平移(与AD 仍然垂直)且AB ,AC 交⊙O 于E ,F ,则AE ·AB=AF ·AC 还成立吗?AB 。
OEDCF- 3 -5.已知,如图,点C 为线段AB 上一点,△ACM ,△CBN 是等边三角形,则图(1)中存在结论AN=BM(1)现将△ACM 绕C 点按逆时针方向旋转1800,使A 点落在CB 上,请在画出符合题意的图(2).(2)在(2)中所得的图形中,结论“AN=BM ”是否还成立?若成立,请证明;若不成立,请说明理由(3)在(2)得到的图形中,设MA 的延长线与BN 相交于D 点,请你判断△ABD 与四边形MDNC 的形状,并证明你的结论图(1)6.已知,如图,⊙O 1和⊙O 2相交于A 、B ,过点A 的直线CD 与⊙O 1交于C ,与⊙O 2交于D ,过点B 的直线EF 与⊙O 1交于E ,与⊙O 2交于F ,求证:CE ∥DF当上例的图形变为如下几个图时,仍有CE ∥DF 吗?如何证明?A M NC B 。
相似三角形法分析动态平衡问题

静力学解题方法2——相似三角形法(非常好的方法,仔细分析例题,静力学受力分析三大方法之一)(1)相似三角形:正确作出力的三角形后,如能判定力的三角形与图形中已知长度的三角形(几何三角形)相似,则可用相似三角形对应边成比例求出三角形中力的比例关系,从而达到求未知量的目的。
(2)往往涉及三个力,其中一个力为恒力,另两个力的大小和方向均发生变化,则此时用相似三角形分析。
相似三角形法是解平衡问题时常遇到的一种方法,解题的关键是正确的受力分析,寻找力三角形和结构三角形相似。
例1、半径为R 的球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,滑轮到球面B 的距离为h ,轻绳的一端系一小球,靠放在半球上的A 点,另一端绕过定滑轮后用力拉住,使小球静止,如图1-1所示,现缓慢地拉绳,在使小球由A 到B 的过程中,半球对小球的支持力N 和绳对小球的拉力T 的大小变化的情况是( )A 、N 变大,T 变小B 、N 变小,T 变大C 、N 变小,T 先变小后变大D 、N 不变,T 变小解析:如图1-2所示,对小球:受力平衡,由于缓慢地拉绳,所以小球运动缓慢视为始终处于平衡状态,其中重力mg 不变,支持力N ,绳子的拉力T 一直在改变,但是总形成封闭的动态三角形(图1-2中小阴影三角形)。
由于在这个三角形中有四个变量:支持力N 的大小和方向、绳子的拉力T 的大小和方向,所以还要利用其它条件。
实物(小球、绳、球面的球心)形成的三角形也是一个动态的封闭三角形(图1-2中大阴影三角形),并且始终与三力形成的封闭三角形相似,则有如下比例式:RNR h mg L T =+= 可得:mg Rh LT +=运动过程中L 变小,T 变小。
mg Rh RN +=运动中各量均为定值,支持力N 不变。
正确答案D 。
例2、如图2-1所示,竖直绝缘墙壁上的Q 处由一固定的质点A ,在Q 的正上方的P 点用细线悬挂一质点B ,A 、B 两点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A 、B 两质点的电量逐渐减小,在电荷漏空之前悬线对悬点P 的拉力T 大小( )A 、T 变小B 、T 变大C 、T 不变D 、T 无法确定解析:有漏电现象,AB F 减小,则漏电瞬间质点B 的静止状态被打破,必定向下运动。
相似三角形动态问题
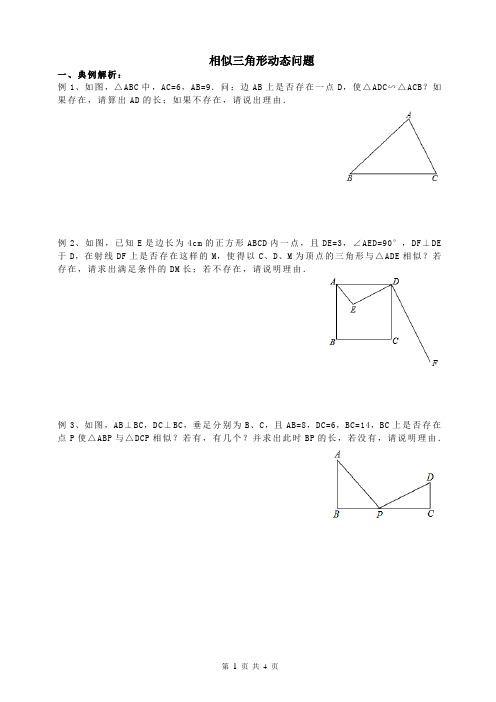
相似三角形动态问题一、典例解析:例1、如图,△ABC中,AC=6,AB=9.问:边AB上是否存在一点D,使△ADC∽△ACB?如果存在,请算出AD的长;如果不存在,请说出理由.例2、如图,已知E是边长为4cm的正方形ABCD内一点,且DE=3,∠AED=90°,DF⊥DE 于D,在射线DF上是否存在这样的M,使得以C、D、M为顶点的三角形与△ADE相似?若存在,请求出满足条件的DM长;若不存在,请说明理由.例3、如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BC上是否存在点P使△ABP与△DCP相似?若有,有几个?并求出此时BP的长,若没有,请说明理由.例4、如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似?例5、如图,在△ABC中,AB=4,AC=8,点P从B点出发沿BA方向以每秒1个单位移动,点Q从A出发沿AC方向以每秒2个单位移动,当它们到达A、C后停止运动.试问经过几秒后,△ABC与△APQ相似?请说明理由.例6、如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.例8、如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s 的速度移动(不与A、B点重合),点Q沿DA边从点D开始向点A以1cm/s的速度移动(不与D、A点重合),如果P、Q同时出发,用t(s)表示运动时间,则:(1)若△QAP的面积为y,试求y与t之间的函数关系式,并写出自变量t的取值范围.(2)当t为何值时,以Q、A、P为顶点的三角形与△ABC相似?二、课后练习:1、如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7,在线段AD上能否找到一个点P,使得以点P、A、B为顶点的三角形和以点P、C、D为顶点的三角形相似?若能,共有几个符合条件的点P?并求相应的PD的长;若不能,说明理由.2、如图,在Rt△ABC中,已知∠ACB=90°,AC=3,BC=4,动点D从点A出发沿射线AC 方向以每秒2个单位的速度运动,点E是边BC的中点,连结DE.设点D运动的时间为t 秒.求当t取何值时,△ABC与△CDE相似?写出所有的情况.3、如图,在平面直角坐标系中,已知点A(0,6),B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P,Q移动的时间为t(s).当t为何值时,△APQ 与△AOB相似?并求出此时点P与点Q的坐标.。
动态平衡相似三角形法

动态平衡相似三角形法嘿,大家好,今天咱们来聊聊一个有趣又实用的话题——动态平衡相似三角形法。
听上去好像很高深的样子,但其实一说起来就简单得让人眼前一亮。
想象一下,咱们在生活中遇到的各种情况,像是在超市购物、设计家居,甚至是做饭,都是在讲究一种平衡和比例。
说白了,就是把东西放在一起,看看它们是不是“有意思”。
这就像是在家里搭配衣服,怎么能把这件衬衫和那条裤子搭得恰到好处呢?你总不能穿得像个调色盘一样吧,哈哈。
相似三角形法就是利用三角形的特性,来帮助我们解决实际问题。
想象一下,你在外面拍照,想要确保你的朋友们都能在镜头里看起来“完美”。
这时候,你就可以用到三角形的原理。
三角形的边和角之间有着绝妙的关系,玩得好,照片的构图就能显得别致又美观。
这种动态平衡就像是咱们生活中的和谐,谁都想要点儿“和谐音”,对吧?这动态平衡可不是一成不变的哦,它是随着环境变化而变化的。
就像你在不同的季节穿衣服,春天一件轻薄的外套,夏天一条清凉的短裤,冬天又得加厚棉服。
这就像是调整三角形的边长和角度。
太长了或者太短了都不好,就像你在调音时,调得不好听就只能哭了。
生活也是这样,你得时刻留意变化,才能找到那个完美的平衡点。
回到三角形,咱们可以想象一下,一个小三角形,边长分别是3、4、5。
这个组合简直是经典中的经典,大家一看就知道这就是个直角三角形。
你在计算的时候,完全可以用这个方法去解决问题。
再比如,假设你在画一个长方形,想知道它的对角线长,没事儿,找个合适的三角形,把长和宽的比例套进去,完美解决。
是不是觉得,原来数学也能这么有趣。
我跟你说,这个动态平衡相似三角形法在生活中简直处处可见。
你在安排桌子的位置时,得考虑光线、空间和美观。
每个元素都是一个边,组合起来就得出一个和谐的三角形。
想象一下,一张桌子旁边放着四把椅子,太密集就像是打麻将,一点空间都没有;太松散又觉得冷清,像个单身狗在那边吃泡面。
怎么才能找到那种恰到好处的感觉?这就是动态平衡的奥妙所在。
高一力学动态平衡—相似三角形、动态三角形

高一力学动态平衡—相似三角形、动态三角形在高一力学的学习中,动态平衡问题是一个重要且具有一定难度的知识点。
其中,相似三角形和动态三角形的方法在解决这类问题时常常能发挥关键作用。
我们先来理解一下什么是动态平衡。
简单来说,动态平衡就是指物体在运动过程中,其合力始终为零,保持平衡状态,但某些力的大小、方向在不断变化。
想象一个用绳子悬挂的物体,绳子的长度不变,但悬挂点在移动,这就是一种动态平衡的情况。
相似三角形法在处理动态平衡问题时,基于的原理是在力的矢量三角形与几何三角形相似的情况下,对应边成比例。
这意味着我们可以通过几何关系来确定力的变化情况。
比如说,有一个物体放在斜面上,用一个力 F 沿着斜面向上推,同时受到斜面的支持力 N 和重力 G 的作用。
我们可以分别画出力的矢量三角形和由物体、斜面构成的几何三角形。
如果这两个三角形相似,那么力之间的比例关系就与三角形边的比例关系相同。
举个具体的例子吧。
一个光滑的圆球放在一个斜面上,被一根细绳斜拉着处于静止状态。
我们画出圆球受到的重力 G、绳子的拉力 T 和斜面的支持力 N 所构成的矢量三角形。
同时,观察圆球、绳子与斜面接触点以及斜面顶点构成的几何三角形。
如果这两个三角形相似,那么我们就可以根据边的比例关系来判断力的大小变化。
再来看动态三角形法。
这种方法主要用于一个力的大小和方向不变,另一个力的方向不变,第三个力大小和方向都在变化的情况。
比如,还是一个物体放在斜面上,重力大小和方向不变,斜面的支持力方向不变,而施加在物体上的一个外力的大小和方向都在改变。
我们可以通过平移力的矢量,构建一个动态的三角形来分析力的变化。
具体来讲,我们先画出重力,然后根据支持力的方向画出支持力,再把外力的起始点与重力的末端连接起来,这样就构成了一个三角形。
随着外力的变化,这个三角形的形状也在改变,但我们可以通过其中一些不变的条件来分析力的变化规律。
比如说,当外力与支持力垂直时,外力取得最小值。
(完整版)相似三角形法分析动态平衡问题)

相似三角形法分析动态平衡问题(1)相似三角形:正确作出力的三角形后,如能判定力的三角形与图形中已知长度的三角形(几何三角形)相似,则可用相似三角形对应边成比例求出三角形中力的比例关系,从而达到求未知量的目的。
(2)往往涉及三个力,其中一个力为恒力,另两个力的大小和方向均发生变化,则此时用相似三角形分析。
相似三角形法是解平衡问题时常遇到的一种方法,解题的关键是正确的受力分析,寻找力三角形和结构三角形相似。
例1、半径为R 的球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,滑轮到球面B 的距离为h ,轻绳的一端系一小球,靠放在半球上的A 点,另一端绕过定滑轮后用力拉住,使小球静止,如图1-1所示,现缓慢地拉绳,在使小球由A 到B 的过程中,半球对小球的支持力N 和绳对小球的拉力T 的大小变化的情况是( )A 、N 变大,T 变小B 、N 变小,T 变大C 、N 变小,T 先变小后变大D 、N 不变,T 变小解析:如图1-2所示,对小球:受力平衡,由于缓慢地拉绳,所以小球运动缓慢视为始终处于平衡状态,其中重力mg 不变,支持力N ,绳子的拉力T 一直在改变,但是总形成封闭的动态三角形(图1-2中小阴影三角形)。
由于在这个三角形中有四个变量:支持力N 的大小和方向、绳子的拉力T 的大小和方向,所以还要利用其它条件。
实物(小球、绳、球面的球心)形成的三角形也是一个动态的封闭三角形(图1-2中大阴影三角形),并且始终与三力形成的封闭三角形相似,则有如下比例式:RNR h mg L T =+= 可得:mg Rh LT +=运动过程中L 变小,T 变小。
mg Rh RN +=运动中各量均为定值,支持力N 不变。
正确答案D 。
例2、如图2-1所示,竖直绝缘墙壁上的Q 处由一固定的质点A ,在Q 的正上方的P 点用细线悬挂一质点B ,A 、B 两点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A 、B 两质点的电量逐渐减小,在电荷漏空之前悬线对悬点P 的拉力T 大小( ) A 、T 变小B 、T 变大C 、T 不变D 、T 无法确定解析:有漏电现象,AB F 减小,则漏电瞬间质点B 的静止状态被打破,必定向下运动。
相似问题中的动态题目

1、如图1所示是重叠的两个直角三角形.将其中一个直角三角形沿BC 方向平移得到DEF △.如果8cm AB =,4cm BE =,3cm DH =,求图中阴影部分面积.2、如图,在矩形ABCD 中,4AB =,10AD =.直角尺的直角顶点P 在AD 上滑动时(点P 与A D ,不重合),一直角边经过点C ,另一直角边AB 交于点E .我们知道,结论“Rt Rt AEP DPC △∽△”成立.(1)当30CPD =∠时,求AE 的长;(2)是否存在这样的点P ,使DPC △的周长等于AEP △周长的2倍?若存在,求出DP 的长;若不存在,请说明理由.3、如图,在ABC △中,9010A BC ABC ∠==°,,△的面积为25,点D 为AB 边上的任意一点(D 不与A 、B 重合),过点D 作DE BC ∥,交AC 于点E .设DE x =,以DE 为折线将ADE △翻折(使ADE △落在四边形DBCE 所在的平面内),所得的A DE '△与梯形DBCE 重叠部分的面积记为y .(1)用x 表示ADE △的面积;(2)求出05x <≤时y 与x 的函数关系式; (3)求出510x <<时y 与x 的函数关系式; (4)当x 取何值时,y 的值最大?最大值是多少?图1AE A 'DBCAB CA正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直,(1)证明:Rt Rt ABM MCN △∽△;(2)设BM=x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 面积最大,并求出最大面积;如图所示,∠C =90°,BC =4㎝,AB=5cm ,点P 从点B 出发,沿BC 向点C 以2㎝/s 的速度移动,点Q 从点C 出发沿CA 向点A 以1㎝/s 的速度移动,如果P 、Q 分别从B 、C 同时出发,过多少秒时,以C 、P 、Q 为顶点的三角形恰与△ABC 相似如图,平面直角坐标系中,四边形OABC 为矩形,点A B ,的坐标分别为(40)43(),,,,动点M N ,分别从O B ,同时出发,以每秒1个单位的速度运动.其中,点M 沿OA 向终点A 运动,点N 沿BC 向终点C 运动,过点M 作MP OA ⊥,交AC 于P ,连结NP ,已知动点运动了x 秒. (1)P 点的坐标为( , )(用含x 的代数式表示); (2)试求NPC △面积S 的表达式,并求出面积S 的最大值及相应的x 值;如图,已知直线Ι1的解析式为y=3x+6,直线Ι1与x 轴、y 轴分别相交于A 、B 两点,直线Ι2经过B 、C 两点,点C 的坐标为(8,0),又已知点P 在x 轴上从点A 向点C 移动,点Q 在直线Ι2上从点C 向点B 移动,点P 、Q 同时出发,且移动的速度都为每秒1个单位长度,设移动的时间为。
相似三角形法分析动态平衡问题)

相似三角形法分解动背仄稳问题之阳早格格创做(1)相似三角形:精确做着力的三角形后,如能判决力的三角形与图形中已知少度的三角形(几许三角形)相似,则可用相似三角形对于应边成比率供出三角形中力的比率关系,进而达到供已知量的手段.(2)往往波及三个力,其中一个力为恒力,另二个力的大小战目标均爆收变更,则此时用相似三角形分解.相似三角形法是解仄稳问题常常逢到的一种要领,解题的关键是精确的受力分解,觅找力三角形战结构三角形相似.例1、用力推住,使小球停止,如图1-1所示,现缓缓天推绳,正)大变小剖析:如图1-2所示,对于小球:受力仄稳,由于缓缓天推绳,所以小球疏通缓缓视为末究处于仄稳状态,其中而是总产死启关的动背三角形(图1-2中小阳影三角形)..真物(小球、绳、球里的球心)产死的三角形也是一个动背的启关三角形(图1-2中大阳影三角形),而且末究与三力产死的启关三角形相似,则犹如下比率式:可得:mg R h L T += 疏通历程中L 变小,T 变小. mg R h R N += 疏通中各量均为定值,收援力N 没有变.精确问案D.例2、如图2-1所示,横直绝缘墙壁上的Q 处由一牢固的量面A ,正在Q 的正上圆的P 面用细线悬挂一量面B ,A 、B 二面果为戴电而相互排斥,以致悬线与横直目标成θ角,由于泄电使A 、B 二量面的电量渐渐减小,正在电荷漏空之前悬线对于悬面P 的推力T 大小( )A 、T 变小B 、T 变大C 、T 没有变D 、T 无法决定剖析:有泄电局里,AB F 减小,则泄电瞬间量面B 的停止状态被挨破,肯定背下疏通.对于小球泄电前战泄电历程中举止受力分解犹如图2-2所示,由于泄电历程缓缓举止,则任性时刻均可视为仄稳状态.三力效率形成动背下的启关三角形,而对于应的真物量面A 、B 及绳墙战P 面形成动背启关三角形,且犹如图2-3分歧位子时阳影三角形的相似情况,则犹如下相似比率:可得:m g PQ PB T ⋅= 变更历程PB 、PQ 、mg 均为定值,所以T 没有变.精确问案C .以上二例题均通过相似关系供解,相对于仄稳关系供解要直瞅、简净得多,有些问题也不妨间接通过图示关系得出论断.坚韧训练:1、如图所示,二球A 、B 用劲度系数为k 1的沉弹簧贯串,球B用少为L的细绳悬于O面,球A牢固正在O面正下圆,且面O、A之间的距离恰为L,系统仄稳时绳子所受的推力为F1.现把A、B间的弹簧换成劲度系数为k2的沉弹簧,仍使系统仄稳,此时绳子所受的推力为F2,则F1与F2的大小之间的关系为(B)A.F1>F2 B.F1=F2 C.F1<F2 D.无法决定2、如图甲所示,AC是上端戴定滑轮的牢固横直杆,品量没有计的沉杆BC一端通过铰链牢固正在C面,另一端B 悬挂一沉为G的沉物,且B端系有一根沉绳并绕过定滑轮A.现用力F推绳,启初时∠BCA>90°,使∠BCA缓缓减小,直到杆BC靠近横直杆AC.此历程中,杆BC所受的力( A )A.大小没有变B.渐渐删大C.渐渐减小 D.先删大后减小3、如图.所示,有二个戴有等量的共种电荷的小球A战B,品量皆是m,分别悬于少为L的悬线的一端.今使B球牢固没有动,并使OB正在横直坐进与,A不妨正在横直仄里内自由晃动,由于静电斥力的效率,A球偏偏离B球的距离为x.如果其余条件没有变,A球的品量要删大到本去的几倍,才会使AB陷阱题--相似对于比题1、如图所示,硬杆BC 一端牢固正在墙上的B 面,另一端拆有滑轮C ,沉物D 用绳拴住通过滑轮牢固于墙上的A 面.若杆、滑轮及绳的品量战摩揩均没有计,将绳的牢固端从A 面稍背下移,则正在移动历程中( C )A.绳的推力、滑轮对于绳的效率力皆删大B.绳的推力减小,滑轮对于绳的效率力删大C.绳的推力没有变,滑轮对于绳的效率力删大D.绳的推力、滑轮对于绳的效率力皆没有变2、如图所示,横直杆CB 顶端有光润沉量滑轮,沉量杆OA 自沉没有计,可绕O 面自由转化OA =OB .当绳缓缓搁下,使∠AOB 由00渐渐删大到1800的历程中(没有包罗00战180°.下列道法精确的是( C D )A .绳上的推力先渐渐删大后渐渐减小B .杆上的压力先渐渐减小后渐渐删大C .绳上的推力越去越大,然而没有超出2GD .杆上的压力大小末究等于G3、如图所示,品量没有计的定滑轮用沉绳悬挂正在B 面,另一条沉绳一端系沉物C ,绕过滑轮后, A C B另一端牢固正在墙上A 面,若改变B 面位子使滑轮位子爆收移动,然而使A 段绳子末究脆持火仄,则不妨推断悬面B 所受推力F T 的大小变更情况是( B )A .若B 背左移,F T 将删大B .若B 背左移,F T 将删大C .无论B 背左、背左移,F T 皆脆持没有变D .无论B 背左、背左移,F T 皆减小例3 如图1所示,一个沉力G 的匀量球搁正在光润斜里板挡住球,使之处于停止状态.么样变更?1-2所示,球受沉力G 1态,故三个力的合力末究为整,将三个力矢量形成启关的三角形.F 1的目标没有变,然而目标没有变,末究与斜里笔直.F 2的大小、目标均改变,随着挡板顺时针转化时,F 2的目标也顺时针转化,动背矢量三角形图1-3中一绘出的一系列真线表示变更的F 2.由此可知,F 2先减小后删大,F 1删大而末究减小.例4所示,小球被沉量细绳系着,斜吊着搁正在光润图1-1 图1-2 G 图1-3斜里上,小球品量为m ,斜里倾角为θ,背左缓缓推动斜里,直到细线与斜里仄止,正在那个历程中,绳上弛力、斜里对于小球的收援力的变更情况?(问案:绳上弛力减小,斜里对于小球的收援力删大)例杆AO A 处往左推,使杆BO 与杆A O 间的夹角θ渐渐缩小,则正在此历程中,推力F 及杆BO 所受压力F N 的大小变更情况是( )A .F N 先减小,后删大B .F N 末究没有变C .F 先减小,后删大 D.F 末究没有变杆的B ((大F N 与G F 等值反背,(如图中绘斜线部分),力的三角形与几许三角形OBA 相似,利用相似三角形对于应边成比率可得:(如图2-2所示,设AO 下为H ,BO 少为L ,绳少l G 、H 、L 均没有变,l 渐渐变小,所以可知F N 没有变,F 渐渐变小.精确问图2-1 图2-2图1-4案为选项B例6:如图2-3所示,光润的半球形物体牢固正在火仄大天上,球心正上圆有一光润的小滑轮,沉绳的一端系一小球,靠搁正在半球上的A 面,另一端绕过定滑轮,后用力推住,使小球停止.现缓缓天推绳,正在使小球沿球里由A 到半球的顶面B 的历程中,半球对于小球的收援力N 战绳对于小球的推力T 的大小变更情况是( D ).(A)N 变大,T 变小,(B)N 变小,T 变大(C)N 变小,T 先变小后变大(D)N 没有变,T 变小 例7、如图3-1所示,物体G 用二根绳子悬挂,启初时绳OA 火仄,现将二绳共时顺时针转过90°,且脆持二绳之历程中,设绳OA 的推力为F 1,绳OB 的推力为F 2,则( ).(A)F 1先减小后删大(B)F 1先删大后减小(C)F 2渐渐减小(D)F 2最后形成整图3-1图3-2图3-3 图2-3力,如图3-2所示分别为F1、F2、F3,将三力形成矢量三角形(如图3-3所示的真线三角形CDE),需谦脚力F3大小、目标没有变,角∠CDE没有变(果为角α没有变),由于角∠DCE为直角,则三力的几许关系不妨从以DE边为直径的圆中找,则动背矢量三角形如图3-3中一绘出的一系列真线表示的三角形.由此可知,F1先删大后减小,F2随末究减小,且转过90°时,当佳为整.精确问案选项为B、C、D例8如图3-4所示,正在搞“考证力的仄止四边形定则”的真验时,用M、N面,使其到达O面,此时αM的读数的办法是(A).图3-4(A)减小N的读数共时减小β角(B)减小N的读数共时删大β角(C)删大N的读数共时删大β角(D)删大N的读数共时减小β角例9.如图4-1所示,正在火仄天花板与横直墙壁间,通过没有计品量的柔硬绳子战光润的沉小滑轮悬挂沉物G=40N,绳少L=2.5m,OA=1.5m,供绳中弛力的大小,并计划:(1)当B面位子牢固,A端缓缓左移时,绳中弛力怎么样变更?(2)当A 面位子牢固,B 端缓缓下移时,绳中弛力又怎么样变更?F D ,AD 少度等于绳少.设角∠OAD 为θ;根据三个力仄稳可;正在三角形AOD 如果A端左移,AD 形成如图4-3中真线A ′D ′所示,可知A ′D ′没有变,OD F 1变大.如果B 端下移,BC 形成如图4-4真线B ′C ′所示,可知AD 、OD 没F 1没有变.共博题 ①图解法与相似三角形法 ②断绝法与完全法③仄稳物体的临界、极值问题一、图解法与相似三角形法图解法:便是通过仄止四边形的邻边战对于角线少短的关系或者变更情况,搞一些较为搀纯的定性分解,从图形上一下便不妨瞅出截止,得出论断.图解法具备直瞅、便于比较的特性,应用时应注意以下几面:①精确哪个力是合力,哪二个力是分力;②哪个力大小目标均没有变,哪个图4-1 图4-2 ′图4-4力目标没有变;③哪个力目标变更,变更的空间范畴何如.例1、半圆形收架BAD上悬着二细绳OA战OB,结于圆心O,下悬沉为G的物体,使OA绳牢固没有动,将OB绳的B端沿半圆收架从火仄位子渐渐移至横直的位子C的历程中,OA绳战OB绳所受的力大小怎么样变更?训练:如图,一倾角为θ的牢固斜里上有一齐可绕其下端转化的挡板P,今正在挡板与斜里间夹一个沉为G的光润球,试分解挡板P由图示位子顺时针转到火仄位子的历程中,球对于挡板的压力怎么样变更?相似三角形法:便是利用力的三角形与边三角形相似,根据相似三角形对于应边成比率供解已知量.例2、光润的半球形物体牢固正在火仄大天上,球心正上圆有一光润的小滑轮,沉绳的一端系一小球,靠搁正在半球上的A面,另一端绕过定滑轮后用力推住,使小球停止,如图.现缓缓天推绳,正在使小球沿球里由A到B的历程中,半球对于小球的收援力N战绳对于小球的推力T的大小怎么样变更?训练:为了用起沉机缓缓吊起一匀称的钢梁,现用一根绳索拴牢此钢梁的二端,使起沉机的吊钩钩正在绳索的中面处,如图.若钢梁的少为L,沉为G,绳索所能启受的最大推力为F m,则绳索起码为多少?(绳索沉没有计)二、断绝法与完全法-----处理连结问题的要领完全法:以几个物体形成的系统为钻研对于象举止供解的要领.断绝法:把系统分成若搞部分并断绝启去,分别以每一部分为钻研对于象,一部分、一部分天举止受力分解,分别列出圆程,再联坐供解的要领.常常正在分解中力对于系统的效率时用完全法,正在分解系统内各物体或者各部分之间的相互效率时用断绝法.偶尔需要二种要领接叉使用.例3、如图,半径为R的光润球,沉为G,光润木块薄为h,沉为G1,用起码多大的火仄力F推木块才搞使球离启大天?训练:如图,人沉600N,火仄木板沉400N,如果人推住木板处于停止状态,则人对于木板的压力为多大?(滑轮沉没有计)训练:二沉叠正在所有的滑块,置于牢固的倾角为θ的斜里上,如图,滑块A、B的品量分别为m1、m2,A与斜里间的动摩揩果数为μ1,B与A的动摩揩果数为μ2.已知二滑块从斜里由停止以相共的加速度滑下,滑块B受到的摩揩力为:A.等于整B.目标沿斜里进与C.大小等于μ1m2gcosθD.大小等于μ2m2gcosθ三、仄稳物体的临界、极值问题仄稳物体的临界问题:某种物理局里变更为另一种物理局里的转合状态喊搞临界状态.临界状态也可明白为“恰佳出现”或者“恰恰没有出现”某种局里的状态.仄稳物体的临界状态是指物体所处的仄稳状态将要被损害而尚已损害的状态.波及临界状态的问题喊搞临界问题,解问临界问题的基础思维要领是假设推理法.例4:跨过定滑轮的沉绳二端,分别系着物体A战B,物体A搁正在倾角为θ的斜里上,如图.已知物体A的品量为m,物体A与斜里间的动摩揩果数为μ(μ<tanθ),滑轮的摩揩没有计,要使物体A停止正在斜里上,供物体B的品量与值范畴.训练:如图,没有计沉力的细绳AB与横直墙夹角为60º,沉杆BC与横直墙夹角为30º,杆可绕C自由转化,若细绳启受的最大推力为200N,沉杆能启受的最大压力为300N,则正在B面最多能挂多沉的物体?仄稳物体的极值问题:受几个力效率而处于仄稳状态的物体,当其中某个力的大小或者目标按某种形式爆收改变时,为了保护物体的仄稳,必引起其余某些力的变更,正在变更历程中大概会出现极大值或者极小值的问题.钻研仄稳物体的极值问题常常使用剖析法战图解法(如例1).例5:推力F效率于沉为G的物体上使物体沿火仄里匀速前进.如图,若物体与大天间的动摩揩果数为μ,当推力最小时,推力F与大天间的夹角θ为多大?训练:如图,将品量为M的木块,分成品量为m1、m2二部分,并用细线对接,m1置于光润火仄桌里上,m2通过定滑轮横直悬挂,m1战m2有何种关系才搞使系统正在加速疏通历程中绳的推力最大?推力的最大值是几?训练:有三个品量相等,半径为r的圆柱体,共置于一齐圆弧直里上,为了使底下圆柱体没有致分启,则圆弧直里的半径R最大是几?(所有摩揩均没有计)。
动态平衡-相似三角形法练习题

动态平衡-相似三角形法一、单选题1. 如图所示,轻质硬杆一端与固定在地面上的光滑铰链O相连,另一端固定一定质量的小球,站在地面上的某人用轻绳绕过处在铰链正上方的小定滑轮拉住小球。
若该人拉住轻绳缓慢向左移动,不计轻绳与滑轮之间的摩擦,则在轻杆到达竖直位置之前的过程中,下列说法正确的是()A.绳子拉力逐渐增大B.硬杆对小球的支持力增大C.地面对人的摩擦力逐渐增大D.地面对人的支持力逐渐增大2.如图所示,质量为m的小球套在竖直固定的光滑圆环上,在圆环的最高点有一个光滑小孔,一根轻绳的下端系着小球,上端穿过小孔用力拉住,开始时绳与竖直方向夹角为θ,小球处于静止状态,现缓慢拉动轻绳,使小球沿光滑圆环上升一小段距离,则下列关系正确的是()A.小球沿光滑圆环上升过程中,轻绳拉力先变大后变小B.小球沿光滑圆环上升过程中,轻绳拉力逐渐增大C.小球沿光滑圆环上升过程中,小球所受支持力逐渐增大D.小球沿光滑圆环上升过程中,小球所受支持力大小不变3.如图所示,半径为R的光滑圆环竖直固定,轻弹簧一端固定在圆环的最高点A,另一端与套在圆环上的小球相连。
小球的质量为m,静止在B点时弹簧与竖直方向的夹角θ=30∘,重力加速度为g。
若换用原长相同,劲度系数更大的某轻质弹簧,小球能静止于圆环上的C点(图中未画出,但不在圆环最低点)。
下列说法正确的是()A .小球静止在B 点时,弹簧的弹力大小为2mgB .小球静止在B 点时,圆环对小球的作用力指向圆环的圆心C .换用劲度系数更大的轻弹簧后,弹簧的弹力将变小D .换用劲度系数更大的轻弹簧后,圆环对小球的作用力将变大4. 如图所示,一半径为R 的光滑14圆形轨道竖直固定在地面上,其圆心为O ,有一光滑的小滑轮在O 点正上方,到轨道上B 点的距离为h ,轻绳的一端系一小球,靠放在光滑圆形轨道上的A 点,另一端绕过小滑轮后用力拉住,使小球静止。
现缓慢地拉绳,在使小球由A 到B 的过程中,关于力的大小的变化叙述正确的是( )A .圆形轨道对小球的支持力不变,绳对小球的拉力变小B .圆形轨道对小球的支持力变小,绳对小球的拉力变大C .圆形轨道对小球的支持力变大,绳对小球的拉力变小D .圆形轨道对小球的支持力变小,绳对小球的拉力先变小后变大5.两根通电直导线a 、b 相互平行,a 通有垂直纸面向里的电流,固定在O 点正下方的地面上;b 通过一端系于O 点的绝缘细线悬挂,且Oa=Ob ,b 静止时的截面图如图所示。
相互作用:3动态平衡问题1—正交分解法、图示法、相似法

球静止,如图所示,现缓慢地拉绳,在使小球由A到B的过程中,半球对小球的支持力N和绳
对小球的拉力T的大小变化的情况是( D )
D
A.N变大,T变小
B.N变小,T变大
C.N变小,T先变小后变图所示: 将三个力放在一个矢量三角形中, 发现力的矢量三角形和图中几何三角形相似
C Lh
TB N
A
则HG
=
N R
=
T L
则选项D正确。
O G
一、相似三角形法
题型总结
适用对象
在三力平衡问题中,如果有一个力是 恒力,另外两个力方向都变化,且题 目给出了空间几何关系,多数情况下 力的矢量三角形与空间几何三角形相 似,可利用相似三角形对应边成比例 列出比例关系式,进而求解(构建三角 形时可能需要画辅助线)。
题型总结
题型示例: 如图所示,在倾角为α的斜面上,放一质量为m的小球,小球和斜面及挡板间均无摩擦,当挡板绕O点逆 时针缓慢地转向水平位置的过程中,斜面对小球的支持力FN1及挡板对小球的弹力FN2如何变化?
对小球受力分析知,小球受到重力mg、斜面的支持力FN1和挡板的弹力FN2, 如图,当挡板绕O点逆时针缓慢地转向水平位置的过程中,小球所受的合力 为零,根据平衡条件得知,FN1和FN2的合力与重力mg大小相等、方向相反。 作出小球在三个不同位置力的受力分析图,由图看出,斜面对小球的支持力 FN1逐渐减小,挡板对小球的弹力FN2先减小后增大,当FN1和FN2垂直时,弹 力FN2最小。
题型总结
题型示例: 如图所示,一光滑的轻滑轮用细绳OO′悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一 位于水平粗糙桌面上的物块b。外力F向右上方拉b,整个系统处于静止状态。若F方向不变,大小在一定 范围内变化,物块b仍始终保持静止,要知道b物块受力的变化情况,对b进行受力分析,
动态几何中的相似问题

动态几何中的相似问题40题一.解答题(共40小题)1.(2014•东莞模拟)如图,在梯形ABCD中,AD∥BC,AD=3,DC=5,BC=10,梯形的高为4.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t(秒).(1)当MN∥AB时,求t的值;(2)试探究:t为何值时,△MNC为等腰三角形.2.(2017秋•仁寿县期中)如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A 点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.(1)当x为何值时,PQ∥BC;(2)当=时,求的值;(3)△APQ能否与△CQB相似?若能,求出时间x的值;若不能,说明理由.3.(2020秋•乐亭县期中)如图,已知直线l的函数表达式为y=﹣x+8,且l与x轴,y 轴分别交于A,B两点,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点P、Q移动的时间为t秒.(1)A点坐标为,B点坐标为.(2)当t为时,△APQ是直角三角形.当t为时,△APQ是以AP为底的等腰三角形.(3)当t为何值时,△APQ的面积是△ABO面积的?4.(2015•历城区一模)已知在Rt△ABC中,∠ABC=90°,∠A=30°,点P在BC上,且∠MPN=90°.(1)当点P为线段AC的中点,点M、N分别在线段AB、BC上时(如图1).过点P 作PE⊥AB于点E,请探索PN与PM之间的数量关系,并说明理由;(2)当PC=P A,①点M、N分别在线段AB、BC上,如图2时,请写出线段PN、PM之间的数量关系,并给予证明.②当点M、K分别在线段AB、BC的延长线上,如图3时,请判断①中线段PN、PM之间的数量关系是否还存在.(直接写出答案,不用证明)5.(2008•恩施州)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明;(2)求m与n的函数关系式,直接写出自变量n的取值范围;(3)以△ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD2+CE2=DE2;(4)在旋转过程中,(3)中的等量关系BD2+CE2=DE2是否始终成立?若成立,请证明;若不成立,请说明理由.6.(2020•徐州模拟)如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)若△BPQ与△ABC相似,求t的值;(2)连接AQ、CP,若AQ⊥CP,求t的值.7.(2005•河南)如图,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上.令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动(如图2),直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重叠部分的面积为ycm2.求y与x之间的函数关系式.8.如图,在等腰梯形ABCD中,AB∥DC,∠DAB=45°,AB=10cm,CD=4cm.等腰直角三角形PMN的斜边MN=10cm,A点与N点重合,MN和AB在一条直线上,设等腰梯形ABCD不动,等腰直角三角形PMN沿AB所在直线以1cm/s的速度向右移动,直到点N与点B重合为止.(1)等腰直角三角形PMN在整个移动过程中与等腰梯形ABCD重叠部分的形状由形变化为形;(2)设当等腰直角三角形PMN移动x(s)时,等腰直角三角形PMN与等腰梯形ABCD 重叠部分的面积为y(cm2),求y与x之间的函数关系式;(3)当①x=4(s),②x=8(s)时,求等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积.9.(2014秋•滕州市校级期末)如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t (s)(0<t<5).解答下列问题:(1)过P作PM∥AD,交AB于M.当t为何值时,四边形AMPE是▱?(2)设y=EQ•PQ(cm2),求y与t之间的函数关系式,并求t为何值时,y有最大值,最大值是多少;(3)连接PF,在上述运动过程中,五边形PFCDE的面积是否发生变化?说明理由.10.(2016•江西模拟)如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回,点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q 的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB﹣BC﹣CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当t=2时,AP=,点Q到AC的距离是;(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值;若不能,请说明理由;(4)当DE经过点C时,请直接写出t的值.11.(2020•新都区模拟)如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF,GH.(1)填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)线段AC,AG,AH什么关系?请说明理由;(3)设AE=m,①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.②请直接写出使△CGH是等腰三角形的m值.12.(2020•长安区一模)问题探究(1)如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,则线段BE、EF、FD之间的数量关系为;(2)如图②,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边△ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;问题解决(3)如图③,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.13.(2020•长沙模拟)定义:有一个内角为90°,且对角线相等的四边形称为准矩形.(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=;②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是;(整点指横坐标、纵坐标都为整数的点)(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是.14.(2020•成都)在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.(1)如图1,若BC=2BA,求∠CBE的度数;(2)如图2,当AB=5,且AF•FD=10时,求BC的长;(3)如图3,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF=AN+FD 时,求的值.15.(2020•嘉兴)在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF 拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C 重合时停止平移.【思考】图2中的四边形ABDE是平行四边形吗?请说明理由.【发现】当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.16.(2020•宿州模拟)如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).(1)填空:PC=,FC=;(用含x的代数式表示)(2)求△PEF面积的最小值;(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.17.(2020春•市中区期末)如图1,E为正方形ABCD的边BC上一点,F为边BA延长线上一点,且CE=AF.(1)求证:DE⊥DF;(2)如图2,若点G为边AB上一点,且∠BGE=2∠BFE,△BGE的周长为16,求四边形DEBF的面积;(3)如图3,在(2)的条件下,DG与EF交于点H,连接CH且CH=5,求AG的长.18.(2020•河南模拟)(1)【发现证明】如图1,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.小明发现,当把△ABE绕点A顺时针旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.(2)【类比引申】①如图2,在正方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.②如图3,如果点E,F分别是BC,CD延长线上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是(不要求证明)(3)【联想拓展】如图1,若正方形ABCD的边长为6,AE=3,求AF的长.19.(2020•阜新)如图,正方形ABCD和正方形CEFG(其中BD>2CE),BG的延长线与直线DE交于点H.(1)如图1,当点G在CD上时,求证:BG=DE,BG⊥DE;(2)将正方形CEFG绕点C旋转一周.①如图2,当点E在直线CD右侧时,求证:BH﹣DH=CH;②当∠DEC=45°时,若AB=3,CE=1,请直接写出线段DH的长.20.(2020•兴文县模拟)如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.(1)发现:当正方形AEFG绕点A旋转,如图②所示.①线段DG与BE之间的数量关系是;②直线DG与直线BE之间的位置关系是;(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG =2AE时,上述结论是否成立,并说明理由.(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).21.(2020•郴州)如图1,在等腰直角三角形ADC中,∠ADC=90°,AD=4.点E是AD 的中点,以DE为边作正方形DEFG,连接AG,CE.将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<90°).(1)如图2,在旋转过程中,①判断△AGD与△CED是否全等,并说明理由;②当CE=CD时,AG与EF交于点H,求GH的长.(2)如图3,延长CE交直线AG于点P.①求证:AG⊥CP;②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.22.(2020•嘉兴模拟)已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;(2)在(1)的条件下,若DE=1,AE=,CE=3,求∠AED的度数;(3)若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=,求CN的长.23.(2020•盘锦)如图,四边形ABCD是正方形,点F是射线AD上的动点,连接CF,以CF为对角线作正方形CGFE(C,G,F,E按逆时针排列),连接BE,DG.(1)当点F在线段AD上时.①求证:BE=DG;②求证:CD﹣FD=BE;(2)设正方形ABCD的面积为S1,正方形CGFE的面积为S2,以C,G,D,F为顶点的四边形的面积为S3,当时,请直接写出的值.24.(2019秋•丰城市期末)如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.【观察猜想】①AE与BD的数量关系是;②∠APD的度数为.【数学思考】如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;【拓展应用】如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为.25.(2020春•历下区期末)如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(提示:正方形的四条边都相等,四个角都是直角)(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为,线段CF、BD的数量关系为;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足条件时,CF⊥BC(点C、F不重合),不用说明理由.26.(2020•新泰市二模)在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明:CE=CF;(2)若∠ABC=90°,G是EF的中点(如图2),求出∠BDG的度数;(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.27.(2020•武汉模拟)已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC为边作平行四边形CEFB,连CD、CF.(1)如图1,当E、D分别在AC和AB上时,求证:CD=CF;(2)如图2,△ADE绕点A旋转一定角度,判断(1)中CD与CF的数量关系是否依然成立,并加以证明;(3)如图3,AE=,AB=,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,直接写出CF的长.28.(2020•浚县模拟)问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73)29.(2020•开封二模)(1)【问题发现】如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为(2)【拓展研究】在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF 的数量关系有无变化?请仅就图2的情形给出证明;(3)【问题发现】当正方形CDEF旋转到B,E,F三点共线的时候,直接写出线段AF的长.30.(2020•西城区校级模拟)如图1,在正方形ABCD中,点F在边BC上,过点F作EF ⊥BC,且FE=FC(CE<CB),连接CE、AE,点G是AE的中点,连接FG.(1)用等式表示线段BF与FG的数量关系是;(2)将图1中的△CEF绕点C按逆时针旋转,使△CEF的顶点F恰好在正方形ABCD 的对角线AC上,点G仍是AE的中点,连接FG、DF.①在图2中,依据题意补全图形;②求证:DF=FG.31.(2020•内江)如图,正方形ABCD中,P是对角线AC上的一个动点(不与A、C重合),连结BP,将BP绕点B顺时针旋转90°到BQ,连结QP交BC于点E,QP延长线与边AD交于点F.(1)连结CQ,求证:AP=CQ;(2)若AP=AC,求CE:BC的值;(3)求证:PF=EQ.32.(2020•锦江区模拟)如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,BP=BE.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.(1)求证:∠BAP=∠BGN;(2)若AB=6,BC=8,求;(3)如图2,在(2)的条件下,连接CF,求tan∠CFM的值.33.(2020•安庆模拟)如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.(1)如图①,当=时,求的值;(2)如图②当DE平分∠CDB时,求证:AF=OA;(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=BG.34.(2020•衢州)【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当=时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.35.(2020•南通)【了解概念】有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.【理解运用】(1)如图①,对余四边形ABCD中,AB=5,BC=6,CD=4,连接AC.若AC=AB,求sin∠CAD的值;(2)如图②,凸四边形ABCD中,AD=BD,AD⊥BD,当2CD2+CB2=CA2时,判断四边形ABCD是否为对余四边形.证明你的结论;【拓展提升】(3)在平面直角坐标系中,点A(﹣1,0),B(3,0),C(1,2),四边形ABCD是对余四边形,点E在对余线BD上,且位于△ABC内部,∠AEC=90°+∠ABC.设=u,点D的纵坐标为t,请直接写出u关于t的函数解析式.36.(2019秋•路北区期末)如图,在△ABC中,∠A=30°,∠C=90°,AB=12,四边形EFPQ是矩形,点P与点C重合,点Q、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).(1)当AE=8时,求EF的长;(2)设AE=x,矩形EFPQ的面积为y.①求y与x的函数关系式;②当x为何值时,y有最大值,最大值是多少?(3)当矩形EFPQ的面积最大时,将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动(当点P到达点B时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.37.(2020•武侯区校级模拟)如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.(1)求线段CE的长;(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设DN=x.①求证四边形AFGD为菱形;②是否存在这样的点N,使△DMN是直角三角形?若存在,请求出x的值;若不存在,请说明理由.38.(2020•太和县模拟)已知在梯形ABCD中,AD∥BC,AC=BC=10,cos∠ACB=,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.(1)如图1,当DF⊥BC时,求AD的长;(2)设EC=y,求y关于x的函数解析式,并直接写出定义域;(3)当△DFC是等腰三角形时,求AD的长.39.(2019秋•咸丰县期末)如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F 在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.(1)试求点E的坐标(用含m,n的式子表示);(2)求证:AM=AN;(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.40.(2020•涪城区模拟)如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.①求∠DAQ的度数;②若AB=6,求PQ的长度.动态几何中的相似问题参考答案与试题解析一.解答题(共40小题)1.(2014•东莞模拟)如图,在梯形ABCD中,AD∥BC,AD=3,DC=5,BC=10,梯形的高为4.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t(秒).(1)当MN∥AB时,求t的值;(2)试探究:t为何值时,△MNC为等腰三角形.【分析】(1)平移梯形的一腰,根据平行四边形的性质和相似三角形的性质求解;(1)因为三边中,每两条边都有相等的可能,所以应考虑三种情况.结合路程=速度×时间求得其中的有关的边,运用等腰三角形的性质和解直角三角形的知识求解.【解答】解:(1)如图1,过D作DG∥AB交BC于G点.则四边形ADGB是平行四边形.∵MN∥AB,∴MN∥DG,∴BG=AD=3.∴GC=10﹣3=7.由题意知,当M、N运动到t秒时,CN=t,CM=10﹣2t.∵DG∥MN,∴△MNC∽△GDC.∴=,即=.解得,t=;(2)分三种情况讨论:①当NC=MC时,如图2,即t=10﹣2t,解得:t=;②当MN=NC时,如图3,过N作NE⊥MC于E.由等腰三角形三线合一性质得EC=MC=(10﹣2t)=5﹣t.在Rt△CEN中,cos C==,又在Rt△DHC中,cos C==,∴=.解得:t=;③当MC=MN时,如图4,过M作MF⊥CN于F点,FC=NC=t.∵∠C=∠C,∠MFC=∠DHC=90°,∴△MFC∽△DHC,∴=,即=,解得:t=.综上所述,当t=、t=或t=时,△MNC为等腰三角形.【点评】此题主要考查了四边形综合应用以及相似三角形的判定与性质和锐角三角函数等知识,注意梯形中常见的辅助线:平移一腰、作两条高.构造等腰三角形的时候的题目,注意分情况讨论.此题的知识综合性较强,能够从中发现平行四边形、等腰三角形等,根据它们的性质求解.2.(2017秋•仁寿县期中)如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A 点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.(1)当x为何值时,PQ∥BC;(2)当=时,求的值;(3)△APQ能否与△CQB相似?若能,求出时间x的值;若不能,说明理由.【分析】(1)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.(2)我们先看当=时能得出什么条件,由于这两个三角形在AC边上的高相等,那么他们的底边的比就应该是面积比,由此可得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积﹣三角形APQ的面积﹣三角形BQC的面积来得出三角形BPQ和三角形ABC的面积比.(3)本题要分两种情况进行讨论.已知了∠A和∠C对应相等,那么就要分成AP和CQ 对应成比例以及AP和BC对应成比例两种情况来求x的值.【解答】解:(1)由题意得,PQ平行于BC,则AP:AB=AQ:AC,AP=4x,AQ=30﹣3x=解得x=;(2)∵S△BCQ:S△ABC=1:3∴CQ:AC=1:3,CQ=10cm∴时间用了秒,AP=cm,∵由(1)知,此时PQ平行于BC∴△APQ∽△ABC,相似比为,∴S△APQ:S△ABC=4:9∴四边形PQCB与三角形ABC面积比为5:9,即S四边形PQCB=S△ABC,又∵S△BCQ:S△ABC=1:3,即S△BCQ=S△ABC,∴S△BPQ=S四边形PQCB﹣S△BCQ═S△ABC﹣S△ABC=S△ABC,∴S△BPQ:S△ABC=2:9=(3)假设两三角形可以相似.情况1:当△APQ∽△CQB时,CQ:AP=BC:AQ,即有=,解得x=,经检验,x=是原分式方程的解.情况2:当△APQ∽△CBQ时,CQ:AQ=BC:AP,即有=,解得x=5,经检验,x=5是原分式方程的解.综上所述,时间x的值是或5.【点评】本题主要考查了相似三角形的判定和性质,根据三角形相似得出线段比或面积比是解题的关键.3.(2020秋•乐亭县期中)如图,已知直线l的函数表达式为y=﹣x+8,且l与x轴,y 轴分别交于A,B两点,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点P、Q移动的时间为t秒.(1)A点坐标为(6,0),B点坐标为(0,8).(2)当t为或时,△APQ是直角三角形.当t为时,△APQ是以AP 为底的等腰三角形.(3)当t为何值时,△APQ的面积是△ABO面积的?【分析】(1)对于y=﹣x+8,令y=﹣x+8=0,解得x=6,令x=0,则y=8,即可求解;(2)利用△BQN∽△QMA∽△BOA,求出Q,P的坐标分别是(t,),(6﹣t,0);①当P AQ为直角三角形时,分∠QP A为直角、∠PQA为直角了两种情况分别求解即可;②当△APQ是以AP为底的等腰三角形,则点Q在AP的中垂线上,进而求解;(3)△APQ的面积=,△AOB的面积=,则,即可求解.【解答】解:(1)对于y=﹣x+8,令y=﹣x+8=0,解得x=6,令x=0,则y=8,故点A、B的坐标分别为:(6,0)、(0,8),故答案为:(6,0)、(0,8);(2)过Q点分别向x轴,y轴引垂线,垂足分别是M,N,∴NQ∥OA,QM∥OB,∴△BNQ∽△QMA∽△BOA,设Q(x,y)∴BQ=2t,AP=t而△BQN∽△QMA∽△BOA,∴,,∴,,即x=,y=(10﹣2t),Q,P的坐标分别是(t,),(6﹣t,0);①当P AQ为直角三角形时,当∠QP A为直角时,则x P=x Q,即t=6﹣t,解得t=;当∠PQA为直角时,在Rt△APQ中,cos∠QAP===,解得t=,故答案为或;②当△APQ是以AP为底的等腰三角形,则点Q在AP的中垂线上,即x Q=(x P+x A),则=(6﹣t+6),解得t=,故答案为;(3)∵△APQ的面积=,△AOB的面积=,∴,解得t1=2,t2=3,当t1=2秒或t2=3秒时,△APQ的面积是△ABO面积的.【点评】本题综合考查了一次函数与几何知识的应用,题中运用平行线的性质、直线的解析式以及直角三角形等知识求出线段的长是解题的关键.4.(2015•历城区一模)已知在Rt△ABC中,∠ABC=90°,∠A=30°,点P在BC上,且∠MPN=90°.(1)当点P为线段AC的中点,点M、N分别在线段AB、BC上时(如图1).过点P 作PE⊥AB于点E,请探索PN与PM之间的数量关系,并说明理由;(2)当PC=P A,①点M、N分别在线段AB、BC上,如图2时,请写出线段PN、PM之间的数量关系,并给予证明.②当点M、K分别在线段AB、BC的延长线上,如图3时,请判断①中线段PN、PM之间的数量关系是否还存在.(直接写出答案,不用证明)【分析】(1)过点P作PE⊥AB于E,PF⊥BC于点F,则四边形BFPE是矩形,所以△PFN∽△PEM得出==,然后根据余切函数即可求得.(2)同(1)证得△PFN∽△PEM得出=,然后在Rt△AEP和Rt△PFC中通过三角函数求得PF=PC,PE=P A,即可求得.【解答】解:(1)PN=PM,理由:如图1,作PF⊥BC,∵∠ABC=90°,PE⊥AB,∴PE∥BC,PF∥AB,∴四边形PFBE是矩形,∴∠EPF=90°∴P是AC的中点,∴PE=BC,PF=AB,∵∠MPN=90°,∠EPF=90°,∴∠MPE=∠NPF,∴△MPE∽△NPF,∴==,∵∠A=30°,在RT△ABC中,cot30°==,∴=,即PN=PM.(2)解;①PN=PM,如图2 在Rt△ABC中,过点P作PE⊥AB于E,PF⊥BC于点F ∴四边形BFPE是矩形,∴△PFN∽△PEM∴=,又∵Rt△AEP和Rt△PFC中,∠A=30°,∠C=60°∴PF=PC,PE=P A∴==∵PC=P A∴=,即:PN=PM②如图3,成立.【点评】本题考查了矩形的判定和性质,相似三角形的判定和性质以及三角函数的应用.5.(2008•恩施州)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明;(2)求m与n的函数关系式,直接写出自变量n的取值范围;(3)以△ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD2+CE2=DE2;(4)在旋转过程中,(3)中的等量关系BD2+CE2=DE2是否始终成立?若成立,请证明;若不成立,请说明理由.【分析】(1)根据已知及相似三角形的判定方法进行分析即可;(2)可根据(1)中的相似三角形BAE和CDA得出关于AB,BE,CD,AC的比例关系,AB,AC可通过等腰直角三角形求出,因此根据比例关系即可得出m,n的函数关系式.(3)根据(2)的函数关系式,即可求出BE,CD的长,从而也就能求出OD,OE,DE,BD,CE的长,那么可通过计算得出本题的结论.(4)根据旋转角,我们知道HB⊥BD,那么DH2=BH2+BD2,而BH=CE,于是关键是证明HD=DE,连接AH,DH那么可通过证三角形AHD和ADE全等来求解.【解答】解:(1)可得△ABE∽△DAE,△ABE∽△DCA.∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°,∴∠BAE=∠CDA.又∵∠ABC=∠ACB=45°,∴△ABE∽△DCA.(2)∵△ABE∽△DCA,∴.由依题意可知CA=BA=.∴.∴m=.自变量n的取值范围为1<n<2.(3)由BD=CE可得BE=CD,即m=n,∵m=,∴m=n=.∵OB=OC=BC=1,∴OE=OD=﹣1.∴D(1﹣,0).∴BD=OB﹣OD=1﹣(﹣1)=2﹣=CE.DE=BC﹣2BD=2﹣2(2﹣)=2﹣2.∵BD2+CE2=2BD2=2(2﹣)2=12﹣8,DE2=(2﹣2)2=12﹣8,∴BD2+CE2=DE2.(4)等量关系BD2+CE2=DE2成立.理由如下:证明:如图,将△ACE绕点A顺时针旋转90°至△ABH的位置,则CE=HB,AE=AH,∠ABH=∠C=45°,旋转角∠EAH=90°.连接HD,在△EAD和△HAD中.∵,∴△EAD≌△HAD.∴DE=DH.∵∠HBD=∠ABH+∠ABD=90°,∴BD2+HB2=DH2.∴BD2+CE2=DE2.【点评】本题主要考查了等腰直角三角形的性质,相似三角形和全等三角形的判定和性质等知识点的综合运用.根据相似三角形或全等三角形得出线段成比例或相等是解题的关键.6.(2020•徐州模拟)如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)若△BPQ与△ABC相似,求t的值;(2)连接AQ、CP,若AQ⊥CP,求t的值.【分析】(1)分两种情况:①当△BPQ∽△BAC时,BP:BA=BQ:BC;当△BPQ∽△BCA时,BP:BC=BQ:BA,再根据BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可;(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8﹣4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.【解答】解:根据勾股定理得:BA=;(1)分两种情况讨论:①当△BPQ∽△BAC时,,∵BP=5t,QC=4t,AB=10,BC=8,∴,解得,t=1,②当△BPQ∽△BCA时,,∴,解得,t=;∴t=1或时,△BPQ∽△BCA;(2)过P作PM⊥BC于点M,AQ,CP交于点N,如图所示:则PB=5t,PM=3t,MC=8﹣4t,∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,∴∠NAC=∠PCM,∵∠ACQ=∠PMC,∴△ACQ∽△CMP,∴,∴,解得t=.【点评】本题考查了相似三角形的判定与性质;由三角形相似得出对应边成比例是解题的关键.。
力学相似原理

力学相似原理
力学相似原理是力学领域中的一个重要概念,用于描述在相似条件下,不同尺度的物体或系统的行为和性质具有相似性。
根据力学相似原理,当两个物体或系统具有相同的几何形状并处于相似的动态条件下,它们的运动行为和内部力的分布情况将相似。
具体而言,如果两个物体或系统在如下的条件下具有相似性:它们的比例因子是相等的,它们的速度、加速度以及所受力的大小和方向的比例也是相等的,那么它们之间的力学行为将相似。
力学相似原理的应用广泛,可以用于研究不同尺度下的流体力学、固体力学等问题。
例如,在飞行器设计中,可以通过设计和测试模型飞行器来预测实际尺寸飞行器的性能。
在这种情况下,力学相似原理可以帮助工程师将模型飞行器的测试结果推广到实际尺寸飞行器上,从而减少开发成本和时间。
总之,力学相似原理是一种重要的力学概念,它描述了在相似条件下,不同尺度的物体或系统的行为和性质具有相似性。
它在工程学和科学研究中有广泛的应用,帮助人们更好地理解和预测物体和系统的力学行为。
流动相似相似原理相似准则及量纲分析全析

流动相似相似原理相似准则及量纲分析全析流动相似(Flow similarity)指的是两个或多个不同的流动在一些条件下具有相同的流动特征。
流动相似原理是通过建立相似性准则,将一个实际流动问题转化为一个更简单的已知流动问题,以便进行分析和计算。
相似准则是基于一些物理模型和经验关系建立的,用于确定相似性的判断依据。
量纲分析是从基本物理方程出发,研究物理量之间的关系,通过将问题的不同物理量以相似形式表示,在相似性的约束条件下简化问题。
流动相似原理是建立在牛顿运动定律和连续性方程等基本方程的基础上。
根据流动的基本物理规律,流体在各个点上都满足相同的动态和物质守恒方程。
因此,流动相似原理可以表述为:如果两个流动有相同的动态和物质守恒方程,并且满足相同的边界条件,则这两个流动是相似的。
这就是流动相似原理的基本思想。
相似准则是用于确定流动相似性的依据。
常用的相似准则有尺寸相似准则和运动相似准则。
尺寸相似准则是指,在相似条件下,物体的几何尺寸与速度、压力等物理量之间存在其中一种关系,如雷诺数、韦伯数等。
运动相似准则是指,在相似条件下,流动的运动状态(如旋转、脉动等)与几何尺寸和流体的物性之间存在其中一种关系。
量纲分析是一种将问题中出现的各个物理量进行无量纲化处理的方法。
通过选择适当的主量和无量纲化的方法,可以将含有多个物理量的复杂方程简化为只包含少数几个无量纲参数的简单方程。
量纲分析的基本原理是,物理方程对不同的物理量的变化都具有相同的形式。
通过消除物理量的量纲,可以得到不含量纲系数的无量纲方程,从而方便进行分析和计算。
量纲分析的具体步骤如下:1.选择主量:根据问题的具体情况,选择与问题最为密切相关的几个主要物理量作为主量。
2.建立主量之间的关系:根据问题的物理性质和经验规律,建立主量之间的关系式,即原方程。
3.形成无量纲方程:通过引入适当的无量纲参数,将原方程化为不含量纲系数的无量纲方程。
4.判定主量的个数:通过判定无量纲方程中无量纲参数的个数,确定主量的个数。
三角形相似之动态展示

三角形相似之动态展示
1,“k字”型相似,也叫“一线三等角”:
注意与光线发射的相似的区别
2,互补型相似:
当α+β=180°时,则有三对三角形相似.
两个特例:
车到山前必有路,不必过多的焦虑,只需要在这些时刻注意点,
如开车拐弯、过路口,走到悬崖附近,快到楼顶边缘,做题出现临界点(临界位置或者数值)等等.
:“铅笔数学”《以微课堂》,由江苏省数学名师、数学奥林匹克国家级教练员,联手四名特级教师共同打造。
七年级数学微课大全
八年级数学微课大全
完整版!中考数学复习大全。
相似三角形中动点问题

ABDCENM相似三角形中动点问题例1: 如图正方形ABCD 的边长为2,AE=EB ,线段MN 的两端点分别在CB 、CD 上滑动,且MN=1,当CM 为何值时△AED 与以M 、N 、C 为顶点的三角形相似?变式练习:如图,在△ABC 中,AB=8,BC=7,AC=6,有一动点P 从A 沿AB 移动到B ,移动速度为2单位/秒,有一动点Q 从C 沿CA 移动到A ,移动速度为1单位/秒,问两动点同时移动多少时间时,△PQA 与△BCA 相似。
例2:如图,已知△ABC 是边长为6cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 匀速运动,其中点P 运动的速度是1cm/s ,点Q 运动的速度是2cm/s ,当点Q 到达点C 时,P 、Q 两点都停止运动,设运动时间为t (s ),解答下列问题: (1)当t =2时,判断△BPQ 的形状,并说明理由;(2)设△BPQ 的面积为S (cm 2),求S 与t 的函数关系式;(3)作QR//BA 交AC 于点R ,连结PR ,当t 为何值时,△APR ∽△PRQ ?变式:1.如图,在矩形ABCD 中,AB=12cm ,BC=8cm .点E 、F 、G 分别从点A 、B 、C 三点同时出发,沿矩形的边按逆时针方向移动.点E 、G 的速度均为2cm/s ,点F 的速度为4cm/s ,当点F 追上点G (即点F 与点G 重合)时,三个点随之停止移动.设移动开始后第t 秒时,△EFG 的面积为S (cm 2)(1)当t=1秒时,S 的值是多少?(2)写出S 和t 之间的函数解析式,并指出自变量t 的取值范围(3)若点F 在矩形的边BC 上移动,当t 为何值时,以点E 、B 、F 为顶点的三角形与以点F 、C 、G 为顶点的三角形相似?请说明理由.例3:如图,在梯形ABCD 中,AD BC ∥,3AD =,5DC =,10BC =,梯形的高为4.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t (秒). (1)当MN AB ∥时,求t 的值;(2)试探究:t 为何值时,MNC △为直角三角形.变式练习1:如图,在直角梯形ABCD 中,AB ∥DC ,∠D=90o ,AC ⊥BC ,AB=10cm,BC=6cm ,FDN CM B A点以2cm /秒的速度在线段AB 上由A 向B 匀速运动,E 点同时以1cm /秒的速度在线段BC 上由B 向C 匀速运动,设运动时间为t 秒(0<t<5). 1)求证:△ACD ∽△BAC ;2)求:DC 的长;3)试探究:△BEF 可以为等腰三角形吗?若能,求t 的值; 若不能,请说明理由.例4:如图①,在△ABC 中,AB =BC =5,AC=6. △ECD 是△ABC 沿BC 方向平移得到的,连接AE.AC 和BE 相交于点O.(1)判断四边形ABCE 是怎样的四边形,说明理由; (2)如图②,P 是线段BC 上一动点(不与点B 、C 重合),连接PO 并延长交线段AB 于点Q ,QR ⊥BD ,垂足为点R.四边形PQED 的面积是否随点P 的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED 的面积;当线段BP 的长为何值时,△PQR 与△BOC 相似?变式:(2008年温州)如图,在Rt ABC △中,90A ∠=,6AB =,8AC =,D E ,分别是边AB AC ,的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ BC ⊥于Q ,过点Q 作QR BA ∥交AC 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ x =,QR y =.(1)求点D 到BC 的距离DH 的长;(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P ,使PQR △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.结合坐标系的解析几何例1:如图,在平面直角坐标系中,已知A (0,6),B (8,0),P 从A 开始在线段AO 上以每秒1个单位长度的速度向O 移,同时Q 从B 开始在线段BA 上以每秒2个单位长度的速度向A 移,设P ,Q 移的时间为t (s ).当t 为何值时,△APQ 与△AOB ?并求出此时P 与Q 的坐标.变式:1.如图,已知直线l 的函数表达式为483y x =-+,且l 与x 轴,y 轴分别交于A B ,两点,动点Q 从B 点开始在线段BA 上以每秒2个单位长度的速度向点A 移动,同时动点P 从A BCD ER P H QA 点开始在线段AO 上以每秒1个单位长度的速度向点O 移动,设点Q P ,移动的时间为t秒.(1)求出点AB ,的坐标; (2)当t 为何值时,APQ △与AOB △相似?(3)求出(2)中当APQ △与AOB △相似时,线段PQ 所在直线的函数表达式.例2.已知:如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB=90°,点A 、C 的坐标分别为A(-3,0),C(1,0), 43=AC BC ,(1)求过点A 、B 的直线的函数表达式; (2)在X 轴上找一点D,连接DB ,使得△ADB 与△ABC 相似(不包括全等),并求点D 的坐标; (3)在(2)的条件下,如P 、Q 分别是AB 和AD 上的动点,连接PQ ,设AP=DQ=m ,问是否存在这样的m 使得△APQ 与△ADB 相似,如存在,请求出m 的值;如不存在,请说明理由.变式:1.如图,在平面直角坐标系中,点(30)C -,,点A B ,分别在x 轴,y 轴的正半轴上,且满足2310OB OA -+-=.(1)求点A ,点B 的坐标.A C OBxyOPA QBy x(2)若点P 从C 点出发,以每秒1个单位的速度沿射线CB 运动,连结AP .设ABP △的面积为S ,点P 的运动时间为t 秒,求S 与t 的函数关系式,并写出自变量的取值范围.(3)在(2)的条件下,是否存在点P ,使以点AB P ,,为顶点的三角形与AOB △相似?若存在,请直接写出点P 的坐标;若不存在,请说明理由.例3.如图直线y=-x+10与x 轴、y 轴分别交于A 、B 两,P 从A 开始在线段AO 上以每秒2个长度单位的速度向原O 运动.直线EF 从x 轴开始以每秒1个长度单位的速度向上平行移动(即EF ∥x 轴),并且分别与y 轴、线段AB 交于E 、F .(当A 运动到O 时,直线EF 随之停止运动) 连接FP ,设P 与直线EF 同时出发,运时间为t 秒. (1)当t=1秒时,求△APF 的面积;(2)设t 的值分别取t 1、t 2时(t 1≠t 2),所对应的三角形分别为△AF 1P 1和△AF 2P 2.试判断这两个三角形是否相似,请证明你的判断;变式:1.如图,A 的坐标为(1,1),点C 是线段OA 上的一个动点(不运动至O ,A 两点),过C 作CD ⊥x 轴,垂足为D ,以CD 为边在右侧作正方形CDEF .连接AF 并延长交x 轴的正半轴于B ,连接OF ,若以B ,E ,F 为顶的三角形与△OFE 相似,B 的坐标是 .y xAOCB图2A D O BC 21MN图1AD B MN12 图3AD O BC 2 1 MN O动态几何中的相似例1、在图1至图3中,直线MN 与线段AB 相交 于点O ,∠1 = ∠2 = 45°.(1)如图1,若AO = OB ,请写出AO 与BD的数量关系和位置关系;(2)将图1中的MN 绕点O 顺时针旋转得到 图2,其中AO = OB .求证:AC = BD ,AC ⊥ BD ;(3)将图2中的OB 拉长为AO 的k 倍得到图3,求AC BD的值.变式练习1:已知在Rt △ABC 中,∠ABC =90º,∠A =30º,点P 在AC 上,且∠MPN =90当点P 为线段AC 的中点,点M 、N 分别在线段AB 、BC 上时(如图1),过点P 作PE ⊥AB 于点E ,PF ⊥BC 于点F ,可证t △PME ∽t △PNF ,得出PN =3PM .(不需证明)当PC =2PA ,点M 、N 分别在线段AB 、BC 或其延长线上,如图2、图3这两种情况时,请写出线段PN 、PM 之间的数量关系,并任选取一给予证明.例2:等腰△ABC ,AB=AC=8,∠BAC=120°,P 为BC 的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P ,三角板绕P 点旋转. (1)如图a ,当三角板的两边分别交AB 、AC 于点E 、F 时.求证:△BPE ∽△CFP ;(2)操作:将三角板绕点P 旋转到图b 情形时,三角板的两边分别交BA 的延长线、边AC 于点E 、F .①探究1:△BPE 与△CFP 还相似吗?(只需写出结论)②探究2:连接EF ,△BPE 与△PFE 是否相似?请说明理由; ③设EF=m ,△EPF 的面积为S ,试用m 的代数式表示S .作业:1.如图,四边形ABCD 中,AD =CD ,∠DAB =∠ACB =90°,过点D 作DE ⊥AC ,垂足为F ,DE 与AB 相交于点E.(1)求证:AB ·AF =CB ·CD(2)已知AB =15cm ,BC =9cm ,P 是射线DE 上的动点.设DP =xcm (x >0),四边形BCDP 的面积为ycm 2.DP AEF CB ①求y 关于x 的函数关系式;②当x 为何值时,△PBC 的周长最小,并求出此时y 的值.2.如图所示,在ΔABC 中,BA=BC=20cm ,AC=30cm ,点P 从A 点出发,沿着AB 以每秒4cm 的速度向B 点运动;同时点Q 从C 点出发,沿CA 以每秒3cm 的速度向A 点运动,设运动时间为x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形动点问题
1、如图,已知一次函数的图象与x轴、y轴分别相交于A、B两点,点C在AB上以每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,当D点到达O点时,C点随之停止运动.运动时间用t(单位:秒)表示.
(1)求AB的长;
(2)当t为何值时,△ACD与△ABO相似?
2、如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm 的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动的时间为t, (1)当t为何值时,PQ∥BC?
(2)△APQ与△CQB能否相似?若能,
求出AP的长;若不能,请说明理由.
3、如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动.点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G (即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2). (1)当t=1秒时,S的值是多少?
(2)若点F在矩形的边BC上移动,当t为何值时,以点E、B、F为顶点的三角形与以点F、C、G 为顶点的三角形相似?请说明理由.
4、(2005•重庆)在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时,四边形OPQB的面积多少个平方单位?
=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,5、(2008•孝感)锐角△ABC中,BC=6,S
△ABC
以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0)(1)△ABC中边BC上高AD= _________ ;
(2)当x= _________ 时,PQ恰好落在边BC上(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
6、(2008•黄冈)已知:如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系,A,(青岛)已知:如图①,在Rt△ACB中,∠C=90°,AC=4 cm,BC=3 cm,点P由B出发沿BA方向向
点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:
(1)当t为何值时,PQ∥BC;
(2)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t 的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
7、(黄冈)三点的坐标分别为A(8,0),B(8,10),C(0,4),点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为t秒.
(1)求直线BC的解析式;
(2)若动点P在线段OA上移动,当t为何值时,四边形OPDC的面积是梯形COAB面积的;
(3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD的面积为S,请直接写出S与t的函数关系式,并指出自变量t的取值范围;
(4)试探究:当动点P在线段AB上移动时,能否在线段OA上找到一点Q,使四边形CQPD为矩形?并求出此时动点P的坐标。
习题补充
1.如图,在平行四边形ABCD 中,E 是边BC 上的点,AE 交BD 于点F ,如果,那么= _________ .
2.如图,在△ABD 中,∠ADB=90°,C 是BD 上一点,若E 、F 分别是AC 、AB 的中点,△DEF 的面积为
3.5,则△ABC 的面积为 _________ .
第二题图 第三题图
第一题图
3.如图,在△ABC 中,∠C=90°,AC=8,CB=6,在斜边AB 上取一点M ,使MB=CB ,过M 作MN ⊥AB 交AC 于N ,则MN= .
4.如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB 于D ,若AD=1,BD=4,则CD= _________ .
5.如图,在△ABC 中,M 、N 是AB 、BC 的中点,AN 、CM 交于点O ,那么△MON 与△AOC 面积的比是 _________ .
第四题图 第五题图 第六题图 第七题图
6.如图,AD=DF=FB ,DE ∥FG ∥BC ,则S Ⅰ:S Ⅱ:S Ⅲ= _________ .
7.如图,已知点D 是AB 边的中点,AF ∥BC ,CG :GA=3:1,BC=8,则AF= _________ .
2.(2009•青岛)如图,在梯形ABCD 中,AD ∥BC ,AD=6cm ,CD=4cm ,BC=BD=10cm ,点P 由B 出发沿BD 方向匀速运动,速度为1cm/s ;同时,线段EF 由DC 出发沿DA 方向匀速运动,速度为1cm/s ,交BD 于Q ,连接PE .若设运动时间为t (s )(0<t <5).解答下列问题:
(1)当t 为何值时,PE ∥AB ;
(2)设△PEQ 的面积为y (cm 2),求y 与t 之间的函数关系式;
(3)是否存在某一时刻t ,使S △PEQ =S △BCD ?若存在,求出此时t 的值;若不存在,说明理由;
(4)连接PF ,在上述运动过程中,五边形PFCDE 的面积是否发生变化?说明理由.
3.(2008•湖州)如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图乙,线段CF,BD之间的位置关系为_________ ,数量关系为_________ .
②当点D在线段BC的延长线时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C,F重合除外)画出相应图形,并说明理由.(画图不写作法)
(3)若AC=4,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP 长的最大值.。
