几何图形中的动态问题
例说立体几何中的动态问题

例说立体几何中的动态问题立体几何中的“动态问题”,是指空间图形中的某些点、线、面的位置关系是不确定的,可变的一类开放问题。
对学生来说,解决这类问题,对其空间想象能力,逻辑推理能力的要求更高,难度一般比较大。
但又因为这类问题是可变的,开放的,更有助于学生空间想象能力及综合思维能力的培养。
这类问题往往把立体几何知识和其他部分的知识有机地结合起来,解决问题的关键就是转化与化归,把空间问题转化为平面问题来解决。
本文归纳了几类动态问题,希望对大家解决立体几何中的动态问题有所启发。
一、与轨迹有关的动态问题例1:如图,正方体中,P为底面上的动点,于E,且则点P的轨迹是()A .线段 B.圆 C.椭圆的一部分D.抛物线的一部分解析:连结,可证,即,即点E是体对角线上的定点,直线AE也是定直线.,∴动点P必定在线段AE的中垂面上,则中垂面与底面的交线就是动点P的轨迹,所以动点P的轨迹是线段.故选A例2:在正方体中,点是侧面内一个动点,它到直线与直线的距离相等,则动点的轨迹所在曲线是()A.直线 B.圆 C.椭圆的一部分 D.抛物线的一部分解析:本题是立体几何与解析几何相结合的一道题目,学生难在空间问题如何转化为平面问题,即解析几何问题。
这里动点到直线的距离易作出,难在到直线的距离的距离是什么。
因垂直平面,所以,即点到点的距离与到直线的距离相等。
所以动点在侧面内的轨迹是一段抛物线。
评注:动点轨迹主要是把空间的关系转化为平面内动点所具有的特性。
这类问题综合了平面几何、立体几何、解析几何等知识,渗透了数形结合思想,转化与化归思想,分类讨论思想,对第一次碰到此类问题的学生有较好的检测功能。
二、与距离有关的动态问题例3:如图,在棱长为2的正方体中,点是的中点,动点在底面内(不包括边界),若平面,则的最小值是()A.B.C.D.解析如图,在上取中点,在上取中点,连接,且,易知平面平面,则动点的轨迹是(不含两点)又平面,则当时,取得最小值此时,评注:本题考查立体几何中动点轨迹及最值的求解问题,关键是能够通过面面平行关系得到动点的轨迹,从而找到最值取得的点.例4:长方体中,且一只小虫子从,点沿长方体的表面爬到点处,则小虫子的最短行程是多少?解析:当小虫子沿侧面与侧面到时,将二侧面展开铺平,在平面内,连即为最短行程,记为。
培优提能10 立体几何中的动态问题

培优提能10 立体几何中的动态问题立体几何中的“动态问题”是指空间中的某些点、线、面的位置是不确定的或可变的一类开放性问题,解答此类问题应该动静结合、化动为静,找到相应的几何关系,具体有以下几种解决方法:(1)函数法:某些点、线、面的运动,必然导致某些位置关系或一些变量的变化.变量变化时会引发其他变量的变化,从而建立函数关系,将立体几何问题转化为函数问题来解.(2)解析法:我们常利用空间直角坐标系解决立体几何问题,即实现几何问题代数化.因此利用空间直角坐标系将空间图形中的若干元素坐标化后,借助向量进行运算和分析,是解决这类问题的常用方法. (3)等价转换法:动和静是相对的,在运动变化过程中,要善于寻找或构造与之相关的一些不变因素,将一些变化的点、线、面进行合理转换,实现变量与不变量的结合.培优点1 以静制动(旋转问题、射影问题)典例1 正四面体ABCD的棱长为1,棱AB∥平面α(如图),则四面体上的所有点在平面α内的射影构成的图形面积的取值范围是.解析:去掉与问题无关的面,将四面体看成是以AB为棱的二面角C-AB-D(二面角大小一定),用纸折出这个二面角,不妨将AB置于平面α内,将二面角绕AB 转动一周,观察点C,D 在平面α上的射影,可以发现点C,D 在平面α上的射影始终在AB 的射影的中垂线上.当CD ∥平面α时,四边形ABCD 的面积最大,为12(如图1).当CD ⊥平面α时,四边形ABCD 的面积最小,为√24(如图2),转动过程中C,D 在平面α上的射影从C,D 变化到C ′,D ′(如图3),故图形面积的取值范围是[√24,12]. 答案:[√24,12]在解决立体几何中的“动态”问题时,需从复杂的图形中分化出最简单的具有实质性意义的点、线、面,让几何图形的实质“形销骨立”,即从混沌中找出秩序,是解决“动态”问题的关键.触类旁通1 如图,直线l ⊥平面α,垂足为O.正方体ABC D −A 1B 1C 1D 1的棱长为2.点A 是直线l 上的动点,点B 1在平面α内,则点O 到线段CD 1的中点P 的距离的最大值为 .解析:从题图中分化出4个点O,A,B1,P,其中△AOB1为直角三角形,固定A,B1,点P的轨迹是在与AB1垂直的平面上且以AB1的中点Q为圆心的圆,从而OP≤OQ+QP=12AB1+2=√2+2,当且仅当OQ⊥AB1,即点O,Q,P共线时,取到等号,此时直线AB1与平面α成45°角.答案:√2+2培优点2 动点轨迹(长度)问题典例2 在棱长为2√2的正方体ABCD-A1B1C1D1中,E,F分别为棱AB,AD 的中点,P为线段C1D上的动点,则直线A1P与平面D1EF的交点Q的轨迹长度为( )A.2√153B.4√33C.2√133D.4√23解析:如图,连接B1D1,因为E,F 分别为棱AB,AD 的中点,所以B 1D 1∥EF,则B 1,D 1,E,F 四点共面.连接A 1C 1,A 1D,设A 1C 1∩B 1D 1=M,A 1D ∩D 1F=N,连接MN,则点Q 的轨迹为线段MN,易得A 1D=√A 1D 12+DD 12=4,△A 1ND 1∽△DNF,且A 1D 1FD=2,所以A 1N=23A 1D=83.易知A 1C 1=C 1D=A 1D=4,所以∠C 1A 1D=60°,又A 1M=2,所以在△A 1MN 中,由余弦定理可得MN 2=A 1N 2+A 1M 2-2A 1N ·A 1Mcos 60°=529,所以MN=2√133,即点Q 的轨迹长度为2√133.故选C.空间中动点轨迹问题变化并不多,一般此类问题可以从三个角度进行分析处理,一是从曲线定义或函数关系出发给出合理解释;二是平面与平面交线得直线或线段;三是平面和曲面(圆锥,圆柱侧面,球面)交线得圆、圆锥曲线.很少有题目会脱离这三个方向.触类旁通2 (多选题)(2022·湖南郴州高三期末)如图,点P 是棱长为2的正方体ABCD-A 1B 1C 1D 1表面上的一个动点,则( AC )A.当点P 在平面BCC 1B 1上运动时,四棱锥P-AA 1D 1D 的体积不变B.当点P 在线段AC 上运动时,D 1P 与A 1C 1所成角的取值范围是[π6,π2]C.当直线AP 与平面ABCD 所成的角为45°时,点P 的轨迹长度为π+4√2D.若F 是A 1B 1的中点,当P 在底面ABCD 上运动,且满足PF ∥平面B 1CD 1时,PF 长度的最小值是 √5解析:当P 在平面BCC 1B 1上运动时,点P 到平面AA 1D 1D 的距离不变,正方形AA 1D 1D 的面积不变,故四棱锥P-AA 1D 1D 的体积不变,故A 正确; 建立如图所示的空间直角坐标系,设P(x,2-x,0),0≤x ≤2,A 1(2,0,2),D 1(0,0,2),C 1(0,2,2),则D 1P →=(x,2-x,-2),A 1C 1→=(-2,2,0),设D 1P 与A 1C 1所成的角为θ(0≤θ≤π2),则cos θ=|cos<D 1P →,A 1C 1→>|=|D 1P →·A 1C 1→||D 1P →||A 1C 1→|=|x -1|√(x -1)2+3,因为0≤|x-1|≤1,当|x-1|=0时,θ=π2,当0<|x-1|≤1时,cos θ=|x -1|√(x -1)2+3=√1+3|x -1|2,0<cos θ≤12,则π3≤θ<π2,综上,π3≤θ≤π2,所以D 1P 与A 1C 1所成角的取值范围是[π3,π2],故B 错误;因为直线AP 与平面ABCD 所成的角为45°,若点P 在平面BCC 1B 1和平面DCC 1D 1内,因为∠B 1AB=45°,∠D 1AD=45°已为最大,不成立,在平面ADD 1A 1内,点P 的轨迹长度是AD 1=2√2,在平面ABB 1A 1内,点P 的轨迹长度是AB 1=2√2, 在平面A 1B 1C 1D 1内,如图所示,作PM ⊥平面ABCD,因为∠PAM=45°,所以PM=AM,又PM=AB,所以AM=AB,则A 1P=AB,所以点P 的轨迹是以A 1为圆心,以2为半径的四分之一圆,所以点P 的轨迹长度为14×2π×2=π,所以点P 的轨迹总长度为π+4√2,故C 正确; 建立如图所示的空间直角坐标系,设P(x,y,0),x,y ∈[0,2],B 1(2,2,2),D 1(0,0,2),C(0,2,0),F(2,1,2),则CB 1→=(2,0,2),CD 1→=(0,-2,2),FP →=(x-2,y-1,-2), 设平面B 1CD 1的法向量为n=(a,b,c),则{CD 1→·n =0,CB 1→·n =0,即{-2b +2c =0,2a +2c =0,令a=1,则n=(1,-1,-1), 因为PF ∥平面B 1CD 1,所以FP →·n=(x-2)-(y-1)+2=0,即y=x+1,所以|FP →|=√(x -2)2+(y -1)2+4=√2x 2-4x +8=√2(x -1)2+6≥√6,当x=1时,等号成立,故D 错误.故选AC.培优点3 翻折问题典例3 如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC 的中心为O.D,E,F 为圆O 上的点,△DBC,△ECA,△FAB 分别是以BC,CA,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB 为折痕折起△DBC,△ECA,△FAB,使得D,E,F 重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积的最大值为 cm 3.解析:如图,连接OD,交BC于点G,由题意,知OD⊥BC,OG=√3BC.6设OG=x,则BC=2√3x,DG=5-x,×2√3x×3x=3√3x2,三棱锥的高h=√DG2-OG2=√25-10x,S△ABC=12则三棱锥的体积V=1S△ABC·h=√3x2·√25-10x=√3·√25x4-10x5.3),则f′(x)=100x3-50x4.令f′(x)=0,得令f(x)=25x4-10x5,x∈(0,52x=2.当x∈(0,2)时,f′(x)>0,f(x)单调递增;当x∈(2,5)时,f′2(x)<0,f(x)单调递减.故当x=2时,f(x)取得最大值80,则V≤√3×√80=4√15.所以三棱锥体积的最大值为4√15 cm3.答案:4√15在解决立体几何中的“动态”问题时,对于一些很难把握运动模型(规律)的求值问题,可以通过构建某个变量的函数,以数解形.触类旁通3 (1)(多选题)(2022·河北唐山高三期末)如图,四边形ABCD是边长为2的正方形,E为AB的中点,将△AED沿DE所在的直线翻折,使A与A′重合,得到四棱锥A′-BCDE,则在翻折的过程中( AB )A.DE⊥AA′B.存在某个位置,使得A′E⊥CDC.存在某个位置,使得A′B∥DED.存在某个位置,使四棱锥A′-BCDE的体积为1(2)(多选题)(2022·广东罗湖高三期末)在△ABC中,AB⊥BC,且AC=2,BC=1,若将△ABC沿AC边上的中线BD折起,使得平面ABD⊥平面BCD.点E在由此得到的四面体ABCD的棱AC上运动,则下列结论正确的为( BCD )A.∠ADC=π2B.四面体ABCD的体积为18C.存在点E使得△BDE的面积为14D.四面体ABCD外接球的表面积为13π3解析:(1)对于A,如图所示,过A′作A′O⊥DE,垂足为O,延长AO交BC于点F,因为DE⊥AO,且AO∩A′O=O,AO,A′O⊂平面A′AO,所以DE⊥平面A′AO,又因为A′A⊂平面A′AO,所以DE⊥AA′,A正确;对于B,取DC的中点G,连接EG,A′G,当A′在平面ABCD上的射影在直线EG上时,此时DC⊥平面A′EG,从而得到A′E⊥CD,B正确;对于C,连接A′B,因为点E∈平面A′BE,点D∉平面A′BE,所以直线A′B与DE是异面直线,所以不存在某个位置,使得A′B∥DE,C错误;对于D,由VA′BCDE =13×12×(1+2)×2×h=1,解得h=1,由A′O⊥DE,可得A′O=A′E·A′DDE =√5=√5,即此时四棱锥的高h∈(0,√5],此时√5<1,所以不存在某个位置,使四棱锥A′-BCDE的体积为1,D错误.故选AB.(2)对于A,取BD的中点M,连接CM,因为BC=CD=1,所以CM⊥BD,又平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,所以CM⊥平面ABD,则CM⊥AD,若∠ADC=π2,则AD⊥CD,所以AD⊥平面CBD,则AD⊥BD,显然不可能,A错误;对于B,易知△BCD的面积为√34,在平面ABD中,过A作BD的垂线,交BD的延长线于点H,易知AH=√32,因为平面ABD ⊥平面BCD,平面ABD ∩平面BCD=BD,所以AH ⊥平面BCD,即三棱锥A-BCD 的高为AH=√32,所以三棱锥A-BCD 的体积V=13×√34×√32=18,即四面体ABCD 的体积为18,B正确;对于C,显然当AC ⊥平面BDE 时,△BDE 的面积取得最小值,易知CD=1,DH=12,由余弦定理可得CH=√72,所以AC=√AH 2+CH 2=√102, 又四面体ABCD 的体积为18, 所以18=13×S ×√102,即S=3√1040<14, 且△BCD 的面积为√34>14,所以存在点E 使得△BDE 的面积为14,C 正确;对于D,设△BCD 与△ABD 的外心依次为O 1,O 2, 过O 1作平面BCD 的垂线l 1,过O 2作平面ABD 的垂线l 2,则四面体ABCD 的外接球球心O 为直线l 1与l 2的交点,延长CO 1交BD 于点M,则M 为BD 的中点,连接O 2M,则四边形MO 1OO 2为矩形,结合正弦定理可求得O 2M=√32,O 1C=√33, 所以四面体ABCD 的外接球半径为R=OC=√O 1O 2+O 1C 2=√O 2M 2+O 1C 2=√34+13=√1312,则四面体ABCD 外接球的表面积为S=4πR 2=4π×1312=13π3,D 正确.故选BCD.培优点4 动态最值问题典例4 (多选题)(2022·江苏常州高三期末)已知正方体ABCD-A 1B 1C 1D 1的棱长为3a,点M 是棱BC 上的定点,且BM=2CM,点P 是棱C 1D 1上的动点,则( )A.当PC 1=23a 时,△PAM 是直角三角形B.四棱锥A 1-PAM 体积的最小值为32a 3 C.存在点P,使得直线BD 1⊥平面PAM D.任意点P,都有直线BB 1∥平面PAM 解析:由已知及计算可得PC 1=23a,AM=√13a,AP=√2113a,MP=√943a,所以AP 2=MP 2+AM 2,所以△PAM 为直角三角形,A 正确;S △AA 1M =12×3a ×√13a=3√132a 2,当P 与C 1重合时,点P 到平面AA 1M 的距离最小,设点P 到平面AA 1M 的距离为h, 在B 1C 1上取M 1,使B 1M 1=2C 1M 1,sin ∠B 1M 1A 1=√13=ℎmin a,所以h min =√13a,所以V A 1PAM =V PAA 1M =13×S △AA 1M ×h ≥13×3√132a 2×√13a=32a 3,B 正确;因为BD 1⊥平面AB 1C,平面AB 1C 与平面PAM 不平行,所以BD 1与平面PAM 不垂直,C 错误;P 与C 1重合时,平面PAM 为平面C 1AM,BB 1∥CC 1,若BB 1∥平面PAM,则CC 1⊂平面C 1AM,与CC 1⊄平面C 1AM 矛盾,D 错误.故选AB.解决与空间图形有关的线段、角、距离、面积、体积等最值问题,一般可以从三方面着手:(1)从问题的几何特征入手,充分利用其几何性质去解决; (2)利用空间几何体的侧面展开图;(3)找出问题中的代数关系,建立目标函数,利用代数方法求目标函数的最值.解题途径很多,在函数建成后,可用一次函数的端点法,二次函数的配方法、公式法,函数有界法(如三角函数等)及导数法等.触类旁通4 (多选题)(2022·广东揭阳高三期末)如图所示,已知正方体ABCD-A 1B 1C 1D 1的棱长为2,M,N 分别是AD,CC 1的中点,P 是线段AB 上的动点,则下列说法正确的是( BD )A.平面PMN 截正方体所得的截面可以是四边形、五边形或六边形B.当点P 与A,B 两点不重合时,平面PMN 截正方体所得的截面是五边形C.△MPN 是锐角三角形D.△MPN 面积的最大值是√212解析:如图所示,当点P 与A,B 两点不重合时,将线段MP 向两端延长,分别交CD,CB 的延长线于点O,Q,连接NO,NQ 分别交DD 1,BB 1于R,S 两点,连接RM,SP,此时截面为五边形MPSNR,故B 正确;当点P 与点A 或点B 重合时,截面为四边形,不可能为六边形,故A 错误;考虑△MPN,当点P 与点A 重合时,MN=√6,PM=1,PN=3, 此时因为MN 2+PM 2<PN 2,故∠PMN 为钝角,故C 错误;当点P 与点B 重合时,点P 到直线MN 的距离取到最大值,△MPN 的面积取到最大值,此时MN=√6,BM=BN=√5,则MN 边上的高为√(√5)2-(√62)2=√142,△MPN的面积为12×√142×√6=√212,即最大值为√212,故D正确.故选BD.。
中考几何-动态试题解法(解析版)

中考几何动态试题解法专题知识点概述一、动态问题概述1.就运动类型而言,有函数中的动点问题有图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。
2.就运动对象而言,几何图形中的动点问题有点动、线动、面动三大类。
3.就图形变化而言,有轴对称(翻折)、平移、旋转(中心对称、滚动)等。
4.动态问题一般分两类,一类是代数综合方面,在坐标系中有动点,动直线,一般是利用多种函数交叉求解。
另一类就是几何综合题,在梯形,矩形,三角形中设立动点、线以及整体平移翻转,对考生的综合分析能力进行考察。
所以说,动态问题是中考数学当中的重中之重,属于初中数学难点,综合性强,只有完全掌握才能拿高分。
二、动点与函数图象问题常见的四种类型1.三角形中的动点问题:动点沿三角形的边运动,根据问题中的常量与变量之间的关系,判断函数图象。
2.四边形中的动点问题:动点沿四边形的边运动,根据问题中的常量与变量之间的关系,判断函数图象。
3.圆中的动点问题:动点沿圆周运动,根据问题中的常量与变量之间的关系,判断函数图象。
4.直线、双曲线、抛物线中的动点问题:动点沿直线、双曲线、抛物线运动,根据问题中的常量与变量之间的关系,判断函数图象。
三、图形运动与函数图象问题常见的三种类型1.线段与多边形的运动图形问题:把一条线段沿一定方向运动经过三角形或四边形,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
2.多边形与多边形的运动图形问题:把一个三角形或四边形沿一定方向运动经过另一个多边形,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
3.多边形与圆的运动图形问题:把一个圆沿一定方向运动经过一个三角形或四边形,或把一个三角形或四边形沿一定方向运动经过一个圆,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
四、动点问题常见的四种类型解题思路1.三角形中的动点问题:动点沿三角形的边运动,通过全等或相似,探究构成的新图形与原图形的边或角的关系。
立体几何的动态问题翻折问题
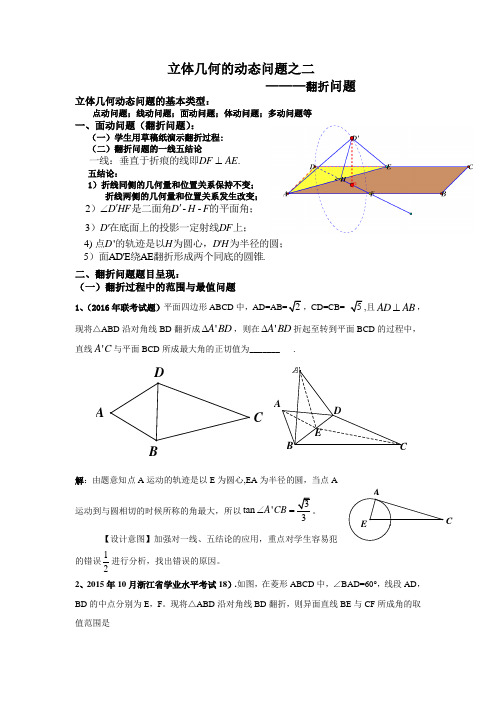
立体几何的动态问题之二———翻折问题立体几何动态问题的基本类型:点动问题;线动问题;面动问题;体动问题;多动问题等一、面动问题(翻折问题):(一)学生用草稿纸演示翻折过程: (二)翻折问题的一线五结论.DF AE ⊥一线:垂直于折痕的线即五结论:1)折线同侧的几何量和位置关系保持不变;折线两侧的几何量和位置关系发生改变; 2--D HF D H F ''∠)是二面角的平面角;3D DF ')在底面上的投影一定射线上; 二、翻折问题题目呈现:(一)翻折过程中的范围与最值问题1、(2016年联考试题)平面四边形ABCD 中,AD=AB=2,CD=CB= 5,且AD AB ⊥,现将△ABD 沿对角线BD 翻折成'A BD ∆,则在'A BD ∆折起至转到平面BCD 的过程中,直线'A C 与平面BCD 所成最大角的正切值为_______ .解:由题意知点A 运动的轨迹是以E 为圆心,EA 为半径的圆,当点A运动到与圆相切的时候所称的角最大,所以3tan 'A CB ∠=。
【设计意图】加强对一线、五结论的应用,重点对学生容易犯的错误12进行分析,找出错误的原因。
2、2015年10月浙江省学业水平考试18).如图,在菱形ABCD 中,∠BAD=60°,线段AD ,BD 的中点分别为E ,F 。
现将△ABD 沿对角线BD 翻折,则异面直线BE 与CF 所成角的取值范围是DABE CDABC4) ''D H DH点的轨迹是以为圆心,为半径的圆;5AD'E AE .)面绕翻折形成两个同底的圆锥ECA.(,)63ππ B. (,]62ππ C. (,]32ππ D. 2(,)33ππ分析:这是一道非常经典的学考试题,本题的解法非常多,很好的考查了空间立体几何线线角的求法。
方法一:特殊值法(可过F 作FH 平行BE,找两个极端情形) 方法二:定义法:利用余弦定理:222254cos 243FH FC CH FHC CH FH FC +-∠==-,有32144CH ≤≤11cos ,22CFH ⎡⎤∴∠∈-⎢⎥⎣⎦异面直线BE 与CF 所成角的取值范围是(,]32ππ 方法三:向量基底法:111()()222BE FC BA BD FC BA FC BF FA FC=+==+111cos ,cos ,,222BE FC FC FA ⎡⎤<>=<>∈-⎢⎥⎣⎦方法四:建系:3、(2015年浙江·理8)如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆折成A CD '∆,所成二面角A CDB '--的平面角为α,则 ( B )A. A DB α'∠≤B. A DB α'∠≥C. A CB α'∠≥D. A CB α'∠≤方法一:特殊值方法二:定义法作出二面角,在进行比较。
初中数学全等三角形中的动态问题(知识点例题解析)

初中数学全等三角形中的动态问题(知识点+例题解析)初中数学中,动点问题是学习的重、难点,在三角形、矩形等一些几何图形上,设计一个或多个动点,探究全等三角形存在性问题,该类题目具有较强的综合性。
解决动点问题常见的答题思路是:1.注意分类讨论;2.仔细探究全等三角形对应边与对应角的变化;3.利用时间表示出相应线段或边的长度,列出方程求解.【典例解析】【例1-1】(2020·周口市月考)如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动______秒时,△DEB与△BCA全等.【例1-2】(2020·江阴市月考)已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.A.1B.1或3C.1或7D.3或7【变式1-1】(2020·无锡市月考)如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.(1)试说明:∠A=∠BCD;(2)当点E运动多长时间时,CF=AB.请说明理由.【变式1-2】(2020·河北灵寿期末)如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m﹣n﹣0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.(1)求OA、OB的长;(2)连接PB,设△POB的面积为S,用t的式子表示S;(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.【例2】(2020·惠州市月考)如图,点C在线段BD上,AB⊥BD于B,ED⊥BD于D.∠ACE=90°,且AC =5cm,CE=6cm,点P以2cm/s的速度沿A→C→E向终点E运动,同时点Q以3cm/s的速度从E开始,在线段EC上往返运动(即沿E→C→E→C→…运动),当点P到达终点时,P,Q同时停止运动.过P,Q分别作BD的垂线,垂足为M,N.设运动时间为ts,当以P,C,M为顶点的三角形与△QCN全等时,t的值为_____.【变式2-1】(2020·江阴市月考)如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D 点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C 作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.(1)试证明:AD∥BC.(2)在移动过程中,小芹发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.【变式2-2】(2020·重庆巴南月考)如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在cm s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它线段AB上以1/们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的cm s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若运动速度为x/不存在,请说明理由.【变式2-3】(2020·江苏兴化月考)如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发,沿折线AC—CB以每秒1个单位长度的速度向终点B运动,点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动,P、Q两点同时出发.分别过P、Q两点作PE⊥l于E,QF⊥l于F.设点P的运动时间为t(秒):(1)当P、Q两点相遇时,求t的值;(2)在整个运动过程中,求CP的长(用含t的代数式表示);(3)当△PEC与△QFC全等时,直接写出所有满足条件的CQ的长.【例3】(2020·惠州市月考)如图,在△ABC中,AB=AC=18cm,BC=10cm,∠B=∠C,AD=2BD.如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过2s后,△BPD与△CQP是否全等,请说明理由;(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP 全等?(3)若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?【变式3-1】(2019·山西太原月考)如图1,在长方形ABCD中,AB=CD=5cm,BC=12cm,点P从点B 出发,以2cm/s的速度沿BC向点C运动,设点P的运动时间为ts.(1)PC=___cm;(用含t的式子表示)(2)当t为何值时,△ABP≌△DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻△ABP与以P,Q,C为顶点的直角三角形全等?若存在,请求出v的值;若不存在,请说明理由.【变式3-2】(2020·四川成都)如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q 三点所构成的三角形全等.【习题精练】=,BC6=,线段PQ=AB,1.(2020·江苏东台月考)如图,有一个直角三角形ABC,∠C=90°,AC10点Q在过点A且垂直于AC的射线AX上来回运动,点P从C点出发,沿射线CA以2cm/s的速度运动,问>,才能使△ABC≌△QPA全等.P点运动___________秒时(t0)2.(2020·江苏泰州月考)如图,AB =12,CA ⊥AB 于A ,DB ⊥AB 于B ,且AC =4m ,P 点从B 向A 运动,每分钟走1m ,Q 点从B 向D 运动,每分钟走2m ,P 、Q 两点同时出发,运动_______分钟后△CAP 与△PQB 全等.3.(2020·常州市月考)如图, ADC 中.∠C =90°,AC =10cm ,BC =5cm .AD ⊥AC ,AB =PQ ,P 、Q 两点分别在AC 、AD 上运动,当AQ =_____时,△ABC 才能和△APQ 全等.4.(2020·江西新余期末)如图,ABC ∆中,90ACB ∠=︒,8cm AC =,15cm BC =,点M 从A 点出发沿A C B →→路径向终点运动,终点为B 点,点N 从B 点出发沿B C A →→路径向终点运动,终点为A 点,点M 和N 分别以每秒2cm 和3cm 的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M 和N 作ME l ⊥于E ,NF l ⊥于F .设运动时间为t 秒,要使以点M ,E ,C 为顶点的三角形与以点N ,F ,C 为顶点的三角形全等,则t 的值为______.5.(2020·武城县月考)如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为多少时,能够使△BPE与以C、P、Q三点所构成的三角形全等?6.(2020·盐城市盐都区月考)如图,有一个直角△ABC,∠C=90°,AC=6,BC=3,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问:当AP=________时,才能使以点P、A、Q 为顶点的三角形与△ABC全等.7.(2020·四川青羊期中)如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4cm,BC=8cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD=cm,CE=cm;(2)当t为多少时,△ABD的面积为12cm2?(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.8.(2020·郑州市月考)如图,在平面直角坐标系中,O 为坐标原点A 、B 两点的坐标分别A (m ,0),B(0,n ),且|m -n -3|=0,点P 从A 出发,以每秒1个单位的速度沿射线AO 匀速运动,设点P 运动时间为t 秒.(1)求OA 、OB 的长;(2)连接PB ,若△POB 的面积不大于3且不等于0,求t 的范围;(3)过P 作直线AB 的垂线,垂足为D ,直线PD 与y 轴交于点E ,在点P 运动的过程中,是否存在这样的点P ,使△EOP ≌△AOB ?若存在,请求出t 的值;若不存在,请说明理由.9.(2020·宜兴市月考)如图,在△ABC 中,∠BAD =∠DAC ,DF ⊥AB ,DM ⊥AC ,AF =10cm ,AC =14cm ,动点E 以2cm /s 的速度从A 点向F 点运动,动点G 以1cm /s 的速度从C 点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t .(1)求证:AF =AM ;(2)当t 取何值时,△DFE 与△DMG 全等;(3)求证:在运动过程中,不管t 取何值,都有2AED DGC S S =△△.10.(2020·江苏工业园区期末)如图①,将长方形纸片沿对角线剪成两个全等的直角三角形ABC、EDF,其中AB=8cm,BC=6cm,AC=10cm.现将△ABC和△EDF按如图②的方式摆放(点A与点D、点B与点E 分别重合).动点P从点A出发,沿AC以2cm/s的速度向点C匀速移动;同时,动点Q从点E出发,沿射线ED以acm/s(0<a<3)的速度匀速移动,连接PQ、CQ、FQ,设移动时间为ts(0≤t≤5).=3S△BQC,则a=;(1)当t=2时,S△AQF(2)当以P、C、Q为顶点的三角形与△BQC全等时,求a的值;(3)如图③,在动点P、Q出发的同时,△ABC也以3cm/s的速度沿射线ED匀速移动,当以A、P、Q为顶点的三角形与△EFQ全等时,求a与t的值.11.(2019·江苏期末)如图①,在ABC ∆中,12AB =cm ,20BC =cm ,过点C 作射线//CD AB .点M 从点B 出发,以3cm /s 的速度沿BC 匀速移动;点N 从点C 出发,以a cm /s 的速度沿CD 匀速移动.点M 、N 同时出发,当点M 到达点C 时,点M 、N 同时停止移动.连接AM 、MN ,设移动时间为t (s ).(1)点M 、N 从移动开始到停止,所用时间为s ;(2)当ABM ∆与MCN ∆全等时,①若点M 、N 的移动速度相同,求t 的值;②若点M 、N 的移动速度不同,求a 的值;(3)如图②,当点M 、N 开始移动时,点P 同时从点A 出发,以2cm /s 的速度沿AB 向点B 匀速移动,到达点B 后立刻以原速度沿BA 返回.当点M 到达点C 时,点M 、N 、P 同时停止移动.在移动的过程中,是否存在PBM ∆与MCN ∆全等的情形?若存在,求出t 的值;若不存在,说明理由.图①图②12.如图,ABC 中,90ACB ∠=︒,8AC cm =,15BC cm =,点M 从A 点出发沿A →C →B 路径向终点运动,终点为B 点,点N 从B 点出发沿B →C →A 路径向终点运动,终点为A 点,点M 和N 分别以每秒2cm 和3cm 的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M 和N 作ME l ⊥于E ,NF l ⊥于F 设运动时间为t 秒,要使以点M ,E ,C 为顶点的三角形与以点N ,F ,C 为顶点的三角形全等,则t 的值为________.13.(2019·湖北襄州)在平面直角坐标系中,点A(0,5),B(12,0),在y轴负半轴上取点E,使OA=EO,作∠CEF=∠AEB,直线CO交BA的延长线于点D.(1)根据题意,可求得OE=;(2)求证:△ADO≌△ECO;(3)动点P从E出发沿E﹣O﹣B路线运动速度为每秒1个单位,到B点处停止运动;动点Q从B出发沿B﹣O﹣E运动速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间△OPM与△OQN全等?14.(2019·福建省惠安期中)如图,在△ABC中,BC=8cm,AG∥BC,AG=8cm,点F从点B出发,沿线段BC以4cm/s的速度连续做往返运动,同时点E从点A出发沿线段AG以2cm/s的速度向终点G运动,当点E到达点G时,E、F两点同时停止运动,EF与AC交于点D,设点E的运动时间为t(秒)(1)分别写出当0≤t≤2和2<t≤4时线段BF的长度(用含t的代数式表示);(2)当BF=AE时,求t的值;(3)若△ADE≌△CDF,求所有满足条件的t值.15.(2020·无锡市月考)△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P 在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q 的运动速度为_____厘米/秒,△BPD与△CQP全等.16.(2020·广东龙岗期末)直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图①,分别过点A、B作AD⊥l于点D,BE⊥l于点E.求证:△ACD≌△CBE.(2)当AC=8,BC=6时,如图②,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿F→C→B→C→F向终点F运动,点M、N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N 作NE⊥l于点E,设运动时间为t秒.①CM=,当N在F→C路径上时,CN=.(用含t的代数式表示)②直接写出当△MDC与△CEN全等时t的值.17.(2020·青岛市黄岛区月考)如图1,直线AM AN ⊥,AB 平分MAN ∠,过点B 作BC BA ⊥交AN 于点C ;动点E 、D 同时从A 点出发,其中动点E 以2/m s 的速度沿射线AN 方向运动,动点D 以1/m s 的速度运动;已知6AC cm =,设动点D ,E 的运动时间为t .图1备用图(1)试求∠ACB 的度数;(2)当点D 在射线AM 上运动时满足ADB S :2BEC S = :3,试求点D ,E 的运动时间t 的值;(3)当动点D 在直线AM 上运动,E 在射线AN 运动过程中,是否存在某个时间t ,使得ADB 与BEC 全等?若存在,请求出时间t 的值;若不存在,请说出理由.参考答案及解析初中数学中,动点问题是学习的重、难点,在三角形、矩形等一些几何图形上,设计一个或多个动点,探究全等三角形存在性问题,该类题目具有较强的综合性。
剖析立体几何中的“动态”问题

ʏ沈建良所谓动态立体几何问题,是指在点㊁线㊁面运动变化的几何图形中,探寻点㊁线㊁面的位置关系或进行有关角与距离的计算㊂立体几何中常求解一些固定不变的点㊁线㊁面的关系,若给静态的立体几何问题赋予 活力 ,渗透了 动态 的点㊁线㊁面元素,立意会更新颖㊁更灵活,能培养同学们的空间想象能力㊂下面是对破解立体几何 动态 问题的一些思考,以期抛砖引玉㊂一㊁ 动态 问题之轨迹问题例1如图1,在边长为a的正方体A B C D-A1B1C1D1中,E,F,G,H,N分别是C C1,C1D1,D D1,C D,B C的中点,M在四边形E F G H边上及其内部运动,若MNʊ面A1B D,则点M轨迹的长度是()㊂图1A.3aB.2aC.32aD.22a解:因为在边长为a的正方体A B C D-A1B1C1D1中,E,F,G,H分别是C C1, C1D1,D D1,C D的中点,N是B C的中点,则G HʊB A1,HNʊB D㊂又G H⊄面A1B D, B A1⊂面A1B D,所以G Hʊ面A1B D㊂同理可得,NHʊ面A1B D㊂又G HɘHN=H,所以面A1B Dʊ面G HN㊂因为点M在四边形E F G H上及其内部运动,MNʊ面A1B D,所以点M一定在线段G H上运动,即满足条件㊂易得G H=22a㊂故点M轨迹的长度是22a㊂应选D㊂本题利用线面平行㊁面面平行,在动态问题中提炼一些不变的 静态 的量,建立不变量与动点之间的关系,从而确定动点的轨迹长度㊂二㊁ 动态 问题之定值问题例2如图2,在单位正方体A B C D-A1B1C1D1中,点P在线段A D1上运动㊂图2给出以下四个命题:①异面直线A1P与B C1间的距离为定值;②三棱锥D-B P C1的体积为定值;③异面直线C1P与C B1所成的角为定值;④二面角P-B C1-D的大小为定值㊂其中真命题的序号是()㊂A.①②B.③④C.①②③D.①②③④解:对于①,异面直线A1P与B C1间的距离即为两平行平面A D D1A1和平面B C C1B1间的距离,即为正方体的棱长,为定值,①正确㊂对于②,V D-B P C1=V P-D B C1,因为SәD B C1为定值,点PɪA D1,A D1ʊ平面B D C1,所以点P到平面B D C1的距离即为正方体的棱长,所以三棱锥D-B P C1的体积为定值,②正确㊂对于③,在正方体A B C D-A1B1C1D1中,因为B1Cʅ平面A B C1D1,而C1P⊂平面A B C1D1,所以B1CʅC1P,即这0 1数学部分㊃知识结构与拓展高一使用2022年4月Copyright©博看网. All Rights Reserved.两条异面直线所成的角为90ʎ,③正确㊂对于④,因为二面角P -B C 1-D 的大小即为平面A B C 1D 1与平面B D C 1所成的二面角的大小,而这两个平面位置固定不变,所以二面角P -B C 1-D 的大小为定值,④正确㊂应选D㊂动态立体几何问题,在变化过程中总蕴含着某些不变的因素,因此要认真分析其变化特点,寻找不变的静态因素,从静态因素中,找到解决问题的突破口㊂三㊁ 动态 问题之翻折问题例3 如图3,在长方形A B C D 中,A B =2,B C =1,E 为D C 的中点,F 为线段E C (端点除外)上一动点㊂现将әAF D 沿A F 折起,使平面A B D ʅ平面A B C F ,得到如图4所示的四棱锥D -A B C F ㊂在平面A B D 内过点D 作D K ʅA B ,垂足为K ㊂设A K =t ,则t 的取值范围是㊂图3 图4解:过点F 作F M ʅA B 交A B 于点M (作法略)㊂设F C =x ,0<x <1,则M F =B C =1,M B =F C =x ㊂易知A K <A D =1,A B =2,所以点K 一定在点M 的左边,则MK =2-t -x ㊂在R t әA D K 中,D K 2=1-t2,在R tәF MK 中,F K 2=1+(2-t -x )2㊂因为平面A B D ʅ平面A B C F ,平面A B D ɘ平面A B C F =A B ,D K ʅA B ,D K ⊂平面A B D ,所以D K ʅ平面A B C F ,所以D K ʅF K ㊂在R t әD F K 中,D F =2-x ,D K 2+F K 2=D F 2,所以1-t 2+1+(2-t -x )2=(2-x )2,化简得1-2t +t x =0,即t =12-x㊂又因为t =12-x在(0,1)上单调递增,所以12<t <1,即t 的取值范围为12,1()㊂本题是一个动态的翻折问题,通过发现不变的垂直关系,从而得到相关变量间的关系,最终转化成函数的值域问题㊂解决折叠问题的关键是分清折叠前后图形的位置和数量关系的变与不变的量㊂四㊁ 动态 问题之展开问题例4 已知某圆锥的母线长为3,底面半径为1,则该圆锥的体积为㊂设线段A B 为该圆锥底面圆的一条直径,一质点从A 出发,沿着该圆锥的侧面运动,到达B 点后再沿侧面回到A 点,则该质点运动路径的最短长度为㊂解:易得该圆锥的高h =32-1=22㊂所以该圆锥的体积V =13ˑπˑ12ˑ22=223π㊂将该圆锥侧面沿母线S A 展开,如图5所示㊂图5因为圆锥底面周长为2π,扇形半径为3,所以侧面展开后得到的扇形的圆心角øA S A '=2π3㊂由题意知点B 是圆锥侧面展开后得到的扇形的弧A A '的中点,则øA S B =π3,所以A B =A 'B =A S =3㊂所以该质点运动路径的最短长度为A B +A 'B =6㊂空间动态问题常转化为平面的动态问题求解㊂化曲为直是求解曲面上路径长度最短问题的关键㊂本题是求解圆锥侧面上质点运动路径的最短长度问题,可将圆锥侧面沿一条母线展开成扇形,从而在平面图形中解决问题㊂作者单位:江苏省盐城市时杨中学(责任编辑 郭正华)11数学部分㊃知识结构与拓展高一使用 2022年4月Copyright ©博看网. All Rights Reserved.。
压轴小题7探究立体几何中的动态问题

压轴小题7 探究立体几何中的动态问题【炎德联考雅礼中学2024届高三月考试卷六T 11】(多选)如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 为菱形,160,2,BAD AB AA P ∠=︒==为1CC 的中点,点Q 满足[][]()10,1,0,1DQ DC DD λμλμ=+∈∈,则下列结论正确的是()A .若13λμ+=,则四面体1A BPQ 的体积为定值B .若1A BQ △的外心为O ,则11A B AO ⋅为定值2C .若1A Q QD .若1λ=且12μ=,则存在点1E A B ∈,使得AE EQ +对于A ,取1,DD DC 的三等分点分别为,由条件确定的轨迹,结合锥体体积公式判断;对于B ,由三角形外心的性质和向量数量积的性质可判断;由条件确定的轨迹为,将原问题转化为平面上两点间的距离最小问题求解;对于C ,由条件确定点的轨迹为圆弧,利用弧长公式求轨迹长度即可判断;对于D ,把1A AB △沿着1A B 进行翻折,使得1A ,A ,B ,P 四点共面,再由勾股定理和余弦定理求出长度.此时有最小值.对于A ,取1,DD DC 的三等分点分别为,如图所示,因为13λμ+=,所以331λμ+=,令,,则,所以.因为,所以1A BQ △的面积为定值,点P 到平面的距离也是定值,故A 正确.对于B ,若1A BQ △的外心为O ,过点O 作于点H ,则H 是1A B 的中点.因为,所以,故B 错误.对于C ,在平面1111D C B A 中作111A K C D ⊥,显然平面11CC D D ,由长度和角度,可得1A K =在中,1A Q =所以KQ =Q 在以为圆心,为半径的圆上运动.设此圆与交于点,因为3KA =且11KD =,所以,则点Q 的轨迹长度是.故C 正确.对于D ,若且,则点Q 与点P 重合.把1A AB △沿着1A B 进行翻折,使得1A ,A ,B ,P 四点共面,此时有最小值AP (这里和后面的A 均为翻折后的点).在中,1A P =PB 1A B =所以1π2PBA ∠=,从而3π4PBA ∠=,在中,由余弦定理得,故D 正确.故选:ACD(2024·湖北·二模)1.如图,棱长为2的正方体1111ABCD A B C D -中,E 为棱1DD 的中点,F 为正方形11C CDD 内一个动点(包括边界),且1//B F 平面1A BE ,则下列说法正确的有( )A .动点FB .三棱锥11B D EF -体积的最小值为13C .1B F 与1A B 不可能垂直D .当三棱锥11B D DF -的体积最大时,其外接球的表面积为25π2(2024·广西南宁·一模)2.在边长为2的正方体1111ABCD A B C D -中,动点M 满足1AM xAB y AD z AA =++,(,,R x y z ∈且0,0,0)x y z ≥≥≥,下列说法正确的是( )A .当[]1,0,0,14x z y ==∈时,1B M MD +B .当11,2x y z ===时,异面直线BM 与1CDC .当1x y z ++=,且AM =时,则MD .当1,0x y z +==时,AM 与平面11AB DA 选项,作出辅助线,结合空间向量基本定理得到,,W Q F 三点共线,得到//WF 平面1PA B ,故点为平面1PA B 的距离为定值,四面体1A BPQ 的体积为定值,A 正确;B 选项,作出辅助线,结合空间向量数量积的几何意义得到11114A B AT B A O A ⋅=⋅= ;C 选项,建立空间直角坐标系,设()0,2,2Q λμ,表达出,故点的轨迹为以()1,2S -为圆心,为半径的圆,落在正方形11CDD C 内的部分,结合弧长公式求出答案;D 选项,求出()0,2,1Q ,,得到AE EQ +=,画出图形,数形结合得到其最小值.A 选项,在1,CD DD 上分别取,使得13DF DC =,,因为,所以,因为13λμ+=,所以331λμ+=,即,故,即,所以,,W Q F 三点共线,因为1//WF CD ,,所以1//WF AB ,故//WF 平面1PA B ,故点为平面1PA B 的距离为定值,又1PA B S 为定值,故四面体1A BPQ 的体积为定值,A 正确;B 选项,取1A B 的中点,因为1A BQ △的外心为,所以⊥1A B ,又题意得,则,B 错误;C 选项,取的中点R ,因为底面为菱形,60BAD ∠=︒,故⊥,以D 为坐标原点,以,1,DC DD 分别为轴,建立空间直角坐标系,故,设()0,2,2Q λμ,则,化简得,点满足,即点在正方形11CDD C 内,包括边界,故点的轨迹为以()1,2S -为圆心,为半径的圆,落在正方形11CDD C 内的部分,如图所示:因为SH =11SD =,故,故1SD H 为等腰直角三角形,π4S ∠=,故点的轨迹长度为,C 正确;D 选项,若且,,即,即()0,2,1Q ,又,)B,设,设,即,解得,即,AE EQ +=,如图所示,设,且⊥,⊥,在线段上取一点,设GL a =,则12LJ a =-,故,显然,直接连接,此时KL VL +取得最小值,最小值即为,由勾股定理得KV ==故AE EQ +=的最小值为,D 正确.故选:ACD(2024·江西鹰潭·一模)3.直四棱柱1111ABCD A B C D -的所有棱长都为4,π3BAD ∠=,点P 在四边形11BDD B 及其内部运动,且满足8PA PC +=,则下列选项正确的是( )A .点P 的轨迹的长度为π.B .直线AP 与平面11BDD B 所成的角为定值.C .点P 到平面11AD B .D .11PA PC ⋅的最小值为-2.(23-24高二下·湖南长沙·开学考试)4.在正方体1111ABCD A B C D -中,1AB =,点P 满足1CP CD CC λμ=+,其中[]0,1λ∈,[]0,1μ∈,则下列结论正确的是( )A .当1B P ∥平面1A BD 时,1B P 不可能垂直1CD B .若1B P 与平面11CCD D 所成角为4π,则点P 的轨迹长度为2πC .当λμ=时,1DP A P +的最小值为D .当1λ=时,正方体经过点1A 、P 、C 的截面面积的取值范围为(2024·湖南·二模)5.如图,点P 是棱长为2的正方体1111ABCD A B C D -的表面上一个动点,F 是线段11A B 的中点,则( )A .若点P 满足1APBC ⊥,则动点P 的轨迹长度为B .三棱锥11A PBD -体积的最大值为163C .当直线AP 与AB 所成的角为45 时,点P 的轨迹长度为π+D .当P 在底面ABCD 上运动,且满足//PF 平面11B CD 时,线段PF 长度最大值为(2024·黑龙江齐齐哈尔·一模)6.已知四面体ABCD 的各个面均为全等的等腰三角形,且24CA CB AB ===.设E 为空间内任一点,且,,,,A B C D E 五点在同一个球面上,则( )A .AB CD⊥B .四面体ABCD 的体积为C .当AE =E 的轨迹长度为4πD .当三棱锥E ABC -E 的轨迹长度为(2024·广东深圳·一模)7.如图,八面体Ω的每一个面都是边长为4的正三角形,且顶点,,,B C D E 在同一个平面内.若点M 在四边形BCDE 内(包含边界)运动,N 为AE 的中点,则( )A .当M 为DE 的中点时,异面直线MN 与CF 所成角为3πB .当MN ∥平面ACD 时,点M 的轨迹长度为C .当MA ME ⊥时,点M 到BCD .存在一个体积为103π的圆柱体可整体放入Ω内(23-24高二上·河北石家庄·期末)8.如图,已知正方体1111ABCD A B C D -的棱长为2,E ,F 分别是棱111,AA A D 的中点,点P 为底面ABCD 内(包括边界)的动点,则以下叙述正确的是( )A .存在点P ,使得1C P ⊥平面BEFB .若点P 在线段CD 上运动,则点P 到直线BFC .若点P 到直线1BB 与到直线AD 的距离相等,则点P 的轨迹为抛物线的一部分D .若直线1D P 与平面BEF 无公共点,则点P (23-24高三上·江西·期末)9.如图,正方体1111ABCD A B C D -的棱长为2,点E 是AB 的中点,点P 为侧面11BCC B 内(含边界)一点,则( )A .若1D P ⊥平面11AC D ,则点P 与点B 重合B .以D 1ACDC .若P 为棱BC 中点,则平面1D EP D .若P 到直线11A B 的距离与到平面11CDD C 的距离相等,则点P 的轨迹为一段圆弧(23-24高二上·安徽马鞍山·期末)10.如图,在长方体1111ABCD A B C D -中,124AB AD AA ===,点E 为1AA 的中点,点F 为侧面11AA B B (含边界)上的动点,则下列说法正确的是 ( )A .不存在点F ,使得1FC FD ⊥B .1FC FD +的最小值为C .满足1FC FD =的点F D .若1//AD 平面EFC ,则线段AF 长度的最小值为35参考答案:1.ABD【分析】对A 由1//B F 平面1A BE ,联想到存在一个过1B F 的平面与平面1A BE 平行,利用正方体特征找到平面1//B MN 平面1BA E ,进而得到F 的轨迹为线段MN ,对B ,根据棱锥体积公式分析即可,对C 举反例即可;对D ,利用勾股定理求出外接球半径即可.【详解】对A ,如图,令1CC 中点为M ,1CD 中点为N ,连接MN ,又正方体1111ABCD A B C D -中,E 为棱1DD 的中点,可得11//B M A E ,11////MN CD BA ,1//B M ∴平面1BA E ,//MN 平面1BA E ,又1B M MN M = ,且1,B M MN ⊂平面1B MN ,∴平面1//B MN 平面1BA E ,又1//B F 平面1A BE ,且1B ∈平面1B MN ,1B F ∴⊂平面1B MN ,又F 为正方形11C CDD 内一个动点(包括边界),F ∴∈平面1B MN 平面11C CDD ,而MN =平面1B MN 平面11C CDD ,F MN ∴∈,即F 的轨迹为线段MN .由棱长为2的正方体得线段MN ,故选项A 正确;对B ,由正方体侧棱11B C ⊥底面11C CDD ,所以三棱锥11B D EF -体积为111112=33D FE D FE V B C S S =⋅ ,所以1D FE 面积1D FE S 最小时,体积最小,如图,F MN ∈ ,易得F 在N 处时1D FE S 最小,此时11111=22D FE S ND D E ⋅= ,所以体积最小值为13,故选项B 正确;对C ,当F 为线段MN 中点时,由11B M B N =可得1B F MN ⊥,又1CC 中点为M ,1CD 中点为N ,1//MN D C ∴,而11//A B D C ,11B F A B ∴⊥,故选项C 不正确;对D ,如图,当F 在M 处时,三棱锥11B D DF -的体积最大时,由已知得此时11FD FD FB ===,所以F 在底面11B DD 的射影为底面外心,12DD =,11B D =1DB =,所以底面11B DD 为直角三角形,所以F 在底面11B DD 的射影为1B D 中点,设为1O ,如图,设外接球半径为R ,由222211113R OO O B OO =+=+,11R OO FO +==可得外接球半径R =,外接球的表面积为2254π2R π=,故选项D 正确.故选:ABD.2.AD【分析】对于A ,确定M 的位置,利用侧面展开的方法,求线段的长,即可判断;对于B ,利用平移法,作出异面直线所成角,解三角形,即可判断;对于C ,结合线面垂直以及距离确定点M 的轨迹形状,即可确定轨迹长度;对于D ,利用等体积法求得M 点到平面11AB D 的距离,结合线面角的定义求得AM 与平面11AB D 所成角的正弦值,即可判断.【详解】对于A ,在AB 上取点H ,使14AH AB = ,在DC 上取点K ,使14DK DC = ,因为[]1,0,0,14x z y ==∈,即14AM AB y AD =+ ,故M 点在HK 上,将平面11B HKC 与平面AHKD 沿着HK 展开到同一平面内,如图:连接1B D 交HK 于P ,此时,,B P D 三点共线,1B M MD +取到最小值即1B D 的长,由于113,422AH AB BH ==∴= ,则152B H ==,故11513,22A B B D =+=∴===即此时1B M MD +,A 正确;对于B ,由于11,2x y z ===时,则111122AM AB AD AA AC CC =++=+ ,此时M 为1CC 的中点,取11C D 的中点为N ,连接,,BM MN BN ,则1MN CD ∥,故BMN ∠即为异面直线BM 与1CD 所成角或其补角,又112MN CD BM ====3BN ===,故222cos 2BM MN BN BMN BM MN+-∠===⋅而异面直线所成角的范围为π(0,]2,故异面直线BM 与1CD B 错误;对于C ,当1x y z ++=时,可得点M 的轨迹在1A BD 内(包括边界),由于1CC ⊥平面ABCD ,BD ⊂平面ABCD ,故1CC BD ⊥,又BD AC ⊥,11,,AC CC C AC CC =⊂ 平面1ACC ,故BD ⊥平面1ACC ,1AC ⊂平面1ACC ,故1BD AC ⊥,同理可证11A B AC ⊥,11,,A B BD B A B BD =⊂ 平面1A BD ,故1AC ⊥平面1A BD ,设1AC 与平面1A BD 交于点P ,由于11113222324A A BD A ABD V V--=⨯⨯==⨯⨯,1A BD 为边长为则点A到平面1A BD的距离为AP =若AM =,则MP ==,即M 点落在以PP 点到1A BD 三遍的距离为13=,即M 点轨迹是以P 为半径的圆的一部分,,C 错误;对于D ,因为11,B D BD BD ⊄∥平面11AB D ,11B D ⊂平面11AB D ,故BD ∥平面11AB D ,因为当1,0x y z +==时,AM AB AD =+ ,即M 在BD 上,点M 到平面11AB D 的距离等于点B 到平面11AB D 的距离,设点B 到平面11AB D 的距离为d ,则111111111142223323B AB D ABB ABB D V V S A D --==⋅=⨯⨯⨯⨯= ,11AB D 为边长为的正三角形,即(12114333A BD S d d ⋅=⨯= ,解得d =又M 在BD 上,当M 为BD 的中点时,AM ,设直线AM 与平面11AB D 所成角为π,[0,2θθ∈,则sin d AM θ===即AM 与平面11AB D ,D 正确,故选:AD【点睛】难点点睛:本题考查了空间几何体中线段和差最值以及几何体中的轨迹问题,以及线线角和线面角的求解,综合性较强,难度较大,解答时要发挥空间想象,明确空间的位置关系,难点在于C ,D 选项的判断,对于C ,要结合空间距离,确定动点的轨迹形状;对于D ,要结合等体积法求得点到平面的距离,结合线面角的定义求解.3.BC【分析】建立空间直角坐标系,表示8PA PC +=,化简后得点P 的轨迹方程,得轨迹长度判断A ;向量法求线面角判断B ,向量法求点到平面距离,结合点P 的轨迹得最小值判断C ;坐标表示向量数量积,结合点P 的轨迹最小值判断D.【详解】直四棱柱1111ABCD A B C D -的所有棱长都为4,则底面ABCD 为菱形,又π3BAD ∠=,则ABD △和CBD △都是等边三角形,设BD 与AC 相交于点O ,由BD AC ⊥,以O 为原点,OA 为x 轴,OB 为y 轴,过O 垂直于底面的直线为z 轴,建立如图所示的空间直角坐标系,则有()()()(),0,2,0,,0,2,0A B C D --,()()()()11114,0,2,4,4,0,2,4A B C D --,点P 在四边形11BDD B 及其内部运动,设()0,,P y z ,22,04y z -≤≤≤≤,由8PA PC +=8+=,即()22422,02y z y z +=-≤≤≤≤,所以点P 的轨迹为yOz 平面内,以O 为圆心,2为半径的半圆弧,所以点P 的轨迹的长度为2π, A 选项错误;平面11BDD B 的法向量为()1,0,0m = ,(),AP y z =- ,直线AP 与平面11BDD B 所成的角为θ,则sin AP m AP m θ⋅=== 又由π0,2θ⎡⎤∈⎢⎥⎣⎦,则π3θ=,所以直线AP 与平面11BDD B 所成的角为定值, B选项正确;()()11=2,4,2,4AB AD ---,设平面11AD B 的一个法向量为(),,n x y z = ,则有11=240=240AB n y z AD n y z ⎧⋅-++=⎪⎨⋅--+=⎪⎩ ,令2x =,得0,y z ==,(n = ,所以点P 到平面11AD B 的距离d 02z ≤≤,所以2z =时,mind所以点P 到平面11AD B C 选项正确;()()11=,4,,4PA y z PC y z --=--- ,()2211=124PA PC y z ⋅-++- ,其几何意义为点(),P y z 到点()0,4距离的平方减12,由224y z +=,点(),P y z 到点()0,4距离最小值为422-=,11PA PC ⋅ 的最小值为22128-=-,D 选项错误.故选:BC.【点睛】方法点睛:空间几何体中的相关问题,要利用好几何体本身的结构特征,点线面的位置关系,图形中的角度和距离等,建立空间直角坐标系,利用向量法解决问题,也是常用的方法.4.BD【分析】建立空间直角坐标系,利用向量的坐标运算即可判断AD ,根据线面角的几何法可判断P 的轨迹是以1C 为圆心,以1为半径的14个圆,即可判断B ,根据展开图,转化为平面中两点距离最小,结合余弦定理即可求解C.【详解】A 选项:建立如图所示的空间直角坐标系A xyz -,则()0,0,0A ,()1,0,0B ,()0,1,0D ,()1,1,0C ,()10,0,1A ,()11,1,1C ,()10,1,1D ,()11,0,1B ,所以()11,0,1CD =- ,()()()()11110,1,11,0,00,0,1,1,1B P B C CP B C CD CC λμλμλμ=+=++=-+-+=-- ,则()11,0,1BA =- ,()1,1,0BD =- ,设平面1A BD 的法向量为(),,n x y z = ,所以10,0,BA n x z BD n x y ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ 令1x =,则1y z ==,即平面1A BD 的一个法向量为()1,1,1n = .若1B P ∥平面1A BD ,则10n B P ⋅= ,即λμ=,111B P CD λμ⋅=+- ,令110B P CD ⋅= ,解得12λμ==.即P 为1CD 中点时,有1B P ∥平面1A BD ,且11B P CD ⊥,故A 错误;B 选项:因为11BC ⊥平面11CCD D ,连接1C P ,则11B PC ∠即为1B P 与平面11CC D D 所成角,若1B P 与平面11CC D D 所成角为π4,则11111tan 1B C B PC C P ∠==,所以1111C P B C ==,即点P 的轨迹是以1C 为圆心,以1为半径的14个圆,于是点P 的轨迹长度为π2,故B 正确;C 选项:当λμ=时,()11CP CD CC CD λλ=+= ,此时点P 在线段1CD 上运动,如图,将平面1CD D 与平面11BCD A 沿1CD展成平面图形,线段1A D 即为1DP A P +的最小值,利用余弦定理可知222111111132cos 24A D A D DD A D DD π=+-⋅⋅=1A D =,故C 错误;D 选项:当1λ=时,11C D P CD C P C CC μμ⇒==+ ,故点P 在线段1DD 上运动,正方体经过点1A 、P 、C 的截面为平行四边形1A PCH ,以A 为坐标原点,建立如图所示的空间直角坐标系A xyz -,则()0,0,0A ,()1,1,0C ,()10,0,1A ,()0,1,P μ,所以()1,0,PC μ=- ,()11,1,1A C =- ,11PC AC μ⋅=+,PC =,1A C = ,所以点P 到直线1AC的距离为d =于是当12μ=时,1PAC △当0μ=或1时,1PAC △,故D 正确.故选:BD【点睛】方法点睛:立体几何中与动点轨迹有关的题目归根到底还是对点线面关系的认知,其中更多涉及了平行和垂直的一些证明方法,在此类问题中要么很容易的看出动点符合什么样的轨迹(定义),要么通过计算(建系)求出具体的轨迹表达式,和解析几何中的轨迹问题并没有太大区别,所求的轨迹一般有四种,即线段型,平面型,二次曲线型,球型.5.CD【分析】利用线面垂直的性质定理可得动点P 的轨迹为矩形11ABC D ,其周长为4+;显然三棱锥11A PB D -体积的最大值即为正四面体11C AB D -,易知最大值为1183C ABD V -=;易知当点P 在线段1,AC AB 和弧 1B C 上时,直线AP 与AB 所成的角为45 ,可知其轨迹长度为π+根据面面平行的判定定理可求出点P 在底面ABCD 上的轨迹为三角形FNM ,易知FP 长度的最大值为FN =【详解】对于A ,易知1B C ⊥平面11,ABC D A ∈平面11ABC D ,故动点P 的轨迹为矩形11ABC D ,动点P 的轨迹长度为矩形11ABC D 的周长,即为4,所以A 错误;对于B ,因为1111A PD D P AB D V V --=,而等边11AB D 的面积为定值要使三棱锥11P AB D -的体积最大,当且仅当点P 到平面11AB D 的距离最大,易知点C 是正方体到平面11AB D 距离最大的点,所以()1111max A PB D C AB D V V --=,此时三棱锥11C AB D -即为棱长是其高为h ==11118323C AB D V -=⨯⨯=,B 错误;对于C :连接AC ,1AB ,以B 为圆心,1BB 为半径画弧 1B C ,如图1所示,当点P 在线段1,AC AB 和弧 1B C 上时,直线AP 与AB 所成的角为45 ,又1AC AB =====,弧 1B C 长度21π2π4⨯⨯=,故点P 的轨迹长度为π+C 正确;对于D ,取1111,,,,,A D D D DC CB BB AB 的中点分别为,,,,,Q R N M T H ,连接,,,,,,,,QR QF FT TM MN NR FH HN HM ,如图2所示,因为FT 1,D C FT ⊄平面111,D B C D C ⊂平面11D B C ,故FT 平面11D B C ,TM 1B C ,TM ⊄平面111,D B C B C ⊂平面11D B C ,故TM 平面11D B C ;又,,FT TM T FT TM ⋂=⊂平面FTM ,故平面FTM 平面11D B C ;又QF ,NM QR ,TM RN FT ,故平面FTMNRQ 与平面FTM 是同一个平面.则点P 的轨迹为线段MN :在三角形FNM 中,FN FM NM =======则2228FM MN FN +==,故三角形FNM 是以FMN ∠为直角的直角三角形;故max FP FN ==,故FP 长度的最大值为D 正确.故选:CD .【点睛】方法点睛:立体几何中动点轨迹问题经常利用不动点的位置和动点位置关系,利用线面、面面平行或垂直的判定定理和性质定理,找出动点的轨迹进而计算出其轨迹长度.6.AC【分析】根据线面的垂直可判断线线垂直,判断A ;根据棱锥的体积公式可判断B ;根据条件,确定轨迹的形状,结合圆的周长求得轨迹长度或范围,即可判断C ,D.【详解】对于A ,依题意,可知4,2DA CB DB AC DC AB ======,设F 为AB 的中点,连接,CF DF ,则,CF AB DF AB ⊥⊥,而,,CF DF F CF DF =⊂ 平面CFD ,故AB ⊥平面CFD ,CD ⊂平面CFD ,故AB CD ⊥,A 正确;对于B ,将四面体ABCD 放入长方体中,设长方体的相邻三条棱长分别为,,x y z ,则2222224,16,16x y x z y z +=+=+=,解得x y z ===由于z =AB 和CD,且AB ⊥平面CFD ,,所以四面体ABCD的体积为11122332DCF S AB ⋅=⨯⨯= ,B 错误;对于C ,由以上分析可知,四面体ABCD=,由AE =E 的轨迹为一个圆,设轨迹圆的半径为r ,则222r +=,解得2r =,所以E 的轨迹长度为2π4πr =,C 正确;对于D,由题意可得sin CF ABC ==∴∠,故ABC的外接圆半径为21=所以球心到ABC=设三棱锥E ABC -的高为h ,由三棱锥E ABC -1112232ABC S h h ⋅=⨯⨯=故h =>E 点轨迹为外接球上平行于平面ABC 且到平面ABC两个截面圆,其中一个圆为外接球的大圆,所以点E的轨迹长度大于2π=,D 错误,故选:AC.【点睛】难点点睛:本题考查了四面体中的线面以及线线的位置关系,以及体积和空间几何体中的轨迹问题,难点在于要发挥空间想象,明确空间几何体中的线线位置关系,特别是选项D 中要明确E 点轨迹,从而确定轨迹长度或其范围.7.ACD 【分析】根据几何体的特征,化空间为平面,逐个推理,计算分析.【详解】因为BCDE 为正方形,连接BD 与CE ,相交于点O ,连接OA ,则OD ,OE ,OA 两两垂直,故以{},,OD OE OA为正交基地,建立如图所示的空间直角坐标系,D,(B -,(0,E,(0,C -,A,(0,0,F -,N 为AE的中点,则N .当M 为DE 的中点时,M,(MN =,(0,CF =- ,设异面直线MN 与CF 所成角为θ,0041cos cos ,242MN CFMN CF MN CFθ+-⋅====⨯,π(0,]2θ∈,故π3θ=,A 正确;设P 为DE 的中点,N 为AE 的中点,则PN ∥AD ,AD ⊂平面ACD ,PN ⊄平面ACD ,则PN ∥平面ACD , 又MN ∥平面ACD ,又MN PN N ⋂=,设Q BC ∈,故平面MNP ∥平面ACD ,平面ACD 平面BCDE CD =,平面MNP 平面BCDE PQ =,则PQ ∥CD ,则Q 为BC 的中点,点M 在四边形BCDE 内(包含边界)运动,则M PQ ∈,点M 的轨迹是过点O 与CD 平行的线段PQ ,长度为4,B 不正确;当MA ME ⊥时,设(,,0)M x y ,(,,MA x y =--,(,,0)ME x y =-- ,2(0MA ME x y y ⋅=+-=,得220x y +-=,即22(2x y +=,即点M 的轨迹以OE 中点K 的圆在四边BCDE 内(包含边界)的一段弧(如下图),K 到BC 的距离为3,弧上的点到BC 的距离最小值为3,因为3<M 到BC C 正确;由于图形的对称性,我们可以先分析正四棱锥A BCDE -内接最大圆柱的体积,设圆柱底面半径为r ,高为h ,P 为DE 的中点,Q 为BC 的中点, 4PQ =,AO =根据AGH 相似AOP ,得GH AG OP AO =,即2r =)h r =-,则圆柱体积22(2)V r h r r π==-,设23()(2)(02)V r r r r -<<,求导得2()(43)V r r r '=-,令()0V r '=得,43r =或0r =,因为02r <<,所以0r =舍去,即43r =,当403r <<时,()0V r '>,当423r <<时,()0V r '<,即43r =时V 有极大值也是最大值,V,503===>53>所以存在一个体积为103π的圆柱体可整体放入Ω内,D 正确.故选:ACD.【点睛】关键点点睛:异面直线所成的角;线面平行性质;空间点的轨迹,圆柱的体积计算,利用导数求体积的最值.8.BCD 【分析】建立空间直角坐标系,利用空间位置关系的向量证明判断A ;利用空间向量求出点到直线距离判断B ;利用抛物线定义判断C ;作出点P 的轨迹并求出长度判断D.【详解】在棱长为2的正方体1111ABCD A B C D -中,建立如图所示的空间直角坐标系,则1(0,2,0),(2,2,0),(0,2,2),(2,0,1),(1,0,2)C B C E F ,对于A ,(1,0,1),(0,2,1)EF EB =-=-,设(,,0),,[0,2]P x y x y ∈,1(,2,2)C P x y =-- ,设平面BEF 的法向量(,,)n a b c = ,则020n EF a c n EB b c ⎧⋅=-+=⎪⎨⋅=-=⎪⎩,令1b =,得(2,1,2)n =,由22212x y --==,解得2,1x y =-=,与[0,2]x ∈矛盾,即1C P 与n 不共线,因此1C P 不垂直于平面BEF ,A 错误;对于B ,(1,2,2)FB =- ,点(0,,0),[0,2]P y y ∈,(2,2,0)BP y =--,则点P 到直线BF的距离d ===≥65y =时取等号,则点P 到直线BF B 正确;对于C ,由1BB ⊥平面ABCD 知,点P 到直线1BB 的距离等于点P 到点B 的距离,因此点P 到点B 的距离等于点P 到直线AD 的距离,由抛物线的定义知点P 的轨迹为抛物线的一部分,C 正确;对于D ,取BC 的中点G ,连接11,,AG AD D G ,如图所示:由,E F 分别是棱111,AA A D 的中点,得1//EF AD ,1AD ⊄平面BEF ,EF ⊂平面BEF ,则1//AD 平面BEF ,由1//D F BG 且1D F BG =,得1D FBG 为平行四边形,则1//D G BF ,又1D G ⊄平面BEF ,BF ⊂平面BEF ,于是1//D G 平面BEF ,而111AD D G D ⋂=,11,AD D G ⊂平面1AGD ,因此平面//BEF 平面1AGD ,由1D P 与平面BEF 无公共点,1D ∈平面1AGD ,得1D P ⊂平面1AGD ,又点P 为底面ABCD 内(包括边界)的一动点,平面1AGD 平面ABCD AG =,则AG 是点P 在底面ABCD 内的轨迹,AG ===所以点P D 正确.故选:BCD 9.ABC 【分析】由线线垂直证明线面垂直判断选项A ;由球面与截面的交线轨迹,计算长度判断选项B ;由位置关系得截面形状,计算面积判断选项C ;由P 点位置特征分析轨迹形状判断选项D.【详解】正方体1111ABCD A B C D -中,BC ⊥平面11DCC D ,1DC ⊂平面11DCC D ,BC ⊥1DC ,正方形11DCC D 中,11⊥D C DC ,1,D C BC ⊂平面1BCD ,1D C BC C ⋂=,则1DC ⊥平面1BCD ,1D B ⊂平面1BCD ,1DC ⊥1D B ,同理,1DA ⊥1D B ,11,DA DC ⊂平面11AC D ,11DA DC D ⋂=, 1D B ⊥平面11ACD ,若点P 不与B 重合,因为1D P ⊥平面11AC D ,则11//D P D B ,与111D P D B D = 矛盾,故当1D P ⊥平面11AC D 时,点P 与B 重合,故A 正确;1DA DC DD ==,11AC AD CD ==,三棱锥1D ACD -为正三棱锥,故顶点D 在底面1ACD 的射影为1ACD △的中心H ,连接DH ,由11D ACD D ACD V V --=,得11112223232⨯⨯⨯⨯=⨯⨯,所以DH =,所以截面圆的半径r ==所以球面与截面1ACD 的交线是以H为半径的圆在1ACD △内部部分,如图所示,13HN =⨯=MF ==222HF HM MF +=,所以π2MHF ∠=,同理,其余两弦所对圆心角也等于π2,所以球面与截面1ACD的交线的长度为π2π32⨯=B 正确;对于C ,过E ,P 的直线分别交DA 、DC 的延长线于点G ,M ,连接1D M 、1D G ,分别交侧棱1C C 于点N ,交侧棱1A A 于点H ,连接EH 和NP ,如图所示:则截面为五边形1D HEPN ,1GA AE EB BP PC CM ======,GE EP PM ===GM=11D G D M ==23HA =,GH =1cos D GM ∠=112GMD G =1sin D GM ∠=,所以112D GM S ==△,12GEH S ==所以五边形1D HEPN 的面积122D GM GEH S S S =-==△△C 正确;因为11A B ⊥平面11BCC B ,1PB ⊂平面11BCC B ,所以111PB A B ⊥,点P 到直线11A B 的距离即点P 到点1B 的距离,因为平面11BCC B ⊥平面11CDD C ,故点P 到平面11CDD C 的距离为点P 到1CC 的距离,由题意知点P 到点1B 的距离等于点P 到1CC 的距离,故点P 的轨迹是以1B 为焦点,以1CC 为准线的抛物线在侧面11BCC B 内的部分,故D 错误.故选:ABC.【点睛】方法点睛:“截面、交线”问题是高考立体几何问题最具创新意识的题型,它渗透了一些动态的线、面等元素,给静态的立体几何题赋予了活力.求截面、交线问题,一是与解三角形、多边形面积、扇形弧长、面积等相结合求解,二是利用空间向量的坐标运算求解. 作几何体截面的方法:(1)利用平行直线找截面;(2)利用相交直线找截面.找交线的方法:(1)线面交点法:各棱线与截平面的交点;(2)面交点法:各棱面与截平面的交线.10.AC【分析】以A 为原点,建立空间直角坐标系,设(,0,)F m n ,由10FC FD ⋅= ,列出方程,可判定A 正确;由点C 关于平面11ABB A 的对称点为(4,4,0)G -,利用111FC FD FG FD GD +=+≥,可判定B 错误;由1FC FD =,求得23m n -=,得到点F 的轨迹为矩形11ABB A 内的线段,可判定C 正确;求得平面EFC 的一个法向量1(1,1,)4s n n m m =---- ,根据10AD s ⋅= ,列出方程,结合二次函数,可判定D 不正确.【详解】以A 为原点,分别以1,,AB AD AA 所在的直线分别为,,x y z 轴,建立空间直角坐标系,如图所示,则1(0,0,0),(4,4,0),(0,4,2),(0,0,1)A C D E ,设(,0,)F m n (其中[0,4],[0,2]m n ∈∈),对于A 中,若1FC FD ⊥,则10FC FD ⋅=,又由1(4,4,),(,4,2)FC m n FD m n =--=--,所以(4,4,)(,4,2)0m n m n --⋅--=,即22(2)(1)110m n -+-+=,此时方程无解,所以不存在点F ,使得1FC FD ⊥,所以A 正确;对于B 中,设点C 关于平面11ABB A 的对称点为G ,则G 的坐标为(4,4,0)-,可得111FC FD FG FD GD =++==≥当且仅当1,,F G D 三点共线时,取等号,所以B 错误;对于C 中,由1FC FD ==整理得23m n -=,即点F 的轨迹为矩形11ABB A 内的线段,因为[0,2]n ∈,当0n =时,13(,0,0)2F ;当2n =时,25(,0,2)2F ,即满足1FC FD =的点F的轨迹长度为12F F ==,所以C 正确;对于D 中,由1(0,4,2),(,0,1),(4,4,1)AD EF m n EC ==-=- ,设平面EFC 的一个法向量为(,,)s x y z = ,则()10440s EF mx n z s EC x y z ⎧⋅=+-=⎪⎨⋅=+-=⎪⎩ ,取1x n =-,可得11,4y n m z m =--=-,所以1(1,1,)4s n n m m =---- ,因为1//AD 平面EFC ,所以10AD s ⋅=,即3440m n +-=,又由点(0,0,0)A,所以AF ===当12[0,4]25m =∈时,可得AF 的最小值为45,所以D 不正确.故选:AC.。
立体几何中的动态问题

立体几何中的动态问题立体几何中的动态问题可以分为平移和旋转两类。
所求变量可以分为相关线、面、体的测度、角度和距离三类。
解决这类问题需要较高的空间想象能力和化归处理能力。
在高考选择题与填空题中,也时常会出现这类问题。
如果能够探寻运动过程中“静”的一面,动中求静,往往能以静制动、克难致胜。
解决立体几何中的动态问题,需要从复杂的图形中分化出最简单的具有实质性意义的点、线、面,让几何图形的实质“形销骨立”,即从混沌中找出秩序。
这是解决动态问题的关键。
例如,在解决某个问题时,可以从图形中分化出几个点,然后找到其中的关系,进而得出答案。
在这个过程中,需要注意极端位置,通过穷尽极端特殊的方法,往往能够直接得出答案。
另外,使用法向量定平面也是解决立体几何中动态问题的一种有效方法。
通过寻找垂直,可以找到两个平面的夹角,从而解决问题。
综上所述,解决立体几何中的动态问题需要一定的数学基础和空间想象能力。
通过分化图形、寻找极端位置和使用法向量定平面等方法,可以有效地解决这类问题。
在解决立体几何中的“动态”问题时,可以利用角度计算和法向量定平面来转化线面角或面面角为线线角。
例如,在长方体ABCD-A1B1C1D1中,已知二面角A1-BD-A的大小为π/6,一条直线l与直线CC1所成的角为π/12.如果空间有π/6,则直线l与平面A1BD所成角的取值范围是π/4.解析如下图所示:过点A作AE⊥BD于点E,连接A1E,则∠A1EA=π/6.过点A作AH⊥A1E于点H,则AH为平面A1BD的法向量,且∠A1AH=π/2.因为l与直线CC1所成角的大小为π/12,即l与直线A1A所成角的大小为π/6,那么l与直线AH所成角的取值范围为π/4 ~ π/3.又因为l与直线AH所成的角和l与平面A1BD所成的角互余,所以直线l与平面A1BD所成角的取值范围是π/4 ~ π/3.在解决立体几何中的“动态”问题时,可以通过锁定垂面来破解翻折或投影问题,将空间化为平面,从而更容易找到问题的核心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何图形中的动态问题★1.如图,在矩形ABCD中,点E在BC边上,动点P 以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从点A出发经x(x>0)秒后,△ABP的面积是y.(1)若AB=8cm,BE=6cm,当点P在线段AE上时,求y关于x的函数表达式;(2)已知点E是BC的中点,当点P在线段ED上时,y=125x;当点P在线段AD上时,y=32-4x.求y关于x的函数表达式.第1题图解:(1)∵四边形ABCD是矩形,∴∠ABE=90°,又∵AB=8cm,BE=6cm,∴AE=AB2+BE2=82+62=10厘米,如解图①,过点B作BH⊥AE于点H,第1题解图①∵S△ABE=12AE·BH=12AB·BE,∴BH=245cm,又∵AP=2x,∴y=12AP·BH=245x(0<x≤5);(2) ∵四边形ABCD是矩形,∴∠B=∠C=90°,AB=DC, AD=BC,∵E为BC中点,∴BE=EC,∴△ABE≌△DCE(SAS),∴AE =DE ,∵y =125x (P 在ED 上), y =32-4x (P 在AD 上), 当点P 运动至点D 时,可联立得,⎩⎪⎨⎪⎧y =125xy =32-4x ,解得x =5,∴AE +ED =2x =10, ∴AE =ED =5cm ,当点P 运动一周回到点A 时,y =0, ∴y =32-4x =0, 解得x =8, ∴AE +DE +AD =16,∴AD =BC =6cm ,∴BE =3cm , 在Rt △ABE 中, AB =AE 2-BE 2=4cm ,如解图②,过点B 作BN ⊥AE 于N ,则BN =125cm ,第1题解图②∴y =125x (0<x ≤2.5), ∴y =⎩⎪⎨⎪⎧125x (0<x ≤5)32-4x (5≤x ≤8).★2. 已知:如图①,菱形ABCD 的边长为4 cm,P 、Q 分别是AB 、BC 两边上的动点,P 、Q 分别从A 、B 两点同时出发,均以1 cm/s 的速度沿AB 、BC 向点B 和点C 匀速运动,当点P 到达点B 时停止运动,点Q 也随之停止运动,设运动时间为t (s),点P 到AD 的距离与点Q 到CD 的距离差的绝对值为y (cm),且y 与t 的函数图象如图②所示.(1)∠A 的度数为 ,M 点的坐标所表示的实际意义是 ; (2)求证:PD =QD ;(3)当y=32时,求t的值.第2题图(1)解:60°,点P到AD的距离与点Q到CD的距离相等;【解法提示】如解图①,过B作BE⊥CD于E,由题图②知,运动时间t=0时,点P到AD的距离为0,点Q到CD的距离是菱形的高为23,即BE=3,在Rt△BCE中,BC=4,BE=23∴sin C=BEBC =32,∴∠A=∠C=60°,由题图②知,点M在t轴上,∴点M的坐标所表示的意义是点P到AD的距离与点Q到CD的距离相等;第2题解图①(2)证明:如解图②,连接BD,由(1)知,∠C=60°,第2题解图②∵在菱形ABCD中,BC=CD,∴△BCD是等边三角形,∴DB=BC=AD,∠DBQ=∠A=60°,由运动的过程知,BQ=AP,在△BDQ和△ADP中,BD AD DBQ ABD BQ AP =∠=∠=⎧⎪⎨⎪⎩, ∴△BDQ ≌△ADP , ∴PD =QD ;(3)解:如解图③,过点P 作PE ⊥AD ,过点Q 作QF ⊥CD,第2题解图③由运动过程知,AP =BQ =t ,(0≤t ≤4) ∴CQ =4-t ,在Rt △APE 中,∠A =60°,AP =t , ∴PE =AP ·sin A =32t , 同理:FQ =32(4-t ), ∴y =33t )|3t -2|,∵y=32,∴3|t-2|=3,化简得2|t-2|=1,∴t=32s或t=52s.★3. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC =8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动.M,N分别是AD,CD的中点,连接MN.设点D运动的时间为t.(1)判断MN与AC的位置关系;(2)求在点D由点A向点B匀速运动的过程中,线段MN 所扫过区域的面积;(3)若△DMN是等腰三角形,求t的值.第3题图解:(1)MN∥AC.证明:在△ADC中,M是AD的中点,N是DC的中点,∴MN∥AC;(2)如解图①,分别取△ABC三边中点E,F,G并连接EG,FG,第3题解图①根据题意,可知线段MN扫过区域的面积就是▱AFGE 的面积.∵AC=6,BC=8,∴AE=3,GC=4,∵∠ACB=90°,∴S▱AFGE=AE·GC=12,∴线段MN扫过区域的面积为12;(3)依题意可知,MD=12AD,DN=12DC,MN=12AC=3.分三种情况讨论:(ⅰ)当MD =MN =3时,△DMN 为等腰三角形,此时AD =AC =6,∴t =6.(ⅱ)当MD =DN 时,AD =DC .如解图②,过点D 作DH ⊥AC 于点H ,则AH =12AC =3,第3题解图②∵cos A =AH AD =ACAB ,AB =10, 即3AD =610. ∴t =AD =5.(ⅲ)当DN =MN =3时,AC =DC , 如解图③,连接MC ,则CM ⊥AD .∵cos A =AM AC =AC AB ,即AM 6=610, ∴AM =185, ∴t =AD =2AM =365.综上所述,当t =5或6或365时,△DMN 为等腰三角形.第3题解图③★4. 如图,在正方形ABCD 中,点E ,G 分别是边AD ,BC 的中点,AF =14AB .(1)求证:EF ⊥AG ;(2)若点F ,G 分别在射线AB ,BC 上同时向右、向上运动,点G 运动速度是点F 运动速度的2倍,EF ⊥AG 是否成立(只写结果,不需说明理由)?(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当S△P AB=S△OAB时,求△P AB周长的最小值.第4题图(1)证明:∵四边形ABCD是正方形,∴AD=AB=BC,∠EAF=∠ABG=90°,∵点E,G分别是边AD,BC的中点,AF=14AB,∴AE AB =12,AFBG=12,∴AE AB =AF BG,又∵∠EAF=∠ABC=90°,∴△AEF∽△BAG,∴∠AEF=∠BAG,又∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠EOA=90°,即EF⊥AG;(2)解:EF⊥AG仍然成立;(3)解:如解图,过点O作MN∥AB分别交AD、BC于点M,N,连接P A,第4题解图∵P是正方形ABCD内一点,当S△P AB=S△OAB,∴点P在线段MN上(不含端点),作点A关于MN的对称点A′,连接BA′交MN于点P,此时P A+PB=P A′+PB=BA′最小,即△P AB的周长最小.∵正方形ABCD的边长为4,∴AE=12AD=2,AF=14AB=1,∴EF=AE2+AF2=5,OA=AE·AFEF =255,∵∠AMO=∠EOA,∠EAO=∠EAO,∴△EOA∽△OMA,∴AE OA =OA AM,∴OA2=AM·AE,∴AM=OA2AE =2 5,∴A′A=2AM=45,∴BA′=A′A2+AB2=4265,故△P AB周长的最小值为4+4265.★5. 如图,在矩形ABCD中,AB=3,BC=2,点M在线段BC上,连接AM,作∠AMN=∠AMB,点N在直线AD 上,MN交CD于点E.(1)求证:△AMN是等腰三角形;(2)求BM·AN的最大值;(3)当M为BC中点时,求ME的长.第5题图(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠NAM=∠AMB,又∵∠AMN=∠AMB,∴∠AMN=∠NAM,∴AN=MN,即△AMN是等腰三角形;(2)解:如解图,作NH⊥AM于点H,第5题解图∵AN =MN ,NH ⊥AM , ∴AH =12AM ,∵∠NHA =∠ABM =90°, ∠AMB =∠NAH , ∴△NAH ∽△AMB , ∴AN AM =AH BM ,∴AN ·BM =AH ·AM =12AM 2, 在Rt △AMB 中,AM 2=AB 2+BM 2=9+BM 2, ∵BM ≤2, ∴9+BM 2≤13,∴AN ·BM ≤132, 即当BM =2时, BM ·AN 的最大值为132; (3)解:∵M 是BC 中点, ∴BM =CM =12BC =1, 由(2)得,AN ·BM =12AM 2, ∵AM 2=32+12=10, ∴AN =5, ∴DN =5-2=3, 设DE =x ,则CE =3-x , ∵AN ∥BC ,∴DN CM =DE CE ,即31=x 3-x ,解得x =94,即DE =94,∴CE =34, ∴ME =CE 2+CM 2=54.★6. 如图①,点O 在线段AB 上,AO =2,OB =1,OC 为射线,且∠BOC =60°,动点P 以每秒2个单位长度的速度从点O 出发,沿射线OC 做匀速运动,设运动时间为t 秒.(1)当t =12秒时,则OP =________,S △ABP =________; (2)当△ABP 是直角三角形时,求t 的值;(3)如图②,当AP =AB 时,过点A 作AQ ∥BP ,并使得∠QOP =∠B ,求证:AQ ·BP =3.第6题图(1)解:1,334;【解法提示】因为动点P 以每秒2个单位长度的速度从点O 出发,故当t =12秒时,OP =12×2=1.如解图①,过点P 作△ABP 的高h ,由于∠BOC =60°,OP =1,故h =OP ·sin 60°=32,即S △ABP =12AB ·h =12(OA +OB )·h =12×(2+1)×32=334.第6题解图①(2)解:①∵∠BAP <∠BOP =60°, ∴∠A 不可能为直角; ②如解图②,当∠B =90°时,第6题解图②∵∠BOC=60°,∴∠OPB=30°,∴OP=2OB=2,即2t=2,∴t=1;③当∠APB=90°时,如解图③,作PD⊥AB,垂足为D,则∠ADP=∠PDB=90°.第6题解图③∵OP=2t,∴OD=t,PD=3t,AD=2+t,BD=1-t,∴BP 2=BD 2+PD 2=(1-t )2+3t 2,AP 2=AD 2+PD 2=(2+t )2+3t 2,∵BP 2+AP 2=AB 2,∴(1-t )2+3t 2+(2+t )2+3t 2=9, 即4t 2+t -2=0,解得t 1=-1+338,t 2=-1-338(舍去). 综上所述,当△ABP 是直角三角形时,t 的值为1或-1+338; (3)证明:∵AP =AB ,∴∠APB =∠B .如解图④,作OE ∥AP 交BP 于点E ,第6题解图④∴∠OEB=∠APB=∠B,∵AQ∥BP,∴∠QAB+∠B=180°,又∵∠3+∠OEB=180°,∴∠3=∠QAB,又∵∠AOC=∠2+∠B=∠1+∠QOP,已知∠B=∠QOP,∴∠1=∠2,∴△QAO∽△OEP,∴AQ EO =AOEP,即AQ·EP=EO·AO,∵OE∥AP,∴△OBE∽△ABP,∴OE AP =BEBP=BOBA=13,∴OE=13AP=1,BP=32EP,∴AQ·BP=AQ·32EP=32AO·OE=32×2×1=3.★7.如图①,在矩形ABCD中,AB=16,BC=8,在AD 边上取一点E,使AE=3,点F是AB边上的一个动点,以EF为一边作菱形EFMN,使点N落在CD上,点M落在矩形ABCD内或其边上,连接BM.(1)当四边形EFMN是正方形时,求AF的长;(2)设△BFM的面积为S,AF=x.①写出S与x之间的函数关系式;②当S由最大值变到最小值时,求点M运动的路线长.第7题图解:(1)在正方形EFMN中,∠FEN=90°,EF=EN;∴∠DEN+∠AEF=90°,在矩形ABCD中,∠A=∠D=90°,∴∠AEF+∠AFE=90°,∴∠DEN=∠AFE,在△DEN与△AFE中,∠D=∠A,∠DEN=∠AFE,EN=EF,∴△DEN≌△AFE(AAS).∴AF=DE=8-3=5,∴AF的长为5;(2)①如解图①,过点M作MH⊥AB于点H,连接NF.第7题解图①在矩形ABCD中,∵AB∥CD,∴∠DNF=∠NFB.∵四边形EFMN是菱形,∴NE∥MF,NE=MF,∴∠ENF=∠MFN,∴∠DNF-∠ENF=∠NFB-∠MFN,即∠DNE=∠MFB,在△DEN与△HMF中,∠D=∠MHF=90°,∠DNE=∠MFB,EN=MF,∴△DEN≌△HMF(AAS),∴MH=DE=5,又∵BF=16-x,∴S=12BF·MH=12(16-x)×5=-52x+40;②当点D与N重合时,S最大(如解图②),第7题解图②此时DE=EF=5,由勾股定理得AF=4,当点M落在BC上时,S最小(如解图③),第7题解图③由①得MB=DE=5,∵点M到AB的距离是定值5,∴点M运动的路径是一条线段M1M2(如解图④),第7题解图④∴M1M2=F1B=16-4=12.∴点M运动的路线长为12.★8.如图①,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A-C-B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ 的面积为y(cm2),y关于x函数图象由C1,C2两段组成,如图②所示.(1)求a的值;(2)求图②中图象C2段的函数表达式;(3)当点P运动到线段BC上某一段时,△APQ的面积大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.第8题图解:(1)如解图①,过点P作PD⊥AB于点D.第8题解图①∵∠A=30°,P A=2x,∴PD=P A·sin30°=2x·12=x,∴y=12AQ·PD=12ax·x=12ax2.由图象得,当x=1时,y=12,则12a·12=12,∴a=1;(2)如解图②,当点P在BC上时,PB=5×2-2x=10-2x.第8题解图②∴PD=PB·sin B=(10-2x)·sin B,∴y=12AQ·PD=12x·(10-2x)·sin B.由图象得,当x=4时,y=43,∴12×4×(10-8)·sin B =43,∴sin B =13, ∴y =12x ·(10-2x )·13=-13x 2+53x ; (3)令12x 2=-13x 2+53x , 解得x 1=0(舍去),x 2=2.由图象得,当x =2时,函数y =12x 2的最大值为y =12×22=2.将y =2代入函数y =-13x 2+53x ,得2=-13x 2+53x , 解得x 1=2,x 2=3.∴由图象得,x 的取值范围是2<x <3.★9.如图①,在长方形ABCD 中,AB =8,AD =6,动点P 、Q 分别从点D 、A 同时出发向点C 、B 运动,点P 的运动速度为每秒2个单位长度,点Q 的运动速度为每秒1个单位长度,当点P 运动到点C 时,两个点都停止运动.设运动的时间为t (s).(1)当t=2时,PQ的长为;(2)在运动过程中,若△BPQ为等腰三角形,求相应时刻的t值;(3)如图②,连接BD,是否存在某个时刻,使得PQ垂直平分BD?若能,求t的值;若不能,说明理由.第9题图解:(1)如解图①,作PH⊥AB于H,第9题解图①由题意得:DP=4,AQ=2,∴QH=2,又∵PH =AD =6, 由勾股定理得: PQ =PH 2+QH 2=210; (2)当PQ =PB 时, QH =BH , ∴2t -t =8-2t ,整理得t +2t =8,解得t =38;当PQ =BQ 时,QH 2+PH 2=PQ 2=BQ 2,即(2t -t )2+62=(8-t )2,解得t =74;当BP =BQ 时,BH 2+PH 2=BP 2=BQ 2,即(8-2t )2+62=(8-t )2,方程无解; 综上所述,当t =38或47时,△BPQ 为等腰三角形; (3)不存在.如解图②,第9题解图②假设PQ垂直平分BD,则QB=QD,PD=PB,7,在Rt△ADQ中,t2+36=(8-t)2,解得:t=425, 在Rt△CPB中,(8-2t)2+36=(2t)2,解得t=8∴不存在某个时刻t,使得PQ垂直平分BD.★10. 如图①,矩形ABCD中,AB=7 cm,AD=4 cm,点E 为AD上一定点,点F为AD延长线上一点,且DF=a cm.点P从A点出发,沿AB边向点B以2 cm/s的速度运动.连接PE,设点P运动的时间为t s,△P AE的面积为y cm2.当0≤t ≤1时,△P AE的面积y(cm2)关于时间t(s)的函数图象如图②所示.连接PF,交CD于点H.(1)t的取值范围为s,AE=cm;(2)如图③,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连接AM,当a为何值时,四边形P AMH为菱形?并求出此时点P的运动时间t;(3)如图④,当点P出发1 s后,AD边上另一动点Q从E 点出发,沿ED边向点D以1 cm/s的速度运动.如果P,Q两点中的任意一点到达终点后,另一点也停止运动,连接PQ,cm,请问△PQH能否构成直角三角形?若能,QH.若a=43请求出点P的运动时间t;若不能,请说明理由.第10题图解:(1)0≤t≤3.5,1;【解法提示】当P运动到点B时,t=3.5 s,∴t 的取值范围为0≤t ≤3.5;由题意知,y =21AP ·AE =21×2t ·AE =AE ·t , 将(0.5,0.5)代入y =AE ·t ,得AE =1.(2)若四边形P AMH 为菱形,则P A ∥HM ,且P A =HM ,AM =P A ,∵∠HDF =∠P AF =90°,∠HFD =∠PF A , ∴△P AF ∽△HDF , ∴12FD HD AF PA ==, ∵DF =a , ∴AF =4+a , ∴412a a +=, ∴a =4.在Rt △ADM 中,AM =P A =2t ,∵△MDF 是由△HDF 沿线段DF 翻折而得, ∴DM =HD =12P A =t , ∵AM 2=DM 2+AD 2,即4t 2=t 2+42,解得t =433或t=-433(舍去),∴当a =4时,四边形P AMH 为菱形,此时点P 的运动时间为43s. (3)△PQH 等构成直角三角形,理由如下:若a =34时,由题意得,AQ =1+1×(t -1)=t ,QD =4-t ,∵413=444+3HD DF PA AF ==, ∴HD =41×2t =2t,过P 作PG 垂直于CD ,垂足为G ,如解图①,第10题解图①则GH =2t -2t=23t , PQ 2=P A 2+AQ 2=5t 2,QH2=QD2+HD2=(4-t)2+14t2,PH2=PG2+HG2=16+94t2,若△PQH为直角三角形,①当Q为直角顶点时,根据勾股定理可得PQ2+QH2=PH2,即5t2+(4-t)2+14t2=16+94t2,解得t=2或t=0(舍去);②当H为直角顶点时,根据勾股定理可得PH2+HQ2=PQ2,8或t=-8(舍去);即16+94t2+(4-t)2+14t2=5t2,解得t=3③当P为直角顶点时,根据勾股定理可得PQ2+PH2=QH2,4(舍去)或t=0(舍去). 即5t2+16+94t2=(4-t)2+14t2,解得t=-38时,△PQH为直角三角形;∴当t=2或t=3。
