线面角习题课
线面角含详细答案

方法二:画出图形,如图,BB1与平 面ACD1所成的角等于DD1与平面ACD1 所成的角,在三棱锥D-ACD1中,由三 条侧棱两两垂直且相等得点D在底面 ACD1内的射影为等边三角形ACD1的 重心,即中心H,连接D1H,DH,则∠DD1H为DD1与平面ACD1所成
1.∵SA=SC,点D为斜边AC的中点,
∴SD⊥AC. 连接BD,在Rt△ABC中,则AD=DC=BD, ∴△ADS≌△BDS, ∴SD⊥BD.又AC∩BD=D,
∴SD⊥平面ABC.
答案:垂直.
求直线与平面所成的角
【技法点拨】求直线与平面所成的角的方法
作(或找)出斜线在平面内的射影,将空间角转变成 平面角,作射影时要过斜线上一点作平面的垂线,再 过垂足和斜足作直线,注意斜线上点的选取以及垂足 的位置与问题中的已知量有关,才能便于计算 证明某平面角就是斜线与平面所成的角 通常在垂线段、斜线和射影所组成的直角三角形中 计算
4.已知正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的中点,
则直线AD与平面B1DC所成的角的正弦值为______.
【解析】作AH⊥CD于H,又B1D⊥平面AA1C1C,所以B1D⊥AH,
从而AH⊥平面B1DC,∠ADH为所求线面角.设正三棱柱的棱长 为1,则AD= 答案: 4
5
5 ,AH= 2
作图
定性
计算
【典例训练】
1.正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成的角的余弦值
为(
(A)
)
2 3 2 6 B C D 3 3 3 3
2.如图所示,三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB 与平面ABC所成的角等于______.
等弹性模量法求线面角测试题(含答案)

等弹性模量法求线面角测试题(含答案)第一题已知钢铁的杨氏模量为 200 GPa,计算以下情况下的线面角:1.1. 应变为 0.002,求应力为多少?1.2. 面内力和面外力分别为 500 N 和 300 N,求线面角大小?答案1.1. 根据杨氏模量的定义,可以使用以下公式计算应力:应力 = 杂氏模量 * 应变将已知数据代入计算,得到:应力 = 200 GPa * 0.002 = 400 MPa所以应力为 400 MPa.1.2. 根据等弹性模量法的定义,可以使用以下公式计算线面角:线面角 = arcsin(面外力 / 面内力)将已知的面内力和面外力代入计算,得到:线面角= arcsin(300 N / 500 N) ≈ 0.6435 rad所以线面角大小约为 0.6435 弧度。
第二题已知铝合金的杨氏模量为 70 GPa,计算以下情况下的线面角:2.1. 应变为 0.003,求应力为多少?2.2. 面内力和面外力分别为 800 N 和 400 N,求线面角大小?答案2.1. 根据杨氏模量的定义,可以使用以下公式计算应力:应力 = 杂氏模量 * 应变将已知数据代入计算,得到:应力 = 70 GPa * 0.003 = 210 MPa所以应力为 210 MPa.2.2. 根据等弹性模量法的定义,可以使用以下公式计算线面角:线面角 = arcsin(面外力 / 面内力)将已知的面内力和面外力代入计算,得到:线面角= arcsin(400 N / 800 N) ≈ 0.5236 rad所以线面角大小约为 0.5236 弧度。
以上是关于等弹性模量法求线面角的测试题目及答案。
希望对您有所帮助!。
第8章立体几何专题7 线面角的求解常考题型专题练习——【含答案】

线面角的求解【方法总结】1、线面角的范围:[0°,90°]2、线面角求法(一):先确定斜线与平面,找到线面的交点A为斜足;找线在面外的一点B,过点B向平面α做垂线,确定垂足O;连结斜足与垂足为斜线AB在面α上的投影;投影AO与斜线AB之间的夹角为线面角;把投影AO与斜线AB归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
注意:以上第二步过面外一点向平面做垂线的方法有一下几种:1)线在面外的一点B与平面上某点的连线正垂直于面α,无需再做辅助线;2)题中已知有与面α垂直的直线,过线在面外的一点B直接做此垂线的平行线;3)过线在面外的一点B做两垂直平面交线的垂线,利用面面垂直的性质证明OB⊥面α(这两个垂直平面一个是面α,另一个是过点B且与α垂直的平面)。
3、线面角求法(二)用等体积法,求出斜线PA在面外的一点P到面的距离,利用三角形的正弦公式进行求解。
114、线面角求法(三)利用空间向量进行求解,高二再学。
【巩固练习】1、已知正方体1111ABCD A B C D -的体积为162,点P 在正方形1111D C B A 上,且1,A C 到P 的距离分别为2,23,则直线CP 与平面11BDD B 所成角的正切值为( )A.2 B.3 C.12D.13【答案】A【解析】易知22AB =;连接1C P ,在直角1CC P ∆中,可计算22112C P CP CC =-=;又1112,4A P A C ==,所以点P 是11A C 的中点;连接AC 与BD 交于点O ,易证AC ⊥平面11BDD B ,直线CP 在平面11BDD B 内的射影是OP ,所以CPO ∠就是直线CP 与平面11BDD B 所成的角,在直角CPO ∆中,2tan 2CO CPO PO ∠== .2、把正方形沿对角线折起,当以四点为顶点的三棱锥体积最大时,直线和平面所成的角的大小为A.B.C.D.[来源网ZXXK]【答案】C【解析】如图所示,当平面平面时,三棱锥的体积最大,取的中点,则平面,故直线和平面所成的角为,则,所以,故选C.3、如图,在三棱锥P-ABC中,,PA AB⊥PC BC⊥,,AB BC⊥22,AB BC==5PC=,则PA与平面ABC所成角的大小为_______.【答案】45︒【解析】如图,作平行四边形ABCD,连接PD,由AB BC⊥,则平行四边形ABCD是矩形.由BC CD⊥,BC PC⊥,PC CD C=,∴BC⊥平面PCD,而PD⊂平面PCD,∴BC PD⊥,同理可得AB PD⊥,又AB BC B⋂=,∴PD⊥平面11ABCD .,PD CD PD AD ⊥⊥,PAD ∠是PA 与平面ABC 所成角.由2,5CD AB PC ===得1PD =,又1AD BC ==,∴45PAD ∠=︒.∴PA 与平面ABC 所成角是45︒.4、已知三棱柱ABC -A 1B 1C 1的侧棱与底面边长都相等,A 1在底面ABC 内的射影为△ABC 的中心O ,则AB 1与底面ABC 所成角的正弦值为( )A .23B .13C .33D .23【答案】A【解析】作1A H ⊥面ABC 于点H ,延长11B A 到D ,延长BA 到E 使得111B A A D =,,BA AE =如图则有11A EAB ,又因为1A O ⊥面ABC ,故1A EO ∠为所求角,且111sin AO A EO A E∠=。
高中数学线面角与线线角例题、习题-学生

线面角与线线角专练(小练习一)【知识网络】1、异面直线所成的角:(1)范围:(0,]2πθ∈;(2)求法;2、直线和平面所成的角:(1)定义:(2)范围:[0,90];(3)求法;【典型例题】例1:(1)在正方体1111ABCD A BC D -中,下列几种说法正确的是 ( )A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1BC 成60角(2)在正方体AC 1中,过它的任意两条棱作平面,则能作得与A 1B 成300角的平面的个数为 ( )A 、2个B 、4个C 、6个D 、8个(3)正六棱柱ABCDEF -A 1B 1C 1D 1E 1F 1底面边长是1,2则这个棱柱的侧 面对角线E 1D 与BC 1所成的角是 ( )A .90ºB .60ºC .45ºD .30º(4)在空间四边形ABCD 中,AB ⊥CD ,BC ⊥DA ,那么对角线AC 与BD 的位置关系是 。
(5)点AB 到平面α距离距离分别为12,20,若斜线AB 与α成030的角,则AB 的长等于__ ___.例2:.如图:已知直三棱柱ABC —A 1B 1C 1,AB =AC ,F 为棱BB 1上一点,BF ∶FB 1=2∶1,BF =BC =2a 。
(I )若D 为BC 的中点,E 为AD 上不同于A 、D 的任意一点,证明EF ⊥FC 1;(II )试问:若AB =2a ,在线段AD 上的E点能否使EF 与平面BB 1C 1C 成60°角,为什么?证明你的结论。
例3: 如图, 四棱锥P-ABCD 的底面是AB=2, BC =2的矩形, 侧面PAB 是等边三角形, 且侧面PAB ⊥底面ABCD.(Ⅰ)证明:BC ⊥侧面PAB;(Ⅱ)证明: 侧面PAD ⊥侧面PAB;(Ⅲ)求侧棱PC 与底面ABCD 所成角的大小; A B C DPA B C H S M 线面角与线线角专练(小练习二)例4:设△ABC 内接于⊙O ,其中AB 为⊙O 的直径,PA ⊥平面ABC 。
线面角练习题

线面角练习题在数学中,线面角是一种常见的概念,用于描述线与面之间的相对关系。
本文将为你提供一系列线面角练习题,帮助你加深对线面角概念的理解并提高解题能力。
练习题一:线与平面的关系1. 建立直角坐标系,并画出平面P:4x - 2y + z = 6。
a) 在该平面上选择一点A(x1, y1, z1),其中x1, y1, z1为任意实数。
画出该平面与点A的关系示意图。
b) 选择另一点B(x2, y2, z2),其中x2, y2, z2为任意实数。
画出该平面、点A和点B之间的关系示意图。
练习题二:线与平面上的点的关系2. 平面P:2x + 3y - 4z = 12与直线L:x = 2 + t, y = 3 - t, z = -1 + 2t相交于点A。
求出点A的坐标。
练习题三:线面角的计算3. 已知平面P:2x - y + 3z = 1和直线L:x = 3 - t, y = 2 + 2t, z = -1 + t。
求出直线L与平面P的线面角。
练习题四:垂直线面角的判断4. 平面P1:2x - y + 2z = 5与平面P2:4x - 2y + 4z = 9之间的夹角为α。
判断平面P1与平面P2是否垂直。
练习题五:平行线面角的计算5. 平面P:3x - 2y + 4z = 7和直线L:x = 1 + 2t, y = -2 + 3t, z = 3 - t 之间的夹角为β。
判断直线L与平面P是否平行。
练习题六:点到平面的距离计算6. 平面P:2x - y + z = 5上有一点A(1, -3, 2)。
求出点A到平面P的距离。
练习题七:平行平面之间的距离计算7. 已知平面P1:2x - 3y + z = 4和平面P2:4x - 6y + 2z = 8平行。
求出平面P1与平面P2之间的距离。
练习题八:垂直线面之间的距离计算8. 平面P:2x - y + 3z = 5与直线L:x = 1 + t, y = 2 - t, z = 3t之间的距离为d。
线线角、线面角、二面角知识点及练习
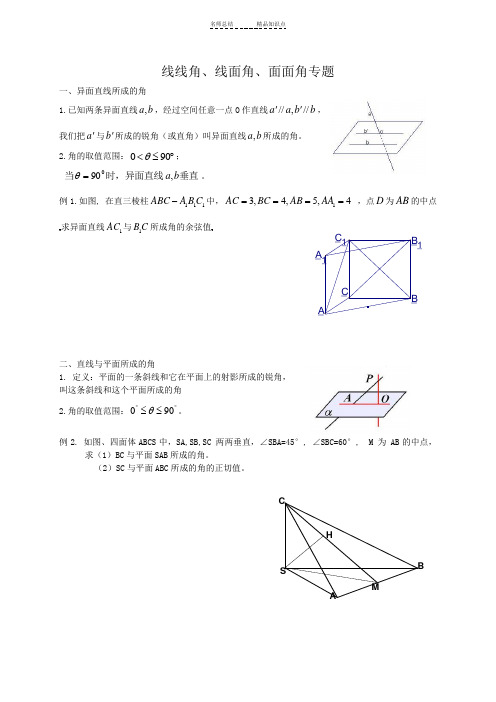
线线角、线面角、面面角专题一、异面直线所成的角1.已知两条异面直线,a b ,经过空间任意一点O 作直线//,//a a b b '',我们把a '与b '所成的锐角(或直角)叫异面直线,a b 所成的角。
2.角的取值范围:090θ<≤︒;垂直时,异面直线当b a ,900=θ。
例1.如图, 在直三棱柱111ABC A B C -中,13,4,5,4AC BC AB AA ==== ,点D 为AB 的中点求异面直线1AC 与1B C 所成角的余弦值二、直线与平面所成的角1. 定义:平面的一条斜线和它在平面上的射影所成的锐角, 叫这条斜线和这个平面所成的角2.角的取值范围:︒︒≤≤900θ。
例2. 如图、四面体ABCS 中,SA,SB,SC 两两垂直,∠SBA=45°, ∠SBC=60°, M 为 AB 的中点,求(1)BC 与平面SAB 所成的角。
(2)SC 与平面ABC 所成的角的正切值。
BMH S CA_1_A一、 二面角:1. 从一条直线出发的两个半平面所组成的图形叫做二面角。
这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
2. 二面角的取值范围:︒︒≤≤1800θ 两个平面垂直:直二面角。
3.作二面角的平面角的常用方法有六种:1.定义法 :在棱上取一点O ,然后在两个平面内分别作过棱上O 点的垂线。
2.三垂线定理法:先找到一个平面的垂线,再过垂足作棱的垂线,连结两个垂足即得二面角的平面角。
3.向量法:分别作出两个半平面的法向量,由向量夹角公式求得。
二面角就是该夹角或其补角。
二面角一般都是在两个平面的相交线上,取恰当的点,经常是端点和中点。
例3.如图,E 为正方体ABCD -A 1B 1C 1D 1的棱CC 1的中点,求 (1)二面角111D C A D --所成的角的余弦值 (2)平面AB 1E 和底面C C BB 11所成锐角的正切值.A 1D 1B 1C 1 EDBCA巩固练习1.若直线a 不平行于平面α,则下列结论成立的是( )A.α内所有的直线都与a 异面;B.α内不存在与a 平行的直线;C.α内所有的直线都与a 相交;D.直线a 与平面α有公共点.2.空间四边形ABCD 中,若AB AD AC CB CD BD =====,则AD 与BC 所成角为( )A.030B.045C.060D.090 3.正方体ABCD-A 1B 1C 1D 1中,与对角线AC 1异面的棱有( )条A.3B.4C.6D.84.如图长方体中,AB=AD=23,CC 1=2,则二面角C 1—BD —C 的大小为( )A.300B.450C.600D.9005.如图,在四面体ABCD 中,CB =CD ,AD ⊥BD ,点E 、F 分别是AB 、BD 的中点.求证:(1)直线EF ∥面ACD .(2)平面EFC ⊥平面BCD .6.如图,DC ⊥平面ABC ,EB ∥DC ,AC =BC =EB =2DC =2,∠ACB =120°,P ,Q 分别为AE ,AB 的中点.(1)证明:PQ ∥平面ACD ;(2)求AD 与平面ABE 所成角的正弦值.ABC D A 1B 1C 1D 17.如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,设SA=4,AB=2,求点A到平面SBD的距离;。
线线角-线面角-二面角的一些题目

B 1D 1A DC 1BCA 1線線角與線面角習題一、復習目標1.理解異面直線所成角の概念,並掌握求異面直線所成角の常用方法.2.理解直線與平面所成角の概念,並掌握求線面角常用方法.3.掌握求角の計算題步驟是“一作、二證、三計算”,思想方法是將空間圖形轉化為平面圖形即“降維”の思想方法. 二、課前預習1.在空間四邊形ABCD 中,AD=BC=2, E 、F 分別為AB 、CD の中點且EF=3,AD 、BC 所成の角為 .2.如圖,在長方體ABCD-A 1B 1C 1D 1中 ,B 1C 和C 1D 與底面所成の角分別為60ο和45ο,則異面直線B 1C 和C 1D 所成角の余弦值為 ( )(A).46 (B).36 (C).62 (D).633.平面α與直線a 所成の角為3π,則直線a 與平面α內所有直線所成の角の取值範圍是 .4.如圖,ABCD 是正方形,PD ⊥平面ABCD,PD=AD,則PA 與BD 所成の角の度數為(A).30ο(B).45ο(C).60ο(D).90ο5.有一個三角尺ABC,∠A=30ο, ∠C=90ο,BC 是貼於桌面上,當三角尺與桌面成45ο角時,AB 邊與桌面所成角の正弦值 是 . 三、典型例題例1.(96·全國) 如圖,正方形ABCD 所在平面與正方形ABEF 所在平面成60ο角,求異面直線AD 與BF 所成角の余弦值. 備課說明:1.求異面直線所成の角常作出所成角の平面圖形.作法有: ①平移法:在異面直線の一條上選擇“特殊點”,作另一條直線平行線 或利用中位線.②補形法:把空間圖形補成熟悉の幾何體,其目の在於容 易發現兩條異面直線の關係.2.解立幾計算題要先作出所求の角,並要 有嚴格の推理論證過程,還要有合理の步驟.例2.如圖在正方體AC 1中, (1) 求BC 1與平面ACC 1A 1所成の角; (2) 求A 1B 1與平面A 1C 1B 所成の角.備課說明:求直線與平面所成角の關鍵是找直線在此平面上の射影,為此必須在這條直線上找一點作平面の垂線. 作垂線の方法常採用:①利用平面垂直の性質找平面の垂線.②點の射影在面內の特殊位置.A CB AD C 1D 1A 1B 1CB D A BPC D A C BF E例3. 已知直三棱住ABC-A 1B 1C 1,AB=AC, F 為棱BB 1上一點,BF ∶FB 1=2∶1, BF=BC=a 2. (1)若D 為BC の中點,E 為線段AD 上不同於A 、D の任意一點,證明:EF ⊥FC 1; (2)試問:若AB=a 2,線上段AD 上のE 點能否使EF 與平面BB 1C 1C 成60ο角,為什麼?證明你の結論. 備課說明:這是一道探索性命題,也是近年高考熱點問題,解決這類問題,常假設命題成立,再研究是否與已知條件矛盾,從而判斷命題是否成立.四、回饋練習1設集合A 、B 、C 分別表示異面直線所成の角、平面の斜線與平面所成の角、直線與平面所成の角の取值範圍,則 (A)A=B=C (B)A=B ⊂C (C)A ⊂B ⊂C (D) B ⊂A ⊂C.2兩條直線a ,b 與平面α所成の角相等,則直線a ,b の位置關係是 (A)平行 (B)相交 (C)異面 (D) 以上均有可能.3設棱長為1の正方體ABCD-A 1B 1C 1D 1中,M 、N 分別為AA 1和BB 1の中點,則直線CM 和D 1N 所成角の正弦值為 . 4已知a 、b 是一對異面直線,且a 、b 成60o 角,則在過空間任意點P の所有直線中,與a 、b 均成60o角の直線有 條.5異面直線a 、b 互相垂直,c 與a 成30o 角,則c 與b 所成角の範圍是 .6∠ACB=90ο在平面α內,PC 與CA 、CB 所成の角∠PCA=∠PCB=60o ,則PC 與平面α所成の角為 .7設線段AB=a ,AB 在平面α內,CA ⊥α,BD 與α成30ο角,BD ⊥AB,C 、D 在α同側,CA=BD=b .求: (1)CD の長;(2)CD 與平面α所成角正弦值.A 1CB A B 1DC 1E F課前預習 1. 60ο2.A3. [3π,2π] 4.C 5.46 典型例題例1解:∵CB ∥AD∴∠CBF 為異面直線AD 與BF 所成の角.連接CF 、CE 設正方形ABCD の邊長為α,則BF=a 2∵CB ⊥AB, EB ⊥AB ∴∠CEB 為平面ABCD 與平面ABEF 所成の角 ∴∠CBE=∠60ο∴CE=a FC=a 2 ∴cos ∠CBF=42例2解:(1)設所求の角為α,先證BD ⊥平面ACC 1A 1,則sin α=sin ∠OC 1B=1BC OB =21.故α=30o .(2)△A 1BC 1是正三角形,且A 1B 1=B 1C 1=BB 1. ∴棱錐B 1-A 1BC 1是正三棱錐.過B 1作B 1H ⊥平面A 1BC 1,連A 1H, ∠B 1A 1H 是直線A 1B 1與平面A 1C 1B 所成の角.設A 1B 1=a 則A 1B =a 2得A 1H =a 36.故cos ∠B 1A 1H=111B A H A =36.所求角為36arccos例3解:(1)連接OF ,容易證明AD ⊥面BB 1C 1C, DF 是EF 在面B 1C 1CB の射影,且DF ⊥FC 1, ∴FC 1⊥EF.(2) ∵AD ⊥面BB 1C 1C , ∠EFD 是EF 與平面BB 1C 1C 所成の角.在△EDF 中,若∠EFD=60ο,則ED =DF ·tan 60ο=3·5=a 15,∵AB=BC=AC=2a ,∴AD=a 3.∵a 15>a 3.∴E 在DA の延長線上,而不線上段AD 上;故線段AD 上のE 點不可能使EF 與平面BB 1C 1C 成60ο角.回饋練習1. D2. D3.954 4. 3 5.[ 60ο,90ο] 6. 45ο7.解:(1)作DD '⊥α於D ',連接AD ',BD '.CA ⊥α,∴CA ∥DD '.四邊形CAD 'D 是直角梯形,∠CAD '=∠D D 'A =90ο,AB α⊂,AB ⊥DD '.又AB ⊥BD,∴AB ⊥平面BDD ',BD '⊂平面BDD '.∴AB ⊥BD '.∵∠DBD '是BD 與α所成の角,∴∠DBD '=30ο,BD =b ,DD '=2b ,BD '=23b .在△ABD '中,AB=a ,BD '=23b ,∠ABD '=90ο,∴AD '=22'BD AB +=4322b a +.在CAD 'D 中,CD=222'2')(b a D D AC AD +=-+.(2)作D 'C '∥DC 交CA 於C ',∠C 'D 'A 是CD 與α所成の角,sin ∠C 'D 'A=22'2''ba bD C AC +=.線面角與面面角練習一、知識與方法要點:1.斜線與平面所成の角就是斜線與它在平面內の射影の夾角。
线面角练习题

线面角练习题线面角练习题在我们的日常生活中,几何形状无处不在。
从建筑物到家具,从自然景观到艺术作品,几何形状都扮演着重要的角色。
而在学习几何学的过程中,线面角是我们必须掌握的基础知识。
今天,我们将通过一些线面角练习题来加深我们对这一概念的理解。
1. 问题一:在一个正方形的角落上,有一只蜘蛛。
它从一个角落出发,每次只能沿着正方形的边缘前进。
蜘蛛最少需要走多少步才能回到起点?解答:蜘蛛只需要走三步就能回到起点。
它可以从一个角落出发,沿着边缘走到下一个角落,再沿着边缘走到下一个角落,最后再沿着边缘走回起点。
2. 问题二:一个圆形的饼干被切成了六个等分的扇形。
如果我们将其中一个扇形的顶点连接到圆心,这个角度是多少度?解答:由于圆形的总角度是360度,而饼干被切成了六个等分的扇形,所以每个扇形的角度是360度除以6,即60度。
因此,连接到圆心的角度也是60度。
3. 问题三:在一个矩形的对角线上,有一只小虫。
它从一个角出发,沿着对角线前进,最后到达另一个角。
如果矩形的长度是8厘米,宽度是6厘米,小虫需要走多少厘米才能到达目的地?解答:根据勾股定理,矩形的对角线的长度可以通过勾股定理计算得出。
对角线的长度等于矩形的长度的平方加上宽度的平方的平方根。
所以,对角线的长度等于√(8^2 + 6^2) = √(64 + 36) = √100 = 10厘米。
因此,小虫需要走10厘米才能到达目的地。
4. 问题四:在一个正三角形的内部,有一只小鸟。
它从一个角出发,沿着三角形的边前进,最后回到起点。
小鸟最少需要走多少条边才能回到起点?解答:正三角形有三条边,所以小鸟最少需要走三条边才能回到起点。
它可以从一个角出发,沿着边前进到下一个角,再沿着边前进到下一个角,最后再沿着边回到起点。
通过以上几个线面角练习题,我们可以看到几何形状和角度之间的关系。
无论是正方形、圆形、矩形还是三角形,它们都有自己独特的特点和角度。
通过解决这些练习题,我们可以更好地理解这些形状,并且培养我们的几何思维能力。
线面角专题 教师版
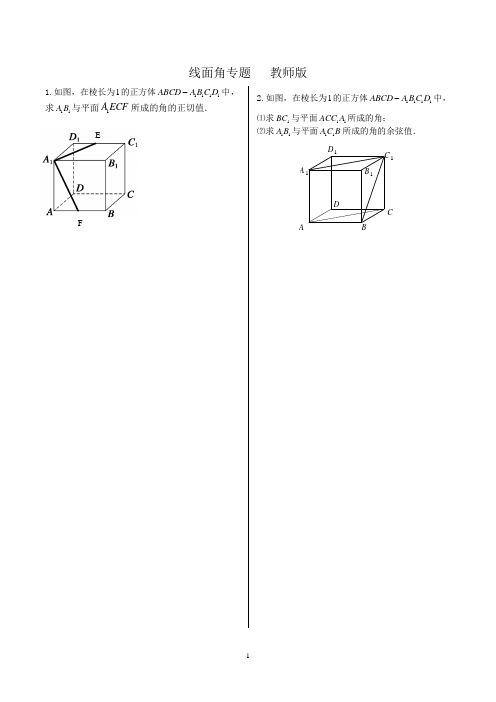
线面角专题 教师版1.如图,在棱长为1的正方体1111ABCD A B C D -中,求11A B 与平面ECF A 1所成的角的正切值.2.如图,在棱长为1的正方体1111ABCD A B C D -中, ⑴求1BC 与平面11ACC A 所成的角; ⑵求11A B 与平面11A C B 所成的角的余弦值.ABCDB 1C 1D 1A 1FE3.已知三棱锥ABC P -中,ABC PA 底面⊥,60=∠BAC ,12===ACAB PA ,D ,E 分别是PB ,BC 中点.(1)求证:PBC AD 面⊥;(2)求直线AB 与平面ADE 所成角的正弦值.【解析】(1)由条件知:PB AD ⊥,BC AB ⊥ ∵ABC PA 底面⊥∴BC PA ⊥, 又∵BC AB ⊥且A AB PA = ∴PAB BC 面⊥又∵PAB AD 面⊂∴BC AD ⊥ 又∵PB AD ⊥且B BC PB = ∴PBC AD 面⊥(2)作DE BH ⊥于点H由(1)知PBC AD 面⊥,则BH AD ⊥ 故ADE BH 面⊥,则BAH ∠是直线AB 与平面ADE 所成角BH AB BHBAH ==∠sin 在Rt △BDE 中,22=BD ,23=BE ,25=DE 由面积法BH DE BD BE ⨯=⨯2121,得1030=BH直线AB 与平面ADE 所成角的正弦值为10304.如图,在四棱锥中,平面平面;,,,.(1)证明:平面;(2)求直线与平面所成的角的正切值.【解析】(1)连结BD ,在直角梯形B C D E 中,由1==BE DE ,得2==BC BD ,由2,2==AB AC 得222BC AC AB +=,即BC AC ⊥,又平面⊥ABC 平面BC DE ,从而⊥AC 平面BC DE .(2)在直角梯形BCDE 中,由2==BC BD ,2=DC 得BC BD ⊥,又平面⊥ABC 平面BC DE ,所以⊥BD 平面ABC .作BD EF //于CB 的延长线交于F ,连结AF ,则⊥EF 平面ABC ,所以EAF ∠是直线AE 与平面ABC 所成的角.在BEF Rt ∆中,由1=EB ,4π=∠EBF ,得22=EF ,22=BF ,在ACF RT ∆中,2=AC ,223=CF ,得226=AF ,在AEF Rt ∆中,由22=EF ,226=AF 得1313tan =∠EAF ,所以直线AE 与平面ABC 所成的角的正切值是1313.2=CD AD EBCABC AE BCDE AC ⊥2AC =1DE BE ==2AB CD ==90CDE BED ∠=∠=︒BCDE ABC ⊥BCDE A -PADCEBHPAD CEB5.在三棱锥P-ABC 中,22AB AC AC AB =⊥⊥,3,2PA ===PB PC 。
线线角、线面角、面面角辅导习题
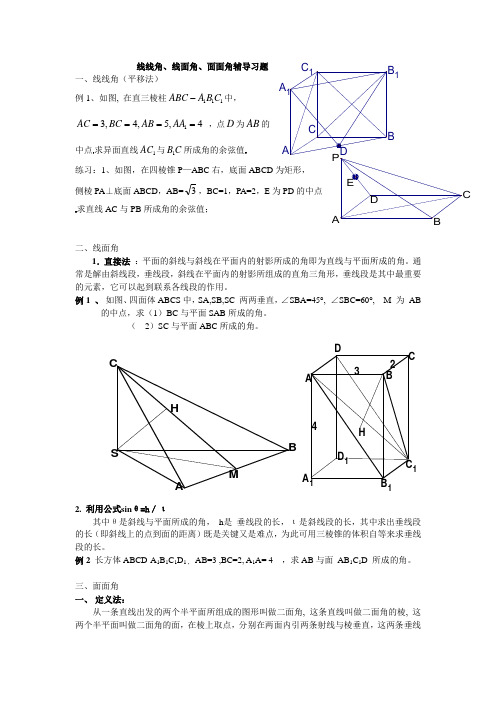
线线角、线面角、面面角辅导习题一、线线角(平移法)例1、如图, 在直三棱柱111ABC A B C -中,13,4,5,4AC BC AB AA ==== ,点D 为AB 的中点求异面直线1AC 与1B C 所成角的余弦值练习:1、如图,在四棱锥P —ABC 右,底面ABCD 为矩形, 侧棱PA ⊥底面ABCD ,AB=3,BC=1,PA=2,E 为PD 的中点求直线AC 与PB 所成角的余弦值;二、线面角1.直接法 :平面的斜线与斜线在平面内的射影所成的角即为直线与平面所成的角。
通常是解由斜线段,垂线段,斜线在平面内的射影所组成的直角三角形,垂线段是其中最重要的元素,它可以起到联系各线段的作用。
例1 、 如图、四面体ABCS 中,SA,SB,SC 两两垂直,∠SBA=45°, ∠SBC=60°, M 为 AB的中点,求(1)BC 与平面SAB 所成的角。
( 2)SC 与平面ABC 所成的角。
BMHSCAA 1C 1D 1H 4CB 123BAD2. 利用公式sin θ=h /ι其中θ是斜线与平面所成的角, h 是 垂线段的长,ι是斜线段的长,其中求出垂线段的长(即斜线上的点到面的距离)既是关键又是难点,为此可用三棱锥的体积自等来求垂线段的长。
例2 长方体ABCD-A 1B 1C 1D 1 , AB=3 ,BC=2, A 1A= 4 ,求AB 与面 AB 1C 1D 所成的角。
三、面面角 一、 定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线1A所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。
例1、把等腰直角三角形ABC 以斜边AB 为轴旋转,使C 点移动的距离等于AC 时停止,并记为点P .求二面角C-BP-A 的余弦。
二、三垂线法三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上则通常用三垂线定理法求二面角的大小。
(完整word版)线面角、二面角专题复习(学生版)

线面角与二面角专题复习编辑\审核:黄志平说明红色为必做题(课堂上展示的) ,其它题可选做,练手感。
一、线面角1、如图,四棱锥S ABCD 中,AB//CD, BC CD,侧面SAB为等边三角形,AB BC 2,C D SD 1(I)证明:SD 平面SAB;(n)求AB与平面SBC所成角的大小.2、如图,在组合体中,ABCD A1 B i C i D i是一个长方体,P ABCD是一个四棱锥.AB 2 , BC 3,点P 平面CC1D1D 且PD PC 罷.(I )证明:PD 平面PBC ;(n )求PA与平面ABCD所成的角的正切值;13、如图,在三棱锥P—ABC中,AB丄BC, AB= BO - PA,点O、D分别是2的中点,OP丄底面ABC.(I )求直线PA与平面PBC所成角的大小;AC PC-1CC i4、如图,棱锥 P —ABCD 的底面ABCD 是矩形,PA 丄平面ABCD, PA=AD=2, BD= 2.(I)求点 C 到平面PBD 的距离. (n)在线段 PD 上是否存在一点 正弦值为込,若存在,指出点 9 Q ,使CQ 与平面PBD 所成的角的 Q 的位置,若不存在,说明理由。
DC5、如图4,在直角梯形ABCD 中, 把^ DAC 沿对角线AC 折起后如图5所示(点D 记为点P ),点P 在平面ABC 上的正投影 E 落在线段AB 上,连接PB . (1)求直线 ABC DAB 90, CAB 30 ,BC 1,AD CD ,AC B 的大小的余弦值.C图5二、二面角 如图,四棱锥 P — ABCD 的底面为矩形,侧面 PAD 是正三角形,且侧面 PAD 丄底面ABCD(I ) 求证:平面 PAD 丄平面 PCD (I I) 当AD = AB 时,求二面角 A — PC — D 的余弦值.C7.如图5,在锥体P ABCD中,ABCD是边长为1 的棱形,且DAB 600, PA PD J2,PBE, F分别是BC,PC的中点,(1)证明:」(2 )求二面角ABCD中,底面ABCD是一直角梯形,底面ABCD ,PD与底面成30°角.PD,E为垂足,求证:BE PD ;的条件下,求异面直线AE与CD所成BAD 90,AD//BC,AB BC a ,2,AD 平面DEF ; IP AD B的余弦值.8、在四棱锥PAD 2a ,PA(1 )若AE(2 )在(1) 角的余弦值;(3)求平面PAB与平面PCD所成的锐二面角的正切值石圉3T9、如图5,在圆锥PO中,已知P0 =丿2, O O的直径的中点.(I)证明:平面POD 平面PAC;(n)求二面角B PA C的余弦值。
线面角习题强化课

课时2 线面角习题强化课目标:会灵活选用方法求直线与平面所成的角重点:用定义四步法和三余关系求线面角难点:向量法求线面角过程1、先复习线面角的的概念,规范找角的过程,回顾求线面角的方法方法一:定义法例1、在正方体1AC 中,求下列线面角⑴1DB 与底面A C ⑵1A B 与平面11A B CD略解:⑴即1arcsinB DB ∠= ⑵即130o BA M ∠= 注意:找证指算四个步骤例2、如图,,,AB ABCD BC CD AB BC AD ⊥⊥=平面与平面ABCD 所成的角为30o⑴求AD 与平面ABC 所成的角⑵AC 与面ABD 所成的角解:⑴易知BD 是AD 在平面BCD 内的射影,故ADB ∠是AD 与平面BCD 所成的角,即30o ADB ∠= 又易证AD 在左面ABC 内的射影是AC ,故DAC ∠是AD 与面ABC 所成的角 设1AB BC ==,则易求45o AC CD DAC ===⑵过C 作CE BD ⊥于E ,则CE ABD ⊥面,连AE ,则AE 是AC 在面ABD 内的射影 从而知CAE ∠为所求由等面积法知CE =arcsin BE CAE CAE ∴=∠=⇒∠=方法二:利用三余弦关系求例3、上节课作业:课本52,2P例4、设,E F 分别为正方体1AC 的棱AB ,11C D 的中点,则11A B 与面1A EF所成角的正切值是析:易知111111B A E B A F A B ∠=∠∴在面1A EF 内的射影为1EA F ∠的平分线,即等腰△1EA F 底边上的中线1A H从而11B A H ∠是11A B 与面1EA F 所成的角由三余弦关系易求11cos B A H ∠=,故11tan2B AH ∠=练习:1、在棱长为1的正方体1AC 中,,E F 分别在11B C 和1CC 上,且111,3EC FC ==求异面直线1A B 与EF 所成角的余弦 2、设空间的不同单位向量1122(,,0),(,,0),(1,1,1)a x y b x y c === 的夹角都为4π,求 ⑴11x y +和11x y 的值⑵,a b 的大小说明:除了坐标处理外,还可置于正方体中,如上图,1(1,1,1),,c DB DM DN == 在面AC内,由三余弦关系:11cos cos B DM B DB BDM ∠=∠∠得cos 2BDM ∠== ,23a b BDM π∴=∠= 方法三:向量法之坐标法例5(三维39P 例3)在长方形ABCD 中,4,2AB BC ==又O 是长方形的中心,OP ⊥面ABCD ,2,OP E =是PC 上一点,13PE PC =,试求BE 与底面ABCD 所成角的余弦 略解:建系如图:(0,0,0)OP ABCD =⊥ 面444,,333BE ⎛⎫=-- ⎪⎝⎭设BE 与底面ABCD 所成角为θ 则sin cos ,cos 33BE OP θθ==⇒= 小结:合适建系,准确运算,注意区分,BE OP 与θ的关系课外高考题探究(2008宁夏)如图,已知点P 在正方体AC '的对角线BD '上,且60oPDA ∠= ⑴求DP 与CC '所成角的大小⑵求DP 与平面AA D D ''所成角的大小分析:⑴即求PDD '∠由三余弦关系知 cos cos cos 45o PDA BDA PDB PDB ∠=∠∠⇒∠=⑵法1:由对称性知45oPDA PDC ∠=∠= 而DC 是面AA D D ''的法向量,故知DP 与左面AA D D ''成30o 角法2:定义法 过P 作PP ADD A '''⊥面于P ',则P D A ''∈,连结P D ',则是在左面内的射影 从而PDP '∠O 为所求不妨设1,2DP DH ==则,122HH DH PP ''=== 1sin 2PP PDP DP ''∴∠==从而sin 30o PDP '∠= 法3:建系如图,不妨设(,)(,P x x Rt DHH Rt DHP '∆∆ 皆为等腰)Rt ∆左面单位法向量(0,1,0)n =设DP 与左面成θ角,则(,)(0,1,0)1sin cos ,212x x DP n x θ=== 30o θ∴=小结:一题两法,并比较两种方法各自的特点(以B 为基点建系就更好)作业:活页十六反思:1、强化课最好用讲义学,事先让学生先预备2、上课最好用多媒体或小黑板3、一题两法中各自难点如何突破很关键,即找角和求坐标4、本课教案需用连实施。
