难点09_立体几何中的“内切”与“外接”问题的探讨(学案)
如何求解立体几何形的内切球和外接球

如何求解立体几何形的内切球和外接球立体几何形的内切球和外接球是数学和几何学中常见的概念。
内切球是指一个球体正好与该立体几何形相切于内部的球,而外接球则是指一个球体正好与该几何形相切于外部的球。
解决这个问题需要一些几何知识和计算技巧。
一、立方体首先,让我们以立方体为例,来讨论如何求解其内切球和外接球。
立方体是一个六个面都是正方形的立体,所有的边长相等。
立方体的内切球和外接球的半径可以通过简单的计算得到。
1. 内切球内切球的半径等于立方体的半边长。
设立方体的边长为a,则内切球的半径r等于a/2。
这是因为内切球的半径与立方体的棱长之比为1:2。
2. 外接球外接球是一个球体,它与立方体的八个顶点相切。
设立方体的边长为a,则外接球的半径R等于立方体对角线的一半。
根据勾股定理,立方体的对角线的长度d等于a√3。
因此,外接球的半径R等于d/2,即R等于a√3/2。
二、圆柱体对于圆柱体来说,内切球和外接球的求解稍微复杂一些。
1. 内切球内切球的半径等于圆柱体的半径。
设圆柱的半径为r,高度为h,则内切球的半径r'等于r。
2. 外接球外接球是一个球体,它与圆柱体的底面相切。
设圆柱的半径为r,高度为h,则外接球的半径R等于圆柱体的斜高。
根据勾股定理,圆柱体的斜高等于√(h^2 + r^2)。
因此,外接球的半径R等于√(h^2 + r^2)。
三、球体球体的内切球和外接球的求解相对简单。
1. 内切球球体的内切球的半径等于球体的半径。
设球体的半径为R,内切球的半径r等于R。
2. 外接球外接球是一个球体,它与球体的表面相切。
设球体的半径为R,则外接球的半径R'等于2R。
结论:通过以上讨论,我们可以得出以下结论:1. 对于立方体来说,内切球的半径等于边长的一半,外接球的半径等于对角线长的一半。
2. 对于圆柱体来说,内切球的半径等于半径,外接球的半径等于斜高。
3. 对于球体来说,内切球的半径等于半径,外接球的半径等于半径的两倍。
专题11立体几何中的内切外接问题11月19日终稿

专题十一 立体几何中的内切外接问题知识点一 棱锥外接问题外接问题常见于球的计算,而一部分棱锥的外接球的问题,常转化为棱锥外接棱柱的外接球问题或将三棱锥补为长方体,本节就先来探究特殊三棱锥的内外接问题.(1)三组对棱分别相等的四面体必内接于唯一的长方体,且四面体的棱分别为长方体的面对角线;(2)正四面体P ABC -内接于正方体且正方体的棱长a =;(3)若四面体有三条棱两两互相垂直.则可将其放入某个长方体内,其中三条互相垂直的棱也为长方体的棱; (4)若四面体的四个面均是直角三角形,该四面体为鳖臑,则可将其放入某个长方体内,其中三条互相垂直的棱也为长方体的棱;(5)三组对棱分别相等的四面体的棱长A B BC A C ''''、、必构成锐角三角形,即为外接长方体的三个面对角线构成的三角形;(6)任一四面体均内接于唯一的平行六面体.每条棱均为平行六面体的面对角线,且四面体体积是平行六面体体积的三分之一;(7)连接两组对棱的中点可组成平行四边形EGFH ,且另一组对棱与该面距离相等,此时平行四边形EGFH 平行于四面体内接平行六面体的一对平行平面;(8)过一组对棱(AB 与CD )中点()E F ,连线的任一平面(E G F H 、、、共面)必平分其()A BCD V -体积,即AC BGFH BD BD BZFH V V V --=-;(9)由正方体性质可知(i)1BD ⊥平面11AC D ,1BD ⊥平面1ACB . (ii)F 为平面11A C D 的中心,E 为平面1ACB 的中心. (iii)E ,F 为1BD 的三等分点.则正方体内接正四面体C AB D 11-高为E D 1,即正方体体对角线的23.【例1】(2009·江西卷)如图所示.在四面体ABCD 中.截面PQMN 是正方形.则在下列命题中.错误的为( )A.AC BD ⊥B.AC 平行于截面PQMNC.AC BD = D .异面直线PM 与BD 所成的角为45【例2】(重庆市七校联考)(多选)如图,在边长为2的正方体1111ABCD A B C D -中,点E ,F 分别是棱1BB ,11B C 的中点,G 是棱1CC 上的动点,则下列说法正确的是( ) A.当G 为中点时,直线AG ∥面1A EFB.当G 为中点时,直线AG 与EF 所成的角为30C.若H 是棱AA 上的动点,且1C G AH =,则平面ACD ⊥平面1B HGD.当G 在1CC 上运动时,直线AG 与平面11AA D D 所成的角的最大值为45︒知识点二 与球有关的内切、外接问题与球有关的内切、外接问题是立体几何的一个重点(切、接问题的解题思路类似,此处以多面体的外接球为例).研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系.一.长方体切割体的外接球设长方体相邻的三条边棱长分别为a ,b ,c .图1墙角体 图2鳖臑 图3挖墙角体 图4对角线相等的四面体图1与图2有重垂线,三视图都是三个直角三角形,图3无重垂线,俯视图是一矩形,AC 为虚线,主视图和左视图为直角三角形,外接球半径均为长方体体对角线一半,R =.图4中2222222222222222222a b BC AD BC AB CD b c AC a b c R AC BD c a AB ααβγβγ⎧+===⎫⎪++⎪=⇒+==⇒++=⇒=⎬⎨⎪⎪=+==⎭⎩abc abc abc V BCD A 31461=⨯-=-.外接球问题遇到墙角体就十分好处理,遇到以下墙角体性质的问题,就可以直接套用公式. 墙角体性质:(1)2222222()AB BC CA a b c ++=++.图 1【解析】如图1,因为Rt PAB △,Rt PBC △,Rt PCA △,所以222222222AB a b BC b c CA a c ⎧=+⎪=+⎨⎪=+⎩,故2222222()AB BC CA a b c ++=++.(2)顶点P 在底面上的投影H 恰为ABC △的垂心.如图 2【解析】如图2,因为Rt PAB △,Rt PBC △,Rt PCA △,又PA ⊥平面PBC ,所以PA BC ⊥. 因为PH ⊥平面ABC ,所以PH BC ⊥,故平面PAH BC ⊥,从而AH BC ⊥. 同理CH BA ⊥,BH AC ⊥,所以H 为ABC △的垂心.(3)设三个侧面和底面的面积分别为ABP S △,BCP S △,CAP S △,ABC S △,则 ①ABP S △是ABH S △与ABC S △的比例中项; ②BCP S △是CBH S △与ABC S △的比例中项; ③CAP S △是CAH S △与ABC S △的比例中项;④2222ABP BCP CAP ABC S S S S ++=△△△△.【解析】因为12BCP S BC PD =⋅△,12CBH S BC HD =⋅△,12ABC S BC AD =⋅△. 在Rt PDA △中,2PD HD AD =⋅.所以2BCP CBH ABC S S S =⋅△△△,所以BCP S △是CBH S △与ABC S △的比例中项. 同理,ABP S △是ABH S △与ABC S △的比例中项. CAP S △是CAH S △与ABC S △的比例中项.2BCP CBH ABC S S S =⋅△△△,2BCP ABH ABC S S S =⋅△△△,2CAP CAH ABC S S S =⋅△△△.三式相加,得222BCP ABP CAP CBH ABC ABH ABC CAH ABC S S S S S S S S S ++=⋅+⋅+⋅△△△△△△△△△2()CBH ABH CAH ABC ABC S S S S S =++⋅=△△△△△.【例3】在球面上有四个点P 、A 、B 、C .如果PA 、PB 、PC 两两互相垂直,且a PC PB PA ===,则这个球的表面积是 .【例4】(张家口期末)在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑 (bi ē n ào).如图,三棱锥D ABC -为一个鳖臑,其中DA ⊥平面ABC ,AB BC ⊥,2DA AB BC ===,AM DC ⊥,M 为垂足,则( )A .AM ⊥平面BCDB .DC 为三棱锥D ABC -的外接球的直径C .三棱锥M ABD -的外接球体积为D .三棱锥M ABC -的外接球体积与三棱锥M ABD -的外接球体积相等 【例5】(市中区校级模拟)在直角梯形ABCD 中,AB CD ∥,AD AB ⊥,22AB DC ==,E 为AD 的中点.将EAB △和ECD △分别沿EB ,EC 折起,使得点A ,D 重合于点F ,构成四面体FBCE .若四面体FBCE 的四个面均为直角三角形,则其外接球的半径为 . 【例6】(江西模拟)在三棱锥P ABC -中,PA ⊥底面ABC ,AB AC ⊥,6AB =,8AC =,D 是线段AC 上一点,且3AD DC =.三棱锥P ABC -的各个顶点都在球O 表面上,过点D 作球O 的截面,若所得截面圆的面积的最大值与最小值之差为16π,则球O 的表面积为( )A .72πB .86πC .112πD .128π【例7】四面体BCD A -中,5==CD AB ,34==BD AC ,41==BC AD ,则四面体BCD A -外接球的表面积为( ) A .π50B .π100C .π150D .π200【例8】(辽宁期末)粽子,古时北方也称“角黍”,是由粽叶包裹糯米、泰米等馅料蒸煮制成的食品,是中国汉族传统节庆食物之一.端午食粽的风俗,千百年来在中国盛行不衰.粽子形状多样,馅料种类繁多,南北方风味各有不同.某四角蛋黄粽可近似看成一个正四面体,蛋黄近似看成一个球体,且每个粽子里仅包裹一个蛋黄.若粽子的棱长为9cm ,则其内可包裹的蛋黄的最大体积约为( )(参考数据:6 2.45≈,3.14)π≈A .320cmB .322cmC .326cmD .330cm【解析】蛋黄近似看成一个棱长为9cm 的正四面体ABCD 的内切球,正四面体为ABCD ,设四面体的内切 【例9】(遵义期末)已知三棱锥P ABC -的顶点P 在底面的射影O 与ABC ∆的垂心重合,且ABC PBCPBC OBCS S S S =△△△△.若三棱锥P ABC -的外接球半径为3,则PAB PBC PAC S S S ++△△△的最大值为( ) A .6 B .8 C .10D .12二. 三棱柱的切割体的外接球⇒图1立着放的模型 图2躺着放的模型图1:立着放的模型一定有重垂线,且重垂线在底面的射影一定位于底面三个顶点中的一个,底面三角形非直角三角形,将重垂线长度设为h ,底面三角形外接圆半径设为r ,A a r sin 2=可以求出,则222⎪⎭⎫⎝⎛+=h r R ; 图2:躺着放的模型,底面是直角三角形或者矩形,侧面非直角三角形,底面一条棱垂直于侧面,222⎪⎭⎫⎝⎛+=h r R .【例10】如图,三棱锥的所有顶点都在一个球面上,在ABC △中,3=AB ,︒=∠60ACB ,︒=∠90BCD ,AB CD ⊥,22=CD ,则该球的体积为 .【例11】(莱西市期末)已知球O 是正三棱锥A BCD -(底面是正三角形,顶点在底面的射影为底面中心)的外接球,3BC =,23AB =,点E 在线段BD 上,且3BD BE =.过点E 作球O 的截面,则所得截面面积的最小值是( ) A .2πB .3πC .4πD .5π三、切瓜模型(两个平面互相垂直,最大高和最小高问题)图1,PAC BAC AB BC ⊥⊥面面 图2底面ABC 固定,P 在球面上运动,ABC P V -最值问题图1:由图可知,小圆ABC 直径AC 长可以求出,平面PAC 必在大圆上,由APCR sin 2=,解出R .图2:先根据ABCr sin 2=求出底面圆的直径MN ,再根据几何性质求出球大圆的直径,最后根据垂径定理算出P 到底面距离的最大值和最小值.双半径单交线公式:4222212l R R R -+=2122212122D O E O D O OO OD R +=+==2222222222121121()()24l O C CE O D O C BC O D R R =-+=-+=+-注意:常见的切瓜模型中,一旦出现21l R =或22lR =时,则2R R =或1R R =.双半径单交线公式适合所有的直二面角模型,两个半平面的外接圆半径分别为1R 和2R ,两半平面交线长度为l ,此公式属于一种开挂般的存在,在前面的直三棱柱切割体模型当中也可以使用,一旦两个半平面的二面角不是︒90时,此公式将不再适用.【例12】(柴桑区校级期末)球O 为三棱锥P ABC -的外接球,ABC △和PBC △都是边长为23的正三角形,平面PBC ⊥平面ABC ,则球的表面积为( ) A .28π B .20π C .18π D .16π【解析】【例13】(驻马店期末)已知平面图形PABCD ,ABCD 为矩形,4AB =,PAD 是以P 为顶点的等腰直角三角形,如图所示,将PAD △沿着AD 翻折至△P AD ',当四棱锥P ABCD '-体积的最大值为163,此时四棱锥P ABCD '-外接球的表面积为( )A .12πB .16πC .24πD .32π四、含二面角的外接球终极公式双距离单交线公式:4sin cos 222222l mn n m R +-+=αα如图,若空间四边形ABCD 中,二面角D AB C --的平面角大小为α,ABD 的外接圆圆心为1O ,ABC 的外接圆圆心为2O ,E 为公共弦AB 中点,则α=∠21EO O ,m E O =1,n E O =2,2lAE =,R OA =,由于21O E O O 、、、四点共圆,且αsin 221O O R OE ='=,根据余弦定理αcos 222221mn n m O O -+=,4sin cos 22222222l mn n m AE OE R +-+=+=αα.(当C ∠与D ∠均为钝角时,外接圆圆心在半平面的另一侧,21EO O ∠为二面角的对顶角,公式不变;当C ∠与D ∠为钝角时,21EO O ∠为二面角的补角,只需将公式中的角α转化为απ-,即4-sin -cos 222222l mn n m R +-+=)()(απαπ) 注意:此公式最好配合剖面图,需要求出两个半平面的外接圆半径,和外接圆圆心到公共弦的距离,通常是,剖面图能很快判断出两条相等弦的优先使用公式()2tan 2222αr h r R -+=.【例14】(亳州模拟)已知空间四边形ABCD ,CD BD ⊥,3CD =,3AB BD AD ===,二面角A BD C --是120︒,若A 、B 、C 、D 四点在同一球面上,则该球的表面积是( ) A .15π B .18π C .21π D .24π 【例15】(北碚区校级期末)如图,在四边形ABCD 中,AD BC ∥,2AD AB ==,45BCD ∠=︒,90BAD ∠=︒,将ABD △沿BD 进行翻折,在这一翻折过程中,下列说法正确的是( )A .始终有AC BD ⊥B .当平面ABD ⊥平面BCD 时,平面ABD ⊥平面ACDC .当平面ABD ⊥平面BCD 时,直线BC 与平面ABD 成45︒角D .当二面角A BD C --的大小为120︒时,三棱锥A BCD -外接球表面积为563π 【例16】在四面体S ABC -中,AB BC ⊥,AB BC =,SAC △为等边三角形,二面角S AC B --的余弦值为,则四面体S ABC -的外接球表面积为 .知识点三 内切球1、内切球的基本概念 (1)内切球定义:①球心到多面体各面距离相等且等于半径的球;②与圆柱两底面以及每条母线都相切的球;③与圆锥底面和各母线都相切的球;④与圆台上下两底面以及每条母线都相切的球. (2)正多面体的内切球和外接球球心重合.(3)正棱锥的内切球和外接球球心都在高线上,除正四面体外,均不重合.(4)任意四面体都有内切球,面数超过四的凸多面体需利用定义判断是否存在内切球. 2、多面体和旋转体的内切球 (1)棱锥内切球半径:①等体积法:由球心到各面距离相等,多面体体积可表示为:123123111111333333n n V rS rS rS rS rS rS ++++=++++==表,所以3V r S =表. ②相似法求解正棱锥内切球半径:(以下以正三棱锥为例)如图,由正三棱锥内切球球心O 在高线上,则球与侧面的切点E 在侧面的高线PD 上,与底面的切点H 为高线垂足,易知POE PDH△∽△,故利用OE PODH PD=,可解出内切球半径R .(2)旋转体内切球半径:(可按照轴截面的内切圆半径计算,外接球同理)如图,已知圆锥高为h ,底面半径为r ,利用两个直角三角形ABD △和AOE △相似可得OE BDAE AD=,故rh=,所以rR rh=().注:圆柱、圆台同样以轴截面的方式处理.(3)常见几何体内切球、外接球半径:棱长为a的正方体:内切球半径2aR=,外接球半径R=.棱长为a的正四面体:内切球半径R,外接球半径R.柱体侧棱长a,底面外接圆半径r:柱体可能不存在内切球,柱体中最大的球的半径min{}2aR r=,.【例17】(昌江区校级期末)正方体的外接球体积与内切球体积的比为()A.3B.C D.2【例18】(山东一模)如图,三棱锥V ABC-中,VA⊥底面ABC,90BAC∠=︒,2AB AC AV===,则该三棱锥的内切球和外接球的半径之比为()A.(2:1B.3):1C.1):3D.1):2【例19】(南京模拟)如图,正三棱柱111ABC A B C-,底面边长为2,D,E,F,M,N分别为棱AC,AB,BC,11A C,11B C的中点,P为线段MN上的动点,则三棱锥P DEF-内切球半径的最大值为.【例20】(青岛开学)已知圆台的上下底面半径分别为1和2,侧面积为,则该圆台的外接球半径为()A B C D【例21】(重庆月考)若正三棱柱111ABC A B C -既有外接球,又有内切球,记该三棱柱的外接球和内切球的半径分别为1R 、2R ,则212()R R =( ) A .5 B .4 C .92D .103同步训练1.在三棱锥A BCD -中,侧棱AB 、AC 、AD 两两垂直,ABC △、ACD △、ADB △、,则三棱锥A BCD -的外接球的体积为( )A B . C . D .2.(凤阳县校级三模)已知正方形123APP P 的边长为4,点B ,C 分别是边12P P ,23P P 的中点,沿AB ,BC ,CA 折叠成一个三棱锥P ABC -(使1P ,2P ,3P 重合于点)P ,则三棱锥P ABC -的外接球的体积为( )A .24πB .C .D .4π3.(瑶海区月考)已知三棱锥P ABC -的顶点P 在底面的射影O 为ABC △的垂心,若2ABC OBC PBC S S S ⋅=△△△,且三棱锥P ABC -的外接球半径为3,则PAB PBC PAC S S S ++△△△的最大值为( ) A .8B .10C .18D .224.已知三棱锥P ABC -的四个顶点均在同一个球面上,底面ABC △满足AB BC =3AC =,若该三棱,则其外接球的半径为( )A .1B .2C .3D .235.(河南模拟)在四面体ABCD 中,ABD △与BDC △都是边长为2的等边三角形,且平面ABD ⊥平面BDC ,则该四面体外接球的体积为 .6.(怀化二模)已知空间四边形ABCD 中,2AB BD AD ===,1BC =,CD 若平面ABD ⊥平面BCD ,则该几何体的外接球表面积为 .7.(江西月考)已知空间四边形ABCD 中,2AB BD AD ===,1BC =,CD ,若二面角A BD C --的大小是120︒,则该几何体的外接球表面积是 .8.(葫芦岛模拟)已知空间四边形ABCD 中,2AB BD AD ===,1BC =,CD ,若二面角A BD C--的取值范围为2[]43ππ,,则该几何体的外接球表面积的取值范围为 .9.(全国四模)已知三棱锥D ABC -所有顶点都在球O 的球面上,ABC △为边长为ABD △是以BD 为斜边的直角三角形,且2AD =,二面角C AB D --为120︒,则球O 的表面积为( )A .1483π B .28π C .373π D .36π10.(江门月考)已知三棱锥P ABC -三条侧棱PA ,PB ,PC 两两互相垂直,且2PA PB PC ===,M ,N分别为该三棱锥的内切球和外接球上的动点,则M ,N 两点间距离的最小值为( )A .2B 1C .2D 2-11.(和平区二模)已知圆锥底面圆的直径为3,该圆锥的内切球也是棱长为a 的正四面体的外接球,则此正四面体的棱长a 为( )A B C .3 D .9212.(山西月考)P ABC -的外接球和内切球的半径分别为1R 和2R ,则12R R -的值为( )A .4BCD .1 13.(大武口区校级三模)正方形ABCD 中,E ,F 分别为线段AB ,BC 的中点,连接DE ,DF ,EF ,将ADE △,CDF △,BEF △分别沿DE ,DF ,EF 折起,使A ,B ,C 三点重合,得到三棱锥O DEF -,则该三棱锥外接球半径R 与内切球半径r 的比值为 .14.(南开区模拟)如果一个八面体各个面都是全等的正三角形,如图所示,则这个几何体叫正八面体,则棱长为4的正八面体的内切球半径是 .15.(黄冈期末)若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积是球体积两倍时,该圆锥的高为( )A .2B .4CD .16.(胶州市期末)在三棱柱111ABC A B C -中,上下底面均为等腰直角三角形,且AB ==1AA ⊥平面ABC ,若该三棱柱存在内切球,则1AA =( )A .2B .2C .2D。
外接球与内切球专题

【典例 1】 已知各顶点都在同一个球面上的正四棱柱的高为 4,体
积为 16,则这个球的表面积是( )
A.16π
B.20π
C.24π
D.32π
【解析】 已知各顶点都在同一个球面上的正四棱柱的高为 4,体积 为 16,可求得底面边长为 2,故球的直径为 22+22+42=2 6,半径为 6, 球的表面积为 24π,故选 C。
【答案】 C
【小结】 本题是运用“正四棱柱的体对角线的长等于其外接球的三视图如图所示,则它的外接球的表 面积为( )
A.16π C.8π
B.4π D.2π
【解析】 由三视图可知该三棱锥的高为 1,底面为一个直角三角形, 由于底面斜边上的中线长为 1,则底面外接圆的半径为 1,顶点在底面上 的投影落在底面外接圆的圆心上。由于顶点到底面的距离与底面外接圆 的半径相等,则三棱锥的外接球的半径 R 为 1,则三棱锥的外接球的表 面积 S=4πR2=4π,故选 B。
【答案】 B
二、构造长方体或正方体确定球心 1.正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角 形的三棱锥,可将三棱锥补形成长方体或正方体; 2.同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱 锥,可将三棱锥补形成长方体或正方体; 3.若已知棱锥含有线面垂直关系,则可将棱锥补形成长方体或正方 体; 4.若三棱锥的三个侧面两两垂直,则可将三棱锥补形成长方体或正 方体。
5 2 4π× 2 2=50π。故选 D。
【答案】 D
三、由性质确定球心 利用球心 O 与截面圆圆心 O′的连线垂直于截面圆及球心 O 与弦中 点的连线垂直于弦的性质,确定球心。
【典例 3】 正三棱锥 A-BCD 内接于球 O,且底面边长为 3,侧 棱长为 2,则球 O 的表面积为________。
立体几何中球的内切和外接问题完美版

性质
内切球的球心位于旋转体 的轴线上,且球的半径等 于旋转体半径。
应用
在几何和工程领域中,内 切球常用于研究旋转体的 体积和表面积。
旋转体的外接球
定义
旋转体的外接球是指与旋 转体外侧相切的球。
性质
外接球的球心位于旋转体 外侧,且球的半径等于旋 转体轴线到旋转体外侧的 垂直距离。
应用
在几何ቤተ መጻሕፍቲ ባይዱ工程领域中,外 接球常用于研究旋转体的 空间位置和关系。
立体几何中球的内 切和外接问题完美 版
目 录
• 球与多面体的内切和外接问题 • 球与旋转体的内切和外接问题 • 球与几何体的内切和外接问题实例 • 总结与展望
01
CATALOGUE
球与多面体的内切和外接问题
多面体的内切球
01
02
03
04
多面体的内切球是指与多面 体的所有顶点和面都相切的
球。
内切球半径的求法:设多面体的 每个面为$S_i$,内切球的半径
03
CATALOGUE
球与几何体的内切和外接问题实例
多面体内切球实例
总结词
多面体内切球是指一个球完全内切于一个多面体,且与多面体的每个面都相切 。
详细描述
多面体内切球的问题可以通过几何定理和公式来解决,例如欧拉公式和球内切 定理。例如,一个正方体的内切球就是其中心,半径等于正方体边长的一半。
旋转体外接球实例
外接球的性质:外接球与 多面体的每个顶点都相切 ,且外接球的直径等于多 面体的对角线长度。
外接球的应用:在几何、 物理和工程领域中,外接 球的概念被广泛应用于研 究多面体的性质和计算。
02
CATALOGUE
球与旋转体的内切和外接问题
立体几何中的“内切”与“外接”问题的探讨

内切球 与外 接球的球心重合 , 且内切球 的
D .
4
c . 9
半径为 1 , 则圆锥的体积 为
P
.
分析 :借助圆锥的内切球与外接 球的 球心重合 , 找准轴截面 , 确定其为正三角形 , 根 据边角关系 求解圆锥 的底 面半径和 高. 解 :过 圆锥 的旋 转轴 作 轴截 面 , 得
重 点放 在与球相关 的外 接与 内切 问题 上. 形 解决正棱柱的外接球的组合体问题.
要 求学生 有较强 的空 间想 象能 力和准确
的计算 能力 . 从 实际 教学来 看 , 这 部分 知
规则 的锥体 , 如正 四面体 、 正棱锥 、 特
角三角形求解. 二是球为正棱锥的 内切球 ,
j
点评 : 如果圆锥 的内切球 与外接球 的
球 心 重 合 ,则截 面 三 角 形 为 正 三 角形 , 记 住这个结论可使解题更加简捷.
由勾股 定理得 O A = ‘ 4 E z + O ,
・
.
.
r 2 = ( 、 / ) ( 4 - r ) 2 ,
解得 r = ,
——●● —●—一
旦 四 ! △
—
—
. . 一
一
一
∥ 与∥ 外 接 问 题 的探 讨 立体 几何 中的 内切
一河北省滦南县司各庄中学 王景川
关键词 : 立体几何
锥体 球 与 圆 锥
球 与柱体
球与
的轴截 面 ,通过 两个截 面图的位置关 系 , 确定好棱 与球 的半径的关系 , 进 而将 空间
式和套路 , 以 至 于 遇 到 类 似 的题 目便 产 生 后 考查几何 体 的体 积或 者表 面积等 相关 畏惧心理。 本 文 就 高 中 阶 段 出现 这 类 问 题 加 以类 型 的总 结 和 方 法 的 探 讨 .
立体几何中球的内切和外接问题

且
,
,
所以知
,
,P
所以
所以可得图形为:
在
中斜边为 ,在
中斜边为 .
取斜边的中点 , 在
中
.
在
中
.
所以在几何体中
,
A
即 为该四面体的外接球的球心.
.
所以该外接球的体积为
.
且
B O
,
C
正三角形ABC的边长为 2 3 ,将它沿高AD翻折,使点B 与点C间的 距离为 3 ,此时四面体ABCD的外接球的体积为 。
A.8 6π B.4 6π C.2 6π D. 6π
【解答】如图, 由 PA=PB=PC,△ABC 是边长为 2 的正三角形,可知三棱锥 P﹣ABC 为正三棱锥,则顶点 P 在底面的射影 O 为底面三角形的中心,连接 BO 并延长,交 AC 于 G,则 AC⊥BG,又 PO⊥AC,PO∩BG=O,可得 AC⊥平面 PBG,则 PB⊥AC, ∵E,F 分别是 PA,AB 的中点,∴EF∥PB, 又∠CEF=90°,即 EF⊥CE,∴PB⊥CE,得 PB⊥平面 PAC, ∴正三棱锥 P﹣ABC 的三条侧棱两两互相垂直, 把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球, 其直径为 2R= PA2+PB2+PC2= 6.
半径为 26,则球 O 的体积为43π×( 26)3= 6π. 故选:D.
求棱长为1的正四面体外接球的体积.
解:设SO1是正四面体S ABCD的高, 外接球的球心O在SO1上, 设外接球半径为R, AO1 r,
则在ABC中,用解直角三角形知识得,r 3 , 3
O
A B
O
D
C
求正多面体外接球的半径
(word完整版)高考数学中的内切球和外接球问题

高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.考查学生的空间想象能力以及化归能力.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.一、直接法(公式法)1、求正方体的外接球的有关问题例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为.例2一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24 ,则该球的体积为.2、求长方体的外接球的有关问题例3一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为.例4已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为().A. 16B. 20C. 24D. 323.求多面体的外接球的有关问题例5一个六棱柱的底面是正六边形, 其侧棱垂直于底面,已知该 六棱柱的顶点都在同一个球面上,且该六棱柱的体积为9,底面周长 为3,则这个球的体积为.解设正六棱柱的底面边长为x ,高为h ,则有 6x 3 9 会 3 2.6 — x h 8 4的半径的常用公式二、构造法(补形法)1、构造正方体例5若三棱锥的三条侧棱两两垂直,且侧棱长均为 V 3 ,则其外 接球的表面积是.例3若三棱锥的三个侧面两两垂直,且侧棱长均为V 3 ,则其外 接球的表面积是.故其外接球的表面积S 4 r 2 9 .小结:一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分 别为a,b,c ,则就可以将这个三棱锥补成一个长方体, 于是长方体的体 对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则 有2R va 2 b 2 c 2.出现“墙角”结构利用补形知识,联系长方体。
复习小专题立体几何中的“内切”与“外接”问题的探究

江苏省口岸中学2017届二轮复习小专题立体几何中的“内切”与“外接”问题的探究1 球与柱体规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题. 1.1球与正方体如图1所示,正方体1111D C B A ABCD -,设正方体的棱长为a ,G H F E ,,,为棱的中点,O 为球的球心。
常见组合方式有三类:一是球为正方体的内切球,截面图为正方形EFHG 和其内切圆,则2a r OJ ==;二是与正方体各棱相切的球,截面图为正方形EFHG 和其外接圆,则a R OG 22==; 三是球为正方体的外接球,截面图为长方形11A ACC 和其外接圆,则23'1a R O A ==.通过这三种类型可以发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题 。
例 1 棱长为1的正方体1111ABCD A BC D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( )A .2B .1C .12+D1.2 球与长方体长方体各顶点可在一个球面上,故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时,截面图为长方体的对角面和其外接圆,和正方体的外接球的道理是一样的,故球的半径2l R == 例 2 在长、宽、高分别为2,2,4的长方体内有一个半径为1的球,任意摆动此长方体,则球经过的空间部分的体积为( ) A.10π3 B.4π C.8π3 D.7π31.3球与正棱柱球与一般的正棱柱的组合体,常以外接形态居多。
下面以正三棱柱为例,介绍本类题目的解法——构造直角三角形法。
立体几何中内切球和外接球问题

立体几何中内切球和外接球问题题目:探索立体几何中的内切球和外接球问题在立体几何中,内切球和外接球问题是一个引人深思的话题。
通过对这个主题的深入探讨,我们可以更好地理解立体几何的原理和性质。
本文将围绕内切球和外接球问题展开讨论,从基本概念到数学推导,深入剖析这一有趣而重要的话题。
1. 内切球和外接球的定义在立体几何中,内切球和外接球分别是指一个球体在一个立体图形内部与其接触,以及一个球体在一个立体图形外部与其接触。
这两个概念可以应用在各种几何图形中,如圆柱体、圆锥体甚至更为复杂的多面体。
内切球和外接球不仅在几何形状中具有重要意义,还在工程学、艺术设计等领域有着广泛的应用价值。
2. 内切球和外接球的性质内切球和外接球在几何中具有许多有趣的性质。
内切球和外接球的半径之比有一定的规律,可以通过数学推导得出。
内切球和外接球的位置关系也有一定的特点,可以通过几何推理进行证明。
这些性质的深入理解有助于我们更好地应用立体几何知识解决实际问题。
3. 内切球和外接球的数学推导从数学角度来看,内切球和外接球问题涉及到许多重要的数学定理和方法。
通过数学推导,我们可以得到内切球和外接球的半径之比、位置关系等具体数学表达式。
这些推导过程需要运用到圆、球体的性质,以及立体几何的相关知识,是一个不可或缺的数学推理过程。
4. 个人观点和理解在我看来,内切球和外接球问题是立体几何中的一个精彩而复杂的主题。
通过对这个问题的探讨,我深刻地感受到数学的美妙和奥妙。
数学不仅是一门实用的科学,更是一个充满乐趣和挑战的学科。
通过不断地学习和探索,我们可以更好地理解立体几何的原理和应用,为我们的工程、设计和科学研究提供有力的支持。
内切球和外接球问题是立体几何中的一个重要而有趣的话题。
通过深入探讨这个主题,我们可以更好地理解立体几何的原理和应用,为我们的学习和工作带来更多的乐趣和启发。
希望本文的内容能够对您有所帮助,也希望您能够对立体几何有着更深入的理解和探索。
高中数学立体几何中的外接球与内切球问题

高中数学立体几何中的外接球与内切球问题
在高中数学的立体几何中,外接球与内切球问题是一个重要的探讨点。
这个问
题涉及到如何在一个给定的立体图形中,找到一个外切于该图形的球和一个内切于该图形的球。
首先,让我们来看外接球问题。
在立体几何中,给定一个多面体,如正方体或
正四面体,我们想找到一个球,使得该球恰好外接于该多面体的每一个面上。
所谓外接,即球与每一个面都有且只有一个公共点,这个点是每个面的外接圆心。
以正方体为例,我们可以观察到正方体的每一个面都是正方形,而正方形的外
接圆心恰好位于该正方形的中心点。
因此,我们可以得出结论:正方体的外接球的圆心与该正方体的每个面的外接圆心重合。
接下来,让我们来看内切球问题。
在立体几何中,给定一个多面体,如正方体
或正四面体,我们想找到一个球,使得该球恰好内切于该多面体的每一个面上。
所谓内切,即球与每一个面都有且只有一个公共点,这个点是每个面的内切圆心。
以正方体为例,我们可以观察到正方体的每一个面都是正方形,而正方形的内
切圆心恰好位于该正方形的中心点。
因此,我们可以得出结论:正方体的内切球的圆心与该正方体的每个面的内切圆心重合。
总结起来,对于任何一个给定的多面体,我们可以找到一个外接球和一个内切球。
外接球的圆心与每个面的外接圆心重合,而内切球的圆心与每个面的内切圆心重合。
这个问题在高中数学的立体几何中十分重要,理解了外接球和内切球的性质,可以帮助我们更好地理解和解决相关的几何问题。
立体几何中球的内切和外接问题(完美版)
C 1
注意:①割补法,② V多面体 3 S全 r内切球
变式训练:一个正方体内接于一个球,过球心作一截面,如 图所示,则截面的可能图形是( )
①
②
③
④
• A .①② B.②④ C.①②③ D.②③④
D A
D1 A1
C
B O
C1 B1
球的内接正方体的对角线等于球直径。
变式训练:已知正四面体内接于一个球,某人画出四 个过球心的平面截球与正四面体所得的图形如下,
的动点,当弦 MN 的长度最大时, PM • PN 的取值范围是
.
感谢阅读
• 感谢阅读
• 感谢阅读
• 感谢阅读
• 感谢阅读
2023最新整理收集 do something
球与多面体的内切、外接
球的半径r和正方体 的棱长a有什么关系?
.r
a
一、 球体的体积与表面积
①
②
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上,
则称这个多面体是这个球的内接多面体,
这个球多是面这体个的外接球
。
定义2:若一个多面体的各面都与一个球的球面相切,
,即 为该四面体的外接球的球心
A
O
C
所以该外接球的体积为
03
破译规律-特别提
醒
2 例题剖析-针对讲 解
04
举一反三-突破提
升
4 举一反三-突破提 升 1、(2015 海淀二模)已知斜三棱柱的三 视图如图所示,该斜三棱柱的体积为 ______.
4 举一反三-突破提 升
2、(2015 郑州三模) 正三角形ABC的2 边3 长
5 正棱锥的外接球的球心是在其 高上
立体几何中的外接球内切球棱切球问题

立体几何中的外接球内切球棱切球问题1. 概述在立体几何中,外接球、内切球和棱切球是常见的几何问题。
它们在工程、建筑、数学等领域都有重要的应用。
本文将围绕外接球、内切球和棱切球展开讨论,探究它们的性质和相关问题。
2. 外接球的定义和性质外接球是指一个球与一个或多个其他物体外接,外接球的半径等于所外接物体相应部分的长度,在立体几何中有着重要的应用。
外接球的性质1)外接球的圆心在被外接物体向外伸出的法线上。
2)外接球的半径等于被外接物体的相应部分的长度。
3)对于凸体而言,外接球存在且唯一。
3. 内切球的定义和性质内切球是指一个球恰好与另一个物体相切,内切球在立体几何中也有着重要的应用。
内切球的性质1)内切球的圆心在被内切物体向内伸出的法线上。
2)对于凸体而言,内切球存在且唯一。
3)内切球在不同物体中的位置可能不同,但其存在性是唯一的。
4. 棱切球的定义和性质棱切球是指一个球与多个物体之间棱切的情况,在立体几何中也有着重要的应用。
棱切球的性质1)棱切球的圆心在被棱切物体所在的平面上。
2)对于凸体而言,棱切球存在且唯一。
3)棱切球在不同物体中的位置可能不同,但其存在性是唯一的。
5. 实际应用举例外接、内切和棱切球在实际应用中有着广泛的应用。
比如在建筑工程中,常常需要计算建筑物的外接球、内切球和棱切球,以确定其结构和稳定性。
在数学建模中,外接、内切和棱切球也常常出现,用于解决各种数学问题。
6. 结论外接球、内切球和棱切球是立体几何中重要的概念,它们的性质和应用涉及到广泛的领域。
对这些几何问题的深入研究和应用可以帮助我们更好地理解立体几何的性质,并且为实际问题的解决提供理论支持。
希望本文能够帮助读者更好地理解外接球、内切球和棱切球的相关问题,并且激发更多人对立体几何的兴趣和研究。
外接球、内切球和棱切球作为立体几何中的重要概念,其性质和应用不仅仅局限于几何学。
它们的相关问题还涉及到数学建模、工程设计、建筑结构等领域,对于实际问题的解决提供了理论支持和指导。
立体几何中的“内切”与“外接”问题的探究(完美版)

立体几何中的“内切”与“外接”问题的探究一、由球心的定义确定球心在空间,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球球心。
二、由上述性质可以得出以下多面体外接球的结论:结论1:正方体或长方体的外接球的球心是其体对角线的中点。
结论2:正棱柱的外接球的球心是上下底面中心的连线的中点。
结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
结论4:正棱锥的外接球的球心是在其高上,具体位置可通过计算得到。
结论5:若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
一、定义法例1、 在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积为A.12512πB.1259πC.1256πD.1253π 解 设矩形对角线的交点为O ,则由矩形对角线互相平分,可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等,即点O 为四面体的外接球的球心,如图2所示.∴外接球的半径52R OA ==.故3412536V R ππ==球.选C.二、求正方体、长方体的外接球的有关问题结论1:正方体或长方体的外接球的球心是其体对角线的中点。
①出现“墙角”结构利用构造法(补形法),联系长方体。
【原理】:长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为222c b a l ++=,几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=例1、若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 . 解 据题意可知,该三棱锥的三条侧棱两两垂直,∴把这个三棱锥可以补成一个棱长为3的正方体,于是正方体的外接球就是三棱锥的外接球.设其外接球的半径为R ,则有()()()()222223339R =++=.∴294R =. 故其外接球的表面积249S R ππ==.小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2222R a b c =++.②出现正四面体外接球时利用构造法(补形法),联系正方体。
立体几何中的与球有关的内切外接问题分解课件

设多边形的边数为$n$,则球的半径$r = frac{a}{2sinfrac{180^circ}{n}}$,其中$a$为多边形的外接圆半径。
球与圆柱体的内切总结词Fra bibliotek详细描述
当一个球完全内切于一个圆柱体时, 圆柱体的底面圆周和顶面圆周都与球 面相切,且圆柱的轴线通过球心。
设圆柱体的底面圆心为$O_1$,顶面 圆心为$O_2$,球心为$O$。由于球 内切于圆柱体,所以$OO_1 = OO_2 = r$,其中$r$为球的半径。同时, 圆柱体的底面圆周和顶面圆周都与球 面相切,所以底面圆心到球心的距离 等于底面圆的半径,顶面圆心到球心 的距离等于顶面圆的半径。
公式
设圆柱体的底面半径为$R_1$,顶面 半径为$R_2$,高为$h$,则球的半 径$r = frac{R_1 + R_2 + h}{2}$。
球与圆锥体的内切
总结词
当一个球完全内切于一个圆锥体时,圆锥体的底面圆周和侧面都与球面相切,且圆锥的轴 线通过球心。
详细描述
设圆锥体的底面圆心为$O_1$,球心为$O$。由于球内切于圆锥体,所以$OO_1 = r$, 其中$r$为球的半径。同时,圆锥体的底面圆周和侧面都与球面相切,所以底面圆心到球 心的距离等于底面圆的半径。
04
球的内切外接问题应用
球在几何题中的应用
球与多面体的内切和外接
在几何题目中,经常涉及到球与多面体的内切和外接问题,需要利用球心到多面 体的顶点的距离等于半径的原理来解决。
球的切线和割线定理
切线和割线定理是球在几何题中的重要应用,通过这些定理可以推导出球与其他 几何形状的位置关系。
球在物理题中的应用
02
球的内切问题
球与多边形的内切
几何体的外接球与内切球的有关问题

几何体的外接球与内切球的有关问题一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点,此类问题实质是计算球的半径或确定球心O 的位置问题,其中球心的确定是关键.(一) 由球的定义确定球心球的定义:在空间中,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论.结论1:正方体或长方体的外接球的球心其体对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点,由球心、底面中心及底面一顶点构成的直角三角形便可得球半径.(在1BOO Rt ∆中,21212OO BO BO +=,即.)结论4:正棱锥的外接球的球心在其高上,具体位置可通过构造直角三角形利用勾股定理求得. (以正三棱锥为例:设正三棱锥的底面△ABC 的边长为a ,高为h ,外接球球心为O ,半径为R .在1AOO Rt ∆中,21212OO AO AO +=,即222)(33R h a R -+⎪⎪⎭⎫ ⎝⎛=.) 结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心,则公共斜边的一半就是其外接球的半径.(二)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处.1.可构造正方体的类型:①正四面体:棱长对应正方体的面对角线.①②③②三条侧棱两两垂直的正三棱锥:底面棱长对应正方体的面对角线,侧棱对应正方体的棱长.③四个面都是是直角三角形的三棱锥:最长的棱长对应正方体的体对角线.2.可构造长方体和正方体的类型①同一个顶点上的三条棱两两垂直的四面体;②三个侧面两两垂直的三棱锥;③有三个面是直角三角形的三棱锥;①与②与③④④相对的棱相等的三棱锥:设对应长方体的长、宽、高分别为a、b、c,则BC2=a2+b2,AC2=a2+c2,AB2=b2+c2. 所以对应长方体的体对角线为.⑤含有其它线面垂直关系的棱锥.(三)由性质确定球心利用球心O与截面圆圆心O’的连线垂直于截面圆,确定球心.记球的半径为R,截面圆的半径为r,球心O与截面圆圆心O’的距离为d,则有R2=r2+d 2.(四)圆柱外接球模型计算球的半径一个底面半径为r,高为h的圆柱,求它的外接球半径.(1)(2)(3)变形一:如果我们对圆柱上下底面对应位置处,取相同数量的点,比如都取三个点,如图(1)所示.我们可以得到(直)三棱柱,它的外接球其实就是这个圆柱的外接球,所以说直棱柱的外接球求半径符合这个模型. 在这里棱柱的高就是公式中的h,而棱柱底面△ABC外接圆的半径则是公式中的r.变形二:如果把三棱柱上面的C1去掉,如图(2)所示,我们得到有一个侧面⊥矩形底面的四棱锥,其中r为垂直底面的侧面△ABC的外接圆半径,h为垂直于那个侧面的底面边长AA1.变形三:如果把上面的那个三棱柱上面的B1,C1两点去掉,如图(3)所示,我们得到一根侧棱⊥底面的三棱锥,其中r为底面△ABC外接圆半径,h为垂直于底面的那条侧棱AA1.二、内切球问题若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.结论1:内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.结论2:正多面体的内切球和外接球的球心重合.结论3:正棱锥的内切球和外接球球心都在高线上,但不重合.结论4:基本方法:构造三角形利用相似比和勾股定理.结论5:体积分割是求内切球半径的通用做法.(一)正方体的的内切球设正方体的棱长为a,求(1)内切球半径;(2)与棱相切的球半径.(1)内切球:截面图为正方形的内切圆,得.(2)棱切球:切点为正方体各棱的中点,截面图为为正方形的外接圆,得.(二)棱锥的内切球(分割法)将内切球的球心与棱锥的各个顶点连线,将棱锥分割成以原棱锥的面为底面,内切球的半径为高的小棱锥,根据分割前后的体积相等,列出关于半径的方程.设三棱锥的棱长为a ,内切球半径为r.V V V V V PAB O PBC O PAC O ABC O ABC P -----+++=r S r S r S r S PAB PBC PAC ABC 31313131+++= r S S S S PAB PBC PAC ABC )(31+++=所以一般地,记棱锥的体积为V ,表面积为S ,则内切球的半径为.(三)圆柱、圆锥的内切球(截面法)(1)圆柱的内切球:圆柱的轴截面为正方形,记圆柱的底面圆的半径r ,内切球的半径R ,则R =r .(2)圆锥的内切球:圆锥的轴截面为三角形的内切圆,记圆锥的底面圆的半径r ,内切球的半径R ,由于在△ABC 中,所以.备注:1.三角形内切圆的半径S S S S AOB AOC BOC ABC ∆∆∆∆++=r c b a cr br ar )(21212121++=++=所以三角形内切圆的半径为,其中S 为△ABC 的面积,C 为△ABC 的周长.2. 三角形外接圆的半径利用正弦定理,.①正三角形:,其中a 为正三角形的边长.②直角三角形:,其中c 为直角三角形的斜边.3. 正三角形的内切圆与外接圆的半径之比正三角形的内切圆与外接圆的两个圆心“二心合一”.设正三角形的边长为a ,内切圆半径为r ,外接圆半径为R.由于,a a a a a a C S r 6360sin 2122=++︒⋅⋅⋅⨯==, 所以,即圆心O 为正三角形高h 的三等分点.4. 正四面体的内切球与外接球的半径之比正四面体的内切球与外接球的两个球心“二心合一”.设正四面体A -BCD 的棱长为a ,内切球半径为r ,外接球半径为R ,则OA=OB=R ,OE=r.∵底面△BCD 为正三角形,∴BE=在BEO Rt ∆中,,即,得∴,即球心O 为正四面体高h 的四等分点.5.正三棱柱的内切球与外接球的半径之比正三棱柱的内切球与外接球的球心是重合的,过侧棱和它们的球心O 作截面如下图所示:设正三棱柱底面边长为. 由于内切球投影到底面的圆是底面正三角形的内切圆,所以,从而正三棱柱的高为.在O D A Rt 11∆中,得, 因此1:5:21=R R .。
专题讲解 立体几何中的外接球与内切球问题(学生版)
专题讲解立体几何中的外接球与内切球问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点与难点,也是高考考查的一个热点。
考查学生的空间想象能力以及化归能力。
研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,解决这类问题的关键是抓住内接的特点,即球心到多面体的顶点的距离等于球的半径.并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用。
球的内切问题主要是指球外切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果外切的是多面体,则作截面时主要抓住多面体过球心的对角面来作。
当球与多面体的各个面相切时,注意球心到各面的距离相等即球的半径,求球的半径时,可用球心与多面体的各顶点连接,球的半径为分成的小棱锥的高,用体积法来求球的半径。
球与多面体的关系是高考考查的重点,但同学们又因为缺乏较强的空间想象能力,较难找到解题的切入点和突破口。
解决这类题目是要认真分析图形,明确切点和接点的位置及球心的位置是关键。
常见题型有求对应外接球或内切球半径、表面积、体积或球内接几何体最值等问题。
本章节将对常见的关于内切球和外接球的模型作一总结,并附有针对性训练题,供教师和学生参考使用。
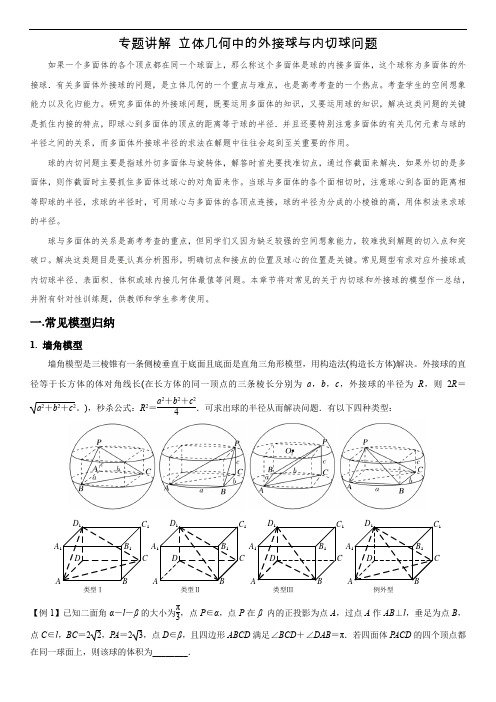
一.常见模型归纳1. 墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决。
外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=a 2+b2+c2。
),秒杀公式:R2=a2+b2+c24.可求出球的半径从而解决问题.有以下四种类型:【例1】已知二面角α-l-β的大小为π3,点P∈α,点P在β内的正投影为点A,过点A作AB⊥l,垂足为点B,点C∈l,BC=22,P A=23,点D∈β,且四边形ABCD满足∠BCD+∠DAB=π.若四面体P ACD的四个顶点都在同一球面上,则该球的体积为________.A BCDA1B1C1D1类型ⅠA BCDA1B1C1D1类型ⅡA BCDA1B1C1D1类型ⅢA BCDA1B1C1D1例外型【例2】已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( ).A .68πB .64πC .62πD .6π【变式练习1】在空间直角坐标系Oxyz 中,四面体ABCD 各顶点的坐标分别为A (2,2,1),B (2,2,-1),C (0,2, 1),D (0,0,1),则该四面体外接球的表面积是( )A .16πB .12πC .43πD .6π【变式练习2】在长方体ABCD -A 1B 1C 1D 1中,底面ABCD 是边长为32的正方形,AA 1=3,E 是线段A 1B 1上一点, 若二面角A -BD -E 的正切值为3,则三棱锥A -A 1D 1E 外接球的表面积为________.2. 对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决。
立体几何外接圆球及内切圆球问题

立体几何外接圆球及内切圆球问题
立体几何是研究三维空间中的图形和体积的学科。
外接圆球和内切圆球问题是立体几何中常见的一个问题。
外接圆球问题
在立体几何中,外接圆球是指一个球能够刚好与一个多面体的所有顶点相切。
对于不规则多面体来说,外接圆球可能无法通过所有的顶点,但可以通过一部分顶点。
外接圆球的半径通常被称为外接球的半径,是从多面体的中心到多面体顶点的最远距离。
要计算外接球的半径,可以使用多面体的顶点坐标来求得多面体的边长和中心点的坐标,然后使用勾股定理来计算半径的长度。
内切圆球问题
内切圆球是指一个球刚好能够与多面体的所有面相切。
与外接
圆球问题类似,对于不规则多面体来说,内切圆球可能无法与所有
的面相切,但可以与一部分面相切。
内切圆球的半径通常被称为内切球的半径,是从多面体的中心
点到多面体的面的最短距离。
要计算内切球的半径,可以使用多面
体的面的法向量和距离公式来求得。
应用和意义
外接圆球和内切圆球问题在立体几何中具有重要的应用和意义。
它们可以用来解决很多实际问题,如计算多面体的体积、表面积,
以及优化多面体的设计。
外接圆球和内切圆球问题也被广泛应用于计算机图形学和计算
机辅助设计领域。
在三维建模和渲染中,可以使用外接圆球和内切
圆球来估计或近似多面体的几何特征,以便更高效地处理和渲染三
维模型。
结论
立体几何中的外接圆球和内切圆球问题是一个有趣且实用的领域。
通过计算外接球和内切球的半径,可以获得关于多面体的重要信息,并应用于多个领域,包括工程设计和计算机图形学。
立体几何中的“内切”与“外接”问题的探究(完美版)

立体几何中的“内切”与“外接”问题的探究(完美版)探究立体几何中“内切”与“外接”问题在立体几何中,我们经常遇到“内切”和“外接”的问题。
在研究这些问题之前,我们需要先明确球心的定义。
如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球球心。
根据上述性质,我们可以得出以下多面体外接球的结论:1.正方体或长方体的外接球的球心是其体对角线的中点。
2.正棱柱的外接球的球心是上下底面中心的连线的中点。
3.直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
4.正棱锥的外接球的球心在其高上,具体位置可通过计算得到。
5.若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
接下来我们来探究一下正方体和长方体的外接球的问题。
根据结论1,正方体或长方体的外接球的球心是其体对角线的中点。
我们可以利用构造法(补形法)来解决这类问题。
例如,对于一个长方体,如果从一个顶点出发的三条棱长分别为a、b、c,则体对角线长为√(a^2+b^2+c^2),几何体的外接球直径2R为体对角线长l,因此R=√(a^2+b^2+c^2)/2.举个例子,如果一个三棱锥的三个侧面两两垂直,且侧棱长均为3,则可以将这个三棱锥补成一个棱长为3的正方体,于是正方体的外接球就是三棱锥的外接球。
设其外接球的半径为R,则有(2R)^2=3^2+3^2+3^2=27.因此,其外接球的表面积为S=4πR^2=36π。
另外,对于一个矩形ABCD,如果AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为(125π)/(1296)。
最后,如果出现正四面体外接球的问题,我们可以利用构造法(补形法),联系正方体。
一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为多少?解析:由于所有棱长都相等,所以可以构造一个正方体,再寻找棱长相等的四面体。
如图2所示,四面体ABDE满足条件,即AB=AD=AE=BD=DE=BE=2.由此可求得正方体的棱长为1,对角线为$\sqrt{3}$,从而外接球的直径也为$\sqrt{3}$,所以此球的表面积为$4\pi$,故选B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
难点09 立体几何中的“内切”与“外接”问题的探讨学案
纵观近几年高考对于组合体的考查,重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类
似的题目便产生畏惧心理.本文就高中阶段出现这类问题加以类型的总结和方法的探讨.
1 球与柱体
规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题.
球与正方体
发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题 例 1 棱长为1的正方体1111ABCD A BC D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( )
A .2
2
B .1
C .212+
D .2
球与长方体 长方体各顶点可在一个球面上,故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时,截面图为长方体的对角面和其外接圆,和正方体的外接球的道理是一样的,故球的半径222
.22l a b c R ++==
例 2 在长、宽、高分别为2,2,4的长方体内有一个半径为1的球,任意摆动此长方体,则球经过的空间部分的体积为( )
A.10π3
B.4π
C.8π3
D.7π3
球与正棱柱
例 3 正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上,则正四棱柱的侧面积有最 值,为 .
2 球与锥体
规则的锥体,如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱锥的棱和高产生联系,然后考查几何体的体积或者表面积等相关问题.
2.1
球与正四面体
2222233a R r a R r CE +=-=,=,解得:66,.412R a r a ==这个解法是通过利用两心合一的思路,建立含有两个球的半径的等量关系进行求解.同时我们可以发现,球心O 为正四面体高的四等分点.如果我们牢记这些数量关系,可为解题带来极大的方便.
例4 将半径都为1的四个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最
小值为 ( ) A.3263+ B. 2+263 C. 4+26
3 D. 43263+
【球的外切正四面体,这个小球球心与外切正四面体的中心重合,而正四面体的中心到顶点的距离是中心到地面距离的3倍.】
2.2 球与三条侧棱互相垂直的三棱锥
球与三条侧棱互相垂直的三棱锥组合问题,主要是体现在球为三棱锥的外接球.
解决的基本方法是补形例 5 在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且AM MN ⊥,若侧棱23SA =,则
正
2.3 球与正棱锥
球与正棱锥的组合,常见的有两类,一是球为三棱锥的外接球,此时三棱锥的各个顶点在球面上,根据截面图的特点,可以构造直角三角形进行求解.二是球为正棱锥的内切球,例如正三棱锥的内切球,球与正三棱锥四个面相切,球心到四个面的距离相等,都为球半径R .这样求球的半径可转化为球球心到三棱锥面的距离,故可采用等体积法解决,即四个小三棱锥的体积和为正三棱锥的体积.
例6 在三棱锥P -ABC 中,PA =PB=PC=3,侧棱PA 与底面ABC 所成的角为60°,则该三棱锥外接球的体积为( )
A .π B.3π C. 4π D.43π
例7 矩形ABCD 中,4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是( ) A.π12125 B.π9125 C.π6125 D.π
3125
3 球与球
对个多个小球结合在一起,组合成复杂的几何体问题,要求有丰富的空间想象能力,解决本类问题需掌握恰当的处理手段,如准确确定各个小球的球心的位置关系,或者巧借截面图等方法,将空间问题转化平面问题求解
.
4 球与几何体的各条棱相切
球与几何体的各条棱相切问题,关键要抓住棱与球相切的几何性质,达到明确球心的位
置为目的,然后通过构造直角三角形进行转换和求解.如与正四面体各棱都相切的球的半径为相对棱的一半:24r a '=
.
例8 把一个皮球放入如图10所示的由8根长均为20 cm 的铁丝接成的四
综合上面的四种类型,解决与球的外切问题主要是指球外切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果外切的是多面体,则作截面时主要抓住多面体过球心的对角面来作;把一个多面体的几个顶点放在球面上即为球的内接问题.解决这类问题的关键是抓住内接的特点,即球心到多面体的顶点的距离等于球的半径.发挥好空间想象力,借助于数形结合进行转化,问题即可得解.如果是一些特殊的几何体,如正方体、正四面体等可以借助结论直接求解,此时结论的记忆必须准确.。
