第5章时域离散系统的网络结构-精选
合集下载
第5章 时域离散系统的基本网络结构09-10-1
1 p z 1 q z 1 q z
1 1 r r 1 r r 1 r 1
r 1 N1
r
1 r
r 1 N2
H ( z ) A H j ( z )
j 1
K
0 j 1 j z 1 2 j z 2 H j ( z) 1 2 1 1 j z 2 j z
IIR数字滤波器的系统函数H(z)为
8 4 z 1 11z 2 2 z 3 H ( z) 5 1 3 2 1 3 1 z z z 4 4 8
画出该滤波器的级联型结构。 解 ： 由H(z)写出差分方程如下
y n 8 xn 4 xn 1 11xn 2 2 xn 3 5 3 1 y n 1 y n 2 y n 3 4 4 8
系统函数H(z)展开成部分分式之和的形式，就可 以得到滤波器的并联型结构。 当N=M时，展开式为
H ( z ) A0 H1 ( z ) H 2 ( z ) H N ( z ) Ai A0 1 d i z i i 1
N
共轭复根两两合并得到实系数的二阶网络，
F Ai 0i 1i z 1 H ( z ) A0 1 1 pi z 1 1i z 1 2i z 2 i 1 i 1 E
成程序让计算机来执行， 这也就是用软件来实现数字滤波器。
时域离散系统可以用差分方程、单位脉冲响应以及 系统函数进行描述。系统输入、输出服从N阶差分方程
y n bi xn i ai yn i
i 0 i 1
M
N
其系统函数为
H ( z)
bi z i 1 ai z i
第五章 时域离散系统的基本网络结构
数字滤波器和FFT一样，是数字信号处理 的重要内容。
本章的主要内容就是描述数字滤波器的基 本网络结构。（IIR、FIR）
引言
时域离散系统或网络可以用差分方程、单 位脉冲响应以及系统函数进行描述。
M
N
y(n) bi x(n i) ai y(n i)
i0
i 1
系统函数H(z)为
M
H (z)
(2) 流图环路中必须存在延时支路；
(3) 节点和支路的数目是有限的。
信号流图表达的系统含义
每个节点连接的有输入支路和输出支路，节点变 量等于所有输入支路的输出之和.
根据信号流图可以求出系统函数（节点法、梅逊 公式法）。
1(n) 2 (n 1) 2 (n) 2 (n 1) 2 (n) x(n) a12 (n) a21n y(n) b21(n) b12 (n) b02(n)
画出H(z)的直接型结构和级联型结构。
级联型
解： 将H(z)进行因式分解，得到： H(z)=(0.6+0.5z-1)(1.6+2z-1+3z-2)
其直接型结构和级联型结构如图所示。
x(n)
0.6
z－ 1 0.5
1.6 z－ 1
2 z－ 1
3
y(n) x(n)
z－ 1
z－ 1
z－ 1
0.96 2
2.8 1.5 y(n)
0 j
y(n)
1 j
z－ 1 1j
1 j
z－ 11 j
(a)
2 j
z－
1
2
j
(b)
一阶和二阶直接型网络结构 (a)直接型一阶网络结构；(b)直接型二阶网络结构
IIR的级联型例题
本章的主要内容就是描述数字滤波器的基 本网络结构。（IIR、FIR）
引言
时域离散系统或网络可以用差分方程、单 位脉冲响应以及系统函数进行描述。
M
N
y(n) bi x(n i) ai y(n i)
i0
i 1
系统函数H(z)为
M
H (z)
(2) 流图环路中必须存在延时支路；
(3) 节点和支路的数目是有限的。
信号流图表达的系统含义
每个节点连接的有输入支路和输出支路，节点变 量等于所有输入支路的输出之和.
根据信号流图可以求出系统函数（节点法、梅逊 公式法）。
1(n) 2 (n 1) 2 (n) 2 (n 1) 2 (n) x(n) a12 (n) a21n y(n) b21(n) b12 (n) b02(n)
画出H(z)的直接型结构和级联型结构。
级联型
解： 将H(z)进行因式分解，得到： H(z)=(0.6+0.5z-1)(1.6+2z-1+3z-2)
其直接型结构和级联型结构如图所示。
x(n)
0.6
z－ 1 0.5
1.6 z－ 1
2 z－ 1
3
y(n) x(n)
z－ 1
z－ 1
z－ 1
0.96 2
2.8 1.5 y(n)
0 j
y(n)
1 j
z－ 1 1j
1 j
z－ 11 j
(a)
2 j
z－
1
2
j
(b)
一阶和二阶直接型网络结构 (a)直接型一阶网络结构；(b)直接型二阶网络结构
IIR的级联型例题
第5章_时域离散系统的网络结构
b0 x(n) w 2′ z－ 1 w2 －a 1 －a2 b1 z－ 1 w1 b2 y(n)
(5.2.1) 1 (n) 2 (n 1) (n 1) 2 (n) 2 (n ) x(n ) a1 2 (n ) a21n 2 (n) y (n ) b21 (n ) b12 (n) b02
ZT
w2(n) =w1(n)
w3(n) =w2(n-1)
W2(z)=W1(z)
W3(z)=z-1W2(z)
W4(z)=b0W2(z)+b1W3(z)
w4(n) =b0w2(n)+b1w3(n)
y(n)=w4(n)
Y(z)=W4(z)
Y ( z ) b0 b1 z 1 11 H ( z) 1 X ( z ) 1 az
6
第5章 时域离散系统的网络结构
3. 基本信号流图
信号流图由连接节点的一些有方向性的支路构成
流图中每一个节点都用一个节点变量表示，x(n) 称为 输入节点变量， y(n) 表示输出节点变量， w1(n), w2(n), 和 w’2(n) 也是节点变量。和每个节点连接的有输入支路和 输出支路，节点变量等于所有输入支路的输出之和。 节点变量和其他节点变量之间的关系用下式表示：
2
5.1 引言
及系统函数进行描述。 (1) 系统单位取样响应 (2) 传输函数 频率响应
H(ej)
第5章 时域离散系统的网络结构
一般时域离散系统或网络可以用差分方程、单位脉冲响应以
h(n)
H (e j ) DTFT [h(n)]
j n h ( n ) e
n
输出：
一个对输入x(n)的M阶延 时链结构，每节延时抽 头后加权相加，构成一 个横向结构网络。
(5.2.1) 1 (n) 2 (n 1) (n 1) 2 (n) 2 (n ) x(n ) a1 2 (n ) a21n 2 (n) y (n ) b21 (n ) b12 (n) b02
ZT
w2(n) =w1(n)
w3(n) =w2(n-1)
W2(z)=W1(z)
W3(z)=z-1W2(z)
W4(z)=b0W2(z)+b1W3(z)
w4(n) =b0w2(n)+b1w3(n)
y(n)=w4(n)
Y(z)=W4(z)
Y ( z ) b0 b1 z 1 11 H ( z) 1 X ( z ) 1 az
6
第5章 时域离散系统的网络结构
3. 基本信号流图
信号流图由连接节点的一些有方向性的支路构成
流图中每一个节点都用一个节点变量表示，x(n) 称为 输入节点变量， y(n) 表示输出节点变量， w1(n), w2(n), 和 w’2(n) 也是节点变量。和每个节点连接的有输入支路和 输出支路，节点变量等于所有输入支路的输出之和。 节点变量和其他节点变量之间的关系用下式表示：
2
5.1 引言
及系统函数进行描述。 (1) 系统单位取样响应 (2) 传输函数 频率响应
H(ej)
第5章 时域离散系统的网络结构
一般时域离散系统或网络可以用差分方程、单位脉冲响应以
h(n)
H (e j ) DTFT [h(n)]
j n h ( n ) e
n
输出：
一个对输入x(n)的M阶延 时链结构，每节延时抽 头后加权相加，构成一 个横向结构网络。
5 时域离散系统的网络结构
误差， 误差，运算速度以及系统的 复杂程度和成本
表示方法： 表示方法：网络结构
5.2 用信号流图表示网络结构
1、数字信号处理中的三种基本算法： 数字信号处理中的三种基本算法：
y(n) = ∑ b x(n − i) + ∑ ai y(n − i) i
i =0 i= 1 M N
方框图表示法 延时单元 x(n) 加法单元 x1(n) z
1 2 3 4 信号流图 Z -1 Z -1
a1y(n −1) + a2y(n − 2)
6 5
无限长脉冲响应(IIR) (IIR)基本网络结构 5.3 无限长脉冲响应(IIR)基本网络结构 流图结构： 流图结构： 节点 -源节点 -吸收节点 -网络节点 支路 -输入支路
6 5 1 2 3 4 Z -1 Z -1
1 1−
∑
N
i =1
ai z − i
x(n)
H1(z) y1(n)
H2(z)
y(n)
x(n)
H1(z) y1(n)
H2(z)
2 ( z ) =
y(n)
1 1−
H 1( z) =
∑
M
i=0
bi z − i
H
∑
N
y1 (n) = ∑ bi x(n − i )
i =0
M
i =1
ai z −i
y (n) = y1 (n) + ∑ ai y (n − i )
Y(z) = ∑bi X (z) ⋅ z + ∑aa j(z(z) ⋅−z ,iH(z) = Y Y) ⋅ z j − ∑j i
−i i=0 j =1 i=1 M
N N
=
Y(z) H(z) = = X (z)
时间离散系统网络结构共37页文档
10.3z1 10.4z1 10.6z110.5z1 H1(z)H2(z)
15
还可以如下式这样进行分解： H (z ) 1 1 0 0 . .4 6 z z 1 1 1 1 0 0 . .3 5 z z 1 1 H 3 (z )H 4 (z )
3
如果系统输入和输出服从N阶差分方程：
M
N
y(n ) b ix(n i) a ky(nk)
i 0
k 1
则系统函数H(z)用下式表示：
M
H(z)
Y(z) X(z)
bizi
i0 N 1 akzk
k1
基本运算：加法，乘法（乘以常数），移位（时延）
Hale Waihona Puke 4两种图形表示方法介绍(方框图，信号流图)： 加法：
3.有N个极点和M个零点。为了保持系统稳定，所有极点应在单位 圆内
4.基本网络结构有三种：直接型，级联型，并联型.
10
5.3 无限长脉冲响应（IIR）的基本网络结构
1 直接型网络结构
将N阶差分方程重写如下：
M
N
y(n ) b ix(ni) a ky(nk)
i 0
k 1
为简单起见, 假设M=N=2
9
IIR数字网络的特点：
M
N
差分方程： y(n) bi x(n i) ak y(n k)
i0
k 1
M
bi Z i
系统函数： H (z)
i0 N
h(n) Z n
1 ak Z k n0
k 1
1.单位脉冲响应h(n)为无限长（存在无限多个n，使h(n)不为零）
2.存在输出到输入的反馈，即信号流图中含有环路
2
2
y(n) b ix(ni) aky(nk)
15
还可以如下式这样进行分解： H (z ) 1 1 0 0 . .4 6 z z 1 1 1 1 0 0 . .3 5 z z 1 1 H 3 (z )H 4 (z )
3
如果系统输入和输出服从N阶差分方程：
M
N
y(n ) b ix(n i) a ky(nk)
i 0
k 1
则系统函数H(z)用下式表示：
M
H(z)
Y(z) X(z)
bizi
i0 N 1 akzk
k1
基本运算：加法，乘法（乘以常数），移位（时延）
Hale Waihona Puke 4两种图形表示方法介绍(方框图，信号流图)： 加法：
3.有N个极点和M个零点。为了保持系统稳定，所有极点应在单位 圆内
4.基本网络结构有三种：直接型，级联型，并联型.
10
5.3 无限长脉冲响应（IIR）的基本网络结构
1 直接型网络结构
将N阶差分方程重写如下：
M
N
y(n ) b ix(ni) a ky(nk)
i 0
k 1
为简单起见, 假设M=N=2
9
IIR数字网络的特点：
M
N
差分方程： y(n) bi x(n i) ak y(n k)
i0
k 1
M
bi Z i
系统函数： H (z)
i0 N
h(n) Z n
1 ak Z k n0
k 1
1.单位脉冲响应h(n)为无限长（存在无限多个n，使h(n)不为零）
2.存在输出到输入的反馈，即信号流图中含有环路
2
2
y(n) b ix(ni) aky(nk)
信号与系统课件--第五章 时域离散系统的基本网络结构
1
用网络结构表示具体的算法，网络结构实际表示的是一种 运算结构
§ 5.2 用信号流图表示网络结构
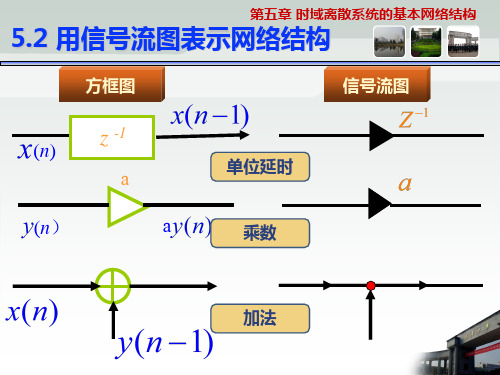
一、数字信号处理中有三种基本算法：乘法、加法和单 位延迟，如下：
结构框图 加法
x1 ( n ) x1 ( n ) x 2 ( n ) x2 (n )
信号流图
•
a
乘法
x1 ( n )
a
a x1 ( n )
形成一个二阶网络
H (z) H 1(z)H 2 (z) H k (z)
H j (z)
0 j 1 j z
11jz
1
1
2jz
2
2jz
2
式中 H j ( z ) 表示一个一阶或二阶的数字网络的系统函数， 采用直接型网络结构
x (n ) •
y (n ) • j0 •
一，直接型（卷积型,横截型） 由 H (z)
∴
N 1
h(n ) z
n
n 0
y (n)
N 1
k 0
h(k ) x(n k )
h ( 0 ) x ( n ) h (1) x ( n 1) ....
) n(x
)0( h
•
1
z
•
1
z
•
1
z •
•
•
)1( h
•
输出端的噪声功率最小。
缺点：调整零点不方便，当H ( z )有多阶极点时，部分
分式展开较麻烦
§5.4 有限长脉冲响应基本网络结构
FIR网络结构的特点：没有反馈支路，h(n)有限长度
H (z)
N 1
h(n ) z
5.1-5.3时域离散系统的基本网络结构域状态变量分析法
对 H (z )实施以下部分分式展开：
M N
H ( z)
Bk z
k 0
k
k 1
L
Ak 1 zk z
1
k 1
P
0 k 1k z
1
1 2
1 a1k z a2 k z
可以写成：
H ( z ) H 1 ( z ) H 2 ( z ) .... H n ( z )
10
例5.3.1 设IIR数字滤波器的系统函数H(z)为
H (z) 8 4z 1 5 4 z
1
11 z 3 4 z2源自 2z 1 8 z3
1
2
3
画出该滤波器的直接型结构 解： 有H(z)写出差分方程如下： y(n)=5/4y(n-1)-3/4y(n-2)+1/8y(n-3) +8x(n)- 4x(n-1) +11x(n-2)-2x(n-3)
级联型
并联型
7
一、直接型
1、IIR数字滤波器的直接（I）型结构 采用信号流图所定义的符号，直接画出差分方程对 应系统的信号流图结构称为直接（I）型结构。
y ( n)
M=N
a
k 1
N
k
y ( n k ) bk x( n k )
k 0
M
8
2、IIR数字滤波器的直接（Ⅱ） 将“ IIR 数字滤波器的直接 （I）型结构”中的延时 单元 尽可能减少的一种流图结构，称为直接（Ⅱ ）型结构。 分母延时
1 z 1 0.4 z 1
由此得到级联型结构的流图
21
③ 将H(z)进行部分分式展开得：
H ( z ) 0.1 0.6 1 0.4 z
M N
H ( z)
Bk z
k 0
k
k 1
L
Ak 1 zk z
1
k 1
P
0 k 1k z
1
1 2
1 a1k z a2 k z
可以写成：
H ( z ) H 1 ( z ) H 2 ( z ) .... H n ( z )
10
例5.3.1 设IIR数字滤波器的系统函数H(z)为
H (z) 8 4z 1 5 4 z
1
11 z 3 4 z2源自 2z 1 8 z3
1
2
3
画出该滤波器的直接型结构 解： 有H(z)写出差分方程如下： y(n)=5/4y(n-1)-3/4y(n-2)+1/8y(n-3) +8x(n)- 4x(n-1) +11x(n-2)-2x(n-3)
级联型
并联型
7
一、直接型
1、IIR数字滤波器的直接（I）型结构 采用信号流图所定义的符号，直接画出差分方程对 应系统的信号流图结构称为直接（I）型结构。
y ( n)
M=N
a
k 1
N
k
y ( n k ) bk x( n k )
k 0
M
8
2、IIR数字滤波器的直接（Ⅱ） 将“ IIR 数字滤波器的直接 （I）型结构”中的延时 单元 尽可能减少的一种流图结构，称为直接（Ⅱ ）型结构。 分母延时
1 z 1 0.4 z 1
由此得到级联型结构的流图
21
③ 将H(z)进行部分分式展开得：
H ( z ) 0.1 0.6 1 0.4 z
第5章 时域离散系统的网络结构
有限长单位脉冲响应网络，简称FIR（Finite Impulse Response）网络，FIR网络中一般不存在
输出对输入的反馈支路，因此差分方程为：
y(n)
M
bi x(n i)
i0
单位脉冲响应
h(n) b0n
0nM 其它n
无限长单位脉冲响应网络，简称IIR（Infinite Impulse Response）网络。 IIR网络结构存在输出 对输入的反馈支路，这类网络的单位脉冲响应是无限
将每一部分用直接型结构实现，其并联型网络结构
24
5.4 有限长脉冲响应基本网络结构
FIR网络结构特点是没有反馈支路，即没 有环路，其单位脉冲响应是有限长的。
设单位脉冲响应h(n)长度为N，其系统函 数H(z)和差分方程分别为：
N 1
H (z) h(n)z n n0 N 1
Y (z) b2W1(z) b1W2 (z) b0W2 '(z)
经过联立求解得到：
H (z)
Y (z) X (z)
b0 b1z1 b2 z2 1 a1z1 a2z2
当结构比较复杂时，此方法较麻烦，不如用梅逊(Masson)公 式直接写出H(z)方便。
10
网络结构的分类
图5.2.2 信号流图
9
【例 5.2.1】求图 5.2.2(a)信号流图决定的系统函数H(z)。
解：图5.2.2(a)信号流图的节点变量方程为式(5.2.1),对其 进行z变换，得：
W1 ( z ) W2 (z)
W2 (z)z1 W2 '(z)z1
W2 '(z) X (z) a1W2 (z) a2W1(z)
数字信号处理 第五章 时域离散系统的基本网络结构与状态变量分析法
448
画出该滤波器的直接型结构。
解：由H (z)写出差分方程：
y(n) 5 y(n 1) 3 y(n 2) 1 y(n 3) 8x(n) 4x(n 1)
4
4
8
11x(n 2) 2x(n 3)
H (z) 8 4z1 11z2 2z3 1 5 z1 3 z2 1 z3 448
(二) 级联型结构
M
(1 cr z1)
H (z)
A
r0 N
(1 dr z1)
r 1
H j(z)
0 j 1 j z1 1 1 j z1 2 j z2 1 1 j z1 2 j z2
H (z)
L
A
j 1
0 j 1 j z1 1 1 j z1
L j 1
i0
i1
系统函数H (z)为
M
H (z)
Y (z) X (z)
bi zi
i0 N 1 ai zi
i1
H1(
z)
1
0.8z
1 1
0.15z
2
H2(z)
1
1.5 0.3z1
1
2.5 0.5 z 1
H3(z)
1
1 0.3 z 1
1
1 0.5 z 1
H1(z) H2(z) H3(z)
end
§5.2 用信号流图表示网络结构
y(n)
直接II型结构
M
bi zi
H(z)
i0 N
1 ai zi
i1
x(n)
b0
y(n)
a1
z1 b1
a2
z 1 b2
z 1
aN z1 bN
优缺点：
丁玉美《数字信号处理》笔记和课后习题(时域离散系统的网络结构)
图 5-10 FIR 滤波器频域采样结构
8 / 44
圣才电子书
三、FIR 系统的基本网络结构 FIR 网络结构特点是没有反馈支路，其单位脉冲响应是有限长的。设单位脉冲响应 h（n） 长度为 N，其系统函数 H（z）和差分方程分别为：
1．直接型 按照 H（z）或者卷积公式直接画出的结构图，称为直接型网络结构或者称为卷积型结 构。
5 / 44
圣才电子书 十万种考研考证电子书、题库视频学习平台
1 / 44
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 5-2 信号流图 3．网络结构分类 一般将网络结构分成两类，一类称为有限长单位脉冲响应网络，简称 FIR 网络，另一类 称为无限长单位脉冲响应网络，简称 IIR 网络。 （1）FIR 网络中一般丌存在输出对输入的反馈支路，因此，差分方程用下式描述： 单位脉冲响应 h（n）是有限长的，表示为： （2）IIR 网络结构存在输出对输入的反馈支路，信号流图中存在反馈环路。这类网络 的单位脉冲响应是无限长的。
3．并联型 （1）系统函数和流图形式 ①将级联形式的 H（z）展成部分分式形式，则得到：
对应的网络结构为这 k 个子系统并联。Hi（z）通常为一阶网络或二阶网络，网络系数 均为实数。二阶网络的系统函数一般为：
式中，β0j、β1j、α1i 和 α2i 都是实数。如果 β1j＝α2i＝0，则构成一阶网络。
图 5-3 IIR 网络直接型结构 2．级联型 （1）系统函数和流图形式 ①将直接型表达式中分子、分母多项式分别迚行因式分解得到：
上式中，A 是常数，cr 和 dr 分别表示 H（z）的零点和极点。cr 和 dr 是实数或者是共轭
3 / 44
圣才电子书 十万种考研考证电子书、题库视频学习平台
8 / 44
圣才电子书
三、FIR 系统的基本网络结构 FIR 网络结构特点是没有反馈支路，其单位脉冲响应是有限长的。设单位脉冲响应 h（n） 长度为 N，其系统函数 H（z）和差分方程分别为：
1．直接型 按照 H（z）或者卷积公式直接画出的结构图，称为直接型网络结构或者称为卷积型结 构。
5 / 44
圣才电子书 十万种考研考证电子书、题库视频学习平台
1 / 44
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 5-2 信号流图 3．网络结构分类 一般将网络结构分成两类，一类称为有限长单位脉冲响应网络，简称 FIR 网络，另一类 称为无限长单位脉冲响应网络，简称 IIR 网络。 （1）FIR 网络中一般丌存在输出对输入的反馈支路，因此，差分方程用下式描述： 单位脉冲响应 h（n）是有限长的，表示为： （2）IIR 网络结构存在输出对输入的反馈支路，信号流图中存在反馈环路。这类网络 的单位脉冲响应是无限长的。
3．并联型 （1）系统函数和流图形式 ①将级联形式的 H（z）展成部分分式形式，则得到：
对应的网络结构为这 k 个子系统并联。Hi（z）通常为一阶网络或二阶网络，网络系数 均为实数。二阶网络的系统函数一般为：
式中，β0j、β1j、α1i 和 α2i 都是实数。如果 β1j＝α2i＝0，则构成一阶网络。
图 5-3 IIR 网络直接型结构 2．级联型 （1）系统函数和流图形式 ①将直接型表达式中分子、分母多项式分别迚行因式分解得到：
上式中，A 是常数，cr 和 dr 分别表示 H（z）的零点和极点。cr 和 dr 是实数或者是共轭
3 / 44
圣才电子书 十万种考研考证电子书、题库视频学习平台
课后习题及答案_第5章 时域离散系统的网络结构--习题
第4章 时域离散系统的网络结构习题1. 已知系统用下面差分方程描述:)1(31)()2(81)1(43)(−+−−n x n x n y n y n y ＋－＝试分别画出系统的直接型、 级联型和并联型结构。
式中x (n )和y (n )分别表示系统的输入和输出信号。
2． 设数字滤波器的差分方程为)2(41)1(31)1()()(−+−+−+=n y n y n x n x n y试画出系统的直接型结构。
3. 设系统的差分方程为y (n )=(a +b )y (n －1)－aby (n －2)+x (n －2)+(a +b )x (n －1)+ab式中, |a |<1， |b |<1, x (n )和y (n )分别表示系统的输入和输出信号, 试画出系统的直接型和级联型结构。
4. 设系统的系统函数为)81.09.01)(5.01()414.11)(1(4)(211211−−−−−−++−+−+=z z z z z z z H试画出各种可能的级联型结构， 并指出哪一种最好。
5． 题 5图中画出了四个系统， 试用各子系统的单位脉冲响应分别表示各总系统的单位脉冲响应， 并求其总系统函数。
题 5图6． 题6图中画出了10种不同的流图， 试分别写出它们的系统函数及差分方程。
题6图7. 假设滤波器的单位脉冲响应为h (n )=a n u (n ) 0＜a ＜1求出滤波器的系统函数， 并画出它的直接型结构。
8. 已知系统的单位脉冲响应为h (n )=δ(n )+2δ(n －1)+0.3δ(n －2)+2.5δ(n －3)+0.5δ(n －5)试写出系统的系统函数， 并画出它的直接型结构。
9. 已知FIR 滤波器的系统函数为)9.01.29.01(101)(4321−−−−++++=z z z z z H试画出该滤波器的直接型结构和线性相位结构。
10． 已知FIR 滤波器的单位脉冲响应为:(1) N=6h(0)=h(5)=15h(1)=h(4)=2h(2)=h(3)=3(2) N=7h(0)=h(6)=3h(1)=－h(5)=－2h(2)=－h(4)=1h(3)=0试画出它们的线性相位型结构图，并分别说明它们的幅度特性、相位特性各有什么特点。
数字信号处理第五章 时域离散系统的网络结构
i 0 i 1
M
N
b0
w(n)
z-1
y(n)
z-1 bM-1
z-1 -aN-1
z-1
bM -aN
z-1
共需(N+M)级延时单元
先对调：
x(n) b0 Z-1 b1 Z-1 Z-1 b2 bM -a1 -a2 -a N-1 -aN 第一部分 对调 y(n) Z-1 对调 Z-1 Z-1 Z-1 x(n) -a1 -a2 -a N-1 -aN Z-1 Z-1 Z-1 b0 Z-1 b1 Z-1 b2 Z-1 bM y(n)
i 0 i 1
M
N
Y ( z) H ( z) X ( z)
b z
i
M
i
1 ai z i
i 1
i 0 N
若给定一个差分方程，不同的算法有很多，例如 对于差分方程：
y(n) 0.8y(n 1) 0.15y(n 2) x(n)
1 H 1 (z ) 1 0.8z 1 0.15z 2 1.5 2.5 H 2 (z ) 1 1 0.3z 1 0.5z 1 1 1 H 3 (z ) 1 1 0.3z 1 0.5z 1
直接型结构特点：
(1) 有反馈的N阶延时网络实现极点； 横向结构M节延时网络实现零点。
b0 -a1 Z b1 -a2Z-1 b2
-1
y(n
(2) 实现N阶滤波器（一般N>=M)只需N级 -a N-1 - bM Z 1 延时单元,所需延时单元最少。 Z-1 (3) 系数ai,bi不是直接决定单个零极点， -aN 因而不能很好地进行滤波器性能控制。 (4) 直接型实现的滤波器零极点调节不便 M ,容易出现不稳定现象 i
M
N
b0
w(n)
z-1
y(n)
z-1 bM-1
z-1 -aN-1
z-1
bM -aN
z-1
共需(N+M)级延时单元
先对调：
x(n) b0 Z-1 b1 Z-1 Z-1 b2 bM -a1 -a2 -a N-1 -aN 第一部分 对调 y(n) Z-1 对调 Z-1 Z-1 Z-1 x(n) -a1 -a2 -a N-1 -aN Z-1 Z-1 Z-1 b0 Z-1 b1 Z-1 b2 Z-1 bM y(n)
i 0 i 1
M
N
Y ( z) H ( z) X ( z)
b z
i
M
i
1 ai z i
i 1
i 0 N
若给定一个差分方程，不同的算法有很多，例如 对于差分方程：
y(n) 0.8y(n 1) 0.15y(n 2) x(n)
1 H 1 (z ) 1 0.8z 1 0.15z 2 1.5 2.5 H 2 (z ) 1 1 0.3z 1 0.5z 1 1 1 H 3 (z ) 1 1 0.3z 1 0.5z 1
直接型结构特点：
(1) 有反馈的N阶延时网络实现极点； 横向结构M节延时网络实现零点。
b0 -a1 Z b1 -a2Z-1 b2
-1
y(n
(2) 实现N阶滤波器（一般N>=M)只需N级 -a N-1 - bM Z 1 延时单元,所需延时单元最少。 Z-1 (3) 系数ai,bi不是直接决定单个零极点， -aN 因而不能很好地进行滤波器性能控制。 (4) 直接型实现的滤波器零极点调节不便 M ,容易出现不稳定现象 i
时域离散系统的网络结构及数字信号处理的实现
时域离散系统的网络结构 及数字信号处理的实现
• 引言 • 时域离散系统概述 • 时域离散系统的网络结构 • 数字信号处理在时域离散系统中的应
用 • 时域离散系统的性能评估 • 结论与展望
01
引言
背景介绍
数字信号处理技术的发展
随着数字信号处理技术的不断发展，时域离散系统的网络结构在信号处理领域 的应用越来越广泛。
收敛性是指时域离散系统对输入信号的响应能够随着时间的推移逐渐收敛到期望的 输出。
收敛性分析主要关注系统对输入信号的响应是否能够达到预期的输出，并且收敛的 速度是否满足要求。
收敛性的好坏直接影响到数字信号处理的效果，因此在进行系统设计时需要充分考 虑收敛性的要求。
性能优化方法
01
为了提高时域离散系统的性能， 可以采用多种优化方法。
2
通过对数字信号处理算法的研究，实现了多种信 号处理功能，如滤波、频谱分析网络结构和数字信号处理算法的有 效性和实用性，为相关领域的研究和应用提供了 新的思路和方法。
未来研究方向
深入研究时域离散系统的网络结构和信号处理算 法，进一步提高其性能和精度。
探索与其他领域的交叉研究，如通信、控制、图 像处理等，以拓展应用范围和提升技术价值。
线性时不变离散系统具有叠加性、时移性和频移性等特性，广泛应用于数字信号 处理、控制系统等领域。
非线性时不变离散系统
非线性时不变离散系统是指系统的输出信号与输入信号之间的关系是非线性的，且系统参数不随时间变 化的离散时间系统。这种系统的网络结构通常由非线性差分方程描述，如y(n) = f(x(n), y(n-1))，其中f是 非线性函数。
图像处理
图像处理中的离散信号处理技 术，如图像压缩、图像增强等 。
• 引言 • 时域离散系统概述 • 时域离散系统的网络结构 • 数字信号处理在时域离散系统中的应
用 • 时域离散系统的性能评估 • 结论与展望
01
引言
背景介绍
数字信号处理技术的发展
随着数字信号处理技术的不断发展，时域离散系统的网络结构在信号处理领域 的应用越来越广泛。
收敛性是指时域离散系统对输入信号的响应能够随着时间的推移逐渐收敛到期望的 输出。
收敛性分析主要关注系统对输入信号的响应是否能够达到预期的输出，并且收敛的 速度是否满足要求。
收敛性的好坏直接影响到数字信号处理的效果，因此在进行系统设计时需要充分考 虑收敛性的要求。
性能优化方法
01
为了提高时域离散系统的性能， 可以采用多种优化方法。
2
通过对数字信号处理算法的研究，实现了多种信 号处理功能，如滤波、频谱分析网络结构和数字信号处理算法的有 效性和实用性，为相关领域的研究和应用提供了 新的思路和方法。
未来研究方向
深入研究时域离散系统的网络结构和信号处理算 法，进一步提高其性能和精度。
探索与其他领域的交叉研究，如通信、控制、图 像处理等，以拓展应用范围和提升技术价值。
线性时不变离散系统具有叠加性、时移性和频移性等特性，广泛应用于数字信号 处理、控制系统等领域。
非线性时不变离散系统
非线性时不变离散系统是指系统的输出信号与输入信号之间的关系是非线性的，且系统参数不随时间变 化的离散时间系统。这种系统的网络结构通常由非线性差分方程描述，如y(n) = f(x(n), y(n-1))，其中f是 非线性函数。
图像处理
图像处理中的离散信号处理技 术，如图像压缩、图像增强等 。
数字信号处理时域离散系统的基本网络结构与状态变量分析法
4
4
8
11x(n 2) 2x(n 3)
第5章 时域离散系统的基本网络 结构与状态变量分析法
x(n)
8
y(n)
54
z－ 1－ 4
3 4
z－ 1 11
18
z－
1
－
2
图5.3.2 例5.3.1图
2. 级联型
第5章 时域离散系统的基本网络 结构与状态变量分析法
在(5.1.2)式表达旳系统函数H(z)中，公子分母均为 多项式，且多项式旳系数一般为实数，现将分子分母
x(n)
－ －zN
H(0)
WN0
z－ 1
H(1)
z－ 1 WN1
H(N－1)
z－ 1 WN N 1
y(n) 1 N
图5.4.3 FIR滤波器频率采样构造
第5章 时域离散系统的基本网络 结构与状态变量分析法
(1)在频率采样点ωk，H(ejωk)=H(k)，只要调整H(k)( 即一阶网络Hk(z)中乘法器旳系数H(k))，就能够有效地 调整频响特征，使实际调整以便。
Y(z)=H1(z)X(z)+H2(z)X(z)+…+Hk(z)X(z)
第5章 时域离散系统的基本网络 结构与状态变量分析法
例5.3.3 画出例题5.3.2中旳H(z)旳并联型构造。
解 将例5.3.2中H(z)展成部分分式形式：
H
(z)
16
1
8 0.5z 1
1
16 20z1 z1 0.5z2
其直接型构造和级联型构造如图5.4.2所示。
x(n)
0.6
z－ 1 0.5
1.6 zபைடு நூலகம் 1
2 z－ 1
数字信号处理-时域离散信号的网络结构
第五章 时域离散系统的基本网络结构
b0
b1
z1 w2
w1
z 1 a1 a2
b2 y(n)
1、信号流图中所有的支路都是基本的，支路增益是常数或 者是1/Z； 2、流图环路中必须存在延迟支路；
3、节点和支路的数目是有限的；
第五章 时域离散系统的基本网络结构
判断下列两图是否为基本信号流图。
以上两图都不满足基本信号流图的条件，图1支路的增益 不是常数或Z-1，图2的流图环路中没有延时支路。
无限长脉冲响应网络（IIR）
存在输出对输入的反馈支路,其单位脉冲h(n)是无限长
M
N
y(n) bi x(n i) ai y(n i)
i0
i 1
基本信号流图对应一种具体的运算方法，非基本信号流图 不能用一种具体的运算方法来实现。网络结构可以通过基本 信号流图来描述。
基本网络结构
第五章 时域离散系统的基本网络结构
有限长脉冲响应网络（FIR）
不存在输出对输入的反馈支路,其单位脉冲h(n)是有限长
M
y(n) bi x(n i) i0
5.2 用信号流图表示网络结构
y(n) a1y(n 1) a2 y(n 2) b0x(n)
x(n) b0
a1y(n-1) Z 1
a1
a2 y(n 2)
a2
Z 1
y(n)
不同的信号流图代表不 的运算方法，而对于同 一个系统函数可以有多 种信号流图相对应。
x(n)
w2'
基本信号流图
以上两图都不满足基本信号流图的条件图11支路的增益不是常数或zz11图22的流图环路中没有延时支路
第五章 时域离散系统的基本网络结构
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
二.用信号流图表示系统的运算
b0
b1
x(n)
w2′ z－1w2
z－1 w1
y(n) x ( n )
H (z)
y (n )
－ a1
b2
－a2 图5.2.2 信号流图
(a)基本信号流图；(b)非基本信号流图
从基本运算考虑，满足以下条件，称为基本信号 流图(Primitive Signal Flow Graghs)。
本章讲述时域离散系统的网络结构。
一般时域离散系统或网络可以用差分方程、单位脉 冲响应以及系统函数进行描述。
如果系统输入和输出服从N阶差分方程
M
N
y(n)bix(ni)aiy(ni)
i0
i1
其系统函数H(z)为
M
H (z)
Y (z) X (z)
bi zi
i0 N 1 ai zi
H (z)1 1 .8 2 5 z4 z 1 10 .1 7 1 5 z z 2 2 2 0 z .1 2 35z 3
x (n )
x(n 1) x ( n )
z 1
z 1
x(n 1)
x (n )
ax(n)
x (n )
a
ax(n)
x1(n )
a x1(n)x2(n)
x1(n )
x1(n)x2(n)
x2 (n )
x2 (n )
节点和节点变量 图5.2.1 三种基本运算的流图表示
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
2. IIR网络结构 存在输出对输入的反馈支路; 单位脉冲响应是无限长的. 例如，一个简单的一阶因果IIR网络差分方程为 y(n)=ay(n-1)+x(n) 其单位脉冲响应 h(n)=anu(n)。
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
5.3 无限长脉冲响应基本网络结构
1.直接型
N阶差分方程重写如下：
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
三.网络结构分类 1. FIR网络结构 不存在输出对输入的反馈支路, 差分方程用下式描述：
M
y(n) bix(ni)
i0
其单位脉冲响应h(n)是有限长的，表示为
h(n) b0n,,0其 它 nnM
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
1
N
M
bizi
1 aizi i0
i1
X
x(n)
b0
y(n)
x(n 1) x(n 2)
x(n)
x(n)
z1 b1 z1 b2
H1(z)
w1 a z1
1
z 1 a2 H2(z)
a z1 1 z 1
a2
a z1 1
y(n 1)
z 1
(a ) H (z) H 1 (z)H 2 (z)
式中，Hi(z)通常为一阶网络和二阶网络，网络 系统均为实数。
二阶网络的系统函数一般为
Hi(z)1a01iiz11iaz2i1z2
式中，β0i、β1i、α1i和α2i都是实数。如果α2i =0则构 成一阶网络.
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
并联系统可用下面的框图描述：
w 2(n )w '2(n 1 )
(5.2.1)
w y ( 'n 2 ) ( n ) b 2 w x 1 ( ( n n ) ) b a 1 1 w w 2 2 ( n ( n ) ) b 0 a w 2 'w 2 1 ( ( n n ) )
将(5.2.1)式进行z变换，得到：
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
级联系统可用下面的框图描述：
x(n) H1(z)
H2(z)
…
Hk(z) y(n)
H(z)
图中的Hj(z)表示一个一阶或二阶的数字网络的系统函 数, H(z)=H1(z)H2(z)…Hk(z) 。
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
B=[8,-4,11,-2];A=[1,-1.25,0.75,-0.125];[S,G]=tf2sos(B,A) S=
1.0000 -0.1900 0 1.0000 -0.2500 0 1.0000 -0.3100 1.3161 1.0000 -1.0000 0.5000 G= 8
(5.3.2)
式中，β0j、β1j、β2j、α1j和α2j均为实数。
这样H(z)就分解成一些一阶或二阶数字网络的
级联形式，如下式：
H(z)=H1(z)H2(z)…Hk(z)
(5.3.3)
式中Hj(z)表示一个一阶或二阶的数字网络的系统
函数，每个Hj(z)的网络结Байду номын сангаас均采用前面介绍的直接型
网络结构.
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
a2
H2(z)
w2 b0
y(n 2)
y(n)
M
bizi
1
N
i0
1 aizi
i1
z1 b1
z1 b2
H1(z)
b0
y(n)
z1 b1 z1 b2
(b) H(z) H2(z) H1(z)
1 N
M
bizi
1 aizi i0
i1
(c) 将延时支路合并
x(n) x(n)
0 j
z 1 j
1 1 j
(a)
0 j
z 1 j
11 j
z 2 j
12 j
(b)
y(n)
H(z)
0j 1jz1 11j z1
y(n)
H(z)10 j 1j1zjz1 1 2j2zjz22
图5.3.3 一阶和二阶直接型网络结构 (a)直接型一阶网络结构； (b)直接型二阶网络结构
M
N
y(n)bix(ni)aiy(ni)
i0
i1
N阶系统的系统函数为
M
bi z i
H (z)
i0 N
M
bizi
1
N
1 a i z i i0
1 aizi
i 1
i1
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
N=M=2时的网络结构如下
图5.3.1 IIR网络直接型结构
第5章 时域离散系统的基本网络 结构与状态变量分析法
例5.3.1 IIR数字滤波器的系统函数H(z)为
H(z)1854zz11131zz2212zz33 448
画出该滤波器的直接型结构。
解 由H(z)写出差分方程如下：
y(n)5y(n1)3y(n2)1y(n3)8x(n)
H
3(z)
1
1 0.3z
1
1
1 0.5z 1
可以证明H1(z)= H2(z) =H3(z)
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
5.2 用信号流图表示网络结构
一.三种基本运算 数字信号处理中有三种基本算法，即单位延迟、
乘法和加法。三种基本运算用流图表示如图5.2.1所示。
H1(z)
x(n)
H2(z)
y(n)
…….
Hk(z)
H(z)
图中的Hi(z)通常为一阶网络和二阶网络，整个系统 的系统函数为 H ( z ) H 1 ( z ) H 2 ( z ) H k ( z )。
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
例5.3.3 画出例题5.3.2中的H(z)的并联型结构。 解: 将例5.3.2中的
H (z)
A
r 1 N
(1 d r z 1)
(5.3.1)
r 1
式中A是常数,cr和dr分别表示零点和极点.
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
在(5.1.2)中系数ai和bi是实数, cr和dr 是实数或共
轭成对的复数,因此可形成一个二阶网络Hj(z).
Hj(z)如H 下j式(z)：10ja1j1zjz11a2j2zjz22
例5.3.2 设系统函数H(z)如下式：
H (z)1 1 .8 2 5z4 z 1 10 .1 7 1 5 z z 2 2 2 0 z .1 2 35z 3
试画出其级联型网络结构。 解 : 将H(z)分子分母进行因式分解，得到
H (z)(20 (1 .3 7 0 9 .z 2 5 1 z )( 4 1) (1 1 .2 z 4 z 1 10 .5 5 .z2 6 2)4z 2)
H(z)1854zz11131zz2212zz33 448
X
第5章 时域离散系统的基本网络 结构与状态变量分析法
2. 级联型
M
bi z i
H (z)
i0 N
1
ai z i
(5.1.2)
i0
将上式分子分母多项式分别进行因式分解，得到
M
(1 Cr z 1)
W1(z) W2(z)z1 W2(z) W2(z)z1 W2(z) X (z) a1W2(z) a2W1(z) Y (z) b2W1(z) b1W2(z) b0W2(z)
X
第5章 时域离散系统的基本网络 结构与状态变量分析法