具变指数非线性拟抛物方程弱解的唯一性

合集下载

两类带非局部项的非线性抛物方程的理论分析

Abstract
STUDY ON TWO CLASSES OF NONLINEAR PARABOLIC EQUATIONS WITH N ONLOCAL TERMS
ABSTRACT
Many problems in applied sciences can be described by partial differential equations. In order to explain some nonlinear phenomenon， and to provide some useful tools for practical fields，one needs to study the existence，uniqueness and stability of solutions to problems of partial differential equations.
保密□，在年解密后适用本授权书。本学位论文属于
不保密√。（请在以上方框内打“√”）
学位论文作者签名：刘桂兰日期： 2008 年 3 月 2 日
指导教师签名：王亚光日期： 2008 年 3 月 2 日
绪论
第一章绪论
1.1 问题背景
非线性抛物方程是一类重要的偏微分方程，来源于自然界中广泛存在的非线性现象．相变理论，渗透理论，图像处理，生物化学理论等领域中的许多问题都可以用这种方程来描述．如相变理论中的 Allen-Cahn 方程，流体力学中的 Cahn-Hilliard 方程等，这些方程不仅有明确的物理背景，而且还有广泛的应用价值，因而，对这些方程的数学理论进行研究是有意义的，也是十分必要的．
4
绪论
第一项：F (g) ，Gσ (g) 同问题 (1.3) 中给出的，这儿 Gσ 的引进是为了对图像进

双非线性抛物型方程解的正则性和唯一性

的唯一性．
ａ（５） ≤ ４ｆＳｆ＋ａ５，口４＞０，５ ≥０，ＳＥＲ；
（４）
－厂（ｓ）ＥＣ（Ｒ），ｙ１ｆ５一ｆ ≤ ｆ（ｓ）ｓ ≤ ｙ２ｆＳｆ＋
｛ “ （州）ｌ加一ｏ，
【ｕ（ｘ，０）一ｏ（ｚ）．
（１
献［６］证明了一般形式的双非线性Ｌａｐｌａｃｉａｎ方
程解的存在性，根据该结果，方程（１）存在弱解
“ （）满足
“ （ｚ，）ＥＣ（０，Ｔ；Ｌ。（））ｎＬ（０，丁；Ｈ（））ｎＬ（０，Ｔ；Ｌ（ｎ））．
性，即“ （￡）∈ Ｈ（ｎ）ＮＬｑ（ｎ）ｎＨ（０）．利用解的正则性和符号函数的性质，证明了方程弱解的
唯一性．
关键词：抛物型方程；正则性；弱解；勒让德变换
中图分类号：Ｏ１７５．２９文献标识码：Ａ
（６）
模，表示ｑ的共轭数，即＋－－７— １，其它类似字
ｑｑ
从上述假设可以看出，非线性项ａ和＿厂都是
母也表示此意义，ｃ表示可能彼此互不相同的常数，有时也用ｃ，ｃ， … 表示．
ＩＳＩ件。一口３ ≤ （ｓ）Ｓ ≤ ２ＩＳｌ件＋ａ３，
口１，ａ２＞０，口３≥ ０，ｒ≥ ０；（３）

非线性方程组解的存在唯一性定理,解的迭代方法和某些应用

非线性方程组解的存在唯一性定理,
解的迭代方法和某些应用
非线性方程组解的存在唯一性定理是世界著名数学家克里斯多福·康威发表于1951年的一项学术成果，它给出了非线性方程组的解的存在唯一性的定理，并被
认为是非线性数学的里程碑。

非线性方程组的解的存在唯一性定理给出了一种把非线性子问题转化为线性子
问题的解法，它将复杂的非线性方程组拆分成多个子问题，逐步对每个子问题求解，并把它们综合起来得到最终结果的方法，是现代非线性数学的重要研究内容。

它的应用被广泛应用在多个学科中，比如金融学，物理学，生物学等。

在这里，我们只讨论它在互联网中的使用场景。

它可以用来解决各种复杂的非线性优化问题，如多轮次排序问题，ID3决策树建模。

它可以有效地帮助我们提高网页排序质量、
构建更智能的搜索引擎等。

有了非线性方程组解的存在唯一性定理，我们也可以使用迭代方法来解决复杂
的非线性问题，比如梯度下降法，牛顿迭代以及二次原型算法。

这些迭代方法可以在互联网中用于实现网页排序，搜索推荐以及机器学习的自主优化等功能，让我们的搜索既“智能”又“高效”。

非线性方程组解的存在唯一性定理至今仍然在发挥重要作用，不仅在数学方面，也在各个行业，特别是在互联网中发挥出了重要的作用，可以大大提高搜索效率和精度，改变人们的网络体验。

一类非线性抛物方程初值问题整体解的存在唯一性

ＣＩ（・ｔ， “ ，其中Ｃ＞是常数和以后的Ｃ（）ｉ２３ …）），０Ｔ（＝，，为仅依赖于的常数．由引理１和引理２ｓ，对任何初始值Ｈ ∈ （，Ｍ＝Ｉ。，。Ｒ）令｛定义集合ＰＭ，） ¨ ∈ ） “ （＝｛Ｉ（，
收稿日期：００—１２１１—２５基金项目：南省教育厅自然科学基金（０９Ｂ１０７）；南工业大学校基金（０Ｔ０河２０１００河１ＸＰ０２）
作者简介：长顺（９Ｏ）男，南平顶山人，南工业大学理学院讲师．侯１８一，河河
（）１
（２）
其中＞０为常数，，，，ｆｈｇ为给定的非线性函数，）给定的初值函数．程（）如下的非线性抛ｕ（为方１和
有紧密联系，中Ｏ，，＞为常数．显然方程（）方程（）特殊情况，含ＧＢ方程和Ｓｂｌ其／０卢１是３的包ＢＭｏｏｅｖ—
引理２假设／Ｒ）０＝， ∈ＨｎＬ且＝［］，中＞．Ｊ ≤Ｍ， ∈Ｃ（，）０Ｍｓ＋１其０若ｌ “ 则有Ｉ（） ≤ ｌｕＩ厂
（），中（）其为依赖于的常数．
引理３
（）ｌ一ｌ，ＩＩ
Ｉｌ）１１ Ⅱ
。，）
Ｖ“ （・ ∈ ）
易见（是一Ｂｎｃ）ａａｈ空间．定义算子Ｊ（一（为再ｓ）：）

一类非线性弹性梁方程弱解存在的唯一性

维普资讯
第３卷
理
工
大
学
学
２００７年１月
ＪＯＵＲＮＡＩＯＦＴＡＩＹＵＡＮＵＮ１ＶＥＲＳＴＹＩＯＦＴＥＣＨＮ０Ｉ０ＧＹ
在本报文㈨
中
Ｖｏ．８Ｎｏ１１３．Ｊｎ２０ａ．０７
和初始条件下，明了一类具非线性本构关系的弹性粱方程弱解的存在性；此弹性梁方程弱解存证在
在的条件下，明了上述方程弱解的唯一性。证关键词：线性弹性梁方程；ｌｒｉ法｝解；在唯一性非Ｇａｅｋｎ弱存中图分类号：７．７ｏ１５２文献标识码：Ａ
一
文章编号：０７９３（０７００卜０１０－４２２０）卜０９４
舫便．
起一
Ｉｌ
一
记；的唯一性～三巩类非线性弹性梁方程弱解存在
闫思青，建文张
（太原理工大学理学院，西太原００２）山３０４
初始条件：
ｕｘ，）一 “ （）（Ｏ０，ｕ（Ｏｘ，）一 “ （．ｌ）（）２
边界条件：
ｕＯｆ（，）：Ｕ（，）一Ｕ（ｆ＝ｆ￡Ｏ，） ‘ （，）：０１￡＝．＝（）３
２弱解的存在性
首先证明初边值问题（）式～（）弱解的３式的存
显然ｘ中的范数与Ｈｎ）的范数相同。（中

具强阻尼非线性弹性梁方程弱解的存在唯一性

0 C (Ω) , 且 ‖u ‖∞ ≤c ‖u ‖, c 为与 u 无关的常数。
α,β为常数。在本文中我们将要研究一类比上述方程更具一般性的非线性弹性梁方程 ¨ u+ u
( 4) l ( 1)
引理 2 [4 ] ( Poincare 不等式 ) 设 f ∈H1 (Ω) , 且设对某个ξ∈ Ω � ,有 f ( ξ ) = 0 ,则 ‖f ‖ ≤ 1 ‖f ( 1) ‖. 2 引理 3[ 2 ] ( Gronwall 不等式 ) 设 f ∈L ∞ ( 0 ,
梁是工程建筑的基本构件之一 , 对于梁方程的研究 ,有着非常重大的理论意义和实际意义。非线性弹性梁方程在数学上是由四阶偏微分方程来描述的。近年来 , 关于弹性梁方程的研究已经取得了不少成果 [1 ] 。Ball 研究了两端固定的弹性梁方程 [ 2] ( ) ¨ u +α u4 l
1 预备知识
2 弱解的存在性
( s ) 下方有界 , 即存在常定理 1 设σ( s) ∈C1 ,σ ′
2 数 c0 , 使σ ′ (s) ≥c0 , u 0 ( x) ∈X , u1 ( x) ∈L (Ω ) , 则问
题 (1 ) - ( 3 ) 存在弱解 u = u ( x , t) , 对于任意的φ∈
和边界条件
u ( 0 , t) = u( l , t) = u u
(2) ( 2)
f ( t) ≤ c0 + k ( 0 , t) = (3) ( l , t) = 0
∫f ( s) d s ,
0
则
f ( t) ≤ c0 e kt .
下的初边值问题。其中 u �(2) 为强阻尼 ,σ( u ( 1) ) (1) 为非线性项。我们以 Sobolev 空间为工具 , 采用 Gal erki n 方法证明了弱解的存在性及唯一性 , 从而解决了该方程弱解的存在唯一性问题。

一类非线性双曲型方程弱解的存在唯一性

ｉｓｔｅｎｃｅａｎｄｕｎｉｑｕｅｎｅｓｓｏｆｗｅａｋｓｏｌｕｔｉｏｎｓｔｏａｃｌａｓｓｏｆｎｏｎｌｉｎｅａｒｈｙｐｅｒｂｏｌｉｃｅｑｕａｔｉｏｎｓ．
Ｋｅｙｗｏｒｄｓ：ｎｏｎｌｉｎｅａｒｈｙｐｅｒｂｏｌｉｃｅｑｕａｔｉｏｎｓ；ＣｏｎｔｒａｃｔｉｏｎＴｈｅｏｒｅｍ；Ｇａｌｅｒｋｉｎ－ａｐｐｒｏｘｉｍａｔｉｏｎ；ｗｅａｋｃｏｎｖｅｒｇｅｎｃｅ
ｇｅｎｅｒａｌｈｙｐｅｒｂｏｌｉｃｏｐｅｒａｔｏｒｓ．ＢｙｍａｋｉｎｇｕｓｅｏｆＧａｌｅｒｋｉｎ－ａｐｐｒｏｘｉｍａｔｉｏｎ，ＣｏｎｔｒａｃｔｉｏｎＴｈｅｏｒｅｍａｎｄｓｏｏｎ，ｅｘｉｓｔｅｎｃｅａｎｄｕｎｉｑｕｅ —
Ｆｅｂ．２Ｏ１３
文章编号：１００７ — ７３８３（２０１３）Ｏ１一Ｏ１２２一Ｏ５
一
类非线性双曲型方程弱解的存在唯一性
夏子伦，曹文慧，杨文斌
（云南民族大学数学与计算机科学学院，昆明６５０５００）
第３１卷
第１期
２０１３年２月
石河子大学学报（自然科学版）ＪｏｕｒｎａｌｏｆＳｈｉｈｅｚｉＵｎｉｖｅｒｓｉｔｙ（ＮａｔｕｒａｌＳｃｉｅｎｃｅ）

解的存在唯一性定理证明

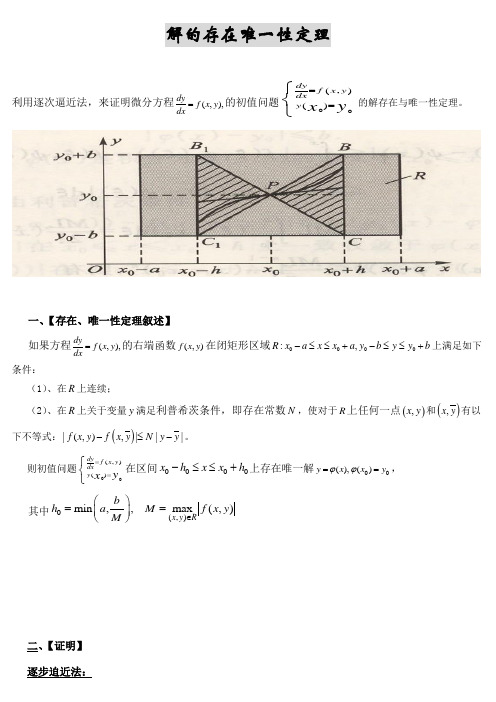
解的存在唯一性定理利用逐次逼近法，来证明微分方程(,),dyf x y dx =的初值问题00(,)()dy f x y dx y y x ==⎧⎨⎩的解存在与唯一性定理。

一、【存在、唯一性定理叙述】如果方程(,),dyf x y dx=的右端函数(,)f x y 在闭矩形区域0000:,R x a x x a y b y y b -≤≤+-≤≤+上满足如下条件：（1）、在R 上连续；（2）、在R 上关于变量y 满足利普希茨条件，即存在常数N ，使对于R 上任何一点(),x y 和(),x y 有以下不等式：()|(,),|||f x y f x y N y y -≤-。

则初值问题00(,)()dyf x y dx y y x ==⎧⎨⎩在区间0000x h x x h -≤≤+上存在唯一解00(),()y x x y ϕϕ==，其中0(,)min ,,max (,)xy R bh a M f x y M∈⎛⎫== ⎪⎝⎭二、【证明】逐步迫近法：微分方程(,)dyf x y dx=等价于积分方程00(,)x x y y f x y dx =+⎰。

取00()x y ϕ=，定义001()(,()),1,2,3, (x)n n x x y f x x dx n ϕϕ-=+=⎰可证明lim ()()n n x x ϕϕ→∞=的()y x ϕ=满足积分方程。

通过逐步迫近法可证明解的存在唯一性。

命题 1：先证积分方程与微分方程等价：设()y x ϕ=是微分方程(,)dyf x y dx=定义于区间0000x h x x h -≤≤+上满足初值条件00()x y ϕ=的解，则()y x ϕ=是积分方程00(,),x x y y f x y dx =+⎰定义于区间0000x h x x h -≤≤+上的连续解。

反之亦然。

证：因()y x ϕ=是微分方程(,)dy f x y dx =的解，有'()()(,())d x x f x x dxϕϕϕ== 两边从0x 到x 取定积分，得：000000()()(,()),xx x x f x x dx x h x x h ϕϕϕ-=-≤≤+⎰代入初值条件00()x y ϕ=得：000000()(,()),xx x y f x x dx x h x x h ϕϕ=+-≤≤+⎰即()y x ϕ=是积分方程00(,)xx y y f x y dx =+⎰定义于区间0000x h x x h -≤≤+上的连续解。

解的存在唯一性定理

一阶微分方程解的存在性定理的其它证明方法姜旭东摘要本文在文[1]对一阶微分方程初值问题解得存在唯一性定理证明的基础上,应用压缩映像原理，Schauder 不动点定理，以及Euler 折线法，给出了一阶微分方程解得存在唯一性定理的其它几种证法.关键词一阶微分方程不动点定理解的存在性唯一性 1、引言微分方程来源于生活实际，研究微分方程的目的在于掌握它所反映的客观规律。

在文[1]第二章里,介绍了能用初等解法求解的一阶方程的若干类型,但同时指出,大量的一阶方程一般是不能用初等解法求解它的通解,而实际问题需要的往往是要求满足某种初始条件的解. 本文在文[1]对一阶微分方程初值问题解的存在唯一性定理证明的基础上,应用压缩映像原理，Schauder 不动点定理，以及Euler 折线法，给出了一阶微分方程解的存在唯一性定理的其它几种证法.考虑一阶微分方程 (,)dyf x y dx= (1.1)这里(,)f x y 是在矩形区域00:||,||R x x a y y b -≤-≤ (1.2)上的连续函数.函数(,)f x y 在R 上满足Lipschitz 条件，即存在常数L ＞0，使得不等式1212|(,)(,)|||f x y f x y L y y -≤- (1.3)对所有12(,),(,)x y x y R ∈都成立, L 称为Lipschitz 常数。

定理1.1、如果(,)f x y 在R 上连续且关于y 满足Lipschitz 条件，则方程(1.1)存在唯一的解()y x ϕ=,定义于区间0||x x h -≤上,连续且满足初始条件00()x y ϕ=这里min(,)bh a M=,(,)max |(,)|x y R M f x y ∈=.文[1]中采用皮卡逐步逼近法来证明这个定理.为了简单起见,只就区间00x x x h≤≤+来讨论,对于00x h x x -≤≤的讨论完全一样.分五个命题来证明这个定理:命题1、设()y x ϕ=是方程(1.1)定义于区间00x x x h ≤≤+上满足初始条件00()x y ϕ=的解,则()y x ϕ=是积分方程0(,)xx y y f x y dx =+⎰ 00x x x h ≤≤+ (1.4)的定义于00x x x h ≤≤+上的连续解.反之亦然. 现在取00()x y ϕ=,构造皮卡逐步逼近函数序列如下:0000100()()(,())x nn x x y x y f d x x x hϕϕξϕξξ-=⎧⎪⎨=+≤≤+⎪⎩⎰ (1.5)(n=1,2,…)命题2 、对于所有的n ，(1.5)中()n x ϕ在00x x x h ≤≤+上有定义、且满足不等式0|()|n x y b ϕ-≤命题3 、函数序列{}()n x ϕ在00x x x h ≤≤+上是一致收敛的. 命题4 、()x ϕ是积分方程(1.4)的定义于00x x x h ≤≤+上的连续解.命题5 、()x ψ是积分方程(1.4)的定义于00x x x h ≤≤+上的一个连续解，则()()x x ϕψ=，00x x x h ≤≤+.综合命题1—5，即得到存在唯一性定理.本文在方程(1.1)在满足定理1.1条件下,应用应用压缩映像原理，Schauder 不动点定理，以及Euler 折线法，给出了一阶微分方程解得存在唯一性定理的其它几种证法.2、预备知识定义 2.1、定义在t αβ≤≤上的实值(m 维)向量函数族{}()F f t =,如果存在数M ＞0，使得对任一f F ∈，都有()f t M ≤，当t αβ≤≤时，则称函数族F 在t αβ≤≤上是一致有界的.定义2.2 、定义在t αβ≤≤上的实值(m 维)向量函数族{}()F f t =，如果对于任给的ε﹥0，总存在δ﹥0，使得对任一f F ∈和任意的12,[,]t t αβ∈，只要12|,|t t -＜δ就有12()()f t f t -＜ε则称函数族F 在 t αβ≤≤上是同等连续.定义2.3、设X 是度量空间，M 是X 中子集，若M 是X 中紧集，则称M 是X 中相对紧集。

一个粘性非线性源的p-Laplace发展方程弱解的唯一性

证明由 ∈ （，；（）及 ∈ （，；（），出ｒｔｔＱ）。ｔｔＱ）得存在函数序列｛｝固的ｔｔｔ，（， ∈ （）当ｋ。２，定对Ｅ（，）・ｔＱ，。２）
（４）
，或者是包括热力学温度０＝“一ｋ
△“ 和传导温度 “ 内的热传导模型】方程（）在．４已被广泛研究，关于解的存在性、唯一性、正则性及其它特殊性质等方面取
ＢＤ．ｏｅａ，Ｊ１ｌ．ＣｌｍｎＲ．．￣ｔ３ｎ和ＶＪＭｉ［研究了关于不稳定的简单断裂流体（ｈａｉｇｆｗ的一种特殊运动状态，出了．．ｌｌ３ｓｅｒｌ）ｎｏ导
ＨＯＩａｎ＝，
（１）
（）２
Ｈ，）ｏ） ∈ｎ，（Ｏ＝ｕ（，
．
（）３
其中ｌＣＲ＂为有界域，ｏ）ｔＵ（为初值函数，＞Ｏ为粘性系数．１中的项ｋ＿衣小．ｔ因子或粘性因此，ｋ（）ａｋ￣伯比松驰／ｕ称方程（）１为
维普资讯 http:/Βιβλιοθήκη
第２卷第２２期
２００７年６月
柳
州
师
专
学
报
Ｖ１２ｏ２０．２Ｎ．
ＪｕａｆＬｕｈｕＴａｈｒｏｌｇｏｒｌｏｉｚｏｅｃｅｓＣｌｅｎｅ
Ｊｎｏ７ｕｅ２０
一
个粘性非线性源的ｐＬｐｃ发展方程弱解的唯一性－ａｌｅａ
郭金勇

一类非线性伪抛物型方程解的性质

∇u (t )
2
Hα (Ω)
≤
C.
(31)
引理
3：令 α
≥
1 2
，
u0
(x)
∈
H α +1
(Ω)
，u
是(1)-(3)有一个弱解，且
µ ∈ C ( R; R), = µ (0) 0, µ ( z) > 0(∀z ∈ R, z ≠ 0),
( ) u t
2 Hα
(Ω)
+
u (t )
2
Hα (Ω)
≤
C,
其中 C 依赖 f。那么运用~Gronwall~引理，可推断出
u (t )
2
Hα (Ω)
≤
C.
引理
2：假设 α
≥
1 2
，
u0
(x)∈
H α +1
(Ω)
，且
µ ∈ C ( R; R), = µ (0) 0, µ ( z) > 0(∀z ∈ R, z ≠ 0),
在性、渐近行为、正则性和衰减性[6] [7] [8] [9]。
描述小振幅长波在非线性色散介质中的传播过程时，经典的伪抛物线方程通常必须考虑耗散机制，
以便准确反映实际情况。但是，引起波衰减的机制非常复杂，人们对其了解不多。在这种情况下，人们
可能被迫依赖耗散的临时模型[10]。在对平面波的单向传播进行建模时，需要在模型中增加非线性和色散
程用于各种领域，例如均匀流体通过裂隙岩石的渗漏[2] (三阶项的系数表示岩石的裂隙程度，其减小程
度对应于增加裂纹的程度)，非线性色散长波的单向传播[3] [4] (其中 u 是振幅或旋度)，种族迁移的描述[5]
(其中 u 是人口密度)。由于伪抛物线方程的广泛应用，它们引起了数学家的极大关注，例如讨论了解的存

一类非局部Cahn-Hilliard方程弱解的存在唯一性

一类非局部Cahn-Hilliard方程弱解的存在唯一性李振邦【摘要】研究一类对流非局部Cahn-Hilliard方程的Neumann问题.通过一致Schauder估计和Leray-Schauder不动点定理,得到了该问题经典解的存在唯一性.进而,利用弱收敛方法得到了该问题弱解的存在唯一性.【期刊名称】《纯粹数学与应用数学》【年(卷),期】2019(035)001【总页数】19页(P15-33)【关键词】对流非局部Cahn-Hilliard方程;Leray-Schauder不动点定理;弱解的存在性;唯一性【作者】李振邦【作者单位】西安工业大学理学院,陕西西安 710021;西北大学数学学院,陕西西安 710127【正文语种】中文【中图分类】O177.21 引言研究如下的Neumann问题:其中,Ω⊂Rn是一个光滑的有界域,u是未知函数,β∈Rn是一个常向量,m(x,t)是一个已知的具有严格正的上下界的光滑函数是一个已知的光滑函数并且满足J(x)=J(−x),J的积分是严格正的.方程(1)可以用来描述许多物理现象,包括在外域上相位分离系统中的合金分离,晶体表面上的非稳定步长移动,晶体生长中面角的形成等[1-4],其中,u(x,t)表示分界面的斜率.光滑函数m(x,t)表示扩散迁移率[5-7].对流项β·∇B(u)来源于具有独立参数的动能,刻画了一种亚稳动力系统中的外部动能[8-9].当驱动系数β→0时,方程(1)形式上成为通常的非局部Cahn-Hilliard方程[10-12].势函数H(u)+f(u)是如下的非局部能量泛函的一阶变分[10-14]:此时,得到如下的非局部形式的势函数:方程(1)有一个基本的守恒量在过去的几十年里,有许多文章是研究经典的具有对流项的Cahn-Hilliard方程的[9,13-16],而对于非局部方程(1),研究成果比较少[5,8].在文献[3]中,作者研究了一类非局部Cahn-Hilliard-Navier-Stokes系统.对于对流非局部Cahn-Hilliard方程,他们得到了三维情形下方程的整体吸引子的存在性结果.近些年来,P.W.Bates和J.Han考虑了一类不具有对流项的非局部Cahn-Hilliard 方程[2-3].一方面,研究了在Dirichelet边界条件下,该模型经典解的存在性,唯一性以及对初值的依赖连续;进一步,证明了该系统存在整体吸引子;另一方面,证明了该方程在Neumann边界条件下弱解的存在唯一性.其他关于非局部问题的结果见文献[10-12,17-18].本文主要考虑具有非线性对流项的非局部 Cahn-Hilliard方程的 Neumann问题(1),其主要困难来源于非局部项和非线性对流项,并且该模型没有能量泛函,很难应用比较原理来研究该模型.为了克服这些困难,应用特殊的迭代技巧[10,19]来得到一些先验估计,而后应用Leray-Schauder不动点定理证明经典解的存在性;进一步,利用弱收敛方法得到其弱解的存在唯一性.本文第二节得到了问题(1)的光滑解的一些先验估计,而后证明经典解的存在性,唯一性以及对初值的连续依赖性.第三节给出了弱解的存在唯一性证明.2 经典解的存在唯一性将方程(1)改写成如下等价的抛物型方程形式:其中本文假设以下条件成立:成立.(A4)∂Ω属于经典的C2+α空间.由条件(A2)可知,存在两个正常数c3和c4,使得首先得到问题(4)的一个先验估计.定理 2.1 假设(A1)-(A4)成立.如果是问题(1)的一个解,则其中正常数只依赖于为了证明上述定理,需要下面这个引理.引理 2.1 假设(A1)-(A4)成立.如果是问题(1)的一个解,则证明在方程(1)左右两边同时乘以u并在Ω上积分,有估算上述等式的右端各项,根据 Hlder不等式,Young不等式,条件 (A1)和条件 (A3),得到和联立(10)式 -(13)式,利用条件(A2)可得应用Gronwall不等式,得到(7)式-(9)式,引理 2.1得证.接下来,证明定理2.1.定理 2.1的证明对p>1,在方程(1)左右两边同时乘以u|u|p−1并且在Ω上积分,分部积分后,利用方程中的边界条件,得到因为和根据条件(A2)和(A3),有联立(15)式-(20)式后立即可得对·∇udx,当p+2q≥ 2r+1 时,利用 Hlder不等式和 Young 不等式和条件(A2),有以下估计而当p+2q<2r+1时,有其中类似地,利用Hlder不等式,Young不等式,条件(A2)-条件(A3)和(7)式,得到和令ε1=m1c2,.从不等式(21)和估计(22)式-(25)式,导出或者从而由条件(A2),有对Gagliardo-Nirenberg不等式,其中α∈(0,1)满足等式此时,令利用Young不等式,得到在 (28)式中令p=µk,把 (31)式代入(28)式,得到取时,有其中而在(31)式中取ε=1时,结合(33)式,可得其中C4(k)=C2(k)+C3.由上述不等式,利用Gronwall不等式,有其中θ(k)=C3(1+µk)β,,并且M0=supx∈Ω|u0|.不等式 (35)说明因为 ,所以有和从而,由(36)式-(38)式及引理2.1,得到其中与 k无关.在 (39)式中令k→ ∞,有∀t∈[0,T]从而由此,根据,得到(6)式,从而定理2.1证毕.有了定理2.1,对进一步的估计,容易证明下面的定理2.2.定理 2.2 对方程任意的解满足条件,有以下结论其中常数K1,K2只与有关,Hlder 模定理2.2的证明类似于文献[20]第五章中定理7.2的证明,这里不再详细证明.为了得到问题(4)经典解的存在性,需要让初值满足相容的边界条件.所以假设并且u0(x)满足如下相容性条件:在方程(4)中,令v(x,t)=u(x,t)−u0(x),得到等价问题其中和因为(43)式说明,所以兼容性条件也满足问题(44).定义和其中c1和m1是条件(A2)和(A3)中的常数.考虑如下问题:引理 2.2 如果是问题(45)的一个解,那么其中k与λ无关.证明因为λ˜a(x,t,v,u0)+(1−λ)c1m1≥ λc1m1+(1−λ)c1m1>0,所以问题 (45)中的各项也满足条件(A1)-(A4)并且不等式(46)由定理2.1直接得到.因此,我们也可以从引理2.2和定理2.2得到:引理 2.3 如果是问题(45)的一个解,那么其中常数K1,K2与δ和λ无关.接下来,需要文献[20]中如下的Leray-Schauder不动点定理:定理 2.3(Leray-Schauder不动点定理)考虑如下变换y=T(x,λ),其中 x,y属于Banach空间X并且0≤λ≤1.假设:(a)对任何已定λ,T(·,λ)在 X 上是连续的.(b)对有界集 X 中的x,当λ属于[0,1]时,T(x,λ)是一致连续的.(c)对任何已定λ,T(·,λ)几乎处处是紧映射,它把有界集X 映到准紧集X.(d)存在一个常数K,使得当λ∈[0,1]时,方程x−T(x,λ)=0的每一个解x满足:.(e)方程x−T(x,0)=0有唯一的解属于X.那么方程x−T(x,1)=0有解.定义 Banach空间 :v(x,0)=0},其中 Hlder 范数空间为通常意义下.对任意函数ω ∈X 满足条件maxQT|ω|≤M 和 maxQT|∇ω|≤M1,考虑如下线性问题:容易证明问题 (59)存在唯一解定义引理 2.4 当ω属于有界集X 时,T(ω,λ)在λ上是一致连续的.证明令ω ∈ X 满足并且令v1=T(ω,λ1),v2=T(ω,λ2),v=v1−v2,有其中和易知|ω|X≤M和成立,再由方程(59)可知其中常数N 与λ2无关.所以,其中N1和N2与λ2无关.易知其中λ∈[0,1].根据线性抛物方程理论,当|λ1−λ2|→0时,问题(49)的解也会趋近于0. 可以用相似的方法得到在X 中,已知的λ,T(x,λ)是连续的.因为是紧的,所以得到T(ω,λ)是一个紧映射.由以上结论,引理2.2-引理2.4和Leray-Schauder不动点定理可得方程(44)解的存在性,并且可得出定理 2.4 令γ>0.满足边界条件(43),那么问题(4)存在唯一一个解 ,并且解对初值具有连续依赖性.关于唯一性及对初值的连续依赖性,有如下定理.定理 2.5 如果u1(x,t)和u2(x,t)是相对应于问题(4)初值u10(x)和u20(x)的两个解,则其中C只与时间T有关.证明任意的满足在∂Ω ×(0,τ)上成立,有其中g(x,ui)=a(x)ui+f(ui).然后其中r(x,t)=|u1|q−|u2|q,并且已知gu(x,u∗)>0,令ξ是如下线性抛物问题的解其中,y∈[0,1]并且γ>0是一个常数.由比较原理,得到所以,由方程(52)有通过条件 (A1),条件 (A3)和u∈L∞(Ω),得到把γ→0和y→sign(u1−u2)+代入不等式(55),得到适当交换u1和u2得到由Gronwall不等式和不等式(57)推导出这样,完成了定理2.4的证明.3 弱解的存在唯一性如果u0(x)∈L∞(Ω),考虑满足如下条件的弱解.定义 3.1设Ω⊆Rn是一个具有光滑边界的有界开区域,QT=Ω×[0,T].称函数u(x,t)是方程(1)的一个弱解,如果它满足如下三个条件:i)ii)在分布意义下,u(x,t)在QT中满足方程(1);iii)对于任意给定的ψ∈H1(Ω),对a.e.t∈[0,T],成立其中g(x,u)=a(x)u+f(u),并且定义函数空间B:=X在L2范数下的完备化.定理 3.1 假设条件(A1)-(A4)都成立并且u0∈L∞(Ω)∩B,那么方程 (1)存在唯一的一个弱解u.证明证明分为四步.第一步构造逼近解.由u0∈L∞(Ω)∩B 可知,存在函数列使得其中常数C与k无关.考虑具有光滑初始值的如下问题:由定理 2.4可知,方程 (62)存在经典解,并且其中常数与 k 无关.第二步一致有界估计.对方程(62)左右两边同时乘以u(k)并且在Ω上积分,得到注意到,以及根据 (64)式 -(67)式,有由 Gronwall不等式,得到其中正常数与 k 无关.通过(63)式,可知u(k)是一直有界的,再由(69)式-(70)式,有和另一方面,根据(71)式-(72)式以及方程(62),可以得到由 (69)式 -(73)式可知,存在的子列,为方便,仍记为,使得由(74)式,利用Aubin-Lions引理可知,在L2((0,T),L2(Ω))中u(k)强收敛于u.又因为,得到第三步 L2中的弱连续性.对所有的,因为在L2([0,T);H1(Ω)中 u(k)⇀u(k→ +∞),所以在L2([0,T)×Ω)中αu(k)⇀αu(k→+∞).由 (64)式,有其中由 (74)式 -(76)式,得到取满足 .∀t0>0,η >0,令,代入(78)式,得到取t0是下列可测函数任意的公共Lebesgue点:那么,有因此,由(79)式-(82)式,得到对任意给定的函数,由方程(62),有根据(77)式,可得令t→t0,得到u(t)是几乎处处从[0,T]到L2(Ω)的一个弱连续函数.∀t>0,若tn是一个时间序列使得(83)式对tn成立并且使得tn→t.得到并且由此及(85)式可知(83)式对所有的t>0成立,进而得到u(t)是从[0,T]到L2(Ω)的一个弱连续函数.第四步连续性:u∈C([0,T);L2(Ω)).由方程解的平移不变性,只需证明又由第三步结论:u(t)是从[0,T]到L2(Ω)的一个弱连续函数,故只需要验证事实上,一方面,由弱收敛性有另一方面,由(83)式有第一步至第四步说明u是方程(1)的一个弱解.唯一性由定理2.5可得.定理3.1证毕. 参考文献【相关文献】[1]Colli P,Frigeri S,Grasselli M.Global existence of weak solutions to a nonlocal Cahn-Hilliard-Navier-Stokes system[J].J.Math.Anal.Appl.,2012,386:428-444.[2]Frigeri S,Grasselli M.Krejčí P,Strong solutions for two-dimensional nonlocal Cahn-Hilliard-Navier-Stokes systems[J].J.Differential Equations,2013,255:2587-2614.[3]Frigeri S,Grasselli M.Global and trajectories attractors for a nonlocal Cahn-Hilliard-Navier-Stokes system[J].J.Dynam.Differential Equations,2012,24:827-856.[4]Frigeri S,Grasselli M.Nonlocal Cahn-Hilliard-Navier-Stokes systems with singular potentials[J].Dyn.Partial Differ.Equ.,2012,9:273-304.[5]Kwek K H.On the Cahn-Hilliard type equation[D].Atlanta:Georgia Institute of Technology,1991.[6]Liu C.On the convective Cahn-Hilliard equation with degeneratemobility[J].J.Math.Anal.Appl.,2008,344:123-144.[7]Zaks M A,Podolny A,Nepomnyashchy A A,et al.Periodic stationary patterns governed bya convective Cahn-Hilliard equation[J].Siam J.Appl.Math.,2005,66:700-720.[8]Cahn J W,Hilliard J E.Free energy of a nonuniform system I,interfacial freeenergy[J].J.Chen.Phys.,1958,28:258-267.[9]Golovin A A,Davis S H,Nepomnyashchy A A.A convective Cahn-Hilliard model for the formation of facets and corners in crystal growth[J].Phys.D.,1998,122:202-230.[10]Bates P W,Han J.The Dirichlet boundary problem for a nonlocal Cahn-Hilliard equation[J].J.Math.Anal.Appl.,2005,311:289-312.[11]Bates P W,Han J.The Neumann boundary problem for a nonlocal Cahn-Hilliard equation[J].J.Differential Equations,2005,212:235-277.[12]Han J.The cauchy problem and steady state solutions for a nonlocal Cahn-Hilliard equation[J].Electron.J.Differential Equations,2004,113:1-9.[13]Giacomin G,Lebowitz J L.Phase segregation dynamics in particle systems with long range interactions.I.Macroscopic limits[J].J.Stat.Phy.,1997,87:37-61.[14]Giacomin G,Lebowitz J L.Phase segregation dynamics in particle systems with long range interactions.II.Phase motion[J].SIAM J.Appl.Math.,1998,58:1707-1729.[15]Eden A,Kalantarov V K.The convective Cahn-Hilliardequation[J].Appl.Math.Lett.,2007,20:455-461.[16]Golovin A A,Nepomnyashchy A A,Davis S H,et al.Convective Cahn-Hilliard models:from coarsening to roughening[J].Phys.Rev.Lett.,2011,86(8):1550-1553. [17]Gajewski H,Zacharias K.On a nonlocal phase separationmodel[J].J.Math.Anal.Appl.,2003,286:11-31.[18]Liu C,Li Z.Existence of solutions for a nonlocal epitaxial thin film growing equation[J].Arch.Math.,2012,99:157-168.[19]Alikakos N D.Lpbounds of solutions of reaction-diffusion equations[J].Comm.Partial Differential equations,1979,4(8):827-868.[20]Ladyzhenskaja O A,Solonikov V A,Uralceva N N.Linear and Quasilinear Equations of Parabolic Type[M].Providence:American Mathematical Society,1968.。

带非抛物项的非线性发展方程的解的适定性

带非抛物项的非线性发展方程的解的适定性非抛物项的非线性发展方程是一类常见的非线性偏微分方程，如Korteweg-de Vries方程、Burgers方程等。

这些方程往往涉及到物理实际问题的建模，具有广泛的应用背景。

在研究非抛物项的非线性发展方程的解的适定性时，我们关注以下几个方面：初值问题的适定性、全局解的存在性和稳定性，以及光滑解的存在性。

首先，我们考虑初值问题的适定性。

对于一个给定的非抛物项的非线性发展方程，我们通常需要考虑其在$t=0$时刻的初值问题。

初值问题的适定性指的是，在给定的初始条件下，方程是否存在唯一的局部解，以及该解在几何上和物理上的特性。

初值问题的适定性可以通过使用合适的函数空间和适当的数学工具来分析。

例如，使用Sobolev空间和能量估计来探讨局部解的存在性和唯一性。

对于一些特殊类型的非线性发展方程，可以使用双曲型方程的理论来证明初值问题的适定性。

其次，我们关注全局解的存在性和稳定性。

全局解是指考虑非抛物项的非线性发展方程在定义域上的解的存在性。

换句话说，我们要证明该方程的解在整个时间范围内是存在的。

全局解的存在性通常要求方程具有良好的非线性性质，例如能量守恒、保持非负性或者一些限制条件。

稳定性是指方程的解对初值和参数的微小扰动是稳定的，即微小扰动不会引起解的显著变化。

全局解和稳定性的研究对于理解方程的动力学行为和长时间演化的特性至关重要。

最后，我们考虑光滑解的存在性。

光滑解是指方程的解在定义域上具有足够的光滑性。

对于非抛物项的非线性发展方程，通常出现的是弱解或者分布解。

弱解通常只具有有限的光滑性，不满足传统的光滑解的定义。

而分布解则可以通过广义函数的理论进行定义，其光滑性更强。

对于光滑解的存在性的研究需要运用一些数学工具，如微分方程的理论、变分方法和极值原理等。

总结起来，非抛物项的非线性发展方程的解的适定性研究涉及到初值问题的适定性、全局解的存在性和稳定性、以及光滑解的存在性等方面。

一类非线性方程解的存在和唯一性及在图像中的应用

学上的证明该问题解的存在性和适定性，时给出对矩形域情况的解的级数形式．后我们给同最基于本模型的数值计算差分模型，且给出几个具体图像在该模型下处理结果．并关键词：多重尺度空间；边界检测；非线性扩散方程
Ｇ（ｚ）一ｆ一Ｐｄ｛。
× ０）１）（丁。，（２
（。）１３
ＭＲ（００主题分类号：５７３Ｊ２０）３Ｋ５；５文献标识码：Ａ中图法分类号：７．９Ｏ１５２
文章编号：０５ — ７７２０）３０２ —６２ ຫໍສະໝຸດ ７９（０２０ —３９０
１引言
在图像分析中，们一般希望精确地确定出图像的边界，数字信号中，谓边界一般人在所描述为周围像素灰度强度有反差变化的那些变化的集合．以往经典理论中，素灰度强度在像有反差变化的集合通常经过对初始灰度函数进行低度滤波然后再对该灰度函数最大值搜索来获得．些理论中［］［］这１，４中有很好的描述．里低度滤波我们指初始灰度函数卷积方差这较小的高斯过程．［］Ｗｉｋｎ注意到卷积高斯过程等价于解经典的以初始灰度函数为在７中ｔｉ初值的热传导方程的解．度滤波或热传导方程的解的主要作用是：低当初始灰度信号很凌乱

常微分方程组解的存在唯一性定理及其应用

常微分方程组解的存在唯一性定理及其应用
近代微分动力学和数学物理学中一个重要且基础性的研究课题是非常重要的。

它不仅涉及到普通微分方程（ODE）的解析或近似解，而且解决微分方程组解的存
在唯一性和存在性也是非常关键的，这也是定义研究这个问题的理论基础。

关于微分方程组解的存在唯一性定理，基本可以归纳为三个部分：定义，定理
以及应用。

从定义来说，微分方程组解的存在唯一性定理指出，一组非线性微分方程的解必须满足它们的一般积分函数的某一唯一的定义拓展，其中，积分函数是原微分方程本身的某种泛函解。

定理上，这个定理被称为Lipschitz不变定理，即：给定一组带有参数的非线
性微分方程组，当该参数在一定范围内发生变化时，其解仍然是唯一的，这一变化度由所谓的Lipschitz条件来度量，即参数改变后该系统的近似的解仍然保持近似关系。

应用上，它主要是用于研究微分动力学系统，而这类系统中出现了新的重要运
动学理论，比如黎曼系统。

使用Lipschitz定理可以搭建一层非常重要的理论框架，帮助我们构建出若干关于微分动力学系统解的重要性质。

此外，该定理也被广泛用于数学物理学中，比如热力学，电磁学，量子力学等。

因此可见，微分方程组解的存在唯一性定理是近代微分动力学和数学物理学中
的一个重要的定理，它的实质和应用也受到广泛的关注，值得引申到包括互联网在内的其它领域深入研究，以期赋予其新的意义及功能。

具非线性边界条件的非牛顿渗流方程整体弱解的存在唯一性

中图分类号
ｌ引
言
考虑非线性边界条件的ｐｌｌｅ渗流方程：－ｐａａｃ
｛一ｉ。ｆｄＶ ‘
ＩＩ。一一
（ｚ
‘￡ｎ ‘丁一ｒｚ ∈ ×０）Ｑ ’ ，，
∈ × （，０丁）一Ｓ，ｒ
ｚ ∈ ｎ，
广ｒ
（）ｎ上（，，０Ｔ；・（）（）Ｗｎ）为１的弱
ＪＩＩ。・一）￡Ｉ￡ｑｄ— Ｉｇｚ，）ｘｌＶｕ（ｑ捌＋，ｘｔ／）０ｄＩｔＳ＇ｚＯ（
ｆＪｓ＿ｒＪｎ
其中检验函数 — Ｌ（，０丁；．ｎ）・０丁；ｎ）且丁）一０Ｗ１（）ｎｐ，（Ｌ（）．关于弱解的存在性及唯一性，们得到以下主要结果．我
・收稿日期：０６０ — ３２０— ５０基金项目：家自然科学基金：线性偏微分方程（０３００国非１１１５）
维普资讯
数学研究
定理１若初值Ｕ。∈ Ｌｎ）ｎＷ（且Ｕ（＇ｎ）一。０那么方程（）在非负的弱解．，１存定理２如果Ｕ分别为方程（），１的具初值为Ｕ， ∈ Ｌ（的弱解，么对任意的丁＞。ｏｎ）那
一
性，的正则性，的初始迹问题的研究已日趋完善Ｃ．解解ｑ但对于非线性第二边值问题的研究
我们还没有见到．本文的目的是给出非线性边值问题解的存在唯一性证明．

一类具有非线性边界条件的退化抛物型方程整体弱解的存在唯一性

摘要：讨论了一类具有非线性边界条件和非线性源项的退化抛物型方程的整体弱解的存在唯一性．首先给出了经典解的一致估计，然后利用弱解的比较原理以及分析方法证明了该问题整体弱解的存在唯一性．在宽松
第３９卷第４期
２０１３年１２月
延边大学学报（自然科学版）
ＪｏｕｒｎａｌｏｆＹａｎｂｉａｎＵｎｉｖｅｒｓｉｔｙ（ＮａｔｕｒａｌＳｃｉｅｎｃｅ）
Ｖｏ【＿３９ＮＯ．４
Ｄｅｃ．２０１３
文章编号：１００４ — ４３５３（２０１３）０４ — ０２４４ — ０４
一
类具有非线性边界条件的退化抛物型方程整体弱解的存在唯一性
朴东哲
（延边大学理学院数学系，吉林延吉１３３００２）
许多学者利用方程（１）的定解问题对多孔媒介中流体的渗流Ⅲ 、某种生物群的扩散跚、非线性媒介中热传导。等实际问题进行了研究，并取得了很多成果．目前为止，有关具有非线性边界条件的退化抛物型方程整体弱解的存在唯一性的研究成果很少．本文证明方程（１）经典解的一致估计后，结合文
ｔｉｏｎｓ．Ｔｈｅｎ，ｗｅｐｒｏｖｅｅｘｉｓｔｅｎｃｅａｎｄｕｎｉｑｕｅｎｅｓｓｏｆｇｌｏｂａｌｗｅａｋｓｏｌｕｔｉｏｎｓｔＯｔｈｅｐｒｏｂｌｅｍｂｙｔｈｅｃｏｍｐａｒｉｓｏｎ

具吸收项的发展型P-Laplace方程组解的存在惟一性

２００８年７月
Ｊｌ２０ｕｙ０８
具吸收项的发展型ＰＬｐａｅ方程组 — ａｌｃ解的存在惟一性
李岩波，辉来李
（吉林大学数学学院，长春１０１）３０２
摘要：究一类发展型ｐＬｐａｅ方程组Ｃｕｈ研－ａｌｃａｃｙ问题弱解的存在惟一性．利用抛物正则化方
法建立了弱解的存在性，并通过把相应的Ｃｕｈａｃｙ问题转化为一个方程的情形，再结合能量估
计和衰减估计两种方法，得到了弱解的惟一性．
关键词：非线性扩散系统；在性；惟一性；吸收项；－ａｌｃ存ｐＬｐａｅ方程组
中图分类号：１５２Ｏ７．文献标识码：Ａ文章编号：６１５８（０８０－５９０１７ —４９２０）４０７－８
ｐＬａ１ｃａｓｓｅｓ．ｐａｉｎｖｔｒｗｅｅｎｖｓｉａｅｎｒｉｅｔｔｄ．Ｔｈｅｓｔｎｅｇｅｘｉｅｃｗａｏｔｉｄｙｉｔｅｆｔｅｓｂａｎｅｂｖｒｕｏｈｐａａｌｃｅｕａｉｅｒｂｏｉｒｇｌｒｚｄ
Ｌｎ．ｏ，ＬＩＨｕ —ａＩＹａｂｉｌｉ
（ｏｌｅｆＭａｈｍｔｓｉｎＵｉｒｉ，ｈｎｃｕ３０２，ｈｎ）Ｃｌｇｔａｉ，ＪｉｎｖｓｙＣａｇｈｎ１０１Ｃｉｅｏｅｃｌｅｔａ
Ａｂｔｃ：ＴｅｘｓｅｃａｄｎｑｅｅｓｆｗａｓｌｔｎｆｒｈＣｕｈｐｏｌｍｏｎｅｏｕｉｎｒｓｒｔｈｅｉｔｎｅｎｕｉｕｎｓｏｅｋｏｕｉｓ０ｔｅａｃｙｒｂｅａｏｆａｖｌｔａｙｏ

非线性热弹耦合偏微分方程弱解的唯一性和稳定性

解的存在唯一性．Ｄｕｖａｕｔ，Ｓｈｉ研究了上述热弹性耦合方程组在不同边界条件下解的存在性、唯一性和稳
定性．
Ｓｈｉ［讨论了热弹耦合杆方程组
ｆｂａ（ｘ，ｔ）一Ｍ ‘ 。 ’ （，ｔ）＋ａＯ ‘ （，ｔ）＝０；
ｅｒｇｙｉｎｅｑｕａｌｉｔｙ．
Ｋｅｙｗｏｒｄｓ：ｔｈｅｒｍｏｅｌａｓｔｉｃ；ｎｏｎｌｉｎｅａｒ；ｕｎｉｑｕｅｎｅｓｓ；ｓｔａｂｉｌｉｔｙ
近些年，不少学者广泛研究了热弹性杆方程，包括热弹性杆耦合方程组合２个杆之间的热黏弹性耦合
ｌｂ（ｘ，ｆ）一０ ‘ （，ｔ）＋ａｉ／ ’ （，ｔ）：０
的解的存在性和唯一性，Ｆａｔｏｒｉ “ 给出了具有记忆项的热弹耦合杆方程
收稿日期：２０１２— ０８一ｌＯ．
作者简介：周道军（１９８０一），男，硕士．主要研究方向：非线性动力系统
云南民族大学学报：自然科学版，２０１３，２２（１）：４４— ４７
ｄｏｉ：１０．３９６９／ｊ．ｉｓｓｎ．１６７２— ８５１３．２０１３．Ｏ１．０１１
ＣＮ５３ — １１９２／ＮＩＳＳＮ１６７２—８５１３
Ａｂｓｔｒａｃｔ：Ｏｎｔｈｅｒｅｓｅａｒｃｈｉｎｆｄｉｎｇｓｏｆｗｅａｋｓｏｌｕｔｉｏｎｓｏｆｔｈｅｎｏｎｌｉｎｅａｒｔｈｅｒｍｏｅｌａｓｔｉｃｃｏｕｐｌｅｄｐａｒｔｉａｌｅｑｕａｔｉｏｎ，ｔｈｅｐａｐｅｒｐｒｏｖｅｄｔｈｅｕｎｉｑｕｅｎｅｓｓｔｈｅｏｒｅｍｏｆｗｅａｋｓｏｌｕｔｉｏｎａｎｄｓｔａｂｉｌｉｔｙｏｆｗｅａｋｓｏｌｕｔｉｏｎｓｆｏｒｔｈｅｅｑｕａｔｉｏｎｓｂｙｕｓｉｎｇｅｎ —

具有非线性奇异项和变指数的拟线性椭圆问题解的存在性

具有非线性奇异项和变指数的拟线性椭圆问题解的存在性初颖;贾小宁【摘要】In this paper,we proved the existence of the solutions for the Dirichlet boundary value problem of quasilin-ear elliptic equation with singular term and variable exponent. Firstly, we constructed an approximation problem, using Sobolev embedding theorem and the supremum and infimum of the variable exponent to overcome difficulties arising from singular term, thus we prove the boundedness of the solution sequence for the approximation problem, then we solved the difficuties caused by p-Laplace operator by selecting the suitable test functions and a priori estimate tech-nique, and with the help of the boundedness of solution sequence for the approximation problem, the sufficient condi-tions of the existence of solutions for this problem are obtained. By contrast,the approximation method we used in this paper is better than the upper and lower solution method in the past.%针对于具有奇异项和变指数的拟线性椭圆方程Dirichlet边值问题,给出了证明该问题解的存在性的方法.首先构造一个逼近问题,利用Sobolev嵌入定理和变指数的上下确界,克服了来自奇异项和变指数的困难,证明了逼近问题解序列的有界性,然后通过选取适当的检验函数和先验估计技巧克服了来自p-Laplace算子的困难,再借助于逼近问题解序列的有界性,得到了该问题解存在的充分条件.通过对比,采用的逼近方法要优于以往常用的上下解方法.【期刊名称】《长春理工大学学报（自然科学版）》【年(卷),期】2016(039)005【总页数】4页(P123-126)【关键词】拟线性椭圆问题;非线性奇异项;变指数;存在性【作者】初颖;贾小宁【作者单位】长春理工大学理学院,长春 130022;长春理工大学理学院,长春130022【正文语种】中文【中图分类】O175.2本文主要研究如式（1）具奇异项和变指数的拟线性椭圆方程解的存在性:其中，Ω是RN(N≥p)上边界光滑的有界开集，p＞2，α(x)是连续函数，是某些Lebesgue空间中的非负函数。