寿险精算课
第八章保险精算

1
本章教学目的
让学生在了解保险精算的产生与发展、基本 任务和基本原理的基础上,掌握非寿险精算中保ห้องสมุดไป่ตู้险费率的厘定方法、“大数”的测定、财务稳定 性分析,以及自留额与分保额的决策;掌握寿险 精算中生命表,趸缴纯保险费、年金保险纯保险 费、年度纯保费和毛保险费的计算,以及理论责 任准备金和实际责任准备金的计算。
D( X1)≤C,D(X2 )≤C,…D(Xn )≤C,…,则对于任意
的ε>0,都有:
lim
n
P
1 n
n k 1
Xk
1 n
n k 1
E(Xk )
1
这一法则的结论运用可以说明,在承保标的数量足够
大时,被保险人所交纳的纯保险费与其所能获得赔款的期
望值相等。这个结论反过来,则说明保险人应如何收取纯
个比率——这类标的发生损失的频率。而在观察次数很多或观察周
期很长的情况下,这一比率将与实际损失概率很接近。换句话说,
当某个所需要求的概率不能通过等可能分析、理论概率分布近似估
计等方法加以确定时,则可通过观察过去大量实验的结果而予以估
计,即用比率代替概率。反过来,经估计得到的比率,可由将来大
量实验所得的实际经验而修正,以增加其真实性。
非寿险精算始终把损失发生的频率、损失发生的规模以及 对损失的控制作为它的研究重心。现在,非寿险精算已经发展 了两个重要分支:一是损失分布理论;二是风险理论。
伴随着金融深化的利率市场化,保险基金的风险也变为精 算研究的核心问题。在这方面要研究的问题包括投资收益的敏 感性分析和投资组合分析、资产和负债的匹配等。
随着国际保险市场的开放和保险精算的发展,有些国家已 经开始授予一定的法定职能于精算师。发生这种转变的主要原 因有:①政府监管部门的职责主要是确保保险市场的整体稳定、 定价合理、保险公司的财务稳定和能够为投保人提供保障。② 寿险品种和保险市场的发展日趋复杂,政府部门难以随时审核 每家保险公司的经营情况。③部分国家和地区的精算师学会对 其会员制定专业指引和守则,以确保其会员可以正确履行精算 师的职能;同时,接受过专业训练的精算师,因为经常参与公 司的业务,可以熟悉保险公司的整体运作。④为了增强保险公 司的竞争能力,有关保险条例必须根据每家公司的不同情况灵 活处理,同时必须顾及保险公司财政状况的稳定。
寿险精算学(第3版)习题答案2

【解2.1】(1)可以被写成=(90−p(r200)18000,又由于达到极限寿命时=0,故=90。
(2)证明:因为,0=1;其次,达到极限寿命=90时,有90=0;且,的导数−110−218000<0,>0。
由此,生存函数的三个条件都被满足。
(3)93333.0)0()10(00010==S S p (4)(030−050)020(5)=−0'(p/0==110+218000−110−2因此,40=0.015833。
【解2.2】作为生存函数的基本属性有:(0)1,S =函数是单调递减的,同时lim ()0x S x →∞=。
(1)由于()exp[0.7(21)](10.72ln 2)xxS x x '=---⨯⨯,(0)0.51480S '=>,说明该函数不满足单调递减的性质。
所以,它不能作为生存函数。
(2)由于(0)1S =,3()2(1)0S x x -'=-+<,21lim ()lim0(1)x x S x x →∞→∞==+。
该函数可以作为生存函数。
(3)由于(0)1S =,()2()(2)0x S x ex -'=-<,lim ()0x S x →∞=。
该函数可以作为生存函数。
【解2.3】(1)4320751001)75(1)75(=--=-=S F (2)20017510040175)()75(=-==-=x x S dx d f (3)501412001)75()75()75(===S f μ【解2.4】(40)40(40)(40)40(40)(40)60(),060(40)60(40)1(),060(40)601()(),06060T t T T t T S t tS t p t S S t t t S t tf x p t t μμ+-===<≤'+=-=<≤+-==<≤【解2.5】()18)100(9)100(6)100(3100)100()100(2)]([2)]([3100)100()100()]([)100()100(222210002221000100022100022x x x x dt x t x t x T E dt p t x T Var xdt x t x dt p x T E x t x l l p xxx t xxx tx t x x t -=---=⎪⎭⎫⎝⎛------=-=-=---==---==⎰⎰⎰⎰----+【解2.6】所有表达式均为非负,因此需要验证是否满足0∞B =∞,使得0)(=∞S (1)∞==∞∞⎰0ln C BC dx BC xx,可以(2)∞=+=+∞∞-⎰001)ln()(x b a dx x b a ,可以(3)21)1(21)1(023=+-=+∞∞-⎰x dx x ,不可以【解2.7】把30.250x q +=代入120.170x q +=式中,得11232120.1700.680x x x x x x q p p q p p ++++++=⋅⋅=⇒=上式与已知条件11210.090x x x q p q+++=⋅=联立求解,解出10.770x p +=,20.117x q +=最后得1212(1)0.230.1170.347x x x x q q p q +++++=-+=+=【解2.8】由()1xS x ω=-,可知~(0,)X U ω,且有(20)~(0,20)T U ω-则[()]2x E T x ω-=,2()[()]12x Var T x ω-=已知020e 40=,即20401002ωω-=⇒=所以2(20)Var[T(20)]533.312ω-==【解2.9】首先计算K 的生存函数k012197k p +1015415则210414()09715151502210422()(21)13509715151513422()()[()]225E K p k k E K k p k k Var K E K E K ==++=∑==+⋅=⋅+⋅+⋅=∑==-=【解2.10】证明:(1)x t x x x t q t T t T p -=<-=≥=1)Pr(1)Pr((2)xu t x t x x x x ut p p u t T t T u t T t q +-=+≥-≥=+≤≤=)Pr()Pr()Pr((3)()()()tx u x t t x x x ut p p u T t T p ++⋅=≥⋂≥=Pr 【解2.11】(1)证明:110111111111+∞+∞+-∞∞+=+≤⋅+=+==⎰⎰⎰⎰⎰⎰x x x t x x t x t x t x t x e dt p dtp p dt p dt p dt p dt p e (2)证明:由于是关于的递减函数,因此有K1B≥所以xk x k k k kx tx t x e p dtp dt p e =≥==∑∑⎰⎰∞=+∞=+∞101【解2.12】证明:()()()()()()()t x t x x t S x t f x t S x t x t p p t t S x S x S x μμ+∂∂++-++====∂∂【解2.13】318.02005exp 20025exp 20015exp )5()25()15(200exp 100exp )(2225101020=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=⎪⎪⎭⎫⎝⎛-=⎭⎬⎫⎩⎨⎧-=⎰S S S q x dt t x S x 【解2.14】[][]8684284p =其中86l 已知,而[][][][][]2848484184841(1)(1)p p p q q ++==--由已知条件推导出[][][]85841848483144508030360.3225550803343640050800.20644556400q q q q q ++-=⋅=⋅=-==⋅⋅=⋅=【解2.15】(1)7[76]=83[76]=1192816608=0.718208(2)6|275+1=82−8475+1=0.084631【解2.16】40+1=40(1−40),40+2=402p [40],43=40+2−40∗2|40,46=43−40+1∗2|340+1.因此343=46/43=1−(1−40)2|340+1/(2p [40]−2|40)=1−(1−0.01608)×0.08964/(0.95977-0.02383)=0.905765【解2.17】151025:2525152540015100.040.04150.06015.40667t t tte p dt p p dtedt eedt--⨯-=+=+=⎰⎰⎰⎰【解2.18】(1)0.752.5=1−53.252.5=1−0.853+0.2540.552+0.553=0.0068381.7|1.252.5=54.2−55.452.5=0.854+0.255−0.655−0.4560.552+0.553=0.022690(2)0.752.5=1−0.5p 52.50.2p 53=1−520.5530.2=0.0068351.7|1.252.5=1.7p 52.51−1.2p 54.2=0.5p 52.5530.2p 541−0.8p 54.20.4p 55=520.553540.21−540.8550.4=0.022668【解2.19】因为{}10102102221exp ()=1exp 2()1exp ()1()1(1)2x x x x x q x t dt x t dt x t dt p q q q μμμ⎡⎤''=--+⎢⎥⎣⎦⎡⎤--+⎢⎥⎣⎦⎡⎤=--+⎢⎥⎣⎦=-=--=-⎰⎰⎰由此推出2x xq q '<。
寿险精算习题及答案
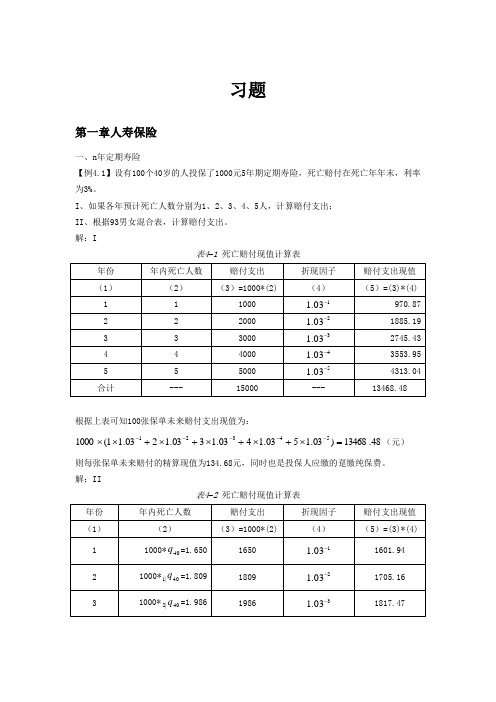
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。
解:I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----(元)则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。
解:II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q (元)则每张保单未来赔付的精算现值为91.25元,同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险,死亡赔付在死亡年年末,利率为5%。
根据93男女混合表计算:I 、单位趸缴纯保费;II 、单位赔付现值期望的方差;III 、(总)趸缴纯保费; 解:I 、单位趸缴纯保费为,)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=(元)。
II 、单位赔付现值期望的方差为,00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为,28.49100001|3:40=⨯A (元) 【例4.3】某人在50岁时投保了100000元30年期定期寿险,利率为8%。
《寿险精算讲义》第四章均衡纯保费

答案
答案
全离散式分两次缴付的年缴纯保费计算 半连续式分两次缴付的年缴纯保费计算
例 4.5.2
对于(40)的人,投保5000元的全离散 式25年定期保险,用换算函数表和年利 率6%。在UDD假设下求:
(1)普通年缴纯保费 (2)季缴纯保费 (3)月缴纯保费
x xx
xa
x
终身寿险-普通
下面考察保险人损失L的方差
(3)Var
(
L)
Var
(v
K
1
Px
a K
1
)
Var(vK 1
Px
1 vK 1 d
)
Var(vK 1(1
Px d
)
Px d
)
(1 Px )2Var(vK 1) d
(1
Px d
)
2[
2
Ax
( Ax )2 ]
2 Ax ( Ax )2 (dax )2
60
【每年分m次缴费的年均纯保费】
在每年分m次缴付的年均纯保费P,每次 缴付纯保费为x元,其计算方法是:
用符号 P(xm)表示保险金额为一个单位的全
离散式普通终身寿险,且每年分m次缴付
的年均衡纯保费.m=2、4、12,故每次缴
纳的纯保费应该是
P(m) x
m
【每年分m次缴费的年均纯保费】
条件:在每一保单年度内,保费分m次缴纳。 终身寿险半连续式寿险为例
m年递延终身生存 保险
P1 x:n
A1 x:n
ax:n Dxn
(Nx Nxn)
P(m
ax
)
A1 x:m
axm
a x:m
Dxm N xm
《保险精算学》课件

总结词
准备金的管理策略包括静态管理、动态管理以及风险管理等 。
详细描述
静态管理是指基于历史数据和当前市场环境确定准备金的数 额;动态管理则是根据市场变化和公司经营状况调整准备金 的数额;风险管理则强调通过建立风险管理体系来降低准备 金的风险。
05
保险风险管理与控制
风险识别与分类
风险识别
识别潜在的风险因素,分析风险发生 的可能性和影响程度。
识,为保险行业的决策提供了更加全面和精确的依据。
02
保险精算的基本原理
概率论基础
随机变量
表示随机事件的数 值结果。
期望值
随机变量的平均值 。
概率
描述随机事件发生 的可能性。
概率分布
描述随机变量取值 的概率规律。
方差
衡量随机变量取值 分散程度的指标。
统计推断
参数估计
根据样本数据推断总体参数的方法。
保险人用于赔付损失的资金。
附加保费确定
附加保费包括经营费用、预期利 润等,是保险人在纯保费基础上
额外收取的费用。
保险费率分类
保险费率可分为单一费率和分类 费率,单一费率适用于相同风险 的多个被保险人,分类费率则根 据被保险人的不同风险等级收取
不同费率。
附加费用的确定
01
02
03
初始费用
初始费用是保险合同签订 时收取的一次性费用,用 于覆盖保险公司的初期成 本。
再保险业务精算案例
比例再保险精算案例
以某保险公司的比例再保险业务为例, 介绍如何根据原保险业务的风险和损失 情况,确定再保险的比例和保费。
VS
非比例再保险精算案例
以某保险公司的非比例再保险业务为例, 介绍如何根据原保险业务的风险和损失情 况,确定再保险的限额和保费。
保险精算课件pptx

财产保险的种类和特点
财产保险精算的基本原理和方法
财产保险精算的风险评估和管理
财产保险精算的未来发展趋势
再保险精算
定义:再保险精算是通过分析再保险合同的详细条款,确定原保险人应向再保险人支付的保费以及再保险人应向原保险人支付的赔款。
目的:确保原保险人的财务稳定,同时为再保险人提供稳定的收入和风险保障。
,a click to unlimited possibilities
保险精算课件
目录
01
保险精算概述02Leabharlann 保险精算数学基础03
保险精算实务
04
保险精算软件应用
05
保险精算前沿问题
06
保险精算职业发展与规划
01
保险精算概述
保险精算的定义
保险精算的主要目标是通过对风险进行评估和管理,为保险公司提供决策支持。
保险精算师需要具备扎实的数学和统计学基础,能够熟练运用各种分析工具和方法,为保险公司提供风险管理和投资策略的建议。
保险精算是保险行业中的一门专业学科。
它涉及到概率统计、金融数学、计算机科学等多方面的知识。
保险精算的作用
添加标题
添加标题
添加标题
添加标题
保费定价:根据风险评估结果,制定合理的保费价格。
汇报人:
感谢观看
职业前景:随着保险市场的不断扩大,精算师的需求也在增加
精算师考试与认证体系
考试科目:数学、统计、金融、法律等
考试难度:较高,需要掌握多学科知识
认证机构:中国精算师协会、北美精算师协会等
职业规划:精算助理、精算师、高级精算师等
精算师职业发展路径与规划
职业定义和定位
精算师的职业规划与职业发展
保险精算培训课件

培训目标与内容设计
培训形式与安排
采用线上+线下的形式,利用多媒体教学资源,实现互动式、案例式、讨论式教学。
培训形式
根据学员实际情况,制定详细的培训时间表和课程安排,确保学员有足够的时间学习和消化所学知识。
培训安排
通过考试、作业、课堂表现等多种方式对学员的学习成果进行评估,了解学员掌握保险精算的程度。
损失分布
索赔频率与索赔强度
预测模型
损失分布与索赔预测的运用
掌握索赔频率和索赔强度的概念及其计算方法,用于评估财产保险的风险。
掌握预测模型的基本原理和方法,如回归分析、时间序列分析等,用于预测索赔行为。
运用损失分布和索赔预测进行保险产品的定价和准备金评估。
保费定价与资金运用
研究保险产品的定价原理和方法,为保险精算提供保费计算工具。
详细描述
保险风险控制与防范
总结词
保险风险监测与报告是保险精算师在风险管理中的重要职责之一,是指对已经实施的风险管理措施进行监测和评估,及时发现和处理潜在的风险。
详细描述
监测是指对已经实施的风险管理措施进行持续的监督和检查,及时发现和处理潜在的风险。报告则是将监测结果和分析结论向保险公司管理层和相关部门进行汇报,以便及时采取相应的措施。在这一过程中,保险精算师需要运用精算技术和风险管理知识,制定科学合理的监测指标和报告制度,以确保风险管理工作的有效性和科学性。
保险精算定义
保险精算具有强烈的数据分析和数理统计特征,需要掌握概率论、统计学、风险理论等相关知识,同时还需要了解保险业务和财务管理的相关知识。
保险精算特点
保险精算的定义与特点
保险精算的角色
保险精算师是保险公司的重要专业人才,负责产品设计、费率厘定、理赔处理等关键环节的数据分析和决策支持。
寿险精算知识点

寿险精算知识点寿险精算是指利用数学、统计学和金融学等理论与方法,对寿险业务进行风险评估、保费定价、赔付准备金计提等工作的过程。
它是寿险行业中的核心技术之一,具有重要的意义。
本文将从寿险精算的基本概念、核心任务以及一些常见的精算方法等方面进行介绍。
我们来了解一下寿险精算的基本概念。
寿险精算是指寿险公司通过对历史数据进行分析和建模,利用数学和统计学的方法,对寿险业务进行风险评估和保费定价的过程。
它主要包括风险评估、保费定价、赔付准备金计提以及风险管理等方面的工作。
寿险精算的核心任务之一是风险评估。
风险评估是指对寿险业务的风险进行测算和评估,主要包括寿险产品的死亡率、残疾率、疾病率等指标的测算和预测。
通过对风险的评估,可以帮助寿险公司合理确定保费水平,确保寿险公司的盈利能力和偿付能力。
保费定价是寿险精算的另一个核心任务。
保费定价是指根据寿险产品的风险特征和市场需求,确定合理的保费水平。
在进行保费定价时,需要考虑到寿险公司的风险承受能力、保险产品的竞争力以及客户的支付能力等因素。
通过合理的保费定价,可以保证寿险公司的盈利能力和可持续发展。
赔付准备金计提是寿险精算的另一个重要任务。
赔付准备金是指寿险公司为支付未来赔款而预先计提的资金。
在进行赔付准备金计提时,需要考虑寿险产品的赔付率、赔付期限、赔付模式等因素。
通过合理的赔付准备金计提,可以确保寿险公司的偿付能力,保障客户的权益。
在寿险精算的实践中,还存在一些常见的精算方法。
例如,死亡率分析是寿险精算中常用的方法之一。
通过对历史死亡率数据的分析和建模,可以预测未来的死亡率,从而为保费定价和赔付准备金计提提供依据。
此外,寿险精算还可以运用生命表、经验法、模型法等方法进行风险评估和保费定价。
寿险精算是寿险行业中的核心技术之一,它通过利用数学、统计学和金融学等理论与方法,对寿险业务进行风险评估、保费定价、赔付准备金计提等工作。
寿险精算的核心任务包括风险评估、保费定价、赔付准备金计提以及风险管理等方面的工作。
寿险精算第七讲 总保费与修正准备金

• 未来保险收入的精算现值为
Ga 40:20
• 故总保费的准备金为
(100000 A40:20
ea 40:20
) Ga 40:10
《寿险精算数学》 --05总保费与修正准备金
5.2.2 总保费准备金对会计报表的影响
下面通过一个例子,说明总保费准备金作为负债对会计报表的影响 考虑一个年缴保费的3 年期生死两全保险,有关情况如下表:
5.2.1 总保费准备金的计算 总保费准备金,是包含费用的准备金。其计算原理与纯保费
准备金相同.根据过去法,有
总保费准备金=过去总保费收入的精算积累值- 过去保险给付 与费用的精算现值
根据未来法,有
总保费准备金= 未来保险给付与费用支出的精算现值 - 未来总保费 收入的精算现值
包含费用的损失变量
包含费用的损失变量= 未来保险给付与费用支出的现值 - 保费总保费 收入的精算现值
一、运用保险资金面发生的费用 例如,员工工资、场地租金、设备费用,其他的服务费及需 缴纳的税金竺。这一类费用称为投资费用。一般在投资收入中扣除, 下面不再分析投资费用。
二、保险费用 因保险业务而发生的费用,称为保险费用。
《寿险精算数学》 --05总保费与修正准备金 表5.1.1 寿险公司可能采用的费用分类制度
费用类别 1. 业务获得费用 2. 保单维持费用
3. 一般费用 4. 理赔费用
费用细目
(1) 销售费用,包括代理人佣金和广告费 (2) 风险分类,包括体检 (3) 新保单制作与记录
(1) 保费收取与记账 (2) 爱益人更换和保单选择权准备 (3)与保单持有人通讯联系
(1) 调查与研究费用 (2) 精算和一般法律服务 (3) 一般会计费用,包括工资、佣金,水电费等 (4) 保费税
寿险精算实务精华版

寿险精算实务讲义第一章 人寿保险的主要类型1.1传统的人寿保险1.1.1 定期寿险定期寿险是指以死亡为给付保险金条件,且保险期限为固定年限的人寿保险。
1.1.2 终身寿险终身寿险是指以死亡为给付保险金条件,且保险期限为终身的人寿保险。
1.1.3 终身寿险两全保险是指在保险期限内以死亡或生存为支付保险金条件的人寿保险。
1.1.4 年金保险年金保险指以生存为支付保险金条件,按约定分期支付生存保险金,且分期支付生存保险金的间隔不超过一年(含一年)的人寿保险。
1.2 新型人寿保险1.2.1分红保险 1.2.2投资连结保险第二章 保单现金价值与红利2.1 保单现金价值2.1.1 保单现金价值的含义现金价值又称解约金、退保金、不丧失保单利益、不丧失价值或不丧失现金价值。
现金价值是指投保人或保险公司解除保险合同时,由保险公司向投保人退还的那部分金额。
现金价值往往特指以现金方式支付的不丧失保单利益。
,0kk k k CV V SC CV =-≥一般情况下,现金价值不大于责任准备金,主要原因是费用在毛保费中重新调整造成的。
其他原因:①财务风险;②死亡率风险;③效益风险;④退保成本。
2.1.2 保单现金价值的计算⑴ 调整保费法 ....()()()()k k C V A k P a k V P P a k αα=-=--, 1..A E P aα+=根据NAIC1941年规则:10.4m in(,0.04)0.25m in(,,0.04)0.02x E P P P ααα=++; 1980年规则:1 1.25m in(,0.04)0.01E P =+优点:是计算现金价值的主要方法,详细定义了费用的确定,得到的不丧失价值更为准确公平; 缺点:计算相对复杂。
⑵ 准备金比例法 k k k C V f V =⨯优点:①简单,便于管理;②不受公司定价假设的影响;③准备金是保单责任的保守估计,对客户较为公平;④能够及时地反映定价时市场利率的变化。
保险精算学6-寿险责任准备金

• 在常数利息力与常数死力假设下,有:
v e , t px eut
Ax
0
vt
t
px
xt dt
et eut dt
0
0.04 e dt (0.060.04)t 0.04 10 0.4 0
ax
1 Ax
10
And we can show :
Axt Ax 0.4, a xt ax 10 tV ( Ax ) Axt P( Ax ) a xt 0
– 责任准备金是已付保费积累值与保险成本积累 值(accumulated cost of insurance)之差。
公式推导:以 Vt x:n 为例
(1)保费差公式
Vt x:n
A xt:nt
P x:n
a xt:nt
A
xt:nt
a xt:nt
P x:n
a xt:nt
P xt:nt
P x:n
a x
h
tV
( Ax:n
)
Axt:nt Axt:nt
h P( Ax:n ) a xt:ht ht n
1 t n
h年限期缴费 n年生存保险
h
1
tV ( Ax:n
)
Ax
1 t:nt
Ax
1 t:nt
1
h P( Ax:n ) axt:ht ht n
1 t n
th
th
m年递延 生存年金
tV (m
ax)
50
0.5508
60
0.8214
4、其他评估方法
• 从未来法推导:
– 保费差公式(premium-difference formula)
• 责任准备金等于剩余缴费期内保费差的精算现值。
保险精算第3章(1)

且分布函数为t q,x 生存函数为 t,px
t qx
s( x) s( x s( x)
t)
t
px
s( x t) s( x)
20
生命函数总结
• t u qx 表示x岁的人将在x+t岁至x+t+u岁之间去世的
概率, t u qx q tu x t qx t px tu px t px qu xt
或 FX (30) FX (10) 0.0587
s(25) s(30)
(4) 5|5 q20
s(20)
0.1303
或 Pr5 T(20) 10 FT (10) FT (5)
或 Pr5 T(20) 10
10
5 fT (t )dt
19
生命函数总结
• X表示新生儿未来的寿命,是一个连续型随机变量, 分布函数为F(x),生存函数为s(x),密度函数为f(x);
t px Pr(T( x) t) Pr( X x t X t) s( x t) s( x)
• 特别: x p0 s( x)
8
符号介绍
• px:x岁的人至少能活到x+1岁的概率 px 1 px
• q x:x岁的人将在1年内去世的概率 qx 1qx • t u q:x x岁的人将在x+t岁至x+t+u岁之间去世的概
0
• 死亡效力表示剩余寿命的密度函数 g(t)
G(t)
1
t
px
s( x) s( x s( x)
t)
g(t)
d G(t) dt
d dt
s(
x)
s(x s( x )
保险精算课程六(人寿保险总保费的计算)20220407003

v v
30 30
0.02G3|
a 30:7|
0.02G
a 30:10|
3
a 30:10|
a 30:20|
G
1000 (M 30 M 50 D50 ) 3D30 2N30 N40 N50
0.98 N30 0.96 N40 0.02 N33 0.25 D30 0.1D31 0.05 D32
N30 N45 96.30
2)年缴总保费
P P 96.30 15 120 .3
1 k 1 0.075
8
费用 分类
1.新契约费 (1)销售费用
佣金 销售事务 其他 (2)风险分类 (3)发行与记录 2.维持费 3.营业费用 (1)研发 (2)精算与法律 (3)会计 (4)税金
每份 保单
• (2)保费税:总保险费的2%; • (3)管理费及承保费用:第一年5元,第二年以后每年2
元,保费缴清后1元。 要求:用换算符号表示该保单的年缴总保费。
16
•设年缴总保费为G,将费用开支情况列表: 0
年龄
X=30 X+1 X+2 X+3 ••• X+9 X+10 ••• X+20
1趸缴纯保费 2佣金 3管理费及承保费用 4保费税
1k
6
课堂练习:
• 某人现年30岁,购买30年定期、限期15年缴费的两全保 险,保险金额为5000元。已知此类业务,每千元保险金额 需支出固定费用15元,另外,每年还需年缴总保费的 7.5%作为其余部分的附加费用,问购买此保单的年缴总 保险费是多少?
7
解:1)年缴纯保费
500015 P30:30| 5000 M 30 M 60 D60
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、单生命生存模型 (6学时)
生存分布,死亡力,生命表的结构,分数年龄段的生存分布的假设,利用EXCEL进行精算实例分析
二、多生命生存模型 (4学时)
联合生存状态与最后生存者状态,生存分布及死亡力,Frank 耦合与共同扰动模型,精算实例分析
三、多元衰减模型 (5学时)
多元衰减模型的定义,衰减力与衰减因素,多元衰减模型与相关的单衰减模型之间的关系,精算实例分析。
联合生存状态和最后生存者状态的精算现值
七、净保费与费用负荷保费 (5学时)
平衡准则,净保费的确定,各种险种的净保费,费用负荷保费,利用EXCEL来计算各种险种的净保费
八、完全离散险种的净准备金 (5学时)
一般的完全离散险种的未来损失量模型,考虑每个保单年度资金变化的模型,净准备金的定义,净准备金的递推公式
英文简介
In this course we will introduce some basic models in life insurance, and the method for calculating net premium and reserve.开课院系数学科学学院通选课领域
是否属于艺术与美育
作业20分, 期中大报告10分,期末考试70分
教学评估
杨静平:
否
平台课性质
平台课类型
授课语言
中文
教材
寿险精算基础,杨静平,北京大学出版社,2002年,第四次印刷,ISBN 7-301-05371-1;
参考书
教学大纲
培养学生利用数学来研究人寿保险中的随机事件的能力。通过教学,要求学生掌握基本的随机给付模型以及相互之间的关系,掌握各种给付的精算现值以及各种险种的净保费、净准备金的计算方法,并能编制Excel 程序来计算净保费及净准备金.
九、普通完全离散险种的净准备金 (4学时)
完全离散的生死合险及终身寿险的净准备金,净准备金的计算方法及现金流分析
十、完全连续险种及其它险种的净准备金 (4学时)
完全连续险种、半连续险种、每年缴纳数次保费的险种及年金的净准备金
课题讲授, 使用多媒体设备. 其中会安排两次课, 安排学生报告他们的大作业.
四、 死亡保险的精算现值 (5学时)
精算现值,死亡保险、生死保险的给付模型及精算现值,利用EXCEL计算各类给付的精算现值的方法。
五、生存保险的精算现值 (4学时)
生存年金,连续生存年金、期初生存年金以及期末生存年金的给付模型及对应的精算现值,精算现值的计算方法。
六、多生命模型的精算现值 (3学时)
寿险精算课程详细信息
课程号
00135810
学分
3
英文名称
Life Insurance Mathematics
先修课程
初等概率论, 利息理论
中文简介
培养学生利用数学来研究人寿保险中的随机事件的能力。通过教学,要求学生掌握基本的随机给付模型以及相互之间的关系,掌握各种给付的精算现值以及各种险种的净保费、净准备金的计算方法,并能编制Excel 程序来计算净保费及净准备金.
