5 条件异方差模型
时间序列条件异方差模型

时间序列条件异方差模型时间序列分析是一种重要的统计分析方法,用于研究时间变量之间的关系。
在金融、经济学、气象学和其他领域,时间序列分析都扮演着重要的角色。
而条件异方差模型则是一种用于捕捉时间序列数据中异方差性质的模型。
本文将介绍时间序列条件异方差模型的概念、原理、应用以及在金融领域的重要性。
一、条件异方差模型的概念条件异方差模型,全称为条件异方差自回归移动平均模型(ARCH),是由Robert F. Engle于1982年提出的一种用于描述时间序列数据中异方差性质的模型。
它认为时间序列数据中的方差是随时间变化的,并受到之前残差的影响,即当前的方差是过去残差的函数。
而在实际应用中,ARCH模型的延伸GARCH模型则是被广泛使用的一种工具,它不仅可以捕捉时间序列数据中的异方差性质,还可以考虑到长期记忆性和其他特征。
二、条件异方差模型的原理条件异方差模型的原理在于将时间序列数据的方差建模为过去残差的函数。
以GARCH(1,1)模型为例,其方差可以表示为:σ^2_t = ω + αε^2_(t-1) + βσ^2_(t-1)其中,σ^2_t为时间t的方差,ω为模型中的常数项,α和β分别表示过去残差和过去方差的权重。
这个模型说明当前的方差受到上一个时期残差的影响,而且方差是随时间变化的。
通过对时间序列数据进行拟合,可以得到最优的α、β和ω参数,从而建立条件异方差模型。
三、条件异方差模型的应用条件异方差模型在金融领域得到了广泛的应用。
由于金融市场的波动性较高,时间序列数据中经常存在着异方差性质。
而条件异方差模型可以帮助金融从业者更好地理解和预测市场的波动性,从而做出更为准确的决策。
例如,投资者可以利用条件异方差模型对金融资产的风险进行度量和管理,而交易员可以利用该模型进行波动性的预测和交易策略的制定。
四、条件异方差模型在金融领域的重要性金融时间序列数据中的异方差性质是一个重要的问题。
大量的实证研究表明,金融资产的收益率往往表现出高度的异方差性,这给投资者和决策者带来了很大的挑战。
《时间序列分析》课程教学大纲

《时间序列分析》课程教学大纲一、课程基本信息二、课程教学目标本课程的目的是使学生掌握时间序列分析的基本理论和方法,让学生借助计算机的存储功能和计算功能来抽象掉其深奥的数学理论和复杂的运算,通过建模练习来掌握时间序列分析的基本思路和方法。
第一,通过这门课程的学习,培养学生对分析方法的理解,使学生初步掌握分析随机数据序列的基本思路和方法。
第二,通过这门课程的学习,使得学生能够运用时间序列分析知识和理论去分析、解决实际问题。
第三,通过这门课程的学习,提高学生利用时间序列的基本思想来处理实际问题,为后续学习打下方法论基础。
三、教学学时分配《时间序列分析》课程理论教学学时分配表《时间序列分析》课程实验内容设置与教学要求一览表四、教学内容和教学要求第一章时间序列分析简介(学时4)(一)教学要求通过本章内容的学习,了解时间序列的定义,理解时间序列的常用分析方法,掌握随机过程、平稳随机过程、非平稳随机过程、自相关基本概念。
(二)教学重点与难点教学重点:时间序列的相关概念。
教学难点:随机过程、系统自相关性。
(三)教学内容第一节引言第二节时间序列的定义(拟采用慕课或翻转课堂)第三节时间序列分析方法1.描述性时序分析2.统计时序分析第四节时间序列分析软件第五节上机指导1.创建时间序列数据集2.时间序列数据集的处理本章习题要点:1、基本概念和特征;2、软件基本操作。
第二章时间序列的预处理(学时6)(拟采用慕课或翻转课堂)(一)教学要求通过本章内容的学习,了解平稳时间序列的定义,理解平稳性和随机性检验的原理,掌握平稳性和随机性检验的方法。
(二)教学重点与难点教学重点:平稳时间序列的定义及统计性质。
教学难点:时间序列的相关统计量。
(三)教学内容第一节平稳性检验1.特征统计量2.平稳时间序列的定义3.平稳时间序列的统计性质4.平稳时间序列的意义5.平稳性的检验第二节纯随机性检验1.纯随机序列的定义2.白噪声序列的性质3.纯随机性的检验第二节上机指导1.绘制时序图2.平稳性与纯随机性检验本章习题要点:1、绘制给定时间序列的相关图;2、计算给定时间序列的相关统计量;3、检验序列的平稳性及纯随机性。
精选-时间序列分析课件-条件异方差模型

方法2:ARCH_LM检验
• ARCH_LM检验 – 1982年,Engle提出检验残差序列是否存在ARCH 效应的拉格朗日乘数检验(Lagrange multiplier test),即ARCH LM检验。
该检验等价于在如下的线性回归中用F统计量检验i 0(i 1, , m) :
at2
0
1at21
m
a2 tm
et ,
t m 1, ,T ,
其他et 表示误差项,m是事先指定的正整数,T是样本容量。
具体的
H0 :1 m 0
令SSR0
T
(at2
t m1
)2,其中
1 T
T
at2 ,
t 1
T
SSR1 eˆt2 ,其中eˆt2是前面线性回归最小二乘估计的残差。 t m1
于是,在原假设下,我们有
at的条件均值 ? at的条件方差 ?
作业:ARCH(p)模型
at的条件均值 ? at的条件方差 ? at的无条件均值 ? at的无条件方差 ?
定义t
at2
2 t
,
可以
证明{
t
}是均
值为
零的
不相关序列。
于是ARCH模型变成
at2 0 1at21 mat2m t , 这是at2的A R(m)形式,但是{ t }不是独立同分布的序列。 因为{ t }不同分布,因此上述模型的最小二乘估计是相合的,
现实金融市场上,许多金融时间序列并没有恒定的均值,大 多数序列在呈现出阶段性的相对平稳的同时,往往伴随着出 现剧烈的波动性。
金融数据的重要特征,包括: ➢ 尖峰厚尾(Leptokurtosis):金融资产收益呈现厚尾(fat
tails)和在均值处呈现过度波峰,即出现过度峰度分布的倾 向; ➢ 波动丛聚性(clustering):金融市场波动往往呈现簇状倾向, 即波动的当期水平往往与它最近的前些时期水平存在正相关 关系。波动率可能在一些时间上高,在另一些时间段上低。 ➢ 杠杆效应(leverage effects):指价格大幅度下降后往往会 出现同样幅度价格上升的倾向,对价格大幅上升和大幅下降 的反应不同 ➢ 波动率以连续方式随时间变化,即波动率的跳跃是很少见的。 ➢ 波动率不发散到无穷,即在固定的范围内变化。
《计量经济学》第五章 异方差性

(二)检验的特点
不仅能对异方差的存在进行判断,而且还能对异 方差随某个解释变量变化的函数形式 进行诊断。 该检验要求变量的观测值为大样本。
36
(三)检验的步骤
1.建立模型并求 ei 根据样本数据建立回归模型,并求残差序列
4
第一节 异方差性的概念
本节基本内容:
●异方差性的实质 ●异方差产生的原因
5
一、异方差性的实质
同方差的含义
同方差性:对所有的 i (i 1,2,...,n)有:
Var(ui ) = σ 2
(5.1)
因为方差是度量被解释变量 Y的观测值围绕回归线
E(Yi ) 1 2 X 2i 3X3i ... k X ki (5.2)
1.求回归估计式并计算 et2
用OLS估计式(5.14),计算残差
差的平方 et2 。
et
Yt
-Yˆt
,并求残
2.求辅助函数
用残差平方
et2
作为异方差
σ
2 t
的估计,并建立
X
2t
,
X
3t
,
X
2 2t
,
X
2 3t
,
X
2t
X
3t
的辅助回归,即
eˆt2
=
αˆ1
+
αˆ2
X
2t
+
αˆ3
X
3t
+
αˆ4
X
2 2t
+
αˆ5
X
2 3t
+
αˆ6
时间序列计量经济学模型概述

时间序列计量经济学模型概述时间序列计量经济学模型是在经济学研究中广泛使用的一种方法,用于分析经济变量随时间的变化。
该模型基于时间序列数据,即经济变量在一段时间内的观测值。
时间序列计量经济学模型的核心是建立经济变量之间的关系,以解释和预测经济现象的变化。
其中最常用的模型是自回归移动平均模型(ARMA)、自回归条件异方差模型(ARCH)和季节性时间序列模型。
自回归移动平均模型(ARMA)是一个包含自回归项和移动平均项的线性模型。
该模型以过去的观测值和随机项为输入,预测当前观测值。
ARMA模型基于假设,即经济变量的行为受到历史观测值的影响。
自回归条件异方差模型(ARCH)是一种考虑了随时间变化方差的模型。
该模型通过引入一个条件异方差项,模拟经济变量中的波动性。
ARCH模型的应用范围广泛,特别是在金融市场波动性分析中。
季节性时间序列模型用于分析具有明显季节性特征的经济变量,如销售额、就业人数等。
这些模型通常基于季节、趋势和随机成分的组合,以预测未来观测值。
在建立时间序列计量经济学模型时,常常需要进行模型识别、参数估计和模型诊断等步骤。
识别模型的目标是确定适当的模型结构,参数估计则是利用历史数据估计模型的参数值。
模型诊断用于检验模型的拟合程度和误差分布是否符合模型假设。
时间序列计量经济学模型在经济研究中有广泛的应用,例如预测未来经济指标、分析经济周期和波动性、评估政策效果等。
它提供了一种量化的方法,使经济学家可以更好地理解和解释经济变量的演变。
时间序列计量经济学模型是经济学研究中一种重要的统计工具,广泛应用于宏观经济、金融市场和企业经营等领域。
它可以帮助我们理解和解释经济变量随时间的变化规律,进行预测和政策分析。
本文将进一步探讨时间序列计量经济学模型的相关概念和应用。
在构建时间序列计量经济学模型之前,首先需要了解时间序列数据的特点。
时间序列数据是按照时间顺序排列的一系列观测值,通常具有趋势性、季节性、周期性和随机性等特征。
GARCH模型

二、ARCH过程
Engle(1982)提出的ARCH模型,正是在不使用特定变量 xt 或数据转 换的情况下,同时对序列的均值和方差进行建模。要理解Engle的方 法,首先我们要估计平稳ARCH模型 yt a0 a1 yt 1 t 并预测 yt 1 , 则 yt 1 的条件均值为 Et yt 1 a0 a1 yt ,若我们用这个条件均值去预 测 yt 1 ,则预测误差方差为 Et [( yt 1 a0 a1 yt )2 ] Ett21 2。 ˆt 表示模型 yt a0 a1 yt 1 t 的残差估计值,那么 yt 1的条件方 若用 差为: var( y y ) E [( y a a y )2 ] E ( )2
GRACH模型
三、GRACH模型
Bollerslev广义自回归条件异方差(Generalized ARCH,GARCH)模型。 GARCH类模型最早是Engle提出的ARCH模型,即自回归条件异方差 模型。设标的资产时间序列为{ yt } , Engle年建立了回归模型ARCH(q),
y t 是因变量,x t 是解释变量的向量, 其中, 是未知参数的向量, 假设 t 的在给定 (t 1) 时间内的信息 t 1 满足正态分布, t | t 1 ~ N ( 0, ht ) , 但其条件方差为:
ARCH模型
一、金融时间序列的异方差性特征
现实金融市场上,许多金融时间序列并没有恒定的均值,大多数 序列在呈现出阶段性的相对平稳的同时,往往伴随着出现剧烈的 波动性。 金融市场中,波动率(volatility)是金融时间序列最重要的特征 之一,因而模拟和预测股票市场的波动性已经成为众多理论和实 证研究的重要领域。然而,金融市场时间序列存在非平稳性,样 本均值并不恒定,有明显的异方差性特征。因此,传统线性结构 模型(以及时间序列模型)并不能很好地解释金融数据的重要特 征。
计量学-向量自回归和自回归条件异方差模型

33
第二节 自回归条件异方差模型
许多学者在分析通货膨胀、汇率、股票 价格等金融时间序列时,都发现时间序 列模型扰动方差的稳定性比通常认为的 差,时间序列数据也存在异方差问题。
经济时间序列数据的这种方差变化也称 为波动集聚性(volatility clustering), 对于研究和控制金融风险等非常有用。
似然比检验实际上就是把不同约束,有约束和 无约束的参数估计、最大似然估计分别代入上 述似然函数,根据是否有显著差异说明参数约 束或者所对应的检验假设是否成立。
24
阶H滞0 :后一的组高变斯量向数量据自由回p归0 阶生而成不。是p1 p0 H1 :这组变量数据是由 p1 p0 阶滞后的 高斯向量自回归生成。
f (Y , YT , ,Y1 Y0 , ,Y p1 T , Y1 Y0 , , Y p1 ; θ)
因为 η Φ1Yt1 Φ pYt p 在时期t为常 数,而 εt ~ iidN[0,Ω],因此
Yt Yt1, Yt2,, Y p1 ~ N[η Φ1Yt1 ΦpYt p ,Ω]
17
1
n1 1,t 1
Y (1)
nn n,t 1
Y ( p)
n1 1,t p
Y ( p) nn n,t p
nt
8
这个展开形式上与一般联立方程组模型相似, 但其实有本质差异:
1、VAR模型不强调变量之间关系的理论根据,模 型形式、变量、滞后期数等并不以特定经济理 论为依据,模型变量也不存在内生、外生之分, 每个方程都包含所有的变量;
18
向量自回归模型的(条件)似然函数为:
L(θ)
f YT ,
,Y1 Y0 ,
(Y , ,Y p1
异方差性和序列相关性在时间序列模型和面板数据模型中的处理方法有何不同

异方差性和序列相关性在时间序列模型和面板数据模型中的处理方法有何不同在时间序列模型和面板数据模型中,异方差性和序列相关性是常见的数据特征。
它们的存在对模型的准确性和鲁棒性有着重要影响,因此需要采取不同的处理方法进行应对。
本文将介绍异方差性和序列相关性在时间序列模型和面板数据模型中的处理方法的不同之处。
一、时间序列模型中的异方差性处理方法时间序列模型是对单一变量随时间变化的模型,如ARIMA模型、GARCH模型等。
在时间序列模型中,异方差性通常表现为随时间变化的方差,并且可能导致模型结果的不准确性。
1. 条件异方差模型最常见的处理异方差性方法之一是采用条件异方差模型,如ARCH模型、GARCH模型等。
这些模型可以通过引入变量来描述方差的变化,并且能够更准确地估计模型参数。
2. 转换变量另一种常见的方法是通过对变量进行转换来减小或消除异方差性。
常用的转换方法包括对数转换、差分变换等。
这些转换可以将异方差性转换为方差齐性,从而提高模型的准确性。
3. 加权最小二乘法加权最小二乘法是一种适应性加权的回归方法,可以通过加权因子对不同时间点的观测值进行不同程度的调整,从而降低异方差性对模型结果的影响。
二、面板数据模型中的序列相关性处理方法面板数据模型是对多个个体在不同时间点上观测到的数据进行建模,如固定效应模型、随机效应模型等。
在面板数据模型中,序列相关性可能存在于个体之间或个体内部,对模型估计和推断都具有重要影响。
1. 面板数据单位根检验面板数据单位根检验可以判断变量是否存在序列相关性。
常用的面板数据单位根检验方法有Levin-Lin-Chu(LLC)检验、Ng-Perron(NP)检验等。
如果变量存在单位根,说明存在序列相关性,需要进一步处理。
2. 区分组间和组内相关性面板数据模型中的序列相关性可以分为组间相关性和组内相关性。
对于组间相关性,可以采用固定效应模型进行估计;对于组内相关性,可以采用随机效应模型进行估计。
九、异方差模型
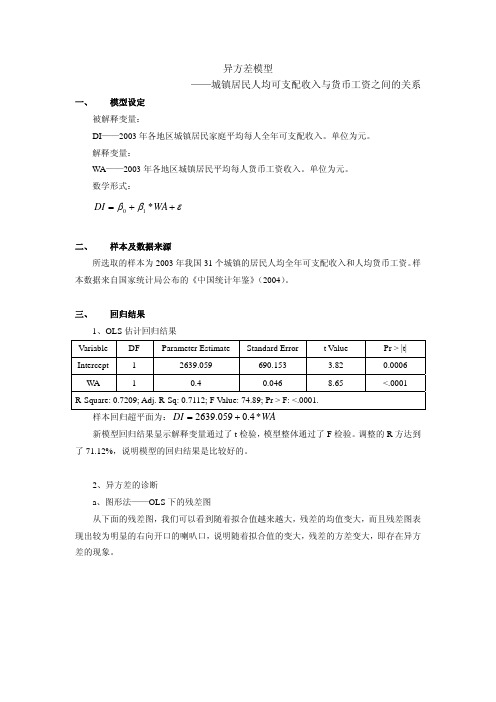
异方差模型——城镇居民人均可支配收入与货币工资之间的关系一、模型设定 被解释变量:DI ——2003年各地区城镇居民家庭平均每人全年可支配收入。
单位为元。
解释变量:WA ——2003年各地区城镇居民平均每人货币工资收入。
单位为元。
数学形式:εββ++=10WA DI *二、样本及数据来源所选取的样本为2003年我国31个城镇的居民人均全年可支配收入和人均货币工资。
样本数据来自国家统计局公布的《中国统计年鉴》(2004)。
三、回归结果1、OLS 估计回归结果 VariableDFParameter EstimateStandard Error t Value Pr > |t| Intercept 1 2639.059 690.153 3.820.0006WA 10.40.0468.65 <.0001R-Square: 0.7209; Adj. R-Sq: 0.7112; F Value: 74.89; Pr > F: <.0001.样本回归超平面为:WA DI *4.0059.2639+=新模型回归结果显示解释变量通过了t 检验,模型整体通过了F 检验。
调整的R 方达到了71.12%,说明模型的回归结果是比较好的。
2、异方差的诊断a 、图形法——OLS 下的残差图从下面的残差图,我们可以看到随着拟合值越来越大,残差的均值变大,而且残差图表现出较为明显的右向开口的喇叭口,说明随着拟合值的变大,残差的方差变大,即存在异方差的现象。
70008000900010000110001200013000-4000-200002000Fitted values R e s i d u a l slm(a$DI ~ a$WA)Residuals vs Fitted261129b 、White 检验利用White 检验的结果如下表所示Heteroscedasticity TestEquation Test Statistic DF Pr> ChiSq Variables DI White's Test12.9420.0016Cross of all varsWhite 检验的结果同样说明了异方差的存在,检验的P 值为0.0016,在1%的水平上能够通过显著性检验。
条件异方差模型

LM检验
总结词
LM检验(拉格朗日乘数检验)是另一种常用的检验条件异方差性的方法。
详细描述
LM检验基于残差的自回归模型,通过构造拉格朗日乘数统计量来检验残差是否存在条件异方差性。如果LM检验 的P值较小,则说明存在条件异方差性,适合使用条件异方差模型。
AIC准则
总结词
AIC准则(赤池信息准则)是一种用于模型 选择的准则,也可以用于选择适合的条件异 方差模型。
资产定价
资产定价
条件异方差模型可以用于资产定价,帮助投资者确定资 产的合理价格。
投资决策
基于资产定价结果,投资者可以做出更加明智的投资决 策,提高投资收益。
06
条件异方差模型的局限性与
未来发展
数据依赖性
模型的有效性依赖于数据的准确性和 完整性,如果数据存在误差或缺失, 可能导致模型预测结果的不准确。
贝叶斯估计法
贝叶斯估计法是一种基于贝叶斯定理 的参数估计方法,通过将模型中的未 知参数视为随机变量,并为其指定一 个先验分布,然后利用观测数据更新 该先验分布,从而得到未知参数的后 验分布。在条件异方差模型中,贝叶 斯估计法可以用来估计模型中的未知 参数。
VS
贝叶斯估计法的优点是灵活且能够处 理不确定性,可以考虑到未知参数的 不确定性,并为其提供一个概率描述。 然而,它对数据和先验分布的要求较 高,且计算复杂度较高,需要借助数 值计算方法进行求解。
TARCH模型
总结词
TARCH模型(门限自回归条件异方差 模型)是条件异方差模型的一种,用 于描述金融时间序列数据的波动性。
详细描述
TARCH模型由Zakoian于1994年提出, 它通过引入门限项来描述波动性的非 对称性。TARCH模型能够较好地拟合 金融时间序列数据的波动性,并预测 未来的波动情况。
ARCH与GARCH模型

ARCH 与GARCH 模型1. 自回归条件异方差模型3.1.1问题的提出对异方差误差分布的修正能够导致更加有效的参数估计。
比如在回归方程εβββttttx x y +++=33221(3.1.1)中的εt的方差可能与xt22成正比,在这种情况下,我们能够使用加权最小二乘法,即令方程的两边同时除以变量xt2,然后用普通最小二乘法估计变化后的回归方程εβββ*23322121ttttttxx x x y +++= (3.1.2)在有些应用场合下,能够认为误差项是随时间变化的同时依靠于过去的误差大小。
通货膨胀与股票市场收益都属于这种情形。
在这些实际应用中,常常有大的误差与小的误差成群出现的情形,换句话说,存在着一种特殊的异方差形式,回归误差的方差依靠于过去不久误差的变化程度。
一个被广泛使用以解决这类异方差模型是由Robert Engle 研究进展出来的,他认为用一个自回归条件异方差模型(Autoregressive conditional heteroscedasticity model ,简计为ARCH 模型)会提高有效性。
3.1.2定义通常的,公式(1)中随机误差项t ε的方差2t σ能够依靠于任意多个滞后变化量it -ε(i=1,2,…p ),记作ARCH (p )εαεαεαασ222221102.......p t p t t t---++++= (3.1.3)注意:(1) 为了保证在给定i t -2ε条件下,02≥t σ,就务必要求0≥α(p ,,1,0 =α); (2) 要保证误差序列t ε的平稳性,系数务必满足:121 p ααα++。
3.1.3检验3.1.3.1Breusch-Pagan 检验 在同方差的假设下条件下:SSR/2~X 2(1)根据Eviews3.1 OLS 处理结果,可根据下式计算检验的统计量SSR/2SSESSR SSRSST SSR R +==2 查自由度为1时的2χ分布表,找出给定显著性水平α条件下临界值,比较检验统计量与临界值的大小,以确定同意还是拒绝模型同方差的零假设3.1.3.2拉格朗日乘子检验法(LM)已经讨论过两种假设检验法:F 检验(Wald 检验)法(第5章)与似然比检验法。
条件异方差模型

测方差t2-1的说明。
通过在极E大V似iew然s函中数AR方C法H估模计型的是。在例扰如动,项对是于条G件A正R态CH分(1布,1的),1假6t 定时下期,
按照通常的想法,自相关的问题是时间序列数据所特有, 而异方差性是横截面数据的特点。但在时间序列数据中,会 不会出现异方差呢?会是怎样出现的?
3
恩格尔和克拉格(Kraft, D., 1983)在分析宏观 数据时,发现这样一些现象:时间序列模型中的扰 动方差稳定性比通常假设的要差。恩格尔的结论说 明在分析通货膨胀模型时,大的及小的预测误差会 大量出现,表明存在一种异方差,其中预测误差的 方差取决于后续扰动项的大小。
大似然估计法进行估计。下面分别介绍这3种分布,其中的
代表参数向量。 1.对于扰动项服从正态分布的GARCH(1, 1)模型,它
的对数似然函数为
ln L(θ ) T ln( 2 π) 1
2
2
T t 1
ln
2 t
1 2
T t 1
( yt
x tγ ) 2
2(6.1.33)
t
这里的t2是ut的条件方差。
2 t
0
1
u
2 t
1
通常用极大似然估计得到参数0, 1, 2, , k(p)过程可以写为:
var(
u
t
)
2 t
0
1
u
2 t 1
u2
2 t2
第9章 条件异方差模型上课讲义

9.5.1 成分GARCH模型介绍
•
此外,在成分GARCH模型的条件方差中,可以包含外生变量 ,外生变量既可以放在长期方程中,也可以放在短期方程 中。
短期方程中的外生变量将对波动产生短期影响,长期方程中 的外生变量将对波动产生长期影响。
非对称成分GARCH模型 •
9.6 多元GARCH模型
随着经济的全球化,很少有国家或地区的金融市场是封闭或孤立的,当 某国出现金融危机后,通常会迅速传导到其它金融市场,多个金融资 产会沿时间方向呈现波动集聚,不同金融资产之间会出现风险交叉传 递。
因此,ARCH模型可以拟合市场波动的集群性现象,但没有说明 波动的方向。
如果时间序列的方差随时间变化,使用ARCH模型可以更精确地 估计参数,提高预测精度,同时还可以知道预测值的可靠性 。当方差较大时,预测值的置信区间就较大,从而可靠性较 差;当方差较小时,预测值的置信区间就较小,从而可靠性 较好。
非对称成分garch模型96多元garch模型随着经济的全球化很少有国家或地区的金融市场是封闭或孤立的当某国出现金融危机后通常会迅速传导到其它金融市场多个金融资产会沿时间方向呈现波动集聚不同金融资产之间会出现风险交叉传一元garch模型无法捕捉到这种跨市场的风险传递或波动溢出
第九章 条件异方差模型(ARCH)
9.1 ARCH模型
•
9.1.1 ARCH(q)模型
•
9.1.1 ARCH(q)模型
•
ARCH(q)模型特点
ARCH(q)模型表明,过去的波动扰动对市场未来波动有着正向而 减缓的影响,即较大幅度的波动后面一般紧接着较大幅度的 波动,较小幅度的波动后面一般紧接着较小幅度的波动,波 动会持续一段时间。
9.4.3 EGARCH模型
条件异方差模型

条件异方差模型介绍条件异方差模型是一种用于建模和分析时间序列数据的统计模型。
在时间序列分析中,我们通常假设序列的方差是恒定的,即服从同方差假设。
然而,在实际应用中,我们经常遇到方差不恒定的情况,这时就需要使用条件异方差模型。
什么是条件异方差条件异方差指的是时间序列数据的方差在不同条件下发生变化。
换句话说,条件异方差模型允许我们在建模过程中考虑方差的非恒定性。
这在金融领域特别常见,因为金融数据通常具有波动性较大的特点。
条件异方差模型的应用条件异方差模型在金融风险管理、投资组合优化、期权定价等领域都有广泛的应用。
通过考虑方差的非恒定性,条件异方差模型能够更准确地捕捉到金融市场的波动性,从而提高模型的预测能力和风险控制能力。
常见的条件异方差模型ARCH模型ARCH(Autoregressive Conditional Heteroskedasticity)模型是最早被提出的条件异方差模型之一。
ARCH模型假设序列的方差是过去方差的线性函数,并且具有自回归结构。
ARCH模型的一阶形式可以表示为:2σt2=α0+α1ϵt−12是时间点t-1的残差的平其中,σt2是时间点t的方差,α0和α1是模型的参数,ϵt−1方。
GARCH模型GARCH(Generalized Autoregressive Conditional Heteroskedasticity)模型是对ARCH模型的拓展,能够更好地捕捉到方差的非恒定性。
GARCH模型引入了条件方差的滞后项,并且具有自回归滑动平均结构。
GARCH模型的一阶形式可以表示为:σt2=α0+∑αipi=1ϵt−i2+∑βjqj=1σt−j2其中,α0,α1,...,αp和β1,β2,...,βq是模型的参数,p和q分别表示条件方差和滞后项的阶数。
EGARCH模型EGARCH(Exponential GARCH)模型是对GARCH模型的改进,能够更好地对称和非对称的影响进行建模。
条件异方差模型

条件异方差模型条件异方差模型是一种用于描述时间序列数据的统计模型,它考虑到了不同时间点上的方差可能是不同的。
这种模型可以用来分析股票价格、汇率等金融数据,也可以用来分析环境变量、气象数据等自然科学数据。
在条件异方差模型中,方差是一个随时间变化的函数,通常被称为条件方差。
这意味着,在给定一些先前观察到的数据之后,我们可以预测未来观测值的方差。
这种方法比传统的线性回归模型更加准确,因为它能够捕捉到随着时间推移而发生变化的不确定性。
条件异方差模型最常见的形式是ARCH(自回归条件异方差)和GARCH(广义自回归条件异方差)模型。
ARCH模型是一种基于过去观测值的平方误差来预测未来观测值误差方差的模型。
GARCH模型则扩展了ARCH模型,并允许过去多个时间点上的平方误差对当前观测值误差方差产生影响。
在实际应用中,我们通常使用最小二乘法或极大似然估计法来拟合条件异方差模型。
最小二乘法是一种通过最小化残差平方和来确定模型参数的方法,而极大似然估计法则是一种基于观测到的数据来估计未知参数的方法。
需要注意的是,条件异方差模型并不适用于所有类型的时间序列数据。
例如,在具有周期性变化或季节性变化的数据中,方差通常是稳定的,因此不需要使用条件异方差模型。
此外,在具有明显趋势或趋势突变的数据中,也可能需要使用其他类型的时间序列模型。
总之,条件异方差模型是一种强大而灵活的统计工具,可以用于分析各种类型的时间序列数据。
它能够捕捉到随着时间推移而发生变化的不确定性,并且可以通过最小二乘法或极大似然估计法来拟合模型参数。
但需要注意,它并不适用于所有类型的时间序列数据,并且在实际应用中需要谨慎选择合适的模型。
06自回归条件异方差(ARCH)模型

够更准确地解释冲击的大小和持续性,因为标准化的 值没有度量单位
(3)EGARCH模型考虑了杠杆效应。如果t-1为正,冲击 对条件方差的对数的影响是a1+1,否则为-a1+1
15
一、ARCH过程
有时,我们可能需要预测序列的条件方差
对于资产持有者,往往对该资产在持有期间的回报率 及其方差感兴趣。
如果投资者打算在t期买进该资产,在t+1期卖出,无条 件方差(即对方差的长期预测)就不重要了
考虑如下模型
yt1 t1xt var( yt1 | xt ) xt2 2
如果xt = xt-1 = … = 常数,则yt就是方差恒定的白噪
GDP增长的标准差相对于1960~1983年减少了61%. Romer(1999)也谈到,良好的货币政策可以使中央银
行更好地促进经济稳定
研究目的:1984年第1季度是否有波动性突变 合理的均值模型:
yt 0.006 0.331yt1 t
(7.14) (5.47)
11
三、EViews应用举例(波动缓和)
② 估计均值方程,求出残差的平方序列 ˆt2
③ 估计辅助回归式
ˆt2 a0 a1ˆt21 apˆt2 p t
④ 用第3步得到的可决系数R2构造统计量LM = TR2。其中T表示辅 助回归式的样本容量。
在原假设成立条件下,LM统计量服从自由度为p的2分布,计算
的LM统计量小于临界值,接受原假设;否则,拒绝原假设。
注意:这里衡量了价格的条件方差对烤鸡供给的负面影响
价格模型:(1 1L 2L2 3L3 4L4 )Pt 0 2t
经检验价格存在异方差,GARCH(1,1)估计结果
条件异方差模型

条件异方差模型
条件异方差模型(ConditionalHeteroskedasticityModels,CHM)是一种用来检验和处理数据中异方差(heteroskedasticity)问题的模型,旨在估计和检验观测数据中异方差的存在,以及其影响程度,来获得更准确的分析结果。
条件异方差模型可分为简单异方差模型和动态异方差模型。
简单异方差模型假设观测值有固定的异方差,而动态异方差模型则假设异方差可以动态变化。
异方差模型通常包括四个步骤:
(1)数据准备:首先,将数据转换为异方差模型可识别的数据格式,其中可能包括数据集的统计量,如平均值,方差,偏度,峰度等;
(2)模型拟合:使用统计模型拟合数据,用于预测观测值的异方差;
(3)异方差识别:利用拟合的模型,采用检验的方法来识别异方差的存在;
(4)异方差处理:对于经识别的异方差,采用最优化的处理办法,以获得更准确和实用的异方差分析结果。
由于条件异方差模型提供了一种有效的方法来理解和处理异方差,因此,它在许多学科中,如财务分析,统计分析,市场营销,投资管理,经济分析等领域中被广泛应用。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5 条件异方差模型
5.1 ARCH 模型
5.1.1 ARCH(1)过程
y t =γ0+γ1x 1t +γ2x 2t +…+γk x kt +u t
t=1, 2, … , T
var(y t ︱Y t-1)=E(y t -γ0-γ1x 1t -γ2x 2t -…-γk x kt )2
=E t-12t u
2t u ~AR(1)
2t u =α0+α121t u -+εt
εt -白噪声过程
E(εt )=0
E(εt ετ)=2,0,t t λττ
⎧=⎨≠⎩
u t ~N[0,(α0+α121t u -)]
扰动项u t 的条件方差依赖于它的前期值u t-1的大小。
ARCH(1)过程的参数γ0, γ1, γ2, …, γk , α0, α1采用极大似然估计。
5.1.2 ARCH(p)过程
y t =γ0+γ1x 1t +γ2x 2t +…+γk x kt +u t
var(u t )=2t σ=α0+α121t u -+α222t u -+…+αp 2
t p u -+εt
均值方程中的(k+1)个参数γ0, γ1, γ2, …, γk ,和方差方程中的(p+1)个参数α0, α1, α2, …, αp 采用极大似然估计。
2t u 协方差平稳的条件
1-α1z-α2z 2-…-αp z p =0
的根全部位于单位圆外。
若αi >0, (i=1,2, … ,p),等价于α1+α2+…+αp <1
5.2 ARCH 检验
ARCH LM 检验
作辅助回归
2
ˆt u =β0+(21p s t s s u
β-=∑)+εt
残差平方滞后联合显著性检验F 统计量。
T×R 2统计量
T-观测值个数
R 2-回归拟合优度
T×R 2~χ2(p)
残差平方相关图:残差平方序列任意指定滞后阶数的自相关系数AC 、偏自相关系数PAC ,判断ARCH 效应。
相应滞后阶数的Ljung-Box Q 统计量若显著,存在ARCH 效应。
5.3 GARCH 模型
5.3.1 GARCH(1,1)模型 y t =X t γ+u t
2t σ=ω+α21t u -+β21t σ- t=1, 2, … , T X t -1×(k+1)维外生变量向量 γ-(k+1)×1维系数向量 ω-常数项
21t u --ARCH 项 21t σ--GARCH 项 y t =X t γ+u t
条件均值方程 2t σ=ω+α21t u -+β21t σ- 条件方差方程 u t 服从条件正态分布的假设下,GARCH(1,1)模型t 时刻的对数似然贡献:
l t =-12ln(2π)-12ln 2t σ-12(y t -X t γ)2/2t σ 2t σ=ω+α(y t-1-X t-1γ)2+β21t σ-
递归替代
2
t σ=1ωβ-+α121j t j j u β∞--=∑
5.3.2 GARCH(p,q)模型 2t σ=ω+21p i t i i u α-=∑+21q i t j j βσ-=∑
误差项u t 服从正态分布的条件下,GARCH(1,1)模型的对数似然函数:
lnL(θ)=-2T ln(2π)-1221ln T t t σ=∑-12221()/T t t t t y X γσ=-∑。
