9.4乘法公式(1)
七年级数学下册 9.4乘法公式(第1课时) 教案2 苏科版

9.4 乘法公式(一)教案班级____________姓名____________学号___________备课时间: 主备人:一、教学目标1.会推导完全平方公式、平方差公式,并能正确运用公式进行简单计算.2.通过图形面积的计算,感受乘法公式的直观解释,了解公式的几何背景.3.在探索公式的过程中,发展学生的符号感和推理能力.4.培养学生主动探索,敢于实践,勇于发现的科学精神,以及合作交流的能力和创新的意识.二、教学重点、难点正确运用公式进行相关的计算三、教具准备:自制长方形、正方形纸板四、教学过程情境创设学生利用准备好的长方形、正方形纸板(图1),拼成一个大正方形(图2).(1)(2)通过这样的拼图过程,你能发现什么吗?探索活动做一做问题一:你是如何表示图(2)中大正方形的面积的?问题二:你能利用多项式乘法法则推导公式2222)(b ab a b a ++=+吗?结论:得到完全平方公式2222)(b ab a b a ++=+问题三:你能够不通过计算直接写出2222)(b ab a b a +-=-?结论:得到完全平方公式2222)(b ab a b a +±=±想一想你能仿照上面的过程,得到平方差公式:22))((b a b a b a -=-+ (可通过计算图形的面积和多项式的乘法来说明.)试一试:1.计算(1)2)2(+x (2)2)2(-x (3))2)(2(-+x x(4)2)52(+a (5)2)52(--a练一练(1)))()((22y x y x y x ++- (2)1)12)(12)(12)(12(842+++++3.计算(1)21.10 (2)2999练一练(1)98102⨯ (2)19952005⨯小结(1) 分别说出完全平方公式、平方差公式的特征(2) 在式子bd ad bc ac d c b a +++=++))((中当a 、b 、c 、d 满足什么关系时,由它可得到乘法公式? 作业:P80练一练1、2、3、4。
9.4乘法公式(1)

例3 用完全平方公式计算
(1)( -x + 2y)2
(2) ( -2a - 5)2
想一想:
你能有那些方法可以利用完全平方行观察 和分析,可以得到不同的解决问 题的方法。
例4 用完全平方公式计算
(1)9982
(2) 1012
运用完全平方公式可以起到 简便运算的作用。
(2) 第一项平方时未加括号;(应该是(-m)2 ) 少了第一数与第二数乘积的2倍 (丢了一项); 应改为: (-m+n)2= (-m)2+2•(-m)n +n2; (3) 第一数平方未添括号, 第一数与第二数乘积的2倍 错了符号; 第二数的平方 这一项错了符号; 应改为: (a−1)2=(a)2−2•(a )•1+12;
a
例题解析
例2 用完全平方公式计算
(1) ( 5 + 3p )2 (2) ( 2x - 7y )2
利用完全平方公式计算,第一步先 选择公 式,明确是哪两数和(或差)的平方;第二步 准确代入公式;第三步化简。
解原式=
第一数 的平方, 5×3p+ (3p)2 + 2× 加上第一数与第二数乘积 2 =25+30p+9p 的2倍, 加上第二数的平方. 52
一个正方形的边长为acm。若 边长减少6cm,则这个正方形的面 积减少了多少?
计算:(a+b+c)2
小兵计算一个二项整式的平方式时,得到
正确结果是4x2+ +25y2,但中间一项
不慎被污染了,这一项应是(
A 10xy B 20xy
)
C±10xy D±20xy
已知a+b=2,ab=1,
求a2+b2、(a-b)2的值.
初中数学七年级下册《9.4 乘法公式》PPT课件 (21)

【例2】用完全平方公式计算:
(1)(5+3p)2;
(2) (2x-7y)2; (3) (-2a-5)2.
9.4 乘法公式(1)——完全平方公式ห้องสมุดไป่ตู้
【练一练】
1.用完全平方公式计算: (1)(1+x)2;(2)(y-4)2; (3)(-3x+2 )2.
9.4 乘法公式(1)——完全平方公式 拓展与提升:
.4 乘法公式(1)
9.4 乘法公式(1)——完全平方公式
聪明的阿凡提
从前有一个贪心的财主,人们叫他巴依老爷. 巴依老爷有两块地,一块面积为 a2,另一块面积为 b2,而阿凡提只有一块地,面积为(a+b)2 .有一天, 巴依老爷眼珠一转对阿凡提说:“我用我的两块地换
你(的一1)块阿地凡,可提以答吧应?了”吗? (2)(a+b)2 与a2 + b2哪个大呢?
9.4 乘法公式(1)——完全平方公式
b a
b
a (a+b)2=a2+2ab+b2 ;
这个公式称为完全平方公式.
用语言叙述为:两项和的平方,等于这两个项的 平方和加上它们的积的2倍.
9.4 乘法公式(1)——完全平方公式
例1 计算: (a-b)2.
(a-b)2=a2-2ab+b2
也称为完全平方公式.
9.4 乘法公式(1)——完全平方公式
完全平方公式:
(a+b)2=a2 + 2ab + b2 (a-b)2=a2- 2ab + b2
语言表述:两数和(差)的平方,等于 它们的平方和加上(减去)它们乘积的两倍.
公式的结构特征:
首平方,尾平方,首尾二倍的积在中央, 符号看前方.
9.4 乘法公式(1)——完全平方公式
9.4乘法公式(1)

1 1 ( x 2 y )( x 2 y ) 2 2 计算: (1) 2
(2)(-4a-1)(4a-1)
B 组题:
1.思考: ( a b) 与 (a b) 相等吗? ( a b) 与 (b a ) 相等吗
2 2 2 2
作业
第 82 页 1、2、4
板 复习 …… …… …… …… …… 教
书
设
计 例1 …… …… 例2 …… …… 板演 …… …… …… …… ……
学
后
记
完全平方公式、平方差公式通常称为乘法公式,在计算时可以直接使用。 练习:第 80 页 第 1、2、3、4 小结: 今天我们学习了乘法公式
(a b) 2 = a 2 2ab b 2 (a b) 2 a 2 2ab b 2 (a b)( a b) a 2 b 2
(a b) 2 a 2 2ab b 2
也可利用多项式乘法法则证明对于任意 a、b 上式都成立
(a b) 2 = a 2 2ab b 2 (a b) 2 a 2 2ab b 2
例题 1:计算 板演 —— 完全平方公式
⑴
( x 2)
2
1 ( y )2 2 ⑵
教学方法 教 师
学 生 活 动
情景设置:
b a ab a
学生回答
b
ab
怎样计算上图的面积?它有哪些表示方法? 新课讲解: 1.完全平方公式 如果把上图看成一个大正方形,它的面积为 ( a b)
2
由学生自己先做(或互 相讨论),然后回答,若 有答不全的,教师(或其 他学生)补充.
苏科版数学七年级下册《9.4乘法公式》说课稿3

苏科版数学七年级下册《9.4 乘法公式》说课稿3一. 教材分析乘法公式是数学中的一种基本公式,广泛应用于各个领域。
苏科版数学七年级下册《9.4 乘法公式》这一节主要介绍了平方差公式和完全平方公式。
平方差公式可以帮助我们简化计算,快速求出两个数的平方差;而完全平方公式则可以帮助我们求出一个数的平方,或者两个数的乘积的平方。
这两个公式在解决实际问题中具有重要的作用。
二. 学情分析学生在学习这一节之前,已经学习了有理数的乘法、乘方等基础知识,对于公式有一定的认识。
但乘法公式较为抽象,需要学生在理解的基础上进行记忆。
同时,学生需要掌握如何将实际问题转化为乘法公式的形式,从而解决问题。
三. 说教学目标1.知识与技能目标:学生能够掌握平方差公式和完全平方公式,并能够灵活运用这两个公式解决实际问题。
2.过程与方法目标:通过小组合作、讨论等方式,培养学生主动探究、合作学习的意识,提高学生的数学思维能力。
3.情感态度与价值观目标:培养学生对数学的兴趣,增强学生自信心,使学生能够积极主动地参与到数学学习中。
四. 说教学重难点1.重点:平方差公式和完全平方公式的记忆与运用。
2.难点:如何将实际问题转化为乘法公式的形式,以及如何在复杂问题中灵活运用乘法公式。
五. 说教学方法与手段1.采用启发式教学,引导学生主动探究、发现规律,培养学生的数学思维能力。
2.利用多媒体课件,生动形象地展示乘法公式的推导过程,帮助学生理解记忆。
3.小组合作、讨论,鼓励学生发表自己的观点,培养学生的合作意识。
4.创设实际问题情境,引导学生运用乘法公式解决问题,提高学生的应用能力。
六. 说教学过程1.导入:通过复习有理数的乘法、乘方等基础知识,引出本节课的主题——乘法公式。
2.讲解:讲解平方差公式和完全平方公式的推导过程,让学生理解并记忆这两个公式。
3.练习:布置一些简单的练习题,让学生运用平方差公式和完全平方公式进行计算,巩固所学知识。
4.应用:创设一些实际问题情境,让学生运用乘法公式解决问题,培养学生的应用能力。
9.4完全平方公式.4完全平方公式

【练一练】
3.用简便方法计算 992.
4.如图所示,内外两个均为正方形,则小正 方形的边长为多少厘米?大正方形的面积比小正方 形大多少?
3
a
9.4 乘法公式(1)——完全平方公式
2=a2+2ab+b2 ; ( a + b ) 完全平方公式: 2 −2ab+b2. 2 a (a−b) =
在解题过程中要正确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不能少乘2.
a
b
(a+b)2= a2+ 2 ab + b2
9.4 乘法公式(1)——完全平方式
想一想
(a+b)2=a2+2ab+b2 ;
(a + b )2 = ( a + b ) ( a + b )
=a2+ab+ ab+b2 =a2+2ab+ b2
你能用多项式的乘法法则来说明它成立吗?
推证
这个公式称为完全平方公式.
9.4
乘法公式(1) ——完全平方公式
9.4 乘法公式(1)——完全平方公式
聪明的阿凡提
从前有一个贪心的财主,人们叫他巴依老爷. 巴依老爷有两块地,一块面积为 a2,另一块面积为 b2,而阿凡提只有一块地,面积为(a+b)2 .有一天, 巴依老爷眼珠一转对阿凡提说:“我用我的两块地 换你的一块地,可以吧?”
公式的结构特征(口诀):
首平方,尾平方,首尾二倍在中央,中央符号看前方.
9.4 乘法公式(1)——完全平方公式
【例1】用完全平方公式计算:
(1)(5+3p)2; (2) (2x-7y)2; (3) (-2a-5)2.
苏科版数学七年级下册《9.4乘法公式》说课稿

苏科版数学七年级下册《9.4 乘法公式》说课稿一. 教材分析苏科版数学七年级下册《9.4 乘法公式》这一节主要介绍乘法公式,包括平方差公式和完全平方公式。
这两个公式在数学运算中具有广泛的应用,对于学生来说,理解和掌握这两个公式对于提高他们的数学运算能力具有重要意义。
二. 学情分析面对七年级的学生,他们在之前的学习中已经掌握了有理数的运算、整式的乘法等基础知识。
对于这部分内容,学生普遍能理解和掌握,但乘法公式的理解和运用还有一定的难度,特别是完全平方公式的推导和应用。
因此,在教学过程中,我们需要关注学生的学习情况,针对性地进行教学。
三. 说教学目标1.知识与技能目标:让学生理解和掌握平方差公式和完全平方公式,能够运用这两个公式进行数学运算。
2.过程与方法目标:通过自主学习、合作交流等方法,提高学生的问题解决能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养他们积极的学习态度。
四. 说教学重难点1.重点:平方差公式和完全平方公式的理解和运用。
2.难点:完全平方公式的推导和应用。
五. 说教学方法与手段1.教学方法:采用自主学习、合作交流、教师讲解等教学方法,引导学生主动参与课堂,提高他们的学习兴趣和效果。
2.教学手段:利用多媒体课件、黑板等教学手段,直观地展示乘法公式的推导和应用过程。
六. 说教学过程1.导入:通过一个实际问题,引发学生对乘法公式的思考,激发他们的学习兴趣。
2.自主学习:让学生自主探究平方差公式和完全平方公式的推导过程,培养他们的自主学习能力。
3.合作交流:学生分组讨论,分享自己的学习心得,共同解决问题,提高合作交流能力。
4.教师讲解:针对学生的学习情况,教师进行有针对性的讲解,帮助学生理解和掌握乘法公式。
5.巩固练习:设计一些相关的练习题,让学生进行巩固练习,提高他们的应用能力。
6.课堂小结:让学生总结本节课的学习内容,巩固知识。
七. 说板书设计板书设计要清晰、简洁,能够直观地展示乘法公式的推导和应用过程。
9.4乘法公式1

1. 若(a+b) 2=7,(a-b) 2=3,求 a24y2+2x-4y+7 的值总是正数.
1 1 1 2 2 3.已知 x x 4, 求 : ①x x 2 ; ②( x x ) .
乘法公式
{
(a+b)2=a2+2ab+b2
2=a2-2ab+b2 (a-b)
乘法公式
b a
a
a2
ab
这个公式称为完全平方公式
b 用语言叙述为:
ab
b2
两数和的平方,等于这两个数 图形的面积表示为 的平方和加上它们的积的2倍.你能利用多
从整体看 从局部看
项式乘以多 项式验证这 个结论吗?
(a+b)2
(a+b) (a+b)
a2+ ab+ ab + b2
a2+2ab+b2
= a2+2ab+b2
做一做
例1 计算
(1) (2) (3)
2 (x+2y) 2 (4+y) 2 (2m+n)
(1)
2 (x+2y) 2 x
解:原式=
x· + 2· 2y +
2 (2y)
= x2+4xy+4y2
(1)
2 (4+y) 2 4
y2 + 2· y + 4· 解:原式= = 16+8y+y2
(1) (2m+n)2
(2m)· + n +2· 解:原式= 2+4mn+n2 = 4m
2 (2m) 2 n
乘法公式课件

=(mn+a)2 =(mn)2+2·mn·a +a2 =m2n2+2amn+a2
初一数学名师课程
计算: (a–b)2 解:(a–b)2= (a–b)(a–b) =a2 –ab–ab+b2 =a2–2ab +b2 (a–b)2=[a+(–b)]2 =a2 +2a(–b)+(–b)2 =a2–2ab +b2
完全平方公式
(a–b)2 = a2 – 2ab + b2
初一数学名师课程
完全平方公式
(a+b)2= a2+2ab+b2
两数和的平方 等于这两数的平方和加上 这两数积的2倍
(a–b)2= a2–2ab+b2
两数差的平方 等于这两数的平方和减去 这两数积的2倍
初一数学名师课程
探究活动二 运用完全平方公式解决问题 1.用完全平方公式计算:
试一试:计算(a+b+c)2
初一数学名师课程
思考:已知a+b=2,ab=1,求a2+b2、(a-b)2的值.
初一数学名师课程
归纳总结:
(a+b)2= a2+2ab+b2
完全平方公式
(a-b)2= a2-2ab+b2
用完全平方公式计算的步骤: (1)先选择公式,明确是哪两数和(或差)的平方 (2)准确代入公式 (3)化简
=10002 – 2×1000×2+22 =1000000 – 4000+4 =996004
运用完全平方公式可以起到简便运算的作用
初一数学名师课程
用完全平方公式计算:1012
9.4乘法公式(完全平方公式)

9.4乘法公式(完全平方公式)主备:黄宏俊 审核:初一数学备课组班级 姓名学习目标:(1) 探索并推导完全平方公式、并能运用公式进行简单的计算; (2)通过图形面积的计算,感受乘法公式的直观解释;(3)经历探索完全平方公式的过程,发展学生的符号感和推理能力。
【探索新知】如右图:你能通过不同的方法计算大正方形的面积吗?从而你发现了什么?问题:将右图看成一个大正方形,则面积为 。
将右图看成是由两个小长方形和两个小正方形组成的图形,那么它的面积为 。
结论利用多项式乘法法则计算:2)(b a + =例1 计算:( a – b )2 想一想:你有几种方法计算 (a-b)2归纳得:完全平方公式:2)(b a + 222b ab a ++=2222)(b ab a b a +-=-两数和 (差)的平方等于这两数的平方和加上 (减去)这两数乘积的两倍【知识运用】例2 用完全平方公式计算(1) ( 5 + 3p )2 (2) ( 2x - 7y )2例3 用完全平方公式计算 (1)( -x + 2y )2 (2) ( -2a - 5)2例4 用完全平方公式计算(1)9982 (2) 1012例5:填空题:(注意分析,找出a、b)①()()2 216=++x;②()()()22243=+-yx③()()2 2=+-aba;④()()2 25025=++aba⑤()-+=⎪⎭⎫⎝⎛-2224116214yxyx⑥()()222bababa++=+-()()222bababa+-=-+例6.已知3=+yx,2=xy,求①22yx+;②yx11+。
17七年级数学下册 9.4乘法公式(第1课时) 教案2 苏科版
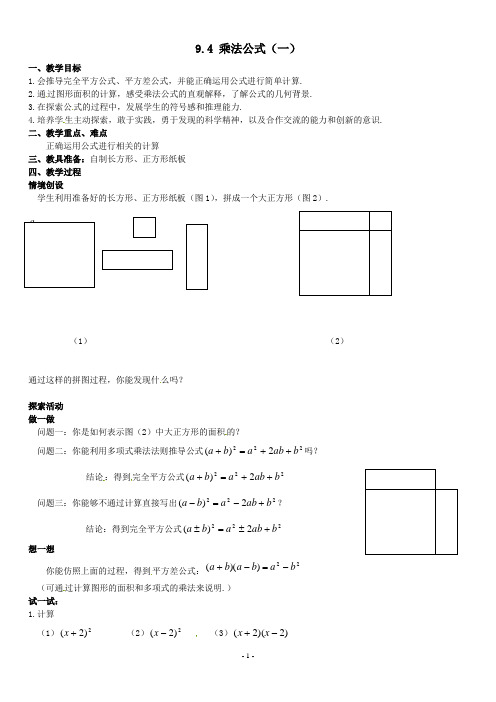
9.4 乘法公式(一)一、教学目标1.会推导完全平方公式、平方差公式,并能正确运用公式进行简单计算.2.通过图形面积的计算,感受乘法公式的直观解释,了解公式的几何背景.3.在探索公式的过程中,发展学生的符号感和推理能力.4.培养学生主动探索,敢于实践,勇于发现的科学精神,以及合作交流的能力和创新的意识.二、教学重点、难点正确运用公式进行相关的计算三、教具准备:自制长方形、正方形纸板四、教学过程情境创设学生利用准备好的长方形、正方形纸板(图1),拼成一个大正方形(图2).(1)(2)通过这样的拼图过程,你能发现什么吗?探索活动做一做问题一:你是如何表示图(2)中大正方形的面积的?问题二:你能利用多项式乘法法则推导公式2222)(b ab a b a ++=+吗?结论:得到完全平方公式2222)(b ab a b a ++=+问题三:你能够不通过计算直接写出2222)(b ab a b a +-=-?结论:得到完全平方公式2222)(b ab a b a +±=±想一想你能仿照上面的过程,得到平方差公式:22))((b a b a b a -=-+ (可通过计算图形的面积和多项式的乘法来说明.)试一试:1.计算(1)2)2(+x (2)2)2(-x (3))2)(2(-+x x(4)2)52(+a (5)2)52(--a练一练(1)))()((22y x y x y x ++- (2)1)12)(12)(12)(12(842+++++3.计算(1)21.10 (2)2999练一练(1)98102⨯ (2)19952005⨯小结(1) 分别说出完全平方公式、平方差公式的特征(2) 在式子bd ad bc ac d c b a +++=++))((中当a 、b 、c 、d 满足什么关系时,由它可得到乘法公式? 作业:P80练一练1、2、3、4。
七下9.4.1乘法公式 (1) 演示文稿

右边是 : 两数的平方和 加上(或减去)这两数乘积的两倍.
a2
a
(a−b)2 = a2−2ab+b2 b a−b
用自己的语 语言表述: 言叙述上面 a−b (a−b)2 b(a−b) 两数和(或差) 的平 的公式 a 方 等于 这两数的平方和 ab b 加上 (或减去)这两数乘积的两倍 2 . (a−b)2 = a2 −ab −b(a−b) = a2−2ab+b
( a b) 2
(a+b)2=a2+2ab+b2
上面的等式是利用面积的不同表示形式得 到的,你还有其他方法吗?
推证
(a+b)2 =(a+b)(a+b) =a2+ab+ ab+b2
=a2+2ab+ b2
一般的,对于任意的a ,b由多项式乘法法则同 样可以得到完全平方公式。
例1 计算:( a – b )
(2xy+ 5 x )2
纠 错 练 习
下 面的计算是否正确?如有错误,请改正: (1) (x+y)2=x2+y2; (2) (-m+n)2=-m2 +n2; (3) (a−1)2=a2−2a−1. 解: (1) 少了第一数与第二数乘积的2倍; 应改为: (x+y)2= x2+2xy+y2;
(2) 第一项平方时未加括号;(应该是(-m)2 ) 少了第一数与第二数乘积的2倍 (丢了一项); 应改为: (-m+n)2= (-m)2+2•(-m)n +n2; (3) 第一数平方未添括号, 第一数与第二数乘积的2倍 错了符号; 第二数的平方 这一项错了符号; 应改为: (a−1)2=(a)2−2•(a )•1+12;
9.4乘法公式

9.4乘法公式(完全平方公式)班级 姓名 学号 等第 教学目标:(1) 探索并推导完全平方公式、并能运用公式进行简单的计算; (2) 引导学生感受转化的数学思想以及知识间的内在联系。
教学重点:完全平方公式;教学难点:正确的应用完全平方公式、进行计算教学方法:探索、引导法教具准备:三角尺、投影仪 a 教学过程:一. 情景创设 b如右图:你能通过不同的方法计算大正方形的面积吗? 从而你发现了什么? 二. 探索活动问题一:如何用字母表示上图中大正方形的面积? 生: 将上图看成一个大正方形,则面积为 2)(b a +。
师:很好,还有没有其它的方法呢?生:可将上图看成是由两个小长方形和两个小正方形组成的图形,那么它的面积为222b ab a ++。
师:两种方法都求出了大正方形的面积,从而我们可以发现什么呢? 生:2)(b a +=222b ab a ++ 这个公式就叫做一个完全平方公式。
问题二:你能用多项式的乘法法则推导公式2)(b a +=222b ab a ++吗? 生:2)(b a +=))((b a b a ++=22b ba ab a +++=222b ab a ++ 师:很好,你能用同样的方法计算2)(b a -吗?生:222222))(()(b ab a b ba ab a b a b a b a +-=---=--=- 即:2222)(b ab a b a +-=-,这是我们要学习的另一个完全平方公式。
完全平方公式:2)(b a + 222b ab a ++=2222)(b ab a b a +-=-师:你能用文字语言叙述这两个公式吗?两数和 (差)的平方等于这两数的平方和加上 (减去)这两数乘积的两倍师:你能说出这两个公式的特点吗?生:左边是:两数和 (差)的平方. 右边是: 两数的平方和加上(减去)这两数乘积的两倍. 三. 范例点睛例1 计算:( a – b )2想一想:你有几种方法计算 (a -b )2例2 用完全平方公式计算(1) ( 5 + 3p )2 (2) ( 2x - 7y )2例3 用完全平方公式计算(1)( -x + 2y )2 (2) ( -2a - 5)2例4 用完全平方公式计算 (1)9982 (2) 1012例4:填空题:(注意分析,找出a 、b )①()()2216=++x ; ②()()()22243=+-y x③()()22=+-ab a ;④()()225025=++ab a ⑤()-+=⎪⎭⎫ ⎝⎛-2224116214y x y x⑥()()222b ab a b a ++=+- ()()222b ab a b a +-=-+例5.已知3=+y x ,2=xy ,求①22y x +;②yx 11+四.随堂练习1、用完全平方公式计算 (1)(1+x )2 (2) (y -4)2(3) ( x − 2y )2 (4) (2x y + x )22. 一个正方形的边长为a c m 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.要给一边长为a米的正方形桌子 铺上桌布,四周均留出0.1米宽, 问桌布面积需要多大? a+0.2 a 2
(a 0.2)
5. 有一块喷泉水池.你能计算出喷泉水池 的面积吗? a
解:喷泉水池的面积为
a-2b
(a 2b) 2 2 a 4ab 4b (平方米)
)
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
4、 填空 : 1 a 6a _______ (a ______) 9 3
2 2
a 2 a 3 3 2 5 2 4 x 2 20 x ______ ( 2 x ______) 25 2 2 2 x 2 2 x 5 5 3 a 2 b 2 (a b) 2 __________ 2ab 2 2 a 2ab b 2ab 2 2 4 xy 4 ( x y ) __________ _ ( x y) 2 2 2 2 x 2 xy y 4 xy x 2 xy y
2
2
2
a 2ab b
2
2
完全平方公式
a b2 a 2 2ab b2 a b2 a 2 2ab b 2
口诀:首平方,尾平方,积的两倍在中间
我们把和的完全平方公式与差的完全 平方公式统称为完全平方公式
(a b) a 2ab b
2 2
2
(3) (
a2 +
b3)2 a 2) 2
解:原式= ( b3 =(
b3)2 - 2× b3×
a2
+
(
a2)2
=
b6 - 2 a2 b3+ a4
2 (口诀:首项为负换位置) (-a+b)2 =(b-a)
(
a2 + b3)2 =
(
b3 -
a2)2
例2. 运用完全平方公式计算:
(1) 1042 解: 1042 = (100+4)2 =10000+800+16 =10816 (2) 99.992 解: 99.992 = (100 –0.01)2 =10000 -2+0.0001 =9998.0001
= a2 - ab - ab +b2
= a2 - 2ab+b2
完全平方公式 的图形理解
验 证 方 法 二 和的平方公式
b ab a
b²
ab b
2 2
(a+b)²
a²
a
2
(a b) a +2 ab +b
完全平方公式 的图形理解
差的平方公式
b a
ab
b²
(a-b)²
a² ab
a b
(a b) a ab ab b
1、在下列各式中,计算正确的是( A、(2m-n)2=4m2-n2
D
)
B、 (5x-2y)2=25x2-10xy+4y2
C、 (-a-1)2=-a2-2a-1
D、 (-a2-0.3ab)2=a4+0.6a3b+0.09a2b2
2、无论x取何值,(x+a)2=x2-x+a2,则常数a 等于 ( D ) A 、2 B 、 -2 C、1/2 D、 -1/2
9.4 乘法公式(1)
大桥实验学校 瞿荣微
想一想
(a+b)2=a2+2ab+b2 ; 2 2 2 a − 2 a b + b . (a−b) =
(1) 你能用多项式的乘法法则来说明它成立吗?
(2) 若 (a−b)2= 是否可行??
推证
[a+(−b)]2
(a+b)2 =(a+b) (a+b)=a2+ab+ ab+b2 =a2+2ab+ b2;
在解题过程中要准确确定a和b、对照公式原形的 两边, 做到不丢项、不弄错符号、2ab时不少乘2;
例1 运用完全平方公式计算:
2 (1)(x+2y)
解:
2 (x+2y) = x2
+2•x •2y +(2y)2
+ 2 ab +
2 +4y
2 b
(a
2 +b) =
2 a
2 =x +4xy
2 (2)(2x-3y)
例3 计算: 19982– 1998 × 3994+19972
解: 19982– 1998 × 3994+19972 = 19982–2 × 1998 × 1997+19972 = (1998 – 1997)2
=1
学会逆用公式:
2 a
2 2 +2ab+b =(a+b)
a2 - 2ab+b2 =(a-b)2
2
2
(a+b)2 = a2+2ab+b2 2 2 2 (a-b) = a -2ab+b
2 2 已知x y 7,xy 10, 求x y 的值.
解: x y 7, xy 10 x y x y 2 xy 2 7 2 10 29
2 2 2
解:(2x-3y)2=(2x)2 -2•2x •3y+(3y)2
(a 2 b) = 2 a
- 2 ab +
2 b
=4x2 -12xy +9y2
( a b c) ?
2
(a b c)(a b c)
[(a b) c] 2 2 (a b) 2(a b)c c
2
(a+b)2 = a2+2ab+b2
2 (a - b ) = 2 2 a -2ab+b
① ②
公式变形
由①得 a2+b2 = (a+b)2-2ab
由②得 a2+b2 = (a-b)2+2ab
① - ②得 (a+b)2- (a-b)2 = 4ab ① + ②得
2 2 (a + b ) + ( a - b ) = 2 2 2(a +b
利用两数和的 完全平方公式 推证公式
(a−b)2= [a+(−b)]2 = a 2 + 2 a (−b) + (−b) 2 = a2 − 2ab + b2.
验证方法一
(a+b)2 =(a+b) (a+b) = a2 +ab +ab +b2 = a2 +2ab+b2
(a-b)2 =(a-b) (a-b)
a2+b2 =(a+b)2 -2ab
1 1 2 已知x 3, 求x 2 的值. x x 1 1 2 1 2 解 : x 2 ( x ) 2( x ) x x x 1 2 (x ) 2 x 2
3 2 7
(a+b)2 = a2+2ab+b2 (a-b)2 = a2-2ab+b2
3.
已知(a b) 13, (a b) 7,
2 2
求a b , a b , (a b) ,2a ab 2b
2 2 2 2 4 2
2
2
a 2ab b 2ac 2bc c
2 2 2 2 2
2
a b c 2ab 2bc 2ac
(4)(- x2y -
)2
(-a-b)2 =(a+b)2
(口诀:两项为负都变正)
解:原式= ( x2y +
)2
+
=( x2y)2 + 2× × x2y = x 4y 2 + x 2y +
