电磁场之恒定磁场
恒定磁场

三、恒定磁场电流或运动电荷在空间产生磁场。
不随时间变化的磁场称恒定磁场。
它是恒定电流周围空间中存在的一种特殊形态的物质。
磁场的基本特征是对置于其中的电流有力的作用。
永久磁铁的磁场也是恒定磁场。
1、磁通密度与毕奥-萨伐尔定律磁通密度是表示磁场的基本物理量之一,又称磁感应强度,符号为B。
电流元受到的安培力 B l d I f d⨯''=毕奥——萨伐尔定律 ⎰⨯=l r r l Id B 2004 πμ对于粗导线,可将导线划分为许多体积元dV 。
⎰⎰⎰⨯=Vrr dV J B 24 πμ 2、磁通连续性定理磁场可以用磁力线描述。
若认为磁场是由电流产生的,按照毕奥-萨伐尔定律,磁力线都是闭合曲线。
磁场中的高斯定理 0d =⋅⎰⎰SS B式中,S 为任一闭合面,即穿出任一闭合面的磁通代数和为零。
应用高斯散度定理⎰⎰⎰⎰⎰⋅∇=⋅VSdV B S B d0=⎰⎰⎰⋅∇VdV B由于V 是任意的,故 0=B⋅∇式中⋅∇为散度算符。
这是磁场的基本性质之一,称为无散性。
磁场是无源场。
3、磁场中的媒质磁场对其中的磁媒质产生磁化作用,即在磁场的作用下磁媒质中出现分子电流。
总的磁场由自由电流与分子电流共同产生。
永磁铁本身有自发的磁化,因而不需要外界自由电流也能产生磁场。
磁媒质的磁化程度用磁化强度M来表征,它是单位体积内的磁偶极矩。
磁偶极矩:环形电流所围面积与该电流的乘机为磁偶极矩,其方向与电流环绕方向符合右螺旋关系。
n IS P m =磁场强度 M B H-=0μ 或 )(0M H B +=μ本构方程 由m H M χ=可得 H B μ=,该式称为磁媒质的成分方程或本构方程。
磁媒质的分类:r m μμχμμ00)1(=+=,顺磁质 1>r μ,抗磁质 1<r μ,铁磁质1>>r μ。
4、安培环路定律磁场强度H沿闭合回路的积分,等于穿过该回路所限定的面上的自由电流。
回路的方向与电流的正向按右螺旋规则选定。
电磁场与电磁波--真空中恒定场的基本规律

=rr
rr
R12 = rr rr
2.3 真空中恒定磁场的基本规律
r
rr
蜒 蜒 r
F12
C2
0
C1 4π
I2dl2
(I1dl1 R132
R12 )
C2
r C1 dF12
r
rr
r dF12
0
4π
I2dl2 (I1dl1 R12 ) R132
对比
r rr dFm Idl B
电流元
r Idl
Er(rr
r ) dl
0
环路定理表明:静电场是无旋场,是保守场,电场力做功与路径无关。
2.2 真空中静电场的基本规律
3. 利用高斯定理计算电场强度 在电场分布具有一定对称性的情况下,可以利用高斯定理计算电场强度。
具有以下几种对称性的场可用高斯定理求解:
• 球对称分布:包括均匀带电的球面,球体和多层同心球壳等。
位于xy 平面上,则所求场点为P (0, 0, z ) , 如图 所示。采用圆柱坐标系,
圆环上的电流元为
位置矢量为 rr erz
r Idl
er
Iad
z ,故得
'
,
其位置矢量为 rr er a,而场点 P 的
rr
rr
r ez
z
r e a,
rr rr (z2 a2)1/2
z
r Idl
(rr
rr)
1 b2 )1/2
z0
0
z0
且
2.2 真空中静电场的基本规律
r E(0,0, z)
r ez
S0z 2 0
1 z
(z2
1 b2 )1/2
z0
电磁场 恒定磁场

工程电磁场导论:恒定磁场
2)无外场时,各分子环流无规取向,总体磁矩为零,此时无宏观 磁场。有外场时,这些微磁矩受到力矩
的作用,趋于沿外场方向排列(
)。此时,出现
的有
序分布,总磁场不再为零,宏观上呈现磁性。这个过程,称为物 质(媒质)的磁化。 3)磁化的后果,就是媒质产生附加的磁场,叠加于外磁场之上, 空间的磁场,由二者共同决定。
(沿 R 方向)那么前者对后者的磁场作用力可表示为
eR方向由施力者指向
受力者
其中 ,称为真空磁导率。
工程电磁场导论:恒定磁场
• 这个规律没有官方的名称,但常常称为 Ampere 定律,
其在磁场中的地位与 Coulomb 定律在电场中的地位相
当。因此,对于真空中的两个载流回路 的作用力 和 , 对
工程电磁场导论:恒定磁场
•
也可以定义磁力线( B 线),其微分方程:
工程电磁场导论:恒定磁场
【例3-1】有限长直线电流的磁场问题。
•
考虑对称性,选取柱坐标,导线中点为坐标原点,导线与 z 轴重 合。显然,磁场与 维度无关。
取元电流
在 z′处,其在 P
点产生的元磁场
其中
工程电磁场导论:恒定磁场 因此
故
工程电磁场导论:恒定磁场
工程电磁场导论:恒定磁场
• 各向同性线性磁介质,有本构方程
称为磁化率,是一个无量纲的纯数。此时有
其中
为相对磁导率,
为磁导率。
工程电磁场导论:恒定磁场 一些磁介质的性能
工程电磁场导论:恒定磁场
• 对于铁磁介质,情况十分复杂。
等式 仍然成立,但是
不成立。 M~H 间没有线性关系。
工程电磁场导论:恒定磁场
大学物理电磁场第3章讲义教材

zˆ4(a20Iaz22)3/2
2
0
d'
B(z)2(a20Iaz22)3/2 z
3.2 真空中的静磁场基本方程
1. 磁通连续性定理
定义穿过磁场中给定曲面S 的磁感应强度B 的通量为磁通:
BdS 单位 韦伯Wb
S
若S面为闭合曲面
ΦBdS0
磁通连续 性定理
上页 下页
ΦBdS0
注意
① 磁通连续性原理也称磁场的高斯定理,表明磁力线是无头
Bdl 2B0I
l
得到
B
0I 2
e
323
I’ II 3 2 2-- 2 22 2 I 3 2 3 2-- 22 2
lBdl2B 0I3 2 3 2--22 2
得到
B
0I 2
32 -2 32 -22
e
同轴电缆的磁场分布
上页 下页
4.真空中的磁场方程
B (r)40 VJR 2R ˆd V '
磁矢位
注意 1 A是从矢量恒等式得出,是引入的辅助计算 量,无明确的物理意义;
2 A适用于整个磁场区域;
③因
mBdSAdS Stokes’ A dl
S
S
l
m Adl
l
A的单位 Wb/m (韦伯/米)
④ 恒定磁场中A满足库仑规范
A0
2 . 磁矢位 A 的求解
应用磁矢位A求解恒定磁场问题也可以分为 场源问题和边值问题。
③ 洛仑兹力垂直于电荷运动方向,只改变电荷运动方向, 对电荷不做功,而库仑力改变电荷运动速度做功。
上页 下页
安培力定律
真空中
描述两个电流回路之间相互作用力的规律。
l1
电磁场4恒定磁场

S
L
S
磁化电流体密度:
Jm M
磁化电流面密度:
JS
M
en
结论:
➢有磁介质存在时,场中任一点的 B 是自由电流和磁化 电流共同作用在真空中产生的磁场;
➢磁化电流具有与传导电流相同的磁效应。
磁偶极子与电偶极子对比
模型
电量
产生的电场与磁场
电 偶
v p P
1 4π0
pv
1 R
pv evR 4π0R2
➢电流与电流之间 存在相互作用
➢磁场对运动电荷的作用 运动电荷既能产生磁效应也 受到磁力的作用
表明: ➢电流与电流之间,磁铁与电流之间都存在力的作用 ➢磁铁和电流周围存在磁场 ➢磁力是通过磁场来传递的
运动电荷
磁场
运动电荷
存在于电流或永久磁铁周围空间且能 对运动电荷和电流施加作用力的物质
(1) 安培定律
dF
Idl
0
4
I
dl
eR
l R2
点电荷q1对点电荷q2 的作用力
F
1
4 0
q2q1 R2
eR
电荷之间相互作用 力通过电场传递
F q
1
4 0
V
dV
R2
eR
qE
点电荷 库仑定律 电场强度
电流元I′dl′对电流元
Idl的作用力
F
0 4
Idl
(
I
dl
eR
)
R2
电流之间相互作用 力通过磁场传递
F
Idl
0
l
4
l
I
dl
eR
R2
Idl B
l
电流元 安培定律 磁感应强度
《电磁波与电磁场》4-恒定磁场

外加磁场时,磁场力使带电粒子的运动方向发生变化或产生 新的电流,使磁矩重新排列,宏观的合成磁矩不再为零,这 种现象称为磁化。
媒质磁化 B
B
B'
磁化结果出磁偶现极的子 合成磁矩产生二次磁场BS,这种二次 磁场影响外加磁场Ba,导致磁化状态发生改变,从而又使J’S
Chapter 4 恒定磁场
磁场是由运动电荷或电流产生的;当产生磁场 的电流恒定时,它所产生的磁场不随时间变化, 这种磁场称为恒定磁场。
4.1 磁感应强度 4.3 磁场的基本方程 4.5 电感 4.7 磁路
4.2 安培环路定律 4.4 磁场位函数 4.6 磁场能量
第4章 恒定磁场
1. 磁场是由运动电荷或电流产生的。 2. 运动电荷或载流导线在磁场中要受到磁场的作用力。 3. 检验磁场是否存在的一种方法是改变载流导线在磁
抗磁性。媒质正常情况下,原子中的合成磁矩为零。当外 加磁场时,电子进动产生的附加磁矩方向总是与外加磁场 的方向相反,导致媒质中合成磁场减弱。如银、铜、铋、 锌、铅及汞等属抗磁性媒质。 顺磁性。媒质在正常情况下,原子中的合成磁矩并不为零, 只是由于热运动结果,宏观的合成磁矩为零。在外加磁场的 作用下,磁偶极子的磁矩方向朝着外加磁场方向转动。使合 成磁场增强。如铝、锡、镁、钨、铂及钯等属顺磁性媒质。
但是,无论抗磁性或者顺磁性媒质,其磁化现象均很微弱,因此,可 以认为它们的相对磁导率基本上等于1。铁磁性媒质的磁化现象非常 显著,其磁导率可以达到很高的数值。值得注意的是,近年来研发的 新型高分子磁性材料,其相对磁导率可达到与介电常数同一数量级。
媒质 金 银 铜
电磁场与电磁波(王家礼 西电第三版)第三章 恒定电流的电场和磁场

3-7 所示)。设土壤的电导率为σ;接地半球的电导率为无穷大。
第三章 恒定电流的电场和磁场
图 3-7 半球形接地器
第三章 恒定电流的电场和磁场
解:导体球的电导率一般总是远大于土壤的电导率,可 将导体球看作等位体。在土壤内,半径r等于常数的半球面是 等位面。假设从接地线流入大地的总电流为I,可以容易地求 出,在土壤内任意点处的电流密度,等于电流I均匀分布在半 个球面上。即:
图 3-5 同轴线横截面
第三章 恒定电流的电场和磁场
两导体间的电位差为
b
U Edr
I
lnb
a
2π a
这样,可求出单位长度的漏电导为
G0
I U
2π
ln b
a
例 3-2 一个同心球电容器的内、外半径为a、b,其间媒质
的电导率为σ,求该电容器的漏电导。
解:媒质内的漏电电流沿径向从内导体流向外导体,设流
过半径为r的任一同心球面的漏电电流为I,则媒质内任一点的
RIP2 4π1(a11b)
第三章 恒定电流的电场和磁场
3.1.7 恒定电流场与静电场的比拟 如果我们把导电媒质中电源外部的恒定电场与不存在体电荷
区域的静电场加以比较,则会发现两者有许多相似之处,如表 3-2 。 可见,恒定电场中的E、j、J、I和σ分别与静电场中的E、 j 、
D、q和ε相互对应,它们在方程和边界中处于相同的地位,因而 它们是对偶量。由于二者的电位都满足拉普拉斯方程,只要两种 情况下的边界条件相同,二者的电位必定是相同的。因此,当某 一特定的静电问题的解已知时,与其相应的恒定电场的解可以通 过对偶量的代换(将静电场中的D、q和ε换为J、I和σ)直接得出。 这种方法称为静电比拟法。例如,将金属导体 1、2 作为正、负极 板置于无限大电介质或无限大导电媒质中,如图 3-6 所示,可以 用静电比拟法从电容计算极板间的电导。因为电容为
高等电磁理论-基本电磁理论

卫星导航系统
卫星导航原理
卫星导航系统通过接收来自卫星的信号来确定接收设备的 位置。高等电磁理论在卫星导航原理、信号处理和误差修 正等方面具有重要应用。
导航精度提升
为了提高卫星导航的定位精度和稳定性,需要进行深入研 究和系统优化。高等电磁理论为导航精度提升提供了重要 的理论支撑和实践指导。
多系统兼容与互操作
天线辐射原理
01
02
03
偶极子天线
是最简单的天线结构,由 两个相反的电荷或电流源 组成,能够向空间辐射电 磁波。
磁偶极子天线
由长直导线绕成线圈构成, 其辐射场呈现环状结构。
电偶极子天线
由两个相距很近的等量异 号点电荷组成,其辐射场 呈现向外的发散状。
电磁散射原理
散射系数
散射相移
描述散射场强度的物理量,与散射体 的形状、大小、介电常数等有关。
电磁场具有物质性,可以与物质 相互作用,产生力的作用和能量
的传递。
电磁场具有波动性,其传播方式 为电磁波,包括无线电波、可见 光、不可见光(紫外线和红外线)
等。
麦克斯韦方程组
麦克斯韦方程组是描述电磁场运动和变化的数学 模型,由四个基本方程构成。
方程组揭示了电场和磁场之间的相互关系,以及 它们与电荷和电流密度的关系。
麦克斯韦方程组是经典电磁理论的基石,是研究 电磁波传播、辐射和吸收等问题的基本工具。
电磁波的传播特性
电磁波在空间中传播时,会受 到介质的影响,其传播速度、 波长和频率会发生变化。
电磁波的传播方向与电场和磁 场的振动方向相互垂直,符合 横波的特征。
电磁波的传播速度与介质的性 质有关,不同的介质对不同频 率的电磁波有不同的折射率和 吸收系数。
磁场的种类

磁场是围绕磁体或电流而存在的物理现象。
根据形成磁场的方式和性质,可以将磁场分为以下几种类型:
恒定磁场:也称为静磁场,指的是保持稳定的磁场,其强度和方向不随时间变化。
例如,磁铁所产生的磁场就是恒定磁场。
电磁场:由电流所产生的磁场被称为电磁场。
当电流通过导线或线圈时,会形成围绕导线或线圈的磁场。
电磁场具有与电流方向和大小相关的特性。
变化磁场:指磁场强度和方向随时间变化的磁场。
这种变化可以是周期性的,也可以是非周期性的。
变化磁场产生的电磁感应现象是电磁感应定律的基础。
自旋磁场:自旋磁场是与粒子的自旋运动相关的磁场。
自旋是微观粒子(如电子)的内禀属性,具有磁矩,因此可以产生磁场。
这些是磁场的一些常见种类。
磁场的研究和应用涉及许多领域,包括物理学、工程学和医学等。
磁场对于电磁感应、电磁波传播和磁性材料等方面有着重要的影响和应用。
南方电网专业课考点总结 电磁场 第三章1

磁力线的性质:
B线是闭合曲线; B线与电流方向成右螺旋关系; B线不能相交 磁场强处,磁力线密集,否则稀疏。
上 页 下 页
第 二 章
恒定电场
B 线方程
B // dl → B = kdl or B × dl = 0
S
Jm = ∇ × M
可以证明面磁化电流 注意
体磁化电流
Km = M × en
磁化电流是一种等效电流,是大量分子电流磁效应的表示。 有磁介质存在时,场中的 B 是传导电流和磁化电流共同 作用在真空中产生的磁场。
上 页
下 页
第 二 章
恒定电场
T(Wb/m2) 1T=104(GS)
或磁通密度 F B Idl α
上 页 下 页
定义
第 二 章
恒定电场
洛仑兹力 电流是电荷以某一速度运动形成的,所以磁场对
电流的作用可以看作是对运动电荷的作用。
dq dF = Idl × B = (vdt ) × B dt
洛仑兹力
dF B v α
F = qv × B
∫ B ⋅ dl = μ I
l 0
交链多个电流
0
∫ B ⋅ dl = μ ∑ I
l
真空中的安 培环路定律
表明在真空的磁场中,沿任意回路磁感应强度B的线积 分等于真空磁导率乘以穿过回路限定面积上电流的代数和。
注意
① 定律中电流I 的正负取决于电流的方向与积分回路的绕 行方向是否符合右螺旋关系,符合时为正,否则为负。 ② 定律中的B是整个场域中所有电流的贡献。
体电流
电磁场导论 第三章]
![电磁场导论 第三章]](https://img.taocdn.com/s3/m/531f55c7240c844769eaee8a.png)
恒定磁场
2) 1 2
得到
B dl 2πB 0 I l 0 I B e 2 π
3) 2 3,
2 32 2 2 2 I I I 2 I 2 2 2 3 2 3 2
图3.2.10 同轴电缆
0 I ( 32 2 ) l B dl 2πB 32 22
根据
B A
A
z Az
B
0 I l
2 2 32
4π ( z )
e
0 I l
4πr
sin e
第 三 章
恒定磁场
例 应用磁矢位 A,试求空气中长直载流细导线产生 的磁场。
A Aez 解: 定性分析场分布,
A
0 I
L
0 I L dz 4π L r
第 三 章
恒定磁场
例
真空中有一载流为 I,半径为R的圆环, 解:元电流 Idl 在 P 点产生的 B 为
试求其轴线上 P 点的 磁感应强度 B 。
0 Idl e r ( Idl dB 2
4 πr
dB
图3.1.3 圆形载流回路
er )
2 4π( R 2 x 2 )
0 Idl sin
图3.3.3 铁磁媒质与空 气分界面
与分界面近似垂直,铁磁媒质表面
近似为等磁面。
返 回
上 页
下 页
第 三 章
恒定磁场
磁矢位及其边值问题
1. 磁矢位 A 的引出 由
B 0 A 0 B A
A 磁矢位
Wb/m(韦伯/米)。
返 回
上 页
电磁场与电磁波 第五章答案

第五章 恒定磁场重点和难点该章重点及处理方法与静电场类似。
但是磁感应强度的定义需要详细介绍,尤其要强调磁场与运动电荷之间没有能量交换,电流元受到的磁场力垂直于电流的流动方向。
说明磁导率与介电常数不同,磁导率可以小于1,而且大多数媒质的磁导率接近1。
讲解恒定磁场时,应与静电场进行对比。
例如,静电场是无散场,而恒定磁场是无旋场。
在任何边界上电场强度的切向分量是连续的,而磁感应强度的法向分量是连续的。
重要公式磁感应强度定义:根据运动电荷受力: B v F ⨯=q根据电流元受力: B l F ⨯=d I 根据电流环受力: B m T ⨯=真空中恒定磁场方程: 积分形式: I ⎰=⋅ll B 0d μ⎰=⋅SS B 0d微分形式:J B 0 μ=⨯∇0=⋅∇B已知电流分布求解电场强度:1,A B ⨯∇=V V ''-'=⎰'d )(4)( 0 r r r J r A πμ2,V V ''-'-⨯'=⎰'d )()( 4)(30 r r r r r J r B πμ 毕奥─萨伐定律。
3,I ⎰=⋅ll B 0d μ安培环路定律。
面电流产生的矢量磁位及磁感应强度分别为S ''-'=⎰'d )(4)(0 r r r J r A S S πμS ''-'-⨯'=⎰'d )()(4)( 30 r r r r r J r B S S πμ 线电流产生的矢量磁位及磁感应强度分别为⎰''-'=l r r l r A d 4)(0I πμ⎰''-'-⨯'=l r r r r l r B 30 )(d 4)(I πμ矢量磁位满足的微分方程:J A 0 2μ-=∇无源区中标量磁位满足的微分方程: 0 2=∇m ϕ 媒质中恒定磁场方程: 积分形式: I l =⋅⎰l H d⎰=⋅SS B 0d微分形式:J H =⨯∇ 0=⋅∇B磁性能均匀线性各向同性的媒质:场方程积分形式:⎰=⋅lI d μl B⎰=⋅BS H 0d场方程微分形式: J B μ=⨯∇ 0=⋅∇H矢量磁位微分方程:J A 2μ-=∇矢量磁位微分方程的解: V V ''-'=⎰'d )(4)(r r r J r A πμ 恒定磁场边界条件:1,t t H H 21=。
工程电磁场--第4章--恒定磁场的基本原理

0 4a
4a
2 时,
整个圆形线电流在圆心产生的磁感应强度
B 2 0 Iez 0 Iez
4a
2a
28
注意:
θ1为A到电流后端, θ2为A到电流前端29
30
4.2 矢量磁位与磁通连续性定理
1.矢量磁位
由体电流(典型情况)产生磁场的磁感应强度
B 0
4
V
J
R
eR
2
dV
0 4
V
J
1 R
16
载流线圈是一种线电流,
所产生磁场的磁感应强度为
B 0
4
l
Idl eR R2
式中: l 为线电流的源区。
17
由面电流产生的磁感应强度为
B
0 4
S
K
e R2
R
dS
式中: S 为面电流的源区。
由体电流产生的磁感应强度为
B 0
4
V
J
R
e
2
R
dV
式中:V 为体电流的源区。
18
5.洛仑兹力
0 4
I1dl1
I2dl2 e21 R221
对比库仑定律,两电荷元之间作用力:
dF12
1 40
dq1
dq2e12 R122
9
电磁场与电磁波问题详解

电磁场与电磁波复习材料简答1.简述恒定磁场的性质,并写出其两个基本方程。
.1、答「恒定盛场是连续的场或无散场,即礙感应强度沿任一闭合曲面的积分尊于專。
产生恒定磁场的源是矢量源0 ©分〉两个基本方程:M-^ = 0 (1 分)(写出徹分形式也对)2.试写出在理想导体表面电位所满足的边界条件。
12•答:设理想导体内部电位为0空空气燥质中电位为孙。
由于理想导体表面电场的切冋分量等于零,或者说电场垂直于理想导体表面,因此有仏=妣(3分)=—(T3.试简述静电平衡状态下带电导体的性质。
答:静电平衡状态下,带电导体是等位体,导体表面为等位面;(2分)导体内部电场强度等于零,在导体表面只有电场的法向分量。
(3分)4.什么是色散?色散将对信号产生什么影响?答:在导电媒质中,电磁波的传播速度随频率变化的现象称为色散。
(3分)色散将使信号产生失真,从而影响通信质量。
(2分)5•已知麦克斯韦第二方程为",试说明其物理意义,并写出方程的积分形式。
答2意义匕随时间变化的磁场可以产生电场。
其和分形式为订事龙二一[罟庖6.试简述唯一性定理,并说明其意义。
答:在静电场中’在给定的边界条件下,拉晋拉斯方程或泊松方程的解是唯一的’这一定理称为唯一性定理. g分)它的意义|给出了定解的充要条件I既满足方程又满足边界条件的解是正确的。
7.什么是群速?试写出群速与相速之间的关系式。
方程的微分形式: VxE = -&B dtii.什么是电磁波的极化?极化分为哪三种?答:电磁波的电场强度矢量的方向随时间变化所描绘的轨迹称为极化。
分为:线极化、圆极化、椭圆极化。
(2分)极化可以12•已知麦克斯韦第一方程为式。
.:D可汇H = J + —ct,试说明其物理意义,并写出方程的积分形答:它表明时变场中械场是由传导电流加位移电溢罟共同产生该方程的积分形式対严"叩+豎■dS答’电磁波包络或能量的传播速度称为群速。
群速%与相速V*的关系式为’V p = J (2分)耳*1一血兀片do&写出位移电流的表达式,它的提出有何意义?悝移电济],=^位移电流产主磁效应代表了变化的电场能够产主磯场,使&麦克斯韦能够预言电谨场以波的形式恃播、为现代通信打下理论基础-9 •简述亥姆霍兹定理,并说明其意义。
磁场的原理

磁场原理
磁场原理指的是磁体产生磁场的基本原理。
在物理学中,磁场是由带有磁性的物质或者通过电流产生的电磁场所产生的。
磁场原理可以通过安培环路定理和洛伦兹力等概念来解释。
安培环路定理指出,一个闭合回路中的总磁通量等于该回路内部产生的总电流。
根据此定理,当电流通过导线时,会形成一个与导线呈环形的磁场。
这个磁场的方向可以用右手规则来确定,规则是将大拇指指向电流的方向,其他手指则会指向磁场线圈的方向。
洛伦兹力是描述电流在磁场中所受力的物理定律。
根据洛伦兹力的原理,电流在磁场中会受到垂直于电流方向和磁场方向的力,这个力的方向可以用右手规则来确定。
右手规则的方法是将大拇指指向电流方向,其他手指指向磁场的方向,大拇指和其他手指的叉乘结果即为所受力的方向。
通过安培环路定理和洛伦兹力的原理,我们可以解释磁体是如何产生磁场的。
当电流通过一个线圈时,由于导线上的电子呈现运动状态,就产生了一个磁场。
这个磁场的强度和方向与电流的大小和方向有关。
当电流增大时,磁场的强度也增大,当电流方向改变时,磁场的方向也相应改变。
除了电流线圈产生的磁场,还有一种特殊的磁场叫做恒定磁场。
恒定磁场是由一根永久磁铁或者一个电磁铁产生的。
永久磁铁的磁场是由其内部的磁矩所产生的,这个磁矩指向磁铁的南北极。
电磁铁的磁场则是通过通电产生的电流所产生的。
总而言之,磁场原理是描述磁体产生磁场的基本原理。
通过电流线圈和恒定磁场的产生过程,可以感受到磁场的强度和方向与电流大小和方向的关系。
这些原理在电磁学和应用中都有重要的应用价值。
《电磁场与电磁波》恒定磁场

分界面磁化电流: Km (M1 M2 ) en
Im
M dl
l
安培环路定理
1.真空中的安培环路定理
l B dl 0 I
真空磁场中,磁感应强度沿任意回路的 环路积分等于真空的磁导率乘以穿过该 回路所限定面的电流的代数和;
2.一般形式的安培环路定理
l B dl 0 ( I Im )
H dl H dl I
PaQ
PbQ
c
I
闭合回路PaQcP:
Q
H dl 2I PaQcP
H dl H dl 2I
PaQ
PcQ
规定:积分路径不穿过电流回路所限定的面。
2.标量磁位的边值问题 微分方程
B 0
H 0
H m
m 0
m m 0 均匀媒质:=0
2m 0 标量磁位的微分方程
Sd
(1)常磁链系统:
Wm
1 2
H BdV
V
V
B2 dV
20
B2Sd
2d
20 20S
f
Wm g
k const
2 20 S
吸力:F 2 f
3.虚位移法举例
例:分析电磁铁吸力,气隙截面积S,长d
1. 恒定磁场基本方程 恒定磁场的性质可由下面一组基本方程描述:
磁通连续性定理 SB dS 0 安培环路定理 l H dl I
各向同性线性媒质的构成方程
B 0 H J
B H
恒定磁场的性质:有旋无散。
2.分界面的衔接条件
B 的衔接条件
2
B2n B2
S h
1 B1
B1n
SB dS 0
B1nS B2nS 0 B1n B2n
电磁场分类

电磁场分类
电磁场是物理学中的一个重要概念,它是由电荷和电流所产生的一种物理场。
根据电磁场的性质和特点,可以将其分为静电场、恒定磁场和电磁波三种类型。
静电场是指在没有电流的情况下,由电荷所产生的电场。
在静电场中,电荷之间的相互作用力是通过电场传递的。
静电场的特点是稳定、静止和不可逆转。
静电场的应用非常广泛,例如电荷分离、电场感应、电容器等。
恒定磁场是指在没有电荷的情况下,由电流所产生的磁场。
在恒定磁场中,电流之间的相互作用力是通过磁场传递的。
恒定磁场的特点是稳定、静止和不可逆转。
恒定磁场的应用也非常广泛,例如电动机、发电机、电磁铁等。
电磁波是指由电场和磁场相互作用所产生的一种波动现象。
电磁波的特点是具有波动性、传播性和相互作用性。
电磁波的应用非常广泛,例如无线电通信、雷达、微波炉等。
电磁场是物理学中非常重要的一个概念,它的分类有助于我们更好地理解和应用电磁场的知识。
静电场、恒定磁场和电磁波分别具有不同的特点和应用,我们需要根据实际情况选择合适的电磁场类型进行研究和应用。
工程电磁场 倪光正第3章静态电磁场Ⅱ:恒定电流的电场和磁场

例 3.1 一接地系统
i
2
土壤 J线
1 a
接地体
等位面
[解] 15106 S/m钢
2102 S/m土 壤
1 895950
2 8 0
3.良导体与理想介质 ( 2 0 ) 分界面上的边界条件
1
+
+
+
+
J c1
+
+ E2t + 2 +
2 0 J1n J2n 0
U
E2n E2
E线
E2t
J c1n 0 J c2n 0
2I
R半球
接地器
I
1
a
屏蔽室接地电阻(深度 20 m) 返回 下页
高压大厅网状接地电阻(深度1米)
返回 上页
3.2.3 跨步电压
I
o
a 土壤
~r
E dl
AB
r
r
I
o
a 土壤
~r E dl
r
I dr
rb r 2
I
r
1 b
1 r
r b
bI r2
U 0 (安全电压)
AB r
r
bI
(3) 推广到其他学科,即可籍以用电测法求得非电 量的相似解答。
3.2.2 接地电阻
1.基本概念
接地——将电气设备的某一部分与大地在电气上相联结。 接地器——埋于地中的导体系统 ( 球、棒、网及其组合 ) 。 接地的工程意义:
• 保护性接地 • 工作接地
ⅰ 电子电路中 ⅱ 电力工程中
A
o
B
短路点
第3章 静态电磁场Ⅱ: 恒定电流的电场和磁场
恒定磁场基本方程

arr sin )d
坐标变换
17
av (avz cos avr sin)
(ar x
sin
avy
cos)
[ar z
cos
r (ax
cos
avy
sin
)
sin
]
r
B
0 Ia 4 R2
2
0
r a
(ar z
cos
ar r
sin )d
avz
0 4
Ia R2
g2
gsin
avz
0 Ia2
2R3
avz
直接求解. B
dB
0
Idl
a
(I
a
Sd
)
4
R az R cos ar R sin
C
I源dl源 R源2 场
aR
闭合 环路C
z
P(0,0,z)
R
a
R R 源点到场点= z 2 a2
y
单位矢量aR ?
x
Idl
aavvBrr电磁场4av与xa0v电RIcx磁aos2波isn02 aravavyy(scarionz scos
联想:
r
• D ——静电场散度方程的微分形式
静电场是有源场
电磁场与电磁波
14
6. 恒定磁场散度方程的积分形式
v Q•B 0
vv
v
ÑS B • dS V ( • B)dV 0
vv
B • dS -----磁通量 S
磁场中通过任何闭合曲面的磁通量恒等于0
v
•B 0 vv
磁通连续性原理、
ÑS B • dS 0 磁场中的高斯定理
电磁场与电磁波典型习题及答案(恒定磁场)
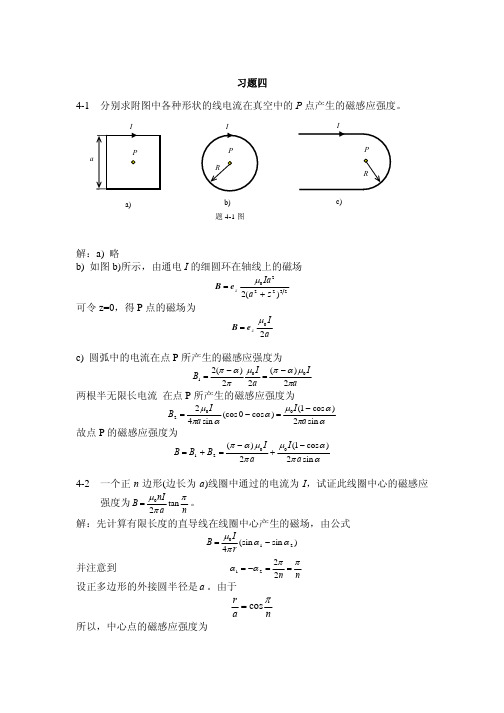
=
8 r
+ 3cotθ
≠
0 ,F
不表示磁感应强度
B。
e) ∇ ⋅ F = − ∂A + ∂A = 0 (A 为常数), J = ∇ ⋅ B = ∇ ⋅ F = 0
∂x ∂y
µ0
µ0
f) ∇ ⋅ F = 1 ∂ (r3r) + ∂2 = 6 ≠ 0 ,F 不表示磁感应强度 B。
r ∂r
∂z
4-4 无限长直线电流垂直于磁导率分别为 µ1 和 µ2 的两种介质的分界面,试求: (1) 两种介质中的磁感应强度 B1 和 B2;(2) 磁化电流分布。
B0x = 0.002 , B0 y = 0.5 , B0z = 0
即
B0 = ex 0.002 + e y 0.5
4-13 真空中有一厚度为 d 的无限大载流块,电流密度为 ez J0 ,在其中心位置有 一半径为 a 的圆柱形空腔。求腔内的磁感应强度。
解:设空腔中同时存在有密度为 ±ez J0 的电流,则可利用安培环路定律和迭加原 理求出空腔内的 B 。
+ π (r 2
− a12 )J 2 ] ⇒
B
=
eφ
⎜⎜⎝⎛
10 3
r
− 10−5 r
⎟⎟⎠⎞
当r
>
a2 时,有 B
= eφ
µ0I 2π r
=
eφ
2 ×10−5 r
4-8 已知在半径为 a 的圆柱区域内有沿轴向方向的电流,其电流密度为
J
= ex
J0r a
,其中 J0 为常数,求圆柱内外的磁感应强度。
1 r
d (r 1) = 0 dr r
在 r=0 处, 具有奇异性。以 z 轴为中心作一个圆形回路 c,由安培环路定律得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上页 下页
I 2 e
B
0 2
I
e
0 a
a
M B H
0
=
0 0
I 2π
e
a
0
a
Jm
M
Mφ z
eρ
1 ρ
( ρMφ ) ρ
ez
0
上页 下页
例
有一磁导率为 µ ,半径为 a 的无限长导磁圆柱,其轴
线处有无限长的线电流 I,圆柱外是空气 µ0 ,试求 B,H
与 M 的分布,并求磁化电流。
B 线微分方程
导线位于铁板上方
长直螺线管的磁场
上页 下页
一对反向电流传输线
一对同向电流传输线
两对反相电流传输线
两对同向电流传输线
上页 下页
3. 真空中的安培环路定律 以无限长直载流导线的磁场为例
B dl Bdlcos
0 I 2
d
0 I 2
2
d
0
0I
若积分回路没有和电流交链
B
dl
0 I 2
方向是否符合右螺旋关系,符合时为正,否则为负。
② 定律中的B是整个场域中所有电流的贡献。
上页 下页
B dl 0(I1 2I2 )
l
② 由 lB d l 0 I
斯托克斯定理 B dS 0 J dS
S
S
B μ0J
恒定磁场是 有旋场
上式两边取旋度 B μ0 J 0
例 试求载流无限长同轴电缆产生的磁感应强度。
解平行平面磁场,
B B()e
1) 0 1
安培环路定律
l B dS u0I
I
I
12
2
I
2 12
B l
dl
2B
0
I 2 12
安培定律示意图
故
B
0 I 2 12
e
上页 下页
2) 1 2
l B dl 2B 0I
得到
B
0 I 2
e
3) 2 3,
②由
B dS 0 散度定理
s
V BdV 0
B 0
表明恒定磁场是无源场可作为判断一个矢量场是否为 恒定磁场的必要条件。
③ 磁通连续性原理可以从毕奥—沙伐定律中导出
上页 下页
2. 磁力线
磁场分布可以用表示磁感应强度的磁力线来形象的描述。规定:
① 磁力线是一些有方向的曲线,曲线上任一点的切线方向
4 2 ρ
0I 4
(sin
1
sin
2 )
当 L1 时,, L2
B
0I 2
e
上页 下页
例 无限大导体平面通有面电流 强度 B 分布。
K ,试K求e磁z 感应
解
取宽度 dx 的一条无限长线电流
dBx
0 Kdx 2
cos
0 Kdx 2
y
0 Kydx 2 (x2 y2 )
根据对称性, By = 0
I
I
I
2 32
22 22
I
32 32
2
2 2
B l
dl
2B
0I (32 32
2 2
2
)
得到
B
0I 2
32 32
2 22
e
同轴电缆的磁场分布
上页 下页
4. 媒质的磁化(magnetization)
几乎所有的气体、液体和固体,不论其内部结构如何,放入 磁场中都会对磁场产生影响,表明所有的物质都有磁性,但大 部分媒质的磁性较弱,只有铁磁物体才有较强的磁性。
磁化强度(magnetization Intensity)
图磁偶极子受磁 场力 而转动
单位体积内的 净偶极距
n
mi
M lim i1 V V 0
Nm (A/m) av
上页 下页
3) 磁化电流 媒质磁化的结果是在表面形成磁化电流。
IM M dl
l
斯托克斯定理
Jm dS M dS
S
S
Jm M 体磁化电流
Km M en
注意 电偶极子总是削弱外电场,磁偶极子则不然。
上页 下页
5.一般形式的安培环路定律
若考虑磁化电流的作用
l B dl μ0 (I Im ) 0I 0 l M dl
移项后
B
( M ) dl I
l 0
定义:磁场强度
H B M A/m
0
则有
H dl I
l
安培环路定律
定义穿过磁场中给定曲面S 的磁 感应强度B 的通量为磁通:
Φ sB dS
若S面为闭合曲面
Wb (韦伯)
Φ B dS 0
磁通连续 性原理
上页 下页
Φ B dS 0
注意
① 磁通连续性原理也称磁场的高斯定理,表明磁力线是无头 无尾的闭合曲线,这一性质建立在自然界不存在磁荷的基 础上,原理适用于恒定磁场也适用于时变场。
空间各处的磁感应强度为:
c
H
eˆ
I
2r
B 0 H eˆ
0I 2r
(2)磁力线如图所示
例 试求无限大截流导板产生的磁感应强度 B。
解 定性分析场分布,取安培环路与电流呈右手螺旋
l B dl B1L B2L 0KL
根据对称性
B1 B2 B
0 K
2
ey
x0
B
0 K
2
e
y
x0
上页 下页
上页 下页
例 试求长直载流导线产生的磁感应强度。
采用圆柱坐标系,取电流 I dz,
解
dB 0 Idl sinθ 4 R2
l tan dl ρ d cos2
Rcos R ρ cos
sin cos
B
0 I 1 4 2
ρ cos cos2
d
ρ2 / cos2
0I 1 cosd
(I 'dl' R2
eR )
注意
① 安培定律说明两载流元之间的作用力与两电流的乘积成 正比,与它们之间的距离成反比,方向为:
dl dl eR
② 电流回路之间的作用力满足牛顿第三定律:F12=F21
③ 式中0为真空中的磁导率,它与真空电容率和真空中光 速满足关系:
c 1 μ0ε0
μ0 4π 107 H / m
上页 下页
② 毕奥—沙伐定律是重要的实验定律,它的重要性在于 定量的描述了电流和它产生的磁场之间的关系,进而 可以导出磁场的基本性质。
③ 对于体分布和面分布电流,毕奥—沙伐定律表述为:
体电流
B
0 4
V
J (r) eR dV R2
面电流
B
0 4
S
K (r) eR R2
dS
另几种元电流段Idl,JdV,KdS
B e 0I (r >b) 2r
表明安培环路定律反映了电流连续性原理。
上页 下页
例 设真空中无限长直导线,电流为I,沿z轴放置,如图所示。求:
(1)空间各处的磁感应强度
(2)画出其磁力线,并标出其方向。 图
解:由电流的柱对称性可知,柱内离轴心r
任一点处的磁场强度大小处处相等,方向为沿柱面切向
由安培环路定律: H dl 2rH I
电子自 旋磁矩
轨道 磁矩
上页 下页
媒质中原子的净磁矩对外的效应相当于一个磁偶极子。
无外磁场作用时,媒质对外不显磁性,
n
mi 0
i 1
在外磁场作用下,磁偶极子发生旋转,
n
mi 0
i 1
上页 下页
转矩为 Ti=mi×B ,旋转方向
使磁偶极矩方向与外磁场方向一 致或相反,对外呈现磁性,称为磁化现象。
上页 下页
2. 毕奥—沙伐定律 • 磁感应强度 从场的观点出发,认为电流之间的相互作用力是通过磁场传递的。
F
μ0 4
l l'
Id
l
I 'd R2
l
eR
)
lId
l
(
μ0
4
l'
I
'd
l R2
eR
)
l
Id
l
B
得任一电流I在空间任意点产生的磁感应强度
B
0 4
Id
l
l eR R2
毕奥—沙伐 定律
注意 ① 毕奥—沙伐定律只适用于恒定磁场中 无限大均匀媒质。
Bx
0Ky 2
dx (x2 y2)
B
0K
2
ex
0K
2
e
x
y0
y0
上页 下页
3.2 磁通连续性原理 • 安培环路定律
Magnetic Flux Continue Theorem & Ampere’s Circuital Law 1. 磁通连续性原理 ( Magnetic Flux Continue Theorem )
l H dl I
H e I
2r
0
① 0<r <a: I
② a<r <b:
H1 B1 0
H
e
1
2r
I b2 a2
r2 a2
a≤r ≤ b
B
e
I 2r
r2 b2
a2 a2
边界条件
法向: e r 切向: e
a<r <b
③ r >b:
ba
I
H e
(r ≥b)
0
2r
I ④ 铁中的磁化强度:
② 洛仑兹力垂直于磁感应强度,而库仑力平行于电场强度
③ 洛仑兹力垂直于电荷运动方向,只改变电荷运动方向, 对电荷不做功,而库仑力改变电荷运动速度做功。
