02324离散数学_202010_试卷
《离散数学》试卷及答案

H(x):x是身体健康的;
S(x):x是科学家
C(x):x是事业获得成功的人
ac>0并且cu>0
若u>0,则c>0,a>0,因此有ac>0;
若u<0,则c<0,a<0,也有ac>0;
因此有(a+bi)R(u+vi)
所以R在C*是传递的。所以R是C*上的等价关系。
2、在一阶逻辑自然推理系统F中,构造下面推理的证明。个体域是人的集合。
“每位科学家都是勤奋的,每个勤奋又身体健康的人在事业中都会获得成功。存在着身体健康的科学家。所以,存在着事业获得成功的人。”(15分)
14、论断:“命题变元不是命题”(A)命题。
A.是;B.不是;C.不可判定
15、设S={a,b,c},T={p,q},作f:S T,则这样的f一共有(C)个。
A.9B.10C.8D.7
得
分
二、填空题(每空2分,共20分)
1、设P:2+5=3,Q:日本在亚洲;于是, 的真值为1。
2、数理逻辑中,进行推理的常用规则有前提引入规则,结论引入规则和
A. B.
C. D.
8、设集合A={a,b,c,d},B={1,2,3,4},则从A到B的函数
f={<a,2 >,<b,1 >,<c,3 >,<d,2 >}是(D)
A. f是双射函数B. f是入射函数
C. f是满射函数D. f即不是满射又不是入射函数
9、下列蕴含式为真的是(B)
A. B.
C. D.
10、设 是A到B的映射, 是B到C的映射, 是双射,则(B)
《离散数学》考试试卷(试卷库20卷)及答案

《离散数学》考试试卷(试卷库20卷)及答案第 1 页/共 4 页《离散数学》考试试卷(试卷库20卷)试题总分: 100 分考试时限:120 分钟、选择题(每题2分,共20分)1. 设论域为全总个体域,M(x):x 是人,Mortal(x):x 是要死的,则“人总是要死的”谓词公式表示为( )(A ))()(x Mortal x M → (B ))()(x Mortal x M ∧(C )))()((x Mortal x M x →?(D )))()((x Mortal x M x ∧?2. 判断下列命题哪个正确?( )(A )若A∪B=A∪C,则B =C (B ){a,b}={b,a}(C )P(A∩B)≠P(A)∩P (B)(P(S)表示S 的幂集)(D )若A 为非空集,则A ≠A∪A 成立3. 集合},2{N n x x A n∈==对( )运算封闭(A )乘法(B )减法(C )加法(D )y x -4. 设≤><,N 是偏序格,其中N 是自然数集合,“≤”是普通的数间“小于等于”关系,则N b a ∈?,有=∨b a ( )(A )a(B )b(C )min(a ,b)(D ) max(a ,b)5. 有向图D=,则41v v 到长度为2的通路有( )条(A )0 (B )1 (C )2 (D )36. 设无向图G 有18条边且每个顶点的度数都是3,则图G 有( )个顶点(A )10 (B )4 (C )8 (D )127. 下面哪一种图不一定是树?()(A )无回路的连通图(B )有n 个结点n-1条边的连通图(C )每对结点间都有通路的图(D )连通但删去一条边则不连通的图 8. 设P :我将去镇上,Q :我有时间。
命题“我将去镇上,仅当我有时间”符号化为()(A )P →Q (B )Q →P (C )P Q (D )Q P ?∨? 9. 下列代数系统中,其中*是加法运算,()不是群。
离散数学试题与答案

离散数学试题及答案一、填空题1设集合A,B,其中A={1,2,3}, B= {1,2}, 则A - B=_____{3}______________; ρ(A) - ρ(B)=____{{3},{1,3},{2,3},{1,2,3}}__________ .2. 设有限集合A, |A| = n, 则|ρ(A×A)| = ___2^(n^2)________.3.设集合A = {a, b}, B = {1, 2}, 则从A到B的所有映射是____A1 = {(a,1), (b,1)}, A2 = {(a,2), (b,2)}, A3 = {(a,1), (b,2)}, A4 = {(a,2), (b,1)},_________ _____________, 其中双射的是______A3, A4__________.4. 已知命题公式G=⌝(P→Q)∧R,则G的主析取式是____P∧⌝Q∧R (m5)____.5.设G是完全二叉树,G有7个点,其中4个叶点,则G的总度数为___12______,分枝点数为_______3_________.6设A、B为两个集合, A= {1,2,4}, B = {3,4}, 则从A⋂B=______{4}______; A⋃B=____{1,2,3,4}_________;A-B=______{1,2}_______ .7. 设R是集合A上的等价关系,则R所具有的关系的三个特性是______自反性____________, _________对称性_________, _________传递性_____________.8. 设命题公式G=⌝(P→(Q∧R)),则使公式G为真的解释有_____(1,0,0)__________,______(1,0,1)________, ________(1,1,0)________.9. 设集合A={1,2,3,4}, A上的关系R1 = {(1,4),(2,3),(3,2)}, R1 = {(2,1),(3,2),(4,3)}, 则 R1•R2= ___{(1,3),(2,2),(3,1)}____,R2•R1 =_____{(2,4), (3,3), (4,2)}_____, R12=_______{(2,2), (3,3)}_________.10. 设有限集A, B,|A| = m, |B| = n, 则| |ρ(A⨯B)| = ______2^(m*n)___________.11设A,B,R是三个集合,其中R是实数集,A = {x | -1≤x≤1, x∈R}, B = {x | 0≤x < 2, x∈R},则A-B = _____{x | -1 ≤x < 0, x ∈R}_______ , B-A = ______{x | 1 < x < 2, x ∈R}_____ ,A∩B = ______{x | 0 ≤x ≤1, x ∈R}__________ , .13.设集合A={2, 3, 4, 5, 6},R是A上的整除,则R以集合形式(列举法)记为___________________{(2, 2),(2, 4),(2, 6),(3, 3),(3, 6),(4, 4),(5, 5),(6, 6)}_________.14. 设一阶逻辑公式G = ∀xP(x)→∃xQ(x),则G的前束式是_____∃y∃x(P(y)→Q(x))________ _____.15.设G是具有8个顶点的树,则G中增加__21___条边才能把G变成完全图。
离散数学考试试题(A、B卷及答案)

离散数学考试试题(A、B卷及答案)离散数学考试试题(A卷及答案)一、证明题(10分)1) (P∧Q∧A→C)∧(A→P∨Q∨C)⇔ (A∧(P↔Q))→C。
P<->Q=(p->Q)合取(Q->p)证明: (P∧Q∧A→C)∧(A→P∨Q∨C)⇔(⌝P∨⌝Q∨⌝A∨C)∧(⌝A∨P∨Q∨C)⇔((⌝P∨⌝Q∨⌝A)∧(⌝A∨P ∨Q))∨C反用分配律⇔⌝((P∧Q∧A)∨(A∧⌝P∧⌝Q))∨C⇔⌝(A∧((P∧Q)∨(⌝P∧⌝Q)))∨C再反用分配律⇔⌝( A∧(P↔Q))∨C⇔(A∧(P↔Q))→C⇔(⌝P∨Q∨R)∧(((⌝P∨Q)∧(⌝P∨R))∨(⌝Q∧⌝R))分配律⇔(⌝P∨Q∨R)∧(⌝P∨Q∨⌝Q)∧(⌝P∨Q∨⌝R)∧(⌝P∨R∨⌝Q)∧(⌝P∨R ∨⌝R)⇔(⌝P∨Q∨R)∧(⌝P∨Q∨⌝R)∧(⌝P∨⌝Q∨R)⇔4M∧5M∧6M使(非P析取Q析取R)为0所赋真值,即100,二进制为4⇔0m∨1m∨2m∨3m∨7m所以,公式(P→(Q∨R))∧(⌝P∨(Q↔R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
真值表法:P Q R Q↔R P→(Q∨R)⌝P∨(Q↔R) (P→(Q∨R))∧(⌝P∨(Q↔R))0 0 0 0 0 1 0 1 0 0 1 1 111111111111111 0 0 1 0 1 1 1 0 1 1 1 11111111由真值表可知,公式(P→(Q∨R))∧(⌝P ∨(Q↔R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
三、推理证明题(10分)1)⌝P∨Q,⌝Q∨R,R→S P→S。
证明:(1)P附加前提(2)⌝P∨Q P(3)Q T(1)(2),I(析取三段论)(4)⌝Q∨R P(5)R T(3)(4),I(析取三段论)(6)R→S P(7)S T(5)(6),I(假言推理)(8)P→S CP2) ∀x(P(x)→Q(y)∧R(x)),∃xP(x)⇒Q(y)∧∃x(P(x)∧R(x))证明(1)∃xP(x)(2)P(a)(3)∀x(P(x)→Q(y)∧R(x))(4)P(a)→Q(y)∧R(a)(5)Q(y)∧R(a)(6)Q(y)(7)R(a)(8)P(a)(9)P(a)∧R(a)(10)∃x(P(x)∧R(x))(11)Q(y)∧∃x(P(x)∧R(x))五、已知A、B、C是三个集合,证明(A∪B)-C=(A-C)∪(B-C) (10分)证明:因为x∈(A∪B)-C⇔x∈(A∪B)-C⇔x∈(A∪B)∧x∉C⇔(x∈A∨x∈B)∧x∉C⇔(x∈A∧x∉C)∨(x∈B ∧x∉C)⇔x∈(A-C)∨x∈(B-C)⇔x∈(A-C)∪(B-C) 所以,(A∪B)-C=(A-C)∪(B-C)。
最新自考离散数学02324真题含答案(.4-2016.4年整理版)

全国2009年4月自学考试离散数学试题(附答案)课程代码:02324一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列为两个命题变元P,Q的小项是()A.P∧Q∧⎤ P B.⎤ P∨QC.⎤ P∧Q D.⎤ P∨P∨Q2.下列语句中是真命题的是()A.我正在说谎B.严禁吸烟C.如果1+2=3,那么雪是黑的D.如果1+2=5,那么雪是黑的3.设P:我们划船,Q:我们跑步。
命题“我们不能既划船又跑步”符号化为()A.⎤ P∧⎤ Q B.⎤ P∨⎤ QC.⎤(P↔Q)D.⎤(⎤ P∨⎤ Q)4.命题公式(P∧(P→Q))→Q是()A.矛盾式B.蕴含式C.重言式D.等价式5.命题公式⎤(P∧Q)→R的成真指派是()A.000,001,110,B.001,011,101,110,111C.全体指派D.无6.在公式(x∀)F(x,y)→(∃y)G(x,y)中变元x是()A.自由变元B.约束变元C.既是自由变元,又是约束变元D.既不是自由变元,又不是约束变元7.集合A={1,2,…,10}上的关系R={<x,y>|x+y=10,x∈A,y∈A},则R的性质是()A.自反的B.对称的C.传递的、对称的D.反自反的、传递的8.若R和S是集合A上的两个关系,则下述结论正确的是()A.若R和S是自反的,则R∩S是自反的B.若R和S是对称的,则R S是对称的C.若R和S是反对称的,则R S是反对称的D.若R和S是传递的,则R∪S是传递的9.R={<1,4>,<2,3>,<3,1>,<4,3>},则下列不是..t(R)中元素的是()A.<1,1> B.<1,2>C.<1,3> D.<1,4>10.设A={{1,2,3},{4,5},{6,7,8}},下列选项正确的是()A.1∈A B.{1,2,3}⊆AC.{{4,5}}⊂A D.∅∈A11.在自然数集N上,下列运算是可结合的是()A.a*b=a-2b B.a*b=min{a,b}C.a*b=-a-b D.a*b=|a-b|12.在代数系统中,整环和域的关系是()A.整环一定是域B.域不一定是整环C.域一定是整环D.域一定不是整环13.下列所示的哈斯图所对应的偏序集中能构成格的是()A.B.C.D.14.设G为有n个结点的简单图,则有()A.Δ(G)<n B.Δ(G)≤nC.Δ(G)>n D.Δ(G)≥n15.具有4个结点的非同构的无向树的数目是()A.2 B.3C.4 D.5二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
离散数学试题及答案
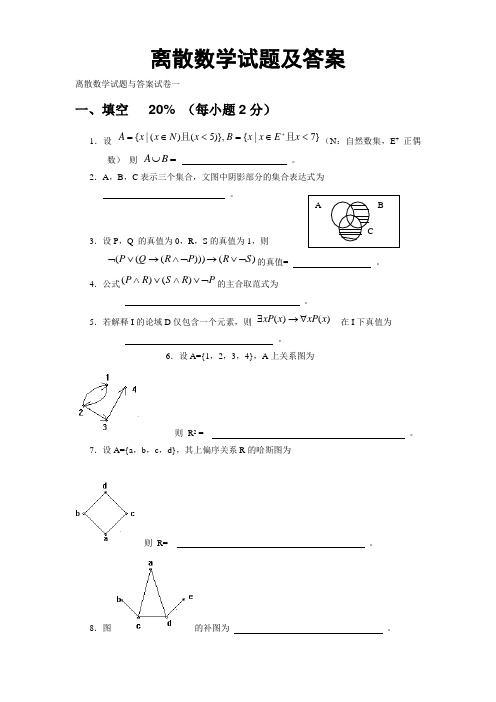
离散数学试题及答案离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E +正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:那么代数系统<A ,*>的幺元是 ,有逆元的元素为 ,它们的逆元分别为 。
10.下图所示的偏序集中,是格的为 。
二、选择 20% (每小题 2分)1、下列是真命题的有( ) A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有()个。
A . 23 ; B . 32 ; C . 332⨯; D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是( ) A .若R ,S 是自反的, 则S R 是自反的; B .若R ,S 是反自反的, 则S R 是反自反的; C .若R ,S 是对称的, 则S R 是对称的; D .若R ,S 是传递的, 则S R 是传递的。
(完整版)自考离散数学02324真题含答案(2009.4-2016.4年整理版),推荐文档.docx

全国 2009 年 4 月自学考试离散数学试题(附答案)课程代码: 02324一、(本大共15 小,每小 1 分,共 15 分)在每小列出的四个中只有一个是符合目要求的,将其代填写在后的括号内。
、多或未均无分。
1.下列两个命元P, Q 的小是()A . P∧Q ∧ P B. P∨ QC. P∧Q D. P∨P∨ Q2.下列句中是真命的是()A .我正在B.禁吸烟C.如果 1+2=3 ,那么雪是黑的D.如果 1+2=5 ,那么雪是黑的3. P:我划船, Q :我跑步。
命“我不能既划船又跑步” 符号化()A . P∧ Q B. P∨ QC.( P Q)D.( P∨ Q)4.命公式( P∧( P→ Q))→ Q 是()A .矛盾式B.含式C.重言式D.等价式5.命公式(P∧ Q)→ R 的成真指派是()A . 000,001, 110,B. 001, 011, 101,110, 111C.全体指派D.无6.在公式(x )F ( x,y)→(y) G( x,y)中元 x 是()A .自由元B.束元C.既是自由元,又是束元D.既不是自由元,又不是束元7.集合 A={1 , 2,⋯,10}上的关系 R={< x,y>|x+y=10, x∈ A , y∈A} , R 的性是()A .自反的B.称的C.的、称的D.反自反的、的8.若 R 和 S 是集合 A 上的两个关系,下述正确的是()A .若 R 和 S 是自反的,R∩ S 是自反的B.若 R 和 S 是称的,R S 是称的C.若 R 和 S 是反称的,R S 是反称的D.若 R 和 S 是的,R∪ S 是的9. R={<1 , 4>,<2 , 3>,<3, 1> , <4, 3>} ,下列不是t( R)中元素的是()A . <1, 1>B. <1, 2>C. <1, 3>D. <1, 4>10.设 A={{1 ,2, 3} , {4 , 5} , {6 ,7, 8}} ,下列选项正确的是()A . 1∈ A B. {1 , 2, 3} AC. {{4 , 5}} A D.∈ A11.在自然数集 N 上,下列运算是可结合的是()A . a b=a-2b B. a b=min{ a,b}C. a b=-a-b D. a b=|a-b|12.在代数系统中,整环和域的关系是()A .整环一定是域B.域不一定是整环C.域一定是整环D.域一定不是整环13.下列所示的哈斯图所对应的偏序集中能构成格的是()A .B.C.D.14.设 G 为有 n 个结点的简单图,则有()A .(G) <n B. (G) ≤nC.(G) >n D. (G) ≥ n15.具有 4 个结点的非同构的无向树的数目是()A . 2B. 3C. 4D. 5二、填空题(本大题共10 小题,每小题 2 分,共 20 分)请在每小题的空格中填上正确答案。
离散数学全部试卷
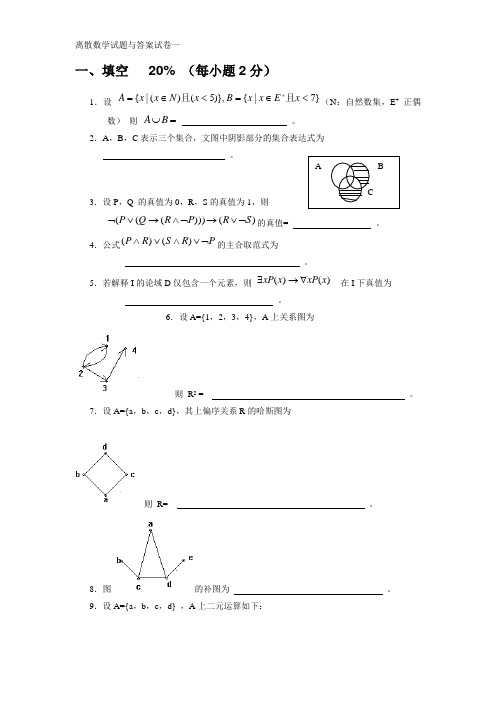
离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:那么代数系统<A ,*>的幺元是 ,有逆元的元素为 ,它们的逆元分别为 。
10.下图所示的偏序集中,是格的为 。
二、选择 20% (每小题 2分)1、下列是真命题的有( ) A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有( )个。
A . 23 ; B . 32 ; C . 332⨯; D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是() A .若R ,S 是自反的, 则S R 是自反的; B .若R ,S 是反自反的, 则S R 是反自反的; C .若R ,S 是对称的, 则S R 是对称的; D .若R ,S 是传递的, 则S R 是传递的。
5、设A={1,2,3,4},P (A )(A 的幂集)上规定二元系如下|}||(|)(,|,{t s A p t s t s R =∧∈><=则P (A )/ R=( )A.A ;B.P(A) ;C.{{{1}},{{1,2}},{{1,2,3}},{{1,2,3,4}}};D.{{Φ},{2},{2,3},{{2,3,4}},{A}}6、设A={Φ,{1},{1,3},{1,2,3}}则A上包含关系“⊆”的哈斯图为()7、下列函数是双射的为()A.f : I→E , f (x) = 2x ;B.f : N→N⨯N, f (n) = <n , n+1> ;C.f : R→I , f (x) = [x] ;D.f :I→N, f (x) = | x | 。
02324离散数学2020年10月试题及答案

绝密★考试结束前全国2020年10月高等教育自学考试离散数学试题课程代码:023241. 请考生按规定用笔将所有试题的答案涂、写在答题纸上。
2. 答题前,考生务必将自己的考试课程名称、姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
选择题部分注意事项:每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
一 、单项选择题:本大题共15小题,每小题1分,共15分。
在每小题列出的备选项中只有一项是最符合题目要求的,请将其选出。
1. 设P:我周末不加班,Q:我去爬山,命题“只要我周末不加班,我就去爬山”符号化为A.-PV-QB. PvQC. P→QD. Q→ P 2. 下列关系矩阵所对应的关系具有对称性的是....3. 下列图为欧拉图的是A. B. C. D.4. 如题4图所示的格中,元e 的补元是A. a 和bB. a 和c C . a 和d D. a 和f 5. 下列命题公式为矛盾式的是A.-(P→Q)^QvRB.(Pv(P^Q))→PC.-(PAQ)v(-P^-Q)D.-(P→Q)^Q题 4 图D C B A6. 设集合A中有4个元素,则A的不同的等价关系的个数为A. 11B. 12C. 15D. 167. 下列选项中与题7图互为补图的是A. B. C. D. 题7 图8. 在自然数集N上,a,b∈N,不满足交换律的运算是A. a*b= min(a,b)B. a*b=a+bC. a*b=a-bD.a*b=max(a,b)9. 下列式子中,不正确的是A.-3xA(x)= Vx-A(x)B.3x(A→B(x))=A→3xB(x)C.-VxB(x)=3x-B(x)D.Vx(A(x)→B)=VxA(x)→B10.下列图中不是哈密顿图的是A. B. C. D.11.设R为实数集,下列关系中能构成函数的是A. {(x,y>|x ∈R^y ∈RA(y²-2x=1)}B. {(x,y》|x ∈RAy ∈RA(x²+2y=1)}C. {(x,y>|x ∈R^y ∈RA(2y/x=1)}D. {<x,y>|x ∈RAy ∈RA(2y ·x=1)}12.谓词公式vx(F(x)^G(y)) →3y(H(x) →S(y,z)) 中量词Vx 的辖域是A.F(x)AG(y)B. F(x)C.Vx(F(x)^G(y))D. F(x),H(x)13.设R、S均为集合A上的二元关系,下列命题错误的是A. 若R和S是自反的,则R-S也是自反的B. 若R和S是反自反的,则R-S也是反自反的C. 若R和S是反对称的,则R-S也是反对称的D. 若R和S是对称的,则R-S也是对称的14.下列度数列可简单图化的是A.(5,4,4,2,1)B.(3,3,1,1)C.(4,4,3,3,2,2)D.(4,3,2,1)15.令S={a,b,c}上的二元运算*如题15表所示,则该代数系统不满足A. 交换律C. 结合律B. 幂等律D. 消去律题15表* a Ca ab bb b b bC b b c非选择题部分注意事项:用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
离散数学试卷及答案
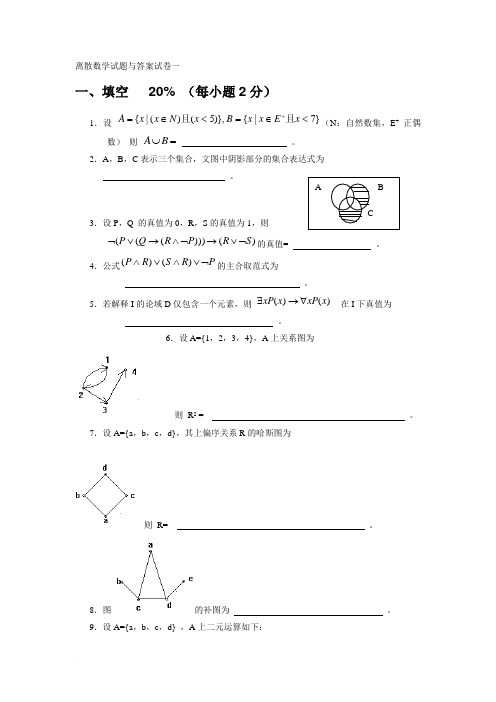
离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:那么代数系统<A ,*>的幺元是 ,有逆元的元素为 ,它们的逆元分别为 。
10.下图所示的偏序集中,是格的为 。
二、选择 20% (每小题 2分)1、下列是真命题的有( ) A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有()个。
A . 23 ; B . 32 ; C . 332⨯; D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是( ) A .若R ,S 是自反的, 则S R 是自反的; B .若R ,S 是反自反的, 则S R 是反自反的; C .若R ,S 是对称的, 则S R 是对称的; D .若R ,S 是传递的, 则S R 是传递的。
5、设A={1,2,3,4},P(A)(A的幂集)上规定二元系如下t st spR=∈=则P(A)/ R=()<A∧>)(||||}s({t,,|A.A ;B.P(A) ;C.{{{1}},{{1,2}},{{1,2,3}},{{1,2,3,4}}};D.{{Φ},{2},{2,3},{{2,3,4}},{A}}6、设A={Φ,{1},{1,3},{1,2,3}}则A上包含关系“⊆”的哈斯图为()7、下列函数是双射的为()A.f : I→E , f (x) = 2x ;B.f : N→N⨯N, f (n) = <n , n+1> ;C.f : R→I , f (x) = [x] ;D.f :I→N, f (x) = | x | 。
离散数学2023年10月真题

2023年10月高等教育自学考试全国统一命题考试离散数学试题(课程代码02324)注意事项:1.本试卷分为两部分,第一部分为选择题,第二部分为非选择题。
2.应考者必须按试题顺序在答题卡(纸)指定位置上作答,答在试卷上无效。
3.涂写部分、画图部分必须使用2B铅笔,书写部分必须使用黑色字迹签字笔。
第一部分选择题一、单项选择题:本大题共15小题,每小题1分,共15分。
在每小题列出的备选项中只有一项是最符合题目要求的,请将其选出。
1.令p:今天我上班,q:今天我休息。
命题“今天我要么上班要么休息”的符号化形式为A.p V qB.q→pC.¬ p∧qD.(¬ q∧p)V(q∧¬ p)2.设令F(x):x是火车,G(x):x是汽车,L(x,y):x比y快。
命题“有的火车比有的汽车快”的符号化形式为A.∀x(F(x)→∀y(G(y)→L(x,y)))B.∃x(F(x)∧∃y(G(y)∧L(x,y)))C.¬∃y(G(y)∧∀x(F(x)→L(y,x)))D.¬∀y(G(y)→∀x(F(x)→L(x,y)))3.下列关于小项和大项的性质表述正确的是A.任意两个不同小项的合取式必为真B.任意两个不同大项的析取式必为假C.任意两个不同小项的析取式必为假D.大项的否定是小项下图中是欧拉图的为4.B. C. D.A.5.设有非空集合A上的全域关系S,则关系S不是A.自反关系B.对称关系C.传递关系D.反对称关系6.简单无向图G有9条边,每个结点都是3度结点,则G的结点数为A.5B.6C.7D.87.下列谓词恒等式,不正确的是A.∀x(P(x)V Q(x))⇔∀xP(x)V∀xQ(x)B.∃x(P(x)V Q(x))⇔∃xP(x)V∃xQ(x)C.∀x(P→Q(x))⇔P→∀xQ(x)D.∃x(P→Q(x))⇔P→∃xQ(x)8.下列度数序列中,不能构成简单无向图的是A.{1,1,1,2,3}B.{1,2,2,3}C.{6,2,2,2,4}D.{3,3,3,3}9.设A={3z|z∈Z),运算为实数加法+和乘法*,则<A,+,*>构成的代数系统是A.环B.整环C.域D.格10.集合A上的自反关系R的关系矩阵为M,则M的元素必定A.对角线上全是0B.关于反对角线对称C.关于对角线对称D.对角线上全是111.已知A、B、C、D是任意集合,则下列各式成立的是A.(A∪B)×(C∪D)=(A×C)∪(B×D)B.(A∩B)×C=(A×C)∩(B×C)C.(A⊕B)×(C⊕D)=(A×C)⊕(B×D)D.(A-B)×(C-D)=(A×C)-(B×D)12.要从完全图K4中得到一棵生成树,需要删除的边数为A.1B.2C.3D.413.设有集合A上的关系R1和R2,下列命题为真的是A.若关系R1和R2是自反的,则R₁⁰ R2也是自反的B.若关系R1和R2是对称的,则R₁⁰ R2也是对称的C.若关系R1和R2是传递的,则R₁⁰ R2也是传递的D.若关系R1和R2是反自反的,则R₁⁰ R2也是反自反的14.下图中4个偏序集的图形,能构成格的是d e e g a afb c b d b fc db c c ea ea dA. B. C. D.15.设有穷集合A的元素个数为m,则A到A的不同单射函数的个数为A.m!B.m mC.m2D.2m第二部分非选择题二、填空题:本大题共10小题,每小题2分,共20分。
新版离散数学试卷及答案-新版-精选.pdf

题目
1
2
3
4
5
6
7
8
9
10
答案 C D
B、 C C A
DCAD
B
A
三、证明 26%
1、 证:
“
”
a, b, c X 若 < a, b >, < a, c > R 由 R 对 称 性 知
< b, a >, < c, a R ,由 R 传递性得 < b, c > R
“ ” 若 < a, b > R , < a, c > R 有 < b, c > R 任 意 a, b X , 因
求出 R 的传递闭包 t (R) 。
(9 分)
2、如下图所示的赋权图表示某七个城市 v1, v2 , , v7 及预先算出它们之间的一些直接通
信线路造价, 试给出一个设计方案, 使得各城市之间能够通信而且总造价最小。
(9分)
试卷一答案: 一、填空 20% (每小题 2 分)
1、{0 ,1,2,3,4,6} ; 2、( B C ) A ;3、1; 4、( P S R) ( P
试卷二试题与答案
一、填空 20% (每小题 2 分)
1、 P:你努力, Q:你失败。“除非你努力,否则你将失败”的翻译为 ;“虽然你努力了,但还是失败了”的翻译为 。
2、论域 D={1 , 2} ,指定谓词 P
P (1,1) P (1,2) P (2,1) P (2,2)
T
T
F
F
则公式 x yP( y, x) 真值为
C. f : R I , f (x) = [x] ; D . f :I N, f (x) = | x | 。
离散数学自学考试真题附答案打印版

离散数学试题课程代码:02324一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1.一个连通的无向图G ,如果它的所有结点的度数都是偶数,那么它具有一条( )A.汉密尔顿回路B.欧拉回路C.汉密尔顿通路D.初级回路2.设G 是连通简单平面图,G 中有11个顶点5个面,则G 中的边是( )3.在布尔代数L 中,表达式(a ∧b)∨(a∧b ∧c)∨(b ∧c)的等价式是( )∧(a ∨c)B.(a ∧b)∨(a ’∧b)C.(a ∨b)∧(a ∨b ∨c)∧(b ∨c)D.(b ∨c)∧(a ∨c)4.设i 是虚数,·是复数乘法运算,则G=<{1,-1,i,-i},·>是群,下列是G的子群是( )A.<{1},·>B.〈{-1},·〉C.〈{i},·〉D.〈{-i},·〉5.设Z 为整数集,A 为集合,A 的幂集为P(A),+、-、/为数的加、减、除运算,∩为集合的交运算,下列系统中是代数系统的有( )A.〈Z ,+,/〉B.〈Z ,/〉C.〈Z ,-,/〉D.〈P(A),∩〉6.下列各代数系统中不含有零元素的是( )A.〈Q ,*〉Q 是全体有理数集,*是数的乘法运算B.〈Mn(R),*〉,Mn(R)是全体n 阶实矩阵集合,*是矩阵乘法运算C.〈Z ,ο〉,Z 是整数集,ο定义为x οxy=xy,∀x,y ∈ZD.〈Z ,+〉,Z 是整数集,+是数的加法运算 7.设A={1,2,3},A 上二元关系R 的关系图如下: R 具有的性质是 A.自反性 B.对称性 C.传递性 D.反自反性 8.设A={a,b,c},A 上二元关系R={〈a,a 〉,〈b,b 〉,〈a,c 〉},则关系R 的对称闭包S(R)是( ) ∪I A ∪{〈c,a 〉} ∩I A 9.设X={a,b,c},Ix 是X 上恒等关系,要使Ix ∪{〈a,b 〉,〈b,c 〉,〈c,a 〉,〈b,a 〉}∪R 为X 上的等价关系,R 应取( ) A.{〈c,a 〉,〈a,c 〉} B.{〈c,b 〉,〈b,a 〉} C.{〈c,a 〉,〈b,a 〉} D.{〈a,c 〉,〈c,b 〉} 10.下列式子正确的是( ) A. ∅∈∅ B.∅⊆∅ C.{∅}⊆∅ D.{∅}∈∅11.设解释R 如下:论域D 为实数集,a=0,f(x,y)=x-y,A(x,y):x<y.下列公式在R 下为真的是( ) A.( ∀ x)( ∀y)( ∀z)(A(x,y))→A(f(x,z),f(y,z)) B.( ∀x)A(f(a,x),a) C.(∀x)(∀y)(A(f(x,y),x)) D.(∀x)(∀y)(A(x,y)→A(f(x,a),a)) 12.设B 是不含变元x 的公式,谓词公式(∀x)(A(x)→B)等价于( ) A.(∃x)A(x)→B B.(∀x)A(x)→B (x)→B D.(∀x)A(x)→(∀x)B 13.谓词公式(∀x)(P(x,y))→(∃z)Q(x,z)∧(∀y)R(x,y)中变元x( )A.是自由变元但不是约束变元B.既不是自由变元又不是约束变元C.既是自由变元又是约束变元D.是约束变元但不是自由变元14.若P :他聪明;Q :他用功;则“他虽聪明,但不用功”,可符号化为( )∨Q ∧┐Q →┐Q ∨┐Q15.以下命题公式中,为永假式的是( )→(p ∨q ∨r)B.(p →┐p)→┐pC.┐(q →q)∧pD.┐(q ∨┐p)→(p ∧┐p)二、填空题(每空1分,共20分)16.在一棵根树中,仅有一个结点的入度为______,称为树根,其余结点的入度均为______。
自考离散数学02324真题含答案(2009.4-2016.4年整理版)

全国2009年4月自学考试离散数学试题(附答案)课程代码:02324一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列为两个命题变元P,Q的小项是()A.P∧Q∧⎤ P B.⎤ P∨QC.⎤ P∧Q D.⎤ P∨P∨Q2.下列语句中是真命题的是()A.我正在说谎B.严禁吸烟C.如果1+2=3,那么雪是黑的D.如果1+2=5,那么雪是黑的3.设P:我们划船,Q:我们跑步。
命题“我们不能既划船又跑步”符号化为()A.⎤ P∧⎤ Q B.⎤ P∨⎤ QC.⎤(P↔Q)D.⎤(⎤ P∨⎤ Q)4.命题公式(P∧(P→Q))→Q是()A.矛盾式B.蕴含式C.重言式D.等价式5.命题公式⎤(P∧Q)→R的成真指派是()A.000,001,110,B.001,011,101,110,111C.全体指派D.无6.在公式(x∀)F(x,y)→(∃y)G(x,y)中变元x是()A.自由变元B.约束变元C.既是自由变元,又是约束变元D.既不是自由变元,又不是约束变元7.集合A={1,2,…,10}上的关系R={<x,y>|x+y=10,x∈A,y∈A},则R的性质是()A.自反的B.对称的C.传递的、对称的D.反自反的、传递的8.若R和S是集合A上的两个关系,则下述结论正确的是()A.若R和S是自反的,则R∩S是自反的B.若R和S是对称的,则R S是对称的C.若R和S是反对称的,则R S是反对称的D.若R和S是传递的,则R∪S是传递的9.R={<1,4>,<2,3>,<3,1>,<4,3>},则下列不是..t(R)中元素的是()A.<1,1> B.<1,2>C.<1,3> D.<1,4>10.设A={{1,2,3},{4,5},{6,7,8}},下列选项正确的是()A.1∈A B.{1,2,3}⊆AC.{{4,5}}⊂A D.∅∈A11.在自然数集N上,下列运算是可结合的是()A.a*b=a-2b B.a*b=min{a,b}C.a*b=-a-b D.a*b=|a-b|12.在代数系统中,整环和域的关系是()A.整环一定是域B.域不一定是整环C.域一定是整环D.域一定不是整环13.下列所示的哈斯图所对应的偏序集中能构成格的是()A.B.C.D.14.设G为有n个结点的简单图,则有()A.Δ(G)<n B.Δ(G)≤nC.Δ(G)>n D.Δ(G)≥n15.具有4个结点的非同构的无向树的数目是()A.2 B.3C.4 D.5二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
离散数学试题及答案解析

离散数学试题及答案解析一、单项选择题(每题2分,共10分)1. 集合A={1,2,3},集合B={2,3,4},则A∩B等于:A. {1,2,3}B. {2,3}C. {1,4}D. {3,4}答案:B2. 以下哪个命题是真命题?A. 所有天鹅都是白色的。
B. 有些天鹅不是白色的。
C. 所有天鹅都不是白色的。
D. 没有天鹅是白色的。
答案:B3. 函数f: A→B的定义域是A,值域是B,那么f是:A. 单射B. 满射C. 双射D. 既不是单射也不是满射答案:D4. 逻辑表达式(p∧q)→r的逆否命题是:A. ¬r→¬(p∧q)B. ¬r→¬p∨¬qC. r→(p∧q)D. ¬r∧¬p∨¬q答案:B5. 有限集合A={a, b, c}的子集个数为:A. 3B. 4C. 7D. 8答案:D二、填空题(每题3分,共15分)1. 如果一个关系R在集合A上是自反的,那么对于A中的每一个元素a,都有___________。
答案:(a, a)∈R2. 命题逻辑中,合取(AND)的逻辑运算符用___________表示。
答案:∧3. 在图论中,一个连通图是指图中任意两个顶点之间都存在___________。
答案:路径4. 集合{1, 2, 3}的幂集包含___________个元素。
答案:85. 如果一个函数f是单射,那么对于任意的x1, x2∈A,如果f(x1)=f(x2),则x1___________x2。
答案:=三、解答题(每题10分,共20分)1. 证明:若p是q的充分条件,q是r的充分条件,则p是r的充分条件。
证明:假设p成立,由于p是q的充分条件,所以q成立。
又因为q是r的充分条件,所以r成立。
因此,p成立可以推出r成立,即p是r的充分条件。
2. 给定一个有向图,其中包含顶点A、B、C、D,边为(A, B),(B, C),(C, D),(D, A),(A, C)。
(完整版)《离散数学》试题及答案解析,推荐文档

则在解释 I 下取真值为 1 的公式是( ).
(A)xyP(x,y) (B)xyP(x,y) (C)xP(x,x) (D)xyP(x,y). 6. 若供选择答案中的数值表示一个简单图中各个顶点的度,能画出图的是( ).
(A)(1,2,2,3,4,5) (B)(1,2,3,4,5,5) (C)(1,1,1,2,3) (D)(2,3,3,4,5,6). 7. 设 G、H 是一阶逻辑公式,P 是一个谓词,G=xP(x), H=xP(x),则一阶逻辑公式
(A)下界 (B)上界 (C)最小上界
(D)以上答案都不对
6
4 下列语句中,( )是命题。
5
(A)请把门关上 (B)地球外的星球上也有人 (C)x + 5 > 6 (D)下午有会吗?
3
4
2
5 设 I 是如下一个解释:D={a,b}, P(a, a) P(a, b) P(b, a) P(b, b)
1
1010
AB=_________________________;A-B= _____________________ . 7. 设 R 是集合 A 上的等价关系,则 R 所具有的关系的三个特性是______________________,
________________________, _______________________________. 8. 设命题公式 G=(P(QR)),则使公式 G 为真的解释有
(1)
1
4
2
3
1 0 0 0
(2)
MR
1 1
1 1
0 1
0 0
1 1 1 1
3. (1)•=((x))=(x)+3=2x+3=2x+3.
