鲁教版七年级下册第七章解二元一次方程组、简单应用导学案(无答案)-word文档

合集下载

鲁教版七年级数学第七章二元一次方程组复习学案

《二元一次方程组》复习学案（一）学习目标:1．了解二元一次方程组及它的解的基本概念。

2．会用代入消元法和加减消元法解简单的二元一次方程组，并能根据方程组的特点，灵活选用适当的解法。

重点：会用适当的方法解二元一次方程组。

难点：理解二元一次方程、二元一次方程组的概念。

一、自主复习：1、二元一次方程和它的解（1）含有未知数，并且未知数的指数都是的方程叫二元一次方程；（2）一般地，二元一次方程的解有组。

2、二元一次方程组和它的解（1）两个二元一次方程合在一起就组成了一个二元一次方程组。

（2）使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值叫做二元一次方程组的解。

3、二元一次方程组的解法解二元一次方程组的基本思想是，方法有代入法的步骤：1)将方程组里的一个方程变形,用含一个未知数的代数式表示另一个未知数;2)用这个代数式代替另一个方程中相应的未知数,使解二元一次方程组转化为解一元一次方程,并求出一个未知数的值.3)把求得的这个未知数的值代入变形后的方程或方程组中任何一个方程,求得另一个未知数的值,从而得到方程组的解加减法步骤;（1）在所解的方程组的两个方程中如果某个未知数的系数互为相反数,可把两个方程相加,即可消去这个未知数;如果某个未知数的系数相等,则可把两方程相减消去这个未知数（2）如果方程组中不存在某个未知数的系数的绝对值相等,那么选取一组系数（最小公倍数最小的一组）,将两个方程分别乘以一个适当的数,使这两个系数的绝对值相等,再用加减消元.二课堂探究：聚焦目标1：1.二元一次方程和二元一次方程组的概念：2.二元一次方程组的解的概念：1．已知：7)8()2()4(22+=-+++-k y k x k x k(1)当k 取何值时，方程为一元一次方程；(2)当k 取何值时，方程为二元一次方程。

2．已知方程5x+3y ＝22(1)请写出方程的三个解；(2)求方程的非负整数解。

3．已知方程组⎩⎨⎧=+=+1102by ax y x 与方程组⎩⎨⎧=+=-652ay bx y x 的解相同，求2005)(b a +的值。

七年级数学下册 7.1 二元一次方程组导学案(无答案) 鲁教版五四制

二元一次方程组【学习目标】能说出二元一次方程、二元一次方程组和它的解的概念，会检验所给的一组未知数的值是否是二元一次方程、二元一次方程组的解。

【学习重点】二元一次方程、二元一次方程组、二元一次方程组的解的概念，以及检验一对数值是不是某个二元一次方程组的解；【学习过程】一、自主学习认真阅读教材P 2——4内容，尝试完成下面的题目，相信你一定能行！1、默写二元一次方程、二元一次方程组和它的解的概念2、判断下列方程是否为二元一次方程，并说明理由。

①y x 23+ ②74=-y x ③62=+y x④23+=xy x ⑤z y x =-43 ⑥y x 312=-3、已知x 、y 都是未知数，判别下列方程组是否为二元一次方程组？ ①⎩⎨⎧=+=+75243y x y x ②⎩⎨⎧=+=32y x xy ③⎩⎨⎧+==+z y y x 75 ④⎩⎨⎧=+=823155y x y 4、篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分。

某队为了争取较好名次想在全部22场比赛中得到40分，那么这个队胜负场数应分别是多少？二、合作交流1、已知下面三对数值：⎩⎨⎧-==20y x ⎩⎨⎧-==32y x ⎩⎨⎧-==51y x（1）哪几对是方程2x-y=7的解；（2）哪几对是方程x+2y=-4的解？2、下面三对数值：⎩⎨⎧-==11y x ⎩⎨⎧==12y x ⎩⎨⎧==54y x哪一对是二元一次方程组的解？（1）⎩⎨⎧=+=-104332y x y x （2）⎩⎨⎧=--=13432y x x y3、判断⎩⎨⎧==26y x 是不是二元一次方程⎩⎨⎧=-=-192325y x y x 的解三、达标测评【必做题】课本5页习题7.1【选做题】1、下列方程组中，是二元一次方程组的为 ( )A 、12x y xy =+⎧⎨=⎩ B 、4123x y y x -=⎧⎨=+⎩C 、2201x x y x ⎧--=⎨=+⎩D 、1130y x x y ⎧-=⎪⎨⎪+=⎩2、下列各式，属于二元一次方程的个数有（）①xy+2x －y=7； ②4x+1=x －y ；③1x +y=5； ④x=y ； ⑤x 2－y 2=2⑥6x －2y ⑦x+y+z=1 ⑧y （y －1）=2y 2－y 2+xA ．1B ．2C ．3D ．43、下列方程组中，是二元一次方程组的是（） A ．228423119 (237)54624x y x y a b x B C D x y b c y x x y +=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩ 【提高题】 4、若方程432+=-x y mx 是二元一次方程，则m 满足（）A 、0≠mB 、2-≠mC 、3≠mD 、4≠m5、先解一元一次方程2x-1=-x+2。

鲁教版(五四制)七年级数学下册：7.1二元一次方程组导学案设计(无答案)

【导预疑学】一、预学导航（一）认识学习目标(1) 通过对实际问题的分析，进一步体会方程是刻画现实世界的有效数学模型。

(2)了解二元一次方程、二元一次方程组及其解等概念，并会判断一组数是不是某个二元一次方程的组的解。

（二）把握学习重点：了解二元一次方程、二元一次方程组及其解等概念，并会运用。

二、预习成果（一）预习检测回忆一下两个问题：（1）方程的概念：（2）一元一次方程的概念：看课本120-122，回答下列问题（3）二元一次方程的概念：（4）二元一次方程组的概念：（5）二元一次方程的一组解：（6）二元一次方程组的解的概念（二）预学质疑你能说出一元一次方程及二元一次方程的区别吗？二元一次方程的解有多少个？二元一次方程组的解有多少个？【导问研学】问题一：如何判断方程是二元一次方程及二元一次方程组？1下列方程中哪些是二元一次方程？在是的后面画对勾。

(1) 2x+y=14 (2) x+y+z =6 （3）132=+yx (4) x²+y=6 (5) 7x+6z+4=16 (6) y=62下列方程中哪些是二元一次方程？在是的后面画对勾。

订正、笔记栏（1）⎩⎨⎧=-=+12y x y x (2) ⎪⎩⎪⎨⎧==+111x y x （3）⎩⎨⎧==+10x y x （4）⎩⎨⎧=-+=521y x y z (5) ⎩⎨⎧==-683xy y x (6)⎩⎨⎧=-=0253y x yx问题二：如何判判断一组数是不是二元一次方程及二元一次方程组的解？1、下面4组数值中,哪些是二元一次方程2x+y=10的解（）(1)⎩⎨⎧=-=62y x （2）⎩⎨⎧==43y x （3）⎩⎨⎧==34y x （4）⎩⎨⎧-==26y x2、二元一次方程组⎩⎨⎧==+xy y x 2102的解是（）（1）⎩⎨⎧==43y x （2）⎩⎨⎧==63y x （3）⎩⎨⎧==42y x（4）⎩⎨⎧==24y x 【导法慧学】1 含有两个未知数，并且含未知数的项都是一次的方程叫二元一次方程。

鲁教版(五四制)七年级下册 7.2 二元一次方程组第3课时学案设计(无答案)

例4解方程组
能否使两个方程中x（或y）的系数相等（或相反）呢？
三、实践与应用：
解下列方程组:
(1) (2)
(3) (4)
四、小结评价
1．解二元一次方程组常采用两种方法——代人法和加减法。两种解法的基本思想都是“消元”，将“二元”转化为“一元”。
2．加减法消元的基本思想是通过“加减”，达到化“二元”为“一元”，即消元的目的。
3．当方程组中某个未知数的系数相同时，应用减法消元。但应注意减式中的各项须变号；当方程组中某个未知数的系数互为相反数时，应用加法消元。
五、达标检测：
用加减法解下列方程组。
(1) (2)
(3) (4)
作业
P12习题7.3
教后信息反馈
重难点分析
重点：用加减法解二元一次方程组。
难点：两上方程组相减消元时对被减的方程各项符号要做变号处理是难点。
整合思路
代入消元法及有理数的运算整合环ຫໍສະໝຸດ 及时控集体备课教学过程设计
个人补充或修改
一、自主学习
1.用加减消元法解二元一次方程组的基本思路:把“二元”转化为 ________
2.加减消元法:通过把两个方程的两边分别________或 ________ 消去其中一个________ 这种解方程组的方法叫作加减消元法,简称加减法
主备教师：总第3课时时间年月日
单元
二元一次方程组
课型
新授课
课题
7．2解二元一次方程组
学习目标
1．会用加减法求未知数系数相等或互为相反数的二元一次方程组的解。
2．通过探求二元一次方程组的解法，经历用加减法把“二元”化为“一元”的过
程，体会消元的思想，以及把“未知”转化为“已知”，把复杂问题转化为简单问题的化归思想。

鲁教版五四制七年级下册数学导学案：7.4二元一次方程和一次函数(无答案)

7.4二元一次方程与一次函数（1）教师寄语：尊重生命，感悟自然，明辨是非，注意细节，享受成长快乐;学会审美，学会宽容，学会感恩，学会思考，领悟完美人生。

教学目标：（1）使学生初步理解二元一次方程与一次函数的关系。

（2）能利用二元一次方程组确定一次函数的表达式。

（3）能根据一次函数图象求出二元一次方程组的近似解。

（4）进一步培养学生画图，识图能力；培养学生初步的数形结合意识和能力。

（5）让学生体会到解决同一问题的办法可多元化二、教学重点、难点教学重点：能根据一次函数的图象求二元一次方程组的近似解。

（即用图象法解二元一次方程组）教学难点：（1）二元一次方程与一次函数图象之间的对应关系。

（2）二元一次方程的解与一次函数图象交点坐标之间的对应关系。

教学方法：探索----研究----发现教学过程：创设情境,以旧引新情境一:（1）方程x+y=5的解有多少个？写出其中的几个。

（2）在直角坐标系中分别描出以这些解为坐标的点，它们在一次函数y=5-x 的图象上吗？（3）在一次函数y=5-x的图象上任取一点，它的坐标适合方程x+y=5吗？（4）以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5-x的图象相同吗？体会到二元一次方程与一次函数图象之间内在的密切的联系：以方程x+y=5的解为坐标的点组成的图象与一次函数y=5-x图象。

１、方程x+y=4的解有个，以方程x+y=4 的解为坐标的点组成一次函数的图象。

2、一次函数ｙ＝３ｘ＋７的图象与y 轴的交点坐标是，且该点的横纵坐标是二元一次方程－２ｘ＋ｂｙ＝１８的解，则ｂ＝。

，）解，其中必有一个解为.。

探索研究,构建模型情境二：2、把下列二元一次方程改写成形如y=ax+b(a≠0) 的一次函数的形式。

已知x+y=5，改写成一次函数为y=________。

已知2x-y=1，改写成一次函数为y=________。

(2)在同一坐标系内作出这两个函数的图象。

(3)(3)观察图象，指出它们的交点坐标。

鲁教版(五四制)七年级下册数学导学案设计：7.3二元一次方程组的应用(2) (无答案)

2、甲、乙两相距36千米两地相向而行，如果甲比乙先走2时，那么他们在乙出发2.5时后相遇；如果乙比甲先走2时，那么他们在甲出发3时后相遇，甲、乙两人每时各走多少千米？
我的收获：
这节课你都有哪些收获？
达标检验：
1.甲、乙两相距6千米，两人同时出发，同向而行，甲3小时可追上乙；相向而行，1小时相遇，两人的平均速度各是多少？
2.某旅馆的客房有三人间和两人间两种，三人间每人每天25元，两人间每人每天35元，一个50人的旅游团50人，租住了若干客房，且每个客房正好住满，一天花了1510元，两
种客房各租住了几间？
3.某体育场的环形跑道长400m,甲、乙分别以一定的速度练习长跑和自行车。

如果反
向而行，那么他们每隔30s相遇一次。

如果同向而行，那么他们每隔80s相遇一次，甲、乙的速度分别为多少？
4.为了保持生态平衡，某地区实施“退耕还林”工程，退耕还林后林场与耕地共有168公顷，其中耕地面积仅占林场面积的20%。

退耕还林后林场和耕地面积分别是多少？。

鲁教版(五四制)七年级下册数学导学案设计：7.3二元一次方程组的应用(一)(无答案)

7.3二元一次方程组的应用（一）二【学习目标】1、经历和体验运用方程（组）解决实际问题的过程，进一步体会方程（组）是刻画现实世界的有效数学模型；三【学习重点】根据等量关系列二元一次方程组解应用题。

四【学习难点】根据题意找出等量关系，列出方程。

五【学习过程】二自学探究初步感受并思考“雉兔同笼”问题。

今有雉（兔）同笼，上有三十五头，下有九十四足，问雉兔各几何？“上有三十五头”的意思是什么？“下有九十四足”呢？1）、如果笼内鸡兔都训练有素，让“鸡们”来个金鸡独立，让“兔们”前足离地，你能否利用小学的算术思想解决这个问题2）、如果设鸡有x只，你能否表示出兔的只数？尝试列一元一次方程解决这个问题3）、如果设鸡有x只，则兔有y只。

尝试列二元一次方程组解决这个问题。

4）、综合对比以上方法，体会三种方法的优缺点。

（二）例题的学习（1）自学教材例1 以绳测井，若将绳三折测之，绳多五尺；若将绳四折测之，绳多一尺.绳长、井深各几何？1）、"将绳三折测之，绳多五尺"，什么意思？(2)、"若将绳四折测之，绳多一尺"，又是什么意思？尝试动手操作，加深理解。

(3)如果设绳长x尺，井深y尺，尝试列二元一次方程组解决这个问题【知识应用与能力形成】1、日本算术书中有名的“龟鹤算”题为：“有一群鹤和乌龟都圈在一个笼子里。

从上边数脑袋是24个，从下边数脚是74只。

问乌龟和鹤各是多少只？2、列方程解古算题："今有牛五、羊二，值金十两；有牛二、羊五，值金八两.牛、羊各值金几何？（题目的大意：5头牛、2只羊共价值10两"金"，2头牛、5只羊共价值8两"金"，每头牛、每只羊各价值多少"金"？）2、〈〈一千零一夜〉〉中有这样一段文字：有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食，树上的一只鸽子对地上觅食的鸽子说：“若从你们中飞上来一只，则树下的鸽子就是整个鸽群的31，若从树上飞下去一只，则树上、树下的鸽子就一样多了。

七年级数学下册7.3二元一次方程组的应用(一)导学案(无答案)鲁教

七年级数学下册7.3二元一次方程组的应用(一)导学案(无答案)鲁教篇一：七年级数学下册 7.3 二元一次方程组的应用(三)导学案(无) 鲁教版五四制二元一次方程组的应用〔三〕【学习目标】1、能将实际问题转化成数学问题，列出方程组解决相应问题。

2、通过稳固练习，培养学生分析问题和解决问题的综合能力。

【学习重点】找等量关系列二元一次方程组解决相应问题。

【学习过程】一、自主学习1、认真阅读课本P17，完成课本上的问题，理解所列方程组的意义。

2、一个三位数，各数位上的数字之和为13，十位上的数字比个位上的数字大2，如果把百位上的数字与个位上的数字对调，那么所得新数比原来的三位数大99，求这个三位数。

【预习自测】题中的两个相等关系：1、每千克售4.2元的糖果销售总价+ = 可列方程为：2、每千克售4.2元的糖果重量+ =可列方程为：〔几何分配问题〕如图：用8块相同的长方形拼成一个宽为48厘米的大长方形，每块小长方形的长和宽分别是多少？解：设小长方形的长是x厘米，宽是y厘米题中的两个相等关系：1、小长方形的长+ =大长方形的宽可列方程为：2、小长方形的长=可列方程为：〔材料分配问题〕一张桌子由桌面和四条脚组成，1立方米的木材可制成桌面50张或制作桌脚300条，现有5立方米的木材，问应如何分配木材，可以使桌面和桌脚配套？解：设有题中的两个相等关系：1、制作桌面的木材+=可列方程为：2、所有桌面的总数：所有桌脚的总数= 可列方程为：〔和差倍问题〕一个两位数，十位上的数字比个位上的数字大5，如果把十位上的数字与个 1篇二：七年级数学下册 7.3 二元一次方程组的应用(二)导学案(无) 鲁教版五四制二元一次方程组的应用〔二〕【学习目标】1、能将实际问题转化成数学问题，列出方程组解决相应问题。

2、通过稳固练习，培养学生分析问题和解决问题的综合能力。

【学习重点】会找等量关系，列出方程组解决相应问题。

【学习过程】一、自主学习列方程解应用题的根本关系量〔1〕行程问题：速度×时间=路程顺水速度=静水速度—水流速度逆水速度=静水速度—水流速度〔2〕工程问题：工作效率×工作时间=工作量〔3〕浓度问题：溶液×浓度=溶质〔4〕银行利率问题：免税利息=本金×利率×时间列方程组解应用题的常见题型〔1〕和差倍总分问题：较大量=较小量+多余量，总量=倍数×倍量〔2〕产品配套问题：加工总量成比例〔3〕速度问题：速度×时间=路程〔4〕航速问题：此类问题分为水中航速和风中航速两类1．顺流〔风〕：航速=静水〔无风〕中的速度+水〔风〕速2．逆流〔风〕：航速=静水〔无风〕中的速度--水〔风〕速〔5〕工程问题：工作量=工作效率×工作时间分为两种，一种是一般的工程问题；另一种是工作总量是单位一的工程问题〔6〕增长率问题：原量×〔1＋增长率〕=增长后的量，原量×〔1＋减少率〕=减少后的量〔7〕浓度问题：溶液×浓度=溶质〔8〕银行利率问题：免税利息=本金×利率×时间，税后利息=本金×利率×时间—本金×利率×时间×税率〔9〕利润问题：利润=售价—进价，利润率=〔售价—进价〕÷进价×100%〔10〕盈亏问题：关键从盈〔过剩〕、亏〔缺乏〕两个角度把握事物的总量〔11〕数字问题：首先要正确掌握自然数、奇数偶数等有关的概念、特征及其表示〔12〕几何问题：必须掌握几何图形的性质、周长、面积等计算公式〔13〕年龄问题：抓住人与人的岁数是同时增长的【预习自测】〔行程问题〕甲、乙二人相距6km，二人同向而行，甲3小时可追上乙；相向而行，1小时相遇。

鲁教版初中数学七年级下册《解二元一次方程组(加减法)》导学案1

7.2 解二元一次方程组（第二课时）导学案【知识回顾】1、解二元一次方程组的基本思想是________，要把二元一次方程组转化为______解决.2、完成下面填空（1）()______,x y x y ++-=（2）()_____.x y x y +--=（3）()()3252____x y x y ++-=，（4）()()334_____.x y x y +--=（5）()()25234_______u v u v ++-=.观察原式与结构，可以发现：每小题中的式子中都含有_____个字母，而结果中含有_____个字母.3、等式的两边都加上（或减去）同一个整式，等式还能成立吗？用代入法解方程组3553423x y x y +=⎧⎨-=⎩，并检验.【学习目标】1.进一步理解解方程组的消元思想.2.了解加减法是消元的又一种基本方法，会用加减法解一些简单的二元一次方程组.【学习重点与难点】重点：会用加减法解二元一次方程组.难点：灵活运用加减消元法的技巧.【学习过程】一、导入新课：上面的方程组中，我们用代入法消去了一个未知数，将“二元”转化为“一元”，从而得到了方程组的解.对于二元一次方程组，是否存在其它方法，也可以消去一个未知数，达到化“二元”为“一元”的目的呢？这就是我们这节课将要学习的内容.二、新知学习（一）同一个未知数的系数相同（或互为相反数）的二元一次方程组的解法1、观察方程组7300,6100.x yy x+=⎧⎨-=⎩①②，并思考：（1）方程①中x的系数是_______，方程②中x的系数是______，这两个数_______.方程①中y的系数是_______，方程②中y的系数是______，这两个数_______.（2）若把方程①、方程②的左右两边分别相加，可得方程____________，得到的这个方程是二元一次方程还是一元一次方程？答：_____________.若把方程①、方程②的左右两边分别相减，可得方程____________，得到的这个方程是二元一次方程还是一元一次方程？答：_____________.（3）通过上面的思考，通过方程两边相加（或相减）的方法，能把二元一次方程组转化为一元一次方程吗？（4）经过上面的思考后，请同学们认真看课本P78至P79例2上面的内容.体会：①课本中给出了这个方程组的几种解法？这种解法与代入法相同吗？你能说出这种解法的根据吗？②什么是加减消元法？通过把两个方程_____或_____消去一个未知数，转化为_________，这种解法叫做加减消元法，简称加减法.2、反馈练习解方程组：（1）325523x yx y+=⎧⎨-=⎩①②；（2）31344x yx y+=⎧⎨-=-⎩①②.提示：方程组325523x yx y+=⎧⎨-=⎩①②中y的系数的特点是________，把这两个方程的两边相_____，可消去未知数y.方程组31344x yx y+=⎧⎨-=-⎩①②中x的系数的特点是________，把这两个方程的两边相_____，可消去未知数x.请写出解答过程.规律总结：在方程组的两个方程中，（1）若同一个未知数的系数相同，可直接把这两个方程相_____（加或减），消去系数相同的这个未知数；（2）若同一个未知数的系数互为相反数，可直接把这两个方程相_____（加或减），消去系数相同的这个未知数；（二）不具备系数相同（或互为相反数）的二元一次方程组的解法1、学前思考能不能由方程524u v+=-得到1048v v+=-？怎么得到的？2、知识探究已知方程组524,3418.u vu v+=-⎧⎨-=-⎩①②.思考（1）在上面的这个方程组中，两个方程中的未知数u和v的系数相同吗？互为相反数吗？能不能直接把这两个方程相加（或相减）消去一个未知数？（2）能利用等式的性质使这两个方程的某一个未知数的系数变为相同或互为相反数吗？如何变化？（3）尝试求出这个方程组的解.求解完后与课本P111例4的解答过程对照.（4）反思在上面给出的方程中，能通过变形消去未知数u 吗？需怎样变化？尝试写出解答过程.3、反馈练习解方程组235,3212.x y x y -=-⎧⎨+=⎩①②三、归纳小结加减消元法解方程组基本思路：加减消元----二元---一元主要步骤有：变形----同一个未知数的系数相同或互为相反数加减----消去一个元求解----分别求出两个未知数的值写解----写出方程组的解【精练反馈】基础部分1、方程组 5 210 x y x y +=⎧⎨+=⎩①②，由②-①，得正确的方程是（）A. 310x =B. 5x =C. 35x =-D. 5x =-2、已知二元一次方程组⎩⎨⎧=--=+72837.08.0y x y x ，用加减法解该方程组时，将方程①两边同时乘以_____，再将得到的方程与方程②两边相______，即可消去_____.3、用加减法解方程组⎩⎨⎧=-=+823132y x y x 时，要使两个方程中同一未知数的系数相等或相反，有以下四种变形的结果：①⎩⎨⎧=-=+846196y x y x ②⎩⎨⎧=-=+869164y x y x ③⎩⎨⎧-=+-=+1646396y x y x ④⎩⎨⎧=-=+2469264y x y x 其中变形正确的是（）A.①②B.③④C.①③D.②④4、方程组⎩⎨⎧=-=+3,5y x y x 的解是 _________．5、解下列方程组（1）4,2 5.x y x y +=⎧⎨-=⎩①② （2）2622x y x y -=⎧⎨+=-⎩ ①②能力提高部分6、小明和小华同时解方程组⎩⎨⎧=-=+1325ny x y mx ,小明看错了m ，解得⎪⎩⎪⎨⎧-==227y x ,小华看错了n ，解得⎩⎨⎧-==73y x ,你能知道原方程组正确的解吗？7、先读阅读材料，然后解方程组材料：解方程组()1045x y x y y --=⎧⎪⎨--=⎪⎩由①得1=-y x ③，把③代入②，得514=-⨯y ，解得1-=y把1-=y 代入③得0=x ，所以01x y =⎧⎨=-⎩ ① ②这种解法称为“整体代入法”，你若留心观察，有很多方程组可采用这种方法解答.请用这种方法解方程组2320 235297x yx yy--=⎧⎪-+⎨+=⎪⎩【课后作业】习题7.3知识技能1数学理解2、3。

鲁教版五四制七年级下册数学导学案设计：7.3二元一次方程组的应用(二)(无答案)

7.3二元一次方程组的应用（二）学习目标：1、知识与能力目标：会根据题意列出二元一次方程组，在抽象二元一次方程组的过程中，进一步体会到方程是描述现实生活中某些问题的有效数学模型，体会代数方法的优越性和多样性2、过程与方法目标：通过积极的思考、互相讨论，经历探索事物之间的数量关系，形成运用方程解决实际问题的过程，进一步体会方程是刻画现实世界的有效数学模型3、情感态度价值观目标：体会方程组在解决生活实际问题过程中的重要地位，感受数学的价值，激发学生学习数学的兴趣探究活动一：小明骑摩托车在公路上匀速行驶，12:00时看到里程碑上的数是一个两位数，它的两个数字之和是7；13:00时看里程碑上的数与12:00时所看到的个位数字和十位数字正好颠倒了；14:00时看到里程碑上的数比12:00时看到的两位数中间多了一个零，你能确定小明在12:00时看到里程碑上的数吗？如果设小明在12:00看到的数的十位数字是x，个位数字是y，那么(1) 小明在12:00看到的数字可表示为__________________________ 根据两个数字之和是7，可列出方程__________________________(2) 小明在13:00看到的数字可表示为___________________________12:00~ 13:00间摩托车行驶的路程是__________________________(3) 小明在14:00看到的数字可表示为___________________________13:00~ 14:00间摩托车行驶的路程是__________________________(4) 12:00～13:00和13:00～14:00两段时间内摩托车行驶的路程有什么关系？你能列出相应的方程吗？___________________________根据以上的分析，得方程组___________________________练一练：1 已知一个两位数，十位数字比个位数字大3 ，将十位数字与个位数字对调所得的新数比原数小27，求这个两位数2 王老师的年龄是个两位数，个位上的数字比十位上的数字的2倍多1，将十位数字与个位数字调换位置，所得的新数比原两位数的2倍还多2，问王老师的年龄多大探究活动二：两个两位数的和是68，在较大的两位数的右边接着写较小的两位数，得到一个四位数；在较大的两位数的左边写上较小的两位数，也得到一个四位数。

七年级数学下册7.6二元一次方程组教案(无答案)鲁教版五四制.doc

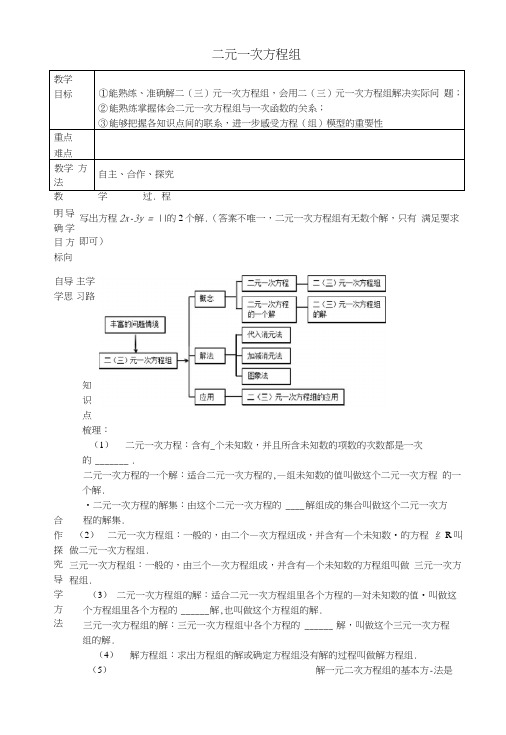
二元一次方程组教学目标 ① 能熟练、准确解二（三）元一次方程组，会用二（三）元一次方程组解决实际问题；② 能熟练掌握体会二元一次方程组与一次函数的关系；③ 能够把握各知识点间的联系，进一步感受方程（组）模型的重要性重点难点教学方法自主、合作、探究教学过. 程写出方程2x-3y = \\的2个解.（答案不唯一，二元一次方程组有无数个解，只有满足要求即可）自导主学学思习路知识点梳理：（1）二元一次方程：含有_个未知数，并且所含未知数的项数的次数都是一次的 _______ .二元一次方程的一个解：适合二元一次方程的,—组未知数的值叫做这个二元一次方程的一个解.•二元一次方程的解集：由这个二元一次方程的 ____ 解组成的集合叫做这个二元一次方程的解集.（2）二元一次方程组：一般的，由二个—次方程纽成，并含有—个未知数•的方程纟R 叫做二元一次方程组.三元一次方程组：一般的，由三个—次方程组成，并含有—个未知数的方程组叫做三元一次方程组.（3）二元一次方程组的解：适合二元一次方程组里各个方程的—対未知数的值•叫做这个方程组里各个方程的 ______ 解,也叫做这个方程组的解. 三元一次方程组的解：三元一次方程组屮各个方程的 ______ 解，叫做这个三元一次方程组的解.（4）解方程组：求出方程组的解或确定方程组没有解的过程叫做解方程组.（5） __________________________________________ 解一元二次方程组的基本方-法是明导确学目方标向合作探究导学方法和_________________________________________ .（6）列二元一次方程纽解应用题的步骤 ________________________ •典型例题: 内容：例1求方程2x + y = 7的正整数解.例2如图，求直线厶：y = x +1和直线仇：y = 2x-l 的交点坐标.x + 2y = 7 + k例3求购进篮球和排球各多少个?2. （1）已知方程+5）小-2" =7是关于X 、y 的二元一次方程，则a=⑵若3/心》7 +兀3）宀+”是单项式，则m =1. 使我们清楚了解二元一次方程、二元一'次方程组及它们的解的基本概念。

鲁教版(五四制)数学七年级下7.4二元一次方程组与一次函数学学案(无答案)

二元一次方程与一次函数学习目标：1、理解二元一次方程与一次函数的关系；2、理解二元一次方程组与一次函数的关系；能利用解二元一次方程组的方法求两直线的交点坐标，反过来，能利用一次函数图象的交点坐标得到相应的二元一次方程组的解。

3、体会转化、数形结合等数学思想在本节课学习中的运用。

课前导入课前老师听到同学们的争论：你知道y=3x+5 这是什么？模块导学自主练习一：1、二元一次方程x+y=5可以转化为y= 。

思考：是不是所有的二元一次方程都能进行这样的转化？2、方程x+y=5的解有（）个。

x=0 x=5 x=2y=5 y=0 y=3 是这个方程的解吗？3、点（0,5），（5,0），（2,3）它们在一次函数y=5－x的图像上吗？4、在函数y=5－x的图像上任取一点，它的坐标适合方程x+y=5吗？5、以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5－x的图像相同吗？跟踪训练一：1、坐标适合方程3x-y=5的点都在一次函数（）图像上。

2、以二元一次方程（）的解为坐标的所有点组成的图象与一次函数y=3x-1的图象相同。

模块二：二元一次方程组与一次函数的关系自主练习二：（1）把下列二元一次方程改写成形如y=kx+b(k≠0) 的一次函数的形式。

已知 x+y=5，改写成一次函数为y=________。

已知2x-y=1，改写成一次函数为y=________。

（2）在同一坐标系内作出这两个函数的图象。

（3）观察图象，指出它们的交点坐标。

（4）解方程组： x+y=52x-y=1（5）观察这个方程组的解与这两个函数图象的交点坐标之间有何关系？（6）根据以上过程，你有什么发现？跟踪训练二：（快速口答）1、一次函数y=5-x与y=2x-1图像的交点为（2,3）,则方程组x+y=52x-y=1的解为（）2、若二元一次方程组x-2y=-2的解为x=2,则函数y=0.5x+1与y=2x-22x-y=2 y=2的图象的交点坐标为（）3、根据下列图像，你能说出是哪些方程组的解？这些解是什么？变形练习：如图中的两条直线L1，L2的交点坐标可以看做方程组的解．（说说你的思路）自主练习三：1、如图，一次函数y=x+1，y=x-2的图像之间有何关系？2、有一组数同时适合方程x-y=-1和x-y=2的解吗？你能从中“悟”出些什么吗？跟踪训练三：关于x 、y 的方程组ax+3y=92x-y=1无解，则a=（）课堂检测1．因为⎩⎨⎧−=−=+124y x y x 的解是⎩⎨⎧==__________y x ，所以一次函数y =－x ＋4与y =2x ＋1的图象交点坐标为．2.若一次函数y =3x －5与y =2x +b 的图象交点为P （1，－2），试确定二元一次方程组 y =3x －5 的解和b 的值．y =2x +b课后延伸基础题：1、若一次函数y =－21x －2与y =2x －7的图象交点为（2，－3），则二元一次方程组⎩⎨⎧=−−=+7242y x y x 的解为． 2、若一次函数y =2x 与y =-x +b 的图象交点为（1，a ），试确定二元一次方程组 y =2x 的 y =-x +b解和a,b 的值．3、求直线y=3x －2和y=－2x ＋3图象的交点坐标。

鲁教版(五四制)(2012)七年级数学下册-7.2 解二元一次方程组-学案设计(无答案)

解二元一次方程组【学习目标】1．会用代入消元法解二元一次方程组。

2．了解解二元一次方程组的消元思想，初步体会数学学习的化归思想。

【学习重难点】1．用代入法解二元一次方程组，基本思想是。

2．消元——化二元为一元。

【学习过程】一、自主学习1．把下列方程写成用含x 的式子表示y 的形式：（1）若2x －y=3，则y=______________。

（2）若3x+y －1=0，则y=______________。

（3）若x 2+y ＝6，则y=______________。

2．已知二元一次方程2x －3y=1。

若x=3，则y=__________。

若y=1，则y=___________。

二、合作交流1．要把方程组 x+y=22 ①2x+y=40 ②转化为一元一次方程，可把①式写成：__________再代入②式，这时方程组就转化成了一元一次方程：__________。

2．二元一次方程组与一元一次方程有什么关系？三、达标检测1．解方程组 3(x －3)=y －1 ①5(y －1)=3(x+5) ②2．若2x ³m －2n+2ym+n 与0.5x5y4n+1中，x 、y 的指数分别相同，求m 与n 的值。

四、课后作业1．已知⎩⎨⎧==12y x 是方程2x+ay=5的解，则a=__________。

2．二元一次方程343x my mx ny -=+=和有一个公共解11x y =⎧⎨=-⎩，则m=______，n=_____。

3．已知2|2|(3)0a b b -++-=，那么______ab =。

4．对于方程组5322(1),(2),(3),(4)161021x y x y x x y x xy x y x y y +=⎧+===⎧⎧⎧⎪⎨⎨⎨⎨-==-+=--=⎩⎩⎩⎪⎩，是二元一次方程组的为（）A ．（1）和（2）B ．（3）和（4）C ．（1）和（3）D ．（2）和（4）5．若25x y =⎧⎨=⎩是方程22kx y -=的一个解，则k 等于（） 858...6.533A B C D - 6．方程组34111238x y x y =⎧⎪⎨-=⎪⎩的解为（） 12142....4333028x x x x A B C D y y y y ⎧==⎧⎧⎪==⎧⎪⎪⎪⎨⎨⎨⎨==⎩⎪⎪⎪==⎩⎩⎪⎩ 7．已知,a b 满足方程组2827a b a b +=⎧⎨+=⎩，则a b -的值为（） A ．－1 B ．0 C ．1 D ．28．解下列方程：（1）⎩⎨⎧=-=-②①.195.02.0,1y x y x （2）⎪⎩⎪⎨⎧=+=184332y x y x。

鲁教版(五四制)七年级数学下册导学案设计：第七章《二元一次方程组》复习 (无答案)

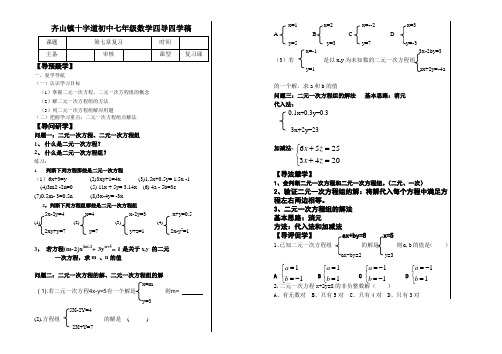
齐山镇十字道初中七年级数学四导四学稿【导预疑学】一、复学导航（一）认识学习目标（1）掌握二元一次方程、二元一次方程组的概念（2）解二元一次方程组的方法（3）列二元一次方程组解应用题（二）把握学习重点：二元一次方程组点解法【导问研学】问题一：二元一次方程、二元一次方程组1、什么是二元一次方程？2、什么是二元一次方程组？练习:1.判断下列方程那些是二元一次方程（1）6x+3=y (2)3xy+1=4x (3)1.5x+0.5y= 1.5x -1 (4)3m2 -2n=0 (5) 11x + 5y= 3.14x (6) 4a - 5b=3c (7)0.5m- 3=0.5n (8)3x-4y= -3x2，判断下列方程组哪些是二元一次方程组5x-2y=4 x=4 x-2y=3 x+y=0.5 (1) (2) (3) (4)2xy+y=7 y=7 y+z=1 2x-y2=1 3，若方程(m-2)x|m|-1+ 3y n+5= 1是关于x,y 的二元一次方程，求m 、n的值问题二：二元一次方程的解、二元一次方程组的解x=my=35X-2Y=4(2).方程组的解是( )2X+Y=7x=1 x=2 x=--2 x=3B Dy=5 y=3 y=7x=-1 3x-2by=3 （3）若是以x,y为未知数的二元一次方程组y=1 ax+2y=-4a的一个解，求a和b的值问题三：二元一次方程组的解法基本思路：消元代入法：0.1x+0.3y=0.33x+2y=23加减法：【导法慧学】1、会判断二元一次方程和二元一次方程组。

（二元、一次）2、验证二元一次方程组的解：将解代入每个方程中满足方程左右两边相等。

3、二元一次方程组的解法基本思路：消元方法：代入法和加减法【导评促学】 ax+by=8 x=51、已知二元一次方程组的解是则a,b的值是（） ax-by=2 y=3A B C D2.二元一次方程x+2y=8的非负整数解（）A、有无数对B、只有5对C、只有4对D、只有3对⎩⎨⎧=+=+20432556zxzx( 1).若二元一次方程4x-y=5则m= ⎩⎨⎧-==11ba⎩⎨⎧==11ba⎩⎨⎧-=-=11ba⎩⎨⎧=-=11ba。

七年级数学下册7.1二元一次方程组教案(无答案)鲁教版五四制.doc

二元一次方程组教学目标（1）理解二元-•次方程（组）及其解的概念，能判别一组数是否是二元一次方程（组）的解；（2）会根据实际问题列简单的二元一次方程或二元一次方程纟无重点难点（1）掌握二元一次方程及二元一次方程组的概念，理解它们解的含义；（2）判断一组数是不是某个二元一次方程组的解. 教学方法自主、合作、探究教•学过程明导确学目方标向在一望无际的呼伦贝尔大草原上，一头老牛和一匹小马驮着包裹吃力地疔走着，老牛喘着气吃力地说：“累死我了”，小马说：“你还累，这么大的个，才比我多驮2 个老牛气不过地说：“哼，我从你背上拿来一个，我的包裹就是你的2倍！”，小马天真而不信地说「'真的？！ ”同学们，你们能否用数学知识帮助小马解决问题呢？门导主学学思习路 1-上面我们列，出的这两个方程与一元一次方程不同•每个方程都有两个耒知数，并且未知项的次数都是1•像这样的方程，我们把它叫做二元一次方程（linear equation with two unknowns'）.把这两个二元一次方程合在一起，就纟R 成了一个二元一次方程组.2.-般地，使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值，叫做二元一次方程组的解.实践1「根据下列语5,分别设适当的未知数，列出二元一次方程或二元•一次方程组: （1）甲数的丄比乙数的4倍多8；3⑵摩托车踽速是货车吩，它们的时速之和是合作探究导学方法200千米/小时;（3）某校现冇校舍20000平方米，计划拆除部分山校舍，改建新校舍，使校舍总面积增加30%,若建造新校舍的血积是被拆除旧校舍面积的4倍，那么应拆除多少旧校舍，建造多少新校舍？（让学生初步体会用二元一次方程或二元一次方程组来表示实际问题中的数量关系，说明二元一次方程（组）是反映现实世界多个量Z 间相等关系的一种有效的数学模型。

）实践2：方程组 3x-2y = \ 厶 A ,的解为（）x + y = 2A.B. C. D. 实践3：如果ax - 4y = 5的解，求a-b的值。

七年级下册数学鲁教版导学案---7.1 二元一次方程组(无答案)

七年级数学下册导学案第___周第___课时课题7.1 二元一次方程组课型新授主备人
备课组审核级部审核学生姓名
教师寄语世界上最宝贵的是今天，最易丧失的也是今天，愿你在今后的学习中无限珍惜这每一个今天。

学习目标1.能根据题意列出方程或方程组，并判断是所学过的哪种方程（组），能举出二元一次方程及二元一次方程组的例子；
2.能列举二元一次方程的解，会判断一组数是不是二元一次方程（组）的解.
（一）课前先学（3分钟）
1.你从上图中获得了哪些数学信息？
2.请利用上述信息列出方程，并说出你列的是不是一元一次方程。

如果不是一元一次方程，它可以叫什么方程？
（二）课中先学活动（1）（4分钟）
1.如果设去了x名成人，去了
y名儿童，根据题意请列出方程？你列的是不是二元一次方程？2.请你总结一下满足什么条件的方程是二元一次方程.请举个二元一次方程的例子.。

鲁教版(五四制)(2012)七年级数学下册-7.3 二元一次方程组的应用-学案设计(无答案)

三、挖掘教材4辆小卡车和5辆大卡车一次共可以运货物27吨，6辆小卡车和10辆大卡车一次共可以运货物51吨，问小卡车和大卡车每辆每次可运货物多少吨？分析：A题型：_________________________________________________________________。

B等量关系；_____________________________________________________________。

C设：___________________________________________________________________。

D列方程组：_____________________________________________________________。

四、达标检测1．今有鸡兔若干，它们共有24个头和74只脚，则鸡兔各有（）A．鸡10兔14 B．鸡11兔13 C．鸡12兔12 D．鸡13兔112．一队敌人一队狗，两队并成一队走，脑袋共有八十个，却有二百条腿走，请君仔细数一数，多少敌军多少狗？3．某制衣厂某车间计划用10天加工一批出口童装和成人装共360件，该车间的加工能力是：每天能单独加工童装45件或成人装30件。

（1）该车间应安排几天加工童装，几天加工成人装，才能如期完成任务？（2）若加工童装一件可获利80元，加工成人装一件可获利120元，那么该车间加工完这批服装后，共可获利多少元？4．某高校共有5个大餐厅和2个小餐厅，经过测试，同时开放1个大餐厅，2个小餐厅，可供1680名学生就餐；同时开放2个ú大餐厅，1个小餐厅，可供2280名学生就餐。

（1）求1个大餐厅，1个小餐厅分别可供多少名学生就餐；（2）若7个餐厅同时开放，能否供全校5300名学生就餐？请说明理由。