抛物线中的三角形面积问题(一)

合集下载

抛物线与坐标轴交点构成的三角形问题

抛物线与坐标轴交点构成的三角形问题--------思考与探索面积篇例1:已知抛物线3+2x +x －=y 2与x 轴交于A,B 两点，其中A 点位于B 点的左侧，与y 轴交于C 点，顶点为P ， _________=S A O C △ _________=S BO C △ _________=S CO P △ _________=S PAB △_________=S PCB △ _________=S A CP △例：在平面直角坐标系中，有两点A （-1，0），B （3，0），如图，小敏发现所有过A ，B 两点的抛物线如果与y 轴负半轴交于点C ，M 为抛物线的顶点，那么△ACM 与△ACB 的面积比不变，请你求出这个比值。

对称篇例2、如图，一元二次方程2230x x +-=的二根12x x ，（ 12x x < ）是抛物线2y ax bx c =++与x 轴的两个交点B,C 的横坐标，且此抛物线过A(3，6)点．（1）求此二次函数的解析式．（2）设此抛物线的顶点为p ，对称轴与线段AC 相交于点Q ，求点P 和点Q 的坐标．（3）在X 轴上有一动点M ，当MQ+MA 取得最小值时，求点M 的坐标（4）设AC 与Y 轴交与D 点，E 点坐标为(0,1)，在X 轴上找一点F ，抛物线对称轴上找一点G ，使四边形AFGE 的周长最短，并求出当四边形周长最短时的点F 、G 点坐标，并求出四边形AFGE 的周长。

形状篇1、已知抛物线c +bx +ax =y 2与x 轴正、负半轴分别交于A 、B 两点，与y 轴负半轴交于点C 。

若OA=4，OB=1，∠ACB=90°，求抛物线解析式。

2、已知：抛物线与x 轴的交点坐标为A(-1,0)和B （3，0）,顶点为C,若∠ACB=90度.问1：C 点的坐标是多少？问2：在抛物线的解析式中，=-ac b 423. 若题设中的A 、B 两点的坐标未知，而已知∠ACB=90度，你能求出 =-ac b 42吗？4. 从上面的探索中我们看到解析式中的△与∠ACB 有关，那么如果△ACB 是等边三角形，则△是多少？最后, ①思因果 ; ②思规律 ; ③思多解 ; ④思变通; ⑤思归类; ⑥思错误．。

【经典压轴题】三角形面积最值问题30题含详细答案

试卷第1页，总14页………外…………○…………订…………○……学：___________考号：___________………内…………○…………订…………○……三角形面积最值问题30题含详细答案1．如图，抛物线2y ax bx c =++与x 轴交于点(1,0)A -，点(3,0)B ，与y 轴交于点C ，且过点(2,3)D -．点P 、Q 是抛物线2y ax bx c =++上的动点．(1)求抛物线的解析式；(2)当点P 在直线OD 下方时，求POD ∆面积的最大值．(3)直线OQ 与线段BC 相交于点E ，当OBE ∆与ABC ∆相似时，求点Q 的坐标．2．如图，在平面直角坐标系xOy 中，已知抛物线22y ax x c =-+与直线y kx b =+都经过(0,3)A -、(3,0)B 两点，该抛物线的顶点为C ．（1）求此抛物线和直线AB 的解析式；（2）设直线AB 与该抛物线的对称轴交于点E ，在射线EB 上是否存在一点M ，过M 作x 轴的垂线交抛物线于点N ，使点M 、N 、C 、E 是平行四边形的四个顶点？若存在，求点M 的坐标；若不存在，请说明理由；（3）设点P 是直线AB 下方抛物线上的一动点，当PAB ∆面积最大时，求点P 的坐标，并求PAB ∆面积的最大值．3．如图，抛物线25(0)y ax bx a =+-≠经过x 轴上的点A （1，0）和点B 及y 轴上的点C ，经过B 、C 两点的直线为y x n =+．试卷第2页，总14页……订…………○……※※内※※答※※题※※……订…………○……①求抛物线的解析式．②点P 从A 出发，在线段AB 上以每秒1个单位的速度向B 运动，同时点E 从B 出发，在线段BC 上以每秒2个单位的速度向C 运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t 秒，求t 为何值时，△PBE 的面积最大并求出最大值． ③过点A 作AM BC ⊥于点M ，过抛物线上一动点N （不与点B 、C 重合）作直线AM 的平行线交直线BC 于点Q ．若点A 、M 、N 、Q 为顶点的四边形是平行四边形，求点N 的横坐标．4．如图，在平面直角坐标系中，已知抛物线22(0)y ax bx a =++≠与x 轴交于()1,0A -），()3,0B 两点，与y 轴交于点C ，连接BC ．（1）求该抛物线的解析式，并写出它的对称轴；（2）点D 为抛物线对称轴上一点，连接CD BD 、，若DCB CBD ∠=∠，求点D 的坐标；（3）已知()1,1F ，若(),E x y 是抛物线上一个动点（其中12x <<），连接CE CF EF 、、，求CEF ∆面积的最大值及此时点E 的坐标．（4）若点N 为抛物线对称轴上一点，抛物线上是否存在点M ，使得以,,,B C M N 为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M 的坐标；若不存在，请说明理由．试卷第3页，总14页…○…………外………………订…………………线…………○……___________考号：______…○…………内………………订…………………线…………○……5．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是，位置关系是；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．6．已知抛物线y ＝a （x ﹣1）2过点（3，4），D 为抛物线的顶点．（1）求抛物线的解析式；（2）若点B 、C 均在抛物线上，其中点B （0，1），且∠BDC ＝90°，求点C 的坐标：（3）如图，直线y ＝kx +1﹣k 与抛物线交于P 、Q 两点，∠PDQ ＝90°，求△PDQ 面积的最小值．7．如图，抛物线y ＝ax 2+bx+c 经过A （0，3）、B （﹣1，0）、D （2，3），抛物线与x试卷第4页，总14页装…………○……………○…………线※要※※在※※装※※订※答※※题※※装…………○……………○…………线轴的另一交点为E ,点P 为直线AE 上方抛物线上一动点，设点P 的横坐标为t ．（1）求抛物线的表达式；（2）当t 为何值时，△PAE 的面积最大？并求出最大面积；（3）是否存在点P 使△PAE 为直角三角形？若存在，求出t 的值；若不存在，说明理由．8．如图，四边形ABCD 是边长为2，一个锐角等于60°的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点D 重合，按顺时针方向旋转三角形纸片，使它的两边分别交CB 、BA （或它们的延长线）于点E 、F ，∠EDF=60°，当CE=AF 时，如图1小芳同学得出的结论是DE=DF ．（1）继续旋转三角形纸片，当CE≠AF 时，如图2小芳的结论是否成立？若成立，加以证明；若不成立，请说明理由；（2）再次旋转三角形纸片，当点E 、F 分别在CB 、BA 的延长线上时，如图3请直接写出DE 与DF 的数量关系；（3）连EF ，若△DEF 的面积为y ，CE=x ，求y 与x 的关系式，并指出当x 为何值时，y 有最小值，最小值是多少？9．已知ABC 和ADE 都是等腰三角形，AB AC =，AD AE =，DAE BAC ∠=∠．（初步感知）（1）特殊情形：如图①，若点D ，E 分别在边AB ，AC 上，则DB __________EC ．（填＞、＜或=）试卷第5页，总14页…………○………………○………………○…………………○……学校:____：___________班级：____：___________…………○………………○………………○…………………○……（2）发现证明：如图②，将图①中的ADE 绕点A 旋转，当点D 在ABC 外部，点E 在ABC 内部时，求证：DB EC =．（深入研究）（3）如图③，ABC 和ADE 都是等边三角形，点C ，E ，D 在同一条直线上，则CDB ∠的度数为__________；线段CE ，BD 之间的数量关系为__________．（4）如图④，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，点C 、D 、E 在同一直线上，AM 为ADE 中DE 边上的高，则CDB ∠的度数为__________；线段AM ，BD ，CD 之间的数量关系为__________．（拓展提升）（5）如图⑤，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，将ADE 绕点A 逆时针旋转，连结BE 、CD ．当5AB =，2AD =时，在旋转过程中，ABE △与ADC 的面积和的最大值为__________．试卷第6页，总14页…○…………外………订…………○………………○……※内※※答※※题※※…○…………内………订…………○………………○……10．如图，在平面直角坐标系xOy 中，反比例函数(0)m y x x =>的图像经过点34,2A ⎛⎫⎪⎝⎭，点B 在y 轴的负半轴上，AB 交x 轴于点C ，C 为线段AB 的中点．（1）m =________，点C 的坐标为________；（2）若点D 为线段AB 上的一个动点，过点D 作//DE y 轴，交反比例函数图像于点E ，求ODE 面积的最大值．11．如图，直线l ：y ＝﹣3x +3与x 轴、y 轴分别相交于A 、B 两点，抛物线y ＝ax 2﹣2ax +a +4（a ＜0）经过点B ，交x 轴正半轴于点C ．（1）求该抛物线的函数表达式；（2）已知点M 是抛物线上的一个动点，并且点M 在第一象限内，连接AM 、BM ，设点M 的横坐标为m ，△ABM 的面积为S ，求S 与m 的函数表达式，并求出S 的最大值及此时动点M 的坐标；（3）将点A 绕原点旋转得点A ′，连接CA ′、BA ′，在旋转过程中，一动点M 从点B 出发，沿线段BA ′以每秒3个单位的速度运动到A ′，再沿线段A ′C 以每秒1个单位长度的速度运动到C 后停止，求点M 在整个运动过程中用时最少是多少？12．（问题提出）试卷第7页，总14页……○…………外装…………○……姓名：___________班级：____……○…………内装…………○……（1）如图①，在等腰Rt ABC 中，斜边4AC =，点D 为AC 上一点，连接BD ，则BD 的最小值为．（问题探究）（2）如图2，在ABC 中，5AB AC ==，6BC =，点M 是BC 上一点，且4BM =，点P 是边AB 上一动点，连接PM ，将BPM △沿PM 翻折得到DPM △，点D 与点B 对应，连接AD ，求AD 的最小值．（问题解决）（3）如图③，四边形ABCD 是规划中的休闲广场示意图，其中135BAD ADC ∠=∠=︒，30DCB ∠=︒，AD =，3AB km =，点M 是BC 上一点，4MC km =．现计划在四边形ABCD 内选取一点P ，把DCP 建成商业活动区，其余部分建成景观绿化区．为方便进入商业区，需修建小路BP 、MP ，从实用和美观的角度，要求满足PMB ABP ∠=∠，且景观绿化区面积足够大，即DCP 区域面积尽可能小．则在四边形ABCD 内是否存在这样的点P ？若存在，请求出DCP 面积的最小值；若不存在，请说明理由．13．在平面直角坐标系中，点O 是原点，四边形AOBC 是矩形，点(5,0)A ，点(0,3)B .以点A 为中心，顺时针旋转矩形AOBC ，得到矩形ADEF ，点O B C ，，的对应点分别为D E F ，，.（1）如图①，当点D 落在BC 边上时，求点D 的坐标；（2）如图②，当点D 落在线段BE 上时，AD 与BC 交于点H .求点H 的坐标；（3）记K 为矩形AOBC 对角线的交点，S 为KDE 的面积，求S 的取值范围（直接写出结果即可）.试卷第8页，总14页……外…………○……………订…………○…※※请※※线※※内※※答※※题※※……内…………○……………订…………○…14．（1）如图1，四边形ABCD 中，//AD BC ，点E 为DC 边的中点，连接AE 并延长交BC 的延长线于点F ，求证：ABF ABCD S S ∆=四边形．（S 表示面积）（2）如图2，在ABC ∆中，过AC 边的中点P 任意作直线EF ，交BC 边于点F ，交BA 的延长线于点E ，试比较EBF ∆与ABC ∆的面积，并说明理由．（3）如图3，在平面直角坐标系中，已知一次函数y kx b =+的图像过点()2,4P 且分别于x 轴正半轴，y 轴正半轴交于点A 、B ，请问AOB ∆的面积是否存在最小值?若存在，求出此时一次函数关系式；若不存在，请说明理由．15．△ABC 为等边三角形，AB =8，AD ⊥BC 于点D ，E 为线段AD 上一点，AE =．以AE 为边在直线AD 右侧构造等边三角形AEF ，连接CE ，N 为CE 的中点．（1）如图1，EF 与AC 交于点G ，连接NG ，求线段NG 的长；（2）如图2，将△AEF 绕点A 逆时针旋转，旋转角为α，M 为线段EF 的中点，连接DN ，MN ．当30°＜α＜120°时，猜想∠DNM 的大小是否为定值，并证明你的结论；（3）连接BN ．在△AEF 绕点A 逆时针旋转过程中，当线段BN 最大时，请直接写出△ADN 的面积．16．如图，已知A ，B 是线段MN 上的两点，4MN =，1MA =，1MB >，以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M ，N 两点重合成一点C ，构成ABC ，设AB x =．试卷第9页，总14页…外…………○………………○…………订………○……学校:_____名：___________班级：___________考号…内…………○………………○…………订………○……（1）求x 的取值范围；（2）求ABC 面积的最大值．17．在平面直角坐标系中，抛物线265y x mx =-+与y 轴的交点为A ，与x 轴的正半轴分别交于点B （b ，0），C （c ，0）.（1）当b =1时，求抛物线相应的函数表达式；（2）当b =1时，如图，E （t ，0）是线段BC 上的一动点,过点E 作平行于y 轴的直线l 与抛物线的交点为P ．求△APC 面积的最大值；（3）当c =b + n .时，且n 为正整数.线段BC （包括端点）上有且只有五个点的横坐标是整数，求b 的值.18．如图，抛物线2y ax bx c =++与坐标轴交于点()()()0, 31,03,0A B E --、、,点P 为抛物线上动点,设点P 的横坐标为t ．（1）若点C 与点A 关于抛物线的对称轴对称,求C 点的坐标及抛物线的解析式；（2）若点P 在第四象限,连接PA PE 、及AE ,当t 为何值时,PAE ∆的面积最大?最大面积是多少?（3）是否存在点P ,使PAE ∆为以AE 为直角边的直角三角形，若存在，直接写出点P试卷第10页，总14页…外…………○…※…内…………○…的坐标；若不存在，请说明理由． 19．综合与实践问题情境：在综合与实践课上，老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合，并让一个三角板固定，另一个绕直角顶点旋转”为主题开展数学活动，如图1，三角板ABC 和三角板CDE 都是等腰直角三角形，90C ∠=︒，点D ，E 分别在边BC ，AC 上，连接AD ，点M ，P ，N 分别为DE ，AD ，AB 的中点．试判断线段PM 与PN 的数量关系和位置关系．探究展示：勤奋小组发现，PM PN =，PM PN ⊥．并展示了如下的证明方法：∵点P ，N 分别是AD ，AB 的中点，∴PNBD ，12PN BD =． ∵点P ，M 分别是AD ，DE 的中点，∴PM AE ∥，12PM AE =．（依据1）∵CA CB =，CD CE =，∴BD AE =，∴PM PN =． ∵PNBD ，∴DPN ADC ∠=∠．∵PM AE ∥，∴DPM DAC ∠=∠．∵90BCA ∠=︒，∴90ADC CAD ∠+∠=︒．（依据2）∴90MPN DPM DPN CAD ADC ∠=∠+∠=∠+∠=︒．∴PM PN ⊥．反思交流：（1）①上述证明过程中的“依据1”，“依据2”分别是指什么？ ②试判断图1中，MN 与AB 的位置关系，请直接回答，不必证明；（2）创新小组受到勤奋小组的启发，继续进行探究，把CDE △绕点C 逆时针方向旋转到如图2的位置，发现PMN 是等腰直角三角形，请你给出证明；（3）缜密小组的同学继续探究，把CDE △绕点C 在平面内自由旋转，当4CD =，10CB =时，求PMN 面积的最大值．20．如图，在平面直角坐标系中，四边形 OABC 为菱形，点 C 的坐标为（4,0），∠AOC = 60°，垂直于 x 轴的直线 l 从 y 轴出发，沿 x 轴正方向以每秒 1 个单位长度的速度运动，设直线 l 与菱形 OABC 的两边分别交与点 M 、N （点 M 在点 N 的上方）．○…………外…………订………………○……级：___________考号：__○…………内…………订………………○……（1）求 A 、B 两点的坐标；（2）设 OMN 的面积为 S ，直线 l 运动时间为 t 秒（0 ≤t ≤6 ），试求 S 与 t 的函数表达式；（3）在题（2）的条件下，t 为何值时，S 的面积最大？最大面积是多少．21．如图，抛物线y=ax 2+bx+c 经过点A （﹣1，0），C （0，3），抛物线的顶点在直线1x =上．（1）求抛物线的解析式；（2）若点P 为第一象限内抛物线上的一点，设△PBC 的面积为S ，求S 的最大值并求出此时点P 的坐标； 22．综合与探究如图，已知抛物线()20y ax bx c a =++≠与x 轴交于A 、()20B ，两点，与y 轴交于点C ，顶点坐标为点1924D ⎛⎫⎪⎝⎭，．（1）求此抛物线的解析式；（2）点P 为抛物线对称轴上一点，当PA PC +最小时，求点P 坐标；（3）在第一象限的抛物线上有一点M ，当BCM ∆面积最大时，求点M 坐标；（4）在x 轴下方抛物线上有一点H ，ABH ∆面积为6，请直接写出点H 的坐标．○…………装………○…………线…………※※请※※不※※要※※在※※○…………装………○…………线…………23．如图，已知抛物线23y ax bx =++与x 轴交于A 、B 两点，过点A 的直线l 与抛物线交于点C ，其中A 点的坐标是(1，0)，C 点坐标是(4，3)．（1）求抛物线的解析式；（2）抛物线的对称轴上是否存在点D ，使△BCD 的周长最小？若存在，求出点D 的坐标，若不存在，请说明理由；（3）点P 是抛物线上AC 下方的一个动点，是否存在点p ，使△PAC 的面积最大？若存在，求出点P 的坐标，若不存在，请说明理由．二、填空题24．如图，直线AB 交坐标轴于A(-2，0)，B(0，-4)，点P 在抛物线1(2)(4)2y x x =--上，则△ABP 面积的最小值为__________．25．如图，在平面直角坐标系xOy 中，半径为2的O 与x 轴的正半轴交于点A ，点B 是O 上一动点，点C 为弦AB 的中点，直线334y x =-与x 轴、y 轴分别交于点D 、E ，则CDE △面积的最小值为________．………○…………装………………订……………线…………○……学校:___________姓名：_级：___________考号：………○…………装………………订……………线…………○……26．如图，30AOB ∠=，C 是BO 上的一点，4CO =，点P 为AO 上的一动点，点D 为CO 上的一动点，则PC PD +的最小值为 ________，当PC PD +的值取最小值时，则OPC ∆的面积为________.27．如图，已知直线433y x =-与x 轴、y 轴分别交于A ，B 两点，P 是以(0,1)C 为圆心，1为半径的圆上一动点，连接PA ，PB ，当PAB ∆的面积最大时，点P 的坐标为__________．28．如图，在Rt ABC ∆中，90ACB ∠=︒，4AB =，点D ，E 分别在边AB ，AC 上，且2DB AD =，3AE EC =连接BE ，CD ，相交于点O ，则ABO ∆面积最大值为__________．…………装…………○…订…………○……线…………○……※请※※不※※要※※在※※装※※订内※※答※※题※※…………装…………○…订…………○……线…………○……29．如图，在△ABC 中，∠ACB ＝120°，AC ＝BC ＝2，D 是AB 边上的动点，连接CD ，将△BCD 绕点C 沿顺时针旋转至△ACE ，连接DE ，则△ADE 面积的最大值＝_____．30．如图，∠AOB=45°，点M 、N 分别在射线OA 、OB 上，MN=7，△OMN 的面积为14，P 是直线MN 上的动点，点P 关于OA 对称的点为P 1，点P 关于OB 对称点为P 2，当点P 在直线NM 上运动时，△OP 1P 2的面积最小值为_____参考答案1．(1)抛物线的表达式为：223y x x =--；(2)POD S ∆有最大值，当14m =时，其最大值为4916；(3) Q -或(或1122⎛-+- ⎝⎭或⎝⎭．【分析】（1）函数的表达式为：y=a （x+1）（x-3），将点D 坐标代入上式，即可求解；（2）设点()2,23P m m m --，求出32OG m =+，根据()12POD D P S OG x x ∆=⨯-1(32)(2)2m m =+-2132m m =-++，利用二次函数的性质即可求解；（3）分∠ACB=∠BOQ 、∠BAC=∠BOQ ，两种情况分别求解，通过角的关系，确定直线OQ 倾斜角，进而求解．【详解】解：(1)函数的表达式为：(1)(3)y a x x =+-，将点D 坐标代入上式并解得：1a =，故抛物线的表达式为：223y x x =--…①；(2)设直线PD 与y 轴交于点G ，设点()2,23P m m m --，将点P 、D 的坐标代入一次函数表达式：y sx t =+并解得，直线PD 的表达式为：32y mx m =--，则32OG m =+， ()12POD D P S OG x x ∆=⨯-1(32)(2)2m m =+-2132m m =-++，∵10-<，故POD S ∆有最大值，当14m =时，其最大值为4916； (3)∵3OB OC ==，∴45OCB OBC ︒∠=∠=，∵ABC OBE ∠=∠，故OBE ∆与ABC ∆相似时，分为两种情况：①当ACB BOQ ∠=∠时，4AB =，BC =AC = 过点A 作AH ⊥BC 与点H ，1122ABC S AH BC AB OC ∆=⨯⨯=⨯，解得：AH =，∴CH 则tan 2ACB ∠=，则直线OQ 的表达式为： 2 y x =-…②，联立①②并解得：x =故点Q -或(； ②BAC BOQ ∠=∠时，3tan 3tan 1OC BAC BOQ OA ∠====∠，则直线OQ 的表达式为： 3 y x =-…③，联立①③并解得：x =故点13,22Q ⎛⎫-+- ⎪ ⎪⎝⎭或1322⎛⎫-+ ⎪ ⎪⎝⎭；综上，点Q -或(或1122⎛-+- ⎝⎭或13,22⎛-+ ⎝⎭．【点睛】本题考查的是二次函数综合运用，涉及到解直角三角形、三角形相似、面积的计算等，其中（3），要注意分类求解，避免遗漏．2．（1）抛物线的解析式为223y x x =--，直线AB 的解析式为3y x =-，（2）(2,1)-或33(22+-+．（3）当32m =时，PAB∆面积的最大值是278，此时P 点坐标为33(,)22-．【解析】【分析】（1）将(0,3)A -、(3,0)B 两点坐标分别代入二次函数的解析式和一次函数解析式即可求解；（2）先求出C 点坐标和E 点坐标，则2CE =，分两种情况讨论：①若点M 在x 轴下方，四边形CEMN 为平行四边形，则CE MN =，②若点M 在x 轴上方，四边形CENM 为平行四边形，则CE MN =，设(,3)M a a -，则2(,23)N a a a --，可分别得到方程求出点M 的坐标；（3）如图，作//PG y 轴交直线AB 于点G ，设2(,23)P m m m --，则(,3)G m m -，可由12PAB S PG OB ∆=，得到m 的表达式，利用二次函数求最值问题配方即可．【详解】解：（1）∵抛物线22y ax x c =-+经过(0,3)A -、(3,0)B 两点，∴9603a c c -+=⎧⎨=-⎩，∴13a c =⎧⎨=-⎩，∴抛物线的解析式为223y x x =--， ∵直线y kx b =+经过(0,3)A -、(3,0)B 两点，∴303k b b +=⎧⎨=-⎩，解得：k 1b 3=⎧⎨=-⎩，∴直线AB 的解析式为3y x =-，（2）∵2223(1)4y x x x =--=--，∴抛物线的顶点C 的坐标为(1,4)-， ∵//CE y 轴， ∴(1,2)E -， ∴2CE =，①如图，若点M 在x 轴下方，四边形CEMN 为平行四边形，则CE MN =，设(,3)M a a -，则2(,23)N a a a --，∴223(23)3MN a a a a a =----=-+， ∴232a a -+=，解得：2a =，1a =（舍去）， ∴(2,1)M -，②如图，若点M 在x 轴上方，四边形CENM 为平行四边形，则CE MN =，设(,3)M a a -，则2(,23)N a a a --，∴2223(3)3MN a a a a a =----=-， ∴232a a -=，解得：a =，a =（舍去），∴M ，综合可得M 点的坐标为(2,1)-或33(22+-+．（3）如图，作//PG y 轴交直线AB 于点G ，设2(,23)P m m m --，则(,3)G m m -， ∴223(23)3PG m m m m m =----=-+， ∴22211393327(3)3()2222228PAB PGA PGB S S S PG OB m m m m m ∆∆∆=+==⨯-+⨯=-+=--+， ∴当32m =时，PAB ∆面积的最大值是278，此时P 点坐标为33(,)22-．【点睛】本题是二次函数综合题，考查了待定系数法求函数解析式，二次函数求最值问题，以及二次函数与平行四边形、三角形面积有关的问题．3．①265y x x =-+-；②当2t =时，△PBE 的面积最大，最大值为；③点N 的横坐标为：4或52+或52．【解析】【分析】①点B 、C 在直线为y x n =+上，则B （﹣n ，0）、C （0，n ），点A （1，0）在抛物线上，所以250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩，解得1a =-，6b =，因此抛物线解析式：265y x x =-+-； ②先求出点P 到BC 的高h为sin 45)BP t ︒=-，于是211)22)22PBE S BE h t t t ∆=⋅=-⨯=-+2t =时，△PBE 的面积最大，最大值为③由①知，BC 所在直线为：5y x =-，所以点A 到直线BC的距离d =N 作x轴的垂线交直线BC 于点P ，交x 轴于点H ．设()2,65N m m m -+-，则(,0)H m 、(,5)P m m -，易证△PQN为等腰直角三角形，即NQ PQ ==4PN =，Ⅰ．4NH HP +=，所以265(5)4m m m -+---=解得11m =（舍去），24m =，Ⅱ．4NH HP +=，()25654m m m ---+-=解得152m +=，252m =（舍去），Ⅲ．4NH HP -=，()265[(5)]4m m m --+----=，解得152m =（舍去），252m =．【详解】解：①∵点B 、C 在直线为y x n =+上， ∴B（﹣n ，0）、C （0，n ）， ∵点A （1，0）在抛物线上，∴250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩， ∴1a =-，6b =，∴抛物线解析式：265y x x =-+-；②由题意，得，4PB t =-，2BE t =，由①知，45OBC ︒∠=，∴点P 到BC 的高h 为sin 45)2BP t ︒=-，∴211(4)2(2)2222PBE S BE h t t t ∆=⋅=⨯-⨯=-+当2t =时，△PBE 的面积最大，最大值为③由①知，BC 所在直线为：5y x =-，∴点A 到直线BC 的距离d =过点N 作x 轴的垂线交直线BC 于点P ，交x 轴于点H ．设()2,65N m m m -+-，则(,0)H m 、(,5)P m m -，易证△PQN 为等腰直角三角形，即NQ PQ ==∴4PN =，Ⅰ．4NH HP +=，∴265(5)4m m m -+---=解得11m =，24m =，∵点A 、M 、N 、Q 为顶点的四边形是平行四边形，∴4m =；Ⅱ．4NH HP +=，∴()25654m m m ---+-=解得152m =，252m =， ∵点A 、M 、N 、Q 为顶点的四边形是平行四边形，5m >，∴m =，Ⅲ．4NH HP -=，∴()265[(5)]4m m m --+----=，解得1m =，2m = ∵点A 、M 、N 、Q 为顶点的四边形是平行四边形，0m <，∴52m =，综上所述，若点A 、M 、N 、Q 为顶点的四边形是平行四边形，点N 的横坐标为：4或52或52-．【点睛】本题考查了二次函数，熟练掌握二次函数的性质、平行四边形的判定与性质是解题的关键．4．（1）224233y x x =-++，对称轴1x =；（2）11,4D ⎛⎫ ⎪⎝⎭；（3）面积有最大值是4948，755,424E ⎛⎫ ⎪⎝⎭；（4）存在点M 使得以,,,B C M N 为顶点的四边形是平行四边形，()2,2M 或104,3M ⎛⎫- ⎪⎝⎭或102,3M ⎛⎫-- ⎪⎝⎭. 【解析】【分析】（1）将点A （-1，0），B （3，0）代入y=ax 2+bx+2即可；（2）过点D 作DG ⊥y 轴于G ，作DH ⊥x 轴于H ，设点D （1，y ），在Rt △CGD 中，CD 2=CG 2+GD 2=（2-y ）2+1，在Rt △BHD 中，BD 2=BH 2+HD 2=4+y 2，可以证明CD=BD ，即可求y 的值；（3）过点E 作EQ ⊥y 轴于点Q ，过点F 作直线FR ⊥y 轴于R ，过点E 作FP ⊥FR 于P ，证明四边形QRPE 是矩形，根据S △CEF =S 矩形QRPE -S △CRF -S △EFP ，代入边即可；（4）根据平行四边形对边平行且相等的性质可以得到存在点M 使得以B ，C ，M ，N 为顶点的四边形是平行四边形，点M （2，2）或M （4，-103）或M （-2，-103）；【详解】解：（1）将点()()1,0,3,0A B -代入22y ax bx =++，可得24,33a b =-=， 224233y x x ∴=-++； ∴对称轴1x =；（2）如图1：过点D 作DG y ⊥轴于G ，作DH x ⊥轴于H ，设点()1,D y ，()()0,2,3,0C B ，∴在Rt CGD ∆中，()222221CD CG GD y =+=-+，∴在Rt BHD ∆中，22224BD BH HD y =+=+，在BCD ∆中，DCB CBD ∠=∠CD BD ∴=，22CD BD ∴=()22214y y ∴-+=+14y ∴=， 11,4D ⎛⎫∴ ⎪⎝⎭；（3）如图2：过点E 作EQ y ⊥轴于点Q ，过点F 作直线FR y ⊥轴于R ，过点E 作FP FR ⊥于P ，90EQR QRP RPE ︒∴∠=∠=∠=，∴四边形QRPE 是矩形，CEF CRF EFP QRPE S S S S ∆∆∆=--矩形，()()(),,0,2,1,1E x y C F ，111•222CEF SEQ QR EQ QC CR RF FP EP ∴=⋅-⨯⋅-⋅- ()()()()111121111222CEF S x y x y x y ∆∴=----⨯⨯--- 224233y x x =-++， 21736CEF S x x ∆∴=-+ ∴当74x =时，面积有最大值是4948，此时755,424E ⎛⎫ ⎪⎝⎭；（4）存在点M 使得以,,,B C M N 为顶点的四边形是平行四边形，设()()1,,,N n M x y ，①四边形CMNB 是平行四边形时，1322x += 2x ∴=-102,3M ⎛⎫∴-- ⎪⎝⎭ ②四边形CNBM 时平行四边形时，3122x += 2x ∴=，()2,2M ∴；③四边形CNNB 时平行四边形时，1322x +=， 4x ∴=，104,3M ⎛⎫∴- ⎪⎝⎭；综上所述：()2,2M 或104,3M ⎛⎫-⎪⎝⎭或102,3M ⎛⎫-- ⎪⎝⎭；【点睛】本题考查了待定系数法求二次函数解析式，二次函数的图象及性质，勾股定理，平行四边形的判定与性质，及分类讨论的数学思想.熟练掌握二次函数的性质、灵活运用勾股定理求边长、掌握平行四边形的判定方法是解题的关键．5．（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492．【分析】（1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【详解】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =，点P ，M 是CD ，DE 的中点， //PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =，利用三角形的中位线得，12PN BD =，12PM CE =， PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠，90BAC ∠=︒，90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，AM ∴=在Rt ABC ∆中，10AB AC ==，AN =MN ∴==最大，22211114922242PMN S PM MN ∆∴==⨯=⨯=最大．方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==， PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大．【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．6．（1）y ＝（x ﹣1）2；（2）点C 的坐标为（2，1）；（3）1【分析】（1）将点（3，4）代入解析式求得a 的值即可；（2）设点C 的坐标为（x 0，y 0），其中y 0＝（x 0﹣1）2，作CF ⊥x 轴，证△BDO ∽△DCF 得BO DF DO CF=，即1＝00x 1y -＝()01x 1-，据此求得x 0的值即可得；（3）过点D 作x 轴的垂线交直线PQ 于点G ，则DG ＝4，根据S △PDQ ＝12DG•MN 列出关于k 的等式求解可得．【详解】解：（1）将点（3，4）代入解析式，得：4a ＝4，解得：a ＝1，所以抛物线解析式为y ＝（x ﹣1）2；（2）由（1）知点D 坐标为（1，0），设点C 的坐标为（x 0，y 0），（x 0＞1、y 0＞0），则y 0＝（x 0﹣1）2，如图1，过点C 作CF ⊥x 轴，∴∠BOD ＝∠DFC ＝90°，∠DCF+∠CDF ＝90°，∵∠BDC ＝90°，∴∠BDO+∠CDF ＝90°，∴∠BDO ＝∠DCF ，∴△BDO ∽△DCF ， ∴BO DF DO CF=， ∴1＝00x 1y -＝()01x 1-，解得：x 0＝2，此时y 0＝1，∴点C 的坐标为（2，1）．（3）设点P 的坐标为（x 1，y 1），点Q 为（x 2，y 2），（其中x 1＜1＜x 2，y 1＞0，y 2＞0），如图2，分别过点P 、Q 作x 轴的垂线，垂足分别为M 、N ，由y=(x-1)2 ，y=kx+1-k ，得x 2﹣（2+k ）x+k ＝0．∴x 1+x 2＝2+k ，x 1•x 2＝k ．∴MN ＝|x 1﹣x 2|＝|2﹣k|．则过点D作x轴的垂线交直线PQ于点G，则点G的坐标为（1，1），所以DG＝1，∴S△PDQ＝12DG•MN＝12×1×|x1﹣x2|＝12|2﹣k|，∴当k＝0时，S△PDQ取得最小值1．【点睛】本题主要考查二次函数的综合问题，解题的关键是熟练掌握待定系数法求函数解析式、相似三角形的判定与性质及一元二次方程根与系数的关系等知识点．7．（1）y＝﹣x2+2x+3；（2）t＝32时，△PAE的面积最大，最大值是278；（3）t的值为1．【分析】（1）由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；（2）由抛物线的对称性可求得E点坐标，从而可求得直线EA的解析式，作PM∥y轴，交直线AE于点M，则可用t表示出PM的长，从而可表示出△PAE的面积，再利用二次函数的性质可求得其最大值即可；（3）由题意可知有∠PAE＝90°或∠APE＝90°两种情况，当∠PAE＝90°时，作PG⊥y轴，利用等腰直角三角形的性质可得到关于t的方程，可求得t的值；当∠APE＝90°时，作PK⊥x 轴，AQ⊥PK，则可证得△PKE∽△AQP，利用相似三角形的性质可得到关于t的方程，可求得t的值．【详解】解：（1）由题意得：0 4233a b ca b cc-+=⎧⎪++=⎨⎪=⎩，解得：123abc=-⎧⎪=⎨⎪=⎩，∴抛物线解析式为y＝﹣x2+2x+3；（2）∵A（0，3），D（2，3），∴抛物线对称轴为x＝1，∴E（3，0），设直线AE的解析式为y＝kx+3，∴3k+3＝0，解得，k＝﹣1，∴直线AE的解析式为y＝﹣x+3，如图1，作PM∥y轴，交直线AE于点M，设P（t，﹣t2+2t+3），M（t，﹣t+3），∴PM＝﹣t2+2t+3+t﹣3＝﹣t2+3t，∴12PAE PMA PMES S S PM OE=+=⋅＝()21332t t⨯⨯-+＝23327228t⎛⎫--+⎪⎝⎭，∴t＝32时，△PAE的面积最大，最大值是278．（3）由图可知∠PEA≠90°，∴只能有∠PAE＝90°或∠APE＝90°，①当∠PAE＝90°时，如图2，作PG⊥y轴，∵OA＝OE，∴∠OAE＝∠OEA＝45°，∴∠PAG＝∠APG＝45°，∴PG＝AG，∴t ＝﹣t 2+2t+3﹣3，即﹣t 2+t ＝0，解得t ＝1或t ＝0（舍去）， ②当∠APE ＝90°时，如图3，作PK ⊥x 轴，AQ ⊥PK ，则PK ＝﹣t 2+2t+3，AQ ＝t ，KE ＝3﹣t ，PQ ＝﹣t 2+2t+3﹣3＝﹣t 2+2t ， ∵∠APQ+∠KPE ＝∠APQ+∠PAQ ＝90°， ∴∠PAQ ＝∠KPE ，且∠PKE ＝∠PQA ， ∴△PKE ∽△AQP ， ∴PK KEAQ PQ=， ∴222332t t t t t t-++-=-+，即t 2﹣t ﹣1＝0，解得：t 或t 0（舍去），综上可知存在满足条件的点P ，t 的值为1或12+．【点睛】本题考查了待定系数法求二次函数解析式、二次函数与几何面积最值问题以及二次函数与特殊三角形的问题，解题的关键是灵活运用二次函数的性质及几何知识．8．(1)成立，证明见解析；（2）DF=DE ．（3）当x=0时，y 最小值【分析】（1）如图1，连接BD ．根据题干条件首先证明∠ADF=∠BDE ，然后证明△ADF ≌△BDE （ASA ），得DF=DE ；（2）如图2，连接BD ．根据题干条件首先证明∠ADF=∠BDE ，然后证明△ADF ≌△BDE（ASA ），得DF=DE ；（3）根据（2）中的△ADF ≌△BDE 得到：S △ADF =S △BDE ，AF=BE ．所以△DEF 的面积转化为：y=S △BEF +S △ABD ．据此列出y 关于x 的二次函数，通过求二次函数的最值来求y 的最小值．【详解】（1）DF=DE ．理由如下：如图1，连接BD ．∵四边形ABCD 是菱形， ∴AD=AB ．又∵∠A=60°，∴△ABD 是等边三角形， ∴AD=BD ，∠ADB=60°， ∴∠DBE=∠A=60° ∵∠EDF=60°， ∴∠ADF=∠BDE ． ∵在△ADF 与△BDE 中，ADF BDE AD BDA DBE ∠=⎧∠=∠=∠⎪⎨⎪⎩， ∴△ADF ≌△BDE （ASA ）， ∴DF=DE ；（2）DF=DE ．理由如下：如图2，连接BD ．∵四边形ABCD 是菱形， ∴AD=AB ．又∵∠A=60°，∴△ABD 是等边三角形， ∴AD=BD ，∠ADB=60°， ∴∠DBE=∠A=60° ∵∠EDF=60°， ∴∠ADF=∠BDE ． ∵在△ADF 与△BDE 中，ADF BDE AD BDA DBE ∠=⎧∠=∠=∠⎪⎨⎪⎩， ∴△ADF ≌△BDE （ASA ）， ∴DF=DE ；（3）由（2）知，△ADF ≌△BDE ．则S △ADF =S △BDE ，AF=BE=x ．依题意得：y=S △BEF +S △ABD =12（2+x ）xsin60°+12×2×2sin60°x+1）2．即x+1）20， ∴该抛物线的开口方向向上， ∴当x=0即点E 、B 重合时，y 最小值=29．（1）=；（2）证明见解析；（3）60°，BD=CE ；（4）90°，AM+BD=CM ；（5）7【分析】（1）由DE ∥BC ，得到DB ECAB AC=，结合AB=AC ，得到DB=EC ；（2）由旋转得到的结论判断出△DAB ≌△EAC ，得到DB=CE ；（3）根据等边三角形的性质和全等三角形的判定定理证明△DAB ≌△EAC ，根据全等三角形的性质求出结论；（4）根据全等三角形的判定和性质和等腰直角三角形的性质即可得到结论；（5）根据旋转的过程中△ADE 的面积始终保持不变，而在旋转的过程中，△ADC 的AC 始终保持不变，即可．【详解】[初步感知]（1）∵DE ∥BC ， ∴DB ECAB AC=， ∵AB=AC ， ∴DB=EC ，故答案为：=，（2）成立．理由：由旋转性质可知∠DAB=∠EAC ，在△DAB 和△EAC 中AD AE DAB EAC AB AC ⎪∠⎪⎩∠⎧⎨＝＝＝， ∴△DAB ≌△EAC （SAS ）， ∴DB=CE ；[深入探究]（3）如图③，设AB ，CD 交于O ，∵△ABC 和△ADE 都是等边三角形， ∴AD=AE ，AB=AC ，∠DAE=∠BAC=60°，∴∠DAB=∠EAC ，在△DAB 和△EAC 中AD AE DAB EAC AB AC ⎪∠⎪⎩∠⎧⎨＝＝＝， ∴△DAB ≌△EAC （SAS ）， ∴DB=CE ，∠ABD=∠ACE ， ∵∠BOD=∠AOC ， ∴∠BDC=∠BAC=60°；（4）∵△DAE 是等腰直角三角形， ∴∠AED=45°， ∴∠AEC=135°，在△DAB 和△EAC 中AD AE DAB EAC AB AC ⎪∠⎪⎩∠⎧⎨＝＝＝， ∴△DAB ≌△EAC （SAS ）， ∴∠ADB=∠AEC=135°，BD=CE ， ∵∠ADE=45°，∴∠BDC=∠ADB-∠ADE=90°，∵△ADE 都是等腰直角三角形，AM 为△ADE 中DE 边上的高， ∴AM=EM=MD ， ∴AM+BD=CM ；故答案为：90°，AM+BD=CM ；【拓展提升】（5）如图，由旋转可知，在旋转的过程中△ADE 的面积始终保持不变， △ADE 与△ADC 面积的和达到最大， ∴△ADC 面积最大，∵在旋转的过程中，AC 始终保持不变， ∴要△ADC 面积最大， ∴点D 到AC 的距离最大， ∴DA ⊥AC ，∴△ADE 与△ADC 面积的和达到的最大为2+12×AC×AD=5+2=7，故答案为7．【点睛】此题是几何变换综合题，主要考查了旋转和全等三角形的性质和判定，旋转过程中面积变化分析，解本题的关键是三角形全等的判定．10．（1）m=6，()2,0；（2）当a=1时，ODE 面积的最大值为278【分析】（1）将点34,2A ⎛⎫ ⎪⎝⎭代入反比例函数解析式求出m ，根据坐标中点公式求出点C 的横坐标即可；（2）由AC 两点坐标求出直线AB 的解析式为3342y x =-，设D 坐标为33,(04)42D a a a ⎛⎫-<≤ ⎪⎝⎭，则6,E a a ⎛⎫⎪⎝⎭，进而得到2327(1)88ODESa =--+，即可解答【详解】解：（1）把点34,2A ⎛⎫ ⎪⎝⎭代入反比例函数(0)m y x x=>，得：324m =，解得：m=6，∵A 点横坐标为：4，B 点横坐标为0，故C 点横坐标为：4022+=，故答案为：6，(2,0)；（2）设直线AB 对应的函数表达式为y kx b =+．将34,2A ⎛⎫ ⎪⎝⎭，(2,0)C 代入得34220k b k b ⎧+=⎪⎨⎪+=⎩，解得3432k b ⎧=⎪⎪⎨⎪=-⎪⎩．所以直线AB 对应的函数表达式为3342y x =-．因为点D 在线段AB 上，可设33,(04)42D a a a ⎛⎫-<≤ ⎪⎝⎭，因为//DE y 轴，交反比例函数图像于点E ．所以6,E a a ⎛⎫ ⎪⎝⎭．所以221633333273(1)2428488ODESa a a a a a ⎛⎫=⋅⋅-+=-++=--+ ⎪⎝⎭．所以当a =1时，ODE 面积的最大值为278．【点睛】本题考查了函数与几何综合，涉及了待定系数法求函数解析式、三角形面积、坐标中点求法、二次函数的应用等知识点，解题关键是用函数解析式表示三角形面积．11．（1）y ＝﹣x 2+2x +3；（2）S 与m 的函数表达式是S ＝252m m --，S 的最大值是258，此时动点M 的坐标是（52，74）；（3）点M在整个运动过程中用时最少是3秒．【分析】（1）首先求出B 点的坐标，根据B 点的坐标即可计算出二次函数的a 值，进而即可计算出二次函数的解析式;。

一题多解三角形面积最大值问题

一题多解三角形面积最大值问题作者：王忠俊来源：《新校园(下)》2017年第01期摘要：二次函数图象抛物线中动点围成三角形面积最大值问题是初中数学最难的一章，是初高中数学知识的衔接点，它考查学生数形结合的思想，是代数与几何有机结合，题型灵活性强、难度大。

本文介绍一题多解的方法，以此提高学生解决此类问题的能力。

关键词：二次函数；三角形面积；最大值；函数图象数学来源于生活，服务于生活。

如何有效地利用数学知识解决实际问题，需要一定的智慧。

相对而言，二次函数在初中数学中是较难的一章，但它的作用却非常大，学好二次函数可以解决生活中的许多实际问题，从而得到意想不到的收获。

例如图1，在平面直角坐标系中，已知抛物线经过A（-1，0），B（3，0），C（0，3）三点：1.求抛物线解析式；2.若点P为第一象限内抛物线上一动点，求△PBC面积最大值时点P的坐标。

分析：1.将三点代入一般式y=ax2+bx+c，求出a、b、c得解析式：y=-x2+2x+32.通过二次函数图象进行分析，具体有三种方法。

一、分补法S△PBC=S△POC+S△POB-S△OBC设P点横坐标为m，则纵坐标为-m2+2m+3，即P（m，-m2+2m+3）S△PBC=S△POC+S△POB-S△OBC=12OC×PD+12OB×PE-12OB×OC=12×3×m+12×3×（-m2+2m+3）-12×3×3=-32m2+92m关于m的二次函数开口向下，有最大值；m=-922×-32=32时，S△BCP面积最大，-m2+2m+3=154，点P32，154。

图1图2二、分割法过P点向x轴作垂线，交BC于点Q，交x轴于点I，PQ越长，△PBC面积越大。

（说明：以动线PQ为底边，△CPQ的高与△BPQ的高的和是固定值3，所以PQ越长，△PBC面积越大。

）设P（m，-m2+2m+3），直线BC解析式为y=-x+3，Q点的横坐标为m，则纵坐标为-m+3，PQ=（-m2+2m+3）-（-m+3）=-m2+3m图3S△PBC=S△CPQ+S△BPQ=12PQ×CH+12PQ×BI=12PQ（CH+BI）=12PQ×BOS△PBC=12（-m2+3m）×3=-32m2+92m同样可得m=32时，S△BCP面积最大，点P为32，154。

二次函数中有关三角形面积的计算

二次函数中有关三角形面积的计算
例1 如图,经过点A(8,0)、B(0,4)的抛物线y=ax c
x 27
2（1）求抛物线的解析式；
（2）若一条与y 轴重合的直线l 以每秒2个单位长度的速度向右平移，分别交线段OA 、AB 和抛物线于点C 、D 和点E ，连接EA 、EB 、AB ，设直线l 移动的时间为t （0<t<4）秒，当t 为何值时，△ABE 的面积最大，最大面积是多少？
2.如图，已知抛物线c
y2经过A、B两点，A、B两点的坐标分
x
bx
别为（-1，0）、（0，-3）
（1）求抛物线的解析式；
（2）点E为抛物线的顶点，点C为抛物线与x 轴的另一个交点，点D为y 轴上一点，若DC=DE，求点D的坐标；
（3）在（2）的条件下，若点P为第四象限内抛物线上一动点，点P的横坐标为m , △DCP面积为S，求S关于m的函数关系式，并求出S的最大值。

第五讲+抛物线中三角形的面积问题

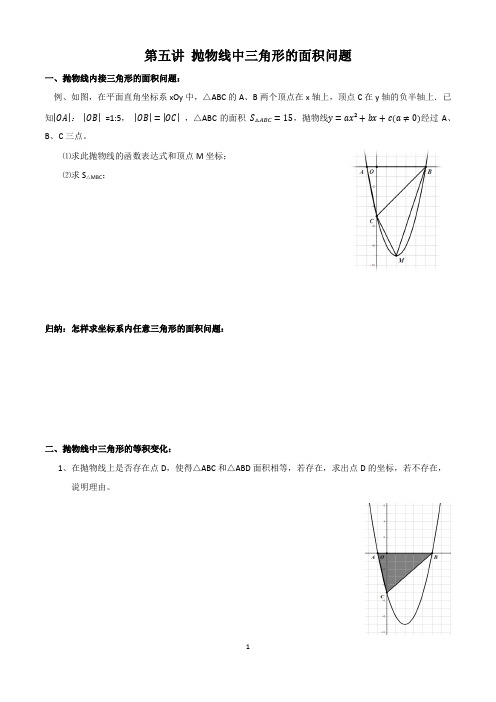
第五讲抛物线中三角形的面积问题一、抛物线内接三角形的面积问题：例、如图，在平面直角坐标系xOy中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知|OA|：|OB|=1:5，|OB|=|OC|，△ABC的面积S△ABC=15，抛物线y=ax²+bx+c(a≠0)经过A、B、C三点。

⑴求此抛物线的函数表达式和顶点M坐标；⑵求S△MBC；归纳：怎样求坐标系内任意三角形的面积问题：二、抛物线中三角形的等积变化：1、在抛物线上是否存在点D，使得△ABC和△ABD面积相等，若存在，求出点D的坐标，若不存在，说明理由。

2、在抛物线上是否存在点E，使得△ABC和△BCE面积相等，若存在，求出点E的坐标，若不存在，说明理由。

S△ABC。

若存在，求出点M的坐标；若不存在，请说明理由3、在抛物线上是否存在点M，使S△MBC= 134、（2011成都）在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为7√？若存在，求出点M的坐标；若不存在，说明理由.5、点P（2，-3）是抛物线对称轴上的一点，在线段OC上有一动点M，以每秒2个单位的速度从O向C 运动，（不与点O，C重合），过点M作MH∥BC，交X轴于点H，设点M的运动时间为t秒，试把△PMH 的面积S表示成t的函数，当t为何值时，S有最大值，并求出最大值；6、在抛物线的对称轴上有一点P的纵坐标为5，在直线上BC求一点M使得S△PBM∶S△ABC=1:5.7、在直线BC下方抛物线上是否存在一个点F，使得△BCF的面积最大，若存在，求出点F的坐标，并求出最大面积，若不存在，说明理由。

练习：1、如图，抛物线与x轴交于A（x1，0）、B（x2，0）两点，且x1＜x2，与y轴交于点C（0，-4），其中x1，x2是方程x2-4x-12=0的两个根．（1）求A、B两点坐标；（2）求抛物线的解析式；（3）点M是线段AB上的一个动点（不与A、B两点重合），过点M作MN∥BC，交AC于点N，连接CM，在M点运动时，△CMN的面积是否存在最大值？若存在，求出△CMN面积最大时点M的坐标；若不存在，请说明理由．2、（2010玉溪）如图，在平面直角坐标系中，点A的坐标为（1，△AOB（1）求点B的坐标；（2）求过点A、O、B的抛物线的解析式；（4）在（2）中x轴下方的抛物线上是否存在一点P，过点P作x轴的垂线，交直线AB于点D，线段OD 把△AOB分成两个三角形．使其中一个三角形面积与四边形BPOD面积比为2：3 ？若存在，求出点P的坐标；若不存在，请说明理由．yAB。

三角形标准二次抛物线的面积形心公式必须牢记

Ai
第6章
6.3 结构位移计算的一般公式单位荷载法
一、虚功方程的意义及应用
[uN
vQ
m
]BI AI

(i)
(i)
BI ( pu qv m)ds
Ai
BI (N Q M )ds ( i ) Ai
1、意义：虚功方程的每一项都是广义力与广义位移的乘积。
第6章
4、上述各种位移统称为“广义位移”。与广义位移相对应的力称为“广义力”。
二、计算结构位移的目的
1、刚度验算：电动吊车梁跨中挠度 fmax≤l/600。
2、计算超静定结构必须考虑位移条件。
3、施工技术的需要。
P
P
P
P
P
P/2
P/2
c
c CV
4、结构的动力计算和稳定分析中，都常需计算结构的位移。
复习思考
（1）图乘法的适用条件是什么？
（2）图乘法的公式是怎样的？说明各符号的物理意义。如何图乘？
（3）使用图乘法时应注意什么问题？
第6章
图乘法应满足的条件 1、杆件为等截面直杆。 2、EI为常数。 3、MK、MP图形中至少有一个为直线图形。
返回
第6章
图乘法公式及其物理意义
ห้องสมุดไป่ตู้
y
MP(x)
d
dx
T P
4、虚功对应的两种状态及应满足的条件：
（1）虚力状态：为求真实位移而虚设的力状态，它应满足静力平衡条件。
（2）虚位移状态：为求真实力而虚设的位移状态，它应满足变形协调条。
第6章
二、变形杆件体系的虚功方程
“杆件AB处于一静力可能的力状态，设另有一与其无关的几何可能的位移状态，则前者的外力由于后者的位移所做的虚外功T等于前者的切割面内力由于后者的变形所作的虚变形功V”。

例谈抛物线中三角形面积最值问题的解法

知识导航三角形面积的最值问题一般比较简单，但抛物线中的三角形面积最值问题却较为复杂，这类三角形的面积常与动点的坐标有关，因而此类问题的难度一般较大.解题时需灵活运用平面几何知识、函数的图象和性质、基本不等式、三角形的性质和面积公式、抛物线的定义和性质等知识.那么，如何解答此类问题呢？一般可运用构造法和分割法来求解.下面我们结合实例来进行探讨.一、构造法构造法是指通过添加辅助线，构造出三角形的底或高，以能直接利用三角形的面积公式求得问题的答案.通常，可过三角形的一个顶点作x 轴或y 轴的垂线，使其与三角形的一条边相交，从而确定三角形的底或高，这样就可以根据三角形的面积公式进行计算了.例1.如图1所示，在平面直角坐标系中，点B 的坐标为（-3，-4），线段OB 绕原点逆时针旋转后与x 轴的正半轴重合，点B 的对应点为A ，如果点P 是抛物线上的一个动点且在x 轴的上方，当点P 运动到什么位置时，△PAB 的面积最大？解析：由于点P 是抛物线上的一个动点，所以我们无法确定△PAB 的形状，也就无法确定三角形的高和底，不能直接利用三角形的面积公式来求解，需要构造出三角形的高和底.可过点P 作PE 垂直x 轴交AB 于点E ，则S △ABP =S △APE +S △BPE ，此时△APE 的底为PE ，高为A 到PE 的距离；△BPE 的底为PE ，高为B 到PE 的距离，而A 、B 到PE 的距离之和为A 、B 的横坐标之差.当|PE |最大时，△PAB 的面积最大.借助两点间的距离公式和二次函数的性质便可顺利求得△PAB 面积的最值.解：过P 点作PE ⊥x 轴交AB 于点E ，如图1所示，设点P 坐标为(m ，-16m 2+56m )，可得到点E 的坐标为（m ，-12m -52）.所以S △ABP =S △APE +S △BPE =12|PE |×8=4|PE |=4×(-16m 2+56m -12m +52)=-23m 2+43m +10，当m =-b 2a=1，S △ABP 取最大值，即S △ABP =（43）2-4×(-23)×104×(-23)=323.所以，当P 点坐标为（1，23）时，S △ABP 取最大值，且最大面积是323.一般地，当三角形底边的长为定值时，三角形的高与面积成正比，高越大其面积越大，只要求得高的最大值，便可求得面积的最大值.二、分割法当求三角形的面积遇到困难时，我们可以运用分割法，将三角形分割为两个或者两个以上的简单几何图形，借助简单几何图形的面积公式求得三角形的面积.当求抛物线中三角形面积的最值时，我们也可以将三角形分割为几个小三角形、平行四边形、梯形等，然后分别利用三角形、平行四边形、梯形面积公式求出各图形的面积，最后综合所得的结果即可求得三角形面积的表达式，借助函数的性质、基本不等式来求得最值.例2.如图2，已知抛物线y =-x 2+bx +c 与直线相交于A （-1，0），C （2，3）两点，与y 轴交于点N ，其顶点为D ，若点P 是该抛物线上位于直线AC 上方的一个动点，试求△APC 面积的最大值.解：，如图2，过点P 作PQ 垂直x 轴于点H ，交AC 于点Q ，过点C 作CG 垂直x 轴于点G .设Q （x ,x +1），则P （x ,-x 2+2x +3），则S △APC =S △APE +S 直角梯形PHGC -S △AGC=12(x +1)(-x 2+2x +3)+12(-x 2+2x +3)(2-x )-12×3×3=-32(x -12)2+278所以△APC 面积的最大值为278.由于点P 是该抛物线上位于直线AC 上方的一个动点，所以我们无法确定△APC 的形状，可以采用分割法来求解.将△APC 分割成两个小三角形△APE 、△AGC 和一个直角梯形形PHGC ，从而把三角形分割成几个规则的简单几何图形，运用三角形的面积公式和梯形的面积公式便可快速求得△APC 面积的表达式，将其视为关于x 的二次函数，借助二次函数的性质就能求得△APC 面积的最大值.总之，同学们在解答抛物线中三角形面积最值问题时，可根据三角形的特点和已知条件合理添加辅助线，构造出三角形的底或高，也可以将三角形分割为几个简单的几何图形，借助简单几何图形的面积公式来求解.在求得三角形面积的表达式后，可借助函数的性质或基本不等式来求得最值.（作者单位：江苏省盐城中学）陈巧巧图1图238。

抛物线焦点弦三角形的面积(抛物线的弦相关的问题)

抛物线焦点弦三角形的面积本内容主要研究抛物线焦点弦三角形的面积.以抛物线的顶点及其焦点弦的两个端点为顶点的三角形，称为抛物线的焦点弦三角形.给出三种抛物线焦点弦三角形的面积公式，根据已知条件合理选择.例：过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,O 为坐标原点.若|AF |=3,则△AOB 的面积为( ) A.22 B.2 C.322 D.22解：抛物线的焦点F 的坐标为(1,0),设A (x 1,y 1),B (x 2,y 2)(y 1>0,y 2<0),因为|AF |=3,所以x 1+1=3,x 1=2,代入抛物线方程得122y =,故A (2,22),所以直线AB 的方程为22(1)=-y x ,由22220,4x y y x⎧--=⎪⎨=⎪⎩得2240y --=. 所以122y y +y 1y 2=－4,则22121219||1()[()4]222AB y y y y ⎡⎤=++-=⎢⎥⎣⎦.又可求得圆点O 到直线AB 的距离为223,故△AOB 的面积为1922322222S =⨯⨯=.[一题多解]设∠AFx =θ(0<θ<π)及|BF |=m ,则点A 到准线l :x =－1的距离为3,得1323cos cos 3θθ=+⇔=,又 232cos()1cos 2,=+π-⇔===+m m BF m m θθ,△AOB 的面积为113||||sin 1(3)22233S OF AB θ=⨯⨯⨯=⨯⨯+⨯=. 答案：C注意：前法是解决此类问题的通法,一般通过求弦长和点到直线的距离进行求解,后法则有一定的技巧性.整理：B AOF过抛物线22(0)y px p =>的焦点F 作直线交抛物线于A ,B 两点,且11(,)A x y ，22(,)B x y ，O 为坐标原点.则△AOB 的面积为(1)121||||2S OF y y =⨯⨯-=; (2) 1||2=⨯⨯S AB d ,d 为点O 到直线AB 的距离; (3)11sin sin 22OAB OBF OAF S S S OF BF OF AF θθ∆∆∆=+=⋅⋅+⋅⋅()11sin sin 22OF AF BF OF AB θθ=⋅+=⋅⋅其中∠AFx =θ(0<θ<π).再看一个例题：例：设F 为抛物线C :y 2=4x 的焦点，过F 且倾斜角为60°的直线交C 于A ，B 两点，O 为坐标原点，则△OAB 的面积为( )解：抛物线的焦点F 的坐标为(1,0),设A (x 1,y 1),B (x 2,y 2)(y 1>0,y 2<0), ∠AFx =60°所以直线AB 的方程为3(1)=-y x ,由23(1),4⎧=-⎪⎨=⎪⎩y x y x得231020-+=x x . 所以12103x x +=,则1216||3AB x x p =++=. 又11sin sin 22OAB OBF OAF S S S OF BF OF AF θθ∆∆∆=+=⋅⋅+⋅⋅ ()11sin sin 22OF AF BF OF AB θθ=⋅+=⋅⋅ 故△AOB 的面积为116341=32323∆=⨯⨯⨯OAB S总结：1.根据已知条件合理选择我三种抛物线焦点弦三角形的面积公式.2.掌握抛物线的焦点弦长计算方法.练习：1.已知抛物线C 的顶点在坐标原点O ,焦点为F (1,0),经过点F 的直线l 与抛物线C 相交于A 、B 两点.(Ⅰ)求抛物线C 的标准方程;(Ⅱ)若△AOB 的面积为4,求|AB |.2. 设F 为抛物线C :y 2=3x 的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，O 为坐标原点，则△OAB 的面积为( )C.6332D.943. 已知抛物线y 2=2px (p >0)的焦点为F ,准线为l ,过点F 的直线交抛物线于A ,B 两点,过点A 作准线l 的垂线,垂足为E ,当A 点坐标为(3,y 0)时,△AEF 为正三角形,则此时△OAB 的面积为( )A.4C.3D.3。

抛物线上动点p的三角形面积-定义说明解析

抛物线上动点p的三角形面积-概述说明以及解释1.引言1.1 概述在数学中，抛物线是一种具有特定形状的曲线，其形状类似于开口向上的U形。

它是由一个定点和一条直线（称为准线或直线段）确定的曲线，其中定点被称为焦点，准线表示为直线段AB。

抛物线是一种非常重要的曲线，广泛应用于物理学、工程学等领域。

本文将围绕着抛物线上的动点P展开讨论。

在抛物线上，动点P具有自由运动的能力，并且可以在曲线上任意选择不同的位置。

我们将重点研究动点P所形成的三角形的面积，并探究如何计算这个面积。

通过研究动点P在抛物线上的运动以及三角形的面积计算方法，我们可以深入理解抛物线曲线的几何特征，并且可以应用这些知识解决实际问题。

同时，对抛物线上动点P的三角形面积的意义和应用也将在文章中进行探讨。

最后，在总结部分我们将对本文的内容进行总结，并展望未来对抛物线相关问题的研究方向。

本文旨在提供一个清晰的抛物线上动点P三角形面积的计算方法，并希望读者通过阅读本文能够对抛物线的几何特性有更深入的了解。

【1.2 文章结构】本文将分为以下几个部分来探讨抛物线上动点P的三角形面积的计算方法。

每个部分的内容如下：（1）引言：在引言部分，我们将概述本文的主题和研究对象，并介绍文章的结构和目的。

同时，我们也将对抛物线的定义和性质进行简要介绍。

（2）正文：在正文部分，我们将分为三个小节来详细阐述抛物线上动点P的三角形面积的计算方法。

首先，我们会介绍抛物线的定义和性质，包括其数学表达和几何特征。

然后，我们会讨论动点P在抛物线上的运动规律，这一部分将包括动点P在不同位置的情况下的三角形面积的变化规律。

最后，我们将介绍具体的计算方法，包括利用向量、坐标和参数方程等不同的方法来计算动点P的三角形面积。

（3）结论：在结论部分，我们将对前面的研究结果进行总结，并探讨抛物线上动点P的三角形面积的一些意义和应用。

同时，我们也会展望未来可能的研究方向和可进一步发展的领域。

通过以上的安排，我们旨在全面而系统地介绍抛物线上动点P的三角形面积的计算方法，并探讨其应用的可能性，为相关领域的研究和实践提供一定的参考和指导。

【高考数学经典题型】抛物线与圆,求三角形面积最值(一题多解)

1/ 5试题出处：2020届湖北省“荆、荆、襄、宜”四地七校联考（改编）抛物线与圆，求三角形面积最值若点P 是抛物线22x y =上的动点,点,M N 在x 轴上，圆22(1)1x y +−=内切于,PMN ∆求PMN ∆面积的最小值. 答案：8解法一：动点设一个参数，利用勾股定理列等式如图,不妨设点2(2,2)P t t (1)t >,圆心为C ,两切点为,D E .分别过点P 作PH x ⊥,作PG x 轴,过点M 作x 轴垂线与PG 交于点G ，且,OM m ON n ==. 在Rt PCE ∆中，由勾股定理得，22222244(21)14PE PC CE t t t =−=+−−=，即22PE t =.在Rt PNH ∆中，由勾股定理得222,PN PH NH =+ 即()224224(2)t n t t n +=+−，可得1t n t =+. 在Rt PMG ∆中，由勾股定理得222,PM PG GM =+ 即()224224(2)t m t t m +=++，可得1t m t =−. 42224122()21121PMNt S m n t t t t ∆∴=⋅+⋅==−− 又2242111111()244t t t −=−−+≥ ∴当22t =时，PMN S ∆有最小值8.2 / 5解法二：动点设两个参数，利用直线与圆相切列等式设00(,),(,0),(,0)P x y M a N b ，其中02y >且a b <.∴直线PN 的方程为：00()y y x b x b=−−，直线PN 与圆相切，∴圆心(0,1)到直线PN 的距离为1， ∴1=∴()2000220y b x b y −+−= 同理可得，()2000220y a x a y −+−=.∴实数,a b 是关于x 的一元二次方程()2000220y x x x y −+−=的两根， ∴0000222x a b y y a b y −⎧+=⎪−⎪⎨−⎪⋅=⎪−⎩, ∴()()()22220002044842x y y a b a b ab y +−−=+−=−,2002x y =∴()()2202042y a b y −=−，0022y a b y −=− 20000014()248222PMNy S b a y y y y ∆∴=⋅−⋅==−++≥−− ∴当04y =时，PMN S ∆有最小值8.解法三：动点设两个参数，利用内切圆性质列等式设点00(,),(,0),(,0)P x y M a N b −圆心为(0,1)C ,两切点为,D E . 在Rt PCD ∆中，PD =2002x y =，∴0PD y = PM PD DM PD MO =+=+3 / 5∴0y a =+，化简得20000002()x y MO a y x y x ===−−同理，可得20000002()x y NO b y x y x ===++0000000011()()22PMN y y S MO NO y y y x y x ∆∴=⋅+⋅=+⋅−+ 32000220000424822PMNy y S y y x y y ∆∴===−++≥−−− ∴当04y =时，PMN S ∆有最小值8.解法四：动点设一个参数、再设直线斜率，利用直线与圆相切列等式设21(,)(2)2P m m m >，直线,PM PN 的斜率一定存在，分别设其为12,k k ，则直线PM 的方程为：211()2y m k x m −=−，1=，化简得：22342111(1)(2)04m k m m k m m −+−+−=……..① 同理可得：22342221(1)(2)04m k m m k m m −+−+−=……..②∴实数12,k k 是关于x 的一元二次方程223421(1)(2)04m x m m x m m −+−+−=的两根， ∴31224212221141m m k k m m m k k m ⎧−+=⎪−⎪⎨−⎪⋅=⎪−⎩，分别令方程①，②中的0y =，得21,2M m x m k =−22,2N m x m k =−222112121122M N k k m m MN x x k k k k −=−=⋅−=2412121228PMNk k m m S MN k k ∆−∴=⋅⋅=⋅48m =4/ 5化简得4222116(48)82824PMNm S m m m ∆==−++≥−− ∴当28m =时，PMN S ∆有最小值8.解法五：动点设两个参数，利用内切圆性质列等式如图，设00(,),P x y 切点分别为,D E 且PMN ∆的内切圆半径1r = 则011()22PMN S MN y PM PN MN r ∆=⋅=++⋅1()2PM PN MN =++ 1()2PMN S OM PE ON PE MN MN PE ∆∴=++++=+MN MN ==0MN y MN =+≥012y MN ∴⋅≥ 016y MN ∴⋅≥0182PMN S y MN ∆∴=⋅≥ ∴PMN S ∆有最小值8.评论与赏析：圆锥曲线中求三角形面积的最值一直是考试的热点、难点问题.解法1跳出了解析几何的大量计算，两次用勾股定理将线段长用动点中的参数表示出.解法2利用直线与圆相切的性质及韦达定理找到线段整体与动点中的参数的关系.解法3利用三角形内切圆的性质和坐标运算将线段长用动点中的参数表示出来.解法4设切线斜率利用韦达定理找到线段与动点中的参数的关系.解法5巧妙利用三角形内切圆性质、这一题的数量特点及基本不等式直接得出面积的最值.5 / 5推广：过抛物线22(0)x py p =>上一点000(,)(2)P x y y p ≥作圆222:()C x y p p +−=的两条切线，分别与x 轴交于,M N 两点，则PMN ∆的最小值为28p .相似题：在平面直角坐标系xoy 中，过点2(2,21)P t t +作圆22:(1)(1)1E x y −+−=的两条切线,PM PN ，切点分别为,M N .当(1,)t ∈+∞时，设切线,PM PN 与y 轴分别交于点,,B C 求PBC ∆面积的最小值. 答案：8。

抛物线中的三角形问题

抛物线中的三角形问题在数学中，抛物线是一种二次曲线，其形状类似于开口朝上的弧线。

抛物线与三角形之间有着紧密的联系，本文将探讨抛物线中的三角形问题。

一、抛物线的定义与性质抛物线是指平面上满足平方差关系的点的集合。

一般来说，抛物线可以由二次方程的图像表示，常见的抛物线方程形式包括标准型、顶点型等。

根据方程的不同形式，可以得到抛物线的不同性质，如焦点、顶点、对称轴等。

二、抛物线中的三角形问题抛物线与三角形之间存在着丰富的几何关系，其中一些经典问题如下：问题一：抛物线上的三点确定一个三角形，该三角形的面积如何计算？解析：设抛物线的方程为y = ax^2 + bx + c，并选取抛物线上三个点A(x1, y1)、B(x2, y2)、C(x3, y3)。

根据三点确定一个三角形，可以利用三角形的高度与底边长度来计算面积。

首先，我们可以通过求解方程组得到顶点的坐标(xv, yv) = (-b/2a, f(-b/2a))，其中f(x)是抛物线的函数。

然后，利用向量的几何性质，求出三角形的高度h，再计算底边长度d，最后利用面积公式S = 0.5 * d * h计算出面积。

问题二：给定一个抛物线和一个点P，如何确定在抛物线上选择两个点形成的三角形，使其面积最大？解析：设抛物线的方程为y = ax^2 + bx + c，设点P的坐标为(xp, yp)。

对于以点P为顶点的抛物线上的任意一条直线，其倾斜角为θ，直线的方程可以表示为y = tanθ * x + C，其中C是常数。

当直线与抛物线相交时，可将两个方程联立求解，得到交点的坐标(x1, y1)和(x2,y2)。

然后，利用这两个交点与点P形成的三角形面积公式S = 0.5 *|x1y2 - x2y1 - x1yp + xpy1 + x2yp - xpy2|，求解出最大的面积。

问题三：已知一个抛物线，如何确定两个定点，使其与抛物线上的另一个点形成的三角形周长最小？解析：设抛物线的方程为y = ax^2 + bx + c。

抛物线中三角形面积最大值问题的解法攻略

抛物线中三角形面积最大值问题的解法攻略
抛物线中三角形面积最大值问题是很多数学教师都会遇到的问题。

求得抛物线中三角形面
积最大值，就先要分析抛物线的基本参数，因为抛物线是一种比较复杂的曲线，需要对其
有一定的了解才可以解答此问题。

抛物线的标准方程为y=ax2+bx+c，a为抛物线的系数，a>0，抛物线呈转弯向上，a<0，呈
转弯向下；b表示抛物线的开口方向，b>0，表示开口向右，b<0，表示开口向左。

因此，
得知抛物线在某一瞬间的顶点位置，以及抛物线的开口位置，就可以求出抛物线上三角形
的端点位置。

在定位了三角形端点位置后，只需要利用海伦公式就可以求出三角形面积：S=√[p(p-
a)(p-b)(p-c)]其中p=(a+b+c)/2，a,b,c分别为三角形的三边长。

最后，把求的所有的三角形面积按从大到小排列，那么最大的面积就是抛物线中三角形面
积最大值了。

抛物线中三角形面积最大值问题，要求求解者要完全把握和理解方程抛物线的特征，以及
三角形的基本定义，之后再结合海伦公式求出最大面积。

海伦公式和抛物线方程是相结合，那么广大教师和学生并不必对此感到困惑，只需要把这两个概念理解深入，就能在一定的
时间内得出满意的答案。

抛物线弓形三角形的面积最大值的探究

抛物线弓形三角形的面积最大值的探究作者：杨建来源：《中学数学杂志(初中版)》2011年第04期我们知道在圆中,弦与弦所对弧组成的图形叫弓形,类似于此,在抛物线中把直线被抛物线截得的线段叫抛物线的弦,抛物线的弦与所对的封闭抛物线组成的图形叫抛物线的弓形,抛物线的弦的两个端点与弓形上任一点组成的三角形叫抛物线的弓形三角形.大凡是抛物线的综合题,绝大多数都会出现这样的图形.对这个图形的考查,是初中的重点和难点,又是初中高中知识的衔接点,更重要的它又是中考的热点问题,历年的中考题中都有类似的中考压轴题出现.本文着重探究抛物线弓形三角形面积最大值的计算的几种方法．2011浙江宁波市第26题,是一道压轴题,其中包含这样的问题：如图1,已知抛物线y=14x2-12x上有两点B(6,6)、O(0,0),N是直线OB右下方抛物线上的任意一点,试求△OBN面积的最大值以及点N的坐标．由于学生积累知识经验不同,从不同角度来探究这个问题,就会得出如下几种不同的解法．1 补型术如果已知直角坐标系中的三个点的坐标,同学们会用割补法来求三角形的面积,本题是要求三角形的面积,我们会想到把三角形OBN通过作垂线,构成规则的三角形来处理这个问题.于是得到第一种解法：如图1,分别过点N,B作x轴的垂线,垂足分别为G,H.设N (x,14x2-12x),则S△BON=S△OBH-S△ONG-S梯形NGHB=12×OH×BH-12×OG×NG-12×(NG+BH)×GH=12×6×6-12×x×(14x2-12x)-12×(14x2-12x+6)×(6-x)=-34x2+92x=-34(x-3)2+274(0所以当x=3时,△BON面积最大,最大值为274,此时点N的坐标为(3,34)．这一种解法,运用了割补法,建立起二次函数的模型,通过二次函数的极值求出抛物线弓形三角形面积的最大值．2 分割法考虑到点N是抛物线弓形上的动点,过这一点作y轴的平行线,就把三角形分成两个部分,所求三角形的面积就等于这两个三角形的面积之和,于是得到如下的解法：如图2,过N作x轴的垂线NG,垂足为G,交OB于点Q,过B作BH⊥x轴于H,设N(x,14x2-12x),由于B点坐标为(6,6),由直线OB的解析式为：y=x.则Q(x,x),于是S△BON=S△QON+S△BQN=12×QN×OG+12×QN×GH=12×QN×(OG+GH)=12×QN×OH=12x-(14x2-12x)×6=-34x2+92x=-34(x-3)2+274(0所以当x=3时,△BON面积最大,最大值为274,此时点N的坐标为(3,34)．3 切线法如果过动点N作弦OB的平行线,则直线与弓形中的抛物线有两个交点,改变点N的位置,则交点之间的距离发生变化,点N到OB的距离也发生变化,两交点之间的距离越小,弓形三角形的面积越大,当两交点之间的距离为零时,弓形三角形的面积最大,于是得到第三种解法：如图3,过点N作OB的平行线ST,当直线ST与抛物线y=14x2-12x相切时,点N到直线OB 的距离最大,△OBN的面积最大．设直线ST的解析式为：y=x+m．解方程组：y=x+my=14x2-12x消去y,得：14x2-32x-m=0，即x2-6x-4m=0,如果ST与抛物线相切,则(-6)2+16m=0,解得m=-94．方程x2-6x-4m=0变为x2-6x+9=0,解得x=3,点N的坐标为(3,34)．有了点O、B、N三点坐标,可求得△OBN面积为274．这一种解法对学生要求比较高,看上去运用了的高中的知识,对初中生来讲超纲了,但仔细想想,我们把圆的切线的知识迁移到抛物线上来,对学业成绩较好的学生来说是可行的,也是有必要的.在我自己的教学实践中,师生一起探究,运用第三种方法来解此题,学生欣喜若狂后,总能品味到数学的深度和广度,大大激发了学生探究数学的兴趣.再说,如果离开的迁移的数学思想,数学学起来就枯燥无味．作者简介：杨建,男,1976年生,江苏海安人,中学一级教师,主要研究中学数学高效课堂教学和教学模式的探讨,曾获南通市初中青年教师优秀课评比一等奖,江苏省初中青年教师优秀课评比一等奖,2010年获县“高效课堂先进个人”,采用的导学案教学模式被同行广泛采用和认同,获得学生好评且教学成绩显著,在省级以上刊物发表论文多篇．。

抛物线中三角形面积最值问题的七种求解策略

图10的正切函数值，则问题便可逐步解决.解析在上找点£，使= 由外角定理，知•①易知直线S C 解析式为y-6.设 £(m ，m -6)，由 fi (6,0)，D (2, -8)，则 B £2 = (m -6)' + (m -6)2, ED 2 = (m - 2)2 + (m + 2)2.由 B £ = £7)，知（;n -6)2 +(m -6)2 = (m -2)2 +(m + 2)2，解得 m =|，即 £(夺，-爭)•又易知 C £>2 + fiC 2 = fi /)2,则乙BCD = 90。

.qi n由 C (0, -6),£(|■，-$)，Z )(2, -8),知 CD =2^",C £=^,P J lain^CED = j .②由①②和 A C(?B = 2 A CflD ,则 tan Z _ C(?B =当点<?在点B 左侧时,(),（ -8,0).当点<?在点B 右侧时,(?2(8,0).综上，(?（ -8,0)或(8,0).从上面题目的解答可以发现:抛物线中角的存在性问题，一般运用角的特殊性及坐标条件构造基本图形，并运用图形的性质，进行推理得出有关相等线段，并表示出有关点的坐标,代入二次函数或一次函数的解析式，或运用勾股定理计算作答.在解答过程中，既要构造几何图形，根据几何直观和几何性质、定理理性分析、推理，还要运用函数与方程知识进行计算和数据分析.综合运用几何推理、函数与方程思想等多方面技能，有较强的综合性及创新探究意识，可以很好地考查学生的综合素养[2].“问题是数学的心脏”，数学的真正组成部分是问题和解，在学习过程中，在一定学习范围或主题内，围绕一定目标或某一中心问题，按照一定的逻辑结构精心设计一组问题，即为“一题多问”，采用“一题多问” 的方式，用同一道题目将多个知识点表现出来，可以帮助学生梳理旧知，形成网络，将数学技能及方法得以综合运用.“一题多问”引导学生从不同角度、不同方位进行不同层次的思考，提高学生分析问题、解决问题和提出问题的能力，可以让学生跳出“题海”，提高解题效益，提升数学素养.参考文献：[1 ]罗峻，段利芳.一次函数与反比例函数图象相交的性质之证明与运用[J ]•数理化学习（初中版），2018(12) :23 -28.[2]罗峻，段利芳.当完美正方形偶遇美丽的45度角[J ]. 理科考试研究（初中），2019,26(22) :29 -32.(收稿日期：2020 -09 -21 )抛物线中三角形面积最值问题的七种求鮮策略段昆山(易县教育局教研室河北保定074200)摘要：以二次函数为栽体，结合几何图形求面积最值问题具有难度大、综合性强，区分度高的特表.本文以某地初三上学期期末考试试卷最后一题为例，谈一谈此类问题的七种求解策略.关键词：最值问题；转化；面积；求解策略纵观近年各地中考试卷，以二次函数为载体，结合几何图形求面积最值问题的题型是各地中考的高频考点之一.这类试题综合运用多种数学思想方法, 不仅考查了二次函数与三角形面积的相关知识，又为后续学习高中知识奠定了基础.1试题呈现题目如图1,在平面直角坐标系中，抛物线y = <M c 2 +心+2(a #0)与.t 轴交于两点（点4在点B作者简介:段昆山（1976 -),男，河北保定人，本科，中学一级教师，研究方向：数学教育.的左侧），与y 轴交于点C ，抛物线经过点£»(- 2，- 3) 和点£(3，2)，点P 是第一象限抛物线上的一个动点.(1) 求抛物线的表达式；(2) 当A B P C 的面积取最大值时，求A fiP C 面积及点P 的坐标.2试题解析 2. 1第（1)问解析将点A £的坐标代人函数表达式，得丄_ 了，3_r故抛物线的表达式为y +2.2.2第（2)问解析 2. 2. 1分割法三角形面积通常用面积公式（底乘髙的一半）来求,在平面直角坐标系中求斜三角形的面积用这个公式难度大，那如何求呢？那就需要运用转化的方法把斜三角形分割成底与高分别与坐标轴平行的三角形，充分利用定点的横纵坐标来求三角形面积•如图2,过点P 作丄;c 轴于点F ，A fiP C 被分割成两个三角形，即A //P C 和所以SA B P C =S 娜c + SAW ，过点C 作C Z )丄/^于点Z ),过点B 作BE _L PF 于点 E ，S A H P C =夸PH x CD.解法1如图3,连接S C ，过点P 作W ///y 轴交S C 于点//，将点C ，S 代入一次函数表达式，可得直线的表达式为y = -+ 2.设点 P U ，+如 +2),则点+2).所以 S A P C B =-％2 +4%.f 4a -2b +2 =-3, 19a +36+2=2,解得,根据二次函数性质，利用配方法，当* = 2时， S apm 的最大值为4.故当A B P C 的面积取最大值时，点P (2,3),S A P C B 二 4.2.2.2补形法在平面直角坐标系中求斜三角形的面积不仅可以运用分割法，也可以转换思路，用补形的方法把不规则图形转化成规则图形，将斜三角形面积转化成矩形面积减去三角形的面积，再充分利用定点的横纵坐标，就可以求斜三角形面积了 • 图4如图4,过点P 作轴，垂足为点£,过点5作 fiZ )丄/)£，垂足为点£»，贝丨J 四边形为矩形•所以S APCB = S 酿形OBOE - S A P E (：一 S APDB _ S a (X b .解法2如图5,过点P 作轴，垂足为点£，过点B 作丄/)£；,垂足为点/)，所以四边形 OBD £为矩形.所以 s A PC b 二 S 四边形〇B D e : — S A P E (： - S _ s A 0C B 二(-+ ^-x + 2) x 4 - (- -^-x2 + -^-x ) x x x ~y - (4-x) x (- ~^x2 ++ 2) x -^--4=-x ~+ 4x.根据二次函数性质，利用配方法，当x =2时，^ A P C B的最大值为4.故当A B P C的面积取最大值时，点P(2,3),■5而=4_2.2.3铅垂法如图6，过A P S C的顶点分别作出水平线的垂线, 外侧两条垂线间的距离叫做水平宽.中间的垂线与 S C相交于点£，线段就叫做铅垂高.如图7,因为S apcb=S A peb+S&PCE二y PE x EU +j PE x EF =所以铅垂法本质上也是分割法.，铅垂高I图7解法3如图8,过点P作P//丄;c轴交B C于点//，设点，-+ 2)，则点 //(x，+ 2)•所以11,312^apcb =^2^~^2X+Y"x+2+y*-2)x4=-x+4x.在直线B C上.根据平行线间的距离相等，所以ABPC 和A B fiC的高相等，底是BC.所以厶B P C和A B//C的面积相等.求A B P C的面积就转化成求A//£C的面积.解法4如图10,过点Z3作户////沉交7轴于点所以 S&P C B= S A C H B-将点c，B代人一次函数表达式，可得直线C B的表达式为y= - 士;'：+ 2.因为W///S C,所以设直线P//的表达式为y根据二次函数性质，利用配方法，当x= 2时，S apos的最大值为4.故当A S P C的面积取得最大值时，点P(2,3),^ APCB=^*2.2.4平行线法如图9，W///B C，点//，P在直线W/上，点5，CH E P设点户(％，- y i2 + y x+ 2)，所以-2 =-—x +b,b22+ ~z~x + 2 + ~z~x2,//C=-y^2+2x+2-2TT22x.x2 +2x+PJflll S A P C B = ^H C xOB =-x2-t-4x.利用配方法，当x= 2时,S A P(：iB的最大值为4.故当A S P C的面积取得最大值时，点P(2,3)，^ APCB=^*2.2.5相似法如图11，求三角形的面积可以用面积公式足为点D.所以BC= VOC2 + OB2 = 7^5.求三角形的面积只要求出高就可以了.高如何求呢？我们仔细观察图形发现丄SO,所以™//y轴.所以 APHC= AOCB•因为P E±B C，所以 APEH=厶COB.所以ABOC w•所以g = I I所以= PH^~° .这样就可以求出高了.解法5如图12,过点P作丄BC,垂足为点 £，PD丄50交 SC 于点由题意，5C= VOC1+ OB2 = 2/5 ,APEH^ABOC.m i0BPH = BC'因为+ 2x,PE PH x BOBC¥(-士解法6如图13,过点P作P£//fiC,因为将点C,B代入一次函数表达式，同理可得直线C Z?的表达式为;^=-士尤+2.所以设直线的表达式为y=-+ 6.1,j=- y x + b-H i2+3+2y= - ~z~x+ ~zrx+1.1/22整理，得-士尤2 +~|~尤+2=-士a:+ 6 一士丨2 +2% +2-6=0.所以 A =4-4 x(-士）x(2 -6) =8 -26 =0.解得6=4_所以点P(2,3)，A P C fi最大值为4 .2.2.7中点法如图14,设直线S C与抛物线交于B,C两点，直线B C的解析式可设为y= ^+ n，抛物线解析式可设为y= m2 +心+ C，求其交点坐标就是联立两解析式’所以 ax2 + + c = n w c + n_ 整理，得[y= mx+ n.ax2+ (b- m)x+ c- n= 0. fffVJs x, + x2 = ——因为直a%2 +2a〇，所以 S A P C fl =^^(-士尤2 +2幻x2V^x士 =-x2 + 4x.利用配方法，当* =2时，S A P efl的最大值为4.故当A S P C的面积取得最大值时，点P(2,3),^ APCB-4-2.2.6切线法如图13,若使点P在抛物线上，S A P eB最大，则需使P£//BC，且与抛物线有且只有一个交点才能使心^8最大.因为底B C确定，只要高最大.因为点P 在抛物线上与抛物线有且只有一个交点时，SC 边上的高才最大.线B C平移到与抛物线只有一个交点时，七即& = 也就是％所以过点P作*轴的垂线，垂足M是O S的中点.所以当抛物线被直线 B C所截,P为抛物线上一动点（此时点P为线段SC 与抛物线所组成的封闭图形上抛物线上一点）丄%轴于点m,交s c于点yv,当点yv为b c中点时，s APC8 的面积有最大值.解法7如图15,过点尸作P////S C,所以& = X B+X C^所以点P 坐标为（2,3).所以=S 四边形"W /Y ;+ S APMB ""SA O R Cx (2+ 3) x 2+冬 x 2x 3_4-x 2x 4=4.' 2 2此法适用于填空、选择或验证.3感悟解法这一类以二次函数为载体，结合几何图形求面积最值问题的题型涉及的知识面多、难度大、综合性强, 要想顺利解答此类问题，必须抓住以下几点.（1)立足转化，抓住动点（设动为定）.合理构造辅助线，以转化思想为基本出发点，抓住动点，根据不同思路过动点作平行，或作垂直等辅助线，把复杂问题转化为简单问题，把未知问题转换为已知问题.（2)数形结合，设出动点坐标.充分挖掘已知条件与隐含条件，要明确角边在数量关系变化中哪些是保持不变的量，哪些是变化的量.哪些是变化的量.这需要在充分理解的基础上，进行多方位思考、多角度着手、多层次探索m ，利用相似、面积公式、根与系数的关系等知识，表示出相关的数量关系.（3)根据相关的数量关系，把面积表示成一个含有某未知量的二次函数关系式，然后利用公式法或配方法求出最值.参考文献：[1] 段昆山.构造图形求准确数形结合找临界一•一类“儿何”型新定义压轴题解法浅析[J ].中学数学教学，2020(01) ：79 -80.[2]周威.圆锥曲线中几个特殊三角形面积最值问题探究[J ].理科考试研究,2020(09) :25 - 27.(收稿日期：2020 _08-15)指向“深度学习”的教学课壹教学策略李娜沈南山(合肥师范学院数学与统计学院安徽合肥230601)摘要：从认知结构观点来看，“深度学习”是一种理解性的学习，注重学习思维的批利性、学习内容的整合性、知识体系的建构性和知识学习的迁移性.指向深度学习的数学课堂教学需要深入追问学什么、怎么学、学得怎么样三个教学本源问题，其教学策略应当注重数学知识对象的多重表征、数学学习脚手架的适时搭建、数学学习问题的逻辑引领、数学学习方法的积极反思等.关键词：初中数学；深度学习；教学策略1 “深度学习”的基本特征“深度学习”（Deep Learning )最早由美国学者 Marlon 等人于1976年提出的一个比较性学习概念，是相对于孤立记忆和非批判性接受知识的浅层学习 (Surface Learning )而言的.随后国内外学者对“深度学习”开展理论与实践研究，其基本内涵是在教师引领下,学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程，并在这个过程中学生掌握学科的核心知识，理解学习的过程,把握学科的本质及思想方法，形成积极的内在学习动机、高级的社会性感情、积极的态度、正确的价值观等m .“深度学习”的基本特征蕴含理论和实践两个层面.理论上，从知识结构观点来看，深度学习是基于学基金项目：合肥师范学院研究生创新基金项目“深度学习理念下初中数学课堂问题提出的教学实践研究”（项目编号:2020yjs 033).作者简介：李娜（ 1995 -)，女，安徽阜阳人，硕士研究生，研究方向：数学教育；沈南山（1964 -),男，安徽六安人，博士，教授，研究方向：数学课程与教学论研究.。

中考数学中二次函数压轴题分类总结

二次函数的压轴题分类复习一、抛物线关于三角形面积问题例题二次函数k m x y ++=2)(的图象，其顶点坐标为M(1，4-). （1）求出图象与x 轴的交点A ，B 的坐标；（2）在二次函数的图象上是否存在点P ，使MAB PAB S S ∆∆=45,若存在，求出P 点的坐标；若不存在，请说明理由；（3）将二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线)1(<+=b b x y 与此图象有两个公共点时，b 的取值范围.练习：1. 如图．平面直角坐标系xOy 中，点A 的坐标为（－2，2），点B 的坐标为（6，6），抛物线经过A 、O 、B 三点，线段AB 交y 轴与点E ．（1）求点E 的坐标；（2）求抛物线的函数解析式；（3）点F 为线段OB 上的一个动点（不与O 、B 重合），直线EF 与抛物线交与M 、N 两点（点N 在y 轴右侧），连结ON 、BN ，当点F 在线段OB 上运动时，求∆BON 的面积的最大值，并求出此时点N 的坐标；yBAMEF2. 如图，已知抛物线4212++-=x x y 交x 轴的正半轴于点A ，交y 轴于点B ．（1）求A 、B 两点的坐标，并求直线AB 的解析式；（2）设),(y x P （0>x ）是直线x y =上的一点，Q 是OP 的中点（O 是原点），以PQ 为对角线作正方形PEQF ．若正方形PEQF 与直线AB 有公共点，求x 的取值范围；（3）在（2）的条件下，记正方形PEQF 与△OAB 公共部分的面积为S ，求S 关于x 的函数解析式，并探究S 的最大值．二、抛物线中线段长度最小问题例题如图，对称轴为直线x ＝－1的抛物线y ＝ax 2＋bx ＋c (a ≠0)与x 轴相交于A 、B 两点，其中点A 的坐标为（－3，0）．（1）求点B 的坐标；（2）已知a =1，C 为抛物线与y 轴的交点．①若点P 在抛物线上，且S △POC ＝4S △BOC ，求点P 的坐标；②设点Q 是线段AC 上的动点，作QD ⊥x 轴，QD 交抛物线于点D ，求线段QD 长度的最大值．OABP EQFxyEN MDCBAOyx练习：1. 如图， Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上，O 为坐标原点，A 、B 两点的坐标分别为（3-，0）、（0，4），抛物线223y x bx c =++经过B 点，且顶点在直线52x =上．（1）求抛物线对应的函数关系式；（2）若△DCE 是由△ABO 沿x 轴向右平移得到的，当四边形ABCD 是菱形时，试判断点C 和点D 是否在该抛物线上，并说明理由；（3）若M 点是CD 所在直线下方该抛物线上的一个动点，过点M 作MN 平行于y 轴交CD 于点N ．设点M 的横坐标为t ，MN 的长度为l ．求l 与t 之间的函数关系式，并求l 取最大值时，点M 的坐标．三、抛物线与线段和最小的问题例题如图，已知抛物线()()()120y x x a a a=-+>与x 轴交于点B 、C ，与y 轴交于点E ，且点B 在点C 的左侧．（1）若抛物线过点M （﹣2，﹣2），求实数a 的值；（2）在（1）的条件下，解答下列问题； ①求出△BCE 的面积；②在抛物线的对称轴上找一点H ，使CH+EH 的值最小，直接写出点H 的坐标．练习：1. 如图，已知二次函数24y ax x c =-+的图象与坐标轴交于点A （-1， 0）和点B （0，-5）．（1）求该二次函数的解析式；（2）已知该函数图象的对称轴上存在一点P ，使得△ABP2. 如图，抛物线y = ax 2 + bx + 4与x 轴的两个交点分别为A （－4，0）、B （2，0），与y 轴交于点C ，顶点为D ．E （1，2）为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别交于F 、G ．（1）求抛物线的函数解析式，并写出顶点D 的坐标；（2）在直线EF 上求一点H ，使△CDH 的周长最小，并求出H 的坐标；（3）若点K 在x 轴上方的抛物线上运动，当K 运动到什么位置时，△EFK 的面积最大？并求出最大面积．四、抛物线与等腰三角形例题：已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．(1)求抛物线的函数关系式；(2)设点P是直线l上的一个动点，当△P AC的周长最小时，求点P的坐标；(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．练习：1. .如图，抛物线与x轴交于A、B两点，与y轴交C点，点A的坐标为（2，0），点C的坐标为（0，3）它的对称轴是直线12 x=-（1）求抛物线的解析式；（2）M是线段AB上的任意一点，当△MBC为等腰三角形时，求M点的坐标．2. 如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n（m＜n）分别是方程x2﹣2x﹣3=0的两根．（1）求抛物线的解析式；（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E两点（点D在y轴右侧），连接OD、BD．①当△OPC为等腰三角形时，求点P的坐标；②求△BOD 面积的最大值，并写出此时点D的坐标．3. 如图，已知抛物线于x轴交于A（－1，0）、B（3，0）两点，与y轴交于点C（0，3）.（1）求抛物线的解析式；（2）设抛物线的顶点为D，在其对称轴的右侧的抛物线上是否存在点P，使得△PDC是等腰三角形，若存在，求出符合条件的点P的坐标；若不存在，请说明理由：（3）若点M是抛物线上一点，以B、C、D、M为顶点的四边形是直角梯形，试求出点M的坐标。

专题01 抛物线中的三角形面积问题-高中数学破题致胜微方法(抛物线中的面积、角度及参数范围问题)

专题01 抛物线中的三角形面积问题本内容主要研究抛物线中的面积问题.直线和抛物线相交，围成的平面图形种类很多，尤其以三角形最为常见，三角形面积的计算是重点，其他平面图形的面积可以转化为三角形面积的计算.直线和抛物线相交时联立方程，利用弦长公式，或者点线距公式，结合韦达定理解决问题.先看例题：例：已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A ,B 两点,|AB |=12,P 为C的准线上一点,则△ABP 的面积为( )A.18B.24C.36D.48解：由题意可知,|AB |是该抛物线的通径,即|AB |=2p =12,且准线上的点到AB 的距离即为焦准距,即为p =6,所以△ABP 的面积为1126362⨯⨯=. 所以本题选C整理：三角形面积（1）过x 轴上一定点H 的直线l 与抛物线交于A 、B 两点，求AOB S ∆1212AOB S OH y y ∆=- （2）过y 轴上一定点H 的直线l 与抛物线交于A 、B 两点，求AOB S ∆1212AOB S OH x x ∆=- （3）弦任意，点任意12S ∆=弦长×点线距注意：要着正确的画出图形，进而求解.再看两个例题，加深印象例：在直角坐标系xOy 中,直线l 过抛物线y 2=4x 的焦点F ,且与该抛物线相交于A ,B 两点,其中点A 在x 轴上方.若直线l 的倾斜角为60°,则△OAF 的面积为________. 解：据题意可知直线AB 方程为3(1)y x =-,与抛物线方程联立消元得243403y y --=, 解得23A y =,故11||123322AOF A S OF y =⨯=⨯⨯=△.再看一个例题：例：已知抛物线y＝ax2－1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为________.解；本小题主要考查抛物线的方程及有关性质.由题意知a＞0,C(0,－1),原方程变形为21 (1)x ya=+,所以1||4OCa=,即14a=,则||4ABa==,所以14122ABCS=⨯⨯=△.总结：1.根据直线和抛物线的位置关系，如果弦任意，选择公式12S∆=弦长×点线距.2.根据直线和抛物线的位置关系，如果直线过x轴上一定点H，设直线方程x my t=+，代入抛物线方程计算弦长.3.根据直线和抛物线的位置关系，如果直线过y轴上一定点H，设直线方程y kx m=+，代入抛物线方程计算弦长.练习：1. O 为坐标原点,F 为抛物线C :2y =的焦点,P 为C 上一点,若||PF =则△POF的面积为( )A.2B.C.D.42. 连接抛物线x 2=4y 的焦点F 与点M (1,0)所得的线段与抛物线交于点A ,设点O 为坐标原点,则三角形OAM 的面积为( )A.1-B.32-C.1D.32+3. 设斜率为2的直线l 过抛物线y 2=ax (a ≠0)的焦点F ,且和y 轴交于点A .若△OAF (O 为坐标原点)的面积为4,则抛物线方程为( )A.y 2=±4xB.y 2=±8xC.y 2=4xD.y 2=8x。

抛物线内接三角形的一个面积公式（初三）

抛物线内接三角形的一个面积公式（初三）
左效平
【期刊名称】《数理天地：初中版》
【年(卷),期】2017(000)012
【摘要】三个顶点都在同一条抛物线上的三角形叫做抛物线的内接三角形.
【总页数】2页(P21-22)
【作者】左效平
【作者单位】山东省沂源县徐家庄中心学校,256116
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.过抛物线顶点的内接三角形的一个性质
2.抛物线内接直角三角形一个性质的研究及其应用
3.抛物线上任一点均存在其一个内接正三角形的证明
4.抛物线外切三角形与内接三角形的一个性质
5.再证抛物线内接三角形的面积公式
因版权原因，仅展示原文概要，查看原文内容请购买。