平面电磁波
电磁场与电磁波第8章 平面电磁波

Ex Hy
O
z
上图表示 t 0时刻,电场及磁场的空间变化特性。
电场强度与磁场强度之比称为电磁波的波阻抗,
以 Z 表示,
即
Z Ex Hy
实数
当平面波在真空中传播时,波阻抗以Z0表示,则
Z0
0 377 Ω 120π Ω 0
均匀平面波的磁场强度与电场强度之间的关系
又可用矢量形式表示为
Ex
Ex Ex 0 ,则只要
x y
以 kc 代替 k 即可求得其解为
Ex
E e jkcz x0
因常数 kc 为复数,令 kc k jk
求得
k
2
1
2
1
k
2
1
2
1
电场强度可表示为
Ex
E e jkcz x0
Ex0ekze jkz
上式表明电场强度的振幅随 z 增加不断衰减,相位 逐渐滞后。
由上求得 式中
vp
1
f f 00
0 f
1
00
r r
0 r r
0
0 为平面波在真空中传播时的波长。
0 的现象称为波长缩短效应,或简称为缩波 效应。
由
Hy
j可E得x
z
Hy
Ex0e jkz
H y0e jkz
H y0 Ex0
可见,在理想介质中,电场与磁场相位相同,
且两者空间相位均与变量z有关,但振幅不会改变。
1. 波动方程 在无限大的各向同性均匀线性介质中,时变
电磁场的方程为
2
E
(r
,
t
)
2 E (r , t ) t 2
J (r,t) t
电磁场-平面电磁波

入射波电场垂直于入射面 (即垂直极化)
注:入射面即y=0的平面,不是分界面
将 H 分解为界面的切线 t 向,上下边界应相等
• .
• 联解(1)(2)得到菲涅耳公式(设μ1 = μ2=μ)
• 考虑到
在介质1中合成波场的分量为:
讨论: 1)场的每一个分量都有因子 向传播,相位沿x方向变化。
,表示合成波也沿x方
第四章 平面电磁波
无线广播,通讯的载波,激光器发出的激光,都 接近正弦电磁波,称谐和波或单色场。
• 通常正弦电流用复数表示:
称为电场的 x(或y, z)分量的复振幅, 复振幅和幅角都是坐标的函数
.
• 利用复指数后,场量对时间的偏导数变得简单。
。将复数表达式代入正弦电磁场情况下的麦克斯韦方程组得:
时称为理想导体。
• (3)0.01 < < 100 称半导体, • 半导体材料对传导电流和位移 电流都必须考虑。
• .注意: 某种材料是导体还是绝缘体或半导体,
• 不但与ζ 还与工作频率 ω有关。 • 例铜的电导率ζ =5 .7x 107 S/m , 在光频以下为良导体 • 对 x射线(设波长为0.1nm), 铜却不是良导体。
电场瞬时值表达式:
为沿 -z 方向传播的平面波
电磁波的极化
• 平面电磁波是横波,它的 E矢量可以在垂直于传 播方向(波矢 K 的方向)的任意方向振动,如 果在垂直于传播方向的平面内,E 的振动限于 某一固定的方向,则称为线偏振或平面偏振,E 的振动方向称为偏振方向或极化方向。 • 沿z轴方向传播的电磁波的电场矢量E 可以分解 为两个互相正交的分量Ex , Ey 它们的振幅分别为 E1、 E2,相位差为φ=φ1-φ2
• .良导体的条件
平面电磁波的性质

uv E
'
积分并取积分常数为0
v k
×
uv E
=
uv kv B
v k
×
uv B
=
−με
uv kv E
结论:E、B、k三个矢量互相垂直,并顺序组成右手坐标系。 电场波E和磁场波B都是横波
回
顾
1.3.2 电磁波的矢量性质
分析:电磁波是由高频振荡的电场E和磁场B按一定的规 律随空间坐标r和时间t传播而形成的。电磁波的波函数描 述了E、 B随r、t的变化规律。在一般情况下,E、B的大 小和方向均随r、t的变化而变化,总是发生在垂直波传播 方向的平面内(横波)。
由于 : k × E = kν B
Qk ⊥ E
且 k = k ⇒ E =νB = 1 B = c B με n
E和B之间的数值关系
r E Qr= B
1 =v
εμ
两波振幅之比是一个正实数, ∴ Er、Br两矢量位相相同。
回 顾
• 平面电磁波的能量传播特性
1.能流密度矢量(各向同性)
电场:u E
=
1 2
•光波在折反射过程中振动分量的状态不变。入射波为s分量时,反射 波和折射波也是s分量,不会出现p分量,反之亦然
这种方向只是一种人为的规定,改变这种规定,并不影响结果的 普遍适用性。
③非铁磁性媒质: μ1 = μ2 = μ0
④
uv E
的正方向的规定:S分量
为正, 为负;P分量:在界面的投影向
右为正,左为负
• 在光学中,常常要处理光波从一种介质到另 一种介质的传播问题,由于两种介质的物理 性质不同(分别以ε1、μ1 和ε2、μ2 表征), 在两种介质的分界面上,电磁场将不连续,
平面电磁波

上一页 下一页 返回
7. 2 自由空间中的平面波
• 式(7 -30) 中 • 为真空中的光速. 由于一切媒质的相对介电常数εr >1. 而且一般媒
质的相对磁导率μr≈1. 因此. 理想电介质中均匀平面波的相速通常 小于真空中的光速. 但是要注意. 电磁波的相速有时可以超过光速. 可 见. 相速不一定代表能量传播速度. • 式(7 -30) 中 • 是频率为f 的平面波在真空中传播时的波长.
上一页 下一页 返回
7. 2 自由空间中的平面波
• 式(7 -9) 是一个二阶常微分方程. 其通解为: • 式中第一项代表沿正z 方向传播的波. 第二项代表沿负z 方向传播的
波. 为了便于讨论平面波的波动特性. 仅考虑沿正z 方向传播的波. 令 上式第二项为零. 即 • 式中. Ex0为z =0 处电场强度的有效值. Ex (z) 对应的瞬时值为:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 媒质电场强度与磁场强度的振幅之比称为波阻抗. 也称为媒质的特征 阻抗. 或者本征阻抗. 以Zc表示. 即
• 由上述讨论可知. 平面波的波阻抗为复数. 电场强度与磁场强度的空间 相位不同. 复能流密度的实部及虚部均不会为零. 意味着平面波在传播 过程中. 既有能量的单向传播. 又有能量的双向或交换传播.
上一页 下一页 返回
7. 2 自由空间中的平面波
• 将ω =2πf 和式(7 -19) 代入式(7 -20). 得: • 式(7 -21) 描述了平面波的相速vp、频率f 与波长λ 之间的关系.
平面波的频率是由波源决定的. 它与源的频率始终相同. 但是平面波的 相速与媒质特性有关. 因此. 平面波的波长也与媒质特性有关. • 将式(7 -14a) 代入式(7 -18) 中. 得:
平面电磁波知识点

平面电磁波知识点电磁波是一种在空间中传播的波动现象,它由电场和磁场相互作用而产生。
平面电磁波作为电磁波的一种形式,具有特定的特性和应用。
本文将介绍平面电磁波的基本知识点,包括定义、特性、产生和传播、应用等内容。
一、平面电磁波的定义平面电磁波是指电场和磁场在空间中沿着一定方向传播的电磁波。
它的波动方向垂直于电场和磁场的传播方向,且电场和磁场的变化情况具有一定的关系。
平面电磁波包含了无线电波、微波、红外线、可见光、紫外线、X射线和γ射线等多个频段。
二、平面电磁波的特性1. 频率和波长:平面电磁波的频率和波长间存在确定的关系,即波长等于光速除以频率。
波长越短,频率越高,能量越大。
不同频段的电磁波对应着不同的波长和频率范围。
2. 周期和振幅:平面电磁波的周期指一个完整波形所经历的时间,振幅指波峰或波谷与波中心的距离。
波形的周期和振幅决定了平面电磁波的能量和强度。
3. 速度:平面电磁波在真空中的传播速度是一个恒定值,即真空中的光速。
它的数值约为299,792,458米每秒,通常记作c。
不同介质中的传播速度与光速有关,由该介质的折射率决定。
4. 方向性:平面电磁波的传播方向是垂直于电场和磁场方向的。
电场和磁场的方向彼此垂直,并且与传播方向形成右手定则。
三、平面电磁波的产生和传播1. 产生:平面电磁波可以通过加速带电粒子、振动电荷或电流等方式产生。
当带电粒子或电流经过加速、振动时,会产生电场和磁场的变化,从而产生平面电磁波。
2. 传播:平面电磁波的传播遵循麦克斯韦方程组。
根据这些方程,平面电磁波在真空中以光速传播,不受介质的影响。
当平面电磁波遇到介质时,会发生折射、反射或透射等现象,具体情况取决于介质的性质。
四、平面电磁波的应用1. 通信:平面电磁波广泛应用于无线通信领域。
不同频段的电磁波用于无线电、电视、手机、卫星通信等通信系统,实现声音、图像和数据的传输。
2. 医学:平面电磁波在医学诊断、治疗和影像技术中起到重要作用。
平面电磁波

入射波
i
r
反射波
x
法 t 折射波 线
1 1 2 2
z y
斯耐尔定律:
①入射线,反射线及折射线位于同一平面;
② 入射角 i 等于反射角 r ; ③ 折射角 t 与入射角 i 的关系为
sin i k2 sin t k1
k1 1 1
Ex Ex 0e jkz H y H y 0e jkz
写成瞬时形式为:
Ez ( z , t ) Ez 0 cos(t kz ) H y ( z , t ) H y 0 cos(t kz )
传播方向
理想介质中均匀平面波的电场和磁场
当 c 2 c1时,R<0,在分界面上电场为最小值,
磁场为最大值
三, ①导电媒质 (1,1,1 0) 对②导电煤
质 ( 2,2, 2 0) 的垂直入射
一区合成波:
E1 ex E (e
i x0
1z
Re )
1z
衰减
入射波,反射波在传播过程中都在衰减 折射波在传播过程中也一样在衰减
则合成场强的大小为
E E E Em
2 x 2 y
合成场强的方向与x轴的夹角有如下关系:
tg Ey Ex sin(t kz y ) cos(t kz y ) tg (t kz y )
右旋圆极化: 时间t越大,合成场强与x 轴的夹角越大,合成波矢 量随着时间的旋转方向与
i x0
i x0
电磁波垂直入射到理想导体表面,电磁波产生 全反射,第一煤质中的电磁波为驻波,具有驻 波的性质!!
二,①为理想介质(1,1 ) ②为理想介质( 2,2)
第6章平面电磁波

磁场强度可表示为: H a H a H ˆx x ˆ y y
电磁场与电磁波
第6章 平面电磁波
三、平面电磁波在无耗介质中的传播特性
1. 波动方程的解
已知电场的波动方程为:
2 Ex 2 Ex 2 2 2 2 E E t 分解为标量方程: z z 2 t 2 2 Ey 2 Ey 2 z t 2 对于随时间按正弦变化的电 2 Ex 2 E x 磁场,因子为 e j t ,因此: z 2
上式两边在给定的体积V内积分,有
1 2 1 2 ( E H )dV ( E H )dV J c EdV V V t V 2 2
电磁场与电磁波
第6章 平面电磁波 欧姆功率损耗
由高斯定律得:
1 2 1 2 ( E H )dV ( E H ) dS J c EdV S V t V 2 2 ——坡印廷定理 坡印廷矢量:流出单位面积的功率密度。 S EH
的复数表示形式;(7)波的平均功率密度。 解 (1)相对介电常数 由电场 E 强度的表达式可知:
k 0 0 r
r
109 rad/s, k 5 rad/m
0 0
25 1018 (3 108 )2 2.25
25 1018
(2)传播速度为 (3)本质阻抗为 (4)波长为
A1 A1me
A2 A2me jx 2
前向行波
Ex A1me j( kz x1 ) A2me j( kz x 2 )
后向行波
同理: Ey A1me
j( kz y1 )
A2me
平面电磁波(HU)

300 10 6 2 8 c. S E H cos (6 10 t 2z ) (e x e y ) (e x e y ) 7 4 10 1500 cos 2 (6 10 8 t 2z ) e z (W / m 2 )
E j H H 0
E 0
令: c (1 j
) 则:
H j c E
相应的波动方程为:
2 2 E (r ) kc E (r ) 0
其中传播常数:
k c c j
y o
H
波阵面
x E
波传播方向
z
均匀平面波
7.1 波动方程
7.1.1 无源区的波动方程:
无源区( J 0, 0
)时谐电磁场方程为:
H j D E j B E 0 H 0
(2)两边取旋度得:
(1)
( 2) (3) ( 4)
E x ( z , t ) E xm cos(t z x )
E y ( z , t ) E ym cos(t z y ) E E x ( z , t )a x E y ( z , t )a y
7.3.1 直线极化
当两电场分量的相位相同或相差180度时,合成电场的极化方式是 直线极化。 Y
例 7.2 巳知自由空间中
上放置一半径为R的圆环,流过圆环的功率P为多少? 解: a.
波沿+Z轴方向传播: k 2 (rad/m), 2 / k 1 m
8
f 2 3 10
(HZ )
v / k 3 10 8
第四章 电磁波的传播 §1. 平面电磁波§2. 电磁波在介质界面上的反射和折射§3. 有导体存在时电磁波的

知 H
E
较大,非铁磁
B
可取 = 0
(2) E k 在与 k 垂直平面上可将 E 分解成两个分量
(3) H k, 且 H E
(4)
nn ((EH22EH1)1
0 )0
即 Et E't E"t Ht H 't H"t
(5) ' ,
sin 2 sin " 1
(1 2 0 )
电磁波:迅变电磁场, 导体内 = ?
电流:J
E
电荷:
E
/
,
J
E
J
0
t
t
J
,
d dt,
t
0e
t = 0 时,导体内 = 0 , 然后 随 t 按指数衰减 t = 时,( = / 特征时间) = 0 / e
导体内的自由电荷分布
t = 0 时,导体内 = 0 , 然后 随 t 按指数衰减
o
y
x
平面电磁波的特性: (证明 see next page)
(1) 电磁波是横波, E k , B k
(2) E B , E B 沿 k 方向
(3) E 和 B同相,振幅比 E / B = v
平面电磁波
证明平面电磁波的特性
E 0
E
E0
ei
(
k
xt
)
E0
ei
( k xt
)i(k
E"
2 1 cos
2sin "cos
E 1 cos 2 cos" sin( ")
振幅关系 Fresnel 公式
(2) E || 入射面: (Ht H )
平面电磁波

第六章主平面电磁波要 内 容 9学时平面电磁波电磁波:变化的电磁场脱离场源后在空间的传播 平面电磁波:等相位面为平面构成的电磁波 均匀平面电磁波:等相位面上E、H 处处相等的 电磁波 若电磁波沿 x 轴方向传播,则H=H(x,t),E=E(x,t) 平面电磁波知识结构框图电磁场基本方程组 电磁波动方程 均匀平面电磁波的传播特性平面电磁波的基本特性1. 理想介质中的均匀平面波 2. 损耗媒质中的均匀平面波 3. 均匀平面波的极化 4. 均匀平面波对平面边界的垂直入射 5. 均匀平面波对平面边界的斜入射 6. 各向异性媒质中的均匀平面波1-120 2-120理想介质中均匀平面波 平面电磁波的极化导电媒质中均匀平面波平面电磁波的垂直入射平面电磁波的斜入射各向异性媒质中的均匀平面波x方向传播的一组均匀平面波3-120平面电磁波知识结构框图数的媒质, σ → ∞ 的媒质称为理想导体。
σ 介 于两者之间的媒质称为有损耗媒质或导电媒质。
6.1 理想介质中的均匀平面波 理想介质是指电导率 σ = 0 ,ε 、 μ 为实常6.1.1波动方程的解其通解为假设电磁场沿着 Z 轴方向传播,且电场仅有指向 X 轴 的方向分量,则磁场必只有 Y 方向的分量,即:z z E x = f1 (t − ) + f 2 (t + ) v v ∂ 2 Ex + β 2 Ex = 0 ∂z 2对于时谐变电磁场:E = ex E x ( z, t )波动方程H = ey H y (z,t)其通解为 则平面波是指波前面,即等相位面或者波前 阵是平面的波。
均匀平面波是指波前面上场量振 幅处处相等的波。
本节介绍最简单的情况,即介绍无源、均 匀(homogeneous)(媒质参数与位置无关)、 线性(linear)(媒质参数与场强大小无关)、 各向同性(isotropic)(媒质参数与场强方向无 关)的无限大理想介质中的时谐平面波。
4-120 5-120则∂E 2 =0 ∂t 2 ∂E 2 ∇ 2 E x − με 2x = 0 ∂t 2 ∂ E x 1 ∂E x2 − =0 ∂z 2 v 2 ∂t 2 ∇ 2 E − με其中: v =其中: β = ω μ εEx = Ex + e− jβ z + Ex − e+ jβ zE x = E x+ cos(ω t − β z ) + E x− cos(ω t + β z )对应的磁场为1∇ × E = −μ6-120με∂H ∂t∂H y ∂E x = −μ ∂z ∂t对应的磁场为∇ × E = −μ其通解为∂H ∂t∂H y ∂E x = −μ ∂z ∂t考察电场的一个分量 ,瞬时值表达式为:Ex ( z, t ) = Ex+ cos(ωt − β z + ϕx )其中Hy =β ⎡ E + cos(ω t − β z ) − E x− cos(ω t + β z ) ⎤ ⎦ ωμ ⎣ xωt 为时间相位 , β z 为空间相位 , ϕ x 是初始相位。
第七章 平面电磁波

与波动方程
d2 dx
f
2
1 v2
d2 f dt 2
0 对比可知,方
程的解同样具有波的形式,是为电磁波。
f f (t x) f (t x)
v
v
4
f f t z
f
v f
t1 > t2 > t3
z固定
z
t
z vt2 t1 vt
5
波的形式取决于边界条件和初始条件
x
驻波
x
行波
等相面在沿波矢 k 方向上距离与时间的关系为
t kr C v dr 1 dt k
是为相速,即等相面沿其法线方向的传播速度, 也即平面波的传播速度。如果媒质的特性与频率 无关,即、与频率无关,则不同频率的平面电 磁波的相速与频率无关,媒质称为无色散媒质。 一般情况下,媒质总是存在色散。
18 109
(J
/
m3)
ez
108
18 109
(J
/
m3)
1.5
108 ( m
/
s)
ez
108
120
(W
/
m2)
25
二、均匀平面波的特征参量
1、平面波的一般表达式
直角坐标系内平面方程为:
ax by cz C
其中矢量 n aex bey cez 为平面的法向矢量
因此平面n方程r可表a达x为:by cz C
9
Re
Er,
t
t
Re
iEre it
ReReexeixiExEmexmictosx t x i sint x
exExm sint x
Em t
Re
E t
工程电磁场5 平面电磁波

2HH t 2tH 2 0 电磁波动方程
2) E ( H )
t
H EE
t
(E)2EE t2tE 2
D0
2EE t 2tE 2 0 电磁波动方程
4.亥姆霍兹方程的平面波解
在正弦稳态下,在均匀、各向同性理想媒质
(ε和μ为常数,γ为0)的无源区域中,电场场量 满足亥姆霍兹方程,即:
电磁场在无耗媒质中 的传播是不衰减的
2E
2E t2
0
vv 2 E k 2 E 0( k 2 2 )
2H
2H t2
0
2 xE 2 v 2 yE 2 v 2 zE 2 vk2E v0
2E
x2 2E
x y
x2
2Ex y 2 2Ey
y 2
2Ex z 2 2Ey
z 2
k2Ex k2Ey
v H
) k
v E
) k 为表示波传播方向
的单位矢量。
同理可以推得:
v E
v H
) k
从公式可知:均匀平面电磁波中电场幅度和磁场幅度
之比为一定值。定义电场幅度和磁场幅度比为媒质本征
阻抗,用 表示,即:
v
E
= v
——媒质本征阻抗
H
特殊地:真空(自由空间)的本振阻抗为:
0
0 0
4107 120377() 361109
结论:当 xy 0或时,电磁波为线极化波。
2、当x
y
且
2
Exm
Eym时
Ex= Exmcos(tx)
Ey= Eymcos(tx2)m Eymsin(tx)
合成电场的模及其与x轴夹角为:
平面电磁波的性质要点

自然光 偏振光
部分偏振光 各种光波电矢量振动示意图(时间平均意义上的)
1.3.3 电场波与磁场波的关系
由于 : k E k B k E 且 k k E B 1 c B B n
物理意义:
E和B之间的数值关系
① 电场的作用大于磁场的作用(讨论光与物质相互作用时) 带电粒子受到的电场力:
Ex Ey Ex ( E ) z E y ' k x Ex ' k y x y x y
Ey
E k E
'
而(3)式右端的可写为:
' B k B t
'
B E t
(3)
得出: k E k B
I A' I A cos L I cos A A L与I , 有关系
入射光波 接收面
同理,对于(4)式可以得出:
'
'
E B t
'
(5)
(4)
k B k E
k E k B
k B k E
(6)
(7)
(8)
证明: k , E , B 三个矢量是互相垂 直,并组成右手坐 标系。
对(5、6)式积分,并取积分的常数项为0,则有:
统计学的方法
I
1
0
E 20 x cos 2 (kz t 0 )dt
1 T E 20 x cos 2 (kz t 0 )dt T 0 1 E 20 x 2
物理意义:在均匀透明介质中,平面电磁波的强度(光强)正比于电场 振幅的平方。
电磁场平面电磁波

(3)为简单起见,我们考察电场的一个分量 E x , 由式(6-7)可写出其瞬时值表达式 Ex ( z, t ) E xm cos(t kz x ) (6-10) x 是 z 0 处在 t 称为时间相位,kz 称为空间相位, 时刻的初始相位。空间相位相同的点所组成的曲面 称为等相位面(plane of constant phase)、波前 z 常数的平面就是等相位面,因 或波阵面。这里, 此这种波称为平面波(plane wave)。又因为场量 z 与x、y无关,在 常数的等相位面上,各点场强 相等,这种等相位面上场强处处相等的平面波称为 均匀平面波(uniform plane wave)。
其中 0 为 t 0 时刻的初始电荷密度。 上式说明: 损耗媒质中的自由电荷密度随时间按指数 规律衰减,与电磁波的形式和变化规律无关,只与媒 质的电磁特性参数( )有关.由于初始时媒质内部 电荷密度一般为零,因此损耗媒质中不存在自由电荷。 即使初始电荷密度不为零,随时间的增加也将被衰减, 例如铜 1.52 1019 秒( 5.8 107 S / m),石墨 r 5), 表示电荷密 3.68 1010 秒( 0.12S / m, 度减小到初始值的 1 / e 所经过的时间,称为弛豫时间, 可见媒质内部自由电荷将迅速趋于零。 方程组(6-17)与理想介质中的麦克斯韦方程组 ~ ~ 相比较,仅有 与 的区别,因此我们只要将 取代 上一节方程中的 ,即可得有损耗媒质中的平面波的 解。
(6-16b)
(6-16c) (6-16d)
r 0 r
6.2 损耗媒质中的均匀平面波
电磁波在媒质中传播时要受到媒质的影响。这一节, 讨论平面波在均匀、线性、各向同性、无源的无限大有 损耗媒质( 0 )中的传播特性。 一、损耗媒质中的平面波场解 在无源的有损耗媒质中,时谐电磁场满足的麦克 斯韦方程组是 ~E (6-17a) H E jE j
平面电磁波的性质

第一章第6讲Wave OpticsWave Optics132回 1.3.2电磁波的矢量性质分析:按一定的规顾电磁波是由高频振荡的电场E 和磁场B按定的规律随空间坐标r 和时间t 传播而形成的。
电磁波的波函数描的变化规律在一般情况下述了E 、B 随r 、t 的变化规律。
在般情况下,E 、B 的大小和方向均随r 、t 的变化而变化,总是发生在垂直波传播方向的平面内(横波)方向的平面内(横波)。
结论EBDH等描述电磁波性质的物理量必须用结论:E、B、D、H等描述电磁波性质的物理量必须用矢量来表示,即电磁波是矢量波。
回矢量分解顾xyE yE x−=)](exp[),()](exp[),(0000y y y x x x t kz j E t z E t kz j E t z E ϕωϕω+−=+14回§1.4电磁波在两种均匀各向同性透明媒质界面上的反射和折射研究的内容:顾电磁波在两种均匀的各向同性的透明媒质界面传播时,会发生反射、折射现象,讨论两种介质中的电磁波(入、反、透)之间在研究的方法:传播方向、能量、位相、振动方向等之间的关系。
研究的方法9从麦克斯韦方程组出发边界条件导出折、反射定律和菲涅耳公式9只讨论入、反、折射的电场波之间的关系只讨反折射的场波间的关系9以简谐平面波为研究对象122E dl E l E l R∴⋅=⋅+⋅+u v v u v u v u v≈E E l −⋅u v u v v横跨界面的矩形积分域1C∫ 212()忽略短边212()0E E l ∴−⋅=u v u v v 结论:结论2122()()E E l l −⊥−−u v u v v vu v u v v v u v u v可为平行于界面的任意方向21212211()//()0cos cos E E u u E E E E θθ⇒×==或在界面两侧,电场强度E的切向分量连续。
2.磁场的边界条件B u v0(13)AB ds ⋅=−∫∫积分域设为横跨界面的小扁盒的整个表面。
平面电磁波的性质要点

Div, Grad, Curl, and still more all The "Curl" of a vector function f : that
f f z f y f x f z f y f x , , y z z x x y
I S
1
② 光波的分类(按矢量性)
自然光 偏振光
部分偏振光 各种光波电矢量振动示意图(时间平均意义上的)
1.3.3 电场波与磁场波的关系
由于 : k E k B k E 且 k k E B 1 c B B n
物理意义:
E和B之间的数值关系
① 电场的作用大于磁场的作用(讨论光与物质相互作用时) 带电粒子受到的电场力:
2
3
定义波印廷矢量S表示电磁波所传递的能流密度
定义: 单位时间内流过与波垂直的单位面积的能流量称为能流密度S。
S uV /( A Dt ) E 2 1
2 E
( J / s m2 )
能量流动具有方向性,所以定义了能流密度矢量:
1 S EB
V = A c Dt
Ex Ey Ex ( E ) z E y ' k x Ex ' k y x y x y
Ey
E k E
'
而(3)式右端的可写为:
' B k B t
'
B E t
(3)
得出: k E k B
1 1 2 3 u E D E ( J / m ) E 电场的能量密度 2 2 1 1 2 3 u H B B ( J / m ) 磁场的能量密度为 m 2 2
沿任意方向传播的平面电磁波

电磁波在现代社会中发挥着至关 重要的作用,它们是无线通信、 卫星通信、导航、雷达和光谱分 析等领域的基础。
电磁波的分类与特点
分类
传播速度
波动特性
能量与频率
穿透能力和吸收
电磁波可以根据频率、 波长和传播方式等特征 进行分类,如无线电波 、微波、红外线、可见 光、紫外线和X射线等。
电磁波在真空中的传播 速度为光速,即每秒约 30万公里。
射角和反射角有关。
折射
当平面电磁波从一种介质进入另 一种介质时,其传播方向会发生 改变,这种现象称为折射。折射 角与入射角和两种介质的折射率
有关。
散射
当平面电磁波遇到微小粒子或粗 糙表面时,会向各个方向散射, 这种现象称为散射。散射的程度 取决于粒子的尺寸、形状和介质
的性质。
干涉与衍射现象
干涉
当两束或多束相干平面电磁波相遇时,它们会相互叠加,产生加强或减弱的现象,这种现象称为干涉。干涉是波 动性质的一种表现,在通信、雷达和光学仪器等领域有广泛应用。
平面电磁波在电磁理论中占据重要地位,对于深入理解电 磁波的传播特性、电磁场与物质的相互作用等基础问题具 有重要意义。
应用领域
平面电磁波在通信、雷达、遥感、医学成像等领域具有广 泛的应用,对于推动相关领域的技术进步和产业发展具有 重要作用。
跨学科领域
平面电磁波的研究涉及到物理学、工程学、材料科学等多 个学科领域,对于促进跨学科交流和合作具有积极意义。
04
平面波的传播特性
传播速度与介质关系
传播速度
平面电磁波在真空中的传播速度为光速,而在介质中的传播 速度受介质折射率的影响,与介质折射率成反比。
介质影响
当平面电磁波从一种介质传播到另一种介质时,其传播方向 会发生改变,这是因为不同介质的折射率不同。
平面电磁波
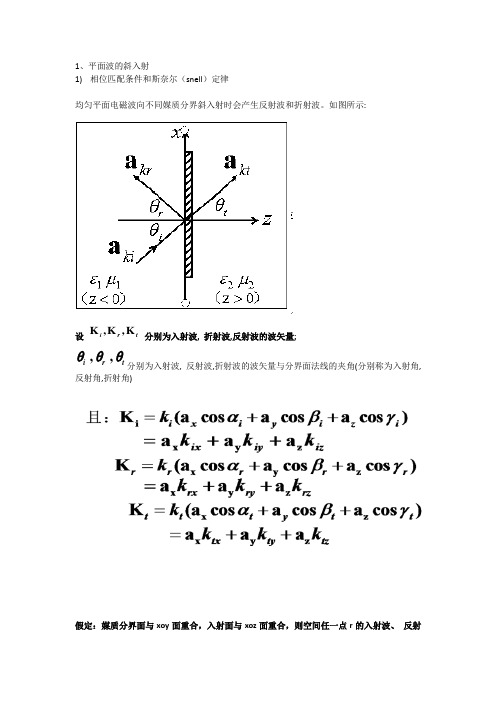
1、平面波的斜入射1) 相位匹配条件和斯奈尔(snell )定律均匀平面电磁波向不同媒质分界斜入射时会产生反射波和折射波。
如图所示:设 K ,K ,K i r t 分别为入射波, 折射波,反射波的波矢量;,,i r t θθθ分别为入射波, 反射波,折射波的波矢量与分界面法线的夹角(分别称为入射角,反射角,折射角)假定:媒质分界面与xoy 面重合,入射面与xoz 面重合,则空间任一点r 的入射波、 反射波、折射波的电场强度为:令: 则有: 所以: 入射角等于反射角2)反射系数和折射系数斜入射的均匀平面波不论何种极化方式,都可以分解为两个正交的线极化波。
其中:极化方向与入射面垂直的称垂直极化波,与入射波平行的(或在入射面内的)称平行极化波,即: 分别求出⊥E 和 ||E 的反射波和入射波,通过叠加就可以获得任意取向的入射波和折射波。
垂直极化波平行极化波3)合成电磁波(垂直极化)112sin sin sin i r t k k k θθθ==()0ix iz j k x k z i e -+=E 0i j i i e -⋅=K r E E (sin cos )0i i i jk x z i e θθ-+=E 0r j r r e -⋅=K r E E ()rx rz j k x k z e -+=r0E (sin cos )r r r jk x z e θθ--=r0E 0t j t t e -⋅=K r E E ()tx tz j k x k z t e -+=0E (sin cos )t t t jk x z t e θθ-+=0E 12;i r t k k k k k ===i r θθ=0E E ⊥=r0i R 2121cos cos cos cos i t i t ηθηθηθηθ-=+0t E E ⊥=0i T 2212cos cos cos i i tηθηθηθ=+0110r i E R E =1212cos cos cos cos i t i t ηθηθηθηθ-=+0110t i E T E =2122cos cos cos i i t ηθηθηθ=+||E E E +=⊥a 、在媒质1中(z<0)b 、在媒质2中(z>0)2、平面电磁波对理想导体的斜入射1)垂直极化波a )反射系数和折射系数将20η=代入一般公式,得: b )合成场(z<0,媒质1区域)c )合成电磁波的性质 在(21)4cos n z k πθ-+=处为E1波腹点,H1x 的波节点。
平面电磁波

平面电磁波1 时变电磁场以电磁波的形式存在于时间和空间这个统一的物理世界。
2 研究某一具体情况下电磁波的激发和传播规律,从数学上讲就是求解在这具体条件下Maxwell equations 或wave equations 的解。
3 在某些特定条件下,Maxwell equations 或wave equations 可以简化,从而导出简化的模型,如传输线模型、集中参数等效电路模型等等。
4 最简单的电磁波是平面波。
等相面(波阵面)为无限大平面电磁波称为平面波。
如果平面波等相面上场强的幅度均匀不变,则称为均匀平面波。
5 许多复杂的电磁波,如柱面波、球面波,可以分解为许多均匀平面波的叠加;反之亦然。
故均匀平面波是最简单最基本的电磁波模式,因此我们从均匀平面波开始电磁波的学习。
§ 6.1 波动方程1 电场波动方程:ερμμε∇+∂∂=∂∂-∇t J t E E ρρρ222磁场波动方程 J t H H ρρρ⨯-∇=∂∂-∇222με 2 如果媒质导电(意味着损耗),有E J ρρσ=代入上面,则波动方程变为ερμεμσ∇=∂∂-∂∂-∇222t E t E E ρρρ0222=∂∂-∂∂-∇tHt H H ρρρμεμσ 如果是时谐电磁场,用场量用复矢量表示,则ερμεωωμσ&&ρ&ρ&ρ∇=+-∇E E j E 22 022=+-∇H H j H &ρ&ρ&ρμεωωμσ采用复介电常数,εμωωεσμεωωμσμεω&222)1(=-=-jj ,上面也可写成 3 在线性、均匀、各向同性非导电媒质的无源区域,波动方程成为齐次方程。
0222=∂∂-∇t EE ρρμε0222=∂∂-∇tHH ρρμε 4在线性、均匀、各向同性、导电媒质的无源区域,波动方程成为齐次方程。
0222=∂∂-∂∂-∇tEt E E ρρρμεμσ0222=∂∂-∂∂-∇tHt H H ρρρμεμσ 如果是时谐电磁场,用场量用复矢量表示,并采用复介电常数,εμωωεσμεωωμσμεω&222)1(=-=-j j ,上面也可写成 022=+∇E E &ρ&&ρεμω022=+∇H H &ρ&&ρεμω注意,介电常数是复数代表有损耗。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7. 2 自由空间中的平面波
• 式(7 -9) 是一个二阶常微分方程. 其通解为: • 式中第一项代表沿正z 方向传播的波. 第二项代表沿负z 方向传播的
波. 为了便于讨论平面波的波动特性. 仅考虑沿正z 方向传播的波. 令 上式第二项为零. 即 • 式中. Ex0为z =0 处电场强度的有效值. Ex (z) 对应的瞬时值为:
7.1 波动方程
• 由此可见. 各个坐标分量满足的方程形式相同. 它们的解应具有同样结 构.
• 可以证明: 在直角坐标系中. 若正弦电磁场的场矢量仅与一个坐标变 量有关. 则该正弦电磁场的场矢量不可能具有该坐标分量. 例如. 若场 矢量仅与z 变量有关. 则可证明Ez = Hz =0. 这是由于. 如果场矢 量与变量x 及y 无关. 则
上一页 下一页 返回
7.1 波动方程
• 在无源区中. ∇·E = 0.∇·H = 0. 由上两式得
• 代入式(7 - 4c) 及式(7 -5c)中. 求得分量Ez = Hz =0. 所 以均匀平面波电磁场的纵向分量(平行于传播方向的电磁场分量. 此处 为z 分量) 等于零.
上一页
返回
7. 2 自由空间中的平面波
上一页 下一页 返回
7. 2 自由间中的平面波
• 由前节分析得知. 电场强度不可能存在z 分量.不失一般性. 令电场强 度方向为x 方向. 即E = ex Ex . 则磁场强度H 为:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 由此可见. 磁场强度仅具有y 分量. 这是因为电场强度仅与z 有关. 因而磁场也仅与z 有关.所以磁场也不可能具有z 分量. 又知电场与 磁场处处垂直. 因此. 若E =ex Ex . 则H =ey Hy . 既然Ex 与 Hy 的关系由式(7 -8) 确定. 所以仅需求解Ex . 然后由式(7 -8) 即可确定Hy .由上一节知. 电场强度的Ex 分量满足齐次标量Hel mholtz 方程式(7 -4a). 由于
• 其中. kc 称为传播常数. εe 称为等效介电常数.
下一页 返回
7.1 波动方程
• 求解上述齐次矢量Helmholtz 方程. 即可以得到平面电磁波 的传播特性.
• 在直角坐标系中. 电场强度E 及磁场强度H 的各个坐标分量分别满足 下列齐次标量Helmholtz 方程:
上一页 下一页 返回
• 空间相位(αz) 变化2p所经过的距离称为波长. 以λ 表示. 由αλ =2 π 关系式. 得:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 电磁波的频率描述相位随时间的变化特性. 而波长描述相位随空间的 变化特性.
下一页 返回
7. 2 自由空间中的平面波
• (6) 由于信号能量在自由空间的扩散. 在传播了一定距离后. 信号能量 也会发生衰减.电磁波的传播与在真空中传播一样. 只存在有扩散损耗 的直线传播. 而不存在反射、折射、绕射、色散、吸收、磁离子分裂 等现象.
• 本节讨论自由空间中平面波的传播特性. 由时变电磁场理论知道. 在自 由空间的无限大媒质中. 无源区内正弦电磁场满足方程式(7 -1). 又 因为在直角坐标系中. 各个分量满足齐次标量Helmholtz 方 程式(7 - 4) 及式(7 - 5). 假设电场强度E 仅与坐标变量z 有关. 即
第7章 平面电磁波
• 7.1 波动方程 • 7.2 自由空间中的平面波 • 7.3 平面波的极化特性 • 7.4 平面边界上的反射和折射 • 7.5 多层媒质中的平面波 • 7.6 波速、 相速和群速 • 7.7 平面波仿真实例
返回
7.1 波动方程
• 根据时谐电磁场理论. 已知在无限大的各向同性的均匀线性媒质中. 无 源区内正弦电磁场满足下列齐次矢量Helmholtz 方程:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 式中. ωt 称为时间相位. kc为复数. 称为传播常数. 令 • 代入式(7 -2) 中. 得:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 将式(7 -13) 代入式(7 -11) 中. 得:
• 式中第一个指数项e- βz表示电场强度的振幅随z 增加按指数规律 不断衰减. 第二个指数项e- jαz表示空间的相位变化. 因此. α 称为相 位常数. 单位为rad/ m. β 称为衰减常数. 单位为Np/ m. 可见. 在 z =常数的平面上. 各点空间相位相等. 因此该电磁波的波面为平面. 称为平面波. 由于在z =常数的波面上. 各点场强的振幅也相等. 这种 平面波称为均匀平面波.
• 自由空间是指无任何衰减、无任何阻挡、无任何多径的传播空间. 自 由空间具有以下特点:
• (1) 没有电荷、电流分布. 即ρ =0. Jf =0. Jf 为分布电流. • (2) 空间中媒质的相对介电常数εr和相对磁导率μr均恒为1. 即磁
导率μ = 真空磁导率μ0. 介电常数ε = 真空介电常数ε0. • (3) 媒质是线性的、均匀的、各向同性的. • (4) 媒质电导率为零. • (5) 电波传播速度等于真空中的光速.
• 将式(7 -15) 代入式(7 -8) 中. 得:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 式中. εeff为等效介电常数. 磁波角频率.
σ 为媒质电导率. ω 为电
• 时间相位(ωt) 变化2p所经历的时间称为电磁波的周期. 以T 表示. 而一秒内相位变化2p的次数称为频率. 以f 表示. 那么由ωT =2π 的关系式. 得:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 由上述讨论知. 无论电场或磁场均与传播方向垂直. 即相对于传播方向. 电场及磁场仅具有横向分量. 因此这种电磁波称为横电磁(Trans verse Electromagnetic. TEM) 波. 均匀平面 波是TEM 波. 只有非均匀平面波才可形成非TEM 波. 但是TEM 波也可以是非均匀平面波. 金属波导只能传输传播方向上具有电场或 磁场纵向分量的非TEM 波. 即TM 波(横磁波) 或TE 波(横电波). 且两者均为非均匀平面波.
