平面应力状态的几何法(2)
平面应力问题
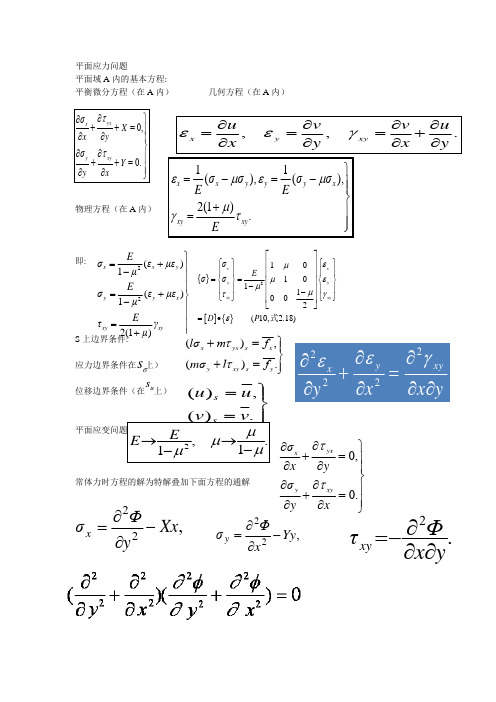
平面应力问题平面域A 内的基本方程:平衡微分方程(在A 内) 几何方程(在A 内)物理方程(在A 内)即: S 上边界条件:应力边界条件在 上)位移边界条件(在 上) 平面应变问题常体力时方程的解为特解叠加下面方程的通解0,0.yx x y xyσX x y σY y x ∂⎫∂++=⎪∂∂⎪⎬∂∂⎪++=⎪∂∂⎭ττ, , .x y xy u v v ux y x yεεγ∂∂∂∂===+∂∂∂∂11(),(),2(1).x x y y y x xy xy σσσσE E Eεμεμμγτ⎫=-=-⎪⎪⎬+⎪=⎪⎭22()1()(a)12(1)x x y y y x xy xyE σεμεμE σεμεμE τγμ⎫=+⎪-⎪⎪=+⎬-⎪⎪=⎪+⎭{}[]{}2101011002(10, 2.18)x x y y xy xy σE σσD P ⎡⎤⎧⎫⎧⎫⎢⎥⎪⎪⎪⎪⎢⎥==⎨⎬⎨⎬⎢⎥-⎪⎪⎪⎪⎢⎥-⎩⎭⎩⎭⎢⎥⎣⎦=•εμμεμμτγε式(),().x yx s x y xy s y l σm f m σl f ττ⎫+=⎪⎬+=⎪⎭σs(),().s s u u v v ⎫=⎪⎬=⎪⎭us 2222y xy x y x x yεγε∂∂∂+=∂∂∂∂.1 ,12μμμμ-→-→E E 0,0.yx x y xyσx y σy x ∂⎫∂+=⎪∂∂⎪⎬∂∂⎪+=⎪∂∂⎭ττ22,y ΦσYy x∂=-∂.2yx Φτxy ∂∂∂-=22,x ΦσXx y∂=-∂二、基本假设 1、连续性假定假定物体是连续的。
因此,各物理量可用连续函数表示。
2、完全弹性假定a.完全弹性—外力取消,变形恢复,无残余变形。
b.线性弹性—应力与应变成正比。
即应力与应变关系可用胡克定律表示(物理线性)。
3、均匀性假定假定物体由同种材料组成,因此, E 、 μ等与位置 无关。
4、各向同性假定假定物体各向同性。
E 、μ与方向无关。
2平面问题的基本理论(平面应力与应变,受力状态,圣维兰原理)

当面积 AB 无限减小而趋于 P 点时,平面 AB 上的 应力就是上述斜面上的应力。 现设斜面上的全应力p可以分解为沿坐标向的分 量( px , py ),或沿法向和切向的分量( σn , τn),如图 2-4b所示。
用n代表斜面AB的外法线方向,其方向余弦为:
cosn, x l, cosn, y m
c
0
,则有
F 0, F Mc 0
x
y
0
yx dy dy dx dx xy dy 1 ( yx dy)dx 1 yx dx 1 0 2 2 y 2 2
力矩方程化简后得到:
xy
1 xy 1 yx dx yx dy 2 x 2 y
x yx fx 0 y x xy y f 0 y x y
4.平衡微分方程适用的条件是,只要求符合连 续性和小变形假定。 5.对于平面应力问题和平面应变问题,平衡微 分方程相同。 6.由于τxy =τyx,以后只作为一个独立未知函数 处理。因此,2个独立的平衡微分方程(2-2) 中含有 3个应力未知函数。
由式(2-4)及(2-5)就可以求得经过P点的任意 斜面上的正应力 n 及切应力 n 。
3.然后,再求出主应力和应力主向
设经过P点的某一斜面上的切应力等于零,则该斜 面上的正应力称为在P点的一个主应力,而该斜面 称为在P点的一个应力主平面,该斜面的法线方向 称为在P点的一个应力主向。
(2)只在侧边上受有平行于板面且不沿厚度变化 的面力和体力,且不沿厚度变化,体力 f x , f y , o 和面 力 f x , f y , o ,只是x,y的函数,并构成平衡力系;
弹性力学平面应力平面应变问题 ppt课件

系,即 σx = Eεx 这就是虎克定律。 应力
(Hooke‘s Law)
Y
弹塑性范围
弹性范围
斜率, E
应变
工程上,一般将应变与应力间的关系表示为
xE 1xyz yE 1yzx
xy
1
G
xy
yz
1
G
yz
zE 1zxy
zx
1
G
zx
称它们为物理方程(广义虎克定律)。
x 1 E 1 1 2 x 1 y 1 z
1
0
对 1 0
称
1
2
对于平面应变问题的弹性矩阵,只须在上式
中,以 E
1 2
代E,
1
代μ即可。
小结
则有
uu vv ww (在 u 上)
用矩阵形式表示为:
uu (在 u 上)
小结
弹性力学基本方程的一般形式为
回顾
平衡微分方程 σb0 (在 内)
几何方程 物理方程
ε tu σDε
(在 内) (在 内)
边界条件
nσt
(在 t 上)
uu
(在 u 上)
其中 t u , 为弹性体的完整边界。
§2-3 平面应变和平面应力问题
平面应变问题
位移:按平面应变的定义,三个方向的位移函数是
uux,y vv(x,y) w0
应变:由几何方程应变-位移关系,得
x
u x
1x,
y,
y
v y
3x,
y,
xy yz
u y
v x
2x,
v w0 z y
y
z
w0, z
zx
u z
弹性力学第二章

(2)平面应变问题的物理方程 由于平面应力问题中:εz = γ zx = γ zy = 0
µ 1− µ2 σx − εx = σy 1− µ E 1− µ2 µ σy − εy = σy E 1− µ
——平面应变问题 ——平面应变问题 物理方程
第三节
平面问题中一点的应力状态
一点的应力
2. 一点的主应力与应力主向 (1)主应力 若某一斜面上τn = 0 ,则该斜面上的正应力σn 称为该点一个主应力σ; 当τn = 0 时,有 σn =σ = p
px =lσ py = m σ
lσx +m xy =lσ τ m y +lτxy = m σ σ
γ xy =
2(1+ µ) τ xy E
在z方向,εz = 0, σz = µ(σx +σy )
变换关系 : 平面应力物理方程 →平面应变物理方程:
E µ E→ , → µ 2 1− µ 1− µ
平面应变物理方程 →平面应力物理方程:
E→
E(1+ 2µ)
(1+ µ)2
, → µ 1+ µ
µ
思考题 1. 试证:由主应力可以求出主应变,且两者方 向一致。 2. 试证:三个主应力均为压应力,有时可以产 生拉裂现象。 3. 试证:在自重作用下,圆环(平面应力问题) 比圆筒(平面应变问题)的变形大。
E
µ
2.平面应变问题 2.平面应变问题 条件是:⑴很长的常截面柱体 ; ⑵体力、面力、约束平行于柱面横截面, 沿长度方向不变。 应力:
σz = µ(σx +σy )
τ zx =τ zy = 0
应变:
εz = 0 γ zx = 0 γ zy = 0
(推荐)平面应力问题

l
yx
m yx l y
yx P xy
x
y A
fx px
x
为 l2、m2,则
y
B fy py
n
tan 2
cos(90 2 ) cos 2
m2 l2
2 x xy
(或 xy ) 2 y
22
应力主向的计算公式:
tan
1
x
(x
dx,
y)
x
(
x,
y)
x (x, x
y)
dx
1 2!
2 x (x,
x2
y)
(dx)2
1 n!
n x (
x
x,
n
y
)
(dx)n
10
略去二阶及二阶以上的微量后便得
x
(
x,
y)
x (x, x
y)
dx
同样 y 、 xy 、 yx 都一样处理,得到图示应力状
l x m yx l
m y l xy m
19
求解得:
m l
x yx
o
m yx
l y
y
2
(
x
y )
(
x
y
2 xy
)
0
yx y
x
P
A
xy
x B
px
n
n
py p
n
p x l x m yx
弹性力学平面应力平面应变问题 ppt课件

系,即 σx = Eεx 这就是虎克定律。 应力
(Hooke‘s Law)
Y
弹塑性范围
弹性范围
斜率, E
应变
工程上,一般将应变与应力间的关系表示为
xE 1xyz yE 1yzx
xy
1
G
xy
yz
1
G
yz
zE 1zxy
zx
1
G
zx
称它们为物理方程(广义虎克定律)。
x 1 E 1 1 2 x 1 y 1 z
则有
uu vv ww (在 u 上)
用矩阵形式表示为:
uu (在 u 上)
小结
弹性力学基本方程的一般形式为
回顾
平衡微分方程 σb0 (在 内)
几何方程 物理方程
ε tu σDε
(在 内) (在 内)
边界条件
nσt
(在 t 上)
uu
(在 u 上)
其中 t u , 为弹性体的完整边界。
§2-3 平面应变和平面应力问题
得
x
1
E
1 x
y
y
1
E
1 y
x
xy
1 G
x
y
21
E
xy
平面应变问题
应力:如果用应变分量来表示应力分量,则有
x
E(1) (1)(12)
x
1y
y
E(1) (1)(12)
1x
y
xy
E
2(1)
xy
E(1) (1)(12)
12 2(1)
xy
由上面的分析可知,独立的应力分量只有 σx、σy 和xy
??2???????????????????1?zyxxe???????????1111??2???????????????????1?zyxye???????????1111???2????????e?e?e??1e???????1?????????????zyxz??????????111??xyxy????12??yzyz????12??zxzx????12若令???????????t?zxyzxyzyx??????tzxyzxyzyx??????代表应变列阵和应力列阵则应力应变关系可写成矩阵形式可写成矩阵形式?????????d其中??d??22???????????????????????????????????11????????11??2????????????221000111111111称对e????????????????1??1??2??22100000210000称为弹性矩阵弹性矩阵由弹性常数e和决定
应力与应力状态分析

应力与应力状态分析拉伸模量拉伸模量是指材料在拉伸时的弹性,其计算公式如下:拉伸模量(㎏/c ㎡)=△f/△h(㎏/c ㎡)其中,△f 表示单位面积两点之间的力变化,△h 表示以上两点之间的应变化。
更具体地说,△h =(L-L0)/L0,其中L0表示拉伸长前的长度,L 表示拉伸长后的长度。
§4-1 几组基本术语与概念一、变形固体的基本假设1、均匀连续性假设:假设在变形固体的整个体积内均匀地、毫无空隙地充满着物质,并且各点处的力学性质完全相同。
根据这一假设,可从变形固体内任意一点取出微小单元体进行研究,且各点处的力学性质完全相同,因而固体内部各质点的位移、各点处的内力都将是连续分布的,可以表示为各点坐标的连续函数。
2、各向同性假设:假设变形固体在所有方向上均具有相同的力学性质。
3、小变形假设:认为构件的变形与构件的原始尺寸相比及其微小。
根据小变形假设,在研究构件上力系的简化、研究构件及其局部的平衡时,均可忽略构件的变形而按构件的原始形状、尺寸进行计算。
二、应力的概念1、正应力的概念分布内力的大小(或称分布集度),用单位面积上的内力大小来度量,称为应力。
由于内力是矢量,因而应力也是矢量,其方向就是分布内力的方向。
沿截面法线方向的应力称为正应力,用希腊字母σ表示。
应力的常用单位有牛/米2 (2/m N ,12/m N 称为1帕,代号a P )、千米/米2(2/m KN ,12/m KN 称为1千帕,代号Ka P ),此外还有更大的单位兆帕(M a P )、吉帕(G a P )。
几种单位的换算关系为:1 K a P =310a P 1 M a P =310K a P 1 G a P =310M a P =610K a P =910a P2、切应力与全应力的概念与截面相切的应力分量称为切应力,用希腊字母τ表示。
K 点处某截面上的全应力K p 等于该点处同一截面上的正应力K σ与切应力K τ的矢量和。
弹性力学平面应力问题和平面应变问题

有限差分法的精度取决于差分格式的选择和网格的划分,同时需要注意数 值稳定性和计算精度的问题。
边界元法
边界元法是一种基于边界积 分方程的数值分析方法,通 过将微分方程转化为边界积
分方程来求解。
变形特点
应用领域
在平面应力问题中,变形主要发生在作用 面上,而在平面应变问题中,变形可以发 生在整个结构中。
平面应力问题在桥梁、建筑和机械等领域 有广泛应用,而平面应变问题在岩土、地 质和材料等领域有广泛应用。
06
结论与展望
结论总结
平面应力问题和平面应变问题在弹性力学中具有重要地位,它们是描述物体在应力作用下的变形和应 力分布的基础。
弹性模量表示材料在受力作用下的刚度,是衡量材料抵 抗弹性变形能力的重要参数。
剪切模量表示材料在剪切力作用下的刚度,与弹性模量 和泊松比有关。
03
平面应变问题
应变状态分析
平面应变条件
应变分量中,只有$varepsilon_{x}$ 、$varepsilon_{y}$和 $gamma_{xy}$不为零,其余分量为 零。
有限元法在弹性力学平面应力问题和平面应变问题中广泛 应用,因为它能够处理复杂的几何形状和边界条件,且计 算精度高。
有限元法的实现需要建立离散化的模型、选择合适的单元 类型和求解算法,并进行数值稳定性和误差分析。
有限差分法
有限差分法是一种基于差分原理的数值分析方法,通过将微分方程转化为 差分方程来求解。
薄板弯曲问题
考虑一个矩形薄板,受到一对相距较远的集中力作用,使板发生弯曲。根据平面应力问题,可以分析 板的应力分布、中性面位置以及挠度等。
过一点所方向面上应力的集合,称为这一点的应力状态

应力是指物体内部受到的力的作用,它可以通过单位面积上的力来描述。
在工程力学中,应力是非常重要的物理量,它与物体的形状、材料特性和外部力的作用密切相关。
本文将围绕应力的概念展开讨论,针对其在材料力学中的应用进行深入分析。
一、应力的定义和分类1.1 应力的概念应力是单位面积上的力,常用符号表示为σ,其计算公式为力F除以面积A,即σ=F/A。
在物体内部,由于外部力的作用,各处都会受到应力的作用,这种应力称为内应力。
而外部施加在物体表面上的力也会导致应力的产生,这种应力称为外部应力。
1.2 应力的分类根据应力的作用方向和大小,可以将应力分为正应力、剪切应力和法向应力三种类型。
正应力是垂直于物体截面的应力,常用符号表示为σn。
而沿着截面方向的应力称为剪切应力,常用符号表示为τ。
另外,法向应力是指作用在物体某一点上的应力。
二、应力状态的描述2.1 应力张量在三维空间中,一个点的应力状态可以由一个3x3的对称矩阵来描述,这个对称矩阵称为应力张量。
应力张量的分量代表了在不同方向上的应力情况,可以通过数学方法进行求解和分析。
2.2 应力状态的表示一个点处的应力状态可以通过应力张量的特征值和特征向量来表示。
特征值代表了应力状态的大小,特征向量则代表了应力作用的方向。
通过对特征值和特征向量的分析,可以判断物体处于何种应力状态,从而进行相应的力学分析和设计。
三、应力的应用3.1 工程材料的性能应力是描述物体受力情况的重要参数,它直接影响着材料的强度、刚度和韧性等性能。
在工程中,通过对材料的应力状态进行分析,可以评估材料的可靠性和安全性,为工程设计提供参考依据。
3.2 结构的稳定性对结构件的受力状态进行分析,可以判断结构在外部载荷作用下的稳定性。
通过对结构的应力分布和应力集中区域的分析,可以预测结构是否会发生破坏或失稳现象,为结构设计和改进提供重要参考。
3.3 力学设计在工程实践中,需要根据实际的力学要求来设计各种零部件和结构件。
2 应力分析

τyz τzy
x A
Sx τzx σz
B y
主平面上的应力
S1 s 1l S2 s 2m S s n 3 3
3 б3 s3 s
s2
l m n 1
2 2 2
1
б2
s1 б1
2
∴
s
S1
2 1
2
s2
S2
2
2
s3
S3
2
2
1
应力椭球面
主应力图
四、主切应力和
最大切应力
3
s
N
s2
1
S 2
切应力取极值的面上的
切应力称为主切应力。
s1 s 3
,
2 S2 s 2
2 2 2
s 1 l 2 s 2 m2 s 3 n 2 (s 1l 2 s 2m2 s 3n 2 )2
s 1 s 2 s 3 为应力主轴
将
n2 1 l 2 m2 代入上式
2 S2 s 2
s 1 l 2 s 2 m2 s 3 n 2 (s 1l 2 s 2m2 s 3n 2 )2
2 2 2
s 23
得
s2 s3
2 s 3 s1 s 31 2 s1 s 2 s 12 2
s2 s3 23 2 s 3 s1 31 2 s1 s 2 12 2
则由第一式得l=±
1 2
一般情况 若s ≠s 2 ≠s 3 1
若l≠0,m≠0,则上式必有
s1 = s 2
与前提条件不符,故这时无解
则得此斜面的方向余弦为: 1 m=0, l =n=± 2 则得此斜面的方向余弦为: n=0, l =m=± 1 2
《弹性力学》第二章_平面问题的基本理论

o
xy
x
y
P
yx
y
A
XN
x
设AB面在xy平面内的长度为dS, 厚度为一个单位长度,N为该面的外 法线方向,其方向余弦为:
B
N
N
N
cos(N , x) l , cos(N , y) m
9
YN S
图2 - 4
斜面AB上全应力沿x轴及y轴的投影分别为XN和YN。由PAB 的平衡条件 Fx 0 可得: X N dS xldS yxmdS
2.主应力的方向
1 与 2 互相垂直。
11
§2-4
几何方程、刚体位移
在平面问题中,弹性体中各点都可能产生任意方向的位移。 通过弹性体内的任一点P,取一单元体PAB,如图2-5所示。弹性 体受力以后P、A、B三点分别移动到P′、A′、B′。 一、P点的正应变
u (u dx) u u x x dx x
二、P点的剪应变
线段PA的转角:
同理可得线段PB的转角:
u y
所以
xy
v u x y
13
因此得到平面问题的几何方程:
u x x v y y v u xy x y
由几何方程可见,当物体的位移分量完全确定时,形变 分量即可完全确定。反之,当形变分量完全确定时,位移分 量却不能完全确定。
z
E
( x y )
16
二、平面应变问题的物理方程 1 2 x ( x y ) E 1 1 2 y ( y x ) E 1 2(1 ) xy xy E 三、平面应力的应力应变关系式与平面应变的关系式之间的 变换关系 1 ( ) y 将平面应力中的关系式: x E x
应力状态分析_图文

一、两个概念:1、极限应力圆: 2、极限曲线:极限应力圆的包络线(envelope)。
t
极限应力圆
s
极限应力圆的包络线
O
近似包络线
二、莫尔强度理论:任意一点的应力圆若与极限曲线相接触,
则材料即将屈服或剪断。
B
s3
O
s2
A
2s0
C
20MPa
s1
s
(MPa)
主应力及主平面如图
B
A
s2
0
s1
t (MPa)Bs3O Nhomakorabeas2
A
2s0
C
20MPa
s1
s
(MPa)
解法2—解析法:分析——建立坐标系如图 60°
y Ox
§9–4 梁的主应力及其主应力迹线
P1
P2
1
2 3 4
5
q 如图,已知梁发生剪切弯 曲(横力弯曲),其上M、 Q>0,试确定截面上各点主 应力大小及主平面位置。
30 x
z
解:由单元
s3
体图知:y
10
s
s2 s1 (M Pa)
z面为主面
A
§9–6 平面内的应变分析
一、叠加法求应变分析公式
y
Ox
剪应变: 直角的增大量! (只有这样,前后才对应)
E1 B
b
E
aA
D1
D
cd
O
E2
B E
b
y Ox
D2
D
A
a cd
O
E3
B
E
b
D3 a
A
第2章 平面问题的基本理论汇总

t= 1
平面应力:z方向应力为零。 平面应变:z方向应力自成平衡。
应用的基本假定: 连续性假定─应力用连续函数来表示。 小变形假定─用变形前的尺寸代替
变形后的尺寸。
二、平衡微分方程(平面任意力系)
合力 = 应力×面积,体力×体积; 以正向物理量来表示。
平面问题中可列出三个平衡条件:
例2(习题2-4) 按平面应变问题特征来分析, 本题中
ox z
y
只有
x x x, y , y y x, y , xy xy x, y
思考题 设有厚度很大(即 z 向很长)的基础梁放置在地基上,如果
想把它近似地简化为平面问题处理,问应如何考虑?
2-2 平面问题的平衡微分方程
将(px,py)向法向、切向投影,得
2-3 平面问题中一点的应力状态
一、斜截面上的应力
2-3 平面问题中一点的应力状态
一、斜截面上的应力
2-4 几何方程 刚体位移
一、几何方程:表示应变与位移之间的关系
x x x, y , y y x, y , xy xy x, y u u x, y,v v x, y
罗建辉
第二章
平面问题的 基本理论
2-1 平面应力问题和平面应变问题
一、弹性力学空间问题的简化
(在特定的条件下)
空间问题
平面问题
二、弹性力学平面问题
1、平面应力问题 (1) 几何特征:
等厚度的薄板,厚度<<长、宽; (2) 受力特征: ∥xy面,沿板厚不变;
体力fx、fy作用于体内; 面力fx、fy作用于板边; 约束u、v 作用于板边。
思考题
1.试检查,同一方程中的各项,其量纲必然相同(可用来 检验方程的正确性)。
弹性力学3-应力状态、几何方程

s x ,s y ,t xy t yx
应力张量: tsyxx
t xy sy
t t
xz yz
t zx t zy s z
s x t xy
t yx
s
y
第二章 平面问题的基本理论 2.3 平面问题中一点的应力状态
一点的应力状态可以用以下三种方法表示:
用包围该点的微元体(微正六面体)表征 过该点的任意斜截面上的应力 用一点的主应力与主方向表征
2.1 平面应力与平面应变 2.2 平衡微分方程 2.3 一点的应力状态 2.4 几何方程 2.5 物理方程 2.6 边界条件 2.7 圣维南原理 2.8 按位移求解平面问题 2.9 按应力求解平面问题 2.10 常体力情况下的简化
第二章 平面问题的基本理论 2.4几何方程
几何方程:应变分量与位移分量之间的关系。
fx
dxdy 2
1 0
上式分别将dx、dy用ds 表达:
pxds
s xlds
t yxmds
fx
ldsmds 2
0
ds趋于零时
O
x
t yx s y
P
A
t t xy
Px
n
px ls x mt xy
(2-3a)
sx
微元体竖直静力平衡条件: Fy 0 可得:
Py s n n
B
y pyds 1 s ydx 1 t xydy 1
过P点的微小三角形,两个边分别 O
平行于坐标轴,当面积SAPB无限减小, 趋近于P点时,平面AB上的应力即成
x
t yx s y
P
A
为过P点斜面上的应力。
P点应力分量(直角坐标面上的应
力)已知:s x ,s y ,t xy t yx
平面问题中一点的应力状态

⑶ 它是在边界上物体保持连续性的条 件,或位移保持连续性的条件。
应力边界条件--设在 s 上给定了面力分 量
fx (s), f y (s).
通过三角形微分体的平衡条件,导出坐标面应力 与斜面应力的关系式,
p l σ m , p m σ l , x x y x y y x y
x y 2 2 xy
2
σ1+σ2=σx+σy
③任一点主应力值是过该点各截面上正应力中的极值。 2 ④最大剪应力所在平面与主 x y 1 2 平面相交45°,其值为 2
m ax
2
⑤主平面上剪应力等于零,但τmax
yx
A
y
x
x l l m p l m l l xy m xy x x x x y x l xy p xyl m m l y ym y xy m xy m l px m y xy l y
问题
§2- 5
平面问题中一点的 应力状态
空间问题有 6 个独立的应力分量,平面问题有 3 个 不为0的应力分量,可决定一点的应力状态。即, 可求出过该点任意斜截面上的正应力与剪应力。
问题的提出:
,xy 已知任一点P处坐标面上应力 σx, σy,
求经过该点的任何斜面上的应力。
问题
斜面应力表示:p ( p ,p ), p ( σ , ). x y n n 求解:取出一个三角形微分体(包含 x 面,
小结: (1)斜面上的应力
p l m yx x x p m l y y x y
(2-3) (2-4)
2 2 l m 2 l m N x y x y (2-5) 2 2 l m ( ) ( l m ) (2-6) N y x x y
工程力学(高教版)教案:8.2 平面应力状态

第二节 平面应力状态如图8-3(a)所示的单元体,因外法线与z 轴重合的平面上其剪应力、正应力均为零,说明该单元体至少有一个主应力的为零,因此该单元体处于平面应力状态。
为便于研究,取其中平面abcd 来代表单元体的受力情况(图8-3b )。
任意斜截面的表示方法及有关规定如下:(1)用x 轴与截面外法线n 间的夹角α表示该截面。
(2)α得正负号:由x 轴向n 旋转,逆时针转向为正,顺时针转向为负(图8-3b 的α角为正)。
(3)ασ得正负号:拉应力为正,压应力为负(图8-3的x σ、y σ、ασ均为正值)。
(4)ατ得正负号:ατ对截面内此任一点的力矩转向,顺时针转向为正,逆时针转向为负(图8-3的x τ、ατ均为正值,y τ为负值)。
图8-3一、任意斜截面上的应力计算任意斜截面上应力有两种方法:解析法和图解法。
(一)解析法因研究的构件是平衡的,因此从构件内一点取单元体,并从单元体上取一部分(图8-3c ),则该部分也处于平衡。
由平衡条件可以求得平面应力状态下单元体任一斜截面上的应力计算公式ατασσσσσα2sin 2cos 22x yx yx --++= (8-1)ατασστα2cos 2sin 2x yx +-=(8-2)应用上式 计算ασ、ατ时,各已知应力x σ、y σ、x τ和α均用其代数值。
例8-1 求图8-4所示各点应力状态下斜截面上的应力(各应力单位是Mpa ),并用图表示出来。
解 (1) 已知:x σ=30Mpa ,y σ=-40 Mpa ,x τ=60 Mpa ,α=30º,将各数值代入式(8-1)、(8-2)得斜截面上的应力46.3960sin 6060cos 240302403030-=-++-=σ Mpa 31.6060cos 6060sin 2403030=++= τ Mpa将 30σ、 30τ方向画在斜截面上,如图8-4(1-b)所示。
(2)已知:x σ=-80Mpa ,y σ=0 Mpa ,x τ=-40 Mpa ,α=120º,将各数值代入式(8-1)、(8-2)得斜截面上的应力64.54240sin 40240cos 280280120-=+-+-=σ Mpa 64.54240cos 40240sin 280120=--=τ Mpa将 120σ、 120τ方向画在斜截面上,如图8-4(2-b)所示。
§2.3 平面应力状态的图解法

应力 方向截面的代表点在 平面上构成一条曲线,由分析可
应变 分析
知这条曲线是一个封闭的圆,称为该点的应力圆,也称莫尔
及应 圆。
力应
变关
系
讲
义
1
莫尔圆(应力圆)的画法
BRY
(1) 斜截面上应力 , 的符号规定
材 料
该点任意平行于 z 轴方向截面上的
力
正应力 ,以拉为“+”;
学 B
切应力 ,以使单元体有顺时针转动趋势为“+”。
料 为单位 1 的直角楔体微元。
力 学
Fnp 0:
r r
B
B 第
p dAcos r dAsin
2
( q dA) cos ( q dA)sin 0
q
p
A
p
np
章
p cos r sin q cos q sin r p
应力 应变 分析
p cos p sin q cos q sin
BRY
§2.3 平面应力状态的图解法
—— 应力圆(莫尔圆)
材
料
力 应力圆(莫尔圆)
学
B
建立直角坐标系 O ,水平轴为正应力 轴,铅垂轴为
第 切应力 轴。某点若为 xy 平面内的平面应力状态,以该点某
2 章
一平行于 z 轴方向斜截面上的正应力 和切应力 的数值为 坐标,可在 平面上得到一个代表点。所有平行于 z 轴
C(
x
y
,
0)
2
B E
P2
系
讲
D A P1 x
义
4
莫尔圆(应力圆)的作用
BRY
莫尔圆(应力圆)图直观地给出了平面应力状态下单元
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面应力状态分析--几何法(2)
平面应力状态分析--几何法(2)
平面应力状态分析—几何法(2)
1. 求任一斜截面上的应力?
可否?
2. 求主应力及方位?
3. 求切应力最值及方位?
平面应力状态分析—几何法(2)
四. 应力圆的应用
1. 求任一斜截面ef上的应力
平面应力状态分析—几何法(2)
从应力圆的半径
CD按方位角α的转向
转动角度2α得到半径
CE。
圆周上E点的坐标
就依次为斜截面上的正
应力σ
α和切应力τ
α。
CD: 起始半径
平面应力状态分析—几何法(2)000cos(22)
cos 2cos 2sin 2sin 2cos 2sin 222x y
x y
x OF OC CF OC CE OC CD CD α
αααααα
σσσσατασ=+=++=+-+-=+-=000sin(22)sin 2cos 2cos 2sin 2sin 2cos 22x y
x FE CE CD CD α
αααααασσατατ=+=
+-=+=证明
横坐标纵坐标
平面应力状态分析—几何法(2)可以看出,应力圆上某点的坐标,对应于单元体某一斜截面上的应力(σα, τα)。
一一对应!
平面应力状态分析—几何法(2)
对比
方位角的起点单元体(解析法)应力圆(几何法)横截面起始半径CD
平面应力状态分析—几何法(2)
对比
方位角的大小单元体(解析法)应力圆(几何法)α2α
转向一致
平面应力状态分析—几何法(2)
2.求主应力及主平面位置
A 1和
B 1两点为
与主平面对应的
点,其横坐标即为
主应力σ1,σ2 。
a. 主应力数值
与解析法一致
22111max 22112min ()22()22x y x y xy x y x y xy OA OC CA OB OC CB σσσστσ=σσσσστσσ⎧+-=+=++=⎪⎪⎨+-⎪=-=-+==⎪⎩
平面应力状态分析—几何法(2) b. 主平面方位角
起始半径CD与半
径CA
的夹角即为应力
1
所在主平面的
圆上σ
1
方位角,且有
∠DCA
=2α0。
1
平面应力状态分析—几何法(2)
由于是顺时针转动,故有:
02tan(2)==xy x y
τDA ασσCA --与解析法一致
二倍角关系
11180A CB ∠= 02tan2=xy x y
τασσ--
平面应力状态分析—几何法(2)
3. 求切应力最值及方位角
G 1和G 2两点的纵坐
标分别代表最大和最小
切应力:
2
2max 1()2x y xy σ-στ=CG =+τ22min 2--()2x y xy σστ=CG =-+τ与解析法一致
平面应力状态分析—几何法(2)
起始半径CD与
的夹角即为
半径CG
1
所在截
应力圆上τ
max
面的方位角,且有
∠DCG
=2 1。
1
由于是逆时针转动,故有:
与解析法一致
1190G CA ∠= 二倍角关系1tan(2)==2x y xy σσDE ατCE
- 平面应力状态分析—几何法(2)。
