阶段提升综合训练一(第十二章第一-四节)
2022年必考点解析沪教版(上海)七年级数学第二学期第十二章实数综合训练试卷(含答案详解)

沪教版(上海)七年级数学第二学期第十二章实数综合训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、平方根和立方根都等于它本身的数是( )A .±1B .1C .0D .﹣12、在实数233,,0.6•2π,1.12112111211112…(每两 个2之间依次多一个1)中,无理数有( )个A .2B .3C .4D .53、a 为有理数,定义运算符号▽:当a >-2时,▽a =-a ;当a <-2时,▽a = a ;当a =-2时,▽a = 0.根据这种运算,则▽[4+▽(2-5)]的值为( )A .1-B .7C .7-D .14、下列各式中正确的是( )A 4±B 34C 3=D 45、观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为2810的末位数字是( )A .2B .4C .8D .66、4的平方根是( )A .±2B .﹣2C .2D .47、16的平方根是( )A .±8B .8C .4D .±48、在实数••133π- ) A .1 B .2 C .3 D .49、下列各数中,最小的数是( )A .0BC .π-D .﹣310、64的立方根为( ).A .2B .4C .8D .-2第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、给定二元数对(p ,q ),其中0p =或1,0q =或1.三种转换器A ,B ,C 对(p ,q )的转换规则如下:(1)在图1所示的“A —B —C ”组合转换器中,若输入()1,0,则输出结果为________;(2)在图2所示的“①—C —②”组合转换器中,若当输入()1,1和()0,0时,输出结果均为0,则该组合转换器为“____—C —____”(写出一种组合即可).2、计算下列各题:(1)|3﹣4|﹣1=_____;(2_____;(3)30=_____;(4)32y xy x+=_____.3、若实数a 、b 、c b ﹣c +1)2=0,则2b ﹣2c +a =________.4、用“*”定义一种新运算:对于任意有理数a 和b ,规定a *b =ab 2+2a ,则3*(-2)=_____________.5、绝对值不大于4且不小于π的整数分别有______.三、解答题(10小题,每小题5分,共计50分)1、计算题:(1)()224332a a a ⋅+-;(2())1012312-⨯+--.2 3、计算:(12(2)2111x x x x -⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭ 4、计算:(1)3173()()()5454---+--;(22)2.5、解方程:(1)x 2=25;(2)8(x +1)3=125.6、已知a 2=16,b 3=27,求a b 的值.7、阅读下面的文字,解答问题.现规定:分别用[]x 和x 〈〉表示实数x 的整数部分和小数部分,如实数3.14的整数部分是[3.14]3=,小数部分是3.140.14〈〉=2-,小数部分是无限不循环小数,无法写完整,2的小数部分,所以2=.(1)= ,= ;= ,= .(2)如果a =,b =,求a b +8、对于有理数a ,b ,定义运算:a b a b a b ⊕=⨯--(1)计算(4)5-⊕的值;(2)填空(2)6-⊕_______6(2)⊕-:(填“>”、“<”或“=”)(3)a b ⊕与b a ⊕相等吗?若相等,请说明理由.9、计算:20201(1)6|3|2π--⨯+-. 10、阅读下列材料:∴34,的整数部分为3,小数部分为3).请你观察上述的规律后试解下面的问题:如果9π的整数部分为a b ,求a b +的值.-参考答案-一、单选题1、C【分析】根据平方根和立方根的定义,可以求出平方根和立方根都是本身数是0.【详解】解:平方根是本身的数有0,立方根是本身的数有1,-1,0;∴平方根和立方根都是本身的数是0.故选C .【点睛】本题主要考查了平方根和立方根的定义,熟知定义是解题的关键:如果有两个数a ,b (b ≥0),满足2a b =,那么a 就叫做b 的平方根;如果有两个数c 、d 满足3c d =,那么c 就叫做d 的立方根.2、C【分析】利用无理数的定义:无限不循环小数称为无理数,进行判断即可,但同时也要掌握有理数的定义:整数和分数统称为有理数.【详解】有理数有:233,0.6•5-,一共四个.无理数有:2π,1.12112111211112…(每两 个2之间依次多一个1),一共四个. 故选:C .【点睛】此题主要是考察了无理数的定义,初中数学中常见的无理数主要是:π,2π等;开方开不尽的数;以及像1.12112111211112…,等有规律的数.3、A【分析】定义运算符号▽:当a >-2时,▽a =-a ;当a <-2时,▽a = a ;当a =-2时,▽a = 0.先判断a 的大小,然后按照题中的运算法则求解即可.【详解】解:2532,-=-<-且当a 2<-时,▽a =a ,∴▽(-3)=-3, 4+▽(2-5)=4-3=1>-2,当a >-2时,▽a =-a ,∴▽[4+▽(2-5)]=▽1=-1,故选:A.【点睛】此题主要考查了定义新运算,以及有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.4、D【分析】由算术平方根的含义可判断A,B,C,由立方根的含义可判断D,从而可得答案.【详解】4,故A不符合题意;3=故B不符合题意;,2C不符合题意;4,运算正确,故D符合题意;故选D【点睛】本题考查的是算术平方根的含义,立方根的含义,掌握“利用算术平方根与立方根的含义求解一个数的算术平方根与立方根”是解本题的关键.5、B【分析】经过观察如果2的次数除以4,余数为1,那末尾数就是2;如果余数是2,那末尾数是4;如果余数为3,那末尾数是8;如果余数是0,那末尾数是6.用810÷4=202…2,余数是2故可知,末尾数是4.2n的个位数字是2,4,8,6循环,所以810÷4=202…2,则2810的末位数字是4.故选:B.【点睛】本题考查了与实数运算相关的规律题,找到2n的末位数的循环规律是解题的关键.6、A【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得2x a=,则x就是a的平方根.【详解】±=解:∵()224∴4的平方根是2±,故选:A.【点睛】本题主要考查平方根的定义,熟练掌握平方根的定义是解题的关键.7、D【分析】根据平方根可直接进行求解.【详解】解:∵(±4)2=16,∴16的平方根是±4.【点睛】本题主要考查平方根,熟练掌握求一个数的平方根是解题的关键.8、B【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【详解】,,∴无理数只有3π2个. 故选:B .【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,3π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.9、C【分析】 有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.【详解】 解:30π-<-<∴所给的各数中,最小的数是π-.故选:C .本题主要考查了有理数大小比较的方法,解题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.10、B【分析】根据立方根的定义进行计算即可.【详解】解:∵43=64,∴实数64,故选:B.【点睛】本题考查立方根,理解立方根的定义是正确解答的关键.二、填空题1、1 A A【分析】(1)利用转换器C的规则即可求出答案.(2)利用转换器A、B、C的规则,写出一组即可.【详解】(1)解:利用转换器C的规则可得:输出结果为1.1,1时,若①对应A,此时经过A、C输出结果为(1,0),②对应A,输出结果恰好(2)解:当输入()为0.0,0时,若①对应A,此时经过A、C输出结果为(0,1),②对应A,输出结果恰好为0.当输入()故答案为:1;A;A.【点睛】本题主要是新定义题目,利用题目所给规则,进行分析判断,即可解答出该题目.2、0 3 1 5 x【分析】(1)先化简绝对值,再计算减法运算即可得;(2)先计算有理数的乘方,再计算算术平方根即可得;(3)计算零指数幂即可得;(4)根据分式的加法运算法则即可得.【详解】解:(1)原式11110=--=-=,故答案为:0;(2)原式3==,故答案为:3;(3)原式1=,故答案为:1;(4)原式325x x x+==,故答案为:5x.【点睛】本题考查了零指数幂、算术平方根、分式的加法等知识点,熟练掌握各运算法则是解题关键.3、1利用绝对值以及平方数的非负性,求出a 的值、b 和c 的关系式,利用整体代入直接求出代数式的值.【详解】解:b ﹣c +1)2=0, 30a ∴-=,10b c -+=,故3a =,1b c -=-,222()2(1)31b c a b c a ∴-+=-+=⨯-+=.故答案为:1.【点睛】本题主要是考查了绝对值以及平方数的非负性、整体代入法求解代数式的值,熟练利用非负性,求出对应字母的值,利用整体代入法,求解代数式的值,这是解决本题的关键.4、18【分析】根据a *b =ab 2+2a ,可得:3*(−2)=3×(−2)2+2×3,据此求出算式的值是多少即可.【详解】解:∵a *b =ab 2+2a ,∴3*(−2),=3×(−2)2+2×3,=3×4+6,=12+6,=18.故答案为:18.此题主要考查了定义新运算,以及有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.5、4【分析】根据绝对值的意义及实数的大小比较可直接进行求解.【详解】解:由绝对值不大于4且不小于π的整数分别有4和4-;故答案为4和4-.【点睛】本题主要考查绝对值的意义及实数的大小比较,熟练掌握绝对值的意义及实数的大小比较是解题的关键.三、解答题1、(1)67a(2)0【分析】(1)先用同底数幂、幂的乘方、积的乘方运算,然后再合并即可;(2)先运用算术平方根、负整数次幂、绝对值、零次幂的知识化简各数,然后再计算即可.(1)解:原式=666+=;347a a a(2)解:原式=2-223-10.⨯+=【点睛】本题主要考查了整式的运算、实数的运算等知识点,灵活运用相关运算法则成为解答本题的关键.2、1【分析】根据平方根与立方根可直接进行求解.【详解】解:原式2231=+-=.【点睛】本题主要考查平方根与立方根,熟练掌握平方根与立方根是解题的关键.3、(1)2;(2)1x-【分析】(1)原式先化简绝对值、二次根式以及立方根,然后再进行外挂;(2)原式先计算括号内的,再把除法转化为乘法,再进行约分即可.【详解】解:(12=2)|3|(3)-----=233-+=2;(2)2111xxx x-⎛⎫⎛⎫-÷-⎪ ⎪⎝⎭⎝⎭=2211x x x x x-+-÷ =2(1)1x x x x -- =1x -.【点睛】 本题主要考查了实数的混合运算以及分式的加减乘除混合运算,掌握运算法则是解答本题的关键.4、(1)52-(2)8- 【分析】(1)根据有理数的混合运算进行计算即可;(24-,进而根据有理数的混合运算进行计算即可 【详解】(1)原式37135544⎡⎤⎛⎫⎛⎫=-+-+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦15222=--=- (2)原式4164448=--÷=--=-【点睛】本题考查了求一个数的立方根,有理数的混合运算,正确的计算是解题的关键.5、(1)5x =±;(2)32x =【分析】(1)根据平方根的定义计算即可;(2)根据立方根的定义计算即可;【详解】解:(1)x2=25 x=±5.(2)3125(1)8x+=x+1=52,x=32.【点睛】本题主要考查平方根、立方根,熟练掌握平方根、立方根的定义是解决本题的关键.6、64或﹣64【分析】根据平方根、立方根、有理数的乘方解决此题.【详解】解:∵a2=16,b3=27,∴a=±4,b=3.当a=4,b=3时,a b=43=64.当a=﹣4,b=3时,a b=(﹣4)3=﹣64.综上:a b=64或﹣64.【点睛】本题主要考查立方根、平方根及有理数的乘方运算,熟练掌握立方根、平方根及有理数的乘方运算是解题的关键.7、(1)11,33;(2)2【分析】(1的范围,再根据题目规定的表示方法写出答案即可;(2a ,b 的值,进一步即可求出结果.【详解】(1<2,34,=11,]=33,故答案为:11,33;(23,1011,a 2,=b =10,∴2108a b +=+=,∴a b +2.【点睛】本题考查了估算无理数的大小和平方根的意义,能够估算出无理数的范围是解决问题的关键.8、(1)21-;(2)=;(3)相等,证明见详解.【分析】(1)按照给定的运算程序,一步一步计算即可;(2)先按新定义运算,再比较大小;(3)按新定义分别运算即可说明理由.【详解】解:(1)()()(4)5=4545204521-⊕-⨯---=-+-=-;(2)()()(2)62626122616-=-⨯---=+-=-⊕,()()6(2)6262126216⊕-=⨯----=--+=-,∴6(2)⊗-=(2)6-⊗,故答案是:=;(3)相等∵a b a b a b ⊗=⨯--,b a b a b a a b a b ⊗=⨯--=⨯--,∴a b ⊗=b a ⊗.【点睛】此题是定义新运算题型,直接把对应的数字代入所给的式子可求出所要的结果. 9、5π-【分析】根据有理数的乘方运算,有理数的乘方运算,化简绝对值,最后进行实数的混合运算即可【详解】解:原式1335ππ=-+-=-.【点睛】本题考查了实数的混合运算,正确的计算是解题的关键.10、a +b 的值为.【分析】由9π≈28.26,可得其整数部分a =28,由27<28<64a +b 的值.【详解】解:∵9π≈28.26,∴a=28,∵27<28<64,<<4,∴b,∴a+b∴a+b的值为【点睛】本题主要考查了估算无理数的大小,根据题意估算出a,b的值是解答此题的关键.。
人教版运动训练 第十二章 周课训练计划与组织题库

人教版运动训练第十二章周课训练计划与组织题库第十二章周课训练的计划与组织第一节训练周的计划与组织1.不同训练周型及其主要任务:1、基本训练周的任务是通过特定的程序和反复练习使运动员掌握和熟练专项技、战术,以及通过负荷的改变引起新的生物适应现象,提高运动员的多种竞技能力。
2、比赛前训练周的任务是使运动员的机体适应比赛的要求和条件,把各种竞技能力集中到专项竞技中去。
3、比赛周的任务是为运动员在各方面培养理想的竞技状态作直接的准备和最后的调整,并参加比赛,力求实现预期的目标。
4、恢复周的任务是消除运动员生理上和心理上疲劳,促进进超量恢复的出现,激发强烈的训练动机,准备投入新的训练。
2.基本训练周训练内容的结构特点:(一)周训练计划中不同内容交替安排的理论基础:(为什么在一周的训练周要安排不同内容的理论依据?08论)由于各种训练内容对机体不同生理系统和心理过程提出的要求不同,因此,在接受了某一内容的负荷之后,机体不同的生理系统及心理过程的反应是不同的,其所需要的恢复时间也不相同。
也就是说,在一次训练后,人体有些系统会产生深度的疲劳,而另一些系统则只产生中度的或轻度的疲劳。
各个系统的恢复过程也呈现出异时性的特征,因此,我们有必要,也有可能在一周中的不同训练日交替安排不同的训练内容。
1、不同的训练内容,对人体各生理系统的要求也不同,如技术要求中枢神经系统与骨骼肌肉系统的高度协调性,耐力训练则要求呼吸与心血管系统承受高度的负荷。
2、不同的训练内容要求不同的供能系统参与运动,在各种运动中三个供能系统参与工作的水平也是不同的3、不同的训练内容要求不同的肌群相同但以不同的工作方式提供运动的主要动力。
4、不同的训练内容对运动员施予不同的心理负荷。
如技术训练要求运动员全神贯注、高度集中,而郊外的越野跑则可使运动员思想放松5、不同目的的训练对运动员机能状态的要求不同,以发展素质、技术及战术等不同竞技能力为目的的训练,对运动员机体状态的要求就不同。
人教版八年级物理下册 第十二章 简单机械 专题训练 综合计算题
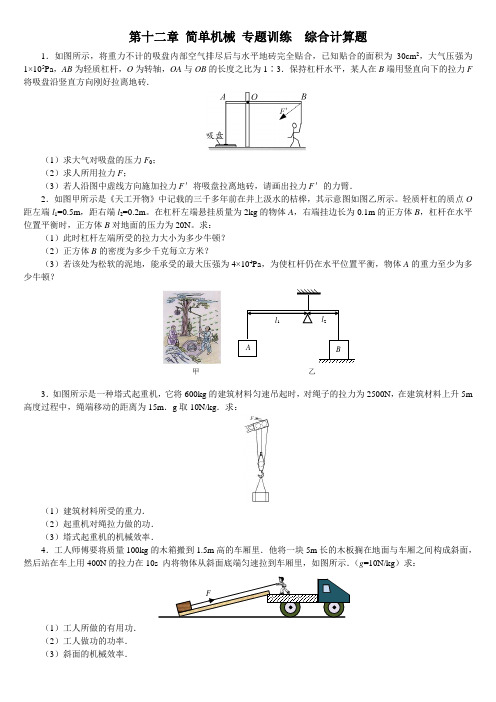
第十二章 简单机械 专题训练 综合计算题1.如图所示,将重力不计的吸盘内部空气排尽后与水平地砖完全贴合,已知贴合的面积为30cm 2,大气压强为1×105Pa ,AB 为轻质杠杆,O 为转轴,OA 与OB 的长度之比为1∶3.保持杠杆水平,某人在B 端用竖直向下的拉力F 将吸盘沿竖直方向刚好拉离地砖.(1)求大气对吸盘的压力F 0; (2)求人所用拉力F ;(3)若人沿图中虚线方向施加拉力F '将吸盘拉离地砖,请画出拉力F '的力臂.2.如图甲所示是《天工开物》中记载的三千多年前在井上汲水的桔槔,其示意图如图乙所示。
轻质杆杠的质点O 距左端l 1=0.5m ,距右端l 2=0.2m 。
在杠杆左端悬挂质量为2kg 的物体A ,右端挂边长为0.1m 的正方体B ,杠杆在水平位置平衡时,正方体B 对地面的压力为20N 。
求:(1)此时杠杆左端所受的拉力大小为多少牛顿? (2)正方体B 的密度为多少千克每立方米?(3)若该处为松软的泥地,能承受的最大压强为4×104Pa ,为使杠杆仍在水平位置平衡,物体A 的重力至少为多少牛顿?3.如图所示是一种塔式起重机,它将600kg 的建筑材料匀速吊起时,对绳子的拉力为2500N ,在建筑材料上升5m 高度过程中,绳端移动的距离为15m .g 取10N/kg .求:(1)建筑材料所受的重力. (2)起重机对绳拉力做的功. (3)塔式起重机的机械效率.4.工人师傅要将质量100kg 的木箱搬到1.5m 高的车厢里.他将一块5m 长的木板搁在地面与车厢之间构成斜面,然后站在车上用400N 的拉力在10s 内将物体从斜面底端匀速拉到车厢里,如图所示.(g =10N/kg )求:(1)工人所做的有用功.(2)工人做功的功率. (3)斜面的机械效率.甲 乙5.用如图所示的滑轮组,将质量为450kg的物体A以0.2m/s的速度沿水平方向匀速向右拉动2m,拉力F大小为200N,物体A与地面间的滑动摩擦力大小是物体A重力的0.1倍,取g=10N/kg。
第十二章识图能力训练 第一节识读电气图的基本方法与步骤

识图能力训练
(1)在绘制电路图时,各种电器元件都应使用国际或 国家统一规定的图形符号和文字符号。
(2)主电路部分采用粗线条画出,控制(辅助)电路部 分采用细线条画出。一般情况下,主电路画在左侧,控 制电路画在右侧。
(3)同一电器的各部分不画在一起,根据其作用原理 分散绘制时,为了便于识别,它们用同一文字符号标注。
识图能力训练
3. 看标题栏 图纸中标题栏也是重要的组成部分,它告诉你电 气图的名称及图号等有关内容,由此可对电气图的类 型、性质、作用等有明确认识,同时可大致了解电气 图的内容。 4. 看概略图(或框图) 看图纸说明后,就要看概略图,从而了解整个系 统或分系统的概况,即它们的基本组成、相互关系及 其主要特征,为进一步理解系统或分系统的工作方式、 原理打下基础。
识图能力训练
三、电气原理图识读举例 现以电动机单向启动控制电路为例(如图12.1所 示),详细介绍电气原理图主电路、辅助电路的识 读方法。 电动机的控制是生产中最主要的电气控制方式 之一。电动机单向启动控制电路是其中应用最广泛、 也是最基本的线路,该线路能实现对电动机启动控 制、停止控制、远距离控制、频繁操作等,并具有 短路、过载、失压等保护。识图的方法与步骤如下:
识图能力训练
3.结合典型电路看图 典型电路就是常见的基本电路,如电动机正、 反转控制电路,顺序控制电路,行程控制电路,晶 体管整流电路,滤波电路,晶体管振荡及放大电路, 晶闸管触发电路等,不管多么复杂的电路,总能将 其分割成若干个典型电路,先搞清每个典型电路的 原理和作用,然后再将典型电路串联组合起来看, 就能大体把一个复杂电路看懂了。这实际上就是一 种从“整体到局部”、再从“局部到整体”的看图 方法。
识图能力训练
第二步,搞清用什么电气元器件控制用电器, 是开关还是启动器或是接触器、继电器。 在本电路中控制电动机的电气元器件是接触器:KM。 第三步,看主电路上还有什么电器,有何用途。 如电源开关、熔断器、热继电器等。 在本电路中还接有电源开关QF、热继电器FR。QF 控制主电路电源的接通和断开,FR对M起过载保护作 用。 第四步,看电源,了解电源电压等级。 本电路的电源是380V三相交流电。
(完整版)第十二章周训练的计划与组织

第十二章周训练的计划与组织班级人数时间教学任务与要求:了解制定周、课时训练计划的意义和作用;正确理解周、课时训练计划的结构和种类;掌握制定多年训练计划方法在实践中的正确应用。
教学重点与难点重点:什么是周、课时训练计划?周、课时训练计划的基本结构如何?难点:如何正确掌握制定周、课训练计划的方法及在训练实践中正确应用。
教学步骤第一节训练周的计划与组织在训练实践中,人们根据自己训练的需要组织小周期训练过程,并从不同的角度出发将训练的小周期分为不同的类型。
这些分类实际上也就是周训练过程的分类。
根据训练任务及内容的不同,可把周的训练计划分为基本训练周、赛前诱导周、比赛周以及恢复周这样四种基本类型(表12-1)。
为适应不同任务而制定的各种相应的周训练计划,也表现出明显不同的负荷变化特点。
一、基本训练周的计划与组织1、基本训练周计划的主要任务基本训练周的任务,是通过特定的程序和反复练习使运动员掌握和熟练专项技、战术,以及通过负荷的改变引起新的生物适应现象,以获得多种竞技能力的提高。
在全年训练中,基本训练周被采用得最多。
2、基本训练周训练内容的结构特点决定周训练计划内容结构的主要依据,是实现训练目标的需要和不同负荷后机体的反应及恢复状况。
前者决定着应该把哪些内容列人训练计划之中,后者则决定着这些内容应该怎样组合在一起。
大多数优秀运动员常常每日训练两次,并取得了出色的训练成果。
这主要应归功于周训练过程中不同内容及不同负荷的交替安排。
(1)周训练计划中不同内容交替安排的理论基础负荷情况下肌肉收缩时人体三个供能系统的参与是非同步的。
人体运动时依赖无氧磷酸原供能、无氧糖酵解供能和有氧供能这样三个系统分别提供完成肌肉工作所需要的能量。
瑞典的奥马特森(1982)论述道:“这三个系统可以释放所需的大量能量。
然而,在大多数情况下,只有一个或两个系统同时发生作用”。
“至于要以哪一个系统供给的能量为主来还原ATP,则取决于练习的强度及其持续时间”。
人教版八年级数学上册《第十一、十二章》综合训练(有解析)

八年级数学上册《第十一、十二章》综合训练一、单选题(3分每题)1.一个三角形三条边长度的比为2:3:4,且其中一条边长是12cm,这个三角形周长不可能是:()A.54cm B.36cm C.27cm D.24cm2.已知一个多边形的内角和为1080°,则这个多边形为()A.七边形B.八边形C.九边形D.十边形3.如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC 和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为().A.115°B.110°C.105°D.100°4.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是()A.BC=DC,∠A=∠D B.BC=EC,AC=DC C.BC=EC,∠B=∠E D.∠B=∠E,∠A=∠D5.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC 分为三个三角形,则S△ABO:S△BCO:S△CAO等于()A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:56.如图所示,在中,P为上一点,,垂足为R,,垂足为S,,.下面三个结论:①;②;③.正确的是()A.①和②B.②和③C.①和③D.全对二、填空题7.在△ABC中,CM是AB边上的中线,已知BC﹣AC=8cm,且△MBC的周长为30cm,则△AMC的周长为_____cm.8.如图①,点E、F分别为长方形纸带ABCD的边AD、BC上的点,∠DEF=19°,将纸带沿EF折叠成图②(G为ED和EF的交点,再沿BF折叠成图③(H为EF和DG的交点),则图③中∠DHF=__.9.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=________10.如图,中,,,平分.交于D,于E,且,的周长为________.11.如图,要测量河岸相对的A,B两点之间的距离,先在的延长线上取一点D,使,再过点D作垂线,使A,C,E在一条直线上,则的依据是________.三、解答题12.如图,在△ABC中,BD⊥AC于D.若∠A:∠ABC:∠ACB=3:4:5,E为线段BD上任一点.(1)试求∠ABD的度数;(2)求证:∠BEC>∠A.13.(1)如图①所示,∠1+∠2与∠B+∠C有什么关系?为什么?(2)如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时,则∠A与∠α+∠β之间有一种数量关系始终保持不变,请写出这个规律并说明理由.14.如图①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA 的平分线,AD、CE相交于点F.(1)请你判断并写出FE与FD之间的数量关系(不需证明);(2)如图②,如果∠ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.15.如图,已知△ABC中,AB=AC=10厘米,∠ABC=∠ACB,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q 在线段CA上由C点向A点运动,设点P运动的时间为t.(1)用含有t的代数式表示线段PC的长度;(2)若点Q的运动速度与点P的运动速度相等,经过1秒后△BPD与△CQP是否全等,请说明理由;(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?16.如图,已知中,是边上的高,是的角平分线,若,,求的度数.17.(1)如图1,在四边形ABCD中,AB=CB,AD=CD.求证:∠C=∠A.(2)如图2,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AB=DE.18.已知△ABC与△中,AC=,BC=,∠BAC=∠,(1)试证明△ABC≌△.(2)上题中,若将条件改为AC=,BC=,∠BAC=∠,结论是否成立?为什么?19.观察、猜想、探究:在中,.如图,当,AD为的角平分线时,求证:;如图,当,AD为的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;如图,当AD为的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.20.探究问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为.拓展问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.推广问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.答案1.D【解析】由三角形三条边长度的比为,可得三边分别占三角形周长的若是最短边,则三角形周长若是较长边,则三角形周长若是最长边,则三角形周长所以三角形周长不可能是.2.B【解析】根据多边形的内角和公式,可知(n-2)·180°=1080°,解得n=8,因此这个多边形是八边形.3.D【解析】∵BE⊥AD,∴∠BED=90°,又∵∠ADC=110°,∴四边形BCDE中,∠BCD+∠CBE=360°-90°-110°=160°,又∵∠EBC和∠DCB的角平分线相交于点F,∴∠BCF+∠CBF=12×160°=80°,∴△BCF中,∠F=180°-80°=100°,4.A【解析】A、已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;B、已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;C、已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC≌△DEC,故此选项不合题意;D、已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意;5.C【解析】本题主要考查三角形的角平分线。
运动训练学十、十一、十二章

以国内外已有的研究成果,考虑不同项群训练的特点, 划分如下表:
2021/6/16
运动训练学
7
全程性多年训练的阶段划分表
阶段
主要任 务
年限
发展一
基础训练
般 运动能
3-5
力
提高专
专项训练
项 竞技能
4-6
力
创造优
最佳竞技
异成 4-8
绩
努力保
竞技保持
持竞 技水
2-5
平
训练的重点内容及顺序
(三)确定比赛时期
在主要比赛阶段前面加上一个历时4-6周的热身比赛阶段,两个阶段合起来就组成了 比赛时期,总时间为8~12周,其间要注意安排必要的热身赛。
(四)确定整个训练大时期
在比赛时期前面加上6-12周的准备时期,后面2-4周的恢复时期,即构成了一个总 时间为14-32周、3.5-7.5个月的训练大周期。
大周期是以成功地参加1-2次重大比赛为目标而设计的。其时间的确定通常采用体现 目标控制思想的“倒数时”充填式方法。14-32周 为例(大比赛)
(一)确定主要比赛日期:由竞赛日程决定
(二)确定主要比赛阶段
在常规大周期中,主要比赛阶段持续4-6周,在主要比赛日后约一周结束。防止比 赛一完,运动员最佳竞技状态消失。
最佳竞技阶段:集中进行训练、积极参加各种比赛, 在适宜的条件下创造运动成绩。一般持续4—8或更长。多 参加国外比赛。
2021/6/16
运动训练学
12
(二)两阶段负荷安排的不同特点
专项提高阶段:较大的负荷。可以是增长式发 展,也可以波浪式发展,有明显的节奏
最佳竞技阶段:逐步达到最大负荷。有明显节 奏。
强化训练沪粤版九年级物理上册第十二章内能与热机综合训练试卷(含答案详解)

沪粤版九年级物理上册第十二章内能与热机综合训练考试时间:90分钟;命题人:物理教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 20分)一、单选题(10小题,每小题2分,共计20分)1、把一瓶酒精倒去一半,则剩下的酒精()A.比热容和热值均变为原来的一半B.比热容变为原来的一半,热值不变C.热值变为原来的一半,比热容不变D.比热容和热值都不变2、汽车的发动机大多数是内燃机,内燃机是热机的一种,下列关于热机和环境保护的说法,正确的是()A.热机排出的尾气没有内能B.热机的效率能达到100%C.热机的大量使用会造成环境污染D.汽油机的做功冲程是将机械能转化成内能3、下列说法正确的是()A.热值大的燃料完全燃烧,放出的热量一定多B.物体的温度不变,它的内能一定不变C.物体的内能增加,可能是从外界吸收了热量D.热量总是从内能大的物体向内能小的物体传递4、下列现象和推断不符合实际的是()A.现象:抽去玻璃板,两瓶中的气体都会变成红棕色。
推断:分子在不停地做无规则运动B.现象:稍稍用力向上拉玻璃板,弹簧测力计示数变大。
推断:分子间只有引力没有斥力C.现象:棉花被点燃。
推断:外界对物体做功,物体的内能增大,温度升高D.现象:当塞子跳起时瓶内出现白雾。
推断:物体对外界做功,物体内能减小,温度降低5、某汽油机的四个冲程如图所示,在该汽油机的一个工作循环中,压缩冲程结束后,下个冲程是()A.①B.②C.③D.④6、甲、乙两物体质量都为2kg,丙物体质量为1kg,三个物体温度都升高1℃,吸收热量如图所示,则()A.甲的比热容为3000J/(kg·℃)B.甲的比热容比乙的大C.乙和丙的比热容相等D.吸收相同热量,甲升高的温度大于丙7、热学世界真了不起,揭开了隐藏在物质世界深处的秘密,瓦特发明的蒸汽机推动了第一次工业革命……。
2019年高考数学(理) 第十二章 全章综合训练

全章综合训练1.[广东惠州2018调研]从0,1,2,3,4中任选两个不同的数字组成一个两位数,其中偶数的个数是( ) A .6 B .8 C .10 D .122.[西藏拉萨2018一模]若8)6(x a x -的展开式中常数项为56,则实数a 的值为( )A .2±B .±1C .21±D.22±3.[广西柳州2018 -模](x-2y )⁶的展开式中,x ²y ⁴的系数为( ) A .60 B .-60 C .240 D .- 2404.[贵州黔东南州2018一模]在n xx )212(-展开式中存在常数项,则正整数n 可以是( )A .2 017B .2 018C .2 019D .2 0205.[江西南昌二中2018月考]某班组织文艺晚会,准备从A ,B 等8个节目中选出4个节目演出,要求:A ,B 两个节目至少有一个选中,且A ,B 同时选中时,它们的演出顺序不能相邻,那么不同演出顺序的和数为( ) A .1 860 B .1 320 C .1 140 D .1 0206.[河北石家庄重点高中2018联考]设(2 -x )⁵=a ₀+a ₁x+ a ₂x ²+…+a ₅x ⁵,则3142a a a a ++的值为( )A .6061-B .121122-C .43-D .12190-7.[湖北长郡中学2018入学考试]若二项式7)2(x a x +的展开式的各项系数之和为-1,则含x ²项的系数为( )A .560B .- 560C .280D .-2808.[山西太原五中等六校2018联考]本周日有5所不同的高校来我校作招生宣传,学校要求每位同学从中任选1所或2所去咨询了解,甲、乙、丙三位同学的选择没有一所是相同的,则不同的选法共有( ) A .330种 B .420种 C .510种 D .600种9.[湖南衡阳八中2018月考]现要给一长、宽、高分别为3.2.1的长方体工艺品各面涂色,有红、橙、黄、蓝、绿五种颜色的涂料可供选择,要求相邻的面不能涂相同的颜色,且橙色跟黄色二选一,红色要涂两个面,则不同的涂色方案种数有( ) A.48种 B .72种 C .96种 D .108种10.在中美组织的暑假中学生交流会结束时,中方组织者将孙悟空、猪八戒、沙憎、唐憎、白龙马彩色陶俑各一个送给来中国的美国中学生汤姆、杰克、索菲亚,每个学生至少一个,且猪八戒不旋送给索菲亚,则不同的送法种数为( ) A. 124 B .100 C .72 D .7611.[辽宁瓦房店2018一模]5)16(xx x +的展开式的常数项是______.12.[陕西吕粱2018 -模](x+1)(x-1)⁵展开式中含x³;项的系数为______.(用数字表示)13.[内蒙古巴彦淖尔中学2018月考]若5)13)(21(+-x a x 的展开式中的常数项为- 12,则a=______.14.[浙江瑞安中学2018期中]nxbax)(-(ab≠0,且a,b为常数)的展开式中,x的系数为10a³b²,则n=______.15.[四川德阳三校2018联考]已知(1 - 2x)⁷=a₀+a₁x+a₂x²+…+a₇x⁷,贝a₁=______.16.[吉林百校联盟2018联考](x+2 018y²)(x-y)¹ᴼ展开式中x⁵y⁶的系数为______.17.[江西南昌二中2018期末]安排A,B,C,D,E,F六名义工照顾甲、乙、丙三位老人,每两位义工照顾一位老人,考虑到义工与老人住址距离问题,不安排义工A照顾老人甲,不安排义工B照顾老人乙,安排方法共有______种.18.[山东济南2018一模]5)12)((xxxax--的展开式中各项系数的和为2,则该展开式中含x⁴项的系数为______.刷真题1.[课标全国Ⅱ理2016·5]如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为()A.24B.18C.12D.92.[四川理2016·4]用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为()A.24B.48C.60D.723.[课标全国Ⅱ理2017·6]安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有()A.12种B.18种C.24种D.36种4.[四川理2016·2]设i为虚数单位,则(x+i)⁶的展开式中含x⁴的项为()A.-15x⁴B .15x ⁴C .-20ix ⁴D .20ix ⁴5.[课标全国I 理2017·6]6)1)(211(x x ++展开式中x ²的系数为( ) A .15 B. 20 C .30 D .356.[课标全国Ⅲ理2017·4](x+y )(2x -y )⁵的展开式中x³y³的系数为( ) A .-80 B .-40 C .40 D .807.[课标全国Ⅲ理2016·12]定义“规范01数列”{}n a 如下:{}n a 共有2m 项,其中m 项为0,m 项为1,且对任意k ≤2m ,a ₁,a ₂,…,ka 中0的个数不少于1的个数,若m=4,则不同的“规范01数列”共有( ) A .18个 B .16个 C .14个 D .12个8.[课标全国I 理2018·15]从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生人选,则不同的选法共有______种.(用数字填写答案)9.[天津理2018·10]在5)21(xx -的展开式中,x ²的系数为______.10.[浙江2018·16]从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成______个没有重复数字的四位数.(用数字作答)11.[天津理2017·14]用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有______个.(用数字作答)12.[浙江2017·16]从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有______种不同的选法.(用数字作答) 13.[山东理2017·11]已知(1+3x )ⁿ的展开式中含有x ²项的系数是54,则n=______. 14.[浙江2018·14]二项式8)213(x x +的展开式的常数项是______. 15.[天津理2016·10]8)12(x x -的展开式中x ⁷的系数为______.(用数字作答)16.[课标全国I 理2016·14]5)52(+x 的展开式中,x³的系数是______(用数字填写答案).17.[浙江2017·13]已知多项式(x+1)³(x+2)²=x ⁵+a ₁x ⁴+ a ₂x³+a ₃x ²+a ₄x+a ₅,则a ₄=______, a ₅=______.18.[上海理2016·8]在nx x )23(-的二项展开式中,所有项的二项式系数之和为256,则常数项等于______.全章综合训练1.C 【解析】由题意,该两位数是偶数时,其个位可能是0,2,4,个位是0时,偶数有4个;个位是2时,偶数有3个;个位是4时,偶数有3个.所以偶数共有4 +3 +3 =10(个).故选C .2.A 解析,8)6(x a x -的展开式中常数项为562282)(6)6(28==-a x a x C ,解得2±=a .故选A . 3.C 【解析】r y r x r C Tr )2(661--=+.∴r =4,2404)2(6=-r C .故选c .4.C 【解析】通项r n x r n C r n r r x r n x r n C T r 32)1()21()2(1---=--=+.依题意得n - 3r= O n =3r.故n 是3的倍数,故选C .5.C 【解析】由题可知可分为两类:第一类,A ,B 只有一个选中,则不同的演出顺序有443612A C C 种;第二类,A ,B 同时选中,则不同演出顺序有232226A C C 种,共有1140232226443612=+A A C A C C 种,故选C .6.C 【解析】由二项式定理,得8042151-=⨯-=C a ,8032252=⨯=C a ;4022353-=⨯-=C a ,102454=⨯=C a ,所以433142-=++a a aa .故选C .7.A 【解析】令x=1,得二项式7)2(x ax +的展开式的各项系数之和为(1+a)⁷,即(1+a)⁷=-1,1+a=-1,a=-2.二项式7)2(x a x -的展开式的通项r x r r C r x x r C T r 314.)2.(7)2.(r 72.71--=--=+)(.令14 -3r =2,得r=4.因此二项式7)2(x a x -的展开式中含x ²项的系数为56042.47=-)(C .故选A .8.A 【解析】由题意,若都选1所,有6035=A 种选法.若有1人选2所,其他2人只选1所,则有180232513=A C C 种选法,若有2人选2所,1人选1所,则有90241513=C C C 种选法,故共有60 +180 +90= 330种选法.故选A .9.C 【解析】按要求,能涂相同颜色的面只能是长方体中相对的面,因为橙色、黄色二选一,且红色必用,所以剩余的蓝色、绿色可以二选一,也可两种颜色都选用,若蓝色、绿色二选一,则不同的涂色方案有24331212=A C C 种,若蓝色、绿色均选用,则不同的涂色方案有7222231312=A A C C 种,故共有24十72= 96种方案.故选C .10.B 【解析】根据索菲亚所得彩色陶俑个数分为三类:第1类,索菲亚得3个,先在除猪八戒外4个中选3个送给索菲亚有34C 种不同方法,再将剩余两个分别送给杰克与汤姆有22A 种不同方法,根据分步乘法计数原理共有2234A C 种不同方法;第2类,索菲亚得2个,先在除猪八戒外4个中选2个送给索菲亚有24C 种不同方法,再将剩余的三个彩色陶俑分成两组有c 23种不同的分组方法,再将这两组分别送给杰克与汤姆有A 22种不同方法,根据分步乘法计数原理共有A C C 222324种不同方法;第3类,索菲亚得1个,先在除猪八戒外4个中选1个送给索菲亚有C 14种不同方法,再将剩余的4个彩色陶俑分成两组有22222434A C C C +种不同的分组方法,再将这两组分别送给杰克与汤姆有22A 种不同方法,共有22)22222434(14A A C C C C +种不同方法,根据分类加法计数原理可得不同的送法种数为10022)22222434(142223242234=++++A A C C C C A C C A C 种,故选B .11.5 解析 二项式5)16(x x x +展开式的通项为r r x r C r x x r x r C T 2153015)1(5)6(5-+=-=,令021530=-r ,解得r=4,∴常数项是545=C .12.0【解析】(x-1)⁵展开式中含x³项的系数为1025=C ,含x ²项的系数为1035-=-C ,所以(x+1)(x-1)⁵展开式中含x³项的系数为10 -10 =0.13.-1【解析】x 1与5)13(+x a 展开式的含x 的项相乘,-2与5)13(+x a 展开式的常数项相乘,结果均为常数,所以5)13).(21(+-x a x 展开式中的常数项为122310325-=-=-a a C ,解得14.5【解析】展开式中x 的系数为232b a nC ,则232b a nC =10a³b ²,即102=nC ,解得n=5.15.- 14【解析】含x 的项的系数为14)2(17-=-⨯C .16. 210【解析】由题意可得(x+2 018y ²)(x-y )¹ᴼ=x (x-y )¹ᴼ+2 018y ²(x -y)¹ᴼ,据此可得只有x(x -y)¹ᴼ中含有x ⁵y ⁶,结合二项式定理可得其系数为2106)1(610=-⨯C ,17. 42【解析】不考虑义工与老人住址距离问题,安排方法有902426=C C 种,当A 照顾老人甲时有302415=C C 种,同理义丁口照顾老人乙也有30种,再加上A ,B 同时分别照顾老人甲和乙有122.24=C 种,所以共有90 - 30 x2 +12= 42种安排方法.18.-48【解析】令x=1可得5)12)((x x x a x --的展开式中各项系数的和为1-a=2,得a=-1,5)12)(1(x x x x -+展开式x ⁴的系数,即为5)12(x x -展开式中的x³与x³系数的和,5)12(x x -展开式通项为r x r r r C Tr 2552.)1(51---=+,令5-2r =3,得r=1,令5-2r =5,得r=0,将r=1与r=0分别代入通项,可得x³与x ⁵的系数分别为- 80与32.∴原展开式x ⁴的系数为- 80 +32=-48,故答案为- 48. 刷真题1.B 【解析】由E 到F 向上和向右各走2段,故有624=C 种走法,同理从F 到G 有313=C 种走法,由分步乘法计数原理可知,共有6×3=18条最短路径.故选B .2.D 【解析】由1,2,3,4,5组成没有重复数字的五位数,个位数为奇数的有C 13种,其余4个数字全排列,所以奇数的个数为44.13A C =3×4×3×2×1=72.故选D . 3.D 【解析】把4项工作分成“三堆”,其中“一堆”包含2项工作,另“两堆”各包含1项工作,其分法有242211.12.24C A C C C =种;然后把这“三堆”分配给3名志愿者,则分法有33A 种,根据分步乘法计数原理可得不同的安排方式共有3633.24=A C 种.故选D.4.A 【解析】二项展开式的通项r ix r C Tr -=+661,令6-r =4,得r=2,所以含x ⁴的项为4154226x x i C -=.故选A .5.C 【解析】x ²的系数由两部分组成,即(1+x)⁶中x ²的系数和x ⁴的系数.∴304626=+C C .故6.C 【解析】令M=x+y ,N=(2x-y)⁵.若M 中取x ,则N 中取含x ²y³的项,即32403)(2)2(35y x y x C -=-,∴3340)3240.(y x y x x -=-.若M 中取y ,则N 中取含x³y ²的项,即23802)(3)2(25y x y x C =-,∴y ·(80x³ y ²)= 80x³ y³.合并同类项得-40x³y³ +80x³y³=40x³y³,系数为40.7.C 【解析】当m=4时,数列共有8项,由题可知,a ₁=0,a ₈ =1,分类考虑:①当前四项全为0时,后四项全为1,满足条件,有1个;②当前四项有三项为0时,第2,3,4项任取两项为0,第5,6,7项任取一项为0,共有913.23=C C 个;③当前四项有两项为0时,则第2或3项为0,第5项一定为o ,第6,7项有一项为0,共有412.12=C C 个.综上,共有1+9 +4=14个.故选C .8. 16 【解析】方法一(直接法):①选1女2男有1224.12=CC 种选法,②选2女1男有414.22=C C 种选法.根据分类加法原理,共12 +4= 16种不同选法.方法二(间接法):6人中选3人有36C 种选法,3人全是男生有34C 种选法,∴符合题意的不同选法有1642034.36=-=C C 种.9.25【解析】5)21(x x -的展开式的通项为r x r C r r x r x r T 2351r 5)21()21(55C -+-=--=,令2235=-r ,解得r=2,所以X ²的系数为25252)21(=-C . 10.1260【解析】方法一:第一类,含有0时有54033132513=A C C C 个;第二类,不含0时,有72044132523=A C C C 个,由分类加法计数原理得共有四位数540 +720 =1 260个.方法二(间接法):不考虑数字0时,共可以组成1440442425=A C C 个;当0在首位时,有180331325=A C C 个,故满足题意的数共有1 440 - 180 =1260个.11.1 080【解析】一个数字是偶数、三个数字是奇数的四位数有960443514=A C C 个;四个数字都是奇数的四位数有12045=A 个,则至多有一个数字是偶数的四位数一共有960 +120 =1080个.12. 660【解析】若不考虑至少有1名女生的要求,则不同的选法种数为840261718=C C C .若选出的服务队中没有女生,则选法种数为180241516=C C C .所以满足题意的选法种数为840 -13.4【解析】n x )31(+的展开式的通项为r x r n C T r )3(1=+,由题意知2x 542)3(2=x n C ,即62)1(=-n n ,解得n=4.14.7【解析】由题知8)21(8)213(31x x x x +=+,由二项式定理得通项为34838311.8)21(..8)21()21.(8)(8r rr x r C r r x x r C r r x r x r C T --+=-=-=,令0348=-r,解得r=2,∴常数项为727841282)21(3=⨯⨯=⨯=C T .15. -56【解析】二项展开式的通项为r x r r C r x r x r C Tr 316)1(8)1.(8)2(81--=--=+,令16 - 3r=7,则r=3.∴x ⁷的系数为(-1)³.38C =-56.16.10【解析】5)2(x x +的展开式的通项为2552521r 25525.5)2(5T rr rr rxr C x r r C x r x r C --+-+=-=-=(r=0,1,…,5).令325=-r,得r=4.∴x³的系数是1045245=-⨯C .17. 16 4【解析】(x+1)³展开式的通项为r x r C Tr -=+331(r =0,1,2,3),(x+2)²=X ² +4x+4,所以一次项系数164334234=⨯+⨯=C C a ,常数项44335=⨯=C a .18. 112【解析】由题意得2562=n,解得n=8.通项为348351.)2(8)2.(.8r rr x r r C r xx r C T --+-=-=.令0348=-r,则r=2,故常数项为1122)2(28=-⨯C .。
运动训练学课件(第十二章)

2 恢复周训练内容及负荷结构的特点
为了实现恢复周训练的主要目标,要求其训练内容广泛而 灵活。应多选择以下内容:
一般性的身体练习。如非专项的球类活动、游泳、各种非 竞技性的健身体操等等;
带有游戏性的练习等等。 恢复周通常大大降低负荷强度、负荷量,或者大幅度地减
➢ 还要注意负荷的合理分配,以便运动员能依次完成全部训 练内容,达到预期的训练目的。
4、测验、检查和比赛课的要求
➢ 训练过程中的测验、检查和比赛是检查训练成果的手段。 要注意采用符合计划要求的测验、检查的练习、手段及方 式、方法,以便准确、客观地反映运动员的训练状态。
二、训练课的结构
➢准备部分 ➢基本部分 ➢结束部分
结束部分
➢ 没有恢复就没有训练,恢复从课上开始 ➢ 各种训练课结束部分的任务主要是解除训练课基本部分所造
成的心理、生理上的紧张状态 ➢ 现代运动训练把恢复作为训练的组成成分。当然,作为训练
课的结束部分并不可能完全消除因紧张训练工作所带来的疲 劳,训练课的结束也就意味着运动员有机体全面恢复过程的 开始。因此,有组织地进行课的结束部分对恢复过程的积极 进行有着重要的作用
星期一 星期二 星期三 星期四 星期五
星期六 星期日
――――――――――――――――――――――――――――――――――――――
上午 小结 力量训练 投篮训练 小结 投篮训练 小结 投篮训练
调整
针对训练 调整 针对训练 调整 针对训练
下午 技战术 技战术
或途中 或休息
晚上
比赛
技战术训练 或途中
比赛
力量训练 或途中
周训练计划的分类
鲍艾尔斯费尔特和施勒特划分为准备小周期、基础负荷小 周期、提高成绩小周期和积极性休息小周期;
苏科版九年级物理上册第十二章机械能和内能综合训练练习题(详解)

苏科版九年级物理上册第十二章机械能和内能综合训练考试时间:90分钟;命题人:物理教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、甲、乙两车同时同地沿同一直线做匀速直线运动,它们的s t 图像如图所示,则()A.甲车的动能大于乙车的动能B.甲、乙两车的重力势能相等C.经过8秒,甲、乙两车相距10米D.运动10米,甲车比乙车少用4秒2、关于分子和物体内能,下列说法正确的是()A.杯子里的水可以任意倒出,说明水分子间没有引力B.固体间能扩散,表明固体物质分子是运动的C.把0℃ 的冰块加热熔化成0℃ 的水,其内能不变D.用力搓手,手发热时的能量转化关系与做功冲程一样3、如图为四冲程汽油机工作过程中某一冲程的示意图,此冲程的名称及能量转化是()A.吸气冲程,机械能转化为内能B.压缩冲程,机械能转化为内能C.做功冲程,内能转化为机械能D.排气冲程,内能转化为机械能4、关于汽油机和柴油机的区别,下列说法中你认为不妥的是()A.柴油机比汽油机费用低廉,但比较笨重B.柴油机的效率一般比汽油机的效率高C.一个工作循环中汽油机做功一次,柴油机做两次功D.在构造上,柴油机汽缸顶部有喷油嘴而没有火花塞5、关于温度、热量和内能,下列说法正确的是()A.物体的温度升高,一定吸收了热量B.物体吸收了热量,温度一定升高C.物体的温度降低,内能一定减小D.物体的内能增大,温度一定升高6、在如图所示事例中,不属于做功改变内能的是()A.冷天搓手取暖B.空气被压缩时内能增大C.烧水时水温升高D.下滑时臀部发热7、一桶汽油用去一半,剩下的半桶汽油不变的物理量是()A.热值,内能B.比热容,密度C.质量,体积D.内能,密度8、下列说法正确的是()A.温度高的物体一定比温度低的物体放出的热量多B.物质的比热容与物体的质量、吸收的热量及温度变化有关C.物体对外做功,其内能可能减少D.热值大的燃料完全燃烧放出的热量一定多9、下列事例中属于内能转化为机械能的是()A.古代人的钻木取火B.锯铁管时锯条发热C.运载火箭点火升空D.汽油机的压缩冲程10、改变物体内能的方法只有做功和热传递。
运动训练学课程第十二章 训练周课过程的计划与组织

12/3/2019
运动训练学
5
(2)基本训练周负荷的变化
周计划的两段结构:上半周的训练后,在一周的中间 安排较小的负荷或其他形式的积极性休息作为调整,在下 半周,从负荷的内容和程度上,常常与上半周相似。
周负荷的加大,是基本训练周负荷变化的主要特点。 加大负荷的途径有:
增加负荷强度,负荷量保持或减少负荷强度; 提高负荷强度,负荷量保持不变或减少; 负荷量和强度都保持不变,通过负荷的累加效应给
机体更深的刺激。
12/3/2019
运动训练学
6
二、 赛前训练周的计划与组织
1、主要任务 赛前训练周主要用于比赛前的专门训练准备。
2、赛前训练周训练内容和负荷结构的特点 训练内容更加专业化,采用的练习更加接近专项的运
动形式,练习的组织形式更加接近专项比赛的特点。
12/3/2019
运动训练学
7
三、 比赛周的计划与组织
1、主要任务
不同时期的比赛周有不周的特点,如准备期的比赛周 就可以稍加调整,随机参加。 2、比赛周训练内容和负荷结构特点 (1)超量恢复的集中安排
4
3、基本训练周负荷的结构特点
(1) 基本训练周的课次安排
不同水平运动员的训练日数和课次差别很大。少年儿童在基本训 练阶段的初期,每周2—4次就可以。
课次的增加,开始增加训练的日数,由每周2—3个训练日增加 到6—7个。以后再将一周中的训练日的训练次数增加为2次,使每周 训练课次达到8—10次。最后做到每日2次训练。个别运动项目和运 动员可更多。目前周训练最高次数是每日训练3—5次,周训练25次, 最长课时为2—3个小时,最短为45分钟。
2021-2022学年度沪科版九年级物理第十二章温度与物态变化综合训练试题(含解析)

沪科版九年级物理第十二章温度与物态变化综合训练考试时间:90分钟;命题人:物理教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、下列数据中,最接近生活实际情况的是()A.八年级物理课本的质量约20gB.光在空气中传播的速度约为340m/sC.唐山市冬季平均气温约-15℃D.全新2B铅笔的长度约为18cm2、下列现象中,可以用分子热运动规律解释的是()A.还未看见瀑布,先听见瀑布的声音B.还未看见花儿,先嗅到花儿的香气C.神舟十三号载人飞船腾空而起D.火车呼啸着从站台驶过3、关于运动和能量以下说法中错误的是()A.灰尘飞舞属于微观运动B.原子由原子核及核外电子组成C.从远处闻到花香说明分子在运动D.行驶中的汽车具有能量4、在国际单位制中,速度的单位是()A.摄氏度(℃)B.米/秒(m/s)C.米(m)D.秒(s)5、小明在实验室做“观察水的沸腾”实验,烧杯下面垫有石棉网,如图所示,下列说法正确的是()A.水在沸腾过程中,温度计示数一定达到100℃B.水在沸腾过程中,继续吸热,温度不变C.杯口冒“白气”,是汽化现象D.撤去酒精灯,水未立刻停止沸腾说明水在沸腾过程中不需要吸热6、下列现中,解释正确的是()A.粉笔用力捏碎变成粉末,说明物体是由分子组成的B.大雪四处飞扬,说明分子在永不停息的做无规则运动C.破镜难圆,说明分子之间在有斥力D.水和酒精混合后体积变小,说明分子之间存在间隙7、下列说法正确是()A.一个鸡蛋的质量约为500gB.人体感觉舒适的温度约为23℃C.冰箱冷冻室的温度约为5℃D.正在考试用的一张物理答题卡质量约为100g8、下列关于物态变化的说法中错误的是()A.晶体凝固过程中放热,温度下降B.汽化的两种方式分别是蒸发和沸腾C.同一晶体的凝固点和熔点是相同的D.液体沸腾过程中吸热,但温度不变9、对于以下估测你认为与实际情况最接近的是()A.人正常步行时的速度约为15m/s B.一只鸡的质量约为16kgC.健康人的正常体温约为36.7℃D.演奏中华人民共和国国歌所需的时间约为4.7min10、下列能说明组成物质的分子都在不停的运动的是()A.新冠病毒的传播B.扫地时灰尘飞扬C.冬日大雪纷飞D.墙里开花墙外香第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题3分,共计15分)1、温度是表示物体______的物理量。
第1-4单元能力提升卷(一)2023-2024学年语文四年级上册统编版.docx

第1-4单元能力提升卷(一)2023-2024学年语文四年级上册统编版一、选择题1.下列加点字注音完全正确的一项是()A.冶.炼(yě)年少.(shǎo)B.扎.实(zā)素昧.平生(mèi)C.竭.力(jié)锁.链(suǒ)D.慎.重(zhèng)嫩.红(nèn)2.下列词语全部正确的一项是()A.操场叶柄浑浊B.缘固阁楼费力C.吟诵侧门卢山D.住宅功夫提目3.“眸”字的意思,正确的是哪一项?()A.睫毛B.眉毛C.眼睛D.眼睑4.下列句子中,加点词语使用不恰当的一项是()A.经过老师的一番教育,他发生了呼风唤雨....的变化。
B.五公里的野外拉练一结束,大家累得横七竖八....的躺在草地上。
C.真是出乎意料....。
今天居然下雨了,美妙的野餐计划泡汤了。
D.飞机起飞或降落时,乘客往往有一种腾云驾雾....的感觉。
5.以下不是用来表示“勤学好问”一项是()A.好问则裕,自用则小。
B.为学患无疑,疑则有进。
C.一言既出,驷马难追。
D.人非生而知之者,孰能无惑?6.“梅须逊雪三分白,雪却输梅一段香。
”对诗句的感悟有偏差的是()A.要用全面的观点看问题。
B.取人之长,补己之短,是正理。
C.只有竞争,才能看出一方的胜负。
D.人各有所长,也各有所短,要有自知之明。
7.下列句子中,运用的修辞手法与其他选项不同的是()A.盘古就像一根柱子,撑在天地之间。
B.浪潮犹如千万匹白色战马飞奔而来。
C.轻而清的东西,缓缓上升,变成了天;重而浊的东西,慢慢下降,变成了地。
D.翠鸟蹬开苇秆,像箭一样飞过去。
二、填空题8.看拼音,写词语。
yán jiūxuǎn zé zhú jiàn zhèn ěr yù lóng( ) ( ) ( ) ( )9.组词。
核( )竖( )既( )题( )幻( )该( )坚( )即( )提( )幼( )10.将下列词语补充完整。
