高一数学暑假作业答案解析
人教版高一数学暑假作业答案

人教版高一数学暑假作业答案(2021最新版)作者:______编写日期:2021年__月__日【一】选择题CCDDB填空题6.57.平行四边形8.29.810.3/2用勾股定理解答题11.都是证明题,忒简单了.12.1)是正方形2)S四边形=213.两种答案T=1或214.同11题,【二】一、填空题(每小题5分,共10分)1.函数f(x)=x2-4x+2,x∈[-4,4]的最小值是________,值是________.【解析】f(x)=(x-2)2-2,作出其在[-4,4]上的图象知f(x)max=f(-4)=34.【答案】-2,342.已知f(x)与g(x)分别由下表给出x1234f(x)4321x1234g(x)3142那么f(g(3))=________.【解析】由表知g(3)=4,f(g(3))=f(4)=1.【答案】1二、解答题(每小题10分,共20分)3.已知函数f(x)的图象是两条线段(如图,不含端点),求f.【解析】由图象知f(x)=,∴f=-1=-,∴f=f=-+1=4.已知函数f(x)=x2+2x+a,f(bx)=9x2-6x+2,其中x∈R,a,b 为常数,求方程f(ax+b)=0的解集.【解析】∵f(x)=x2+2x+a,∴f(bx)=(bx)2+2(bx)+a=b2x2+2bx+a.又∵f(bx)=9x2-6x+2,∴b2x2+2bx+a=9x2-6x+2即(b2-9)x2+2(b+3)x+a-2=0.∵x∈R,∴,即,∴f(a x+b)=f(2x-3)=(2x-3)2+2(2x-3)+2=4x2-8x+5=0.∵Δ=(-8)2-4×4×5=-16<0,∴f(ax+b)=0的解集是?.【答案】?5.(10分)某市出租车的计价标准是:4km以内10元,超过4km 且不超过18km的部分1.2元/km,超过18km的部分1.8元/km.(1)如果不计等待时间的费用,建立车费与行车里程的函数关系式;(2)如果某人乘车行驶了20km,他要付多少车费?【解析】(1)设车费为y元,行车里程为xkm,则根据题意得y=1 (2)当x=20时,y=1.8×20-5.6=30.4,即当乘车20km时,要付30.4元车费.。
高一数学暑假作业(含解析)

高一数学暑假作业(含解析)2021年高一数学暑假作业为您引见了试题及答案,希望你喜欢。
一选择题(本大题共小题,每题5分,在每题给出的四个选项中,只要一项为哪一项契合标题要求的。
1.,那么是的( )A.充沛但不用要条件B.必要但不充沛条件C.充要条件D.既不充沛也不用要条件2.在区间上为增函数的是: ( )A. B. C. D.3.抛物线y=的顶点在第三象限,试确定m的取值范围是( )A.m-1或mB.m0或mC.-14.等差数列{}的公差不为零,首项=1,是和的等比中项,那么数列的前10项之和是A. 90B. 100C. 145D. 190 5.假定△ABC的三边长为a,b,c,且那么f(x)的图象( )(A)在x轴的上方 (B)在x轴的下方(C)与x轴相切 (D)与x轴交于两点6.向量a = (2,1), ab = 10,︱a + b ︱= ,那么︱b ︱=(A) (B) (C)5 (D)257.设集合( )A. B.C. D.8.如图,该顺序运转后输入的结果为( )A.1B.10C.19D.28本大题共小题,每题5分,9.设A={x|x2+x-6=0},B={x|mx+1=0},且AB=A,那么m的取值范围是 .10.抛物线y=-b+3的对称轴是___,顶点是___。
11.假定是一个等比数列的延续三项,那么的值为 .12.在△ABC中,假定,那么______。
本大题共小题,每题分,13.设函数的最小正周期为.(Ⅰ)求的最小正周期(Ⅱ)假定函数的图像是由的图像向右平移个单位长度失掉,求的单调增区间.14.一个有穷等比数列的首项为,项数为偶数,假设其奇数项的和为,偶数项的和为,求此数列的公比和项数。
15.求关于x的方程ax+1=-x2+2x+2a(a0且a1)的实数解的个数.16.解不等式 (1)(2)1.B2.D3.D4.B解析:设公差为,那么.∵0,解得=2,=1005.A6.解析:此题考察平面向量数量积运算和性质,由知(a+b)2=a2+b2+2ab=50,得|b|=5 选C。
暑假作业高一数学含详解
α
的值.
tan α π cos α
3.已知
0,
4
,
4
,
0
,
cos
4
3 5
,
cos
β
π 4
5 13
.
(1)求 sin 2 的值;
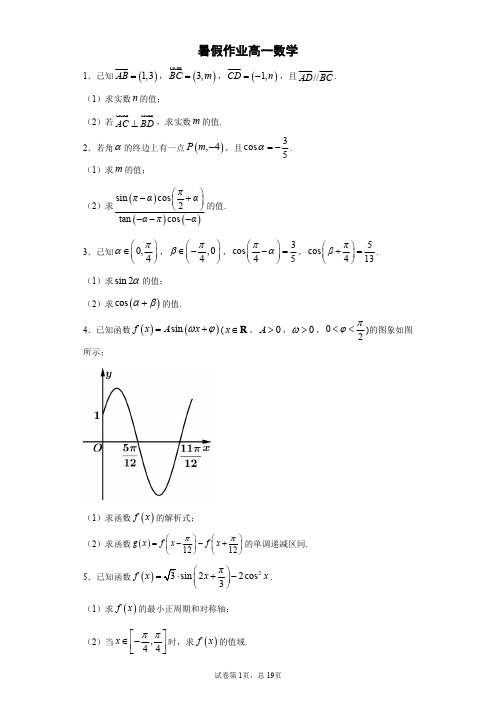
(2)求 cos 的值. 4.已知函数 f x Asin x ( x R , A 0 , 0 , 0 )的图象如图
2
(2)将函数 f x 的图象先向左平移 个单位,再把图象上各点的横坐标伸长为原来 6
的
2
倍,得到函数
h
x
的图象.若对任意的
x
0,
2
,不等式
p
h
x
1
h
x
2
1
h
2x
成立,求实数
p
的取值范围.
44.在 ABC 中,角 A , B , C 对应的边分别是 a , b , c .已知
cos 2A 3cos B C 1.
41.已知向量 a 与 b 的夹角为
60°,
a
3,
b
ur 2,m
r rr r r 2a 3b , n 3a kb .
(1)若 m n ,求实数 k 的值
ur r (2)是否存在实数 k ,使得 m//n ,说明理由.
42.如图是函数
f
(x) sin(x )(
0,
) 一个周期内的图象,已知点
g x
f
xk
在区间
6
, 13 12
上有三个零点,求实数 k
的取值范围.
32.已知函数 f x 是定义域为 R 的奇函数,且当 x 0 时,
高一数学暑假作业答案解析

2021年高一数学暑假作业答案解析不得不说暑假作业在暑假期间对学生的学习也是起一定作用的,精品小编准备了2021年高一数学暑假作业答案,希望你喜欢。
一选择题(本大题共小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知f(x)在区间(,+)上是增函数,a、bR且a+b0,则下列不等式中正确的是A.f(a)+f(b)f(a)+f(b)]B.f(a)+f(b)f(a)+f(b)C.f(a)+f(b)f(a)+f(b)]D.f (a)+f(b)f(a)+f(b)2.等差数列的一个通项公式为( )A. B. C. D.3.在△ABC中,,,A=120,则B等于( )A. 30B. 60C. 150D. 30或1504.已知向量若与平行,则实数的值是( )A.2B.0C.1D.25.若,,则与的关系是( )A. B. C. D.6.算法的有穷性是指( )A、算法的最后包含输出B、算法中的每个步骤都是可执行的C、算法的步骤必须有限D、以上说法都不正确7.以下各式能成立的是A. B.且C.且D.8.有下列说法:(1)0与{0}表示同一个集合;(2)由1,2,3组成的集合可表示为或;(3)方程的所有解的集合可表示为;(4)集合是有限集. 其中正确的说法是A. 只有(1)和(4)B. 只有(2)和(3)C. 只有(2)D. 以上四种说法都不对本大题共小题,每小题5分,9.设函数,函数的零点个数为______10.函数是R上的单调函数且对任意实数有.则不等式的解集为__________11.等差数列中,,,则 .12.若向量则。
本大题共小题,每小题分,13.平面向量,若存在不同时为的实数和,使且,试求函数关系式。
14.已知是等差数列,且(1)求数列的通项公式(2)令,求的前项的和.15.不等式的解集为,求实数的取值范围。
16.任意给定一个大于1的正整数n,设计一个算法求出n的所有因数.1.B 2.D 3.A4.D解析1:因为,所以由于与平行,得,解得。
高一数学暑假作业(1)参考答案

4
2
f(3)=cos
3π π 2 + = , 2 4 2
π 2 f(4)=cos2π + = .
4 2 所以 f(1)+f(2)+f(3)+f(4)=0, 所以 f(1)+f(2)+…+f(2 015)=f(2 013)+f(2 014)+f(2 015)=f(1)+f(2)+f(3) =- 2 . 2 答案:B π 7 解析:由 y=sin x 的对称轴为 x=kπ + (k∈Z), 2 π π 可得 3× +φ =kπ + (k∈Z), 12 2 π 则 φ =kπ + ( k∈Z), 4
高一数学暑假作业(1)参考答案
1 解析:因为-2π <-5<- 答案:A 3π ,所以角α 在第一象限. 2
1 2 解析:由题意知 g(x)=sin 2× x +1=sin x+1.故 T=2π . 2 答案:A
3 解析:a=tan-π - π π 3 =-tan =- , 6 6 3 23 π π 2 b=cos π =cos6π - =cos = , 4 4 4 2 4 4 4 2 所以 b>a> c. 答案:A 4 解析:函数 f(x)=sin(2x+θ )的图象向右平移 φ (φ >0)个单位长度后得到函数 g(x) =sin(2x+θ -2φ ),若 f(x),g(x)的图象的对称轴重合,则-2φ =kπ (k∈Z),即 φ = kπ π - (k∈Z),当 k=-1 得 φ = . 2 2 答案:C 1 π π 5 解析: T= -- , 4 12 6 所以 T=π ,所以 ω =2,排除 A、C. π f =1 代入可排除 B. 12 答案:D nπ π 6 解析:f(n)=cos + 的周期 T=4; 2 4 π π 3π 2 且 f(1)=cos + =cos =- , 2 4 4 2 π 2 f(2)=cosπ + =- , 33 π π 2 c=sin- π =sin-8π - =-sin =- ,
高中暑假作业:高一数学暑假作业参考答案

高中暑假作业:高一数学暑假作业参考答案高中暑假作业:高一数学暑假作业参考答案高中暑假作业:高一数学暑假作业参考答案【】高中暑假作业:高一数学暑假作业参考答案是查字典数学网为您整理的最新学习资料,请您详细阅读!一、选择题(本大题共12小题,每小题4分,共48分)题号 1 2 3 4 5 6 7 8 9 10 11 12答案 B A A B D B A D C A B B二、填空题(本大题共4小题,每小题4分,共16分)13. ; 14. ; 15. ; 16.三.解答题(本大题共4大题,共36分,解答应写出文字说明、证明过程或演算步骤)17. (本小题8分)已知 , 且 , ,求 .解∵ ,cos =- ,sin = . (2)分又∵0 , , ,又sin( + )= ,,cos( + )=-=- =- , ...............................4分sin =sin[( + )- ]=sin( + )cos -cos( + )sin= - = . ...............................8分又∵ = - =ma+nb- a=(m- )a+nb.= - =b- a=- a+b.又∵C、M、B三点共线,与共线.存在实数t1,使得 =t1 ,(m- )a+nb=t1(- a+b)消去t1得,4m+n=1 ②...............................6分由①②得m= ,n= ,= a+ b. ...............................8分注:本题解法较多,只要正确合理均可酌情给分.查字典数学网的编辑为大家带来的高中暑假作业:高一数学暑假作业参考答案,希望能为大家提供帮助。
高一数学暑假作业及答案

XX年高一数学暑假作业及答案一、填空题(每题5分,共10分)1.函数f(x)=x2-4x+2,x∈[-4,4]的最小值是,最大值是.【解析】 f(x)=(x-2)2-2,作出其在[-4,4]上的图象知f(x)max=f(-4)=34.【答案】 -2,342.f(x)与g(x)分别由下表给出x1234 f(x)4321x1234 g(x)3142 那么f(g(3))=.【解析】由表知g(3)=4,f(g(3))=f(4)=1.【答案】 1二、解答题(每题10分,共20分)3.函数f(x)的图象是两条线段(如图,不含端点),求f.【解析】由图象知f(x)=,∴f=-1=-,∴f=f=-+1=4.函数f(x)=x2+2x+a,f(bx)=9x2-6x+2,其中x∈R,a,b为常数,求方程f(ax+b)=0的解集.【解析】∵f(x)=x2+2x+a,∴f(bx)=(bx)2+2(bx)+a=b2x2+2bx+a.又∵f(bx)=9x2-6x+2,∴b2x2+2bx+a=9x2-6x+2即(b2-9)x2+2(b+3)x+a-2=0.∵x∈R,∴,即,∴f(ax+b)=f(2x-3)=(2x-3)2+2(2x-3)+2=4x2-8x+5=0.∵Δ=(-8)2-4×4×5=-16<0,∴f(ax+b)=0的解集是?.【答案】 ?5.(10分)某市出租车的计价标准是:4 km以内10元,超过4 km且不超过18 km的局部1.2元/km,超过18 km的局部1.8元/km.(1)如果不计等待时间的费用,建立车费与行车里程的函数关系式;(2)如果某人乘车行驶了20 km,他要付多少车费?【解析】 (1)设车费为y元,行车里程为x km,那么根据题意得y=1(2)当x=20时,y=1.8×20-5.6=30.4,即当乘车20 km时,要付30.4 元车费.精品为大家提供的高一数学暑假作业练习题及答案大家仔细阅读了吗?最后祝同学们学习进步。
高一暑假数学作业本答案(必修1必修4)-精选教育文档

高一暑假数学作业本答案(必修1-必修4)高一学生需要多加练习,才可以巩固暑假期间的知识,精品小编准备了高一暑假数学作业本答案,希望对你有所帮助。
一选择题(本大题共小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若,则是成等差数列的( )A.充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件2.已知函数在区间上是减函数,则实数a的取值范围是( )A.aB.aC.aD.a33.等差数列的一个通项公式为( )A. B.C. D.4.在△ABC中,若,则△ABC的形状是( )A 直角三角形B 等腰或直角三角形C 不能确定D 等腰三角形5.在中,有命题:③若,则为等腰三角形;④若,则为锐角三角形.上述命题正确的是A.①②B.①④C.②③D.②③④6.7.设,用二分法求方程内近似解的过程中得则方程的根落在区间( )A. B. C. D.不能确定8.已知定义域为R的函数f(x)在区间(-,5)上单调递减,对任意实数t,都有f(5+t)=f(5-t),那么下列式子一定成立的是 ( )A.f(-1)C.f(9)本大题共小题,每小题5分,9.集合M={a| N,且aZ},用列举法表示集合M=_____ ___.10.等差数列中,,,则 .11.在ABC中,三边a,b,c与面积s的关系式为则角C为12.若的解集是,则的值为___________。
本大题共小题,每小题分,13.已知集合A={-3,4},B={x|x2-2px+q=0},B,且BA,求实数p,q的值.14.已知.(1)求的值;(2)求的值.15.设非零向量,满足,求证:16.解不等式 (1)(2)1.C2.B3.D4.B5.C6.B7.B 解析:8.C9.10.2111.12. 解析:13.解析:若B=若B,若B={-3,4}则则14.(1)(2)解得,从而,故所求=15.证明:以上高一暑假数学作业本答案就介绍到这里,祝同学们学业有成。
2022年高一年级数学暑假作业参考答案

2022年高一年级数学暑假作业参考答案高一年级数学暑假作业参考答案一、选择题1.已知f(x)=x-1x+1,则f(2)=()A.1B.12C.13D.14【解析】f(2)=2-12+1=13.X【答案】C2.下列各组函数中,表示同一个函数的是()A.y=x-1和y=x2-1x+1B.y=x0和y=1C.y=x2和y=(x+1)2D.f(x)=?x?2x和g(x)=x?x?2【解析】A中y=x-1定义域为R,而y=x2-1x+1定义域为{x|x≠1};B中函数y=x0定义域{x|x≠0},而y=1定义域为R;C中两函数的解析式不同;D中f(x)与g(x)定义域都为(0,+∞),化简后f(x)=1,g(x)=1,所以是同一个函数.【答案】D3.用固定的速度向如图2-2-1所示形状的瓶子中注水,则水面的高度h和时间t之间的关系是()图2-2-1【解析】水面的高度h随时间t的增加而增加,而且增加的速度越来越快.【答案】B4.函数f(x)=x-1x-2的定义域为()A.[1,2)∪(2,+∞)B.(1,+∞)C.[1,2]D.[1,+∞)【解析】要使函数有意义,需x-1≥0,x-2≠0,解得x≥1且x≠2,所以函数的定义域是{x|x≥1且x≠2}.【答案】A5.函数f(x)=1x2+1(x∈R)的值域是()A.(0,1)B.(0,1]C.[0,1)D.[0,1]【解析】由于x∈R,所以x2+1≥1,0<1x2+1≤1,即0【答案】B二、填空题6.集合{x|-1≤x<0或1【解析】结合区间的定义知,用区间表示为[-1,0)∪(1,2].【答案】[-1,0)∪(1,2]7.函数y=31-x-1的定义域为.【解析】要使函数有意义,自变量x须满足x-1≥01-x-1≠0解得:x≥1且x≠2.∴函数的定义域为[1,2)∪(2,+∞).【答案】[1,2)∪(2,+∞)8.设函数f(x)=41-x,若f(a)=2,则实数a=.【解析】由f(a)=2,得41-a=2,解得a=-1.【答案】-1三、解答题9.已知函数f(x)=x+1x,求:(1)函数f(x)的定义域;(2)f(4)的值.【解】(1)由x≥0,x≠0,得x>0,所以函数f(x)的定义域为(0,+∞).(2)f(4)=4+14=2+14=94.10.求下列函数的定义域:(1)y=-x2x2-3x-2;(2)y=34x+83x-2.【解】(1)要使y=-x2x2-3x-2有意义,则必须-x≥0,2x2-3x-2≠0,解得x≤0且x≠-12,故所求函数的定义域为{x|x≤0,且x≠-12}.(2)要使y=34x+83x-2有意义,则必须3x-2>0,即x>23,故所求函数的定义域为{x|x>23}.11.已知f(x)=x21+x2,x∈R,(1)计算f(a)+f(1a)的值;(2)计算f(1)+f(2)+f(12)+f(3)+f(13)+f(4)+f(14)的值.【解】(1)由于f(a)=a21+a2,f(1a)=11+a2,所以f(a)+f(1a)=1.(2)法一因为f(1)=121+12=12,f(2)=221+22=45,f(12)=?12?21+?12?2=15,f(3)=321+32=910,f(13)=?13?21+?13?2=110,f(4)=421+42=1617,f(14)=?14?21+?14?2=117,所以f(1)+f(2)+f(12)+f(3)+f(13)+f(4)+f(14)=12+45+15+910+110+1617+117=72.法二由(1)知,f(a)+f(1a)=1,则f(2)+f(12)=f(3)+f(13)=f(4)+f(14)=1,即[f(2)+f(12)]+[f(3)+f(13)]+[f(4)+f(14)]=3,而f(1)=12,所以f(1)+f(2)+f(12)+f(3)+f(13)+f(4)+f(14)=72.高中理科学霸各科学习技巧【语文】结合大纲,注重积累明确教学内容和要求《教学大纲》将高中语文的“教学内容和要求”分为阅读、写作、口语交际和综合性学习等部分。
高一数学暑假作业(含解析)

高一数学暑假作业(含解析)2021年高一数学暑假作业为您介绍了试题及答案,期望你喜爱。
一选择题(本大题共小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知,则是的( )A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要条件2.在区间上为增函数的是: ( )A. B. C. D.3.抛物线y=的顶点在第三象限,试确定m的取值范畴是( )A.m-1或mB.m0或mC.-14.等差数列{}的公差不为零,首项=1,是和的等比中项,则数列的前10项之和是A. 90B. 100C. 145D. 190 5.若△ABC的三边长为a,b,c,且则f (x)的图象( )(A)在x轴的上方(B)在x轴的下方(C)与x轴相切(D)与x轴交于两点6.已知向量a = (2,1),ab = 10,︱a + b ︱= ,则︱b ︱=(A) (B) (C)5 (D)257.设集合( )A. B.C. D.8.如图,该程序运行后输出的结果为( )A.1B.10C.19D.28本大题共小题,每小题5分,9.设A={x|x2+x-6=0},B={x|mx+1=0},且AB=A,则m的取值范畴是.10.抛物线y=-b+3的对称轴是___,顶点是___。
11.若是一个等比数列的连续三项,则的值为.12.在△ABC中,若,则______。
本大题共小题,每小题分,13.设函数的最小正周期为.(Ⅰ)求的最小正周期(Ⅱ)若函数的图像是由的图像向右平移个单位长度得到,求的单调增区间.14.一个有穷等比数列的首项为,项数为偶数,假如其奇数项的和为,偶数项的和为,求此数列的公比和项数。
15.求关于x的方程ax+1=-x2+2x+2a(a0且a1)的实数解的个数.16.解不等式(1)(2)1.B2.D3.D4.B解析:设公差为,则.∵0,解得=2,=1005.A6.解析:本题考查平面向量数量积运算和性质,由知(a+b)2=a2+b2+2ab =50,得|b|=5 选C。
高中暑假作业:高一数学暑假作业参考答案-最新教学文档

高中暑假作业:高一数学暑假作业参考答案高中暑假作业:高一数学暑假作业参考答案【】高中暑假作业:高一数学暑假作业参考答案是查字典数学网为您整理的最新学习资料,请您详细阅读!一、选择题(本大题共12小题,每小题4分,共48分)题号 1 2 3 4 5 6 7 8 9 10 11 12答案 B A A B D B A D C A B B二、填空题(本大题共4小题,每小题4分,共16分)13. ; 14. ; 15. ; 16.三.解答题(本大题共4大题,共36分,解答应写出文字说明、证明过程或演算步骤)17. (本小题8分)已知 , 且 , ,求 .解∵ ,cos =- ,sin = . (2)分又∵0 , , ,又sin( + )= ,,cos( + )=-=- =- , ...............................4分sin =sin[( + )- ]=sin( + )cos -cos( + )sin= - = . ...............................8分18. (本小题8分)已知:、、是同一平面内的三个向量,其中 =(1,2)⑴若| | ,且,求的坐标;⑵若| |= 且与垂直,求与的夹角.解:⑴设由或...............................4分代入(※)中, ...............................8分19.(本小题8分)如图所示,在△ABO中, = , ,AD与BC相交于点M,设 = , = .试用和表示向量 .解设 =ma+nb,则 = - =ma+nb-a=(m-1)a+nb.= - = - =-a+ b.又∵A、M、D三点共线,与共线.存在实数t,使得=t , ...............................2分(m-1)a+nb=t(-a+ b). (m-1)a+nb=-ta+ tb.,消去t得:m-1=-2n.即m+2n=1. ①...............................4分又∵ = - =ma+nb- a=(m- )a+nb.= - =b- a=- a+b.又∵C、M、B三点共线,与共线.存在实数t1,使得 =t1 ,(m- )a+nb=t1(- a+b)消去t1得,4m+n=1 ②...............................6分由①②得m= ,n= ,= a+ b. ...............................8分注:本题解法较多,只要正确合理均可酌情给分.查字典数学网的编辑为大家带来的高中暑假作业:高一数学暑假作业参考答案,希望能为大家提供帮助。
高一数学暑期作业本(必修2、5含参考答案)

高一数学暑期作业(必修2、5)1.解三角形(1)1. 在△ABC中,若==,则△ABC的形状是( )A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形2. 在△ABC中,若A=60°,b=16,且此三角形的面积S=220,则a的值是( )A. B.25 C.55 D.493. 在△ABC中,若acosA=bcosB,则△ABC是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角4. 在△ABC中,A=120°,B=30°,a=8,则c= .5. 在△ABC中,已知a=3,cosC=,S△ABC=4,则b= .6.△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.7.在△ABC中,已知角A,B,C的对边分别为a,b,c,且bcosB+ccosC=acosA,试判断△ABC的形状.2.解三角形(2)1、设m、m+1、m+2是钝角三角形的三边长,则实数m的取值范围是( )A.0<m<3B.1<m<3C.3<m<4D.4<m<62、在△ABC中,已知sinA∶sinB∶sinC=3∶5∶7,则此三角形的最大内角的度数等于 ( )A.75°B.120°C.135°D.150°3、 ⊿ABC中,若c=,则角C的度数是( )A.60°B.120°C.60°或120° D.45°4、 在△ABC中,A=60°,b=1,面积为,则= .5、 在△ABC中,已知A、B、C成等差数列,且边b=2,则外接圆半径R= .6、在中,,.(Ⅰ)求角的大小;(Ⅱ)若最大边的边长为,求最小边的边长.7. 如图,海中有一小岛,周围3.8海里内有暗礁。
一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°。
高一数学暑假作业答案解析

高一数学暑假作业答案解析
解法2因为与平行,则存在常数,使,即,根据向量共线的条件知,向量与共线,故。
5.A 解析:,
6.C
7.C
8.C
9.2
10.(-1,)
11.10
12. 解析:由平行四边形中对角线的平方和等于四边的平方和得
13.解析:由得
14.. 解(1)
(2)
15.解析:
当时,并不恒成立;
当时,则
得
16.解析:第一步:给定一个大于一的正整数n,
第二步:依次以(2――n-1)的整数d为除数去除n,检查余数是否为0,若是,则d是n的因数;若不是,则d不是n 的因数。
第三步:在n的因数中加入1和n,
第四步:输出n的所有因数。
2019年高一数学暑假作业答案就为大家介绍到这里,希望对你有所帮助。
高一暑假数学作业解析新人教A版

高一暑假数学作业解析新人教A版高一暑假数学作业答案2021为你介绍高一试题,请多加演练,期望对你有所关心。
一选择题(本大题共小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数,且,则A. B. C. D.2.某程序的框图如图所示,运行该程序时,若输入的x=0.1,则运行后输出的y值是A.﹣1B.0.5C.2D.103.如图所示,满足a0的函数y=的图像是( )4.设是公差不为0的等差数列,且成等比数列,则的前项和=( )A. B. C. D.5.在△ABC中,已知三边a、b、c满足(a+b+c)(a+b-c)=3ab,则C等于( )A.15B.30C.45D.606.已知向量a = (2,1),ab = 10,︱a + b ︱= ,则︱b ︱=(A) (B) (C)5 (D)257.设集合( )A. B.C. D.8.算法的有穷性是指( )A、算法的最后包含输出B、算法中的每个步骤差不多上可执行的C、算法的步骤必须有限D、以上说法都不正确本大题共小题,每小题5分,9.已知集合A={x|y=x2-2x-2,xR},B={y|y=x2-2x+2,xR},则AB=_ ___.10.11.若为等差数列, .12.在△ABC中,若,则的值是_________。
本大题共小题,每小题分,13.在中,角的对边分别为,。
(Ⅰ)求的值;(Ⅱ)求的面积.14.已知,,,,求。
15.已知△ABC的三边且,求16.1.A2.A3.C4.A解析:设数列的公差为,则依照题意得,解得或(舍去),因此数列的前项和5.D6.解析:本题考查平面向量数量积运算和性质,由知(a+b)2=a2+b2+2ab =50,得|b|=5 选C。
7.B 解析:8.C9.{y|-33}10.11.2612. 解析:13.解析:本题要紧考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基础知识,要紧考查差不多运算能力.(Ⅰ)∵A、B、C为△ABC的内角,且,(Ⅱ)由(Ⅰ)知,又∵,在△ABC中,由正弦定理,得△ABC的面积.14.为点(4,7)。
高一数学暑假作业精选(附解析)

高一数学暑假作业精选(附解析)C.03,x0+11,即x00,无解;当x02时,log2x03,x023,即x08,x08.4.函数f(x)=ax+loga(2x+1)(a0且a1)在[0,2]上的最大值与最小值之和为a2,则a的值为()A. B.5 C. D.4[答案] A[解析] 当a1时,ax随x的增大而增大,loga(2x+1)随x的增大而增大,函数f(x)在[0,2]上为增函数,f(x)max=a2+loga5,f(x)min=1,a2+loga5+1=a2,loga5+1=0,loga5=-1,a=(不合题意舍去).当0f(x)max=1,f(x)min=a2+loga5,1+a2+loga5=a2,loga5=-1,a=.二、填空题5.(2019~2019学年度江西南昌市联考)定义在R上的偶函数f(x)在[0,+)上单调递减,且f()=0,则满足f(x)0的集合为____________.[答案] (0,)(2,+)[解析] 本题主要考查函数的奇偶性、单调性的应用和对数不等式的解法.因为定义在R上的偶函数f(x)在[0,+)上单调递减,所以在(-,0]上单调递增.又f()=0,所以f(-)=0,由f(x)0可得x-,或x,解得x(0,)(2,+).6.(2019福建文,15)函数f(x)=的零点个数是________.[答案] 2[解析] 当x2,令x2-2=0,得x=-;当x0时,令2x-6+lnx=0,即lnx=6-2x,在同一坐标系中,画出函数y=6-2x与y=lnx的图象如图所示.由图象可知,当x0时,函数y=6-2x与y=lnx的图象只有一个交点,即函数f(x)有一个零点.综上可知,函数f(x)有2个零点.三、解答题7.已知函数f(x)=lg(4-x2).(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性,并证明.[解析] (1)要使函数f(x)有意义,应满足4-x20,x24,-20,且a1)的图象关于原点对称.(1)求m的值;(2)判断函数f(x)在(1,+)上的单调性.[解析] (1)f(x)=loga(a0,且a1)的图象关于原点对称,f(x)为奇函数.f(-x)=-f(x).loga=-loga=loga,1-m2x2=1-x2,m2=1,m=1或m=-1.当m=1时,不满足题意,舍去,故m=-1.(2)f(x)=loga=loga.设x1,x2(1,+),且x10,x1x2-x1+x2-1x1x2-x2+x1-1,又x1,x2(1,+),(x1+1)(x2-1)=x1x2-x1+x2-10,(x2+1)(x1-1)=x1x2-x2+x1-10,1.当01时,loga0,即f(x1)f(x2),故函数f(x)在(1,+)上是减函数.综上可知,当a1时, f(x)在(1,+)上为减函数;当0f(1)=-2,即x1时, f(x)的值域是(-2,+).当x1时, f(x)=logx是减函数,所以f(x)f(1)=0,即x1, f(x)的值域是(-,0].于是函数f(x)的值域是(-,0](-2,+)=R.(2)若函数f(x)是(-,+)上的减函数,则下列三个条件同时成立:当x1时, f(x)=x2-(4a+1)x-8a+4是减函数,于是1,则a当x1时, f(x)=logax是减函数,则0以上就是高一数学暑假作业精选,希望能帮助到大家。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年高一数学暑假作业答案解析不得不说暑假作业在暑假期间对学生的学习也是起一
定作用的,精品小编准备了2019年高一数学暑假作业答案,希望你喜欢。
一选择题(本大题共小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知f(x)在区间(-,+)上是增函数,a、bR且a+b0,则下列不等式中正确的是
A.f(a)+f(b)-f(a)+f(b)]
B.f(a)+f(b)f(-a)+f(-b)
C.f(a)+f(b)-f(a)+f(b)]
D.f (a)+f(b)f(-a)+f(-b)
2.等差数列的一个通项公式为( )
A. B. C. D.
3.在△ABC中,,,A=120,则B等于( )
A. 30
B. 60
C. 150
D. 30或150
4.已知向量若与平行,则实数的值是( )
A.-2
B.0
C.1
D.2
5.若,,则与的关系是( )
A. B. C. D.
6.算法的有穷性是指( )
A、算法的最后包含输出
B、算法中的每个步骤都是可执行的
C、算法的步骤必须有限
D、以上说法都不正确
7.以下各式能成立的是
A. B.且
C.且
D.
8.有下列说法:(1)0与{0}表示同一个集合;(2)由1,2,3组成的集合可表示为或;(3)方程的所有解的集合可表示为;(4)集合是有限集. 其中正确的说法是
A. 只有(1)和(4)
B. 只有(2)和(3)
C. 只有(2)
D. 以上四种说法都不对
本大题共小题,每小题5分,9.设函数,函数的零点个数为______
10.函数是R上的单调函数且对任意实数有.则不等式的解集为__________
11.等差数列中,,,则 .
12.若向量则。
本大题共小题,每小题分,13.平面向量,若存在不同时为的实数和,使且,试求函数关系式。
14.已知是等差数列,且
(1)求数列的通项公式(2)令,求的前项的和.
15.不等式的解集为,求实数的取值范围。
16.任意给定一个大于1的正整数n,设计一个算法求出n的所有因数.1.B 2.D 3.A
4.D解析1:因为,所以
由于与平行,得,解得。
解法2因为与平行,则存在常数,使,即,根据向量共线的条件知,向量与共线,故。
5.A 解析:,
6.C
7.C
8.C
9.2
10.(-1,)
11.10
12. 解析:由平行四边形中对角线的平方和等于四边的平方和得
13.解析:由得
14.. 解(1)
(2)
15.解析:
当时,并不恒成立;
当时,则
得
16.解析:第一步:给定一个大于一的正整数n,
第二步:依次以(2――n-1)的整数d为除数去除n,检查余数是否为0,若是,则d是n的因数;若不是,则d不是n的因数。
第三步:在n的因数中加入1和n,
第四步:输出n的所有因数。
2019年高一数学暑假作业答案就为大家介绍到这里,希望对你有所帮助。
