7.1.2 三角形的高、中线与角平分线(含答案)
7.1.2三角形的高、中线与角平分线(平行班) 初中八年级上册数学教案教学设计课后反思 人教版

7.1.2三角形的高、中线与角平分线【课题】:三角形的高、中线与角平分线【设计与执教者】:广州市五羊中学,高惠平,33065525@【教学时间】:2008年5月【学情分析】:平行班学生在小学已学过三角形的高和中线的画法及概念,对锐角三角形和直角三角形的高都能画得较好,但对于平行班的学生来说,钝角三角形的三条高的画法是一个相当薄弱的知识点,大多数学生需要针对此在课内课外进行突破训练。
角平分线的画线在初一上学期学生已学过,在这里要让学生明确一般的角平分线是射线,而三角形的角平分线是线段。
在本节课中,要让学生学会在三角形中用几何语言表示三角形的中线、角平分线、高,并尝试在较复杂的图形进行分析与推理。
【教学目标】:(1)理解三角形的中线、角平分线、高的概念,并掌握这三种三角形重要线段的画法(2)让学生在实践中得出三角形的三条中线、三条角平分线、三条高各交于一点。
能根据三角形的三条高的交点的位置(在三角形内、在三角形外、在三角形的顶点处)判断三角形的形状。
(3)掌握三角形的中线、角平分线、高的几何语言表示方法。
(4)学会识别较复杂图形中的三角形的重要线段。
【教学重点】:三角形的中线、角平分线、高的画法与几何语言表示。
【教学难点】:钝角三角形的高的画法。
【教学突破点】:通过让学生动手画图,使学生掌握三角形的中线、角平分线、高的画法,体会和掌握三角形的中线、角平分线、高的几何语言表示方法。
【教法、学法设计】:教法:讲授法,举例法;学法:动手画图、观察图形【课前准备】:教师:PPT课件及几何画板课件,学生:直尺和三角板三、形成性训练【形成性练习】(1)下列选项中,表示△ABC 中AB边上的高是()(A)(B)(C)(D)(2)如图,CD、CE、CF分别是ABC的高、角平分线、中线,则下列各式中错误的是()(A)AB=2AF(B)∠ACE=21∠ACB(C)AE=BE(D)CD⊥BE(3)如右图所示,D、E分别为△ABC的边AC、BC的中点,则下列说法不正确的是()A.DE是△BDC的中线B.BD是△ABC的中线C.AD=DC,BE=ECD.图中∠C的对边是DE通过形成性练习(1),引导学生学会辨别三角形的边与高的位置关系。
三角形的高、中线、角平分线

三角形内部 三角形内部 三角形内部
梳理归纳
三角形的高、中线与角平分线有 什么共同的特征?
(1)都是线段;
(2)这些线段一个端点是三角 形的顶点,另一端点在这个顶点 的对边上。
• 1、AD是ΔABC的角平分线(如左图),那么
∠BAC= ∠BAD;
• 2、AE是ΔABC的中线(如右图),
那么BC=
BE。
A
A
B
D
C
B
E
C
探究 如图,在△ABC中,AD是△ABC的
线与它的对边相交,这个角的顶点与
交点之间的 线段 叫做三角形的角平
分线。
如图,∠BAC的平分
A
线交BC于点D,线段AD
就是ΔABC的一条角平
分线。
B
DC
理解定义
如图,∠BAC的平分线交BC于点D,线 段AD就是ΔABC的一条角平分线。
A 线段AD是△ABC
1 2 的角平分线
B
DC
∠1= ∠ 2= 1 ∠BAC 2
A
B
D
C
三角形中线定义
在三角形中,连接一个顶点与它对 边中点的线段,叫做三角形的中线。
如图,D为BC的中
点,线段AD就是
ΔABC的BC边上的
中线。
B
A
D
C
理解定义 如图,D为BC的中点,线
A 段AD就是ΔABC的BC边上 的中线。
线段AD是
B
D
C △ABC的中线
BD= CD= 1 BC
2
观察思考
思考
有同学说:“三角形的一个角的 平分线就是三角形的角平分线. ”这 种说法对吗?为什么?
解:这种说法不对,三角形一个角
三角形的高、中线与角平分线练习题及答案
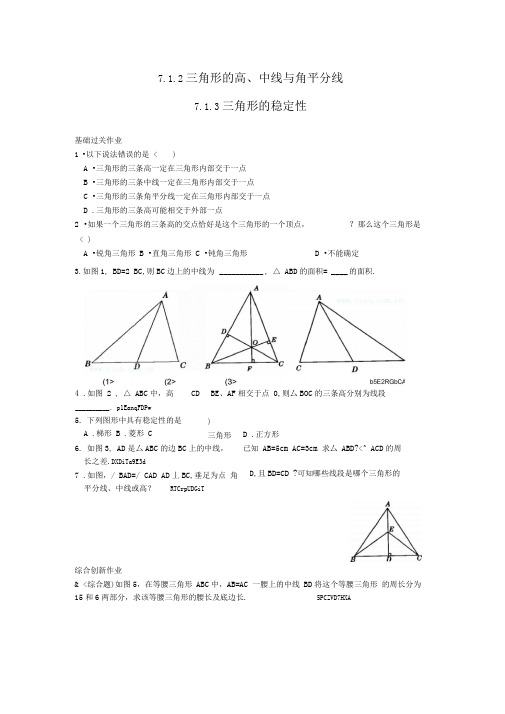
7.1.2三角形的高、中线与角平分线7.1.3三角形的稳定性基础过关作业1 •以下说法错误的是 < )A •三角形的三条高一定在三角形内部交于一点B •三角形的三条中线一定在三角形内部交于一点C •三角形的三条角平分线一定在三角形内部交于一点D .三角形的三条高可能相交于外部一点2 •如果一个三角形的三条高的交点恰好是这个三角形的一个顶点, ?那么这个三角形是< )A •锐角三角形B •直角三角形C •钝角三角形D •不能确定3.如图1, BD=2 BC,则BC 边上的中线为 ___________ , △ ABD 的面积= ____ 的面积.综合创新作业& <综合题)如图5,在等腰三角形 ABC 中,AB=AC 一腰上的中线 BD 将这个等腰三角形 的周长分为15和6两部分,求该等腰三角形的腰长及底边长.5PCZVD7HXA4 .如图 2 , △ ABC 中,高__________ . p1EanqFDPw5. 下列图形中具有稳定性的是 A .梯形 B .菱形 CCD )三角形 6. 如图3, AD 是厶ABC 的边BC 上的中线, 长之差.DXDiTa9E3d7 .如图,/ BAD=/ CAD AD 丄BC,垂足为点 角平分线、中线或高?RTCrpUDGiTD .正方形已知 AB=5cm AC=3cm 求厶 ABD?<^ ACD 的周D,且BD=CD ?可知哪些线段是哪个三角形的BE 、AF 相交于点 0,则厶BOC 的三条高分别为线段9 •有一块三角形优良品种实验基地,如图所示,?由于引进四个优良品种进行对比实验,需将这块土地分成面积相等的四块,请你制定出两种以上的划分方案供选择<画图说明).jLBHrnAlLg11.<2004年,陕西)如图,在锐角厶ABC 中,CD BE 分别是AB AC 上的高,?且CD BE 交于一点 P ,若/ A=50° 则/ BPC 的度数是<)LDAYtRyKfEA . 150°B . 130°C . 120°D . 100 °培优作业12. <探究题)<1)如图7-1-2-9 , AD 是厶ABC 的角平分线, DE// AB,DF// AC, EF 交 AD 于点 O.请问:DO>A DEF 的角 平分线吗?如果是,请给予证明;如果不是,请说明理 由.Zzz6ZB2Ltk<2)若将结论与 AD 是厶ABC 的角平分线、DE// AB DF// AC 中的任一条件交换,?所得命题10 . <创新题)如图,在△ABC 中,D 、E 分别是 BCA正确吗?/ / \13.<开放题)要使四边形木架<用4根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?dvzfvkwMIl14.<趣味题)《三国演义》中有关木牛流马的叙述:“孔明即手书一纸,付众观看,众将环绕而视•造木牛之法云:’方腹曲头,一脚四足;头入领中,舌着于腹•载多而行少,独行者数十里,群行者二十里•曲者为牛头,双者为牛脚,横者为牛领,转者为牛足,覆者为牛背,方者为牛腹,垂者为牛舌,曲者为牛肋,刻者为牛齿,立者为牛角,细者为牛鞅,摄者为牛轴•牛仰双辕,人行六尺,牛行四步•’每牛载十人所食一月之粮,人不大劳,牛不饮食•”rqyn14ZNXI你知道木牛流马中运用了什么数学知识吗?数学世界探险家的“难极”有一个探险家,挖空心思想出一个“难极”来.什么是探险家的“难极”呢?一般情况下,如果从某地出发,先往北走100公里,再往东走100公里,然后往南走100公里,这时,终止地总要在出发地正东100公里处.EmxvxOtOco而若从某地出发,先往北走100公里,再往东走100公里,然后往南走100?公里,能正好回到原来的出发地•这个出发地被探险家称其为“难极”.SixE2yXPq5 你知道探险家的“难极”在哪里吗?答案:1. A 点拨:锐角三角形的三条高在三角形内部交于一点,?直角三角形的三条高交于直角顶点,钝角三角形的三条高在三角形外部交于一点. 6ewMyirQFL2. B 3 . AD △ ACD 4 . BD, CE OF 5 . C6.解:T ABC的中线,••• BD=CD•••△ ABD与△ ACD的周长之差为:<AB+BD+AD )Y AC+CD+AD =AB-AC=5-3=2<cm).7.解:I/ BAD=/ CAD • AD>^ ABC的角平分线,。
七年级数学下册 7.1.2《三角形的高、中线、角平分线》

课题:三角形的高、中线与角平分线(课堂实录)(课型新授)【预习反馈】师:(1)什么叫三角形的高?三角形的高与垂线有何区别和联系? 生:(抢着站起来)三角形的高是从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段,而从三角形一个顶点向它对边所在的直线作垂线这条垂线是直线.师:(赞许地点点头)(2)什么叫三角形的中线?连结两点的线段与过两点的直线有何区别和联系?生:(很有把握地)三角形的中线是连结一个顶点和它对边的中点的线段, 而过两点的直线有着本质的不同,一个代表的是线段,另一个却是直线.师:(3)什么叫三角形的角平分线?三角形的角平分线与角平分线有何区别和联系?生:三角形的角平分线是三角形的一个内角平分线与它的对边相交, 这个角顶点与交点之间的线段,而角平分线指的是一条射线.师:3.三角形的高、中线和角平分线是代表线段还是代表射线或直线?生:集体回答(线段)生:三角形的高、中线和角平分线都代表线段, 这些线段的一个端点是三角形的一个顶点,另一个端点在这个顶点的对边上.〖评析〗通过图表的体现,便于学生对本节课知识的掌握,利用建构主义理论达到教学目的。
让学生对符号语言的运用有进一步的认识和更深的理解,渐渐学会运用几何语言解题。
【探索新知】师:让学生在练习本上画出三角形,并在这个三角形中画出它的三条高. (如果他们所画的是锐角三角形,接着提出在直角三角形的三条高在哪里?钝角三角形的三条高在那里?)观察这三条高所在的直线的位置有何关系?同学们可以互相议论一下。
三条高的位置生:三角形按角分类锐角三角形的三条高都在内部,交于一点。
生:(补充)直角三角形两条高在边上,一条高在内部,且交于直角的顶点生:(接着补充)钝角三角形两条高在外部,一条在内部,且延长线交于一点。
师:(颔首微笑)同学们总结得真仔细!(归纳)三角形的三条高交于一点,锐角三角形三条高交点在直角三角形内,直角三角形三条高线交点在直角三角形顶点,而钝角三角形的三条高的交点在三角形的外部.师:(描述)2.让学生在练习本上画三角形,并在这个三角形中画出它的三条中线.( 如果他们所画的是锐角三角形,接着让他们画出直角三角形和钝角三角形,看看这些三角形的中线在哪里)?观察这三条中线的位置有何关系?生:(脱口而出)三角形的三条中线都在三角形内部,它们交于一点,这个交点在三角形内师:三角形的一条中线把三角形的面积怎样了?生:平分(等底同高)生:(鼓掌同意)真好!师: 3.让学生在练习本上画一个三角形,并在这三角形中画出它的三条角平分线,观察这三条角平分线的位置有何关系?生:(接着回答,用手指示)锐角三角形还是直角三角形或钝角三角形, 它们的三条角平分线都在三角形内,并且交于一点.师:很好!完全正确。
七年级7.1.2 三角形的高、中线与角平分线(专题课时练含答案)-

7.1.2 三角形的高、中线与角平分线◆知能点分类训练知能点1 三角形的高、中线与角平分线1.下列说法正确的是().A.直角三角形只有一条高B.如果一个三角形有两条高与这个三角形的两边重合,•那么这个三角形是直角三角形 C.三角形的三条高,可能都在三角形内部,也可能都在三角形外部D.三角形三条高中,在三角形外部的最多只有1条2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是().A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形3.如图所示,画△ABC的一边上的高,下列画法正确的是().4.三角形的角平分线是().A.直线 B.射线 C.线段 D.以上都不对5.如图所示,AM是△ABC的中线,那么若用S1表示△ABM的面积,用S1表示△ACM的面积,则S1与S2的大小关系是().A.S1>S2B.S1<S2C.S1=S2D.以上三种情况都可能6.下列说法:①三角形的角平分线、中线、高线都是线段;•②直角三角形只有一条高线;③三角形的中线可能在三角形的外部;④三角形的高线都在三角形的内部,并且相交于一点,其中说法正确的有().A.1个 B.2个 C.3个 D.4个7.如图所示,已知△ABC:(1)过A画出中线AD;(2)画出角平分线CE;(3)作AC边上的高.知能点2 三角形的稳定性8.下列四个图形中,具有不稳定性的图形是().9.照相机的支架是三条腿,这是利用了三角形的_________.•现实生活中还有利用三角形的这个特性的例子吗?如果知道,请写出来:________.10.如图所示,建筑工人在安装门窗时,先要把木头门窗固定好,这样搬运和安装起来才不会变形,请你设计一种方法固定木头门窗,这样做依据的数学道理是什么?◆规律方法应用11.如图所示,在△ABC中,AD⊥BC,BE⊥AC,BC=12,AC=8,AD=6,求BE的长.12.在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12cm和15cm两部分,求三角形各边的长.◆开放探索创新13.将一个三角形的三边中点顺次连结可得到一个新的三角形,通常称为“中点三角形”,如图①所示,△DEF是△ABC的中点三角形.(1)画出图中另外两个三角形的中点三角形.(2)用量角器和刻度尺量△DEF和△ABC的三个内角和三条边,看看你有什么发现?并通过三个图的重复度量实验,验证你的发现.(3)你知道S△ABC和S△EDF的关系吗?怎样得出来的?(4)根据(2)中的结论,解答下列问题,如图所示,CD是△ABC的中线,DE是△ACD的中线,EF为△ADE的中线,若△AEF的面积为1cm2,求△ABC的面积.①②③④答案:1.B 2.C 3.C 4.C5.C (点拨:等底等高)6.A 7.略 8.D9.稳定性三条腿的凳子等10.可在门(窗)角上钉一根木条,或用木杆顶在门(窗)角上,•这样做根据的数学道理是三角形的稳定性.11.解:∵S△ABC =12BC·AD=12AC·BE,∴BC·AD=AC·BE,∴BE=1268BC ADAC⨯==9.12.解:设AB=x(cm),则AD=DC=12x(cm).(1)若AB+AD=12,即x+12x=12.所以x=8.即AB=AC=8cm,则DC=4cm,故BC=15-4=11cm,此时AB+AC>BC,所以三边长分别为8cm,8cm,11cm.(2)若AB+AD=15,即x+12x=15,所以x=10,则DC=5cm,故BC=12-5=7cm,显然此时三角形存在,所以三边长分别为10cm,10cm,7cm.综上所述,此三角形的三边长分别为:8cm,8cm,11cm或10cm,10cm,7cm.13.(1)略(2)角度相同,中点三角形各边是原三角形各边长度的一半.(3)经度量知中点三角形与原三角形相比,底和高的长度分别是原三角形的底与高的12,所以面积是原三角形面积的14.(4)△ABC面积为8cm2,解略.。
三角形的高中线与角平分线知识点

三角形的高中线与角平分线知识点
嘿,朋友们!咱今天来聊聊三角形的高中线与角平分线这些超有意思的知识点呀!
咱先说这三角形的高吧,嘿,这高不就像是三角形的支柱嘛!比如说一个直角三角形,那直角边不就是斜边上的高嘛,它可决定着三角形的“身高”呢!这高如果画得歪了或者短了,那这个三角形感觉都要站不稳啦!
接着是中线呀,这中线就好像是三角形的对称轴一样嘞!比如三角形ABC,AB 边上的中线,不就是把 AB 分成了相等的两段嘛。
中线一拉,两
边就对称起来了,是不是超神奇呀?
还有角平分线,这就好像是个公平的裁判呢!比如在三角形 DEF 中,
角 D 的角平分线,会把角 D 公平地分成相等的两份,多公道呀!
三角形的高中线与角平分线,它们可是三角形的重要组成部分呀,少了它们可不行嘞!它们就像是三角形的好朋友,一直守护着三角形呢!我觉得呀,了解它们真的超级有趣,能让我们对三角形有更深的认识呢!。
初中数学八年级《三角形的高、中线、角平分线》优秀教学设计
7.1.2《三角形的高、中线、角平分线》教案
教学目标分析
本节课的教学设计力图体现“尊重学生,注重发展”的教学理念,着重培养和发展学生基本作图能力、语言表达能力、观察能力等,根据这一目的确定本节教学目标为:
教学流程
依据本节课的教材知识结构及学生认知规律和发展水平,为优化教学过程,实现“尊
教学过程
2 你能描述三角形的高
3 一个三角形有几边?那么高有几条呢?
4 你能做出下列三角形的高吗?
②若一个三角形有高在它的外部,则这个三角形为
∆的中线交于点ABC
线吗?
ABC中的A
∠的平分线,。
7.1.2三角形的高,中线、角分线课件

6.下列各阴影部分的面积有何关系?
S乙>S甲=S丙
同底 等高
7.填空:如图,在ΔABC中,AE是 中线,AD是角平分线,AF是高。 1 BC ; (1)BE= CE = 2 1 (2)∠BAD= ∠CAD = 2 ∠BAC ;
A
(3)∠AFB= ∠AFC = 90°
C
E D F
B
8、在△ABC中,AE,AD分别是BC边上 的中线和高。说明△ABE的面积与 △AEC的面积相等。
B
A
C
这节课你有那些收获?
有哪些困惑?
做一做:观察图中三角形的面积,看看有何发现?
等底同高
E D
C
三角形的三条中线交于一点
CF 其中,AB边上的中线是______ AD BC边上的中线是______ BE AC边上的中线是______
∵BE是中线
1 AC ∴____=_____= AE CE 2 _____
A
F
O
B D
E
∵CF是中线
C
做一做
直角三角形的三条高
A
画出直角三角形的三条高线, 它们有怎样的位置关系呢?
直角三角形的三条 高线相交于直角顶点
D B ; C
口答:
直角边BC边上的高是 AB
直角边AB边上的高是 CB ; 斜边AC边上的高是 BD ;
议一议
钝角三角形的三条高
A
钝角三角形的三条高线 也相交于一点吗?试通过 画图来验证。
AF BF ∴AB=2______=2_______
思考:任意三角形的三条中线的交点都在三角形的内部吗?
三角形的角平分线的定义:
• 在三角形中,一个内角的角平分线与它的 对边相交,这个角的顶点与交点之间的线 段叫做三角形的角平分线。 A ∵AD是 △ ABC的 角平分线 C
7.1.2三角形的高、中线、角平分线

1、一个三角形的三条中线位置为( A.一定都在三角形内 B.一定都在三角形外 C.可能在三角形外,也可能在三角形内 D.可能与三 角 E
三角形的中线
连接三角形一个顶点与对边中点的线段 叫做三角形的中线 A
B
D
C
关于三角形的中线
• 三角形的中线是一条线段 • 三角形有三条中线,三条中线的交点叫做 三角形的重心(重心都在三角形内部) • 三角形每一条中线分成两个面积相等的三 角形 • 重心到顶点的距离是到对边中点距离的 倍 重心到顶点的距离是到对边中点距离的2倍
三角形的角平分线
三角形一个内角的角平分线与对边相 交,顶点与交点的线段,叫做三角形的 角平分线 A
D B C
关于三角形的角平分线
• 三角形的角平分是一条线段 • 三角形有三条角平分线,三条角平分线交 于一点,这点叫做三角形的内心(内心都在 三角形内部) • 内心到三边的距离相等
1、请完成课本66页-练习第一题
7.1.2 三角形的高、中线与角平 分线
三角形的高、中线与角平分线
三角形的高 三角形的中线 三角形的角平分线
三角形的高
从三角形的一个顶点作对边(对边的延长 线)的垂线,顶点与垂足的之间的线段,叫 三角形的高。 A
C
D
B
关于三角形的高
• 三角形的高都是线段 • 三角形有三条高交于一点,这个交点叫三 角形的垂心 • 锐角三角形垂心在三角形内部,直角三角 形垂心在直角顶点上,钝角三角形垂心在 三角形外部
第二讲 三角形的高、中线与角平分线(含解析)(人教版)

第二讲三角形的高、中线与角平分线【学习目标】1.掌握三角形的高,中线及角平分线的概念。
2.掌握三角形的高,中线及角平分线的画法。
3.掌握钝角三角形的两短边上高的画法。
【温故知新】1.垂线的定义2.线段中点的概念3.角平分线的定义当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。
把一条线段分成两条相等的线段的点叫做线段中点。
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
【新课学习】知识点1:三角形的高1.定义:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的高。
2.如图所示,AD是边BC上的高。
3.三角形的高的做法:锐角三角形的高直角三角形的高钝角三角形的高4. 三角形的三条边上的高的交点锐角三角形的高交于三角形内部一点;交点在内部的三角形是锐角三角形。
直角三角形的高交于直角顶点;交点在顶点的三角形是直角三角形。
钝角三角形的高所在的直线交于三角形外部一点。
交点在外部的三角形是钝角三角形。
5.与三角形高相关的解题方法(1)记住三角形面积公式=BC AD/2(2)等面积法。
=BC AD/2= AC BE/2= AB CF/26.例题演练【例题1】如图,于点B,于点C,且AC与BD相交于点E,则的边DE上的高是____,边AE上的高是_____;若,,,则______.【答案】AB;DC;.【解析】的边DE上的高为线段AB,边AE上的高为线段DC.知识点2:三角形的中线1. 三角形的中线定义在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线. AE是BC边上的中线.2. 三角形的重心.每一个三角形都有三条中线,并且三角形的三条中线交于一点,这个交点就是三角形的重心.【例题2】在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,求ΔADC的周长。
【答案】20cm.【解析】∵CD是△ABC的中线,∴BD=AD,∴△DBC的周长=BC+BD+CD=25cm,则BD+CD=25-BC.∴△ADC的周长=AD+CD+AC=BD+CD+AC=25-BC+AC=25-(BC-AC)=25-5=20cm.知识点3:三角形的角平分线1.三角形的角平分线的定义在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.注意:“三角形的角平分线”是一条线段.如上图线段AD是∠A的平分线。
7.1.2三角形的高线、中线、角平分线

A
A
F B D 图1
E C
B
F 1 2 3 D 图2
E 4 C
4.如图,在ΔABC中,AE是中线, AD是角平分线,AF是高。填空: CE = 1 BE ; (1)BE= (2)∠BAD= ∠CAD = 1 ∠BAC (3)∠AFB= =90°; 2 ∠AFC (4)SΔABC= 1 。 BC•AF C
三角形中线的理解
●
A E
O ∵AD是△ ABC的中线 ● B C 1 ∴BD=CD= BC D 2 三角形的三条中线相交于一 点,交点在三角形的内部.
F
任意画一个三角形,然后利用刻度尺画出 这个三角形三条边的中线,你发现了什么?
三角形的角平分线
在三角形中,一个内角的角平分线与它的对边相交,
A
这个角的顶点与交点之间的线段,叫做三角形的角平分线。 ∵AD是 △ ABC的角平分线 1 ∴∠ BAD = ∠ CAD = 2∠BAC
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部。
直角三角形的三条高
在纸上画出一个直角三角形。 (1) 画出直角三角形的三条高, 它们有怎样的位置关系? 将你的结果与同伴进行交流. A
D
直角三角形的三条高 交于直角顶点.
直角边BC边上的高是 直角边AB边上的高是 AB ; CB ;
E
G
D
C
三角形的高、中线与角平分线都是线段
本课小结
今天我们学了什么呀? 1.三角形的高、中线、角平分 线等有关概念及它们的画法. 2. 三角形的高、中线、角平分线 的几何表达及简单应用.
你和别人的差距知道是什么吗? 就是看你会不会思考,能不能抓住 你身边的每一分每一秒的空闲时间!
三角形的高、中线与角平分线专题(含答案)

11.1.2三角形的高、中线与角平分线一、选择题1.以下说法正确的有() ①三角形的中线、角平分线都是射线; ②三角形的三条高所在直线相交于一点; ③三角形的三条角平分线在三角形内部交于一点; ④三角形的中线把三角形分成面积相等的两部分; ⑤直角三角形的三条高相交于直角顶点.A.5个B.4个C.3个D.2个2.如图所示,CD、CE、CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是()A.BA=2BFB.∠ACE=12∠ACBC.AE=BED.CD⊥AB3.画△ABC中AB边上的高,下列画法中正确的是()A. B. C. D.4.如图,AC⊥BC于点C,CD⊥AB于点D,则图中可以作为三角形“高”的线段有()A.1条B.2条C.3条D.5条5.若AD是△ABC的中线,下列结论错误的是()A.AB=BCB.BD=DCC.AD平分BCD.BC=2DC6.如图,△ABC中AB边上的高线是()A.线段DAB.线段CAC.线段CDD.线段BD7.如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列各式中错误的是()A.AE=CEB.∠ADC=90∘C.∠CAD=∠CBED.∠ACB=2∠ACF8.如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,S△ABC=4cm2,则S△BEF等于()A.2cm2B.1cm2C.12cm2D.14cm29.如果AD是△ABC的中线,那么下列结论: ①BD=12CB; ②AB=AC; ③S△ABD=S△ACD.其中一定成立的有()A.3个B.2个C.1个D.0个10.如图,已知P是△ABC的重心,连接AP并延长交BC于点D,若△ABC的面积为20,则△ADC的面积为()A.10B.8C.6D.511.填空:(1)如图(1),AD,BE,CF是△ABC的三条中线,则AB=2,BD=,AE=12.(2)如图(2),AD,BE,CF是△ABC的三条角平分线,则∠1=∠,∠3=12,∠ACB=2.12.如图,AB⊥BD于点B,AC⊥CD于点C,且AC与BD交于点E.已知AE=5,DE=2,CD=95,则AB的长为.13.若AD是△ABC的高,∠BAD=70∘,∠CAD=20∘,则∠BAC的度数为.14.如图,在△ABC中,CD平分∠ACB,DE//BC,交AC于点E.若∠AED=50°,则∠D的度数为______.15.如图,在△ABC中,AD⊥BC,垂足为点D,EC⊥BC交AB于点E,CF⊥AB,垂足为点F,BG⊥AC,垂足为点G.(1)分别写出△ABC各条边上的高;(2)CF是哪几个三角形的高?16.如图,D是△ABC中BC边上的一点,DE//AC交AB于点E,若∠EDA=∠EAD,试说明AD是△ABC的角平分线.17.如图,在△ABC中,AB=2,BC=4.△ABC的高AD与CE的比是多少?(提示:利用三角形的面积公式.)18.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90∘.试求:(1)AD的长;(2)△ABE的面积;(3)△ACE与△ABE的周长的差.19.如图,AD是△ABC的角平分线.DE // AC,DE交AB于点E,DF // AB,DF交AC于点F.图中∠1与∠2有什么关系?为什么?20.在如图所示的方格纸中,每个小正方形的边长均为1,点A,点B,点C均在小正方形的顶点上.(1)画出△ABC中BC边上的高AD;(2)画出△ABC中AC边上的中线BE;(3)直接写出△ABE的面积为.11.1.2三角形的高、中线与角平分线1.【答案】B2.【答案】C3.【答案】C4.【答案】D5.【答案】A6.【答案】C7.【答案】C8.【答案】B9.【答案】B10.【答案】A11.【答案】AF或BFCDAC∠2∠ABC∠4或∠ACF12.【答案】9213.【答案】90∘或50∘14.【答案】25°15.【答案】解:(1)由题意,可得△ABC中,AB边上的高是CF,BC边上的高是AD,AC边上的高是BG;(2)∵CF⊥AB,垂足为点F,∴CF是△BCF,△BCE,△BCA,△FCE,△FCA,△ECA的高.16.【答案】解:∵DE//AC,∴∠ADE=∠CAD,∵∠EDA=∠EAD,∴∠CAD=∠EAD,∴AD是△ABC的角平分线.17.【答案】解:∵AD和CE分别是△ABC边BC和边AB上的高,∴S△ABC=12BC·AD=12AB·CE,即2AD=CE,.18.【答案】解:(1)∵∠BAC=90∘,AD是边BC上的高,∴12AB⋅AC=12BC⋅AD,∴AD=AB⋅AC BC=6×810=4.8(cm),即AD的长为4.8cm.(2)∵△ABC是直角三角形,∠BAC=90∘,AB=6cm,AC=8cm,∴S△ABC=12AB⋅AC=12×6×8=24(cm2).又∵AE是△ABC的中线,∴BE=EC,∴12BE⋅AD=12EC⋅AD,即S△ABE=S△AEC,∴S△ABE=12S△ABC=12(cm2),∴△ABE的面积是12cm2.(3)∵AE为BC边上的中线,∴BE=CE,∴△ACE的周长−△ABE的周长=AC+AE+CE−(AB+BE+AE)=AC−AB=8−6=2(cm),即△ACE与△ABE的周长的差是2cm.19.【答案】解:∠1=∠2.理由如下:因为AD平分∠BAC,所以∠BAD=∠DAC.因为DE//AC,所以∠DAC=∠1.因为DF//AB,所以∠DAB=∠2.所以∠1=∠2.20.【答案】解:(1)如图所示,线段AD即为所求.(2)如图所示,线段BE即为所求.(3)4.。
三角形的高、中线和角平分线教案

7.1.2三角形的高、中线与角平分线教案【教学重点与难点】教学重点:1.了解三角形的高、中线与角平分线的概念.2.能利用三角形的高、中线和角平分线的性质进行简单计算.教学难点:1.能用自己的语言说出三角形高、中线与角平分线的概念.2.熟练运用三角形的高、中线和角平分线的性质进行有关计算.【教学目标】1.了解三角形的高、中线与角平分线的概念2.准确区分三角形的高、中线与角平分线.3.能够独立完成与三角形的高、中线和角平分线有关的计算.【教学方法】以学生实践为主,在已学内容的基础上进行更进一步的探究,从而发现新的结论,以此培养学生发现和解决问题的能力.【教学过程】一.回顾旧知(设计说明:通过对已学知识的回忆来巩固基础知识的运用,并借此引入新课.)问题1:数一数,图中共有多少个三角形?请将它们全部用符号表示出来.学生回答:图中共有5个三角形.它们分别是:△ABC、△ABD、△ACD、△ADE、△CDE.问题2:利用长为3、5、6、9的四条线段可以组成几个三角形?为什么?学生回答:可以组成2个三角形.从四条线段中任选三条组成三角形,共有四种选法:①3、5、6,②3、5、9,③3、6、9,④5、6、9,其中,满足“三角形两边之和大于第三边”的只有第①、④这两组.问题3:利用△ABC的一条边长为4cm,面积是24 cm2这两个条件,你能求出什么结论?学生回答:能够求出的△ABC高是3 cm.(教学说明:教师利用问题让学生回顾所学知识,特别是问题3内容的变化,可以引起学生注意和疑问,将学生的思路引入与三角形有关的线段中.)二、自主探究1.通过作图探索三角形的高(设计说明:通过经历画三角形的高的过程,使学生在头脑中留下清晰形象,并能结合这些具体形象叙述高的定义.)问题1:你能画出下列三角形的所有的高吗?学生画出三角形所有的高,观察这些高的特点.问题2:根据画高的过程说明什么叫三角形的高?学生讨论回答,师完善并归纳:从三角形的一个顶点向它的对边所在直线作垂线,连接顶点和垂足之间的线段称为三角形的高.问题3:在这些三角形中你能画出几条高?它们有什么相同点和不同点?学生回答:每个三角形都能画出三条高.相同点是:三角形的三条高交于同一点.不同点是:锐角三角形的高交于三角形内一点,直角三角形的高交于直角的顶点,钝角三角形的高交于三角形外一点.问题4:如图所示,如果AD是△ABC的高,你能得到哪些结论?学生回答:如果AD是△ABC的高,则有:AD⊥BC于D,∠ADB=∠ADC=90°.(教学说明:三角形的高的概念在书中并没有具体给出,所以学生在归纳定义的时候会有一定的困难.那么在授课时就要留给学生充足的时间进行思考和讨论,教师可以引导学生先利用具体图形进行定义,再由具体图形中抽出准确、简明的语言,同时要强调:三角形的高是一条线段.在问题3中,有些学生会认为直角三角形只能画出斜边上的一条高,这时教师要给予讲解,说明另外两条直角边也是这个直角三角形的高.而问题4是要将三角形的高用符号语言表示出来,这是为以后学习证明打基础.)2.类比探索三角形的高的过程探索三角形的中线(设计说明:利用类比的方法进行探索,可以留给学生更多思考与探究的空间,有得于拓展学生的思维,培养学生自主探究的学习习惯.)问题1:如图,如果点C是线段AB的中点,你能得到什么结论?学生回答:.问题2:如图,如果点D是线段BC的中点,那么线段AD就称为△ABC 的中线.类比三角形的高的概念,试说明什么叫三角形的中线?由三角形的中线能得到什么结论?学生回答:三角形中连结一个顶点和它对边中点的线段称为三角形的中线.如果线段AD是△ABC的中线,那么.问题3:画出下列三角形的所有的中线,并讨论说明三角形的中线有什么特点?学生回答:无论哪种三角形,它们都有三条中线,并且这三条中线都会交于一点,这一点都在三角形的内部.问题4:如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?学生回答:△ABD和△ACD的面积相等.理由:∵AD是△ABC的中线∴BD=CD∵AE既是△ABD的高,也是△ACD的高∴△ABD和△ACD的面积相等.问题5:通过问题4你能发现什么规律?学生回答:三角形的中线将三角形的面积平均分成两份.(教学说明:让学生利用对三角形的高的探究过程,利用类比的方法进行对三角形的中线的探究.“类比思想”是数学学习中常用的一种思想,所以在授课过程中要让学生体会运用这种思想进行探究的好处,培养自主探究的能力.问题4和问题5的设立是对三角形中线的知识进行扩展,并不是教科书中的内容,但能够使学生更深刻地体会三角形中线的特点,同时,根据课堂时间的需要,对于这两个问题的讲授,教师可以自行调节.)3.通过类比的方法探究三角形的角平分线(设计说明:再次使用类比的方法进行探究,让学生经历动脑思考探索的过程,对知识有进一步的理解.)问题1:如图,若OC是∠AOB的平分线,你能得到什么结论?学生回答:.问题2:如图,在△ABC中,如果∠BAC的平分线AD交BC边于点D,我们就称AD是△ABC的角平分线.类比探索三角形的高和中线的过程,你能得到哪些结论?三角形的角平分线与角的角平分线相同吗?为什么?学生回答:三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段称为三角形的角平分线.三角形有三条角平分线,并且这三条角平分线在三角形内交于一点.如果AD是△ABC的角平分线,那么就有.三角形的角平分线与一个角的角平分线不一样,三角形的角平分线是一条线段,有长度,而角的平分线是一条射线,没有长度.(教学说明:对于三角形的角平分线的探究,教师要给学生足够的空间和时间,如果漏下了哪一点没有探究到,教师可以给予提示.)三、尝试应用(设计说明:通过比较练习,帮助学生掌握三角形的高、中线和角平分线的基本性质,熟练基本技能.)练习1:如图,在△ABC中画出这个三角形的高BD,中线CE和角平分线BF.练习2:如图,已知AD,BE,CF都是△ABC的三条中线.则AE= =,BC=2 ,AF= .学生:CE,AC,BD或CD,BF.练习3:如图,已知AD,BE,CF都是△ABC的三条角平分线.则∠1=,∠2= =,∠ABC=2 .学生:∠BAC,∠3,∠ACB,∠4或∠ABE.练习3:如图,△ABC中,AC=12 cm,BC=18 cm,△ABC的高AD与BE 的比是多少?学生:解:由三角形的面积公式得所以有解得(教学说明:练习的设计以基础知识为主,要让学生独立完成.而练习3是所学知识的一个应用,要让学生有利用面积求高的意识,开阔思路.)四、成果展示(设计说明:围绕三个问题,师生以谈话交流的形式,共同总结本节课的学习收获。
7.1.2三角形的高中线角分线7.1.3三角形稳定性(六中珠中杨敏浩)

解:
F
A
E D
C
B
如图所示,BF为△ABC的AC边上的高,BD为△ABC 的AC边上的中线,BE为△ABC的角平分线。
几种典型错误:1、没写解;2、没标字母表示线段;3、没下结论 .
复习回顾
书第69页第1、2题, 第70页第7题. 1、一个三角形的两边分别是2和7,则第三边x取 值范围是__________ 5<x<9 ;若周长为偶数,则第三 边长是__________. 7 2、如图,线段AB,CD相交于点O, 能否确定AB+CD与AD+BC的大小关系, 请说明理由.
19、参考答案: A`(5,-3) B`(5,-4) C`(2,-3) D`(2,-1)
20题:
解:这样的C点共有12个,分别是 (5,1)、 (5,2) 、(5,3)、 (5,4) 、(5,5)、 (5,6)
(1,1)、 (1,2) 、(1,3)、 (1,4) 、(1,5) 、(1,6)
错因:①没有“等底等高等面积”的意识;
F 1 2 D C
盖房子时,在窗框未安装 好之前,木工师傅常常现在窗 框上斜钉一根木条.为什么要 这样做?
三角形 具有稳定性, 四边形 不具有稳定性.
思考: 如图(1),将三根木条用钉子钉成一个三角形 木架,然后扭动它,它的形状会改变吗? 如图(2),将四根木条用钉子钉成一个四边形 木架,然后扭动它,它的形状会改变吗? 如图(3),在四边形木架上再钉一根木条,将 它的一对顶点连接起来,然后再扭动它,这时 木架的形状还会改变吗?为什么?
(3) A`(1,1)、B`(6,4)、C`(3,5)
解:(2)将△ABC补成 长方形ADEF,则 S△ABC=S长方形ADEFF S△ADB-S△BEC-S△AFC =5×4-5×3÷2-1×3÷22×4÷2=7
三角形的高、中线与角平分线(分层作业)(解析版)docx

11.1.2三角形的高、中线与角平分线夯实基础篇一、单选题:(每题3分,共18分)1.在△AB C中,画边BC上的高,正确的是()A.B.C.D.【答案】A【解析】【详解】解:A.此图形中AD是BC边上的高,符合题意;B.此图形中CE不是BC边上的高,不符合题意;C.此图形中BE是AC边上的高,不符合题意;D.此图形中BG是△BCG中BC边上的高,不符合题意;故选:A.【点睛】本题考查三角形高的画法,解题关键在理解底与高的对应关系,作钝角三角形的高是易错点. 中,BC边上的高为()2.如图,在ABCA.BD B.CF C.AE D.BF【解析】【分析】根据三角形高的定义是从一个顶点到它对边的垂线段即可判断.【详解】根据三角形的高的定义,在△AB C中,BC边上的高应是过点A垂直于BC的线段,从图中可以看出,过点A垂直于BC的线段是AE,所以AE是BC边上的高.故选:C.【点睛】本题考查了三角形高的定义,熟练掌握三角形的高概念,仔细观察图形中符合定义的线段即可.3.下列叙述中错误的一项是().A.三角形的中线、角平分线、高都是线段.B.三角形的三条高线中至少存在一条在三角形内部.C.只有一条高在三角形内部的三角形一定是钝角三角形.D.三角形的三条角平分线都在三角形内部.【答案】C【解析】【分析】根据三角形的角平分线、中线、高的概念和性质进行一一判断.【详解】A:三角形的中线、角平分线、高都是线段,正确;B:锐角三角形三条高在三角形内部,直角三角形一条高在三角形内部,钝角三角形一条高在三角形内部,正确;C:只有一条高在三角形内部的三角形是钝角三角形或直角三角形,错误;D:锐角三角形、钝角三角形、直角三角形的三条角平分线都在三角形内部,正确【点睛】本题考查三角形的三线,掌握高、中线、角平分线的定义是解题关键.4.已知,AE、BD是ABC的高线,AE=6cm,BD=5cm,BC=8cm,则AC的长度是()A.8cm B.8.6cm C.9cm D.9.6cm【答案】D【解析】【分析】根据等面积法即可求解.【详解】解:∵AE、BD是ABC的高线,AE=6cm,BD=5cm,BC=8cm,∴1122AC BD AE BC,即68489.655AE BCACBDcm.故选D.【点睛】本题考查了三角形高线的相关计算,理解三角形的高线的意义是解题的关键.5.如图,在△AB C中,AB=5,AC=3,AD为BC边上的中线,则△ABD与△ACD的周长之差为()A.2B.3C.4D.5【答案】A【解析】【分析】根据题意,AD是△ABC的边BC上的中线,可得BD=CD,进而得出△ABD的周长=AB+BD+AD,△ACD的周长=AC+CD+AD,相减即可得到周长差.【详解】解:∵AD是△ABC的中线,∴BD=CD,∴△ABD与△ACD的周长之差为:(AB+BD+AD)-(AC+CD+AD)=AB+BD+AD-AC-CD-AD=AB-AC=5-3=2;故选:A.【点睛】本题主要考查了三角形的中线、高和三角形周长的求法,熟练掌握三角形周长公式是解题的关键.的中线,角平分线,高,下列各式中错误的是()6.如图,AD,AE,AF分别是ABCA .2BC CDB .12BAE BAC C .90AFBD .AE CE 【答案】D【解析】【分析】根据三角形的高线,角平分线和中线解答即可;【详解】解:A .∵AD 是ABC 的中线∴2BC CD ,故选项正确,不符合题意;B .∵AE 是ABC 的角平分线∴12BAE BAC 故选项正确,不符合题意;C .∵AF 分别是ABC 的高,∴90AFB故选项正确,不符合题意;D .AE CE 不一定成立,故选项错误,符合题意.故选:D .【点睛】此题考查三角形的高线,角平分线和中线,关键是根据三角形的高线,角平分线和中线的定义进行判断即可.二、填空题:(每题3分,共15分)7.如图,90CBD E F ,则线段______是ABC 中BC 边上的高.【答案】AE【解析】【分析】根据三角形高线的定义判断即可;【详解】∵AE BC ,∴ABC 中BC 边上的高是AE .故答案是AE .【点睛】本题主要考查了三角形的角平分线、中线和高线,准确分析判断是解题的关键.8.如图,△AB C 中,AD 是BC 上的中线,BE 是△AB D 中AD 边的中线,若△ABC 的面积是24,AE =3,则点B 到直线AD 的距离为________.【答案】4【解析】【分析】由三角形的中线平分三角形面积的性质可得△ABE 的面积,再由三角形面积公式即可求得结果.【详解】∵AD 是△ABC 的BC 边上的中线,24ABC S ,∴1122ABD ABC S S .∵BE 是△AB D 中AD 边上的中线,∴162ABE ABD S S .设点B 到直线AD 的距离为h ,则162ABE S AE h,即1362h ,∴h =4.即点B 到直线AD 的距离为4.故答案为:4.【点睛】本题考查了三角形一边上的中线平分三角形面积的性质、三角形面积等知识,掌握三角形一9.如图,在△AB C 中,AD 、AE 分别是BC 边上的中线和高,AE =6,S △ABD =15,则CD =_____.【答案】5【解析】【分析】由利用三角形的面积公式可求得BD 的长,再由中线的定义可得CD =BD ,从而得解.【详解】解:∵S △ABD =15,AE 是BC 边上的高,∴12BD •AE =15,则12×6BD =15,解得:BD =5,∵AD 是BC 边上的中线,∴CD =BD =5.故答案为:5.【点睛】本题主要考查三角形的中线,三角形的高,解答的关键是由三角形的面积公式求得BD 的长.10.如图,在三角形ABC 中,AB AC ,AD BC ,垂足为D ,3AB ,4AC ,5BC ,则AD ______.【答案】2.4【解析】【分析】根据面积相等可列式1122AB AC BC AD ,代入相关数据求解即可.【详解】解:∵AB AC ,AD BC ,∴1122AB AC BC AD ∵3AB ,4AC ,5BC ,∴12 2.45AB AC AD BC 故答案諀:2.4【点睛】此题主要考查了运用等积关系求线段的长,准确识图是解答本题的关键.11.已知ABC 中,30cm AC ,中线AD 把ABC 分成两个三角形,这两个三角形的周长差是12cm ,则AB 的长是__________.【答案】42cm 或18cm【解析】【分析】先根据三角形中线的定义可得BD =CD ,再求出AD 把△ABC 周长分为的两部分的差等于|AB -AC |,然后分AB >AC ,AB <AC 两种情况分别列式计算即可得解.【详解】∵AD 是△AB C 中线,∴BD =C D .∵AD 是两个三角形的公共边,两个三角形的周长差是12cm ,∴如果AB >AC ,那么AB -AC =12cm ,即AB -30=12cm∴AB =42cm ;如果AB <AC ,那么AC -AB =12cm ,即30-AB =12cmAB =18cm .综上所述:AB 的长为42cm 或18cm .故答案为:42cm 或18cm .【点睛】考查了三角形的中线,三角形一边的中点与此边所对顶点的连线叫做三角形的中线.三、解答题:(每题8分,共40分)12.如图,BD 和CE 是△ABC 的中线,AE =3cm ,CD =2cm ,若△ABC 周长为15cm ,求BC 边的长.【答案】5cm【解析】【分析】根据中线定义可得AB ,AC ,根据△ABC 周长公式即可求解.【详解】∵BD 和CE 是△ABC 的中线,∴2236AB AE cm ,2224AC CD cm ,∵△ABC 周长为15cm ,即15AB AC BC cm ,∴1515645BC AB AC cm .【点睛】本题考查三角形中线定义、三角形周长公式,解题的关键是根据三角形中线求出AB 和AC 的长.13.如图,△ABC 的周长是21cm ,AB =AC ,中线BD 分△ABC 为两个三角形,且△ABD 的周长比△BCD 的周长大6cm ,求AB ,B C .【答案】AB=9cm,BC=3cm.【解析】【分析】由BD是中线,可得AD=CD,又由△ABD的周长比△BCD的周长大6cm,△ABC的周长是21cm,AB=AC,可得AB-BC=6cm,2AB+BC=21cm,继而求得答案.【详解】解:∵BD是中线,∴AD=CD=12AC,∵△ABD的周长比△BCD的周长大6cm,∴(AB+AD+BD)﹣(BD+CD+BC)=AB﹣BC=6cm①,∵△ABC的周长是21cm,AB=AC,∴2AB+BC=21cm②,联立①②得:AB=9cm,BC=3cm.【点睛】本题考查了三角形周长与三角形的中线.注意掌握数形结合思想与方程思想的应用.14.如图,△ABC的顶点都在边长为1的正方形方格纸的格点上,将△ABC向上平移4格.(1)请在图中画出平移后的三角形A′B′C′;(2)在图中画出三角形△ABC的高CD、中线BE;(3)△ABC的面积是.【答案】(1)见解析(2)见解析(3)8【解析】【分析】(1)根据图形平移的性质画出平移后的△A′B′C′即可;(2)找出线段AC的中点E,然后连接B E,再过点C向AB所在的直线作垂线,垂足为D 即可;(3)直接根据三角形的面积公式即可得出结论.(1)如图所示,三角形A′B′C′就是所要求做的图形;(2)如图所示,三角形△ABC的高CD、中线BE;(3)S △ABC =1144822AB CD .故△ABC 的面积是8.【点睛】本题考查作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.15.如图,已知AD ,AE 分别是ABC 的高和中线,9cm AB ,12cm AC ,15cm BC ,90BAC .(1)求AD 的长度;(2)求ABE △的面积.【答案】(1)36cm 5(2)227cm 【解析】【分析】(1)利用等面积法,根据1122ABC S AB AC BC AD ,代值求解即可;(2)根据已知条件和(1)中求出的AD 长,利用三角形面积公式得出12ABE S BE AD ,代值求解即可.(1)解:在ABC 中,90BAC ,AD 是边BC 上的高,∵9cm AB ,12cm AC ,15cm BC ,根据1122ABC S AB AC BC AD 可得91236155cm AB AC AD BC ;(2)解:在ABC 中,BE 是边BC 上的中线,且15cm BC ,1152m 2c BE BC ,在ABE 中,AD 是边BE 上的高,且由(1)知5cm 36AD ,2111536272225cm ABE S BE AD .【点睛】本题考查三角形面积公式,熟练掌握三角形的中线与高线是解决问题的关键.16.请补全证明过程及推理依据.已知:如图,BC //ED ,BD 平分∠ABC ,EF 平分∠AE D .求证:BD ∥EF .证明:∵BD平分∠ABC,EF平分∠AED,∴∠1=12∠AED,∠2=12∠ABC(______________)∵BC∥ED(________)∴∠AED=________(________________)∴12∠AED=12∠ABC∴∠1=________∴BD∥EF(________________).【答案】角平分线的定义;已知;∠ABC;两直线平行,同位角相等;∠2;同位角相等,两直线平行【解析】【分析】根据角平分线的定义得出∠1=12∠AED,∠2=12∠ABC,根据平行线的性质定理得出∠AED=∠ABC,求出∠1=∠2,再根据平行线的判定定理推出即可.【详解】证明:∵BD平分∠ABC,EF平分∠AED,∴∠1=12∠AED,∠2=12∠ABC(角平分线的定义)∵BC∥ED(已知)∴∠AED=∠ABC(两直线平行,同位角相等)∴12∠AED=12∠ABC∴∠1=∠2∴BD∥EF(同位角相等,两直线平行).故答案为:角平分线的定义;已知;∠ABC;两直线平行,同位角相等;∠2;同位角相等,两直线平行.【点睛】本题考查了角平分线的定义,平行线的性质定理和判定定理等知识点,能熟记平行线的性质定理和判定定理是解此题的关键.能力提升篇一、单选题:(每题3分,共9分)1.在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为()A.7B.10C.7或11D.7或10【答案】C【解析】【分析】题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.【详解】设等腰三角形的底边长为x,腰长为y,则根据题意,得①152122yxyy==或②122152yxyy==解方程组①得118xy==,根据三角形三边关系定理,此时能组成三角形;解方程组②得710 xy==,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7;故选:C.【点睛】本题考查等腰三角形的性质及相关计算.学生在解决本题时,有的同学会审题错误,以为15,12中包含着中线BD的长,从而无法解决问题,有的同学会忽略掉等腰三角形的分情况讨论而漏掉其中一种情况;注意:求出的结果要看看是否符合三角形的三边关系定理.2.如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为()A.13B.710C.35D.1320【答案】B【解析】【分析】连接CP.设△CPE的面积是x,△CDP的面积是y.根据BD:DC=2:1,E为AC的中点,得△BDP的面积是2y,△APE的面积是x,进而得到△ABP的面积是4x.再根据△ABE的面积是△BCE的面积相等,得4x+x=2y+x+y,解得y=43x,再根据△ABC的面积是3即可求得x、y的值,从而求解.【详解】连接CP,设△CPE的面积是x,△CDP的面积是y.∵BD:DC=2:1,E为AC的中点,∴△BDP的面积是2y,△APE的面积是x,∵BD:DC=2:1∴△ABD的面积是4x+2y∴△ABP的面积是4x.∴4x+x=2y+x+y,解得y=43x.又∵△ABC的面积为3∴4x+x=3 2,x=3 10.则四边形PDCE的面积为x+y=7 10.故选B.【点睛】此题能够根据三角形的面积公式求得三角形的面积之间的关系.等高的两个三角形的面积比3.如图,△ABC的面积是24,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG 的面积是()A.9B.10C.11D.12【答案】A【解析】【分析】首先根据点E 是AD 的中点,可知ABE BDE S S ,ACE CDE S S V ,再根据点D 是BC 的中点,可得BDE CDE S S V ,即可得164ABE BDE ACE CDE ABCS S S S S V V V V ,然后根据点F ,G 是BE ,CE 的中点,得132AEF ABE S S V V ,132AEG ACE S S V V ,可知FG 是△CBE 的中位线,可得134EFG BCE S SV V ,即可得出答案.【详解】∵点E 是AD 的中点,∴ABE BDE S S ,ACE CDE S S V .∵点D 是BC 的中点,∴BDE CDE S S V ,∴164ABE BDE ACE CDE ABCS S S S SV V V V .∵点F ,G 是BE ,CE 的中点,∴132AEF ABE S S V V ,13AEG ACE S S V V ,∴FG 是△CBE 的中位线,∴134EFG BCES S V V ,∴+=9AFG AEF AEG EFG S S S S V V V V .故选:A .【点睛】本题主要考查了三角形的面积和中线的关系,三角形中位线的定义和性质等,将一个三角形的面积转化为求三个小三角形的面积是解题的关键.二、填空题:(每题3分,共9分)4.如图,在ABC 中,2AB AC ,P 是BC 边上的任意一点,PE AB 于点E ,PF AC于点F .若2ABC S ,则PE PF ______.【答案】2【解析】【分析】根据1122ABC ABP APC S S S AB PE AC PF,结合已知条件,即可求得PE PF 的值.【详解】解:如图,连接AP ∵PE AB 于点E ,PF AC 于点F1122ABC ABP APC S S S AB PE AC PF 2AB AC ∵,2ABC S 1122AB PE AC PF 2PE PF 2【点睛】本题考查了三角形的高,掌握三角形的高的定义是解题的关键.5.如图,在 AB C 中,已知点D ,E ,F 分别为边BC ,AD ,CE 的中点,且 ABC 的面积等于24cm 2,则阴影部分图形面积等于_____cm 2【答案】6【解析】【分析】因为点F是CE的中点,所以△BEF的底是△BEC的底的一半,△BEF高等于△BEC的高;同理,D、E、分别是BC、AD的中点,可得△EBC的面积是△ABC面积的一半;利用三角形的等积变换可解答.【详解】解:如图,点F是CE的中点,∴△BEF的底是EF,△BEC的底是EC,即EF=12EC,而高相等,∴S△BEF=12S△BEC,∵E是AD的中点,∴S△BDE=12S△ABD,S△CDE=12S△ACD,∴S△EBC=12S△ABC,∴S△BEF=14S△ABC,且S△ABC=24cm2,∴S△BEF=6cm2,即阴影部分的面积为6cm2.故答案为6.【点睛】本题考查了三角形面积的等积变换:若两个三角形的高(或底)相等,面积之比等于底边(高)之比.6.在ABC 中,90B ,8AB cm ,6BC cm ,点D 是AB 的中点,点P 从A 点出发,沿线段AD 以每秒2cm 的速度运动到B .当点P 的运动时间t ____________秒时,PCD 的面积为26cm .【答案】1或3【解析】【分析】分为两种情况讨论:当点P 在AD 上时,当点P 在DB 上时,根据三角形的面积公式建立方程求出其解即可.【详解】∵8AB cm ,点D 是AB 的中点,∴AD =BD =4cm ,当点P 在AD 上时,AP =2t ,∴PD =4-2t∵PCD 的面积为26cm ,∴12PD ×BC =6,即 142662t 解得t =1s ,当点P 在BD 上时,AP =2t ,∴DP =2t -4,∵PCD 的面积为26cm ,∴12DP ×BC =6,即 124662t ,解得t =3s ,综上,当点P 运动时间t 1或3秒时,PCD 的面积为26cm .故答案为:1或3.【点睛】本题考查了三角形的中线,三角形的面积公式的运用,解答时灵活运用三角形的面积公式求解是关键.三、解答题:(9分)7.如图,在ABC 中,CD 、CE 分别是ABC 的高和角平分线,,()BAC B .(1)若70,40 ,求DCE 的度数;(2)试用 、 的代数式表示DCE 的度数_________.【答案】(1)15DCE (2)2【解析】【分析】(1)根据三角形的内角和定理求出∠ACB 的值,再由角平分线的性质以及直角三角形的性质求出∠DCE .(2)由(1)的解题思路即可得正确结果.(1)解:∵70BAC ,40B180()180704070ACB BAC B ,∵CE 是ACB 的平分线, 1352ACE ACB .∵CD 是高线,90ADC ,9020ACD BAC ,352015DCE ACE ACD .(2)解:∵BAC ,B180()180ACB BAC B ,∵CE 是ACB 的平分线, 1118090222ACE ACB .∵CD 是高线,90ADC ,9090ACD BAC , 909022DCE ACE ACD.【点睛】思维拓展篇1.阅读下列材料:阳阳同学遇到这样一个问题:如图1,在ABC 中AB AC ,BD 是ABC 的高,P 是BC 边上一点,PM 、PN 分别与直线AB ,AC 垂直,垂足分别为点M 、N .求证:BD PM PN .阳阳发现,连接AP ,有ABC ABP ACP S S S ,即111222AC BD AB PM AC PN .由AB AC ,可得BD PM PN .他又画出了当点P 在CB 的延长线上,且上面问题中其他条件不变时的图形,如图2所示,他猜想此时BD 、PM 、PN 之间的数量关系是:BD PN PM .请回答:(1)请补全阳阳同学证明猜想的过程;证明:连接AP .ABC APC S S ∵________,1122AC BD AC ________12AB ________.AB AC ∵,BD PN PM .(2)参考阳阳同学思考问题的方法,解决下列问题:在ABC 中,AB AC BC ,BD 是ABC 的高.P 是ABC 所在平面上一点,PM 、PN 、PQ 分别与直线AB 、AC 、BC 垂直,垂足分别为点M 、N 、Q .①如图3,若点P 在ABC 的内部,猜想BD 、PM 、PN 、PQ 之间的数量关系并写出推理过程.②若点P 在如图4所示的位置,利用图4探究得此时BD 、PM 、PN 、PQ 之间的数量关系是:_______.(直接写出结论即可)【答案】(1)S △APB ;PN ;PM ;(2)①BD =PM +PN +PQ ,证明见解析②BD =PM +PQ −PN .【解析】【分析】(1)根据图形,结合阅读材料填写即可;(2)①连接AP 、BP 、CP ,根据S △ABC =S △APC +S △APB +S △BPC 得出12AC •BD =12AC •PN +12AB •PM +12BC •PQ ,由AB =AC =BC ,即可得出BD =PM +PN +PQ ;②连接AP 、BP 、CP ,根据S △ABC =S △APB +S △BPC −S △APC ,得出12AC •BD =12AB •PM +1 2BC•PQ−12AC•PN,由于AB=AC=BC,即可证得BD=PM+PQ−PN.【详解】解:(1)证明:连接AP.∵S△ABC=S△APC−S△APB,∴12AC•BD=12AC•PN−12AB•PM.∵AB=AC,∴BD=PN−PM.故答案为:S△APB;PN;PM;(2)①BD=PM+PN+PQ;如图3,连接AP、BP、CP,∵S△ABC=S△APC+S△APB+S△BPC∴12AC•BD=12AC•PN+12AB•PM+12BC•PQ,∵AB=AC=BC,∴BD=PM+PN+PQ;②BD=PM+PQ−PN;如图4,连接AP、BP、CP,∵S△ABC=S△APB+S△BPC−S△AP C.∴12AC•BD=12AB•PM+12BC•PQ−12AC•PN,∵AB=AC=BC,∴BD=PM+PQ−PN.【点睛】本题考查了等边三角形的性质,三角形的面积等,作出辅助线构建三个三角形是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.1.2 三角形的高、中线与角平分线
7.1.3 三角形的稳定性
基础过关作业
1.以下说法错误的是()
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.三角形的三条高可能相交于外部一点
2.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,•那么这个三角形是()
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.如图1,BD=1
2
BC,则BC边上的中线为______,△ABD的面积=_____的面积.
(1) (2) (3)
4.如图2,△ABC中,高CD、BE、AF相交于点O,则△BOC•的三条高分别为线段________.5.下列图形中具有稳定性的是()
A.梯形 B.菱形 C.三角形 D.正方形
6.如图3,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,求△ABD•与△ACD的周长之差.
7.如图,∠BAD=∠CAD,AD⊥BC,垂足为点D,且BD=CD.•可知哪些线段是哪个三角形的角平分线、中线或高?
综合创新作业
8.(综合题)如图5,在等腰三角形ABC中,AB=AC,一腰上的中线BD将这个等腰三角形的周长分为15和6两部分,求该等腰三角形的腰长及底边长.
9.有一块三角形优良品种试验基地,如图所示,•由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制定出两种以上的划分方案供选择(画图说明).
10.(创新题)如图,在△ABC 中,D 、E 分别是BC 、AD 的中点,S △ABC =4cm 2,求S △ABE .
11.(2004年,陕西)如图,在锐角△ABC 中,CD 、BE 分别是AB 、AC 上的高,•且CD 、BE 交于一点P ,若∠A=50°,则∠BPC 的度数是( )
A .150°
B .130°
C .120°
D .100°
培优作业
12.(探究题)(1)如图7-1-2-9,AD 是△ABC 的角平分线,
DE ∥AB ,DF ∥AC ,EF 交AD 于点O .请问:DO 是△DEF 的角平分线吗?如果是,请给予证明;如果不是,请说明理由.
(2)若将结论与AD 是△ABC 的角平分线、DE ∥AB 、DF ∥AC 中的任一条件交换,•所得命题正确吗?
13.(开放题)要使四边形木架(用4根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n 边形木架呢?
14.(趣味题)《三国演义》中有关木牛流马的叙述:
“孔明即手书一纸,付众观看,众将环绕而视.造木牛之法云:‘方腹曲头,一脚四足;头入领中,舌着于腹.载多而行少,独行者数十里,群行者二十里.曲者为牛头,双者为牛脚,横者为牛领,转者为牛足,覆者为牛背,方者为牛腹,垂者为牛舌,曲者为牛肋,刻者为牛齿,立者为牛角,细者为牛鞅,摄者为牛轴.牛仰双辕,人行六尺,牛行四步.’每牛载十人所食一月之粮,人不大劳,牛不饮食.”
你知道木牛流马中运用了什么数学知识吗?
数学世界
探险家的“难极”
有一个探险家,挖空心思想出一个“难极”来.
什么是探险家的“难极”呢?
一般情况下,如果从某地出发,先往北走100公里,再往东走100公里,然后往南走100公里,这时,终止地总要在出发地正东100公里处.
而若从某地出发,先往北走100公里,再往东走100公里,然后往南走100•公里,能正好回到原来的出发地.这个出发地被探险家称其为“难极”.
你知道探险家的“难极”在哪里吗?
答案:
1.A 点拨:锐角三角形的三条高在三角形内部交于一点,•直角三角形的三条高交于直角顶点,钝角三角形的三条高在三角形外部交于一点. 2.B 3.AD ;△ACD 4.BD ,CE ,OF 5.C 6.解:∵AD 为△ABC 的中线, ∴BD=CD ,
∴△ABD 与△ACD 的周长之差为:
(AB+BD+AD )-(AC+CD+AD )=AB-AC=5-3=2(cm ).
7.解:∵∠BAD=∠CAD ,∴AD 是△ABC 的角平分线,DE 是△BEC 的角平分线. ∵AD ⊥BC ,垂足为点D ,∴AD 是△ABC 的高,DE 是△BEC 的高. ∵BD=CD ,∴AD 是△ABC 的中线,DE 是△BEC 的中线. 点拨:本题是考查三角形的角平分线、中线和高的概念. 8.解:设AB=AC=2x ,则AD=CD=x . (1)AB+AD=15,BC+CD=6时, 有2x+x=15,解得x=5. ∴2x=10,BC=6-5=1.
(2)当BC+CD=15,AB+AD=6时, 有2x+x=6,解得x=2. ∴2x=4,BC=15-2=13.
∵4+4>13,∴此时构不成三角形.
∴这个等腰三角形的腰长及底边长分别为10,1.
点拨:要注意检验结果是否满足三角形三边关系定理.
9.解:方案1:如答图1,在BC 上取D 、E 、F ,使BD=ED=EF=FC ,连接AE 、ED 、•AF .
(1) (2) (3)
方案2:如答图2,分别取AB 、BC 、CA 的中点D 、E 、F ,连接DE 、EF 、DF . 方案3:如答图3,分别取BC 的中点D ,CD 的中点E ,AB 的中点F ,连接AD 、AE 、DF .同学们,你还有别的方法吗?试试看. 点拨:三角形面积计算公式为
1
2
×底×高,因此解题的关键是找出底、高分别相等的四个三角形.
10.解:∵AD 是△ABC 的边BC 上的中线,
∴S△ABD=1
2
S△ABC=
1
2
×4=2(cm2).
∵BE是△ABD的边AD上的中线,
∴S△ABE=1
2
S△ABD=
1
2
×2=1(cm2).
点拨:三角形的任一中线将三角形分为面积相等的两个小三角形.
11.B 点拨:∵CD、BE分别是AB、AC边上的高,
∴∠AEB=∠CDB=90°,
∵∠A=•50°,∴∠ABE=40°,
∴∠BPD=180°-∠CDB-∠ABE=180°-90°-40°=50°,•
∴∠BPC=180°-∠BPD=180°-50°=130°.
12.解:(1)DO是△DEF的角平分线.
证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD.
∵DE∥AB,DF∥AC,
∴∠EDA=∠FAD,∠FDA=∠EAD(两直线平行,内错角相等).
∴∠EDA=∠FDA.
∴DO是△DEF的角平分线.
(2)所得命题正确.
13.解:要使四边形木架不变形,至少要再钉上1根木条.
要使五边形木架不变形,至少要再钉上2根木条.
要使六边形木架不变形,至少要再钉上3根木条.
要使n边形木架不变形,至少要再钉上(n-3)根木条.
14.答:用手抬按木牛的双辕或木马的头部,木牛流马会稳稳地向前迈进.用手操作的时候,人和木牛流马总是呈三角形.
这符合三角形稳定性原理,•这也是木牛流马“上山下岭,各尽其便”的原因.数学世界答案:探险家的“难极”就是南极点.。
