湘教版数学九上34相似多边形同步测试一
湘教版九年级数学上3.3相似的图形同步测试题及答案

湘教版九年级数学上册第3章图形的相似 3.3 相似的图形同步测试题1.观察如图所示的四组图形,不相似的图形是( )2.已知△DEF∽△ABC,且∠A=50°,∠B=40°,则∠F的度数是( ) A.50°B.20°C.70°D.90°3.在△ABC中,BC=13,AC=11,AB=15,另一个与它相似的三角形的最大边长为10,则它的最小边长为( )A.223B.203C.172D.1524.小张用手机拍摄得到图①,经放大后得到图②.图①中的线段AB在图②中的对应线段是( )A.FG B.FH C.EH D.EF5.如果△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为k1,△A′B′C′与△ABC的相似比为k2,则k1与k2的关系是( )A.k1=k2B.k1+k2=0 C.k1·k2=-1 D.k1·k2=1 6.如图,△ABC∽△ADE,且∠ADE=∠B,则下列比例式正确的是( )A.AEBE=ADDCB.AEAB=ADACC.ADAC=DEBCD.AEAC=DEBC7.如图,△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12,∠A=58°,∠AOB =72°,求AB,OC的长和∠C的度数.8.下列图形中,是相似形的是( )A.所有平行四边形 B.所有矩形 C.所有菱形 D.所有正方形9.两个相似多边形的一组对应边分别为 3 cm,4.5 cm,那么它们的相似比为( )A.23B.32C.49D.9410.如图,下列两个四边形若相似,则下列结论不正确的是( )A.∠α=100° B.x=32 5C.y=245D.x=711.(易错题)在△ABC,点D,E分别在AB,AC上,且ADDB=AEEC=2,则△ADE与△ABC的相似比为( )A.12B.2 C.32D.2312.如图,Rt△ABC∽Rt△DEF,∠A=35°,则∠E的度数为( )A.35° B.45° C.55° D.65°13.如图,△ABC∽△ACD,若∠ACB=80°,则∠ADC的度数为( )A.30° B.50° C.80° D.无法确定14.若如图所示的两个四边形相似,则∠α的度数是( )A.60° B.75° C.87° D.120°15.如图,在▱ABCD中,AB=10,AD=6,E是AD的中点,点F在AB上,且△BCF∽△DCE,则BF的长是( )A.8.2 B.3.6 C.5 D.1.816.已知△ABC与△A′B′C′相似,相似比为2∶3;△A′B′C′与△A″B″C″相似,相似比为5∶4,那么△ABC与△A″B″C″的相似比为( )A.5∶6 B.6∶5 C.15∶8 D.8∶1517.如图,有两个相似的星星图案,则x的值是( )A.15 B.12 C.10 D.818.如图,△ADE∽△ABC,若AD=1,AB=3,则△ADE与△ABC的相似比是_________.19.矩形ABCD与矩形A′B′C′D′中,AB=40,BC=20,A′B′=20,B′C′=10,则矩形ABCD与矩形A′B′C′D′_______相似.(填“一定”或“不一定”) 20.如图,已知△ABC∽△ADE,AE=5 cm,EC=3 cm,BC=7 cm,∠BAC=45°,∠C=40°.(1)求∠AED和∠ADE的大小;(2)求DE的长.21.如图,已知四边形ABCD∽四边形A′B′C′D′,求∠A的度数及x的值.22.在一矩形ABCD的花坛四周修筑小路,使得相对两条小路的宽均相等,如果花坛AB=20米,AD=30米,问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A ′B ′C ′D ′与矩形ABCD 相似?请说明理由.答案:1---6 CDADDD7. 解:根据题意有:OD =AD -OA =7,OA OD =OB OC =AB CD ,∴OB OC =AB CD =27,∴5OC =AB 12=27,∴OC =17.5,AB =247,∠C =∠B =180°-∠A -∠AOB =50°8----17 DADDC CCDAD 18. 1:319. 一定20. 解:(1)∠AED =40°,∠ADE =95°(2)∵△ABC∽△ADE ,∴AE AC =DE BC ,即55+3=DE7,∴DE =4.375 cm21. 解:∵四边形ABCD∽四边形A′B′C′D′,∴∠A =∠A ′,ABA′B′=AD A′D′.又∵∠A′=107°,AB =5,AD =4,A ′B ′=2,∴∠A =107°,52=4x,∴x =8522. 解:由题意知20∶(20+2y )=30∶(30+2x ),∴3y =2x ,即y x =23,即x y =32时,矩形A′B′C′D′与矩形ABCD 相似。
2016湘教版九年级数学上3.4.1相似三角形的判定同步练习含答案解析

《3.4.1 相似三角形的判定》一、填空题1.三角形一边的和其他两边,所构成的三角形与原三角形相似.2.如果两个三角形的对应边的,那么这两个三角形相似.3.如果两个三角形的对应边的比相等,并且相等,那么这两个三角形相似.4.如果一个三角形的角与另一个三角形的,那么这两个三角形相似.5.在△ABC和△A′B′C′中,如果∠A=56°,∠B=28°,∠A′=56°,∠C′=28°,那么这两个三角形能否相似的结论是,理由是.6.在△ABC和△A′B′C′中,如果∠A=48°,∠C=102°,∠A′=48°,∠B′=30°,那么这两个三角形能否相似的结论是,理由是.7.在△ABC和△A′B′C′中,如果∠A=34°,AC=5cm,AB=4cm,∠A′=34°,A′C′=2cm,A′B′=1.6cm,那么这两个三角形能否相似的结论是,理由是.8.在△ABC和△DEF中,如果AB=4,BC=3,AC=6,DE=2.4,EF=1.2,FD=1.6.那么这两个三角形能否相似的结论是,理由是.9.如图,△ABC的两条高AD、BE交于点H,则图中的相似三角形共有对.10.如图所示,?ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有对.二、选择题11.如图,不能判定△ABC∽△DAC的条件是()A.∠B=∠DAC B.∠BAC=∠ADC C.AC2=DC?BC D.AD2=BD?BC12.如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是()A.5 B.8.2 C.6.4 D.1.813.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是()A. B. C.D.三、解答题14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.(1)图中有哪两个三角形相似?(2)求证:AC2=AD?AB;BC2=BD?BA;CD2=AD?BD;(3)若AD=2,DB=8,求AC,BC,CD的长;(4)若AC=6,DB=9,求AD,CD,BC的长;(5)求证:AC?BC=AB?CD.15.如图所示,如果D、E、F分别在OA、OB、OC上,且DF∥AC,EF∥BC.求证:(1)OD:OA=OE:OB;(2)△ODE∽△OAB;(3)△ABC∽△DEF.16.如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE?FB.17.已知:如图,在梯形ABCD中,AB∥CD,∠B=90°,以AD为直径的半圆与BC相切于E点.求证:AB?CD=BE?EC.18.如图,AB是⊙O的直径,BC是⊙O的切线,切点为点B,点D是⊙O上的一点,且AD∥OC.求证:AD?BC=OB?BD.19.已知:如图,在⊙O中,CD过圆心O,且CD⊥AB,垂足为D,过点C任作一弦CF交⊙O于F,交AB于E.求证:CB2=CF?CE.20.已知D是BC边延长线上的一点,BC=3CD,DF交AC边于E点,且AE=2EC,试求AF与FB的比.21.已知:如图,在△ABC中,∠BAC=90°,AH⊥BC于H,以AB和AC为边在Rt△ABC外作等边△ABD和△ACE,试判断△BDH与△AEH是否相似,并说明理由.22.如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过点P作PE⊥AB交AC 边于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,求y与x之间的函数关系式.《3.4.1 相似三角形的判定》参考答案与试题解析一、填空题1.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.【考点】相似三角形的判定.【分析】平行于三角形一边的直线和其他两边(或两边的延长线)相交,所得的三角形与原三角形的三边对应成比例.所以所构成的三角形与原三角形相似.【解答】解:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.故答案是:平行于;直线;相交.【点评】本题考查了相似三角形的判定.(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.2.如果两个三角形的三组对应边的比相等,那么这两个三角形相似.【考点】相似三角形的判定.【分析】由三边法:三组对应边的比相等的两个三角形相似;即可求得答案.【解答】解:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.故答案为:三组,比相等.【点评】此题考查了相似三角形的判定.注意熟记相似三角形的判定定理是关键.3.如果两个三角形的两组对应边的比相等,并且夹角对应相等,那么这两个三角形相似.【考点】相似三角形的判定.【分析】由两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;即可求得答案.【解答】解:如果两个三角形的两组对应边的比相等,并且夹角对应相等,那么这两个三角形相似.。
【湘教版】九年级数学上册:3.3《相似图形》同步试题(含答案)

3.3相似图形01 基础丿 知识点1相似图形的概念1•下列选项中,是相似图形的木质属性的是(0A.大小不同 B.大小相同 C.形状相同 D.形状不同2•观察如图所示的四组图形,不相似的图形是(0知识点2相似三角形的概念及性质3.如果△ ABCsff C' , BC=3, B' C =1.8,那么△才 B' C'与△遊的相似比为⑵A. 5 : 3C. 2 : 3 4•如图所示,筑\ABC S \DEF,则ZE 的度数为(。
C. 42°D. 52°5.己知△ ABCsM s' c 等于(Qf ,且相似比为3 : 2,若才B' =10 cm,则肋 20 A. ■— cm oB. 15 cm A. 28°C. 30 cmD. 20 cmB. 3 : 2 D. 3 : 5ABCD10.两个相似多边形一组对应边分别为3 c 叫4. 5 cm 那么它们的相似比为 (A)2A -33 B -2 4C -9 9D -411 •若如图所示的两个四边形相似,则Za 的度数是(0A. 60°B. 75°C. 87°6.两个相似三角形的童应边的比值叫作相似比.7.两个三角形相似,其中一个三角形的两个内角分别是40° .60。
,那么另 -个三角形的最大角为80° ,最小角为40° .8•如图,'ABCs'AED 、找出对应角并写出对应边的比例式.解:对应角:与上E ; ZC 与上D ; ZBAC 与ZDAE ; ,-、.,,11 / I AB AC BC 对应边的比例式:廷=沪丽 知识点3相似多边形的概念及性质9•如下的各组多边形中,相似的是(3>正六边形和一般六边形 (I)□A. (1) (2) (3)B. (2) (3)C. (1) (3)D. (1) (2)正方形 (2) ⑶D. 120°12.如图,正五边形尸6曲艸与正五边形肋宓相似,若肋:FG=2 : 3,则下列结论正确的是(BA. 2DE=3MNB. 3DE=2MNC. 3ZJ=2Z FD. 2Z^=3Z FM d c心N F E A02 中档题13.给出四个判断:①所有的等腰三角形都相似;②所有的等边三角形都相似;③所有的直角三角形都相似;④所有的等腰直角三角形都相似.其中判断正确的个数是(BA. 1B. 2C. 3D. 414.F列命题是真命题的是(BA.所有的等腰三角形都相似B.所有的对角线互相垂直平分且相等的四边形都相似C.四个角都是直角的两个四边形一定相似D.四条边对应成比例的两个四边形相似15.如图所示,'ABCsHADE,肚/ADE=ZB,则下列比例式正确的是(0)AB AD A,BE_ DCAE AD B 一=一*AB ACAD DE r —=—AC BCAE DED —AC BCA16.如图,有两个相似的星星图案,则x的值是⑵A. 15B. 12C. 10D. 8x cm17.(南岸区一模)如图,'ABCs 仞=2, M=3, BC=4,那么仙的值等于(B解:(1) AAED=W , Z^=95° ・(2) •: 'ABC S 'ADE 、・・・防=曽cm.O19•如图,己知四边形如"四边形才B f C l D f ,求Z 力的度数及左的值.解:•・•四边形宓M 四边形才B' C D' , ZA =107° ,肋=5,仙=4,A 1B 1 =2,15 cm 20 cmil I A. 5 B. 6C. 7 1& 如图,己巩 5 ABCs HADE,处=5 cm, EC=3 cm, BC=1 cm, ABAC=45° , Zr=40° ・ (1)求上AED 和Z 血疗的大小;⑵求防的长.5 DE•燈老即5+3 7 D. 403 综合题20.我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但 形状完全相同,就把它们叫作相似体•如图,甲.乙是两个不同的正方体, 正方体都是相似体,它们的一切对应线段之比都等于相似比:日:方,设S 甲, s 乙分别表示这两个正方体的表面积,则尹=驚=《)訂又设孑甲,卩乙分别 表示这两个正方体的体积,则—⑴下列几何体中,一定属于相似体的是G4)B. 两个圆锥体 ⑵请归纳出相似体的3条主要性质:① 相似体的一切对应线段(或弧)长之比等于似也② 相似体表而积之比等于相似比的平方;③ 相似体体积之比等于相似比的立方 ・・・Z4Z 才, AB AD A' B‘_A Z DC. 两个圆柱体D. 两个长方体A.两个球体即 Z 力=107° ,。
湘教版九年级数学上册《3.4 相似三角形的判定与性质》练习题-带参考答案

湘教版九年级数学上册《3.4 相似三角形的判定与性质》练习题-带参考答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.已知△ABC∽△A′B′C′且ABA′B′=12,则S△ABC∶S△A′B′C′为( )A.1∶2B.2∶1C.1∶4D.4∶12.如图,△ABC与△DE F相似,相似比为1∶2,BC的对应边是EF,若BC=1,则EF的长是( )A.1B.2C.3D.43.已知△ABC∽△DEF,且AB∶DE=1∶2,则△ABC的面积与△DEF的面积之比为( )A.1∶2B.1∶4C.2∶1D.4∶14.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF :S△ABF=4:25,则DE:EC=()A.2:3 B.2:5 C.3:5 D.3:25.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )A.1对B.2对C.3对D.4对6.如图,P是Rt△ABC的斜边BC上异于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )A.1条B.2条C.3条D.4条7.如图,点P是△ABC的边AB上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )A.2条B.3条C.4条D.5条8.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在格点为( )A.P1 B.P2C.P3D.P49.要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么符合条件的三角形框架乙共有( )A.1种B.2种C.3种D.4种10.如图,在△ABC中,CD⊥AB,且CD2=AD•DB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DF•DC.则下列结论正确的是( )A.①②④B.②③④C.①②③④D.①③二、填空题11.若△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,则△ABC与△DEF的面积比值为.12.若两个相似三角形的周长比为2:3,则它们的面积比是.13.若△ABC∽△A′B′C′,且AB:A′B′=3:4,△ABC的周长为12 cm,则△A′B′C′的周长为____________.14.下图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是.(写出满足条件的所有的点)15.如图,平行四边形ABCD中,E是BC边延长线上一点,AE交CD于F,则图中相似三角形有对.16.如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则Cn的坐标是.三、解答题17.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°. 求证:△ADC∽△DEB.18.如图,A、B、C、P四点均在边长为1的小正方形网格格点上.(1)判断△PBA与△ABC是否相似,并说明理由;(2)求∠BAC的度数.19.如图所示,已知AB∥CD,AD,BC相交于点E,F为BC上一点,且∠EAF=∠C.求证:(1) ∠EAF=∠B;(2) AF2=FE·FB.20.如图,在△ABC中,AD和BG是△ABC的高,连接GD.(1)求证△ADC∽△BGC;(2)求证CG·AB=CB·DG.21.如图,已知P是正方形ABCD边BC上一点,BP=3PC,Q是CD的中点(1)求证:△ADQ∽△QCP;(2)若AB=10,连接BD交AP于点M,交AQ于点N,求BM,QN的长.22.在等腰三角形ABC中,AB=AC,D是AB延长线上一点,E是AC上一点,DE交BC于点F.(1)如图①,若BD=CE,求证:DF=EF.(2)如图②,若BD=1nCE,试写出DF和EF之间的数量关系,并证明.(3)如图③,在(2)的条件下,若点E在CA的延长线上,那么(2)中结论还成立吗?试证明.答案1.C2.B3.B4.A5.C.6.C7.C.8.B9.C.10.C.11.答案为:1:4.12.答案为:4:9.13.答案为:16cm.14.答案为:Q.15.答案为:4.16.答案为(﹣3×4n﹣1,4n).17.证明:∵△ABC是等边三角形∴∠B=∠C=60°∴∠ADB=∠CAD+∠C=∠CAD+60°∵∠ADE=60°∴∠ADB=∠BDE+60°∴∠CAD=∠BDE∴△ADC∽△DEB.18.解:(1)△PBA与△ABC相似,理由如下:∵AB=5,BC=5,BP=1∴∵∠PBA=∠ABC∴△PBA∽△ABC;(2)∵△PBA∽△ABC∴∠BAC=∠BPA∵∠BPA=90°+45°=135°∴∠BAC=135°.19.证明:(1)∵AB∥CD∴∠B=∠C又∠C=∠EAF∴∠EAF=∠B(2)∵∠EAF=∠B,∠AFE=∠BFA ∴△AFE∽△BFA则AFBF=FEFA∴AF2=FE·FB20.解:(1) ∵在△ABC中,AD和BG是△ABC的高∴∠BGC=∠ADC=90°.又∠C=∠C∴△ADC∽△BGC.(2)∵△ADC∽△BGC∴CGDC=BCAC.∴CGBC=DCAC.又∠C=∠C∴△GDC∽△BAC.∴CGBC=DGAB.∴CG·AB=CB·DG.21.证明:(1)∵正方形ABCD中,BP=3PC,Q是CD的中点∴PC=14﹣BC,CQ=DQ=12CD,且BC=CD=AD∴PC :DQ =CQ :AD =1:2 ∵∠PCQ =∠ADQ =90° ∴△PCQ ∽△ADQ (2)∵△BMP ∽△AMD ∴BM :DM =BP :AD =3:4 ∵AB =10 ∴BD =10 2 ∴BM =同理QN =53 5.22.证明:(1)在题图①中作EG ∥AB 交BC 于点G 则∠ABC =∠EGC ,∠D =∠FEG. ∵AB =AC ,∴∠ABC =∠C. ∴∠EGC =∠C.∴EG =EC. ∵BD =CE ,∴BD =EG. ∵∠D =∠FEG ,∠BFD =∠GFE ∴△BFD ≌△GFE. ∴DF =EF. (2)解:DF =1nEF.证明:在题图②中作EG ∥AB 交BC 于点G ,则∠D =∠FEG.由(1)得EG =EC. ∵∠D =∠FEG ,∠BFD =∠EFG ∴△BFD ∽△GFE.∴BD EG =DF EF. ∵BD =1n CE =1n EG∴DF =1n EF.(3)解:成立.证明:在题图③中作EG ∥AB 交CB 的延长线于点G则仍有EG=EC,△BFD∽△GFE.∴BDEG=DFEF.∵BD=1nCE=1nEG,∴DF=1nEF.。
湘教版九年级上第3章图形的相似检测题含答案详解.doc
第3章图形的相似检测题(时间:90分钟,满分:100分)一、选择题(每小题3分,共30分)1.下列四组图形中,不是相似图形的是( )3.在比例尺;Njrri'jTi 的地图上,量得两地的距离是)A•朋加 B .麻汹C.坦加D. -bti4.若 a5 C,且 一,则丽掘厂猛 的值是( )8A.14B.42C.714D.—35.如图,在△ 瞬中,点泳卜;分别是的中点,则下列结论:① ……;—L △.二一; A.3个AD AB③——:其中正确的有( )AE ACD.0个6.如图,獗〃_[,二〃],服刚分别交:賈于点. ,则图中共有相似三角形( )A.4对B.5对C. 6对D.7对'r “,则这两地的实际距离是(第5题第T 题4057•已知△貞置如图所示,则下列4个三角形中,与△.踞亍:相似的是( )8. 下列说法中正确的是( )① 在两个边数相同的多边形中,如果对应边成比例,那么这两个多边形相似; ② 如果两个矩形有一组邻边对应成比例,那么这两个矩形相似; ③ 有一个角对应相等的平行四边形都相似; ④ 有一个角对应相等的菱形都相似. A.①②B.②③C.③④D.②④9.已知,如图,点一是线段耀的黄金分割点 於沪邈,则下列结论中正确的是()B.1 ?二卜:AC v5—1D.— --BC 2血二弼腿二3, AC=4 AS 的垂直平分线 二交二 的延长线于点 「,则二 的长为()3 7 25A.—B. 一C. —D.2 6 6二、填空题(每小题3分,共24分)ii.已知= 312,且 a+& = lfl',则0 二 _________ .BC 岳-1C.—----AC 210.如图,在 Rt△ 妣中,5H第10题图12.已知仝I f. d是成比例线段,即. 「其中-■■■■■ - ■- -「二…,则d 二—…-13•如图,在△.―中,二…一一•二一「二一「则」--------------------- ------ -15.如图,_是遥的黄金分割点,跟匚般,以側为边的正方形的面积为「以眾霭为边的矩形的面积为',则5______ (填“〉”“v”“= ”).16.五边形卿就s五边形n曲,24 = 120*, zr = 13F, ZC = W5S 少二851 则上E 二_____________ .17.如图,在△般中,一二分别是帆駅边上的点,——一…匸二…「二-,-「二♦则撫二——.18.如图,△薦押三个顶点的坐标分别为蚊丄几林込时呎N 2],以原点为位似中心,将△缩小,位似比为1:2,则线段4C的中点P变换后对应点的坐标为 ___________ _三、解答题(共46分)19.(5分)如图,在平行四边形 朋霭中,一为边戒延长线上的一点,且 _为二 的黄金分割点,即.二•亠;湍交…于点「,已知蜩三和E ,求二的长.20. (4分)如图,在 △做中,朋=』C ,册平分/眦,胚//就.求证:DE 二EC . 21.(5分)已知:如图,_是朋上一点,鵰熬匚歪,二一分别交于点.仁/ 2, 探索线段 即,幡「器之间的关系,并说明理由•第旧题图第勿题图第可题国D第22题图22. (8 分)如图,梯形鋼彩中,二//亦,点-在垃上,连接膳并延长与#仲的延长线交于点一.(i)求证:△[饬;△…;;(2)当点是^ 的中点时,过点. 作_ // 「交臓于点],若-.…::....,求二的长.23.(8分)如图,在梯形-中,二//__,点一是边二的中点,连接「交一.一于;,「的延长线交強j的延长线于一…_EG AE(1)求证2)若鑼:□?,密□?,求线段乔•的长.GE BC ---.- -券:,点在边蹴上,弼与鵰相交于点,且/ _ '.求证:(I— - s△郦;(225. (8 分)如图,在正方形獅中,一. 分别是边冊,僞;上的点,.1 i T K_并延长交…的延长线于点_4(1)求证:△ ABE DEF ;(2)若正方形的边长为4,求氾的长.24. (8 分)已知:如图,在△影中, 朋:□雜顷//策羽题图A第25题图第3章 图形的相似检测题参考答案A 、B 、C 项都为相似图形,D 项中一个是等边三角形,A 、B 、D 项都正确,C 项不正确.3. D 解析:.:口工口-诃応c- 9『以;.4. D解析:设I =加8 *,则1二、:.=•.门下、二一.「=:「所以.;-;:-】所以-- . - _」聲.I.A解析:因为点屠::此分别是 AB 、 M 的中点,所以 「是△的中位线•由中位线的性质可推出①②③全部正确 6. C 解析:△ f 熔;s 窗谕's △炭 £“△:;/$;• 7. C解析:由一二L ;能 Zfl = 7S\ 知 ZC 二出 ZA = 30S 对照四个选项知,C 项中的三角形与△..二相似• 8. D解析:①虽然对应边成比例,但是对应角不一定相等,所以不一定相似,比如:所有菱 形的对应边成比例,但是它们不一定相似;②两个矩形有一组邻边对应成比例,就可以 得出四条边对应成比例,并且它们的角都是90°所以这两个矩形相似;③有一个角对应相等的平行四边形的对应边不一定成比例,所以不一定相似;④有一个角对应相等就可 以得出菱形的其他角对应相等,并且菱形的对应边成比例,所以相似•故选D .BC vi-i9. C解析:根据黄金分割的定义可知,^•AC 210. B 解析:在由勾股定理得 AB 二 5.因为.―亠…巴 所以一 -'•又因为亠化戸必惋=毅厶;=心;所以卄盟曲 25 皿 nr 2 25 、 7△F.枷:s △測#.所以,所以…二 二,所以讹:二二 二二 [二. AB BC乳 661. D解析:根据相似图形的定义知, 个是直角三角形,不是相似图形 2. C 解析:由比例的基本性质知11.4解析:因为倉璨弍刈,所以设迟:,II 「」二-一-一'., 所以、-;所以;;'二甌二如a c佗4解析:把「二代入.「得一壮迫13.9解析:在△赠中因为]]//「,所以/綱阮期麗 羽霭匸,所以△AD AE 23—L △二,所以…,所以一…,所以」15•一 解析:由黄金分割的概念知= -J » f _,又探T 曲 所以 _ =f所以;],:--16.i :『解析:因为五边形册饨鬧s 五边形:护『m 所以―__…—一 一 一又因为五边形的内角和为[一,所以—二二二.仃•二解析:在*和△腮中,•••____..,△汹r △妙.其中点坐标 为(4, 3),又以原点为位似中心,将 △绅;『缩小,位似比为j 0 ■;,/19.解:T 四边形期畫鹭为平行四边形,/ /灯擀1亠/編期,/吃丫也i.» ,14.一解析:由b 诗 f“5,得E 弘E ・5d ,2脚,所以窘f1.5b -d 0.5f 3b -2d f= 0.5.18.解析:••• (2, 2), (6, 4),/线段槍的中点变换后对应点的坐标为又••朋□<,「是淤「Il 平分/瞬」/珈—…」/…/…, •m 哦,•••二21. 解—「理由:•••二〃…〔•- /〕—[.又m ;EF FG又△二一 S △二二,•二[「即…二「「22. (1)证明:「梯形.匚 __ 中,二 II __ ,• ___ / 一 _「丄,• △…s △邂-(2)解:由(1)知,△ CDF _ .■.,又一是… 的中点,•8.r = FC宀 ' ' GB BC ,GB EF2 EF「一 一,於:纟’二 一’•燼 R1.2+3+FF224.证明:(1「•猷口献• / - 「一CF BC CF AD—: ----- ,即—=—23.(1)证明::册1 :器,二/空卫二/朋〔•…,-(2)由△牌s△聃,得匹二匹,.•. DE2二DB EF .DE EF由△_」s△觑,得—溺匸儕••• DG DF 二DB EF .25.(1)证明:在正方形 .—中,―--.,二卫二綁•「.匚一二・I 一「:二脱,•• JAB =些.•. △ ABE s\DEFDE DF '(2)解:r J _ . • BE 二4222= 2 5 ,• ABE "DEF , AEB ABE = AEB DEF =90 ,• BEG = 90 .由:_//_「,得.AEB - EBG ,• △豚s△…,AE BE BE 一BG BG 二B^10.AE•••/颤匚/颐,•△溯S△瞬••••匹二匹..•• DE DG DF .DE DF。
湘教版九年级数学上册测试题3.3 相似图形

3.3 相似图形01 基础题知识点1 相似图形的概念1.下列选项中,是相似图形的本质属性的是(C)A .大小不同B .大小相同C .形状相同D .形状不同2.观察如图所示的四组图形,不相似的图形是(C)知识点2 相似三角形的概念及性质3.如果△ABC ∽△A′B′C′,BC =3,B′C′=1.8,那么△A′B′C′与△ABC 的相似比为(D)A .5∶3B .3∶2C .2∶3D .3∶54.如图所示,若△ABC ∽△DEF ,则∠E 的度数为(C)A .28°B .32°C .42°D .52°5.已知△ABC ∽△A′B′C′,且相似比为3∶2,若A′B′=10 cm ,则AB 等于(B)A.203cm B .15 cm C .30 cm D .20 cm6.两个相似三角形的对应边的比值叫作相似比.7.两个三角形相似,其中一个三角形的两个内角分别是40°、60°,那么另一个三角形的最大角为80°,最小角为40°.8.如图,△ABC ∽△AED ,找出对应角并写出对应边的比例式.解:对应角:∠B 与∠E ;∠C 与∠D ;∠BAC 与∠DAE ;对应边的比例式:AB AE =AC AD =BC ED.知识点3 相似多边形的概念及性质9.如下的各组多边形中,相似的是(B)A .(1)(2)(3)B .(2)(3)C .(1)(3)D .(1)(2)10.两个相似多边形一组对应边分别为3 cm ,4.5 cm ,那么它们的相似比为(A)A.23B.32C.49D.9411.若如图所示的两个四边形相似,则∠α的度数是(C)A .60°B .75°C .87°D .120°12.如图,正五边形FGHMN 与正五边形ABCDE 相似,若AB ∶FG =2∶3,则下列结论正确的是(B)A .2DE =3MNB .3DE =2MNC .3∠A =2∠FD .2∠A =3∠F02中档题13.给出四个判断:①所有的等腰三角形都相似;②所有的等边三角形都相似;③所有的直角三角形都相似;④所有的等腰直角三角形都相似.其中判断正确的个数是(B)。
湘教版九年级数学上册第3章 图形的相似测试题

湘教版九年级数学上册第3章 图形的相似测试题一、选择题(本大题共7小题,每题4分,共28分)1.5x =6y ,那么x y等于( ) A .5 B .6 C.56 D.652.C 是线段AB 的黄金联系点,且AB =6 cm ,那么BC 的长为( )A .(3 5-3)cmB .(9-3 5)cmC .(3 5-3)cm 或(9-3 5)cmD .(9-3 5)cm 或(6 5-6)cm3.如图3-Z -1,在四边形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于点O ,AD =1,BC =4,那么△AOD 与△BOC 的面积之比等于( )A.12B.14C.18D.1164.以下选项中能判定△ABC ∽△DEF 的是( )A .∠A =45°,∠B =55°;∠D =45°,∠F =75°B .AB =5,BC =4,∠A =45°;DE =10,EF =8,∠D =45°C .AB =6,BC =5,∠B =40°;DE =5,EF =4,∠E =40°D .BC =4,AC =6,AB =9;DE =18,EF =8,DF =12图3-Z -1图3-Z -25.如图3-Z -2,线段AB 两个端点的坐标区分为A (6,6),B (8,2),以原点O 为位似中心,在第一象限内将线段AB 增加为原来的12后失掉线段CD ,那么端点C 的坐标为( ) A .(3,3) B .(4,3)C .(3,1)D .(4,1)6.如图3-Z -3,在△ABC 中,中线BE ,CD 相交于点O ,衔接DE ,以下结论:①DE BC=12;②S △DOE S △COB =12;③AD AB =OE OB ;④S △DOE S △ADE =13.其中正确的有( ) A .1个 B .2个 C .3个 D .4个图3-Z -3图3-Z -47.如图3-Z -4,在Rt △ABC 中,∠ABC =90°,AB =6,BC =8,∠BAC ,∠ACB 的平分线相交于点E ,过点E 作EF ∥BC 交AC 于点F ,那么EF 的长为( )A.52B.83C.103D.154二、填空题(本大题共4小题,每题4分,共16分)8.在比例尺为1∶40000的地图上,某条路途的长为7 cm ,那么该路途的实践长度是________ km.9.如图3-Z -5,在△ABC 中,MN ∥BC 区分交AB ,AC 于点M ,N .假定AM =1,MB =2,BC =3,那么MN 的长为________.10.在△ABC 中,AB =6,AC =5,点D 在边AB 上,且AD =2,点E 在边AC 上,当AE =________时,以A ,D ,E 为顶点的三角形与△ABC 相似.图3-Z -5图3-Z -611.如图3-Z -6,铁路道口的栏杆短臂长1 m ,长臂长16 m .当短臂端点下降0.5 m 时,长臂端点降低________m .(杆的宽度疏忽不计)三、解答题(本大题共5小题,共56分)12.(10分)如图3-Z -7所示,AD ,BE 区分是钝角三角形ABC 的边BC ,AC 上的高,求证:AD BE =AC BC. 图3-Z -713.(10分)如图3-Z -8,四边形ABCD 中,E ,F ,G 区分在AD ,BD ,CD 上,且EF ∥AB ,FG ∥BC .求证:△DEG ∽△DAC .图3-Z -814.(10分)如图3-Z -9,在10×10的正方形网格中,点A ,B ,C ,D 均在格点上,以点A 为位似中心画四边形AB ′C ′D ′,使它与四边形ABCD 位似,且位似比为2.(1)在图中画出四边形AB ′C ′D ′;(2)填空:△AC ′D ′是________三角形.图3-Z -915.(12分)为测量操场上旗杆的高度,设计的测量方案如图3-Z -10所示,标杆高度CD =3 m ,标杆与旗杆的水平距离BD =15 m ,人的眼睛距空中的高度EF =1.6 m ,人与标杆CD 的水平距离DF =2 m ,E ,C ,A 三点共线,求旗杆AB 的高度.图3-Z -1016.(14分)如图3-Z -11,四边形ABCD 中,AB =AC =AD ,AC 平分∠BAD ,点P 是AC 延伸线上一点,且PD ⊥AD .(1)证明:∠BDC =∠PDC ;(2)假定AC 与BD 相交于点E ,AB =1,CE ∶CP =2∶3,求AE 的长.图3-Z -11详解详析1.D2.C [解析] ∵C 是线段AB 的黄金联系点,且AB =6 cm ,∴BC =5-12AB =(3 5-3)cm 或BC =3-52AB =(9-3 5)cm.应选C.3.D [解析] 在梯形ABCD 中,AD ∥BC ,所以△AOD ∽△COB .又由AD =1,BC =4,依据相似三角形的面积比等于相似比的平方,即可求得△AOD 与△BOC 的面积之比.4.D 5.A6.C [解析] 由BE ,CD 均为△ABC 的中线可知,DE 为△ABC 的中位线,所以DE =12BC ,DE ∥BC ,所以DE BC =12,故①正确; 由DE ∥BC 可得△DOE ∽△COB ,所以S △DOE S △COB =(DE BC)2=14,故②错误;由DE ∥BC 可得AD AB =DE BC ,DE BC =OE OB ,所以AD AB =OE OB ,故③正确;由于DE ∥BC ,所以△ADE ∽△ABC ,所以S △ADE S △ABC =(DE BC )2=14,设△DOE 的高OH 为h ,DE =a ,那么BC =2a ,△BOC 的高为2h ,△ABC 的高为6h ,△ADE 的高为3h ,所以S △DOE S △ADE =12ah 12·a ·3h =13,故④正确.应选择C. 7.C [解析] 延伸FE 交AB 于点D ,作EG ⊥BC 于点G ,作EH ⊥AC 于点H ,∵EF ∥BC ,∠ABC =90°,∴FD ⊥AB .又∵EG ⊥BC ,∴四边形BDEG 是矩形.∵AE 平分∠BAC ,CE 平分∠ACB ,∴ED =EH =EG ,∠DAE =∠HAE ,∴四边形BDEG 是正方形.在△DAE 和△HAE中,∵⎩⎪⎨⎪⎧∠DAE =∠HAE ,∠ADE =∠AHE ,AE =AE ,∴△DAE ≌△HAE (AAS),∴AD =AH .同理△CGE ≌△CHE ,∴CG =CH .设BD =BG =x ,那么AD =AH =6-x ,CG =CH =8-x .∵AC =AB 2+BC 2=62+82=10,∴6-x +8-x =10,解得x =2,∴BD =DE =2,AD =4.∵DF ∥BC ,∴△ADF ∽△ABC ,∴AD AB =DF BC ,即46=DF 8,解得DF =163, 那么EF =DF -DE =163-2=103.应选C. 8.2.8 [解析] 设这条路途的实践长度为x ,那么140000=7x,解得x =280000 cm =2.8 km. 9.1 [解析] ∵MN ∥BC ,∴△AMN ∽△ABC ,∴AM AB =MN BC, 即11+2=MN 3,∴MN =1. 10.125或53 [解析] 当AE AD =AB AC时, ∵∠A =∠A ,∴△AED ∽△ABC ,此时AE =AB ·AD AC =6×25=125;当AD AE =AB AC时,∵∠A =∠A , ∴△ADE ∽△ABC ,此时AE =AC ·AD AB =5×26=53. 故答案为125或53. 11.812.证明:∵AD ,BE 是钝角三角形ABC 的高,∴∠ADC =∠BEC =90°.又∵∠DCA =∠BCE ,∴△DAC ∽△EBC ,∴AD BE =AC BC. 13.证明:∵EF ∥AB ,∴DE DA =DF DB. ∵FG ∥BC ,∴DG DC =DF DB , ∴DE DA =DG DC. 又∵∠EDG =∠ADC ,∴△DEG ∽△DAC .14.解:(1)如图,四边形AB ′C ′D ′即为所求作图形.(2)依据网格的特点,应用勾股定理可以求出AD ′=C ′D ′=210,应用勾股定理的逆定理可以得出∠AD ′C ′=90°,故△AC ′D ′是等腰直角三角形.15.解:如图,过点E 作EH ⊥AB 于点H ,交CD 于点G ,那么EF =DG =BH =1.6 m ,GH =BD =15 m ,EG =DF =2 m ,∴CG =CD -DG =3-1.6=1.4(m).∵CG ∥AH ,∴△ECG ∽△EAH ,∴CG AH =EG EH , 即1.4AH =22+15, 解得AH =11.9(m),∴AB =AH +BH =11.9+1.6=13.5(m).答:旗杆AB 的高度为13.5 m.16.解:(1)证明:∵AB =AD ,AC 平分∠BAD ,∴AC ⊥BD ,∴∠ACD +∠BDC =90°.∵AC =AD ,∴∠ACD =∠ADC ,∴∠ADC +∠BDC =90°.∵PD ⊥AD ,∴∠ADC +∠PDC =90°,∴∠BDC =∠PDC .(2)过点C 作CM ⊥PD 于点M , ∵∠BDC =∠PDC ,∴CE =CM .∵∠CMP =∠ADP =90°,∠P =∠P , ∴△CPM ∽△APD ,∴CM AD =PC P A. 设CM =CE =x .∵CE ∶CP =2∶3,∴PC =32x . ∵AB =AD =AC =1,∴x 1=32x 32x +1, 解得x =13(x =0不合题意,舍去), 故AE =1-13=23.。
《3.3 相似图形》课时同步练习 湘教版九年级数学上册

《3.3 相似图形》课时同步练习2020-2021年数学湘教版九(上)一.选择题(共11小题)1.观察下列图形中,是相似图形的一组是()A.B.C.D.2.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是()A.B.C.D.3.选项图形与如图所示图形相似的是()A.B.C.D.4.下列各组图形中,一定相似的是()A.任意两个正方形B.任意两个平行四边形C.任意两个菱形D.任意两个矩形5.下列说法正确的是()A.所有的等腰三角形都相似B.所有的菱形都相似C.边数相同的正多边形相似D.所有的矩形都相似6.下列结论①两个全等三角形是相似三角形;②所有正方形都相似;③任意两个等腰三角形都相似;④所有菱形都相似;⑤两个等腰直角三角形相似.其中结论正确的有()A.5个B.4个C.3个D.2个7.如图,已知△ABC的六个元素,其中a、b、c表示三角形三边的长,则下面甲、乙、丙、丁四个三角形中与△ABC不一定相似的图形是()A.甲B.乙C.丙D.丁8.分别画出下列四组图形,必是相似三角形的为()A.两个直角三角形B.有一个角为110°的两个等腰三角形C.有一个角为55°的两个等腰三角形D.两条边对应成比例,其中一边的对角对应相等的两个三角形9.下列各组图形中,是相似图形的是()A.B.C.D.10.下图是世界休闲博览会吉祥物“晶晶”.右边的“晶晶”可由左边的“晶晶”经下列哪个变换得到的()A.轴对称B.平移C.旋转D.相似11.在如图所示的各组图形中,相似的是()A.①②B.①③C.②③D.②④二.填空题(共5小题)12.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为.13.四边形ABCD和四边形A'B'C'D'是相似图形,点A、B、C、D分别与A'、B'、C'、D'对应,已知BC=3,CD=2.4,B'C′=2,那么C′D'的长是.14.如图,用放大镜将图形放大,应属于哪一种变换:(请选填:对称变换、平移变换、旋转变换、相似变换).15.如图,相似的正方形共有个,相似的三角形共有个.16.如图,与相似.三.解答题(共4小题)17.如图所示,若△ABE∽△DCE,分别写出相似图形中的对应角与对应边.18.设四边形ABCD与四边形EFGH是相似图形.且A与E,B与F,C与G,D与H是对应点.已知AB=10.BC=8,CD=8,AD=6,EF=8,求四边形EFGH的周长.19.如图,四边形ABCD与四边形A'B'C'D'相似的图形,点A与点A′、点B与点B′、点C与点C′、点D与点D′分别是对应顶点,已知数据如图所示,求未知边x、y的长度和角α、β的大小.20.在下列两组图形中,每组的两个三角形相似,m表示已知数.试分别确定α、x的值.参考答案一.选择题(共11小题)1.解:A.形状不相同,不符合相似形的定义,此选项不符合题意;B.形状相同,但大小不同,符合相似形的定义,此选项符合题意;C.形状不相同,不符合相似形的定义,此选项不符合题意;D.形状不相同,不符合相似形的定义,此选项不符合题意;故选:B.2.解:A、两图形形状相同,是相似图形,不符合题意;B、两图形形状不同,不是相似图形,符合题意;C、两图形形状相同,是相似图形,不符合题意;D、两图形形状相同,是相似图形,不符合题意;故选:B.3.解:因为相似图形的形状相同,所以A、B、C中形状不同,故选:D.4.解:A、任意两个正方形的对应角相等,对应边的比也相等,故一定相似,符合题意;B、任意两个平行四边形对应边的比不一定相等,对应角也不一定相等,故不一定相似,不符合题意;C、任意两个菱形的对应边的比相等,但对应角不一定相等,故不一定相似,不符合题意;D、任意两个矩形对应角相等,但对应边的比不一定相等,故不一定相似,不符合题意,故选:A.5.解:A、所有的等腰三角形都相似,说法错误;B、所有的菱形都相似,说法错误;C、边数相同的正多边形相似.说法正确;D、所有的矩形都相似,说法错误;故选:C.6.解:①两个全等三角形是相似三角形,正确,符合题意;②所有正方形都相似,正确,符合题意;③任意两个等腰三角形对应边不一定相等,所以不一定都相似,不正确,不符合题意;④所有菱形的对应角不一定都相等,所以不一定都相似,不符合题意;⑤两个等腰直角三角形相似,正确,符合题意,正确的有3个,故选:C.7.解:甲三角形的两边AC,BC的夹角不一定等于72度,故与△ABC不一定相似的图形,故选此选项正确;乙可以利用两边对应成比例且夹角相等得出相似;丙、丁可以利用两角对应相等得出相似;故选:A.8.解:两个直角三角形不一定相似;因为只有一个直角相等,∴A不一定相似;有有一个角为110°的两个等腰三角形一定相似;因为110°的角只能是顶角,所以两个等腰三角形的顶角和底角分别相等,∴B一定相似;一个角为55°的两个等腰三角形不一定相似;因为55°的角可能是顶角,也可能是底角,∴C不一定相似;两条边对应成比例,一个对应角相等的两个三角形不一定相似;因为这个对应角不一定是夹角;∴D不一定相似;故选:B.9.解:A.形状不相同,不符合相似形的定义,此选项不符合题意;B.形状不相同,不符合相似形的定义,此选项不符合题意;C.形状不相同,不符合相似形的定义,此选项不符合题意;D.形状相同,但大小不同,符合相似形的定义,此选项符合题意;故选:D.10.解:A、轴对称变换是反射产生一个图形的映象的过程,不符合题意,故错误;B、平移变换是原图形中的点都沿着平行的途径运动一个恒等的距离,不符合题意,故错误;C、旋转变换原图形中的点都绕着一个固定的中心点转动一个恒等的角度,不符合题意,故错误;D、相似变换,图形的形状相同,但大小不一定相同的变换,符合题意,故正确.故选:D.11.解:①∵正六边形与一般六边形的对应边不成比例,∴两图形不相似;②∵正方形的各角相等,且对应边的比相等,∴两正方形相似;③∵菱形的角相等,对应边的比也相等,∴两个菱形相似.④两个矩形的对应角相等,但对应边的比不相等,∴两个矩形不一定相似.故选:C.二.填空题(共5小题)12.解:∵△ABC∽△DEF,∴∠BAC=∠EDF,又∠EDF=90°+45°=135°,∴∠BAC=135°.故答案是:135°.13.解:∵四边形ABCD∽四边形A'B'C'D',∴CD:C′D′=BC:B′C′,∵BC=3,CD=2.4,B'C′=2,∴C′D′=1.6,故答案为:1.6.14.解:由一个图形到另一个图形,在改变的过程中形状不变,大小产生变化,属于相似变化.15.解:如图,相似的正方形共有5个,相似的三角形共有16个,故答案为:5,16.16.解:利用相似图形对应角相等,对应边成比例,只有(1),(4)图形全等,符合题意.故答案为:(1),(4).三.解答题(共4小题)17.解:对应角是:∠A与∠D,∠B与∠C,∠DEC与∠AEB.对应边是:AB与DC,AE与DE,BE与CE.18.解:四边形ABCD的周长=AB+BC+CD+AD=10+8+8+6=32,∵四边形ABCD与四边形EEGH是相似图形,∴四边形ABCD的周长:四边形EEGH的周长=AB:EF,∴四边形EEGH的周长=×32=25.6.19.解:在四边形ABCD中,∠D=∠D'=β=55°,∠A=α=360°﹣55°﹣90°﹣60°=155°,∵四边形ABCD∽四边形A'B'C'D',∴==,∴x=6,y=15.20.解:如图1中,∵△ABC∽△A′B′C′,∴,α=40°,∴x=9;如图2中,∵∠D=180°﹣65°﹣70°=45°,∵△ABC∽△A′B′C′,∴α=∠D=45°.。
湘教版数学九年级上册同步训练《相似图形》
湘教版数学九年级上册同步训练《3.3 相似图形》一、单选题1..下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是()A. B. C. D.2..如图,从图甲到图乙的变换是()A. 轴对称变换B. 平移变换C. 旋转变换D. 相似变换3.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为()A. 70°B. 80°C. 90°D. 120°4.把一张矩形的纸片对折后和原矩形相似,那么大矩形与小矩形的相似比是()A. :1B. 4:1C. 3:1D. 2:15..下列每个选项的两个图形,不是相似图形的是()A. B.C. D.6.如图,将- -张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么我们把这样的纸张叫做标准纸.则标准纸的宽和长的比值为()A. B. C. D.7..下列说法中,正确的是()A. 两个矩形必相似B. 两个含角的等腰三角形必相似C. 两个菱形必相似D. 两个含角的直角三角形必相似8..下面图形是相似形的为()A. 所有矩形B. 所有正方形C. 所有菱形D. 所有平行四边形9.如图,在的小正方形网格中,勤奋学习小组的同学画出了五边形和五边形则下列说法中,错误的是()A. 五边形五边形B.C. 五边形的周长是五边形周长的倍.D.10.一个五边形的边长分别为2,3,4,5,6,另一个和它相似的五边形的最长边长为24,则这个五边形的最短边长为()A. 6B. 8C. 12D. 10二、填空题11.下列命题中,正确命题的个数为________.①所有的正方形都相似②所有的菱形都相似③边长相等的两个菱形都相似④对角线相等的两个矩形都相似12..下列五组图形中,①两个等腰三角形;②两个等边三角形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有 1 (填序号)13.秋天红透的枫叶,总能牵动人们无尽的思绪,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花”如图是两片形状完全相同,大小不同的枫叶,则的值为________ .14..如图所示,矩形ABCD的长AB=30,宽BC=20,x为 1 时,图中的两个矩形ABCD与A'B'C'D'相似?15..在矩形中,点分别在上(点E与点F不重合)矩形与矩形相似,那么的长为 1 .16.两个相似多边形一组对应边分别为3cm,5cm,那么它们的相似比为________.三、解答题17..如图,ABCD是边长为1的正方形,在它的左側补一个矩形ABFE,使得新矩形CEFD与矩形ABEF相似,求BE的长.18.如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.19..如图,四边形四边形,求边、的长度和角的大小.20.若四边形ABCD与四边形A1B1C1D1相似,相似比为k1= ,又四边形A1B1C1D1与四边形A2B2C2D2相似,相似比为k2= ,请问四边形ABCD与四边形A2B2C2D2相似吗?若相似,相似比是多少?21..观察下列图形,指出哪些是相似图形:22.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.请回答下列问题:(1)你认为上述两个观点是否正确?请说明理由.(2)如图3,已知,AC=6,BC=8,AB=10,将按图3的方式向外扩张,得到,它们对应的边间距都为1,DE=15,求的面积.答案解析部分一、单选题1.【答案】B2.【答案】D3.【答案】B4.【答案】A5.【答案】D6.【答案】A7.【答案】D8.【答案】B9.【答案】D10.【答案】B二、填空题11.【答案】①12.【答案】②⑤13.【答案】614.【答案】1.515.【答案】16.【答案】3:5三、解答题17.【答案】解:设BE=x,则BC=1,CE=x+1,∵矩形CEFD与矩形ABEF相似,∴或,代入数据,∴或,解得:,(舍去),或不存在,∴BE的长为,故答案为.18.【答案】解:∵矩形ABFE∽矩形DEFC,且相似比为1:2,∴= = ,∵四边形ABCD为矩形,∴CD=AB=4∴DE=8,AE=2,∴AD=AE+DE=2+8=1019.【答案】解:∵四边形四边形,∴,,.∴,,.20.【答案】解:相似.理由:∵四边形ABCD与四边形A1B1C1D1相似,四边形A1B1C1D1与四边形A2B2C2D2相似,∴四边形ABCD与四边形A2B2C2D2相似;∵四边形ABCD与四边形A1B1C1D1相似,相似比为k1= ,又四边形A1B1C1D1与四边形A2B2C2D2相似,相似比为k2= ,∴四边形ABCD与四边形A2B2C2D2相似比是:21.【答案】解:观察、分析可得上述图形中:(1)和(8)是相似图形;(2)和(6)是相似图形;(3)和(7)是相似图形.22.【答案】(1)解:观点一正确;观点二不正确.理由:①如图(1)连接并延长DA,交FC的延长线于点O,∵△ABC和△DEF对应的边的距离都为1,∴AB//DE,AC//DF,∴∠FDO=∠CAO,∠ODE=∠OAB,∴∠FDO+∠ODE=∠CAO+∠OAB,即∠FDE=∠CAB,同理∠DEF=∠ABC,∴△ABC∽△DEF,∴观点一正确;②如图(2)由题意可知,原矩形的邻边为6和10,则新矩形邻边为4和8,∴,∴新矩形于原矩形不相似,∴观点二不正确;(2)解:∵AC=6,BC=8,AB=10,∴△ABC是直角三角形,∴∠ACB=90°,由(1)知△ABC∽△DEF,∴∠DFE=90°,,∴,,∴DF=9,EF=12,∴△DEF的面积为:9×12=54.。
湘教版九年级上册数学第三章 图形的相似 单元测试题(含答案)

湘教版九年级数学上册第三章图形的相似单元检测试卷一、单选题(共10题;共30分)1.在相同的时刻,太阳光下物高与影长成正比.如果高为1.5米的人的影长为2.5米,那么影长为30米的旗杆的高是().A. 18米B. 16米C. 20米D. 15米2.△ABC∽△A,B,C,,相似比为3:4,那么面积的比是_____。
A. 3:4B. 9:16C. 6:8D. 4:53.如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是()A. 2 cm2B. 4 cm2C. 8 cm2D. 16 cm24.在上科学课时,老师让同学利用手中的放大镜对蜗牛进行观察,同学们在放大镜中看到蜗牛与实际的蜗牛属于什么变换()。
A. 相似变换B. 平移变换C. 旋转变换D. 轴对称变换5.如图,在△ABC中,DE∥BC ,,DE=4,则BC的长是()A. 8B. 10C. 11D. 126.若相似△ABC与△DEF的相似比为1 :3,则△ABC与△DEF的面积比( )A. 1 :3B. 1 :9C. 3 :1D. 1 :7.如图,在ΔABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN的长为()A. B. C. D.8.如图,在平面直角坐标系中,点P的坐标为(0,2),直线y= 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为()A. 3B. 4C. 5D. 69.若△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为1:2,则△ABC与△A′B′C′的面积比是()A. 1:1B. 1:2C. 1:3D. 1:410.若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为()A. 1:2B. 2:1C. 1:4D. 4:1二、填空题(共10题;共30分)11.已知8:x =6:9,则x的值等于________。
【湘教版】九年级数学上册:第3章图形的相似同步训练(含答案)
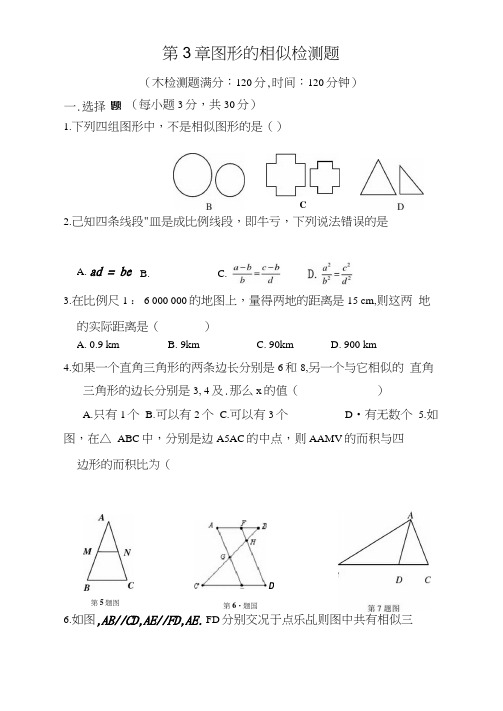
第3章图形的相似检测题(木检测题满分:120分,时间:120分钟)1.下列四组图形中,不是相似图形的是()2.己知四条线段"皿是成比例线段,即牛亏,下列说法错误的是3.在比例尺1 : 6 000 000的地图上,量得两地的距离是15 cm,则这两 地的实际距离是()4.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的 直角三角形的边长分别是3, 4及.那么x 的值()A.只有1个B.可以有2个C.可以有3个D •有无数个 5.如图,在△ ABC 中,分别是边A5AC 的中点,则AAMV 的而积与四 边形的而积比为(6.如图,AB//CD,AE//FD,AE. FD 分别交况于点乐乩则图中共有相似三一.选择(每小题3分,共30分)A. ad = beB.A. 0.9 kmB. 9kmC. 90kmD. 900 kmDCC.第5题图第6•题国46 角形( )A. 4对B. 5对C. 6对D. 7对7. 如图,D 是△ ABC 的边上任一点,己知AB = 4,AD = 2, Z DAC= ZB .若AABD 的面积为d,则/XACD 的面积为()A. " B-如 c- D- ? 8. 下列说法中正确的是()① 在两个边数相同的多边形中,如果对应边成比例,那么这两个多 边形相似;② 如果两个矩形有一组邻边对应成比例,那么这两个矩形相似; ③ 有一个角对应相等的平行四边形都相似; ④ 有一个角对应相等的菱形都相似.A.①②B.②③C.③④D.②④9. 如图,点c 是线段肋的黄金分割点(AOBC ),则下列结论中正确的是()pA. AB 2= AC 2+ BC 2B ・ 5C 2= AC^BA/小ECV 5 — 1 、AC'ClC.—— ---------D.—=—— / 、L AC 2BC2L_SF 1.b(第10题怡9A CB第9题因交况的延长线于点E,则CE的长为()D. 2二.填空题(每小题3分,共24分)11.己知a:& = 3:2,且a+b 二10,则0 二______ 4 612•己知© b, C 是成比例线段,即"刁其中0 da = 3 cm,b = 2 cm,c 二 6 cm,贝赧= ___ cm.13.如图,在AABC 中,点D, E 分别是边ABAC 的中点,则ZMDE 与AABC的周长之比等于 ______ .15.如图丄是月日的黄金分割点,BG =A 召,以C4为边的正方形的面积为S 」,以亦而为边的矩形的面积为足,则S, ____________________ S2 (填心,将△朋£缩小,位似比为2 : 2,则线段M 的中点P 变换后对应点的 坐标为 _________ .14•若d£ = £ = o ・5,则 b d j3a -2c +e3b — 2d第15题因弟17逊因三.解答题(共66分)19. (6分)如图,在平行四边形MCD中,E为边月D延长线上的一点,且D为4E的黄金分割点,即AD二竽恥,BE交M于点F,已知鮎=苗+ 1,求CF的长.第⑴题圈20. (8 分)如图,在△ ABC^9AB = AC9 BE平分ZABJDE//BC.求证: DE=EC.第20题创21. (8分)如图卫是££上一点,毗〃船BE = AD, AE分别交加、BC J:点F、G, Z1=Z2,探索线段BF、FG、EF之间的关系,并说明理由.22. (10分)如图,在梯形ABCD中,朋〃CD,点卩在EC上,连接DF并延长与丽的延长线交于点G.(1)求证:gDFs/\BGF;24. (12分)如图,在△舶£中,AB = 4C, DE//BC,点F 在边AC 上,DF 与相交于点6且ZEDF=ZABE.求证:⑴Z\DEFs/\BDE ; (2)DG ・DF=DB ・EF.25. (12分)如图,在正方形ABCD 中,E 、F 分(2)当点F 是*C 的中点时,过点F 作EF // CD 交4D 于点E,若AB = 6 cm, Ef = 4cm,・23.( 10分)(2013 •江苏扬州中考)如图,在/MBC中,ZACB = 90° , AC = BC,点D 在边AB 上,连接CD,将线段CD 绕点C 顺时针旋90。
2021秋九上3、3相似图形习题湘教版

2.相似三角形的对应角__相__等____,对应边__成__比__例__.
3.对于两个边数相同的多边形,如果它们的对应角 __相__等____、对应边__成__比__例__,那么这两个多边形叫作相 似多边形.
1.下列图形不一定相似的是( C ) A.两个圆 B.两个等边三角形 C.两个菱形 D.国旗上的五角星
2.若△ABC∽△DEF,∠A=50°,则∠D的度数是( A ) A.50° B.60° C.70° D.80°
3.
若△ABC与△DEF的相似比为4∶3,则△DEF与
△ABC的相似比为( B )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
【点拨】本题易错点是忽略相似比具有方向性,相似 三角形的顺序不同,它们的相似比也可能不同.
2?请说明理由. 解:不存在,理由如下:
若k=2,则a=2a1,b=2b1,c=2c1. 又∵b=a1,c=b1,∴a=2a1=2b=4b1=4c. ∴b=2c. ∴b+c=2c+c<4c. 又∵4c=a,∴b+c<a,这与三角形的任意两边之和大于 第三边相矛盾.
故不存在△ABC和△A1B1C1,使得k=2.
第3章 图形的相似
3.3 相似图形
提示:点击 进入习题
Байду номын сангаас
新知笔记 1 相等;成比例 2 相等;成比例 3 相等;成比例
1C 2A 3B 4B
5A
答案显示
6 见习题 7 见习题 8 见习题
答案显示
1.把三个角对应__相__等____,且三条边对应__成__比__例__的 两个三角形叫作相似三角形.
7.【2021·宁波期末】如图,E,F分别为矩形ABCD的边 AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1, 求AD的长.
湘教版数学九上34相似多边形同步测试一

相似多边形自主研练一、仔认真细,记录自信1.下列各组图形中必然相似的图形是()A.底角对应相等的两个等腰梯形B.有一个角为60°的两个菱形C.两邻边之比相等的两个平行四边形D.两个矩形2.在梯形ABCD中,AD∥BC,AC与BD相交于O,若是AD∶BC=1∶3,那么下列结论中正确的是()A.S△COD=9S△AOD B.S△AB C=9S△ACDC.S△BOC=9S△AOD D.S△BDC=9S△AOD3.如图1,将一个矩形纸片ABCD沿边AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形的长与宽的比应为()A.2:1B.3:1C.2:1D.1:14.某校有两块相似的多边形草坪,其面积比为9∶4,其中一块草坪的周长是36米,则另一块草坪的周长是()A.24米B.54米 C.24米或54米 D.36米或54米5.在一张比例尺为1∶50 000的地图上,一块多边形地域的面积是320cm2,那个地域的实际面积是()A.8×107m2 B.8×108m2C.8×1010m2 D.8×1011m2二、认认真真,书写欢乐6.只增加一个条件,使矩形ABCD与矩形A′B′C′D′相似,那个条件能够是.7.一个四边形的边长别离是3,4,5,6,另一个与它相似的四边形最小边长为6,则另一个四边形的周长是.8.如图2,BC∥DE,AB∶AD=1∶3,则S△ABC∶S四边形BDE C=.9.如图3,在大小为4×4的正方形网格中,是相似三角形的是(请填上编号).三、心平气和,展现聪慧10.如图4,要测量湖岸AB之间的距离,在与湖岸平行的公路上选择两点C、D,确信AD与BC交于点O,测得CD为75m,CO为45m,BO为60m,求湖面AB之间的距离.相似多边形答案一、1~5.BCCCA二、6.AB A BBC B C''=''(答案不惟一) 7.36 8.1:8 9.①,③三、10.AB的距离是100m.。
湘教版九年级上册数学3.3 相似的图形1同步练习

3.3 相似的图形
1.在比例尺为1:5000的地图上,量得甲,乙两地的距离为25cm,则甲,乙两地的实际距离是( )
A.1250km
B.125km
C.12.5km
D.1.25km
2.已知⊿ABC 的三边长分别为2,6,2,⊿A ′B ′C ′的两边长分别是1和3,如果⊿ABC 与⊿A ′B ′C ′相似,那么⊿A ′B ′C ′的第三边长应该是( ) A.2 B.2
2 C.26 D.3
3
3.如图,AB 是斜靠在墙上的长梯,梯脚B 距墙脚1.6m,梯上点D 距墙1.4m,BD 长0.55m,则梯子的长为( )
A.3.85m
B.4.00m
C.4.40m
D.4.50m
5.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC ∽⊿CAD,只要CD 等于( ) A.c b 2 B.a
b 2 C.c
ab D.c a 2
(第3题图) (第4题图) (第5题图)
4.一个钢筋三角架三边长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm 和50cm 的两根钢筋,要求以其中的一根为一边,从另一
根截下两段(允许有余料)作为另两边,则不同的截法有( )
A.一种
B.两种
C.三种
D.四种
5.如图,⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
(1)试说明⊿ABD≌⊿BCE.
(3)BD2=AD·DF吗?请说明理由.。
湘教版九年级数学上册3.3《相似图形》【同步练习】

《相似图形》同步练习1.在下列说法中,正确的是()A .两个钝角三角形一定相似B .两个等腰三角形一定相似C .两个直角三角形一定相似D .两个等边三角形一定相似2.如图5,在ABC △中,D ,E 分别是AB 、AC 边上的点,DE BC ∥,30ADE =∠,120C =∠,则A =∠( )A .60°B .45°C .30°D .20°3.如果三角形的每条边都扩大为原来的5倍,那么三角形的每个角( )A .都扩大为原来的5倍B .都扩大为原来的10倍C .都扩大为原来的25倍D .都与原来相等 4.如图6,在Rt ABC △中,90ACB =∠,CD AB ⊥于D ,若1AD =,4BD =,则CD =( )A .2B .4C .2D .35.如图7,6BC =,E ,F 分别是线段AB 和线段AC 的中点,那么线段EF 的长是( )◆ 选择题A .6B .5C .4.5D .36.如图8,点E 是ABCD 的边BC 延长线上的一点,AE 与CD 相交于点G ,AC 是ABCD 的对角线,则图中相似三角形共有( )A .2对B .3对C .4对D .5对7.如图9,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC 相似的是( )8.如图10,梯形ABCD 的对角线交于点O ,有以下四个结论:①AOB COD △∽△; ②AOD ACB △∽△;③::DOC AOD S S DC AB =△△;④AOD BOC S S =△△.其中始终正确的有( )A . 1个B .2个C .3个D .4个9.用作相似图形的方法,可以将一个图形放大或缩小,相似中心位置可选在( )A .原图形的外部B .原图形的内部C .原图形的边上D .任意位置10.如图11是小孔成像原理的示意图,根据图中所标注的尺寸,这支蜡烛在暗盒中所成的像CD 的长是( )A .16cm B.13cm C .12 cm D .1cm 11.在比例尺为1∶50 0000的福建省地图上,量得省会福州到漳州的距离约为46厘米,则福州到漳州实际距离约为 千米。
湘教版数学九年级上册第三章相似图形试题(含答案)

数学九年级第三章图形的相似试卷(含答案)一、填空题(每小题3分,共24分)1.如果四条线段m, n, x, y 成比例,若m=2 , n=8 , y=20 .则线段x 的长是__________.2.边长为12cm 的等边三角形按2:1的比例缩小后的三角形是边长为_____的____三角形.3.已知△ABC ∽△DEF, AB =6 , DE =8 , 则:ABC DEF S S ∆∆=________.4.已知三个数2,请你再添一个数,写出一个比例式________.5.点P 是△ABC 中AB 边上的一点,过点P 作直线 (不与直线AB 重合)截△ABC,使截得三角形与△ABC 相似,满足这样条件的直线最多________条.6.电视节目主持人在主持节目时,站在舞台上的黄金分割点处最自然得体,若舞台AB 长为20cm,试计算主持人应走到离A 点至少____________________m 处.(结果精确到0.1m)7.一个4米高的电线杆的影长是6米,它临近的一个建筑物的影长是36米.则这个建筑的高度是_________.8.如图,若DE ∥BC,FD ∥AB,AD ∶AC =2∶3 ,AB =9,BC =6,则四边形BEDF 的周长为_____.二、选择题(每小题4分,共40分)1.若果mn ab =,则下列比例式中不正确的是( ) A.a n m b = B.a m n b = C.m n a b = D.m b a n= 2.已知:如图2,在△ABC 中,∠ADE=∠C,则下列等式成立的是( ) A.AD AE AB AC = B.AE AD BC BD= C.DE AE BC AB = D.DE AD BC DB= 3.已知正五边形ABCDE 与正五边形'''''A B C D E 的面积比为1:2,则它们的相似比为( )A. 1:2B. 2:1C.4.如图,两个位似图形△ABO 和△'''C B A ,若OA:'OA =3:1,则正确的是( )A.AB:''A B =3:1B.'AA :'BB =AB:'ABC.OA:'OB =2:1D.∠A =∠'B5.在比例尺是1:3800的南京交通游览图上,玄武湖隧道长约7cm,它的实际长度约为( )6.下列判断正确的是( )A.不全等的三角形一定不是相似三角形B.不相似的三角形一定不是全等三角形C.相似三角形一定不是全等三角形D.全等三角形不一定是相似三角形7.如图, D 、E 是AB 的三等分点, DF ∥EG ∥BC , 图中三部分的面积分别为S 1,S 2,S 3, 则S 1:S 2:S 3( )A.1:2:3B.1:2:4C.1:3:5D.2:3:48.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )A.小明的影子比小强的影子长B.小明的影子比小强的影子短C.小明的影子和小强的影子一样长D.无法判断谁的影子长9.把△ABC 的各边都扩大为原来的2倍,得到△'''A B C ,下面结论不正确的是( )A.△ABC ∽△'''A B CB.△ABC 和△'''A B C 的各边、各角对应相等C.△ABC 和△'''A B C 的相似比为1:2D.△ABC 和△'''A B C 的相似比为1:310.如图,四边形ABCD 是平行四边形,则图中与△DEF 相似的三角形共有( )A.1个B.2个C.3个D.4个三、解答题(每题8分,共24分)1. 如图,在△ABC 中,∠C=90°,DE ⊥AB 于E,DF ⊥BC 于F.求证: △DEH ~△BCA2.如图,四边形AEFD 与EBCF 是相似的梯形,AE:EB =2:3,EF =12 cm,求AD 、BC 的长.3.如图, 平行四边形ABCD 中,点E 是DC 中点, 连AE 并延长与BC 延长线交于点F, 若CEF S =10 , 求四边形ABCE 的面积.四.(12分)已知如图,平行四边形ABCD 中,AE:EB =1:2 .(1)求AE:DC 的值.(2)△AEF 与△CDF 相似吗若相似,请说明理由,并求出相似比.(3)如果AEF S ∆=6cm 2,求CDF S ∆数学九年级第三章图形相似试题的答案1、5,2、6cm ,等边,3、9︰16,4、略,5、4、,6、7.6m ,7、24m ,8、14二、选择题:CCCAA BCDDB三、解答题⑴证明:∵DE ⊥AB,DF ⊥BC,∴∠D+∠DHE=∠B+∠BHF=90°而∠BHF=∠DHE ∴∠D=∠B,又∵∠HFB=∠C=90°△DEH ∽△BCA⑵解:∵四边形AEFD ∽四边形EBCF ∴EF AD =EB AB ,BC EF =EB AB,∴AD=8,BC=18⑶ 解:∵四边形ABCD 为平行四边形∴EC ∥AB,DC=AB,由E 为DC 中点,∴EC=21DC=21AB,∵EC ∥AB,有∠ECF=∠ABF,∠F=∠F,△ECF ∽△ABF:4:1ABF ECF S S = ∴12123,0cos 2x x α==≤四.提高题 解:① ∵ A B C D ,∴DC=AB 由12AE EB = ∴ 21EB AE =∴31AB AE =,∴13AE DC =②相似,∵ABCD,有DC∥AB,∴∠DCF=∠EAF,∠FDC=∠EFA ∴△AEF∽△CDF,相似比为:13 AE DC=③∵△AEF∽△CDF ∴21:3AEF CDFS S⎛⎫= ⎪⎝⎭∴254CDFS cm=。
湘教版九年级数学同步练习:3.3 相似图形

湘教版九年级数学同步练习:33.3 相似图形知识点 1 相似图形1.以下图形中,不是相似图形的是( )图3-3-12.以下图形不是相似图形的是( )A .同一底片冲洗出来的两张照片B .某人的正面照和他的侧身照C .一棵树和它倒映在水中的像D .用缩小镜观察某一图形,缩小镜中的图形和原图形知识点 2 相似三角形及对应边、对应角的性质3.以下判别正确的选项是( )A .不全等的三角形一定不是相似三角形B .不相似的三角形一定不是全等三角形C .相似三角形一定是全等三角形D .全等三角形不一定是相似三角形4.如图3-3-2,△ABC ∽△DEF ,相似比为1∶2.假定BC =1,那么EF 的长是( )图3-3-2A .1B .2C .3D .45.△ABC 与△A 1B 1C 1相似,顶点A ,B ,C 的对应点区分是A 1,B 1,C 1,∠A =55°,∠B =100°,那么∠C 1的度数是( )A .55°B .100°C .25°D .不能确定6. 全等三角形是相似比为________的相似三角形.7.假定△ABC ∽△DEF ,且AB =1,BC =3,DE =2,那么EF =________.图3-3-38.如图3-3-3,假定△ADE ∽△ACB ,且AD AC =23,DE =10,那么BC =________. 9.如图3-3-4,△ABC ∽△AED ,找出对应角并写出对应边的比例式.图3-3-410.在如图3-3-5所示的两组图形中,每组的两个三角形相似((1)△ABC ∽△A′B′C′,(2)△ABC ∽△DEF),试区分确定x 的值和∠E 的度数.图3-3-5知识点 3 相似多边形及对应边、对应角的性质11.以下各组中的两个图形,一定相似的是( )A .有一个角对应相等的两个菱形B .对应边成比例的两个多边形C .两条对角线对应成比例的两个平行四边形D .恣意两个矩形12.假设多边形ABCDE ∽多边形A′B′C′D′E′,且∠A =72°,那么∠A′的度数为( )A .54°B .112°C .18°D .72°13.如图3-3-6,△ABC ∽△ADE ,且∠ADE =∠B ,那么以下比例式成立的是( )A .AE BE =AD DCB .AE AB =AD ACC .AD AC =DE BC D .AE AC =DE BC图3-3-6图3-3-714.教材习题3.3第4题变式如图3-3-7所示,在矩形ABCD 中,AB =1,在BC 上取一点E ,沿AE 将△ABE 向上折叠,使点B 落在AD 上的点F 处,假定四边形EFDC 与矩形ABCD 相似,那么AD 的长度为( )A .5-12B .5+12C . 3D .215.假设一个三角形的三边长为5,12,13,与其相似的三角形的最长边的长为39,那么较大的三角形的面积为( )A .90B .180C .270D .540图3-3-816.如图3-3-8,△ACP ∽△ABC ,AC =4,AP =2,那么AB 的长为________.17.如图3-3-9,AD =2,AC =4,BC =6,∠B =36°,∠D =117°,△ABC ∽△DAC.求AB ,CD 的长及∠BAD 的度数.图3-3-918.如图3-3-10,在▱ABCD 中,AC 与BD 交于点O ,F ,E ,M ,N 区分是AO ,BO ,CO ,DO 的中点,这样构成一个▱FEMN ,求证:▱ABCD ∽▱FEMN.图3-3-1019.探求以下效果:(1)图3-3-11①中的两个矩形相似吗?(2)图3-3-11②中的两个矩形能否相似?假定能相似,那么x ,y 满足什么关系?(3)图3-3-11③中的矩形ABCD 与矩形AFED 能否相似?假定能相似,那么x 的值是多少(其中a>b)?图3-3-111.C [解析] A ,B ,D 三个选项中的图形外形相反,但大小不同,契合相似图形的定义,故不契合题意.C 选项中的图形外形不相反,不契合相似图形的定义,故契合题意.应选C.2.B [解析] 由于选项B 中的正面照与侧身照外形不同,所以不相似.3.B4.B [解析] ∵△ABC ∽△DEF ,相似比为1∶2,∴BC EF =12,∴EF =2BC =2. 5.C [解析] ∠C 1=∠C =180°-55°-100°=25°. 6.17.6 [解析] ∵△ABC ∽△DEF ,∴AB DE =BC EF . ∵AB =1,BC =3,DE =2, ∴12=3EF ,解得EF = 6. 8.15 [解析] ∵△ADE ∽△ACB ,∴AD AC =DE BC .又AD AC =23,DE =10,∴BC =15.9.解: 对应角:∠B 与∠E ,∠C 与∠D ,∠BAC 与∠EAD ;对应边的比例式:AB AE =AC AD=BC DE. 10.解:(1)∵△ABC ∽△A ′B ′C ′,∴BC ∶B ′C ′=AC ∶A ′C ′,即2∶4=2∶x ,∴x =2 2.(2)∵∠A =110°,∠C =28°,∴∠B =42°.∵△ABC ∽△DEF ,∴∠B =∠E ,∴∠E =42°.11.A [解析] A .有一个角对应相等,其他三个角一定对应相等,对应边成比例,所以这两个菱形一定相似,故本选项正确;B.对应边成比例的两个多边形的对应角不一定相等,故本选项错误;C.两条对角线对应成比例的两个平行四边形,对应边不一定成比例,对应角不一定相等,故本选项错误;D.恣意两个矩形,对应角一定相等,但对应边不一定成比例,故本选项错误.应选A.12.D 13.D14. B [解析] ∵AB =1,设AD =x ,那么FD =x -1,FE =1.∵四边形EFDC 与矩形ABCD 相似,∴EF FD =AD AB ,即1x -1=x 1, 解得x 1=1+52,x 2=1-52(负值舍去), 经检验,x =1+52是原方程的解. 应选B.15.C [解析] 与其相似的三角形的三边长区分为15,36,39,∵152+362=392,∴三边长为15,36,39的三角形是直角三角形,其面积=12×15×36=270. 16. 8 [解析] ∵△ACP ∽△ABC ,∴AC AB =AP AC, 即4AB =24,∴AB =8. 17.解:∵△ABC ∽△DAC ,∴∠DAC =∠B =36°,∠BAC =∠D =117°,AB AD =AC CD =BC AC. 又AD =2,AC =4,BC =6,∴AB =3,CD =83, ∠BAD =∠DAC +∠BAC =36°+117°=153°.18.证明:∵F ,E ,M ,N 区分是AO ,BO ,CO ,DO 的中点,∴FN ∥EM ∥AD ∥BC ,EF ∥NM ∥AB ∥CD ,EM =FN =12BC =12AD ,EF =NM =12AB =12CD , ∴∠OFN =∠OAD ,∠OFE =∠OAB ,∴∠BAD =∠EFN .同理可得∠ABC =∠FEM ,∠ADC =∠FNM ,∠BCD =∠EMN .由EM =FN =12BC =12AD ,EF =NM =12AB =12CD ,得BC EM =AD FN =AB EF =CD MN=2, ∴▱ABCD ∽▱FEMN .19. (1)假设两个矩形相似,只能是20-x 20=16-x 16,由此失掉x =0,不合题意,故图①中的两个矩形不相似.(2)能相似.假定相似,那么20-x 20=16-y 16或20-x 16=16-y 20, 即x y =54(0<y <16)或y =54x -9(7.2<x <20). (3)能相似.假定相似,那么a b =b a -x, 所以x =a 2-b 2a .。
湘教版-数学-九年级上册-数学3.3相似图形同步测试

3.3相似图形同步测试一、选择题1.我们已经学习了相似三角形,也知道,如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长、对角线等所有元素都对应成比例,就可以称它们为相似图形.现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形,是相似图形的有()A. ①③B. ①②C. ①④D. ②③2.下列两个图形一定相似的是()A. 任意两个等腰梯形B. 任意两个菱形C. 任意两个正方形D. 任意两个矩形3.下列说法中不一定正确的是()A. 所有的等腰直角三角形都相似B. 所有等边三角形相似C. 所有矩形相似D. 直角三角形被斜边上的高分成两个三角形相似4.下列叙述正确的是()A. 任意两个正方形一定是相似的B. 任意两个矩形一定是相似的C. 任意两个菱形一定是相似的D. 任意两个等腰梯形一定是相似的5.下列说法不一定正确的是()A. 所有的等边三角形都相似B. 有一个角是100°的等腰三角形相似C. 所有的正方形都相似D. 所有的矩形都相似6.下列命题正确的是( )A. 所有等腰三角形都相似B. 所有的矩形都相似C. 所有的菱形一定相似D. 有一对锐角相等的直角三角形一定相似7.在一张由复印机放大复印出来的纸上,一个多边形的一条边由原来的1cm变成了4cm,那么这次复印的面积变为原来的()A. 不变B. 2倍C. 3倍D. 16倍8.下列各组图形中一定相似的有()A. 两个矩形B. 两个等腰梯形C. 两个等腰三角形D. 两个等边三角形9.如图的各组图形中,相似的是()A. (1)(2)(3)B. (2)(3)(4)C. (1)(3)(4)D. (1)(2)(4)10.下列图形中不一定是相似图形的是()A. 两个等边三角形B. 两个等腰直角三角形C. 两个长方形D. 两个正方形二、填空题11.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm 变成3cm,则这次复印出来的图案的面积是________ cm2.12.给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有________ (填序号).13.甲、乙是两个形状相同,大小不相同的五棱柱.像这样,两个形状相同,大小不一定相同的几何体称为相似体.两个相似体的一切对应线段之比都等于相似比(即有a:a′=b:b′=c:c′=k).解答下列问题:(1)下列几何体中,一定属于相似体的是________A.两个正方体B.两个圆锥体C.两个圆柱体D.两个长方体(2)请归纳出相似体的三条主要性质:①相似体一切对应线段(或弧)长的比等于________②相似体表面积的比等于________③相似体体积的比等于________14.下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图象是相似的图形;②用彩笔在黑板上写上三个大字1,2,3,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是________ ,错误的是________ (填序号)15.挂在墙上的中国地图与课本上的中国地图________ 相似的图形.16.(1)同一张底片印出来的不同尺寸的照片是________图形;(2)正对且平行平面镜的一幅画在平面镜里的像与原画之间的关系是________;用放大镜看这幅画,看到的放大后的像与原画之间的关系是________;(3)下列各组图形中,肯定是相似图形的是________(只填序号).①半径不等的两个圆;②边长不等的两个正方形;③周长不等的两个正六边形;④面积不等的两个矩形;③边长不等的两个菱形.17.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的________倍.18.如图,E、P、F分别是AB、AC、AD的中点,则四边形AEPF与四边形ABCD________ (填“是”或“不是”)位似图形.三、解答题19.将三角形各边向外平移1个单位并适当延长,得到如图(1)所示的图形,变化前后的两个三角形相似吗?如果把三角形改为正方形、长方形呢?20.请任意画出两个相似的图形.21.如图所示,小芳用画正方形的办法画出下列一组图案,你能按规律继续画下去吗?想想其中有哪些相似图形?22.如图是两个相似圆柱,它们的相似比为2:3,求它们的体积之比.23.如图所示,将下列图形分别分成四小块,使它们的形状、大小完全相同,并且与原图形相似,应怎样分?(画出大致图形即可)参考答案一、选择题1.C2.C3.C4.A5.D6.D7.D8.D9.B 10.C二、填空题11.18 12.①②④⑤13.A;相似比;相似比的平方;相似比的立方14.①;②③15.是16.相似;全等;相似;①②③17.5 18.是三、解答题19.解:∵三角形、矩形对应边外平移1个单位后,对应边的比值不一定相等,∴变化前后的两个三角形、矩形都不相似,∵正方形边长改变后对应比值仍相等,且对应角相等,∴变化前后的两个正方形相似.20.解:如图:正方形ABCD和正方形EFGH是相似的图形.正△ABC和正△DEF是相似的图形.21.解:这组图形的规律是:后面的图案比前面的图案多两个全等的正方形,且多出的这两个正方形的边长等于前面正方形对角线的长.按此规律可以继续画图.其中每两个全等的正方形组成的图形与后面多出的两个全等的正方形形成的图形都是相似的.22. 解:小圆柱的体积是:(2a)2π•2b=23a2bπ,大圆柱的体积是:(3a)2π•3b=33a2bπ,所以小圆柱与大圆柱的体积之比为23:33.所以它们的体积的比为:8:27.23.解:根据相似多边形面积的比等于相似比的平方,可以按如下方法分割:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似多边形自主研练
一、仔仔细细,记录自信
1.下列各组图形中一定相似的图形是()
A.底角对应相等的两个等腰梯形B.有一个角为60°的两个菱形
C.两邻边之比相等的两个平行四边形D.两个矩形
2.在梯形ABCD中,AD∥BC,AC与BD相交于O,如果AD∶BC=1∶3,那么下列结论中正确的是()
A.S△COD=9S△AOD B.S△AB C=9S△ACD
C.S△BOC=9S△AOD D.S△BDC=9S△AOD
3.如图1,将一个矩形纸片ABCD沿边AD和BC的中点连线EF对折,要
使矩形AEFB与原矩形相似,则原矩形的长与宽的比应为()
A.2:1B.3:1C.2:1D.1:1
4.某校有两块相似的多边形草坪,其面积比为9∶4,其中一块草坪的周长是36米,则另一块草坪的周长是()
A.24米B.54米 C.24米或54米 D.36米或54米
5.在一张比例尺为1∶50 000的地图上,一块多边形地区的面积是320cm2,这个地区的实际面积是()
A.8×107m2 B.8×108m2C.8×1010m2 D.8×1011m2
二、认认真真,书写快乐
6.只增加一个条件,使矩形ABCD与矩形A′B′C′D′相似,这个条件可以是.7.一个四边形的边长分别是3,4,5,6,另一个与它相似的四边形最小边长为6,则另一个四边形的周长是.
8.如图2,BC∥DE,AB∶AD=1∶3,则S△ABC∶S四边形BDE C=.
9.如图3,在大小为4×4的正方形网格中,是相似三角形的是(请填上编号).三、平心静气,展示智慧
10.如图4,要测量湖岸AB之间的距离,在与湖岸平行的公路上选择两点C、D,确定AD 与BC交于点O,测得CD为75m,CO为45m,BO为60m,求湖面AB之间的距离.
相似多边形答案一、1~5.BCCCA
二、6.AB A B
BC B C
''
=
''
(答案不惟一) 7.36 8.1:8 9.①,③
三、10.AB的距离是100m.。
