第三章整式的加减
第三章 整式的加减

第三章整式的加减学情分析本章在学习有理数的基础上,结合学生已知的生活经验,引入用字母表示有理数,使学生的思维跨越由数到式的飞跃,继而介绍了代数式、代数式的值、整式、单项式与多项式及其相关概念,以及多项式的升(降)幂排列,并在这些概念的基础上逐步展开同类项的概念、合并同类项的法则以及去括号与添括号的法则,最后将这些法则应用于本章的重点——整式的加减,使得全章的知识体系井然有序,层层深入,结构分明,重点突出。
学生由“数”的学习转到“式”的学习,刚开始不懂,不过他们会逐步适应的。
列代数是本章的一个难点,刚开始时可以学习简单的列代数式,等全章学完后再适当补充结合生活实际的列代数式的题目;求代数式的值,在用数值代替代数式里的字母时,注意不要写错,特别是代入的数值是负数或分数时,要注意加括号;本章的概念较多,注意紧扣概念进行学习,注意单项式与多项式及其次数和系数、整式、同类项等的识别,教学时教师可补充这些概念的运用题,以进一步巩固所学的概念;在将一个多项式的按某字母升(降)幂排列时,注意是按题目要求的字母的次数,而不是这项的次数;本章学习的法则也很多,教师要帮助学生理解法则,并讲解典型题目紧扣法则进行训练,补充一些题目让学生练习,以巩固所学的法则的运用,其中在去括号与添括号时括号前面是负号,这是难点,学生特别容易做错,应加强训练,在学习本章的重点——整式的加减时,更要根据法则进行,在去括号时注意符号,计算时注意同类项的识别,运算时要细心,防止计算错误,也应多练习,以熟练掌握整式的加减运算。
在本章的学习中,让学生经历探索数量关系和变化规律的过程;学习时,对知识的呈现过程尽量能联系学生已有的生活经验,以发展学生用数学的意识和能力;在重视基础知识的同时,适当插入一些开放题,培养学生的发散思维。
在学习中,充分发挥学生的主体作用,让学生自主学习、主动探索、小组讨论、合作学习、归纳总结、练习训练,牢固地掌握所学的知识。
苏科版(2024)七年级上册数学第3章 代数式3.3 整式的加减 教案

苏科版(2024)七年级上册数学第3章代数式3.3 整式的加减教案【教材分析和学情分析】教材分析:整式的加减是苏科版七年级上册代数式这一章的重要内容,主要介绍了如何对含有相同字母的多项式进行合并同类项,以及如何在实际问题中应用整式的加减法则。
这一部分的知识点是代数运算的基础,为后续的代数学习,如解一元一次方程、二次方程等奠定了基础。
教材通过丰富的实例和练习,引导学生理解并掌握整式加减的规则,同时培养他们的抽象思维能力和逻辑推理能力。
此外,通过解决实际问题,也锻炼了学生应用数学知识解决实际问题的能力。
学情分析:七年级的学生已经学习了基本的代数知识,如变量、常量、单项式、多项式等,对数学符号和运算规则有一定的理解和应用能力。
然而,对于抽象的整式加减,尤其是如何识别和合并同类项,可能会感到一定的困难。
部分学生可能还停留在具体的数的运算上,对于字母表示的数的运算可能会感到陌生和困惑。
此外,这个阶段的学生好奇心强,喜欢探索,但注意力集中时间可能较短,需要教师通过生动有趣的教学方式,激发他们的学习兴趣,保持他们的学习动力。
【教学目标】1. 知识与技能:学生应能理解整式的加减运算法则,掌握同类项的概念,能正确地进行整式的加减运算。
2. 过程与方法:通过实例,让学生经历整式加减的抽象过程,培养他们的观察、比较、抽象和概括能力,提高他们的运算能力。
3. 情感态度与价值观:培养学生严谨的数学思维习惯,体验数学的简洁美,提高学习数学的兴趣。
【教学重难点】1. 整式的加减运算法则及其应用。
2. 同类项的识别和整式加减的简化过程。
【教学过程】一、情境导入1. 展示几个生活中的实际问题,如:苹果和香蕉的总数,两本书的总价格等,引出含有加减运算的数学表达式。
二、新知探究1. 整式和同类项的概念:通过实例,引导学生总结出整式的定义,即字母和数字的乘积,且字母可以是任意次幂。
引导学生发现同类项的特征,即字母相同,字母的指数也相同的项。
第三章《整式及其加减》基础知识
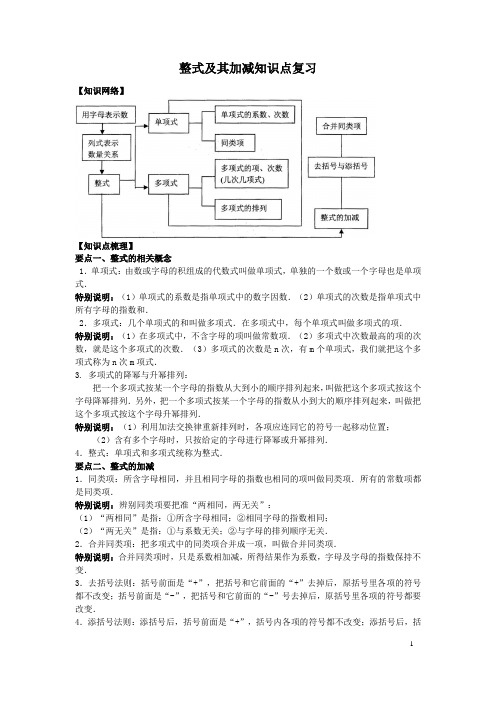
整式及其加减知识点复习【知识网络】【知识点梳理】要点一、整式的相关概念1.单项式:由数或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.特别说明:(1)单项式的系数是指单项式中的数字因数.(2)单项式的次数是指单项式中所有字母的指数和.2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.特别说明:(1)在多项式中,不含字母的项叫做常数项.(2)多项式中次数最高的项的次数,就是这个多项式的次数.(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.3. 多项式的降幂与升幂排列:把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.特别说明:(1)利用加法交换律重新排列时,各项应连同它的符号一起移动位置;(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.4.整式:单项式和多项式统称为整式.要点二、整式的加减1.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.特别说明:辨别同类项要把准“两相同,两无关”:(1)“两相同”是指:①所含字母相同;②相同字母的指数相同;(2)“两无关”是指:①与系数无关;②与字母的排列顺序无关.2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.特别说明:合并同类项时,只是系数相加减,所得结果作为系数,字母及字母的指数保持不变.3.去括号法则:括号前面是“+”,把括号和它前面的“+”去掉后,原括号里各项的符号都不改变;括号前面是“-”,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.4.添括号法则:添括号后,括号前面是“+”,括号内各项的符号都不改变;添括号后,括号前面是“-”,括号内各项的符号都要改变.5.整式的加减运算法则:几个整式相加减,通常用括号把每一个整式括起来,再用加、减号连接,然后去括号,合并同类项.【典型例题】类型一、整式的相关概念1.在式子①﹣14x 2,①﹣2xy ,①xy 2﹣12x 2,①1y ①b a ﹣x ,①312x -,①0中,整式有_____个.【变式1】 在代数式①ab ,①1a ,①3x y +,①32x +,①3y -,①221b b =+,①2pq -,①2aπ中单项式有________;多项式有________;整式有________.【变式2】下列代数式:(1)12-mn ,(2)m ,(3)12 ,(4)b a ,(5)2m +1,(6)5x y -,(7)2x y x y +-,(8)x 2+2x +23,(9)y 3﹣5y +3y 中,整式有______.(填序号) 类型二、同类项及合并同类项2.若2|2|(1)03nm -+-=,则单项式213x m n y +-和224x n m y -是同类项吗?如果是,请把它们进行加法运算;如果不是同类项,请从下列代数式中找出同类项进行加法运算:242x y -,645x y -【变式1】在 2x 2y ,-2xy 2 ,3x 2y ,-xy 这四个代数式中,哪两项是同类项,并合并这两项.【变式2】合并同类项:(1)5(32)(37)a a a -+--- (2)3338(5)53a a a --+-类型三、去(添)括号3、a b c d a b --+=--(_________)a =+(_________)a =-(__________).4、计算:(2xy -y)-(-y +xy)=________.【变式1】m +n -p 的相反数为__________.【变式2】在等式的括号内填上恰当的项,x 2﹣y 2+8y ﹣4=x 2﹣(___________). 类型四、整式的加减5、整式的加减(1)化简:3b +5a +2a -4b ; (2)化简:(a 2+2ab +b 2)-(a 2-2ab +b 2).(3)化简并代入求值:(4a 2-3a)-2(1-2a +2a 2),其中a =-2【变式1】已知22m x y 与3n xy -是同类项,计算()()223423m m n m n nm n -+-+-的值.【变式2】 计算:( 1)3x 2y-3xy 2-12xy 2+23x 2y; (2)4(a-2b+1)-3(-4a+b-5).【变式3】 嘉淇准备完成题目:化简:22(68)(652)x x x x ++-++,发现系数“”印刷不清楚.(1)他把“”猜成3,请你化简:(3x 2+6x +8)–(6x +5x 2+2); (2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“”是几?类型五、综合应用6、如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.(1)用含字母a,b的代数式表示矩形中空白部分的面积;(2)当a=3,b=2时,求矩形中空白部分的面积.【变式1】设A=2x2﹣3xy+y2+2x+2y,B=4x2﹣6xy+2y2﹣3x﹣y,(1)求B-2A(2)若|x﹣2a|+(y﹣3)2=0,且B﹣2A=a,求a的值.【变式2】“十一”期间,某中学七年级(1)班的三位老师带领本班a名学生(学生人数不少于3名)去北京旅游,春风旅行社的收费标准为:教师全价,学生半价;华北旅行社不论教师、学生一律八折优惠,这两家旅行社的基本收费都是每人500元.(1)用代数式表示,选择这两家旅行各需要多少钱?(2)如果有学生20名,你认为选择哪家旅行社较为合算,为什么?。
北师大版七年级数学上册 第三章3 整式的加减

用括号括起来。(2)整式加减的最后结果中:①不能含有同类项, 即要合并到不能再合并为止;②不能出现带分数,带分数要化 成假分数。
知识点2:整式化简求值的步骤(重难点) 一化:利用整式加减运算法则将整式化简;二代:把已知字母或某 个整式的值代入化简后的式子; 三计算:依据有理数的运算法则进行计算。
例4:一名同学做一道题,“已知两个多项式A、B,计算A+B” 时,
他误将A+B看成A-B,求得结果是9x2-2x+7,若B=x2+ 3x解:A=9x2-2x+7+x2+3x-2=10x2+x+5,所以A+B=
1-0x22,+求x+出5A++xB2+的3正x确-答2=案1。1x2+4x+3。
【题型三】整式加减运算中的无关型问题(拓展) 例5:已知代数式A=x2+xy-2y,B=2x2-2xy+x-1。
【题型一】整式的加减运算
例1:化简:(1)(7m2n-5m)-(4m2n-5m);(2)2x2{- 5x -1 ( x-3) 2
+ 2}x2 。
解:(1)原式=7m2n-5m-4m2n+5m=3m2n。(2)原式=2x2-5x +
12x-3-2x2=-92x-3。
例 2:先化简,再求值:21x2+2x2-3xy+13y2-332x2-2xy-19y2, 其中x,y满足(x-2)2+|y+3|=0。
如果用a,b分别表示一个两位数的十位数字和个位数字,那 么这个两位数可以表示为10a+b。交换这个两位数的十位 数字和个位数字,得到的数是10b+a,这两个数相加得 (10a+b)+(10b+a)=11a+11b
2.请同学们在完成上面任务后思考以下问题:
两个数相减后的结果有什么规律?这个规律对任意一个三位数都 成立吗? 规律是它们的差为百位数字与个位数字的差的99倍,对任意一个 三位数都成立
【精编】六年级数学上册《整式的加减》全章知识点总结及练习

第三章 整式的加减 基础知识复习知识点1、单项式的概念式子x 3,m t xy a ---,6.2,,32它们都是数或字母的积,像这样的式子叫做单项式,单独的一个数或一个字母也是单项式。
注意:单项式是一种特殊的式子,它包含一种运算、三种类型。
一种运算是指数与字母、字母与字母之间只能是乘法的一种运算,不能有加、减、除等运算符号;三种类型是指:一是数字与字母相乘组成的式子,如ab 2;二是字母与字母组成的式子,如3xy ;三是单独的一个数或字母,如m a ,2-,。
【特别注意】分母中只要含有字母一定不是单项式,也不是多项式,而是分式。
知识点2、单项式的系数单项式中的数字因数叫做这个单项式的系数。
注意:(1)单项式的系数可以是整数,也可能是分数或小数。
如42x 的系数是2;3ab 的系数是31,2.7m 的系数是2.7。
(2)单项式的系数有正有负,确定一个单项式的系数,要注意包含在它前面的符号,如-()xy 2的系数是-2,(注意:千万不要忘记前边的符号)(3)对于只含有字母因素的单项式,其系数是1或-1,不能认为是0,如-2xy 的系数是-1;2xy 的系数是1。
(单项式前边的系数是1或-1时,1可以省略不写。
)(4)表示圆周率的π,在数学中是一个固定的常数,当它出现在单项式中时,应将其作为系数的一部分,而不能当成字母。
如-2πxy 的系数就是-2π知识点3、单项式的次数一个单项式中,所有字母的指数和叫做这个单项式的次数。
注意:(1)计算单项式的次数时,应注意是所有字母的指数和,不要漏掉字母指数是1的情况。
如单项式z y x 342的次数是字母z y x ,,的指数和,即4+3+1=8,而不是7次,应注意字母Z 的指数是1而不是0.(2)单项式是一个单独字母时,它的指数是1,如单项式m 的指数是1,单项式是单独的一个常数时,一般不讨论它的次数。
(非要讨论的话,单独的一个数字的系数是它本身,次数是0)(3)单项式的指数只和字母的指数有关,与系数的指数无关。
第三章整式及其加减第4节整式的加减(教案)

同学们,今天我们将要学习的是《整式的加减》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要合并同类项或计算总价的情况?”(如购物时计算多件商品的价格)。这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索整式加减的奥秘。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了整式的概念、加减运算法则以及它在实际生活中的应用。通过实践活动和小组讨论,我们加深了对整式加减的理解。我希望大家能够掌握这些知识点,并在解决实际问题时灵活运用。如果有任何疑问或不明白的地方,请随时向我提问。
具体内容包括:
-单项式、多项式的定义与性质;
-整式的加减法则与运算技巧;
-合并同类项、去括号等方法;
-应用整式加减解决实际问题。
二、核心素养目标
1.培养学生的逻辑思维能力,通过整式的加减运算,使学生能够理解数学的内在联系,提高推理与论证能力;
2.培养学生的数学建模素养,使学生能够将实际问题转化为整式的加减问题,建立数学模型,增强解决实际问题的能力;
3.培养学生的数学运算素养,使学生熟练掌握整式的加减法则,提高运算速度和准确性;
4.培养学生的创新意识,鼓励学生在解决整式加减问题时,探索不同的解题方法和技巧,提升数学思维品质。
三、教学难点与重点
1.教学重点
-单项式与多项式的概念:明确单项式的系数与次数,多项式的项数与次数的概念,以及它们的表示方法。
2024秋七年级数学上册第三章整式的加减3.4整式的加减2去括号与添括号教案(新版)华东师大版
简短介绍整式的基本概念和重要性,为接下来的学习打下基础。
2.整式基础知识讲解(10分钟)
目标:让学生了解整式的基本概念、组成部分和原理。
过程:
讲解整式的定义,包括其主要组成元素或结构。
详细介绍整式的组成部分或功能,使用图表或示意图帮助学生理解。
-分类:单项式和多项式。
2.整式的加减法则:
-同类项的定义和加减法。
3.去括号与添括号的方法:
-原则:正数去括号,负数去括号,添括号保持等式平衡。
-示例:去括号和添括号的具体步骤。
4.练习题:
-加减运算题目和去括号添括号题目。
5.作业布置与反馈:
-课后练习题和作业要求。
2024秋七年级数学上册第三章整式的加减3.4整式的加减2去括号与添括号教案(新版)华东师大版
授课内容
授课时数
授课班级
授课人数
授课地点
授课时间ห้องสมุดไป่ตู้
教学内容
本节课的教学内容来自于2024秋七年级数学上册第三章整式的加减3.4节,主要涉及整式的加减法则,特别是去括号与添括号的方法。具体内容包括:
1.掌握去括号的原则,即如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
(2)视频:播放一些与整式加减相关的视频,让学生更直观地了解去括号与添括号的过程。
(3)在线工具:利用在线工具,让学生进行整式加减的练习,及时反馈学生的学习情况,提高教学效果。
教学过程设计
1.导入新课(5分钟)
目标:引起学生对整式加减的兴趣,激发其探索欲望。
数学第三章代数式的运算

数学第三章代数式的运算数学第三章:代数式的运算在数学中,代数式是由数、变量和运算符组成的表达式。
代数式的运算是指对代数式进行各种加减乘除等运算的过程。
在第三章中,我们将学习如何进行代数式的运算,包括整式与分式的加减乘除、括号展开、因式分解等内容。
本文将详细介绍代数式的运算方法。
一、整式的基本运算1. 整式的加减法在进行整式的加减法时,我们只需按照相同项合并的原则进行合并即可。
例如:3x^2 + 4x + 2x^2 - 6x = (3x^2 + 2x^2) + (4x - 6x) = 5x^2 - 2x2. 整式的乘法整式的乘法可以使用分配律,即将每个项分别相乘后进行合并。
例如:(2x + 3y)(4x - 5y) = (2x)*(4x) + (2x)*(-5y) + (3y)*(4x) + (3y)*(-5y) = 8x^2 - 10xy + 12xy - 15y^2= 8x^2 + 2xy - 15y^23. 整式的除法整式的除法是通过因式分解的方法进行。
例如:8x^2 - 2x = 2x(4x - 1)二、分式的基本运算1. 分式的加减法在进行分式的加减法时,我们需要先找到分母的最小公倍数,并将分子进行相应的转化,然后进行合并。
例如:(2/x + 3/y) = (2y + 3x) / (xy)2. 分式的乘法分式的乘法是将分子与分母分别相乘后再进行合并。
例如:(2/x) * (3/y) = 6 / (xy)3. 分式的除法分式的除法可以转化为乘法,即将除法转化为倒数的乘法。
例如:(2/x) / (3/y) = (2/y) * (y/3x) = 2y / 3x三、括号展开与因式分解1. 括号展开括号展开是指将一个代数式中的括号去掉,并将括号外的项与括号内的每一项进行相乘。
例如:2(3x + 4) = 6x + 82. 因式分解因式分解是指将一个代数式分解成若干个乘积的形式,其中每个乘积的项都不能再进行因式分解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 整式的加减
3.1 整式 同类项
基础知识训练
1.把下列各代数式中的整式找出来,并说明它是单项式还是多项式:
(1)22b a + (2)π34ab - (3)32++n m n (4)1323++x x (5)-4 (6)
a a 33+ (7)322d bc a (8)xy x 232+
2.填表:
3.下列多项式是哪几个单项式的和,各项的系数分别是什么?
(1)6223-+-xy y x
(2)22222
1434ab b a ab b a -
+-
4.写出系数是-1,含字母b a ,的所有六次单项式.
5.单项式213
1c ab m -是一个五次单项式,求m 的值.
6.单项式z y x b a 25是一个四次单项式,求ab 应满足什么关系?
7.分别写出下列多项式的项,并说出是几次几项式,常数项是几.
(1) 5+-x ; (2)6322-+x x ;
(3)2327a a --; (4)222b ab a ++;
(5)c bc abc c ab bc a ab +-++-222458.
8.关于x 的多项式2242)1(++--m x x m mx 是五次三项式,求m 的值,并求出这个多项式.
9.已知:y x m 1+-与222+n y x 是同类项,求:232++n m 的值.
10.将多项式532342++-a a a 先按字母a 降幂排列,再按字母a 升幂排列.
11.将多项式5322323--+n m n m mn
(1)按字母m 降幂排列;(2)按字母m 升幂排列.
综合提高训练
1.写出系数是2,含字母b a ,中的1个或2个的所有4次单项式.
2.写出系数是1,含字母c b a ,,中的1个或2个或3个的所有三次单项式.
3.观察多项式,b a +22b ab a ++,将b a ,的位置交换,得a b +和22a ba b ++,与原多项式相等,这种多项式叫对称式,你能写出一些对称式吗?
3.2整式的加减
基础知识训练
1.填空:
(1)化简:=+--)523(b a ;
(2)化简=---)]}23[({y x ;
(3)如果0<-+z y x ,那么化简=-+||z y x ;
(4)-=+-a c b a 323( );
(5)+-=---+-+){())((m x n m y x n m y x ( )--)][(m x ( )];
(6)单项式b a 23与b a 24-的差是 ;
(7)化简b b a a 3)35(++-的结果是 .
2.化简:(1);)]3(5[)23(a b a b a -+---
(2)2)313()83(5222++---+-x x x x x .
3.计算:
(1)22222)3()2(3ab ab b a b a --+-+;
(2))232()543(22-+---x x x x ;
(3))1896(3
1)524(212322y xy x y xy x -+++--。
4.已知:2222752,32n n m m B n mn m A ---=+-=
求:(1)B A +; (2))3(2A B A +-.
5.解方程:.2723y y -=+
6.化简求值:
)]},2(53[2{4222abc ab b a ab abc ----其中.4,2,2
1=-==c b a
7.三个连续奇数的和是-39,求这三个奇数.
综合提高训练
1.有理数在数轴上表示的点如图
化简:.||2||2||b c b a c a --+--
2.两个多项式m b a 2543与66
1b a n -的和是一个单项式,求n m ,以及这两个单项式的和.
3.将多项式262222222+--+-y a y y y a a 先按字母y 的同类项合并,再按照字母a 的同类项合并.
4.填空:(1)34632=+-x x ( ); (2)5
172512-=-+-x x ( ). 5.已知:,64,223=+-=+y x y x 求:y x 10+的值.
6.美国学生的怪题.
蓬蓬国王为了获得贫穷老百姓的支持,图一个“乐善好施”的好名声,决定施舍男人1美元,每个女人40美分(1美分等于100美分).为了不使他花费过多,这位陛下盘算来盘算去,最后想出一个妙法,决定将他的直升机于正午12时在一个贫困的山村着陆.因为他十分清楚,在那个时刻,村庄里有60%个男的都外出打猎去了,该村庄里共有成年人口3085人,儿童忽略不计,女性比男性多,请问,这位“精打细算”的国王要施舍多少钱?
本章实力测评
一.填空
1.若c b c a 2,7-==,则c b a 32-+= .
2.多项式xy x y x 34423-+-的最高次项的系数是 .
3.当=a 时,212y x a -与7223+-a x y 是同类项.
4.有理数b a ,在数轴上的对应点如图,化简:b a b 2|2|+-= .
5.如果a 3的倒数与3
92-a 互为相反数,那么=a . 6.三个连续偶数的和是18,那么它们的积是 .
7.多项式2244b ab a +--减去一个多项式,得ab a 322-,那么这个多项式是 .
8.把232ax a x ax --+按x 的降幂排列是 .
9.五个代数式:3
,4,2,1,23b a b a m a ---其中单项式是 ,整式是 .
10.代数式)232(2)32(322x x x x x +--++化简后是 次 项式,按x 的升幂排列是 . 11.-=-+-a d c b a 2
151413121( ) 12.将b a bm am --+添上括号,使每个括号里面有两项,那么可能是 (至少写出三种可能).
13.多项式4
122-x 中的常数项是 . 14.当3,2==b a 时,)4()3(22222b a ab b a ab ---的值等于 . 15.5)3(5
121++--x n y x m 为二次三项式的条件是=m , =n . 二.选择题
16.下列各组单项中,是同类项的是( )
A .a 4与2a
B .-2.5与12
C .b a 25与25ab
D .m 3与n 3
17.A 和B 均为x 的四次多项式,A +B 是( )
A .8次多项式
B .4次多项式
C .3次多项式
D .不能确定是几次多项式
18.下列说明中,正确的是( )
A .x 的系数是0
B .x 的次数是0
C .22xy -的系数是2
D .y x 33-的次数是4
19.下列各式,一定能成立的是( )
A .ab b a 422=+
B .mn mn n m 25322-=-
C .963x x x =+
D .03322=-yx y x
10.当3-<x 时,|24||3|x x -++化简得( )
A .x -7
B .73+x
C .x 37-
D .x 31-
三.解答题
21.计算:
(1)16423522--++-x x x x ; (2)222223
1321yx x y xy y x --+; (3)).(3)()(5)(7b a b a b a b a -++---+
22.计算:
(1)]6)6(43[25--+-y x x x ; (2))]2(2[232222n m mn n mn m -+---.
23.合并同类项:1116343---+-+-m m m m m x x x x x .
24.已知:x x B x x A +-=-+=2325,13 求:B A B A 2)(2+--
25.将多项式5224234623y y x xy y x y x -++-按字母y 降幂排列.
26.求下列代数式的值.
(1))32(3)21(2222x x x x x ++-++--,其中5
1-=x ; (2))](41[2)2(214223232xy y x y x xy y x xy ----+;其中.2
1,21-==y x
27.多项式1211++++-+-x mx x x n n n 是关于x 的三次多项式,求n m ,的值.
28.形如2232b ab a +-是各项都是二次的多项式,这种多项式称二次齐次式,请写出一些三次齐次式,四次齐一次式.
29.数轴上的点A、B、C、D分别表示有理数-5,-3,1,2,数a表示点E在线段AB上移动,数b表示的点FD在线段CD上移动,求:(1)a和b的取值范围;(2)代数式)
b
a+
a
-
-的最大值和最小值.
3
(
2
3b
30.已知:,2
a
+b
b
a求代数式b
=
3,4
=
2-
-
9+的值.
a4。
