赏析一道高考题的多种解法
高考语文诗歌鉴赏题的解答方法

高考语文诗歌鉴赏题的解答方法高考语文这门科目会涉及到各种题型,其中诗词歌赋题就是考生比较难以学会的一种题。
这种类型题型解答,不仅需要讲解诗词,诗句所包含的感情考生要需要表达出来。
那这种类型题型的解答方法是什么呢?下面就一起来看一下吧!一、读标题,抓重要信息诗词歌赋这种类型题标题是非常重要的,毕竟标题当中一般都包含重要信息,对于解题很有协助。
有的是包含了时间、地点,有的也蕴含某种情感。
例如《秋思》这首诗当中,就表达一种惆怅的思想感情。
而在《晓出净慈寺送林子方》这首诗中,就包含了时间,以及内容送别。
假如考生答题的时候,抓到了这些重要信息,答题的方向也会愈加的准确。
因此,考生答题必须要仔细的剖析标题,不要错过得分点。
二、仔细的品一品注释诗词当中一般是必不可少注释的,而注释的用途就是让考生更好的理解整首诗。
具体来说,注释一方面是为知道释难题,另一方面就是交代诗词的历史背景。
考生答题的时候就不可以放过这些答题的细则,要去细细的品读注释。
说不定结合注释剖析诗词,考生会更了解诗词的内容以及所表达的情感。
三、剖析作者的经历和写作风格作者写的每首诗都是有感而作的,其中会有作者的写作风格以及自己的经历。
因而,考生在评析诗词的时候,就可以结合作者的经历和风格来剖析整首诗。
例如,杜甫自己经历过贬官,他做的诗也会有仕途不畅,抑郁不得志的情感,再结合他的风格是沉郁顿挫的,考生答题的时候就有明确的方向了。
而其他的诗人,例如李清照是属于婉约派的,因而她的风格就是曲折委婉的。
考生在答题的时候,只须分清每一个诗人的写作风格,知道他们的经历,答题就容易了。
四、全方位剖析,仔细剖析整首诗考生在解答这种类型题的时候,不仅对于重要句要去剖析,对于每一句的意思和情感也要去剖析,也就是全方位剖析,仔细剖析整首诗。
一般首尾句都是起到抒情和画龙点睛的用途的,中间的诗句大多数是描写内容。
考生站在整体上剖析每一句,就能理解全诗的意思了。
以上,就是高考语文诗歌鉴赏题型的解答方法。
一道向量组线性相关性试题的多种解法及其思政元素

一道向量组线性相关性试题的多种解法及其思政元素随着信息技术的发展,向量组的线性相关性的研究被越来越多的应用到各个领域。
它在国防领域、航空航天领域、电子工程领域均有着重要的作用。
本文旨在探讨向量组的线性相关性的多种解法及其思维元素。
首先,我们来谈谈向量组的线性相关性的定义和涵义。
线性相关性是指xx 向量组两两成对之间存在明确的线性关系,即给定一组输入自变量值 x1、x2、 x3 和 y,使用回归分析法可以正确确定 y 的解析解 y1、 y2 和 y3;它们的关系可以表示为:y=a*x1+b*x2+c*x3+d。
其次,对于向量组的线性相关性问题,有多种解法可以提供参考。
常见的解法有:1、线性回归法:给定 T 个样本(Xi),求出 k 维参数矩阵 A,使得条件最优,这里 k 是系数矩阵的维度(也就是参数的个数)。
2、最小二乘法:求解以 A 为参数,根据样本 T 的均方误差(SSE)来拟合模型的优度,也就是使得 SSE 最小的参数矩阵 A 的求解。
3、偏最小二乘法:给定偏最小二乘法的系数矩阵,求其最优解。
最后,我们来说说解决向量组的线性相关性问题的思维元素。
总的来说,解决这类问题的思维模式主要有:1、确定函数原型:要确定函数原型,也就是要确定最恰当的函数形式,以把问题表述出来。
2、求解参数值:求解参数值,函数需要通过参数来述说,而参数又需要通过数学算法来计算得出。
3、函数评价:最后,根据函数以及确定的参数,需要对函数效果进行客观评价,以验证此函数能否完美地拟合数据。
有了上面的思维元素,才能有助于我们更加熟练的掌握解决向量组的线性相关性问题的各种解法。
综上所述,向量组的线性相关性对于很多领域具有重要作用,而其解法及其思维模式也需要我们充分认识,以获得更好的解决线性相关性问题的效。
一题多解之五种方法解一道经典数学题

O BCD①A 一题多解之五种方法解一道经典数学题江苏海安紫石中学 黄本华一题多解是我们学习数学的特好方法!通过一题多解,我们可以多角度、多方位地去思考解题的方案,这样不仅能加强知识间的联系,同时也增添新颖性和趣味性,优化我们的思维结构,提升我们的思维能力。
更重要的是,一题多解让我们不仅只满足解题目标的实现,而是让我们拥有了研究学问的态度!例题 如图,在平面直角坐标系中,点A (-1,0),B (0,3),直线BC 交坐标轴于B ,C 两点,且∠CBA =45°.求直线BC 的解析式.【分析】要求BC 解析式,现在已经知道了B 点坐标,所以只要求到C 点坐标就好了。
这就要用到条件∠CBA =45°。
但这个条件如何用呢?这是本题的难点,也是关键点。
考虑到这个角是45°,我们可以尝试做垂线,构造等腰直角三角形。
如图①,作AD ⊥BC 于D ,由A 、B 的坐标可知1OA =,3OB =,根据勾股定理2210AB OA OB =+=,5BD AD ==AC x =,则1OC x =+,25DC x =-255BC x =-,在RT OBC ∆中,根据勾股定理得出222OC OB BC +=,即()222213(55)x x ++=-,解得152x =-(舍去),25x =,求得6OC =,得出C (﹣6,0),然后根据待定系数法即可求得BC 的解析式.解法一:如图①,作AD ⊥BC 于D , ∵点A (﹣1,0),B (0,3),∴1OA =,3OB =,∴2210AB OA OB =+=, ∵∠CBA =45°,∴△ABD 是等腰直角三角形, ∴5BD AD ==设AC x =,则1OC x =+, ∴25DC x =-,∴BC=+255BC x =-+,在152x =-中,222OC OB BC +=2,即()222213(55)x x ++=-), 解得x 1=﹣(舍去),25x =,②③∴5AC =,6OC =,∴C (﹣6,0), 设直线BC 的解析式为3y kx =+, 解得12k =,∴直线BC 的解析式为132y x =+. 【点评】虽然这种解法思路比较清晰,但是用勾股定理得出的方程比较复杂,解方程很繁,很费时,很累。
高考古诗鉴赏题的八种答题模板

第一种模式:分析形象型 概括形象特征 + 分析形象特征 + 形象的意义 第二种模式:分析意境型 描绘诗中图景画面 + 概括景物所营造的环境氛围特点 + 分析作者的思 想感情 第三种模式:分析技巧(手法)型 指出手法 + 结合诗句说明怎样运用这种手法 + 手法效果(感情) 第四种模式:分析语言型 点明语言特色 + 分析这种特色 + 表现了作者怎样的感情(效果) 第五种模式:炼字型、诗眼型 解释该字的含义 + 把该字放入原句中描述景象 + 该字烘托了怎样的意 境,或表达了怎样的感情 第六种模式:炼句型 写什么内容 + 用什么手法 + 效果(情感、结构) 或用什么手法 +写什么内容 + 效果(情感、结构) 第七种模式:观点不同型 观点(同意或不同意) + 理由 第八种模式:情感型 结合诗句分析 + 情感概括 或 情感概括 + 结合诗句分析 实用类文本(传记文)题型模式 题型一:概括传主的性格特点 答题模式:概括特点(形象、性格) + 举例分析 (分点答题,一般三点) 题型二:手法题: 答题模式:指出手法 + 举例分析 + 分析效果(分点答题,一般三点) 题型三:作用题 答题模式:内容作用 + 结构作用 (分点答题,一般三点) 题型四:探究题 亮出观点 + 引据论述 + 联系现实 + 总结陈词(分点答题,一般四点) • 1.唯一观点型(谈谈看法、启示、是否赞同等) : • 模式:观点 + 理由 1 + 理由 2 + 理由 3 (每一点理由,先概括+再结合文本 分析) • 2.多观点型(哪些型、多启示型) : • 模式: (1)观点 1+ 结合文本分析 (2)观点 2+ 结合文本分析 (3)观点 3+ 结合文本分析 (4)观点 4+ 结合文本分析
一题多解之五种方法解一道经典数学题
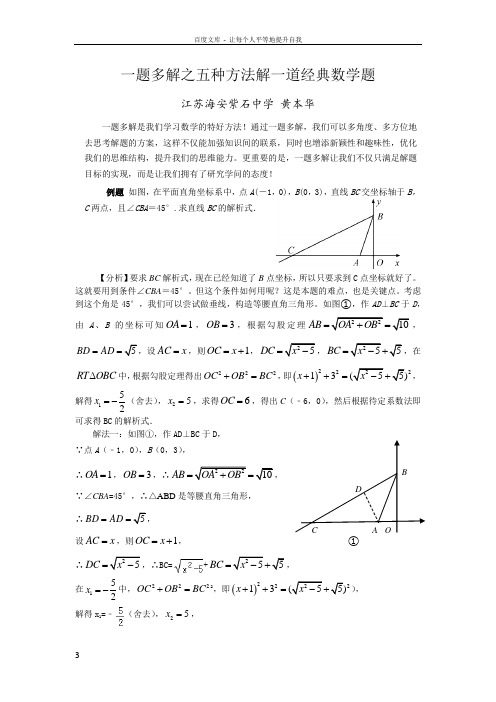
O BCD①A 一题多解之五种方法解一道经典数学题江苏海安紫石中学 黄本华一题多解是我们学习数学的特好方法!通过一题多解,我们可以多角度、多方位地去思考解题的方案,这样不仅能加强知识间的联系,同时也增添新颖性和趣味性,优化我们的思维结构,提升我们的思维能力。
更重要的是,一题多解让我们不仅只满足解题目标的实现,而是让我们拥有了研究学问的态度!例题 如图,在平面直角坐标系中,点A (-1,0),B (0,3),直线BC 交坐标轴于B ,C 两点,且∠CBA =45°.求直线BC 的解析式.【分析】要求BC 解析式,现在已经知道了B 点坐标,所以只要求到C 点坐标就好了。
这就要用到条件∠CBA =45°。
但这个条件如何用呢?这是本题的难点,也是关键点。
考虑到这个角是45°,我们可以尝试做垂线,构造等腰直角三角形。
如图①,作AD ⊥BC 于D ,由A 、B 的坐标可知1OA =,3OB =,根据勾股定理2210AB OA OB =+=,5BD AD ==AC x =,则1OC x =+,25DC x =-255BC x =-,在RT OBC ∆中,根据勾股定理得出222OC OB BC +=,即()222213(55)x x ++=-,解得152x =-(舍去),25x =,求得6OC =,得出C (﹣6,0),然后根据待定系数法即可求得BC 的解析式.解法一:如图①,作AD ⊥BC 于D , ∵点A (﹣1,0),B (0,3),∴1OA =,3OB =,∴2210AB OA OB =+=, ∵∠CBA =45°,∴△ABD 是等腰直角三角形, ∴5BD AD ==设AC x =,则1OC x =+, ∴25DC x =-,∴BC=+255BC x =-+,在152x =-中,222OC OB BC +=2,即()222213(55)x x ++=-), 解得x 1=﹣(舍去),25x =,②③∴5AC =,6OC =,∴C (﹣6,0), 设直线BC 的解析式为3y kx =+, 解得12k =,∴直线BC 的解析式为132y x =+. 【点评】虽然这种解法思路比较清晰,但是用勾股定理得出的方程比较复杂,解方程很繁,很费时,很累。
高考语文赏析句子答题公式

高考语文赏析句子答题公式高考语文赏析句子答题公式是考生在应对高中语文阅读领域时必须要熟知的一种技巧。
下面将从七个方面给大家介绍一下赏析句子答题公式并给出相应的案例。
一、排除干扰项法“排除干扰项法”是指在选择题答题时,先看选项中哪些是明显错误的,将其排除,更快地找到正确答案。
例如:“闪烁的灯光使他的表情显得越来越专注。
”这句话中的“闪烁”的灯光是对他表情的一种增强修饰,显得格外动人。
正确选项应该是“使表情显得动人”。
二、寻找创新词汇装点词汇,不仅让文章越发绚丽多彩,还能调动观者的感官,产生视觉变化。
所以在高考答题的时候,如果一道选项中出现了新的汉字或者意义有所变化的词汇,往往就是正确的选项。
例如:“记忆在岁月中堆积,青春却褪色了它的色彩。
”这句话表达了时间对记忆的影响,并且运用了“堆积”这一创新词汇,选项中出现“堆积”二字,可以很确定地选择此项。
三、关注情感、态度高考语文答题时,经常要求考生对文章的情感、态度进行把握。
因此,答题过程中要注意筛选出文章中的重点态度、情感,并且判断选项中是否与文章中表达的情感保持一致。
例如:“绿地上竖起了新一轮朝阳,那粉墙黑瓦的双重轮廓清晰可见。
”表达的是诗意和欣喜,选项中出现“喜悦”和“美好”的形容词,可以很确信这是正确选项。
四、强调语言运用文章中的语言运用是高考语文考试不可缺少的一部分,所以在答题时,考生需要对文章中的修辞手法、句式变化等作出分析,寻找合适的选项。
如:“多么伟大的信仰,它促使我们懂得用眼睛去看世界的无限美好。
”强调的是信仰的伟大,运用了排比句及修辞手法,选项中出现的排比句则是正确选项。
五、看文中所涉及的知识有时,在文中出现某些单词或专业术语,可作为突破口,帮助寻找正确的答案。
如:“绝代有佳人,幽居在空谷,自云良家子,零落依草木。
”这句话出自欧阳修的《玉楼春·绝代有佳人》,人物形象的描写和行为表现在文学上的贡献是宏大的,选项中出现的“良家子”可判断为正确答案。
高考古诗鉴赏题的十二种答题模式讲课讲稿

高考古诗鉴赏题的十二种答题模式高考古诗鉴赏题的十二种答题模式第一种模式:分析意境型一般提问方式:这首诗营造了一种怎样的意境?变式提问:这首诗描绘了一幅怎样的画面?表达了诗人怎样的思想感情?答题步骤:(1)描绘诗中展现的图景画面。
考生应抓住诗中的主要景物,用自己的语言再现画面。
描述时一要忠实于原诗,二要用自己的联想和想象加以再创造,语言力求优美。
(2)概括景物所营造的环境氛围特点。
一般用两个双音节词即可,例如孤寂冷清、恬静优美、清新明丽、雄浑壮阔、悲壮慷慨、萧瑟凄凉等,注意要能准确地体现景物的特点和情调。
(3)分析作者的思想感情。
切忌空洞,要答具体。
比如光答“表达了作者感伤的情怀”是不行的,应答出为什么而“感伤”。
解答分析:意境,是指寄托诗人情感的物象(即意象)综合起来构建的让人产生想象的境界。
它包括景、情、境三个方面。
答题时三方面缺一不可。
常见错误:学生在解答此类问题时常见的失误有两点:一是描摹景物时采用直译的方法,变描摹为翻译;二是学生往往着重于“思于境偕、情景相融”的正衬模式,而忽落了一些诗歌是通过景物来反衬思想感情,造成理解思想感情的错误。
在这种情况下,应多从诗人的生平、抱负或标题来思考,避免出错。
答题示例:阅读下面一首唐诗,然后回答问题。
(8分)绝句二首(其一) 杜甫迟日江山丽,春风花草香。
泥融飞燕子,沙暖睡鸳鸯。
注:此诗写于诗人经过“一岁四行役”的奔波流离之后,暂时定居成都草堂时。
此诗描绘了怎样的景物?表达了诗人怎样的感情?请简要分析。
答:此诗描绘了一派美丽的初春景象:春天阳光普照,四野青绿,江水映日,春风送来花草的馨香,泥融土湿,燕子正繁忙地衔泥筑巢,日丽沙暖,鸳鸯在沙洲上静睡不动(步骤一)。
这是一幅明净绚丽的春景图(步骤二)。
表现了诗人结束奔波流离生活安定后愉悦闲适的心境(步骤三)。
练习1:阅读下面一首唐诗,然后回答问题。
西楼曾巩海浪如云去却回,北风吹起数声雷。
朱楼四面钩疏箔,卧看千山急雨来。
2023年新高考Ⅰ卷第22题的五种解法

2023年新高考Ⅰ卷第22题的五种解法卢会玉(西北师范大学附属中学ꎬ甘肃兰州730070)摘㊀要:文章从三角函数㊁直线的参数方程等五个角度解析了2023年新高考Ⅰ卷第22题ꎬ通过对新鲜出炉的真题的研究与分析ꎬ剖开了题目的内核ꎬ感受数学思维的变通性㊁反思性㊁严密性㊁开放性的重要性.关键词:新高考ꎻ数学ꎻ五种方法中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2024)01-0020-04收稿日期:2023-10-05作者简介:卢会玉(1981.7-)ꎬ女ꎬ甘肃省天水人ꎬ本科ꎬ中学高级教师ꎬ从事中学数学教学研究.㊀㊀自新高考施行以来ꎬ有很多学生吐槽数学题通常都是 满纸的不超纲ꎬ但就是不正常说话! 不难发现ꎬ命题者是想通过改变固定的命题模式ꎬ指导教师和学生实现两个转变:从解题到解决问题的转变ꎻ从死板的刷题到培养思维的转变[1].这是在大力推行核心素养的背景下进行的一次具有革命性的变化!2023年新高考Ⅰ卷第22题让我们再一次感受到了数学思维训练的重要性ꎬ下文从三角函数㊁直线的参数方程等五种不同的角度对该题进行了解析.1试题呈现题目㊀(2023年新高考Ⅰ卷第22题)在直角坐标系xOy中ꎬ点P到x轴的距离等于点P到点(0ꎬ12)的距离ꎬ记动点P的轨迹为W.(1)求W的方程ꎻ(2)已知矩形ABCD有三个点在W上ꎬ证明:矩形ABCD的周长大于33.2试题解析2.1第(1)问解析解析㊀设动点P(xꎬy)ꎬ则由题意可得y=x2+(y-12)2.化简可得x2=y-14.也可用抛物线的定义解决:点P的轨迹是以(0ꎬ12)为焦点ꎬ以x轴为准线的抛物线ꎬ所以抛物线的焦准距p=12ꎬ故抛物线的方程为x2=2p(y-14)ꎬ即x2=y-14.2.2第(2)问解析解法1㊀(利用三角函数和放缩法解题)不妨设AꎬBꎬD在W上ꎬ显然矩形ABCD每条边所在直线的斜率都存在.因为此时ABʅADꎬ则设AB的倾斜角为θꎬ所以AD的倾斜角为90ʎ+θ.设点A(xAꎬx2A+14)ꎬ则直线AB的方程为y=tanθ(x-xA)+x2A+14.由抛物线和矩形的对称性ꎬ不妨设0<θɤ45ʎ.由x2=y-14ꎬy=tanθ(x-xA)+x2A+14ꎬìîíïïïï得x2-xtanθ+xAtanθ-x2A=0ꎬΔ=tan2θ-4xAtanθ+4x2A>0ꎬ所以xA+xB=tanθ.则xB=tanθ-xA.所以AB=xA-xBcosθ=tanθ-2xAcosθ.同理AD=cotθ+2xAsinθ.所以矩形ABCD的周长为2(AB+AD)=2(tanθ-2xAcosθ+cotθ+2xAsinθ).因为0<θɤ45ʎꎬ所以0<sinθɤcosθ.则2(AB+AD)ȡ2ˑtanθ-2xA+cotθ+2xAcosθ(当且仅当θ=45ʎ时取等号).㊀又根据a+bȡa+b(当且仅当abȡ0时取等号)ꎬ所以2(AB+AD)ȡ2cosθtanθ+1tanθ=2cosθˑ1sinθcosθ=2sinθcos2θ=2-sin3θ+sinθ.令f(x)=-x3+xꎬxɪ0ꎬ22æèç]ꎬ则fᶄ(x)=-3x2+1=-3(x+33)(x-33).令fᶄ(x)>0ꎬ得0<x<33ꎬ此时函数单调递增.令fᶄ(x)<0ꎬ得33<x<22ꎬ此时函数单调递减.所以f(x)max=f(33)=239ꎬ此时sinθ=33.所以2(AB+AD)>223/9=33.即矩形ABCD的周长大于33.解法2㊀(利用直线参数方程和放缩法解题)不妨设AꎬBꎬD在W上ꎬ显然矩形ABCD每条边所在直线的斜率都存在.因为此时ABʅADꎬ则设AB的倾斜角为θꎬ所以AD的倾斜角为90ʎ+θ.设点A(mꎬm2+14)ꎬ则直线AB的参数方程为x=m+tcosθꎬy=m2+14+tsinθìîíïïï(t为参数ꎬ0<θɤ45ʎ)ꎬ直线AD的参数方程为x=m-tsinθꎬy=m2+14+tcosθìîíïïï(t为参数ꎬ0<θɤ45ʎ).将x=m+tcosθꎬy=m2+14+tsinθꎬìîíïïï代入x2=y-14ꎬ得t2cos2θ+t(2mcosθ-sinθ)=0.所以tB=sinθ-2mcosθcos2θ=tanθ-2mcosθ.则AB=tanθ-2mcosθ.同理AD=1/tanθ+2msinθ.所以矩形ABCD的周长为2(AB+AD)=2(tanθ-2mcosθ+cotθ+2msinθ).因为0<θɤ45ʎꎬ所以0<sinθɤcosθꎬ则2(AB+AD)ȡ2ˑtanθ-2m+cotθ+2mcosθ(当且仅当θ=45ʎ时取等号).又根据a+bȡa+b(当且仅当abȡ0时取等号)ꎬ所以2(AB+AD)ȡ2cosθtanθ+1tanθ.以下同解法1.解法3㊀(利用常规根与系数关系和放缩法解题)不妨设AꎬBꎬD在W上ꎬ显然矩形ABCD每条边所在直线的斜率都存在.因为此时ABʅADꎬ则设AB的斜率为kꎬ所以AD的斜率为-1k.设点A(xAꎬx2A+14)ꎬ则直线AB的方程为y=k(x-xA)+x2A+14.由x2=y-14ꎬy=k(x-xA)+x2A+14ꎬìîíïïïï得x2-kx+kxA-x2A=0ꎬΔ=k2-4kxA+4x2A>0.所以xA+xB=kꎬ则xB=k-xAꎬ所以AB=1+k2k-2xA.同理AD=1+1k2xA-xD=1+1k2-1k-2xA=1+1k21k+2xA.所以矩形ABCD的周长为2(AB+AD)=2(1+k2k-2xA+1+1k21k+2xA).又由抛物线和矩形的对称性可知ꎬ-1ɤkɤ1ꎬkʂ0ꎬ不妨使0<kɤ1ꎬ则2(AB+AD)=2(1+k2k-2xA+1+1k21k+2xA)ȡ21+k2(k-2xA+1k+2xA)(当且仅当k=1时取等号).又根据a+bȡa+b(当且仅当abȡ0时取等号)ꎬ所以2(AB+AD)ȡ21+k2k+1k=2(1+k2)(k+1k)2=2(1+k2)(k2+2+1k2).令f(x)=(1+x)(x+2+1x)ꎬxɪ0ꎬ1(]ꎬ则fᶄ(x)=2x-1x2+3=2x3+3x2-1x2=(2x-1)(x+1)2x2ꎬ令fᶄ(x)>0ꎬ得12<x<1ꎬ此时函数单调递增ꎻ令fᶄ(x)<0ꎬ得0<x<12ꎬ此时函数单调递减.所以f(x)min=f(12)=274ꎬ此时k2=12.所以2(AB+AD)>2ˑ274=33.即矩形ABCD的周长大于33.解法4㊀(利用常规根与系数关系和分段函数解题)不妨设AꎬBꎬD在W上ꎬ显然矩形ABCD每条边所在直线的斜率都存在.因为此时ABʅADꎬ则设AB的斜率为kꎬ所以AD的斜率为-1k.设直线AB的方程为y=kx+mꎬ直线AD的方程为y=-1kx+n.由x2=y-14ꎬy=kx+mꎬìîíïïï得x2-kx-m+14=0.Δ=k2+4m-1>0ꎬ所以xA+xB=kꎬ则xB=k-xAꎬ所以AB=1+k2k-2xA.同理可得AD=1+1k21k+2xA.所以矩形ABCD的周长为2(AB+AD)=2(1+k2k-2xA+1+1k21k+2xA)=21+k2(2xA-k+2kxA+1k2).令f(xA)=2xA-k+2kxA+1k2ꎬ由抛物线和矩形的对称性可知ꎬ-1ɤkɤ1ꎬkʂ0ꎬ不妨使0<kɤ1ꎬ则f(xA)=2xA-k+2kxA+1k2=-(2k+2)xA+k-1k2ꎬxA<-12kꎬ(2k-2)xA+k+1k2ꎬ-12kɤxA<k2ꎬ(2k+2)xA-k+1k2ꎬxAȡk2.ìîíïïïïïïïï则f(xA)在(-¥ꎬ-12k)上单调递减ꎬ在(-12kꎬ+¥)上单调递增.所以f(xA)ȡf(-12k)=k+1k.所以2(AB+AD)ȡ21+k2k+1k.以下同解法3.解法5㊀(利用坐标运算和放缩法解题)不妨设A(x1ꎬy1)ꎬB(x2ꎬy2)ꎬD(x3ꎬy3)在W上ꎬ则y1=x21+14ꎬy2=x22+14ꎬy3=x23+14.因为ABʅADꎬ则ABң ADң=0.即(x1-x2)(x1-x3)+(y1-y2)(y1-y3)=0.所以(x1-x2)(x1-x3)+(x21-x22)(x21-x23)=(x1-x2)(x1-x3)1+(x1+x2)(x1+x3)[]=0.所以1+(x1+x2)(x1+x3)=0.即(x1+x2)(x1+x3)=-1.所以矩形ABCD的周长为2(AB+AD)=2((x1-x2)2+(y1-y2)2+(x1-x3)2+(y1-y3)2)=2[x1-x21+(x1+x2)2+x1-x31+1/(x1+x2)2]因为(x1+x2)(x1+x3)=-1ꎬ所以不妨设(x1+x2)2ɤ(x1+x3)2ꎬ所以2(AB+AD)ȡ21+(x1+x2)2(x1-x2+x1-x3)[]ꎬ当且仅当x2+x3=2x1时取等号.又根据a+bȡa-b(当且仅当abɤ0时取等号)ꎬ所以x1-x2+x1-x3ȡx2-x3=(x1+x2)-(x1+x3)=(x1+x2)+1(x1+x2).即2(AB+AD)ȡ21+(x1+x2)2(x1+x2)+1(x1+x2).令m=x1+x2ꎬ由(x1+x2)(x1+x3)=-1ꎬ可不妨设mɪ0ꎬ1(]ꎬ则2(AB+AD)ȡ21+m2m+1m.以下同解法3.3结束语不难发现ꎬ以上五种方法有一个共同的特点ꎬ就是都利用了不等式性质进行了放缩运算ꎬ达到了减少变量的目的ꎬ最后基本都变换为一个利用函数单调性求最值的问题.所以ꎬ遇到思维量较大的题目ꎬ我们一定要有明确的目标ꎬ有的放矢.参考文献:[1]丁益民ꎬ金鹏. 一 以贯之:高三专题复习的教学组织:以解析几何解题教学为例[J].数学通讯ꎬ2023(08):48-51ꎬ54.[责任编辑:李㊀璟]。
