浙江省三门县城关中学2014届九年级10月月考数学试题

合集下载

浙江省台州市三门县城关中学2015届中考数学模拟试题二(含解析)

浙江省台州市三门县城关中学2015届中考数学模拟试题二一．选择题（共10小题）1．﹣5的绝对值是（）A．B．5 C．﹣5 D．﹣2．函数中，自变量x的取值范围是（）A．x≠3 B．x≥3 C．x＞3 D．x≤33．已知一次函数y=kx+k﹣1和反比例函数y=，则这两个函数在同一平面直角坐标系中的图象不可能是（）A．B． C． D．4．二次函数的图象如图所示，当﹣1≤x≤0时，该函数的最大值是（）A．3.125 B．4 C．2 D．05．如图，一只花猫发现一只老鼠溜进了一个内部连通的鼠洞，鼠洞只有三个出口A，B，C，要想同时顾及这三个出口以防老鼠出洞，这只花猫最好蹲守在（）A．△ABC的三边高线的交点P处B．△ABC的三角平分线的交点P处C．△ABC的三边中线的交点P处D．△ABC的三边中垂线的交点P处6．北海到南宁的铁路长210千米，动车运行后的平均速度是原来火车的1.8倍，这样由北海到南宁的行驶时间缩短了1.5小时．设原来火车的平均速度为x千米/时，则下列方程正确的是（）A． +1.8=B．﹣1.8=C． +1.5=D．﹣1.5=7．正方形网格中，∠AOB如图放置，则cos∠AOB的值为（）A．B．C．D．8．如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=kx﹣3k+4与⊙O 交于B、C两点，则弦BC的长的最小值为（）A．22 B．24 C．10D．129．如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为（）A．3 B．4 C．5 D．610．一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是（）A．5：4 B．5：2 C．：2 D．：二．填空题（共6小题）11．因式分解：x3﹣xy2= ．12．正十边形的一个外角为度．13．有50个数据，共分成6组，第1～4组的频数分别为10，8，7，11．第5组的频率是0.16，则第6组的频数是．14．如图所示，半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动．且滚动至扇形O′A′B′处，则顶点O所经过的路线总长是．15．如图，直角坐标系中，点P（t，0）是x轴正半轴上的一个动点，过点P作y轴的平行线，分别与直线，直线y=﹣x交于A，B两点，以AB为边向右侧作正方形ABCD．当点（3，0）在正方形ABCD内部时，t的取值范围是．16．如图，在矩形ABCD中，AD=6，AB=4，点E、G、H、F分别在AB、BC、CD、AD上，且AF=CG=2，BE=DH=1，点P是直线EF、GH之间任意一点，连接PE、PF、PG、PH，则△PEF和△PGH的面积和等于．三．解答题（共7小题）17．计算：18．解方程：x2﹣5x﹣6=0．19．如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，其中点A（5，4），B（1，3），将△AOB绕点O逆时针旋转90°后得到△A1OB1．（1）画出△A1OB1；（2）在旋转过程中点B所经过的路径长为；（3）求在旋转过程中线段AB、BO扫过的图形的面积之和．20．如图，⊙O中，FG、AC是直径，AB是弦，FG⊥AB，垂足为点P，过点C的直线交AB的延长线于点D，交GF的延长线于点E，已知AB=4，⊙O的半径为．（1）分别求出线段AP、CB的长；（2）如果OE=5，求证：DE是⊙O的切线；（3）如果tan∠E=，求DE的长．21．在东西方向的海岸线l上有一长为1km的码头MN（如图），在码头西端M的正西19.5km处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°，且与A相距40km的B处；经过1小时20分钟，又测得该轮船位于A的北偏东60°，且与A相距km的C处．（1）求该轮船航行的速度（保留精确结果）；（2）如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸？请说明理由．22．我县实施新课程改革后，学生的自主字习、合作交流能力有很大提高．张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调査，并将调査结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调査结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：（1）本次调查中，张老师一共调査了名同学，其中C类女生有名，D类男生有名；（2）将上面的条形统计图补充完整；（3）为了共同进步，张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．23．如图，已知抛物线y=ax2+bx+c经过 A（0，4），B（4，0），C（﹣1，0）三点．过点A作垂直于y轴的直线l．在抛物线上有一动点P，过点P作直线PQ平行于y轴交直线l于点Q．连接AP．（1）求抛物线y=ax2+bx+c的解析式；（2）是否存在点P，使得以A、P、Q三点构成的三角形与△AOC相似？如果存在，请求出点P的坐标；若不存在，请说明理由；（3）当点P位于抛物线y=ax2+bx+c的对称轴的右侧．若将△APQ沿AP对折，点Q的对应点为点M．求当点M落在坐标轴上时直线AP的解析式．2015年浙江省台州市三门县城关中学中考数学模拟试卷（二）参考答案与试题解析一．选择题（共10小题） 1．﹣5的绝对值是（）A ．B ．5C ．﹣5D ．﹣【考点】绝对值．【分析】利用绝对值的定义求解即可．【解答】解：﹣5的绝对值是5，故选：B ．【点评】本题主要考查了绝对值，解题的关键是熟记绝对值的定义． 2．函数中，自变量x 的取值范围是（）A ．x≠3B ．x≥3C ．x ＞3D ．x≤3 【考点】函数自变量的取值范围．【分析】根据二次根式有意义的条件，即根号下大于等于0，求出即可．【解答】解：∵有意义的条件是：x ﹣3≥0．∴x≥3．故选：B ．【点评】此题主要考查了函数变量的取值范围，此题是中考考查重点，同学们应重点掌握，特别注意根号下可以等于0这一条件．3．已知一次函数y=kx+k ﹣1和反比例函数y=，则这两个函数在同一平面直角坐标系中的图象不可能是（）A ．B ．C ．D ．【考点】反比例函数的图象；一次函数的图象．【分析】因为k的符号不确定，所以应根据k﹣1的符号及一次函数与反比例函数图象的性质解答．【解答】解：当k＜0时，k﹣1＜0，反比例函数y=的图象在二，四象限，一次函数y=kx+k﹣1的图象过二、三、四象限，故选项C错误，符合题意；而选项D正确，不合题意；当k＞0时，k﹣1的符号不确定，则反比例函数y=的图象在一、三象限，一次函数y=kx+k﹣1的图象过一、三、四象限或一、二、三象限故选项A，B正确，不符合题意．故选C．【点评】本题主要考查了反比例函数和一次函数的图象性质，正确掌握它们的性质才能灵活解题．4．二次函数的图象如图所示，当﹣1≤x≤0时，该函数的最大值是（）A．3.125 B．4 C．2 D．0【考点】二次函数的最值．【分析】由图可知，x≤1.5时，y随x的增大而减小，可知在﹣1≤x≤0范围内，x=0时取得最大值，然后进行计算即可得解．【解答】解：∵x≤1.5时，y随x的增大而减小，∴当﹣1≤x≤0时，x=0取得最大值，为y=2．故选C．【点评】本题考查了二次函数的最值问题，主要利用了二次函数的增减性求最值，准确识图是解题的关键．5．如图，一只花猫发现一只老鼠溜进了一个内部连通的鼠洞，鼠洞只有三个出口A，B，C，要想同时顾及这三个出口以防老鼠出洞，这只花猫最好蹲守在（）A．△ABC的三边高线的交点P处B．△ABC的三角平分线的交点P处C．△ABC的三边中线的交点P处D．△ABC的三边中垂线的交点P处【考点】三角形的外接圆与外心．【专题】应用题；压轴题．【分析】根据题意，知猫应该到三个洞口的距离相等，则此点就是三角形三边垂直平分线的交点．【解答】解：三角形三边垂直平分线的交点到三个顶点的距离相等．故选D．【点评】考查了三角形的外心的概念和性质．要熟知三角形三边垂直平分线的交点到三个顶点的距离相等．6．北海到南宁的铁路长210千米，动车运行后的平均速度是原来火车的1.8倍，这样由北海到南宁的行驶时间缩短了1.5小时．设原来火车的平均速度为x千米/时，则下列方程正确的是（）A． +1.8=B．﹣1.8=C． +1.5=D．﹣1.5=【考点】由实际问题抽象出分式方程．【分析】设原来火车的平均速度为x千米/时，则动车运行后的平均速度为1.8x，根据题意可得：由北海到南宁的行驶时间动车比原来的火车少用1.5小时，列方程即可．【解答】解：设原来火车的平均速度为x千米/时，则动车运行后的平均速度为1.8x，由题意得，﹣1.5=．故选：D．【点评】本题考查了由实际问题抽象出分式方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列出方程．7．正方形网格中，∠AOB如图放置，则cos∠AOB的值为（）A．B．C．D．【考点】锐角三角函数的定义；勾股定理的逆定理．【专题】常规题型．【分析】找出OB边上的格点C，连接AC，利用勾股定理求出AO、AC、CO的长度，再利用勾股定理逆定理证明△AOC是直角三角形，然后根据余弦=计算即可得解．【解答】解：如图，C为OB边上的格点，连接AC，根据勾股定理，AO==2，AC==，OC==，所以，AO2=AC2+OC2=20，所以，△AOC是直角三角形，cos∠AOB===．故选B．【点评】本题考查了锐角三角函数的定义，勾股定理，勾股定理逆定理，找出格点C并作辅助线构造出直角三角形是解题的关键．8．如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=kx﹣3k+4与⊙O 交于B、C两点，则弦BC的长的最小值为（）A．22 B．24 C．10D．12【考点】圆的综合题．【分析】易知直线y=kx﹣3k+4过定点D（3，4），运用勾股定理可求出OD，由条件可求出半径OB，由于过圆内定点D的所有弦中，与OD垂直的弦最短，因此只需运用垂径定理及勾股定理就可解决问题．【解答】解：对于直线y=kx﹣3k+4，当x=3时，y=4，故直线y=kx﹣3k+4恒经过点（3，4），记为点D．过点D作DH⊥x轴于点H，则有OH=3，DH=4，OD==5．∵点A（13，0），∴OA=13，∴OB=OA=13．由于过圆内定点D的所有弦中，与OD垂直的弦最短，如图所示，因此运用垂径定理及勾股定理可得：BC的最小值为2BD=2=2×=2×12=24．故选：B．【点评】本题主要考查了直线上点的坐标特征、垂径定理、勾股定理等知识，发现直线恒经过点（3，4）以及运用“过圆内定点D的所有弦中，与OD垂直的弦最短”这个经验是解决该选择题的关键．9．如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为（）A．3 B．4 C．5 D．6【考点】反比例函数综合题．【专题】计算题．【分析】先设P（0，b），由直线AB∥x轴，则A，B两点的纵坐标都为b，而A，B分别在反比例函数的图象上，可得到A点坐标为（﹣，b），B点坐标为（，b），从而求出AB的长，然后根据三角形的面积公式计算即可．【解答】解：设P（0，b），∵直线AB∥x轴，∴A，B两点的纵坐标都为b，而点A在反比例函数y=﹣的图象上，∴当y=b，x=﹣，即A点坐标为（﹣，b），又∵点B在反比例函数y=的图象上，∴当y=b，x=，即B点坐标为（，b），∴AB=﹣（﹣）=，∴S△ABC=•AB•OP=•b=3．故选：A．【点评】本题考查了点在函数图象上，点的横纵坐标满足函数图象的解析式．也考查了与坐标轴平行的直线上的点的坐标特点以及三角形的面积公式．10．一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是（）A．5：4 B．5：2 C．：2 D．：【考点】正多边形和圆；勾股定理．【专题】计算题；压轴题．【分析】先画出图形，分别求出扇形和圆的半径，再根据面积公式求出面积，最后求出比值即可．【解答】解：如图1，连接OD，∵四边形ABCD是正方形，∴∠DCB=∠ABO=90°，AB=BC=CD=1，∵∠AOB=45°，∴OB=AB=1，由勾股定理得：OD==，∴扇形的面积是=π；如图2，连接MB、MC，∵四边形ABCD是⊙M的内接四边形，四边形ABCD是正方形，∴∠BMC=90°，MB=MC，∴∠MCB=∠MBC=45°，∵BC=1，∴MC=MB=，∴⊙M的面积是π×（）2=π，∴扇形和圆形纸板的面积比是π÷（π）=．故选：A．【点评】本题考查了正方形性质，圆内接四边形性质，扇形的面积公式的应用，解此题的关键是求出扇形和圆的面积，题目比较好，难度适中．二．填空题（共6小题）11．因式分解：x3﹣xy2= x（x﹣y）（x+y）．【考点】提公因式法与公式法的综合运用．【分析】先提取公因式x，再对余下的多项式利用平方差公式继续分解．【解答】解：x3﹣xy2=x（x2﹣y2）=x（x﹣y）（x+y）．故答案为：x（x﹣y）（x+y）．【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．12．正十边形的一个外角为36 度．【考点】多边形内角与外角．【分析】利用正十边形的外角和是360度，并且每个外角都相等，即可求出答案．【解答】解：正十边形的一个外角为360÷10=36度．【点评】本题主要考查了正多边形的性质：正多边形的各个外角相等，外角和是360度．13．有50个数据，共分成6组，第1～4组的频数分别为10，8，7，11．第5组的频率是0.16，则第6组的频数是 6 ．【考点】频数与频率．【分析】首先根据频率=频数÷数据总数求得第5组的频数，然后根据6个组的频数和等于数据总数即可求得第6组的频数．【解答】解：∵有50个数据，共分成6组，第5组的频率是0.16，∴第5组的频数为50×0.16=8；又∵第1～4组的频数分别为10，8，7，11，∴第6组的频数为50﹣（10+8+7+11+8）=6．故答案为：6．【点评】本题是对频率、频数灵活运用的综合考查，各小组频数之和等于数据总数，各小组频率之和等于1．频率、频数的关系：频率=频数÷数据总数．14．如图所示，半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动．且滚动至扇形O′A′B′处，则顶点O所经过的路线总长是π．【考点】弧长的计算；旋转的性质．【分析】仔细观察顶点O经过的路线可得，顶点O到O′所经过的路线可以分为三段，分别求出三段的长，再求出其和即可．【解答】解：顶点O经过的路线可以分为三段，当弧AB切直线l于点B时，有OB⊥直线l，此时O 点绕不动点B转过了90°；第二段：OB⊥直线l到OA⊥直线l，O点绕动点转动，而这一过程中弧AB始终是切于直线l的，所以O与转动点的连线始终⊥直线l，所以O点在水平运动，此时O点经过的路线长=BA′=AB的弧长；第三段：OA⊥直线l到O点落在直线l上，O点绕不动点A转过了90°．所以，O点经过的路线总长S=π+π+π=π．故答案是：．【点评】本题考查了旋转的性质，弧长的计算，根据题意，准确分析得到三段的运动过程是解题的关键．15．如图，直角坐标系中，点P（t，0）是x轴正半轴上的一个动点，过点P作y轴的平行线，分别与直线，直线y=﹣x交于A，B两点，以AB为边向右侧作正方形ABCD．当点（3，0）在正方形ABCD内部时，t的取值范围是＜t＜3 ．【考点】正方形的性质；一次函数图象上点的坐标特征．【分析】根据点P的横坐标表示出AB，由点C的横坐标大于3列出不等式求解即可．【解答】解：∵点P（t，0），AB∥y轴，∴点A（t， t），B（t，﹣t），∴AB=|t﹣（﹣t）|=|t|，∵t＞0时，点C的横坐标为t+t=t，∵点（2，0）在正方形ABCD内部，∴t＞3，且t＜3，解得t＞且t＜3，∴＜t＜3；故答案为：＜t＜3．【点评】本题是一次函数综合题型，主要利用了一次函数图象上点的坐标特征，正方形的性质；由点C的横坐标大于3列出不等式求解是解题的关键．16．如图，在矩形ABCD中，AD=6，AB=4，点E、G、H、F分别在AB、BC、CD、AD上，且AF=CG=2，BE=DH=1，点P是直线EF、GH之间任意一点，连接PE、PF、PG、PH，则△PEF和△PGH的面积和等于7 ．【考点】矩形的性质；平行四边形的判定与性质．【专题】计算题；压轴题．【分析】连接EG，FH，根据题目数据可以证明△AEF与△CGH全等，根据全等三角形对应边相等可得EF=GH，同理可得EG=FH，然后根据两组对边相等的四边形是平行四边形可得四边形EGHF是平行四边形，所以△PEF和△PGH的面积和等于平行四边形EGHF的面积的一半，再利用平行四边形EGHF 的面积等于矩形ABCD的面积减去四周四个小直角三角形的面积即可求解．【解答】解：∵在矩形ABCD中，AD=6，AB=4，AF=CG=2，BE=DH=1，∴AE=AB﹣BE=4﹣1=3，CH=CD﹣DH=4﹣1=3，∴AE=CH，在△AEF与△CGH中，，∴△AEF≌△CGH（SAS），∴EF=GH，同理可得，△BGE≌△DFH，∴EG=FH，∴四边形EGHF是平行四边形，∵△PEF和△PGH的高的和等于点H到直线EF的距离，∴△PEF和△PGH的面积和=×平行四边形EGHF的面积，平行四边形EGHF的面积=4×6﹣×2×3﹣×1×（6﹣2）﹣×2×3﹣×1×（6﹣2），=24﹣3﹣2﹣3﹣2，=14，∴△PEF和△PGH的面积和=×14=7．故答案为：7．【点评】本题考查了矩形的性质，平行四边形的判定与性质，作出辅助线并证明出四边形EGHF是平行四边形是解题的关键．三．解答题（共7小题）17．计算：【考点】实数的运算．【分析】本题涉及绝对值、负整数指数幂、特殊角的三角函数值、二次根式化简四个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．【解答】解：原式=2=．【点评】本题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算．18．解方程：x2﹣5x﹣6=0．【考点】解一元二次方程-因式分解法．【分析】把方程左边进行因式分解得到（x﹣6）（x+1）=0，则方程就可化为两个一元一次方程x﹣6=0，或x+1=0，解两个一元一次方程即可．【解答】解：x2﹣5x﹣6=0，∴（x﹣6）（x+1）=0，∴x﹣6=0或x+1=0，∴x1=6，x2=﹣1．【点评】本题考查了运用因式分解法解一元二次方程ax2+bx+c=0（a≠0）的方法：先把方程化为一般式，再把方程左边进行因式分解，然后一元二次方程就可化为两个一元一次方程，解两个一元一次方程即可．19．如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，其中点A（5，4），B（1，3），将△AOB绕点O逆时针旋转90°后得到△A1OB1．（1）画出△A1OB1；（2）在旋转过程中点B所经过的路径长为π；（3）求在旋转过程中线段AB、BO扫过的图形的面积之和．【考点】作图-旋转变换；勾股定理；弧长的计算；扇形面积的计算．【专题】作图题．【分析】（1）根据网格结构找出点A、B绕点O逆时针旋转90°后的对应点A1、B1的位置，然后顺次连接即可；（2）利用勾股定理列式求OB，再利用弧长公式计算即可得解；（3）利用勾股定理列式求出OA，再根据AB所扫过的面积=S扇形A1OA+S△A1B1O﹣S扇形B1OB﹣S△AOB=S扇形A1OA﹣S求解，再求出BO扫过的面积=S扇形B1OB，然后计算即可得解．扇形B1OB【解答】解：（1）△A1OB1如图所示；（2）由勾股定理得，BO==，所以，点B所经过的路径长==π；故答案为：π．（3）由勾股定理得，OA==，∵AB所扫过的面积=S扇形A1OA+S△A1B1O﹣S扇形B1OB﹣S△AOB=S扇形A1OA﹣S扇形B1OB，BO扫过的面积=S扇形B1OB，∴线段AB、BO扫过的图形的面积之和=S扇形A1OA﹣S扇形B1OB+S扇形B1OB，=S扇形A1OA，=，=π．【点评】本题考查了利用旋转变换作图，弧长公式，扇形的面积，勾股定理，熟练掌握网格结构准确找出对应点的位置是解题的关键，难点在于（3）表示出两线段扫过的面积之和等于扇形的面积．20．如图，⊙O中，FG、AC是直径，AB是弦，FG⊥AB，垂足为点P，过点C的直线交AB的延长线于点D，交GF的延长线于点E，已知AB=4，⊙O的半径为．（1）分别求出线段AP、CB的长；（2）如果OE=5，求证：DE是⊙O的切线；（3）如果tan∠E=，求DE的长．【考点】切线的判定．【专题】证明题．【分析】（1）根据圆周角定理由AC为直径得∠ABC=90°，在Rt△ABC中，根据勾股定理可计算出BC=2，再根据垂径定理由直径FG⊥AB得到AP=BP=AB=2；（2）易得OP为△ABC的中位线，则OP=BC=1，再计算出==，根据相似三角形的判定方法得到△EOC∽△AOP，根据相似的性质得到∠OCE=∠OPA=90°，然后根据切线的判定定理得到DE是⊙O 的切线；（3）根据平行线的性质由BC∥EP得到∠DCB=∠E，则tan∠DCB=tan∠E=，在Rt△BCD中，根据正切的定义计算出BD=3，根据勾股定理计算出CD=，然后根据平行线分线段成比例定理得=，再利用比例性质可计算出DE=．【解答】（1）解：∵AC为直径，∴∠ABC=90°，在Rt△ABC中，AC=2，AB=4，∴BC==2，∵直径FG⊥AB，∴A P=BP=AB=2；（2）证明∵AP=BP，AO=OC∴OP为△ABC的中位线，∴OP=BC=1，∴=，而==，∴=，∵∠EOC=∠AOP，∴△EOC∽△AOP，∴∠OCE=∠OPA=90°，∴OC⊥DE，∴DE是⊙O的切线；（3）解：∵BC∥EP，∴∠DCB=∠E，∴tan∠DCB=tan∠E=在Rt△BCD中，BC=2，tan∠DCB==，∴CD==，∵BC∥EP，∴=，即=，∴DE=．【点评】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了垂径定理、圆周角定理、勾股定理和相似三角形的判定与性质．21．在东西方向的海岸线l上有一长为1km的码头MN（如图），在码头西端M的正西19.5km处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°，且与A相距40km的B处；经过1小时20分钟，又测得该轮船位于A的北偏东60°，且与A相距km的C处．（1）求该轮船航行的速度（保留精确结果）；（2）如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸？请说明理由．【考点】解直角三角形的应用-方向角问题．【分析】（1）根据∠1=30°，∠2=60°，可知△ABC为直角三角形．根据勾股定理解答．（2）延长BC交l于T，比较AT与AM、AN的大小即可得出结论．【解答】解：（1）∵∠1=30°，∠2=60°，∴△ABC为直角三角形．∵AB=40km，AC=km，∴BC===16（km）．∵1小时20分钟=80分钟，1小时=60分钟，∴×60=12（千米/小时）．理由：作线段BR⊥AN于R，作线段CS⊥AN于S，延长BC交l于T．∵∠2=60°，∴∠4=90°﹣60°=30°．∵AC=8（km），∴CS=8sin30°=4（km）．∴AS=8cos30°=8×=12（km）．又∵∠1=30°，∴∠3=90°﹣30°=60°．∵AB=40km，∴BR=40•sin60°=20（km）．∴AR=40×cos60°=40×=20（km）．易得，△STC∽△RTB，所以=，，解得：ST=8（km）．所以AT=12+8=20（km）．又因为AM=19.5km，MN长为1km，∴AN=20.5km，∵19.5＜AT＜20.5故轮船能够正好行至码头MN靠岸．【点评】此题结合方向角，考查了阅读理解能力、解直角三角形的能力．计算出相关特殊角和作出辅助线构造相似三角形是解题的关键．22．我县实施新课程改革后，学生的自主字习、合作交流能力有很大提高．张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调査，并将调査结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调査结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：（1）本次调查中，张老师一共调査了20 名同学，其中C类女生有 2 名，D类男生有 1 名；（2）将上面的条形统计图补充完整；（3）为了共同进步，张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．【考点】条形统计图；扇形统计图；列表法与树状图法．【分析】（1）由扇形统计图可知，特别好的占总数的15%，人数有条形图可知3人，所以调查的样本容量是：3÷15%，即可得出C类女生和D类男生人数；（2）根据（1）中所求数据得出条形图的高度即可；（3）根据被调査的A类和D类学生男女生人数列表即可得出答案．【解答】解：（1）3÷15%=20，20×25%=5．女生：5﹣3=2，1﹣25%﹣50%﹣15%=10%，20×10%=2，男生：2﹣1=1，故答案为：20，2，1；（2）如图所示：（3）根据张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，可以将A类与D类学生分为以下几种情况：∴共有6种结果，每种结果出现可能性相等，∴两位同学恰好是一位男同学和一位女同学的概率为：P（一男一女）==．【点评】此题主要考查了条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．23．如图，已知抛物线y=ax2+bx+c经过 A（0，4），B（4，0），C（﹣1，0）三点．过点A作垂直于y轴的直线l．在抛物线上有一动点P，过点P作直线PQ平行于y轴交直线l于点Q．连接AP．（1）求抛物线y=ax2+bx+c的解析式；（2）是否存在点P，使得以A、P、Q三点构成的三角形与△AOC相似？如果存在，请求出点P的坐标；若不存在，请说明理由；（3）当点P位于抛物线y=ax2+bx+c的对称轴的右侧．若将△APQ沿AP对折，点Q的对应点为点M．求当点M落在坐标轴上时直线AP的解析式．【考点】二次函数综合题．【专题】计算题；压轴题．【分析】（1）将A（0，4），B（4，0），C（﹣1，0）分别代入抛物线y=ax2+bx+c，列出方程组，即可求出函数解析式．（2）当P在l下方时，令△AOC∽△AQP，△AOC∽△PQA，根据相似三角形的性质，列比例式，求出点的坐标；当P在l上方时，令△AOC∽△AQP，△AOC∽△PQA，根据相似三角形的性质，列比例式，求出点的坐标；（3）画出函数图形，利用三角形相似，求出P点坐标，再利用待定系数法求出函数解析式．【解答】解：（1）将A（0，4），B（4，0），C（﹣1，0）分别代入抛物线y=ax2+bx+c得，，解得，函数解析式为y=﹣x2+3x+4．（2）P在l下方时，令①△AOC∽△AQP，=，即，由于y=﹣x2+3x+4，则有=，解得x=0（舍去）或x=，此时，y=，P点坐标为（，）．②△AOC∽△PQA，，即，由于y=﹣x2+3x+4，则有，解得，x=0（舍去）或x=7，P点坐标为（7，﹣24）．③P在l上方时，令△AOC∽△PQA，，即，∵y=﹣x2+3x+4，∴，解得，x=0（舍去）或x=﹣1，P点坐标为（﹣1，0）（不合题意舍去）．④△AOC∽△AQP，=，即∴，解得，x=0（舍去）或x=，P点坐标为（，）．（3）如图（1），若对称点M在y轴，则∠PAQ=45°，设AP解析式为y=kx+b，则k=1或﹣1，当k=1时，把A（0，4）代入得y=x+4，当k=﹣1时，把A（0，4）代入得y=﹣x+4，此时P在对称轴右侧，符合题意，∴y=x+4，或y=﹣x+4，设点Q（x，4），P（x，﹣x2+3x+4），则PQ=x2﹣3x=PM，∵△AEM∽△MFP．则有=，∵ME=OA=4，AM=AQ=x，PM=PQ=x2﹣3x，∴=，解得：PF=4x﹣12，∴OM=（4x﹣12）﹣x=3x﹣12，Rt△AOM中，由勾股定理得OM2+OA2=AM2，∴（3x﹣12）2+42=x2，解得x1=4，x2=5，均在抛物线对称轴的右侧，故点P的坐标为（4，0）或（5，﹣6）．设一次函数解析式为y=kx+b，把（0，4）（4，0）分别代入解析式得，解得，函数解析式为y=﹣x+4．把（0，4）（5，﹣6）分别代入解析式得，解得，函数解析式为y=﹣2x+4．综上所述，函数解析式为y=x+4，y=﹣x+4，y=﹣2x+4．【点评】本题考查了二次函数解析式的求法、二次函数解析式、相似三角形的性质、翻折变换、待定系数法求一次函数解析式等，题目错综复杂，涉及知识面广，旨在考查逻辑思维能力．。

2014-2015年浙江省台州市三门县城关中学八年级上学期期中数学试卷和答案

2014-2015学年浙江省台州市三门县城关中学八年级（上）期中数学试卷一、选择题（本题有10小题，每小题3分，共30分）1．（3分）在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）A．B．C．D．2．（3分）下列图形中具有不稳定性的是（）A．长方形B．等腰三角形C．直角三角形D．锐角三角形3．（3分）小芳有两根长度为4cm和9cm的木条，他想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择的木条的长度只能是（）A．5 cm B．3 cmC．17 cm D．12 cm4．（3分）在直角坐标系中，点M（1，2）关于x轴对称的点的坐标为（）A．（﹣1，2）B．（2，﹣1）C．（﹣1，﹣2）D．（1，﹣2）5．（3分）如图，△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD 的面积是（）A．2 B．5 C．10 D．206．（3分）如图，AB∥DC，AB=DC，要使∠A=∠C，直接利用三角形全等的判定方法是（）A．AAS B．SAS C．ASA D．SSS7．（3分）小明在镜子里看到自己的像在用右手拿着梳子向左梳头，那么他实际是（）A．用右手向左梳头 B．用左手向右梳头C．用右手向右梳头 D．用左手向左梳头8．（3分）若n边形恰好有n条对角线，则n为（）A．4 B．5 C．6 D．79．（3分）如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，当∠A的位置及大小变化时，线段EF和BE+CF的大小关系（）A．EF＞BE+CF B．EF=BE+CF C．EF＜BE+CF D．不能确定10．（3分）如图，△ABC的中线BE与CD交于点G，连结DE，下列结论不正确的是（）A．点G叫做△ABC的重心B．S△ADC=2S△BDEC．S△BDG=S△CEG D．S△ABC=3S△ADE二、填空题（本题有6小题，每小题3分，共18分）11．（3分）一个外角和与内角和相等的多边形是．12．（3分）如图，如果直线m是多边形ABCDE的对称轴，其中∠A=130°，∠B=110°．那么∠BCD的度数等于度．13．（3分）如图，在△ABC中，∠ACB=90°，∠BAC=30°，在直线BC或AC上取一点P，使得△PAB为等腰三角形，这样的点P共有个．14．（3分）如图，在△ABC中，AB=AC，DE是AB的中垂线，△BCE的周长为14，BC=6，则AB的长为．15．（3分）已知△ABC的三边长a、b、c，化简|a+b﹣c|﹣|b﹣a﹣c|的结果是．16．（3分）如图是用黑白两种颜色的正六边形地砖，按规律拼成的若干个图案，按此规律请你写出：第5个图案中有白色地砖块；第n块图案中有白色地砖块．三、解答题（本题有8小题，第17～18题每题4分，第19～21题每题6分，第22，23题每题8分，第24题10分，共52分）17．（4分）如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：（用直尺画图）（1）画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1；（2）在DE上画出点Q，使△QAC的周长最小．18．（4分）已知等腰三角形底角的度数是顶角度数的三倍少15°，求这个等腰三角形顶角的度数．19．（6分）如图，已知∠ACB=∠ADB=90°，AC=AD，E在AB上，连接CE、DE （1）请你找出与点E有关的所有全等的三角形．（2）选择（1）中的一对全等三角形加以证明．20．（6分）如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°，求∠DAE的度数．21．（6分）如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．22．（8分）如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC．CF平分∠DCE．求证：（1）△ACD≌△BEC；（2）CF⊥DE．23．（8分）如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重叠部分；…；将余下部分沿∠B n A n C 的平分线A n B n+1折叠，点B n与点C重合，无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的好角．小丽展示了确定∠BAC是△ABC的好角的两种情况．情形一：如图2，沿等腰三角形△ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿△ABC的∠BAC的平分线AB1折叠，剪掉重叠部分；将余下的部分沿∠B1A1C 的平分线A1B2折叠，此时点B1与点C重合．探究发现：（1）△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？．（填“是”或“不是”）（2）小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B＞∠C）之间的等量关系．根据以上内容猜想：若经过n 次折叠∠BAC是△ABC的好角，则∠B与∠C不妨设∠B＞∠C）之间的等量关系为．应用提升：（3）小丽找到一个三角形，三个角分别为15°，60°，105°，发现60°和105°的两个角都是此三角形的好角，请你完成，如果一个三角形的最小角是18°，试直接写出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．24．（10分）学完“几何的回顾”一章后，老师布置了一道思考题：如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．求证：∠BQM=60度．（1）请你完成这道思考题；（2）做完（1）后，同学们在老师的启发下进行了反思，提出了许多问题，如：①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题？②若将题中的点M，N分别移动到BC，CA的延长线上，是否仍能得到∠BQM=60°？③若将题中的条件“点M，N分别在正三角形ABC的BC，CA边上”改为“点M，N 分别在正方形ABCD的BC，CD边上”，是否仍能得到∠BQM=60°？…请你作出判断，在下列横线上填写“是”或“否”：①；②；③．并对②，③的判断，选择一个给出证明．2014-2015学年浙江省台州市三门县城关中学八年级（上）期中数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分）1．（3分）在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）A．B．C．D．【解答】解：A、是轴对称图形，故A符合题意；B、不是轴对称图形，故B不符合题意；C、不是轴对称图形，故C不符合题意；D、不是轴对称图形，故D不符合题意．故选：A．2．（3分）下列图形中具有不稳定性的是（）A．长方形B．等腰三角形C．直角三角形D．锐角三角形【解答】解：等腰三角形，直角三角形，锐角三角形都具有稳定性，长方形不具有稳定性．故选：A．3．（3分）小芳有两根长度为4cm和9cm的木条，他想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择的木条的长度只能是（）A．5 cm B．3 cmC．17 cm D．12 cm【解答】解：设木条的长度为lcm，则9﹣4＜l＜9+4，即5＜l＜13．故选：D．4．（3分）在直角坐标系中，点M（1，2）关于x轴对称的点的坐标为（）A．（﹣1，2）B．（2，﹣1）C．（﹣1，﹣2）D．（1，﹣2）【解答】解：点M（1，2）关于x轴对称的点的坐标为：（1，﹣2）．故选：D．5．（3分）如图，△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD 的面积是（）A．2 B．5 C．10 D．20【解答】解：过D作DE⊥AB于E，∵∠C=90°，∴DC⊥AC，∵AD平分∠BAC，CD=2，∴CD=DE=2，∴S=×AB×DE=×5×2=5，△ABD故选：B．6．（3分）如图，AB∥DC，AB=DC，要使∠A=∠C，直接利用三角形全等的判定方法是（）A．AAS B．SAS C．ASA D．SSS【解答】解：∵AB∥∥DC，∴∠ABD=∠CDB，在△ABD和△CDB中∵，∴△ABD≌△CDB（SAS），∴∠A=∠C．故选：B．7．（3分）小明在镜子里看到自己的像在用右手拿着梳子向左梳头，那么他实际是（）A．用右手向左梳头 B．用左手向右梳头C．用右手向右梳头 D．用左手向左梳头【解答】解：根据镜面对称的性质，当你面对镜子的时候，右手拿着梳子向左梳头，对于镜子中的像来说是左手拿着梳子，向右梳头．故选：B．8．（3分）若n边形恰好有n条对角线，则n为（）A．4 B．5 C．6 D．7【解答】解：依题意有=n，n（n﹣5）=0，解得n=0（不合题意舍去）或n=5．故选：B．9．（3分）如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，当∠A的位置及大小变化时，线段EF和BE+CF的大小关系（）A．EF＞BE+CF B．EF=BE+CF C．EF＜BE+CF D．不能确定【解答】解：由BD平分∠ABC得，∠EBD=∠ABC，∵EF∥BC，∴∠AEF=∠ABC=2∠EBD，∠AEF=∠EBD+∠EDB，∴∠EBD=∠EDB，∴△BED是等腰三角形，∴ED=BE，同理可得，DF=FC，（△CFD是等腰三角形）∴EF=ED+EF=BE+FC，∴EF=BE+CF．故选：B．10．（3分）如图，△ABC的中线BE与CD交于点G，连结DE，下列结论不正确的是（）A．点G叫做△ABC的重心B．S△ADC=2S△BDEC．S△BDG=S△CEG D．S△ABC=3S△ADE【解答】解：∵△ABC的中线BE与CD交于点G，∴G是△ABC的重心，故（A）正确；∵△ABC的中线BE与CD交于点G，=S△ADC=S△ABC，S△BDE=S△ABE，∴S△ABE=2S△BDE，故（B）正确；∴S△ADC∵△ABC的中线BE与CD交于点G，∴DE是△ABC的中位线，∴DE∥BC，DE=BC，=S△BCE，∴S△BCD∴S=S△CEG，故（C）正确；△BDG∵DE∥BC，∴△ADE∽△ABC，∴=，=4S△ADE，故（D）错误；∴S△ABC故选：D．二、填空题（本题有6小题，每小题3分，共18分）11．（3分）一个外角和与内角和相等的多边形是四边形．【解答】解：设多边形的边数为n，根据题意得（n﹣2）•180°=360°，解得n=4．故答案是：四边形．12．（3分）如图，如果直线m是多边形ABCDE的对称轴，其中∠A=130°，∠B=110°．那么∠BCD的度数等于60度．【解答】解：把AE与直线m的交点记作F，∵在四边形ABCF中，∠A=130°，∠B=110°，且直线m是多边形的对称轴；∴∠BCD=2∠BCF=2×（360°﹣130°﹣110°﹣90°）=60°．故填60°．13．（3分）如图，在△ABC中，∠ACB=90°，∠BAC=30°，在直线BC或AC上取一点P，使得△PAB为等腰三角形，这样的点P共有6个．【解答】解：如图，①AB的垂直平分线交AC一点P 1（PA=PB），交直线BC于点P2；②以A为圆心，AB为半径画圆，交AC有二点P3，P4，交BC有一点P2，（此时AB=AP）；③以B为圆心，BA为半径画圆，交BC有二点P5，P2，交AC有一点P6（此时BP=BA）．故符合条件的点有6个．故答案为：6．14．（3分）如图，在△ABC中，AB=AC，DE是AB的中垂线，△BCE的周长为14，BC=6，则AB的长为8．【解答】解：∵DE是AB的中垂线∴AE=BE，∵△BCE的周长为14∴BC+CE+BE=BC+CE+AE=BC+AC=14∵BC=6∴AC=8∴AB=AC=8．故填8．15．（3分）已知△ABC的三边长a、b、c，化简|a+b﹣c|﹣|b﹣a﹣c|的结果是2（b﹣c）．【解答】解：∵△ABC的三边长分别是a、b、c，∴a+b＞c，b﹣a＜c，∴a+b﹣c＞0，b﹣a﹣c＜0，∴|a+b﹣c|﹣|b﹣a﹣c|=a+b﹣c﹣（﹣b+a+c）=a+b﹣c+b﹣a﹣c=2（b﹣c）；故答案为：2（b﹣c）16．（3分）如图是用黑白两种颜色的正六边形地砖，按规律拼成的若干个图案，按此规律请你写出：第5个图案中有白色地砖22块；第n块图案中有白色地砖4n+2块．【解答】解：第一个图形中有6块白色地砖；第二个图形中有6+4=10块白色地砖；第三个图形中有6+2×4=14块白色地砖；第4个图形中有6+3×4=18块白色地砖；第5个图形中有6+4×4=22块白色地砖；…第n个图形中有6+（n﹣1）×4=4n+2块白色地砖．故答案为：22，4n+2．故答案为：18，4n+2．三、解答题（本题有8小题，第17～18题每题4分，第19～21题每题6分，第22，23题每题8分，第24题10分，共52分）17．（4分）如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：（用直尺画图）（1）画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1；（2）在DE上画出点Q，使△QAC的周长最小．【解答】解：（1）所作图形如图所示：（2）如图所示：利用轴对称图形的性质可得点C关于直线DE的对称点C1，连接AC1，交直线DE于点Q，点Q即为所求，此时△QAC的周长最小．18．（4分）已知等腰三角形底角的度数是顶角度数的三倍少15°，求这个等腰三角形顶角的度数．【解答】解：设顶角为x度，则底角为（3x﹣15）°，则：3x﹣15+3x﹣15+x=180，解得：x=30，所以这个等腰三角形顶角的度数是30°．19．（6分）如图，已知∠ACB=∠ADB=90°，AC=AD，E在AB上，连接CE、DE （1）请你找出与点E有关的所有全等的三角形．（2）选择（1）中的一对全等三角形加以证明．【解答】（1）△ACE≌△ADE，△BCE≌△BDE；（2）在RT△ABC和RT△ABD中，，∴△ABC≌△ABD（HL），∴∠CAB=∠DAB，在△ACE和△ADE中，，∴△ACE≌△ADE（SAS）．20．（6分）如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°，求∠DAE的度数．【解答】解：在△ABC中∠BAC=180﹣∠B﹣∠C=80°，又∵AE平分∠BAC，∴∠EAC=40°，在直角△ACD中，∠DAC=90﹣∠C=60°，∴∠DAE=∠DAC﹣∠EAC=20°．21．（6分）如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．【解答】证明：连接AF，（1分）∵AB=AC，∠BAC=120°，∴∠B=∠C==30°，（1分）∵AC的垂直平分线EF交AC于点E，交BC于点F，∴CF=AF（线段垂直平分线上的点到线段两端点的距离相等），∴∠FAC=∠C=30°（等边对等角），（2分）∴∠BAF=∠BAC﹣∠FAC=120°﹣30°=90°，（1分）在Rt△ABF中，∠B=30°，∴BF=2AF（在直角三角形中，30°角所对的直角边等于斜边的一半），（1分）∴BF=2CF（等量代换）．22．（8分）如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC．CF平分∠DCE．求证：（1）△ACD≌△BEC；（2）CF⊥DE．【解答】证明：（1）∵AD∥BE，∴∠A=∠B，在△ACD和△BEC中∴△ACD≌△BEC（SAS），（2）∵△ACD≌△BEC，∴CD=CE，又∵CF平分∠DCE，∴CF⊥DE．23．（8分）如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重叠部分；…；将余下部分沿∠B n A n C 的平分线A n B n+1折叠，点B n与点C重合，无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的好角．小丽展示了确定∠BAC是△ABC的好角的两种情况．情形一：如图2，沿等腰三角形△ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿△ABC的∠BAC的平分线AB1折叠，剪掉重叠部分；将余下的部分沿∠B1A1C 的平分线A1B2折叠，此时点B1与点C重合．探究发现：（1）△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？是．（填“是”或“不是”）（2）小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B＞∠C）之间的等量关系∠B=3∠C．根据以上内容猜想：若经过n 次折叠∠BAC是△ABC的好角，则∠B与∠C不妨设∠B＞∠C）之间的等量关系为∠B=n∠C．应用提升：（3）小丽找到一个三角形，三个角分别为15°，60°，105°，发现60°和105°的两个角都是此三角形的好角，请你完成，如果一个三角形的最小角是18°，试直接写出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．【解答】解：（1）△ABC中，∠B=2∠C，经过两次折叠，∠BAC是△ABC的好角；理由如下：小丽展示的情形二中，∵沿∠BAC的平分线AB1折叠，∴∠B=∠AA1B1；又∵将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合，∴∠A1B1C=∠C；∵∠AA1B1=∠C+∠A1B1C（外角定理），∴∠B=2∠C；故答案是：是；（2）∠B=3∠C；在△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C 的平分线A1B2折叠，剪掉重复部分，将余下部分沿∠B2A2C的平分线A2B3折叠，点B2与点C重合，则∠BAC是△ABC的好角．证明如下：∵根据折叠的性质知，∠B=∠AA1B1，∠C=∠A2B2C，∠A1B1C=∠A1A2B2，∴根据三角形的外角定理知，∠A1A2B2=∠C+∠A2B2C=2∠C；∵根据四边形的外角定理知，∠BAC+∠B+∠AA1B1﹣∠A1B1C=∠BAC+2∠B﹣2C=180°，根据三角形ABC的内角和定理知，∠BAC+∠B+∠C=180°，∴∠B=3∠C；由小丽展示的情形一知，当∠B=∠C时，∠BAC是△ABC的好角；由小丽展示的情形二知，当∠B=2∠C时，∠BAC是△ABC的好角；由小丽展示的情形三知，当∠B=3∠C时，∠BAC是△ABC的好角；故若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为∠B=n∠C；故答案为：∠B=3∠C；∠B=n∠C（3）由（2）知，∠B=n∠C，∠BAC是△ABC的好角，因为最小角是18°是△ABC的好角，根据好角定义，则可设另两角分别为18m°，18mn°（其中m、n都是正整数）．由题意，得18m+18mn+18=180，所以m（n+1）=9．因为m、n都是正整数，所以m与n+1是9的整数因子，因此有：m=1，n+1=9；m=3，n+1=3；所以m=1，n=8；m=3，n=2；所以18m=18°，18mn=144°；18m=54°，18mn=108°．所以该三角形的另外两个角的度数分别为：18°，144°；54°，108°；24．（10分）学完“几何的回顾”一章后，老师布置了一道思考题：如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．求证：∠BQM=60度．（1）请你完成这道思考题；（2）做完（1）后，同学们在老师的启发下进行了反思，提出了许多问题，如：①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题？②若将题中的点M，N分别移动到BC，CA的延长线上，是否仍能得到∠BQM=60°？③若将题中的条件“点M，N分别在正三角形ABC的BC，CA边上”改为“点M，N 分别在正方形ABCD的BC，CD边上”，是否仍能得到∠BQM=60°？…请你作出判断，在下列横线上填写“是”或“否”：①是；②是；③否．并对②，③的判断，选择一个给出证明．【解答】（1）证明：在△ABM和△BCN中，，∴△ABM≌△BCN（SAS），∴∠BAM=∠CBN，∴∠BQM=∠BAQ+∠ABQ=∠MBQ+∠ABQ=60°．（2）①是；②是；③否．②的证明：如图，在△ACM和△BAN中，，∴△ACM≌△BAN（SAS），∴∠AMC=∠BNA，∴∠NQA=∠NBC+∠BMQ=∠NBC+∠BNA=180°﹣60°=120°，∴∠BQM=60°．③的证明：如图，在Rt△ABM和Rt△BCN中，，∴Rt△ABM≌Rt△BCN（SAS），∴∠AMB=∠BNC．又∵∠NBM+∠BNC=90°，∴∠QBM+∠QMB=90°，∴∠BQM=90°，即∠BQM≠60°．赠送初中数学几何模型【模型一】“一线三等角”模型：图形特征：60°60°60°45°45°45°运用举例：1.如图，若点B 在x 轴正半轴上，点A (4，4)、C (1，－1)，且AB ＝BC ，AB ⊥BC ，求点B 的坐标；2.如图，在直线l 上依次摆放着七个正方形（如图所示），已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ，则14S S += ．ls 4s 3s 2s 13213. 如图，Rt △ABC 中，∠BAC =90°，AB =AC =2，点D 在BC 上运动（不与点B ，C 重合），过D 作∠ADE =45°，DE 交AC 于E ．（1）求证：△ABD ∽△DCE ；（2）设BD =x ，AE =y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围；（3）当△ADE 是等腰三角形时，求AE 的长．B4.如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0)。

2014年九年级数学第三次月考试卷

2014年九年级数学第三次月考试卷一、细心选一选。

（每小题3分，共42分）1．下列各图中，是中心对称图形的是（）2．下列事件中是必然事件的为（）。

A ．打开电视，正在播放《新闻联播》节目。

B ．三角形任意两边之和大于第三边。

C ．在一个装着白球和黑球的袋中摸球，摸出红球。

D ．某种彩票中奖率是1%，买这种彩票100张一定会中奖。

3．已知⊙O 的半径是5cm,圆心O 到直线L 的距离是3cm,则直线L 与⊙O 的位置关系是（）。

A ．相交 B ．相切 C ．相离 D ．以上答案都不是 4．教练对小明推铅球的录像进行技术分析，发现铅球行进高度y （m ）与水平距离x （m ）之间的关系为，由此可知铅球推出的距离是（）5．如果一个扇形的弧长是34π，半径是6，那么此扇形的圆心角为（）。

A ．40° B ．45° C ．60° D ．80°6．抛物线y=x 2的图象向左平移2个单位，再向下平移1个单位，则所得抛物线的解析式为（）A.y=x 2+4x+3B. y=x 2+4x+5C. y=x 2－4x+3D.y=x 2－4x －57．下列二次函数中，图象以直线x=2为对称轴、且经过点（0，1）的是 A ．2y (x 21=-+）B ．2y (x+21=+）C ．2y (x 23=--）D ．2y (x+23=-）8．已知1=x 是方程022=++ax x 的一个根，则方程的另一个根为（）。

A ．2B ． 2-C ．3D ．3-9．若关于x 的一元二次方程022=+-m x x 有两个不相等的实数根，则m 的取值范围是（）。

A ．1-<mB ． 1<mC ．1->mD ．1>m10．如图，点A ，B ，C 在⊙O 上，∠A=50°，则∠BOC 的度数为（）。

A ．40°B ．50°C ．80°D ．100° 11．如图，将△ABC 绕点A 逆时针旋转一定角度，得到△ADE ．若∠CAE=65°，∠E=70°，且AD ⊥BC ，∠BAC 的度数为（）。

2013-2014学年九年级数学第一学期10月月考试卷 (新人教版第53套)

浙江省三门县城关中学2013-2014学年第一学期10月月考九年级数学试卷考生须知：1．全卷满分150分，考试时间120分钟．试题卷共4页，有三大题，共24小题。

2．全卷答案必须做在答题卷的相应位置上，做在试题卷上无效. 3. 考试时不能使用计算器。

温馨提示：请仔细审题，细心答题，答题前仔细阅读答题纸上的“注意事项”。

一、选择题（本大题有10小题，每小题4分，共40分．请选出各题中唯一的正确选项，不选、多选、错选，均不得分）1．下列计算正确的是 ( ▲ ) A ．16= ±4Ｂ．24÷ 6= 4Ｃ． 2 +3= 5 Ｄ．D ．32×6=22. 若2=x 是关于x 的一元二次方程082=+-mx x 的一个解,则m 的值是 ( ▲ )A. 6 B . 6- C. 5 D . 23．已知x ＜1，则122+-x x 的化简的结果是 ( ▲ ) A ．x －1 B ．x ＋1 C ．1－x D ．－x －14. 对右图的对称性表述，正确的是（ ▲ ）A 、轴对称图形B 、中心对称图形C 、既是轴对称图形又是中心对称图形D 、既不是轴对称图形又不是中心对称图形5. 下列一元二次方程中，两个实数根的和是- 2的是 ( ▲ )A ．0232=-+x xB ．0322=+-x xC ．0322=++x xD ．0322=-+x x6. 已知点P （0,-3）与点Q(2a+b,a+2b)关于原点对称，则ab 的值为 ( ▲ )A.2B.-2C. 0.5D. -0.57.如图，数轴上A ，B 两点表示的数分别为－1和3，点B 关于点A 的对称点为C ，则点C 所表示的数为 ( ▲ )8．化简xx x 13--- 的结果是 ( ▲ ) A ．－2－3B ．－1－3C ．－2＋3D ．1＋3A. x x --)1(B. x x --)1(C. x x )1(+-D. x x )1(- 9．如图，在△ABC 中，∠CAB ＝70°.在同一平面内，将△ABC 绕点A 旋转到△A ′B ′C 的位置，使得CC ′∥AB ，则∠BAB ′＝ ( ▲ ) A ．30° B ．35° C ．40° D ．50° 10.定义新运算“※”如下：当a ≥b 时，a ※b=ba a +, 当a ＜b 时，a ※b=b aa -，若(2x-1)※(x+2)=0,则x 的值为 ( ▲ ) A ．,21,321=-=x x B ．21,121=-=x xC ． 1,21,3321-==-=x x x D ．以上答案均不正确二、填空题（本大题有6小题，每题5分，共30分） 11．函数41-=x y 中自变量x 的取值范围是 ▲ ．12.一元二次方程x 2=2x 的解是 ▲ ．方程x ＋6＝x 的根是 ▲ ． 13. 某校九年级学生毕业时，每个同学都将自己的相片向全班其他同学各送一张留作纪念，全班共送了2070张相片，如果全班有x 名学生，根据题意，列出方程为 ▲ ． 14．已知关于x的一元二次方程210x --=有实数根，则k 的取值范围是 ▲ ． 15．在直角梯形ABCD 中，AD ∥BC ，∠B ＝90°，AD ＝2，BC ＝4，以点D 为旋转中心将腰DC 逆时针旋转90°至DE ，连接AE ，则△ADE 的面积为 ▲ .16．如图，在标有刻度的直线l 上，从点A 开始，以AB ＝1为直径画半圆，记为第1个半圆；以BC ＝2为直径画半圆，记为第2个半圆；以CD ＝4为直径画半圆，记为第3个半圆；以DE ＝8为直径画半圆，记为第4个半圆，…按此规律，继续画半圆，则第4个半圆的面积是第3个半圆面积的 ▲ 倍，第n 个半圆的面积为▲ (结果保留π)．三、解答题（本大题有8小题，第17～19题每题8分，第20～22题每题10分，第23题12分，第24题14分，共80分） 17.（本题8分）（1）计算：()1214.3313--+π （2）已知32,32-=+=b a ，试求22ab b a +的值.18.（本题8分）解方程①2210x x --= ②02323=+-x x x19. （本题8分）如图，在边长为1的正方形组成的网格中建立直角坐标系，△AOB 的顶点均在格点上，点O 为原点，点A 、B 的坐标分别是A （3，2）、B （1，3）。

城关中学2014.答题卡doc

城关中学2014---2015学年度第一学期九年级中考班第一次测试答卷（满分150分，考试时间120分钟）一、选择题、（本题共10小题，每小题3分，满分30分）小题 1 2 3 4 5 6 7 8 9 10 答案二、填空题：（本大题共8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上.11、_______________________； 12、______________________; 13、________________________; 1 4、_______________________;15、________________________; 1 6、_______________________;17、_______________________; 18、_______________________.三、解答题：（本大题共9个小题，，共88分）解答时每小题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上.19．（6分）计算：()12614201434-⎪⎭⎫ ⎝⎛+-⨯--+20．（8分）先化简，再求值：11121122++⎪⎪⎭⎫ ⎝⎛---+÷x x x x x x ，其中x 的值为方程152-=x x 的解.21．( 8分）如图，解：（1）（2）22、（本题10分）如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E.（1）求证：△ACD≌△AED；（2）若∠B=30°，CD=1，求BD的长。

23．（10分）（1）本次调查活动的样本容量是；（2）调查中属于“基本了解”的市民有人；（3）补全条形统计图；（4）“略有知晓”类占扇形统计图的圆心角是多少度？“知之甚少”类市民占被调查人数的百分比是多少？ 24、（10分）“六·一”儿童节前，某玩具商店根据市场调查，用2500元购进一批儿童玩具，上市后很快脱销，接着又用4500元购进第二批这种玩具，所购数量是第一批数量的1.5倍，但每套进价多了10元。

2014届全国名校数学试题解析汇编专题(9)三角形(解析版)

一、选择题1．【温州市七校2013-2014学年上学期12月联考九年级数学试题】如图，点D在△ABC的边BC上，过点D作DF∥AB，交AC于点E，连结BF，已知BD：DC＝1：2，DE：EF＝1：3，则S△ABC：S△BDF ＝…（）A．3：2 B. 4：3 C. 6：5 D. 9：82．【衢州市衢江区2013-2014学年第一学期九年级第三次联考数学试题】已知在Rt△ABC中，∠C=90°，∠A=α，AC=3，那么AB的长为（）A．3sinα B．3cosα C．3cosαD．3sinα【答案】C 【解析】试题分析：如解析图cosα=3ACAB AB=,所以AB=考点：锐角三角函数3．【云南省临沧区云县后箐中学2014届九年级10月综合练习数学试题】已知1sin A2，则锐角A的度数是（）A．30° B．45° C．60° D．75°4 【云南省临沧区云县后箐中学2014届九年级10月综合练习数学试题】已知△ABC∽△DEF，且AB:DE = 1:2，△AB C的周长与△DEF的周长之比为（）A．2:1 B．1:2 C．1:4 D． 4:15．【浙江省金华市聚仁教育集团2014九年级上学期第二阶段考试数学试题】夏季的一天，身高为1.6m 的小玲想测量一下屋前大树的高度，她沿着树影BA由B到A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m，CA=0.8m，于是得出树的高度为( )A．8m B．6.4m C．4.8m D．10m【答案】A.【解析】试题分析：因为人和树均垂直于地面，所以和光线构成的两个直角三角形相似，设树高x米，则AC 1.6=AB x，即0.8 1.6=0.8+3.2x，解得，x=8. 故选A.考点：相似三角形的应用.6．【浙江省金华市聚仁教育集团2014九年级上学期第二阶段考试数学试题】已知△ABC∽△DEF，若△ABC与△DEF的相似比为3∶4，则△ABC与△DEF的面积比为()A．4∶3 B．3∶4 C．16∶9 D．9∶167．【浙江省三门县城关中学2013-2014学年第一学期10月月考九年级数学试卷】如图，在△ABC中，∠CAB＝70°.在同一平面内，将△ABC绕点A旋转到△A′B′C的位置，使得CC′∥AB，则∠BAB′＝( ▲ )A．30° B．35° C．40° D．50°考点：1.旋转的性质；2.三角形全等的性质；3.等腰三角形的性质；4.三角形内角和定理. 8．【浙江省三门县城关中学2013-2014学年第一学期10月月考九年级数学试卷】在直角梯形ABCD 中，AD∥BC，∠B＝90°，AD＝2，BC＝4，以点D为旋转中心将腰DC逆时针旋转90°至DE，连接AE，则△ADE的面积为▲ .5. 【江西省新干县思源实验学校第一学期初中八年级期中考试数学试题】满足下列条件的三角形中，不是直角三角形的是（）A.三内角之比为1∶2∶3B.三边长的平方之比为1∶2∶3C.三边长之比为3∶4∶5D.三内角之比为3∶4∶5【答案】D【解析】9. 【江西省新干县思源实验学校第一学期初中八年级期中考试数学试题】已知直角三角形两边的长分别为3和4，则此三角形的周长为（）A．12 B．7＋7C．12或7＋7D．以上都不对10.【江西省新干县思源实验学校第一学期初中八年级期中考试数学试题】在∆ABC中，AB=10cm，AC=17cm，BC边上的高为8cm，则∆ABC的面积为（）A. 84B. 36C. 36或84D. 无法确定考点：勾股定理．11.【广东省温州地区2013-2014学年八年级上学期第三次月考数学试卷】如图，△ABC中，∠ABC 与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE；③△ADE的周长等于AB与AC的和；④BF=CF．其中有（）A．①②③ B．①②③④ C．①② D．①12. 【江西省新干县思源实验学校第一学期初中八年级期中考试数学试题】如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2 m，梯子的顶端B到地面的距离为7 m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m，同时梯子的顶端B 下降至B′，那么BB′（）A．小于1m B．大于1mC．等于1m D．小于或等于1m考点：勾股定理的应用.13. 【江西省新干县思源实验学校第一学期初中八年级期中考试数学试题】将一根24 cm的筷子置于底面直径为15 cm，高为8 cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度为h cm，则h的取值范围是（）A．h≤17 B．h≥8 C．15≤h≤16 D．7≤h≤1614.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】下列几组线段能组成三角形的是（）A ．3cm，5cm，8cm B．8cm，8cm，18cmC．0.1cm，0.1cm，0.1cm D．3cm，4cm，8cm15.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】下列各图中，正确画出AC边上的高的是（）A B C D16.【广东省温州地区2013-2014学年八年级上学期第三次月考数学试卷】下列判断正确的是（）A 有一直角边相等的两个直角三角形全等B 腰相等的两个等腰三角形全等C 斜边相等的两个等腰直角三角形全等D 两个锐角对应相等的两个直角三角形全等17.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】适合条件∠A=∠B=∠C的三角形是（）A．锐角三角形 B．直角三角形C．钝角三角形 D．都有可能18.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】下列说法中正确的是（）A．两个直角三角形全等 B．两个等腰三角形全等C．两个等边三角形全等 D．两条直角边对应相等的直角三角形全等D【答案】19.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（）A. CB=CDB.．∠BAC=∠DACC.．∠BCA=∠DCAD.．∠B=∠D=90°20.【江西省新干县思源实验学校第一学期初中八年级期中考试数学试题】下列4组数中，不能构成直角三角形的是（）A. 20，21，29B. 16，28，34C. 3a，4a，5a（a>0）D. 5，12，13B、22+（ 5 ）2=9=32，故是直角三角形，不符合题意；C、42+52=41≠72，故不是直角三角形，符合题意；C、12+（ 2 ）2=（ 3 ）2，故是直角三角形，不符合题意．故选C．考点：勾股定理的逆定理21.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】下列命题中：（1）形状相同的两个三角形是全等形；（2）在两个全等三角形中，相等的角是对应角，相等的边是对应边；（3）全等三角形对应边上的高、中线及对应角平分线分别相等，其中真命题的个数有（）A.．3个B.．2个 C． 1个D． 0个22.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（）去．A．① B．② C.．③ D.．①和②二、填空题：23.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】如图，共有______个三角形．24.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】如图，△ABC的一个外角等于120°，∠B=40°，则∠C的度数是_______．25.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）】如图，若△ABC≌△A1B1C1，且∠A=110°，∠B=40°，则∠C1=________度．考点：(1)三角形内角和。

2014届全国名校数学试题解析汇编专题(4)图形的变换(解析版)

一．选择题1【江苏省泰兴市济川中学初三数学阶段试题】下列图形中，既是轴对称图形又是中心对称图形的有()A.4个B. 3个C. 2个D. 1个2【湛师附中、东方实验学校2013-2014学年度上学期第一次月考九年级数学试题】下列图形中，是中心对称图形的是（）3.【湛师附中、东方实验学校2013-2014学年度上学期第一次月考九年级数学试题】下列图形中，对称轴最多的是（）A ．等边三角形B ．矩形C ．正方形D ．圆4.【湛师附中、东方实验学校2013-2014学年度上学期第一次月考九年级数学试题】点M （3，2-）关于原点对称的对称点的坐标是（）A.（3-，2）B.（3，2）C.（3-，2-）D.（2，3）5 【温州市七校2013-2014学年上学期12月联考九年级数学试题】按如下方法，将△ABC 的三边缩小到原来的21，如图，任取一点O ，连接AO 、BO 、CO ，并取它们的中点D 、E 、F ，得到△DEF，则下列说法错误的是（）A.△ABC 与△DEF 是位似图形B.△ABC 与△DEF 是相似图形C.△ABC 与△DEF 的面积之比为4:1D.△ABC 与△DEF 的周长之比为1:2考点：位似图形的性质.6.【湛师附中、东方实验学校2013-2014学年度上学期第一次月考九年级数学试题】某几何体的三视图如图2所示，那么该几何体是（）A．棱柱 B．圆锥 C．圆柱 D．长方体7 【云南省临沧区云县后箐中学2014届九年级10月综合练习数学试题】如图，A、B、C三点在正方形网格线的交点处.若将△ACB绕着点A逆时针旋转得到△AC′B′，则tan B′的值为( )A．14B．13C．12D．1【答案】B.【解析】试题分析：如图，过C点作CD⊥AB，垂足为D，根据旋转性质可知，∠B′=∠B．8.【云南省临沧区云县后箐中学2014届九年级10月综合练习数学试题】直角三角形纸片的两直角边长分别为6，8，现将△ABC 如图那样折叠，使点A 与点B 重合，折痕为DE ，则tan∠CBE 的值是（）A ．247BC ．724D ．139.【北京市海淀区九年级第一学期期中测评数学试题】如图所示的图案绕旋转中心旋转一定角度后能够与自身重合，那么这个旋转角可能是( )A ． 60B ． 72C ．90D ．12010．【浙江省桐乡市实验中学2013-2014学年上学期基础调研九年级数学试卷】对下图的对称性表述，正确的是（）．（A）轴对称图形（B）中心对称图形（C）既是轴对称图形又是中心对称图形（D）既不是轴对称图形又不是中心对称图形11．【诸暨市陶朱中学2013-2014学年第一学期10月月考九年级数学试卷】如图，矩形纸片ABCD 中，BC=4，AB=3，点P是BC边上的动点(点P不与点B、C重合)．现将△PCD沿PD翻折，得到△PC’D；作∠BPC’的角平分线，交AB于点E．设BP= x,BE= y,则下列图象中，能表示y与x的函数关系的图象大致是( )12．【北京市海淀区九年级第一学期期中测评数学试题】在角、等边三角形、平行四边形、圆中，既是中心对称图形又是轴对称图形的是( )A．角 B．等边三角形 C．平行四边形 D．圆13、【江苏省无锡市惠山六校联考2014届九年级上学期期中考试数学试题】如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB＝65°，则∠AED′等于（）A. 70°B.65°C.50°D.25°14.【广东省温州地区2013-2014学年八年级上学期第三次月考数学试卷】右图中几何体的左视图是（）A B C D二．填空题15．【温州市七校2013-2014学年上学期12月联考九年级数学试题ABCD 绕点A 逆时针方向旋转30o 后得到正方形AB ＇C ＇D ＇，则图中阴影部分面积为【解析】试题分析：设CD 与B'C'的交点是M ，连结AM ，则 ∠DAM=30° ∴AM=2DM 由勾股定理得DM=1考点：1.旋转的性质；2.正方形的性质.正面14题16.【广东省温州地区2013-2014学年八年级上学期第三次月考数学试卷】如图所示，用一根长度足够的长方形纸带，先对折长方形得折痕l,再折纸使折线过点B，且使得A在折痕l上，这时折线CB与DB所成的角为：。

九年级上第二次月考数学精品试卷

城关中学2013-2014学年九年级上第二次月考数学试卷本卷满分150分一、选择题（每小题4分，共40分） 1．在Rt △ABC 中，∠C =90°，若22sin =A ，则cosB 的值为（）． A ．21 B ．22C ．23 D ．12. 已知点A( -2 ,y 1 ) , B( -1 ,y 2 ) , C( 3 ,y 3 )都在反比例函数xy 4=的图象上,则（）A. y 1＜y 2＜y 3B. y 3＜y 2＜y 1C. y 3 ＜y 1＜y 2D. y 2＜y 1＜y 33．甲、乙两地相距60km ，则汽车由甲地行驶到乙地所用时间y （小时）与行驶速度x （千米/时）之间的函数图像大致是（）4.已知函数)0(>=k xky 经过点),(),,(222111yx P y x P ,如果021<<y y ,那么( ) A.012<<x xB.021<<x xC.012>>x xD.021>>x x5.由若干个相同的小立方体搭成的几何体的三视图如图所示，则搭成这个几何体的小立方体的个数是（） A ．3 B ．4 C ．5 D ．6主视图左视图俯视图6、已知函数1y x=的图象如图所示，当y ≥－1时，y 的取值范围是（） A .x ＜－1B..x ≤－1C . x ＜－1或x ≥0D . x ≤－1或x ＞0BC7、在同一直角坐标系中，函数y =kx -k 与ky=(k ≠0)的图象大致是（）8、对于函数xy 6=，下列说法错误．．的是（） A . 它的图像分布在一、三象限 B . 它的图像是轴对称图形 C . 它的图像是中心对称图形 D . y 的值随x 的增大而减小9、如图：AD ⊥CD ，AB=13，BC=12，CD=3，AD=4 ，则sinB=( )A B C D10.如图，已知正方形ABCD 的边长为2，如果将线段BD 绕着点B 旋转后，点D 落在CB 延长线上的D'处，那么tan ∠BAD'等于（） A 、2 B 、22C 、22D 、1 二、填空题（每小题4分，共24分） 11.若点（-2，1）在双曲线ky x=上，则k 的值为_______。

2014届全国名校数学试题解析汇编专题(15)阅读理解(解析版)

一．填空题1. 【江西省新干县思源实验学校第一学期初中八年级期中考试数学试题】（8分）阅读下列解题过程：已知为△的三边长，且满足，试判断△的形状．解：因为，①所以. ②所以．③所以△是直角三角形. ④回答下列问题：（1）上述解题过程，从哪一步开始出现错误?该步的序号为；（2）错误的原因为；（3）请你将正确的解答过程写下来.2.【广东省广州市南沙区珠江中学2013-2014学年第一学期八年级月考（9月份）数学试卷】完成下面的证明过程已知：如图，AB∥CD，AE⊥BD于E，CF⊥BD于F，BF=DE．求证：△ABE≌△CDF．证明：∵AB∥CD，∴∠1=_________ ．（两直线平行，内错角相等）∵AE⊥BD，CF⊥BD，∴∠AEB= _________ =90°． ∵BF=DE，∴BE= _________ ．在△ABE 和△CDF 中，∴△ABE≌△CDF _________ ．二．解答题3．【北京市海淀区九年级第一学期期中测评数学试题】阅读下面的材料：小明在研究中心对称问题时发现：如图1，当点1A 为旋转中心时，点P 绕着点1A 旋转180°得到1P 点，点1P 再绕着点1A 旋转180°得到2P 点，这时点P 与点2P 重合.如图2，当点1A 、2A 为旋转中心时，点P 绕着点1A 旋转180°得到1P 点，点1P 绕着点2A 旋转180°得到2P 点，点2P 绕着点1A 旋转180°得到3P 点，点3P 绕着点2A 旋转180°得到4P 点,小明发现P 、4P 两点关于点2P 中心对称.（1）请在图2中画出点3P 、4P ，小明在证明P 、4P 两点关于点2P 中心对称时，除了说明P 、2P 、4P 三点共线之外，还需证明；（2）如图3，在平面直角坐标系xOy 中，当)3,0(1A 、)0,2(2 A 、)0,2(3A 为旋转中心时，点)4,0(P 绕着点1A 旋转180°得到1P 点；点1P 绕着点2A 旋转180°得到2P 点；点2P 绕着点3A 旋转180°得到3P 点；点3P 绕着点1A 旋转180°得到点4P 点. 继续如此操作若干次得到点56P P 、、，则点2P 的坐标为（），点2017P 的坐为．4. 【浙江省三门县城关中学2014届九年级10月月考数学试题专题】（本题12分）阅读材料：已知方程22p p 101q q 0--=--= ，且pq 1≠，求pq 1q+的值. 解：由2p p 10--=，及21q q 0--=可知p 0q 0≠≠，，又∵pq 1≠，∴1p q≠. ∵21q q 0--=可变形为21110q q ⎛⎫--= ⎪⎝⎭，根据2p p 10--=和21110q q⎛⎫--= ⎪⎝⎭的特征.∴1p q、是方程2x x 10--=的两个不相等的实数根，则1p 1q +=，即pq 11q +=.根据阅读材料所提供的方法，完成下面的解答.已知：22152m 5m 1020n n --=+-=，，且m n ≠，求下列各式的值（1）11m n+；（2）()2m n -.5.【无锡南菁中学2013-2014学年度上学期第一次阶段性测试九年级数学试题】（本小题10分）阅读理解：如图1，在四边形ABCD的边AB上任取一点E（点E不与点A、点B重合），分别连接ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB 上的强相似点．解决问题：（1）如图1，∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；（2）如图2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD 的边AB上的一个强相似点E；拓展探究：（3）如图3，将矩形ABCD 沿CM 折叠，使点D 落在AB 边上的点E 处．若点E 恰好是四边形ABCM 的边AB 上的一个强相似点，试探究AB 和BC 的数量关系．（3）利用折叠找出图中相等的线段和相等的角；由相似找出图中相等的角；可知30=∠BCE ，由直角三角形的性质可得EC BE 21=,而AB CD EC ==,所以AB BE 21=，由33tan ==∠BC BE BCE 可得332=BC AB 试题解析：（2）作图如下：考点：1、相似三角形的判定.2、利用直径所对的圆周角是直角找符合条件的点.3、三角函数.。

城关中学2014学年第三次中考模拟测试卷数学

城关中学2014学年第三次中考模拟测试卷数学一．选择题（每题4分，共48分）1.计算:32a a ⋅等于（）A.5aB.6aC.8aD.9a2.雾霾PM2.5是指大气中直径小于或等于0.0000025的颗粒物，将它用科学计数法表示为（）A.0.25×510-B.7105.2-⨯C.6105.2-⨯D.81025-⨯3.比较π，-1，3的大小，下列判断正确的是（）A.π<-1<3B.-1<π<3C.-1<3<πD.3<-1<π4.如图，在⊙O 中，OC ⊥弦AB 于点C ，AB=4,OC=1,则OB 的长度是（） A.3 B.5 C.15 D.175.某校有A,B,C 三个餐馆，甲、乙两名学生各自随机选择其中的餐厅用餐，则甲、乙两名学生在同一个餐厅用餐的概率为（）A.61B.31C.21D.32 6.如图，△ABC 中，AB=AC=17,BC=16,M 是△ABC 的重心，AM 的长度是（）A.8 B.10 C.217 D.302897.某工程队准备修建一条长1200m 的道路，由于采用新的施工方式，实际每天修建道路的速度比原计划快20％，结果提前两天完成任务，若设原计划每天修建道路xm ，则根据题意可列方程为（）A. .-=2 B. -=2 C.-=2 D..-=28.如图①为一张三角形ABC 纸片，P 点在BC 上，今将A 折至P 时，出现折线BD ，其中D 点在AC 上，如图②所示，若△ABC 的面积为80，△DBC 的面积为50，则BP 与PC 的长度比是（）A.3:2B.5:3C.8:5D.13:8 9.如图，直角三角形ABC 有一外接圆，其中∠B=90°，AB>BC,在上找一点P ，使得,=,以下是甲乙两人的做法：甲：（1）取AB 中点D （2）过D 作直线AC 的平行线，交于P ，则P 即为所求乙：（1）取AC 中点E （2）过E 作直线AB 的并行线，交于P ，则P 即为所求对于甲、乙两人的作法，下列判断何者正确？（）A ．两人皆正确B ．两人皆错误C ．甲正确，乙错误D ．甲错误，乙正确10.如图所示，分别以直角三角形ABC 的三边作正三角形，已知AC=6，AB=10,阴影部分的面积分别记为S 1,S 2,S 3，则S 1+S 2-S 3的值为（） A.24 B.48 C.50243- D.253二．填空题（每题5分，共30分）11.分解因式：=+-y xy y x 22_______ 12.某茶厂用甲乙两台分装机分装某种茶叶（每袋茶叶的标准重量为200g ）.为了监控分装重量，该厂从它们各自分装的茶叶中随机抽取了50袋，测得它们的实际质量分析如下：则这两台分装机中，分装的茶叶质量更稳定的是（填“甲”或“乙”）．13.小明用一块含30°的直角三角形在已知线段AB 上作出△ABC （如图所示）若AB=6，则△ABC 的面积为_______.14.函数c bx x y ++=2的图象如图所示，有以下结论：①042<-ac b ;②c-b+1=0;③3b+c+6=0;④当1<x<3时，0)1(2<+-+c x b x ，其中正确的结论为 _______.平均数（g ）方差甲分装机 200 16.23乙分装机 200 5.84第13题第14题第15题15.如图，A 为双曲线xy 4=(x>0)上一点，B 为x 轴正半轴上一点，线段AB 的中点C 恰好在双曲线上，则△OAC 的面积为_______. 16.如图，射线QP 与等边△ABC 的两边AB ，AC 分别交于点M,N ，且BC//QP ，AM=MB=2,QP=8,将等边△ABC 从如图位置（点Q 与点M 重合）沿射线QP 以1cm/s 的速度向右移动，经过t(s)，以点P 为圆心，3cm 为半径的圆与△ABC 的边相切（切点在边上），请写出t 可取的一切值_______.三．解答题（本大题有8题，第17-20题每题8分，第21题10分，第22、23小题每小题12分，第24题14分，共80分，解答需写出必要的文字说明，演算步骤或证明方式）17.（1）计算：︒--+++-60sin )2()21(2320 （2）先化简，再求值：)2()(2b a a b a ---,其中a=1,b=218.某游泳池内现存水20003m ，已知该游泳池的排水速度是灌水速度的2倍，假设在换水时需要经历“排水—清洗—灌水”的过程，其中游泳池内剩余的水量y 3m 与th 换水时间之间的函数关系如图所示，根据图象解答下列问题：（1）根据图中提供的信息，求排水的速度及清洗该游泳池所用的时间；（2）求灌水过程中的y 3m 与换水时间th 之间的函数关系式，并写出自变量的取值范围.19.感恩是中华民族的传统美德，在4月份某校提出了“感恩父母，感恩老师，感恩他人”的三感教育活动，感恩事例有：A 给父母过一次生日；B 为父母做一次家务活，让父母休息一天；C 给老师一个发自内心的拥抱，并且与老师谈心；D 帮助有困难的同学度过难过，为了解学生对四中感恩事例的情况，在全校范围内随机抽取若干名学生，进行问卷调查（每个被调查的学生在4种感恩事例里选择一项），将数据进行整理并绘制成以下两幅统计图（未画完整）。

2013-2014学年九年级语文第一学期10月月考试卷新人教版第86套)

浙江省三门县城关中学2013-2014学年第一学期10月月考九年级语文试卷（本试卷共150分，考试时间为120分钟）一、基础知识积累与运用。

（31分） 1、结合语境，根据拼音写出正确汉字。

（4桂姑娘袭一身浸满香气的衣裙，迈步在这金色的田p ǔ（）上，俯首n íng （）望着农人脸上绽出的金灿灿的笑，抬头仰望着q ī（）息在电线杆上舒适快乐的麻雀……她醉了：三门的秋天，分外妖r áo （）。

2、依次填入下列句子横线处的词语，最恰当的一项是（）（3分） ①毋庸，三门有着良好的治安环境和丰富的海产资源。

②谁来为这些弱势人群正义？③我正在赏着这里的景致，一位老人骑着一头小毛驴地走过我的身旁。

A 、质疑声张泰然自若 B 、置疑声张泰然自若 C 、置疑伸张悠然自得 D 、质疑伸张悠然自得 3、下列句子标点符号使用有误的一项是（）（3分）A 、如果你喜欢自然，喜欢绿色，就来关注一下刚刚诞生在澳洲的“生态住宅”吧。

B 、春花灼灼，难免林黛玉葬花之悲；秋色如水，亦有欧阳修夜读之凉。

C 、卡罗琳听了我的话，笑了：“明天就开始吧。

当然，今天开始最好不过。

”D 、“卖青蟹啰”！小姑娘又亮开了又甜又脆的嗓门。

4、古诗文默写。

（10分）1．足蒸暑土气，。

⒉ 陈涉太息曰“嗟乎！！” 3．今夜偏知春气暖，。

⒋ ，人迹板桥霜。

5．无意苦争春，一任群芳妒。

，。

《卜算子咏梅》 6．《沁园春•雪》一词中承上启下的句子是：，。

7．《观刈麦》诗中与“可怜身上衣正单，心忧炭贱愿天寒”同样表现隐含的矛盾心理的诗句是，。

5、阅读名著片段，回答下列问题。

（5分）鲁提辖假意道：“你这厮诈死，酒家再打！”只见面皮渐渐的变了。

鲁达寻思道：“俺只指望痛打这厮一顿，不想三拳真个打死了他。

酒家须吃官司，又没人送饭，不如及早撒开。

”拔步便走，回头指着郑屠尸道：“你诈死！酒家和你慢慢理会！”一头骂，一头大踏步去了。

2014届全国名校数学试题解析汇编专题(14)操作性问题(解析版)

一．选择题1. 【浙江省三门县城关中学2013-2014学年第一学期10月月考九年级数学试卷】定义新运算“※”如下：当a≥b 时，a※b=a a b +，当a ＜b 时，a※b=a a b -，若()()2x 1x 20-+=※，则x 的值为 ( ▲ )A ．121x 3x 2=-=， B ．121x 1x 2=-=， C ．1231x 3x x 12=-==-，， D ．以上答案均不正确2．【衢州市衢江区2013-2014学年第一学期九年级第三次联考数学试题】如图，将一个有45°角的三角板ABC 的直角顶点放在一张宽为3cm 的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，则三角板的最大边AB 的长为（）A. 3 cmB.6cmC.二．填空题3．【温州市七校2013-2014学年上学期12月联考九年级数学试题】将一副三角尺如图拼接：含30°角的三角尺（△ABC）的长直角边与含45°角的三角尺（△ACD）的斜边恰好重合．已知AB=23，E是AC上的一点(AE>CE)，且DE=BE，则AE的长为 .4.【浙江省杭州市翠苑中学2013-2014学年上学期10月质量检测九年级数学试题】(10分)如图，矩形ABCD为一本书，AB=12π,AD=2，当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧)，如第一张纸AB对应为»AB，最后一张纸CD对应为»CD（»CD 为半圆），（1）连结OB，求钝角∠AOB=；（2）如果该书共有100张纸，求第40张纸对应的弧超出半圆部分的长.三．解答题5．【浙江省金华市聚仁教育集团2014九年级上学期第二阶段考试数学试题】将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n].（1）如图①，对△ABC作变换[60°，]得△AB′C′，则S△AB′C′：S△ABC=____；直线BC 与直线B′C′所夹的锐角为______度；（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值.6.【浙江省桐乡市实验中学2013-2014学年上学期基础调研九年级数学试卷】（6分）（1）解方程：1x x2x136-+-=-（2）x,y表示两个数，规定新运算“*”及“”如下：x*y=mx+ny，x△y=kxy,其中m，n，k 均为自然数（零除外），已知1*2=5，（2*3）△4=64，求（1△2）*3的值.∴1△2=2×1×2=4.∴（1△2）*3=4*3=4+2×3=10.考点：1.解一元一次方程；2.新定义；3.简单推理.7．【衢州市衢江区2013-2014学年第一学期九年级第三次联考数学试题】（本题10分）数学课上，王老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF交正方形外角∠DCG的平行线CF于点F，求证：AE=EF．经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF．在此基础上，同学们作了进一步的研究：（1）观点一：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立．观点二：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．请从以上两个观点中选择一个观点判断是否正确，如果正确，写出证明过程；如果不正确，请说明理由.（2）拓展：如图4，当四边形ABCD是矩形，且AB=2AD时，点E是边BC上的任意一点（不与B、C重合），∠AEF=90°，且AE=2EF，连接CF，求tan∠FCG的值．试题解析：（1）观点一正确.证明：在AB上取一点M，使AM＝EC，连接ME．∴BM＝BE．∴∠BME ＝45°.∴∠AME＝135°．∵CF是外角平分线，∴∠DCF＝45°.∴∠ECF＝135°．∴∠AME ＝∠ECF．8．【云南省临沧区云县后箐中学2014届九年级10月综合练习数学试题】当060α︒︒＜＜时，下列关系式中有且仅有一个正确.A. ()2sin 30sin αα+︒=+B. ()2sin 302sin αα+︒=C. ()2sin 30cos ααα+︒=+（1）正确的选项是；（2）如图1，△ABC 中， AC 1B 30A α=∠=︒∠=，，，请利用此图证明（1）中的结论；（3）两块分别含45︒ 和30︒的直角三角板如图2方式放置在同一平面内，BD =，求ADC S ∆.（3）由（2）证明的等式易得()sin 30α+︒= 如图2，过点A 作AG⊥CD 交CD 的延长线于点G ．∵△ABD 和△BCD 是两个含45°和30°的直角三角形，BD =，∴∠ADG=75°，AD=8，CD ＝考点：1.解直角三角形；2.三角形外角性质；3. 锐角三角函数定义；4.特殊角的三角函数值；5.三角形面积．9.【江苏省无锡市惠山六校联考2014届九年级上学期期中考试数学试题】(10分)某数学兴趣小组开展了一次课外活动，过程如下：如图，正方形ABCD中，AB＝6，将三角板放在正方形ABCD上，使三角板的直角顶点与D点重合。

浙江省三门县城关中学2014届九年级上学期英语10月月考试题

浙江省三门县城关中学2013-2014学年第一学期10月月考九年级英语试卷（考试时间100分钟，总分120分）亲爱的考生：欢迎参加考试！请你认真审题，积极思考，仔细答题，发挥最佳水平。

听力部分(25分)一、听力（本题有15小题，第一节每小题1分，第二、三节每小题2分，共25分）第一节：听小对话，请从A、B、C三个选项中选出符合对话内容的图片1. What will people use in this city in ten years ?A．B. C.2. What did Lucy’s father use to be?A. B. C.3. Which sign are they talking about?A. B. C.4. Where does the conversation probably happen?A. B. C.5. Which animal is Amy afraid of?A. B. C. 第二节：听长对话，回答问题听下面一段较长的对话，回答第6～7两小题。

6. Where is the woman going?A. To the bus station.B. To the train station.C. To the airport.7. Why does the woman stay in the city?A. For vacationB. For a meeting.C. For studying.听下面第二段较长的对话，回答第8-10两小题。

8. Why does Linda look so tired?A. Because she didn’t sleep well.B. Because she did too much homework.C. Because she has a cough.9. What does Linda want to do?A. To go to hospital.B. To watch TV at home.C. To have a rest.10. Where is Linda now?A. At home.B. In the hospital.C. At school.11. A. play games B. go to the movies C. go to the concerts12. A. reading B. doing her homework C. watching TV13. A. shopping B. picnics C. dinner14. A. take different classes B. do housework C. play the piano15. A. interested B. happy C. bored笔试部分(95分)二、单项选择 (10分)16. —What should I buy for Tom’s birthday?— How about ______camera? He loves taking photos.A. aB. anC. theD. /17. —_____do you learn English so well?— _____ asking the teacher for help.A. What; ByB. How; WithC. How; ByD. What; With18. —_________ work in Microsoft? —Yes, I did.A. Did you used toB. Did you use toC. Do you used toD. Was you use to19. ___________ should not be allowed to go out at night.A. Twelve-years -oldB. Twelve-year-oldsC. Twelve years oldD. Twelve year olds20. Don’t worry, Mom. I’m to look after myself.A. enough oldB. enough youngC. old enoughD. young enough21. —I don’t know how to pronounce this word. Can you help me?—Sorry, I don’t know, either. Let’s _________ in my dictionary right now.A. look it upB. look up itC. look them upD. look up them22. To ________ , I won the first prize.A. me surpriseB. my surprisedC. I surprisedD. my surprise23. You can’t go to the mall with John, he has got his driver’s license.A. even thoughB. becauseC. soD. if24. —On summer nights, the weather is usually hot at night in the south of China.— Yes, so I often go to sleep ______ the window ________.A. let, openB. with, openedC. with, closedD. with, open25. — I will take an English test tomorrow.— Oh, really?________!A. Good luckB. Have a good timeC. Well doneD. Good idea三、完型填空（本题有15小题，每小题1分，共计15分）阅读下面短文，然后从各题所给的四个选项中选出一个最佳答案。

2014年中考数学海门三模

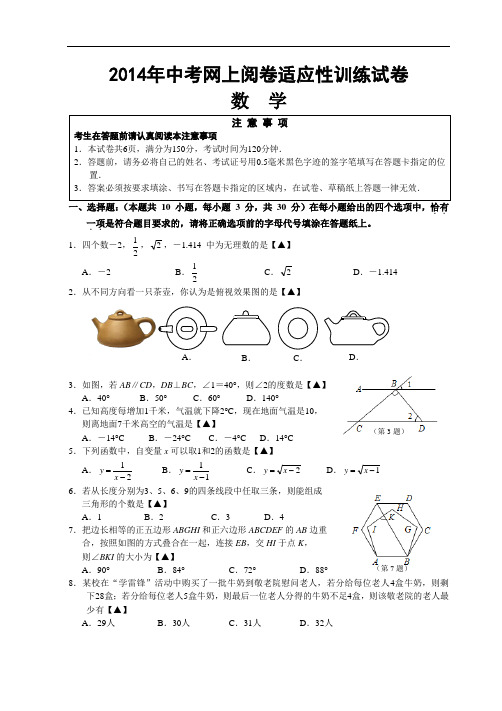
2014年中考网上阅卷适应性训练试卷数学一、选择题：（本题共 10 小题，每小题 3 分，共 30 分）在每小题给出的四个选项中，恰有．．一项．．是符合题目要求的，请将正确选项前的字母代号填涂在答题纸上。

1．四个数－2，21，2，－1.414 中为无理数的是【▲】A ．－2B ．21C ．2D ．－1.4142．从不同方向看一只茶壶，你认为是俯视效果图的是【▲】3．如图，若AB ∥CD ，DB ⊥BC ，∠1＝40°，则∠2的度数是【▲】 A ．40° B ．50° C ．60° D ．140° 4．已知高度每增加1千米，气温就下降2°C ，现在地面气温是10，则离地面7千米高空的气温是【▲】 A ．－14°C B ．－24°C C ．－4°C D ．14°C 5．下列函数中，自变量x 可以取1和2的函数是【▲】 A ．21-=x y B ．11-=x y C ．2-=x y D ．1-=x y6．若从长度分别为3、5、6、9的四条线段中任取三条，则能组成三角形的个数是【▲】 A ．1 B ．2 C ．3 D ．47．把边长相等的正五边形ABGHI 和正六边形ABCDEF 的AB 边重合，按照如图的方式叠合在一起，连接EB ，交HI 于点K ，则∠BKI 的大小为【▲】A ．90°B ．84°C ．72°D ．88°8．某校在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人，若分给每位老人4盒牛奶，则剩下28盒；若分给每位老人5盒牛奶，则最后一位老人分得的牛奶不足4盒，则该敬老院的老人最少有【▲】 A ．29人 B ．30人 C ．31人 D ．32人A ．B ．C ．D ．注意事项考生在答题前请认真阅读本注意事项1．本试卷共6页，满分为150分，考试时间为120分钟．2．答题前，请务必将自己的姓名、考试证号用0.5毫米黑色字迹的签字笔填写在答题卡指定的位置．3．答案必须按要求填涂、书写在答题卡指定的区域内，在试卷、草稿纸上答题一律无效．（第3题）（第7题）9．如图，已知第一象限内的点A 在反比例函数xy 2=上，第二象限的点B 在反比例函数xky =上，且OA ⊥OB ，sinA ＝33，则k 的值为【▲】 A ．－1B ．－2C ．21-D ．22-10．已知x 1，x 2 是方程 x 2－(2k －1)x ＋k 2＋1＝0 的两个实数根，则 x 12＋x 22 的最小值是【▲】A ．－3B ．43C ．87 D ．825 二、填空题：（本题共8小题，每小题3分，共24分）不需写出解答过程，把最后结果填在答题纸对应的位置上。

浙江省三门初级中学九年级第二次月考数学试题(无答案)

亲爱的考生：欢迎参加考试！请你认真审题，仔细答题，发挥最佳水平．请注意以下几点： 1.全卷共4页，满分150分，考试时间110分钟．2.答案必须写在答题纸相对应的位置上,写在试题卷、草稿纸上无效．3.本次考试不得使用计算器．祝你成功！一、选择题（本题有10小题，每小题4分，共40分．请选出各题中一个符合题意的准确选项，不选、多选、错选，均不给分）1．已知⊙O 1和⊙O 2的半径分别为3cm 和4cm ，圆心距O 1O 2＝9cm ，那么⊙O 1和⊙O 2的位置关系是（ ▲ ）A ．内切B ．相交C ．外切D ．外离 2．平面直角坐标系内一点P （-2，3）关于原点对称的点坐标是（ ▲ ） A ．（2，3）B ．（3，-2）C ．（2，-3）D ．（-2，-3）3. 如图，冰淇淋蛋筒下部呈圆锥形，若蛋筒圆锥部分包装纸的面积(接缝忽略不计)是20πcm 2，则将包装纸拆开，得到扇形的半径（▲ ）A ．4cm B. 8cm C. 4πcm D. 8πcm4. 如图，△ABC 是⊙O 的内接三角形，∠ABC=30°，∠BAC =60°，AB=10，则⊙O 的半径是（ ▲ ） A ．5 B ．6 C ．7 D ．535.如图，直线y=kx+b 交坐标轴于A ，B 两点，则不等式kx+b ＞0的解集是（ ▲ ） A.x >-2 B ．x >3 C ．x <-2 D ．x <36．如图，⊙O 的直径CD 与AB 相交于点E ，∠AOC=60°，∠CDB=30°，则下列说法不准确的是 ( ▲ )A ．CD ⊥AB B ．OE=CEC ．CD=BD D. AE=BE7.用配方法解方程2420x x -+=,下列配方结果准确的是（ ▲ ） A. 2(2)2x += B. 2(2)2x -= C. 2(2)2x -=- D. 2(2)6x -=8.如图，在平面直角坐标系中，点A 、B 、C 的坐标分别为（1，4），（5，4），（1，-2），则ABC ∆外接圆的圆心坐标是（ ▲ ） A ．（2，3） B ．（3，2） C ．（1，3） D ．（3，1）9.如图，在△ABC 中，AB=2，AC=1，以AB 为直径的圆与AC 相切，与边BC 交于点D ，则AD 的长为（ ▲ ） 45543525523510.如图（甲），水平地面上有一圆心角为60°的扇形OAB ，其中OA 的长度为6cm ，且与地面垂直，若在没有滑动的情况下，将图（甲）的扇形向右滚动至OB 与地面垂直为止，如图（乙）所示，则点O 移动的距离是（ ▲ ）A ． 6 cmB ．cmC ．2cm D ．4cm二、填空题（本题有6小题，每小题5分，共30分） 11.在函数11y x =-中，自变量x 的取值范围是 ▲ . 12．正十边形的中心角等于 ▲ °13. 如图，在⊙O 中，∠AOC=100°，则∠A +∠C = ▲ . 14. 已知四边形ABCD 是圆的内接四边形，AC,BD 是对角线，则 ∠1 +∠2+∠3 +∠4= ▲ . 15.如图，P 是射线35y x =上的一动点，以P 为圆心的⊙P 与y 轴相切于C 点，与x 轴的正半轴交于A 、B 两点．若⊙P 的半径为5，则点P 的坐标是（▲ ， ▲ ），点A 的坐标是（ ▲ ， ▲ ）.16.如图，AB 是⊙O 的弦，AB=8，点P 是优弧AB 上一动点，若△ABP 的最大面积是32，则⊙O 的半径是 ▲ .三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分）17. （1）解不等式：2143x x -<+ （2）解方程：22011x x x -=+-18.已知2223,23,x y x xy y =+=-++求的值.19. 如图，两个圆都以点O 为圆心，求证：AB=CD.20．已知：如图，E,F 是□ ABCD 是对角线AC 上的两点，AE = CF ，求证：四边形DEBF 是平行四边形.21.如图线段AB 的端点在边长为1的正方形网格的格点上，现将线段AB 绕点A 按逆时针方向旋转90°得到线段AC ．（1）请你在所给的网格中画出线段AC 及点B 经过的路径；（2）若将此网格放在一平面直角坐标系中，已知点A 的坐标为（1，3），点B 的坐标为（-2，-1），则点C 的坐标为。

浙江初三初中数学月考试卷带答案解析

浙江初三初中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.下列各图是选自历届世博会徽中的图案，其中是中心对称图形的是（）.2.下列根式中属最简二次根式的是（）.A．B．C．D．3.两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是（）.A．内切B．相交C．外切D．外离4.如图，⊙O是△ABC的外接圆，已知∠ABO=30º，则∠ACB的大小为（）A．60ºB．30ºC．45ºD．50º5.设a＞0，b＞0，则下列运算错误的是（）.A．＝·B．＝＋C．()2＝a D．＝6.若是方程的一个根，则代数式的值等于（）A．0B．2009C．2008D．－2009 7.如图，AB是⊙O的直径，弦CD⊥AB于E，如果AB=20，CD=16，那么线段OE的长为（）. A．10B．8C．6D．48.如图所示，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转至在△ADE处，使点B落在BC的延长线上的D点处，则∠BDE=( )．A．90°B．85°C．80°D．40°9.如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形的上底AD、下底BC以及腰AB均相切，切点分别是D、C、E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是（）.A．9B．10C．12D．1410..一个均匀的立方体骰子六个面上标有数1，2，3，4，5，6，若以连续掷两次骰子得到的数作为点的坐标，则点落在反比例函数图象与坐标轴所围成区域内（含落在此反比例函数的图象上的点）的概率是（）A．B．C．D．二、填空题1.如图，点A、B、C在⊙O上，若∠BAC= 24°，则∠BOC= °2.如图，圆形转盘中，A，B，C三个扇形区域的圆心角分别为150°，120°和90°. 转动圆盘后，指针停止在任何位置的可能性都相同（若指针停在分界线上，则重新转动圆盘），则转动圆盘一次，指针停在B区域的概率是 .3.圆锥的底面半径为4cm，母线长为12cm，则该圆锥的侧面积为cm2．4.若式子有意义，则x的取值范围是．5.在半径为2的⊙O中，弦AB的长为2，则弦AB所对的圆周角的度数为6.（1）如图一，等边三角形MNP的边长为1，线段AB的长为4，点M与A重合，点N在线段AB上. △MNP 沿线段AB按的方向滚动，直至△MNP中有一个点与点B重合为止，则点P经过的路程为；（2）如图二，正方形MNPQ的边长为1，正方形ABCD的边长为2，点M与点A重合，点N在线段AB上，点P在正方形内部，正方形MNPQ沿正方形ABCD的边按的方向滚动，始终保持M,N,P,Q四点在正方形内部或边界上，直至正方形MNPQ回到初始位置为止，则点P经过的最短路程为 .（注：以△MNP为例，△MNP沿线段AB按的方向滚动指的是先以顶点N为中心顺时针旋转，当顶点P落在线段AB上时，再以顶点P为中心顺时针旋转，如此继续. 多边形沿直线滚动与此类似.）三、计算题．计算与化简（本题满分8分，每小题4分）⑴⑵四、解答题1.解下列方程（本题满分8分,每题4分）⑴⑵2.（本题满分8分）已知在平面直角坐标系中的位置如下图所示．（1）分别写出图中点的坐标；（2）画出绕点按逆时针方向旋转后的；（3）求点旋转到点所经过的路线长（结果保留）．3.有四张背面图案相同的卡片A、B、C、D，其正面分别画有四个不同的几何图形（如图）.小敏将这四张卡片背面朝上洗匀摸出一张，放回洗匀再摸出一张.（1）用树状图（或列表法）表示两次摸出卡片所有可能的结果.（卡片可用A、B、C、D表示）（2）求摸出的两张卡片图形都是中心对称图形的概率.4.已知：如图，AB是⊙O的切线，切点为A，OB交⊙O于C，且点C为OB中点，∠ACD＝45°，弧AD的长为，求弦AD、AC的长．5.世界最长跨海大桥港珠澳大桥开工已经一年了．若2016年通车后，珠海A地准备开辟香港方向的运输路线，即货物从A地经港珠澳大桥公路运输到香港，再从香港运输另一批货物到澳门B地．若有几辆货车（不超过10辆）从A地按此路线运输货物到B地的运费需5920元，其中从A地经港珠澳大桥到香港的运输费用是每车380元，而从香港到澳门B地的运费的计费方式是：一辆车500元，当货车每增加1辆时，每车的运费就减少20元．若有x辆车运输货物．（1）用含x的代数式表示每辆车从香港到澳门B地的运费P；（2）求有多少辆车运送货物？6.如图，△ABC中，∠BAC=90°，AC=2，AB=，△ACD是等边三角形.（1）求∠ABC的度数.（2）以点A为中心，把△ABD顺时针旋转60°，画出旋转后的图形.（3）求BD的长度.7.如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为－1,直线l y=－X－与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.(1) 求点A的坐标及∠CAO的度数;(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?(3)如图2.过A,O,C三点作⊙O,点E是劣弧上一点,连接EC,EA.EO,当点E在劣弧上运动时(不与A,O两1点重合),的值是否发生变化?如果不变,求其值,如果变化,说明理由..浙江初三初中数学月考试卷答案及解析一、选择题1.下列各图是选自历届世博会徽中的图案，其中是中心对称图形的是（）.【答案】C【解析】在同一平面内，如果把一个图形绕某一点旋转180度，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形，A、B、D不满足中心对称图形的定义，故选C2.下列根式中属最简二次根式的是（）.A．B．C．D．【答案】A【解析】根据最简二次根式的定义（被开方数不含有能开的尽方的因式或因数，被开方数不含有分数），判断即可,,，=，故选A3.两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是（）.A．内切B．相交C．外切D．外离【答案】B【解析】两圆的位置关系有：外离（d＞R+r）、内含（d＜R-r）、相切（外切：d=R+r或内切：d=R-r）、相交（R-r＜d＜R+r）,因为3+5＞7＞5-3，所以两圆的位置关系是相交，故选B4.如图，⊙O是△ABC的外接圆，已知∠ABO=30º，则∠ACB的大小为（）A．60ºB．30ºC．45ºD．50º【答案】A【解析】：△AOB中，OA=OB，∠ABO=30°；∴∠AOB=180°-2∠ABO=120°；∴∠ACB= ∠AOB=60°；故选A5.设a＞0，b＞0，则下列运算错误的是（）.A．＝·B．＝＋C．()2＝a D．＝【答案】B【解析】分别根据二次根式的乘除法及二次根式的加法法则进行逐一分析,A、正确，符合二次根式乘法的逆运算；B、错误，不符合二次根式的加法法则；C、正确，符合二次根式乘法法则；D、正确，符合二次根式的除法法则．故选B．6.若是方程的一个根，则代数式的值等于（）A．0B．2009C．2008D．－2009【答案】D【解析】由一元二次方程的解的定义，可将a代入已知方程可得a2+a+2009=0，即a（a+1）=-2009故选D7.如图，AB是⊙O的直径，弦CD⊥AB于E，如果AB=20，CD=16，那么线段OE的长为（）.A．10B．8C．6D．4【答案】C【解析】连接OD,先求出DE和圆的半径，再利用勾股定理即可求出OE=68.如图所示，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转至在△ADE处，使点B落在BC的延长线上的D点处，则∠BDE=( )．A．90°B．85°C．80°D．40°【答案】C【解析】：∵点B落在BC的延长线上的D点处，∴AB=AD，∠ADB=40°，∴∠BDE=∠ADB+∠ADE=80°,故选C9.如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形的上底AD、下底BC以及腰AB均相切，切点分别是D、C、E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是（）.A．9B．10C．12D．14【答案】D【解析】根据切线长定理，得AD=AE，BC=BE，所以梯形的周长是5×2+4=14．故选D10..一个均匀的立方体骰子六个面上标有数1，2，3，4，5，6，若以连续掷两次骰子得到的数作为点的坐标，则点落在反比例函数图象与坐标轴所围成区域内（含落在此反比例函数的图象上的点）的概率是（）A．B．C．D．【答案】D【解析】因为掷骰子的概率一样，每次都有六种可能性，因此掷两次共有36种可能．而要使P点落在反比例图象的区域内，则有14种可能，因此可得出概率为14/36=7/18，故选D二、填空题1.如图，点A、B、C在⊙O上，若∠BAC= 24°，则∠BOC= °【答案】48【解析】∵∠BOC、∠BAC是同弧所对的圆心角和圆周角，∴∠BOC=2∠BAC=48°2.如图，圆形转盘中，A，B，C三个扇形区域的圆心角分别为150°，120°和90°. 转动圆盘后，指针停止在任何位置的可能性都相同（若指针停在分界线上，则重新转动圆盘），则转动圆盘一次，指针停在B区域的概率是 .【答案】【解析】：∵B扇形区域的圆心角为120°，∴B区域所占的面积比例为120/360=1/3，即转动圆盘一次，指针停在B区域的概率是1/3．3.圆锥的底面半径为4cm，母线长为12cm，则该圆锥的侧面积为cm2．【答案】【解析】圆锥的侧面积=底面周长×母线长÷2=1/2×8×12=4.若式子有意义，则x的取值范围是．【答案】X≥—1且X≠0【解析】根据二次根式的性质可知：1+x≥0，即x≥-1，又因为分式的分母不能为0，所以x的取值范围是x≥-1且x≠05.在半径为2的⊙O中，弦AB的长为2，则弦AB所对的圆周角的度数为【答案】30度或150度【解析】如图，弦AB所对的圆周角为∠C，∠D，连接OA、OB，因为AB=OA=OB=2，所以，∠AOB=60°，根据圆周角定理知，∠C="1" 2 ∠AOB=30°，根据圆内接四边形的性质可知，∠D=180°-∠C=150°，所以，弦AB 所对的圆周角的度数30°或150°6. （1）如图一，等边三角形MNP 的边长为1，线段AB 的长为4，点M 与A 重合，点N 在线段AB 上. △MNP 沿线段AB 按的方向滚动，直至△MNP 中有一个点与点B 重合为止，则点P 经过的路程为；（2）如图二，正方形MNPQ 的边长为1，正方形ABCD 的边长为2，点M 与点A 重合，点N 在线段AB 上，点P 在正方形内部，正方形MNPQ 沿正方形ABCD 的边按的方向滚动，始终保持M ,N ,P ,Q 四点在正方形内部或边界上，直至正方形MNPQ 回到初始位置为止，则点P 经过的最短路程为 .（注：以△MNP 为例，△MNP 沿线段AB 按的方向滚动指的是先以顶点N 为中心顺时针旋转，当顶点P 落在线段AB 上时，再以顶点P 为中心顺时针旋转，如此继续. 多边形沿直线滚动与此类似.）【答案】π，2π【解析】（1）点P 经过的路程是两段弧，半径为1，圆心角为120°, 点P 经过的路程是：（2）点P 经过的路程是四段弧，半径为1，圆心角为90°点P 经过的最短路程是：三、计算题．计算与化简（本题满分8分，每小题4分）⑴⑵【答案】（1）===（2）原式=1--2+=【解析】此题考查二次根式的运算和实数运算四、解答题1.解下列方程（本题满分8分,每题4分） ⑴ ⑵【答案】(1)开平方，去括号得：x 2+8x+16=5x+20 整理得x 2+3x-4=0 即（x-1）(x+4)=0 所以x 1=1,x 2=-4(2)方程变形为：（x-1）（x+3）=0,解得x 1=1,x 2=-3【解析】将原方程化为一般式，然后再用因式分解法求解2.（本题满分8分）已知在平面直角坐标系中的位置如下图所示．（1）分别写出图中点的坐标；（2）画出绕点按逆时针方向旋转后的；（3）求点旋转到点所经过的路线长（结果保留）．【答案】解：（1）点A的坐标（2，1），点B的坐标（6，0）………………………………2分（2）如图，为所求作的图形……………………………………………3分（3）………………………………………………………1分点旋转到点所经过的路线长：………………………………………………………2分【解析】（1）在直角坐标系中读出A的坐标，点C的坐标；（2）根据旋转的性质画出△ABC绕点A按逆时针方向旋转90°后的△A′B′C′；（3）先根据勾股定理求出AC的长，然后利用弧长的计算公式求解即可3.有四张背面图案相同的卡片A、B、C、D，其正面分别画有四个不同的几何图形（如图）.小敏将这四张卡片背面朝上洗匀摸出一张，放回洗匀再摸出一张.（1）用树状图（或列表法）表示两次摸出卡片所有可能的结果.（卡片可用A、B、C、D表示）（2）求摸出的两张卡片图形都是中心对称图形的概率.【答案】解：（1）树状图……………………………………………………………4分或列表法是中心对称图形（记为事件A）有4种，即：（B，B）（B，D）（D，B）（D，D）.∴P（A）＝………………………………4分【解析】（1）列举出所有情况即可；（2）中心对称图形是绕某点旋转180°后能够和原来的图形完全重合，那么B，D是中心对称图形，看所求的情况占总情况的多少即可4.已知：如图，AB是⊙O的切线，切点为A，OB交⊙O于C，且点C为OB中点，∠ACD＝45°，弧AD的长为，求弦AD、AC的长．【答案】解：连接OA …………………1分（看图或文字描述即可给分）∵∠ACD＝45°，∴∠AOD＝90°，∴AD弧的长为．∴．∴．…………………5分∵AB是⊙O的切线∴OA⊥AB．∵点C为Rt△AOB的斜边的中点．∴．…………4分【解析】连接OA，根据弧AD的长可求得圆的半径，利用解直角三角形求得AD，AC的长5.世界最长跨海大桥港珠澳大桥开工已经一年了．若2016年通车后，珠海A地准备开辟香港方向的运输路线，即货物从A地经港珠澳大桥公路运输到香港，再从香港运输另一批货物到澳门B地．若有几辆货车（不超过10辆）从A地按此路线运输货物到B地的运费需5920元，其中从A地经港珠澳大桥到香港的运输费用是每车380元，而从香港到澳门B地的运费的计费方式是：一辆车500元，当货车每增加1辆时，每车的运费就减少20元．若有x辆车运输货物．（1）用含x的代数式表示每辆车从香港到澳门B地的运费P；（2）求有多少辆车运送货物？【答案】解：（1）p=500―20(x―1)=520―20x……………3分（2）由题意得，……………4分整理得，解得，（不合题意，舍去），答：有8辆货车运输货物．……………5分（没有检验舍去一个扣2分）【解析】（1）用原来一辆车500元减去增加的（x-1）辆汽车所减少的运费即可列出；（2）利用从A地经港珠澳大桥到香港的运输费用+从香港到澳门B地的运费=总费用列方程解答即可6.如图，△ABC中，∠BAC=90°，AC=2，AB=，△ACD是等边三角形.（1）求∠ABC的度数.（2）以点A为中心，把△ABD顺时针旋转60°，画出旋转后的图形.（3）求BD的长度.【答案】（1）Rt△ABC中∴-------------------4分（2）如图-----------------3分（3）方法1 ：连接BE.由（2）知：△ACE≌△ADB∴AE=AB，∠BAE=60°，BD=EC∴∠EBC=90°又BC=2AC=4∴Rt△EBC中，EC=∴---------------------------------------- 5分方法2：过点D作DF⊥BC，交BC延长线于点F，则求得DF= BF =5,∴按方法1 相应给分方法3：过点D作DG⊥BA，交BA延长线于点G，按照方法1给分【解析】（1）利用正切的知识可得出答案．（2）根据旋转角度、旋转中心、旋转方向找出各点的对称点，顺次连接即可；（3）根据旋转的性质可得△ACE≌△ADB，从而确定∠EBC=90°，然后利用勾股定理即可解答7.如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为－1,直线l y=－X－与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.(1) 求点A的坐标及∠CAO的度数;(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?,点E是劣弧上一点,连接EC,EA.EO,当点E在劣弧上运动时(不与A,O两(3)如图2.过A,O,C三点作⊙O1点重合),的值是否发生变化?如果不变,求其值,如果变化,说明理由..【答案】解：（1）、A （－，0）∵C （0，－），∴OA=OC 。