立体几何中的向量公式
高中数学立体几何向量公式

高中数学立体几何向量公式
在三维空间中,向量有着相应的公式。
第一个公式是向量a加向量b,即a+b=a+b。
这表示将两个向量相加,得到一个新的向量。
下一个公式是a×b,它表示两个向量的点积,这意味着它们的方向是相反的,但它们的大小是不同的。
还有另一个公式叫平行向量,它表示两个向量具有相同的方向。
它可以写成:a∥b,这意味着它们之间的另一个角度被视为0度。
另外,向量也有一个公式,它可以用来描述两个向量的向量积,这是一个形状向量,表示另一个向量的方向或大小与其相似。
最后,还有一个叫作法向量的公式,它表示了一个向量和一个平面的关系,这被用来描述法线的方向,它可以写为n=b-a。
总而言之,立体几何中向量的公式涉及加减、点积和叉积等内容,是高中学习数学中十分重要的一部分。
了解并掌握这些公式有助于学生更好地理解数学知识,更好的运用到学习中去。
空间向量与立体几何公式

空间向量与立体几何公式一、空间向量1、空间向量是一种简单的数学表达形式,表示一组相同类型数据成员之间的关系。
它可以描述空间中的每个点与另一个点之间的连接情况,而连接情况是由三个不同的坐标表示的。
换言之,空间向量就是描述空间中一个点到另一个点的方向及距离,作为一种数学实体而存在的。
2、空间向量可以用一个有向箭头来表示,并用数学记号标注出来。
通常来说,它的数学记号是表示坐标系中的另一个点在第一个点的坐标上的偏移量,如a→b表示b点在a点上的偏移量。
3、空间向量形式可以表示一条从原点到某个点的路径,通过它可以确定在x、y和z轴上的平移量,即偏移量,从而避免了我们有时在空间中运行物体时会误解运动方向的困难。
从更宏观的角度来说,空间向量可以用来表示以位置、速度和加速度等。
二、立体几何公式1、立体几何是几何学分支之一,它学习的内容是空间中的点、线、面和体的特性、关系及其变化规律,其中关于立体图形的内容被称为立体几何。
立体几何的定义是关于空间中的点、线、面和体的研究,以及它们之间的关系,其中主要考虑的就是位置、形状、大小以及一般的空间概念。
2、立体几何公式包括:立体几何定义、立体几何变换、立体几何性质、其他立体几何相关概念以及三角几何相关公式。
例如,立体几何定义涉及的公式有:空间中的点的位置关系(a-b=c),线的距离关系(L=1/2×Z1×Z2),面的面积关系(S=1/2×Z1×Z2×cosX),以及球体表面积(S=4×π×R2)等公式。
3、另外,立体几何公式还包括三角几何公式,它主要涉及到角度、正弦、余弦、正切、反正切等相关公式。
这些公式用来解决各种形状三角形以及其他更复杂的立体图形以及相关空间距离关系的问题。
高中数学立体几何向量法归纳

B
练习
D1F (0,1, 2)
D
E C
AE D1F 0, DA D1F 0 AE D1F, DA D1F D1F 平面AED 平面A1FD 平面AED
F
Y
A
B X
或证明两平面的法向量垂直
练习
如图,直三棱柱ABC A1B1C1中,CA CB 1,
BCA 90O,棱AA1 2,M、N分别是A1B1、AA1的
n
α
5、平面法向量的求法
设a=( x1,y1,z1)、b=(x2,y2,z2)是平面α内的两个不共 线的非零向量,由直线与平面垂直的判定定理知,若 n⊥a且n⊥b,则n⊥α.换句话说,若n·a = 0且n·b = 0, 则n⊥α.可按如下步骤求出平面的法向量的坐标
1、假设平面法向量的坐标为n=(x,y,z).
6、中点坐标公式 7、重心坐标公式
x
x1
x2 2
y
y1 y2 2
z
z1
z2 2
x
x1
x2 3
x3
y
y1
y2 3
y3
z
z1
z2 3
z3
8、直线与直线所成角公式
cos | AB CD |
| AB | | CD |
9、直线与平面所成角公式
sin | PM n |
| PM || n |
二、基本公式:
1、两点间的距离公式(线段的长度)
AB AB x2 x1 2 y2 y1 2 z2 z1 2
2、向量的长度公式(向量的模)
a
2
a
x2 y2 z2
3、向量的坐标运算公式
若 a (x1, y1, z1) b (x2, y2, z2) 那么
立体几何证明的向量公式和定理证明

立体几何证明的向量公式和定理证明立体几何中的向量公式和定理证明非常多,下面仅列举其中几个常见的向量公式和定理的证明。
1.向量叉乘的模长公式证明:对于两个三维向量A=(a1,a2,a3)和B=(b1,b2,b3),它们的叉乘C=A×B定义为C=(a2b3-a3b2,a3b1-a1b3,a1b2-a2b1)。
根据向量的定义,我们有C,^2=(a2b3-a3b2)^2+(a3b1-a1b3)^2+(a1b2-a2b1)^2=(a2^2b3^2-2a2a3b2b3+a3^2b2^2)+(a3^2b1^2-2a1a3b1b3+a1^2b3^2)+(a1^2b2^2-2a1a2b1b2+a2^2b1^2)=a2^2b3^2+a3^2b1^2+a1^2b2^2-2a2a3b2b3-2a1a3b1b3-2a1a2b1b2+a3^2b2^2+a1^2b3^2+a2^2b1^2-2a1a2b1b2-2a2a3b2b3+a1^2b2^2=a1^2(b2^2+b3^2)+a2^2(b1^2+b3^2)+a3^2(b1^2+b2^2)-2(a1a2b1b2+a2a3b2b3+a1a3b1b3)=a1^2,B,^2+a2^2,B,^2+a3^2,B,^2-2(a1a2b1b2+a2a3b2b3+a1a3b1b3)=(a1^2+a2^2+a3^2),B,^2=,A,^2,B,^2因此,可以得出,C, = ,A × B, = ,A,B,sinθ,其中θ为A和B的夹角。
2.向量线性组合的余子定理证明:设有n个非零向量v1, v2, ..., vn,如果它们的线性组合为零向量,即存在一组不全为零的实数c1, c2, ..., cn,使得c1v1 + c2v2 + ...+ cnvn = 0,则对于其中任意一个向量,它的余子向量与其余子式满足如下关系:v1 × (v2 × ... × vn) = (v1 · vn) (v2 × ... × vn) -(v1 · vn-1)(v2 × ... × vn-1)vn为了证明上述关系,我们可以使用向量叉乘的定义进行展开计算。
立体几何中的向量方法(平行与垂直)

——证明平行与垂直
例1 四棱锥P-ABCD中,底面ABCD是正方 形, PD⊥底面ABCD,PD=DC=6, E是PB的
中点,DF:FB=CG:GP=1:2 . 求证:AE//FG. 证 :如图所示, 建立 Z E(3,3,3), 空间直角坐标系. A(6,0,0), P
F(2,2,0),
G(0,4,2),
几何法呢?
AE =(-3, 3, 3), FG =(-2, 2, 2)
3 AE = FG AE // FG 2 AE与FG不共线
E
D
G
C Y
AE//FG
A X
F
B
例2.如图:ABCD与 ABEF是正方形, CB⊥平面ABEF, AH=GF. 求证: HG∥平面CBE. E
F B
C y
例5 正方体 ABCD A1 B1C1 D1 ,E是AA1中点, 求证:平面EBD 平面C1BD. 证明: 设正方体棱长为2, 建立如图所示坐标系
E(0,0,1) B(2,0,0) D(0,2,0)
EB (2,0, 1) ED (0,2, 1)
设平面EBD的一个法向量是
E
C
D
M B N G
H
A F
证明:由已知得:AB、 C BC、BE两两垂直,故可 建立如图所示的空间直 角坐标系o-xyz. 设正方形边长为1, oB AH=FG=a, 则 2 2 H(0,1- 2 a , 2 a)、 E
x
2 2 (1 a,0, a) ,而平面CBE的法向 故 HG H 2 2
G F B1
C1
A1
E
D A B
C
AD∥GF,AD=GF 平行四边形ADGE AE∥DG 又EH∥B1D1,GF∥B1D1 EH∥GF
立体几何中的向量方法

利用直线方向向量
直线a的方向向量a , 直线b的方向向量b a b a // b a // b
证明平行问题
证明线面平行的方法
利用线线平行 若 a , b , a // b,则 a //
利用面面平行
若 a // , a , 则a // .
利用向量共面充要条件
点到直线距离
点到直线的距离:一点到它在一直线上的射影的距 离叫做这一点到这条直线的距离 定义法:作出距离线段(常利用三垂线定理作出), 解三角形求之 A 向量法:
1.取斜线AB上的向量BA, 取直线方向向量l 2.计算 BA在l方向上的投影的绝对值 即 BO ) ( BO BA cos BA, l BA l l 3.利用勾股定理求 AO (点到线的距离 )
小结
画出下列空间几何体,思考如何建立坐标系? 正方体、长方体 正三棱锥、正四棱锥 正三棱柱、直三棱柱 …… 注意:要建立右手系:x→y→z按逆时针顺序转. 用向量解立体几何问题步骤: 建系(必须用文字表述,并在图中标出) 写点坐标 写向量坐标 计算…… 回归到立体几何结论
向量方法与传统立体几何方法 “两手都要抓,两手都要硬”
立体几何中的向量方法
空间角的计算
异面直线所成的角
平移法:平移其中一条,或者利用中位线平移,或者 利用补形平移,用余弦定理求角 向量法:取两直线的方向向量a , b,cos a , b a b ab
两异面直线所成角, cos a , b cos
小结论: 三面角余弦公式
证明平行问题
证明线线平行的方法
利用平行公理 若a // b, b // c , 则a // c.
利用线面平行 若 a // , a , b, 则a // b.
平面向量直线和圆立体几何公式定理

平面向量 坐标运算:(1)设a =11(,)x y ,b =22(,)x y ,则a +b =1212(,)x x y y ++. (2)设a =11(,)x y ,b =22(,)x y ,则a -b =1212(,)x x y y --. (3)设A 11(,)x y ,B 22(,)x y ,则2121(,)AB OB OA x x y y =-=-- . (4)设a =(,),x y R λ∈,则λa =(,)x y λλ. (5)设a =11(,)x y ,b =22(,)x y ,则a ·b =1212()x x y y +.向量内积:a 与b 的数量积(或内积):a ·b =|a ||b |cos θ 两向量的夹角公式:121222221122cos ||||x x y y a b a b x y x y θ+⋅==⋅+⋅+ (a =11(,)x y ,b =22(,)x y ).平面两点间的距离公式:,A B d 222121()()x x y y =-+- (A 11(,)x y ,B 22(,)x y ). 向量的平行与垂直 :设a =11(,)x y ,b =22(,)x y ,且b ≠0 ,则:a ||b 12210x y x y ⇔-=.(交叉相乘差为零) a ⊥b (a ≠0 )⇔ a ·b =012120x x y y ⇔+=.(对应相乘和为零)线段的定比分公式 :设111(,)P x y ,222(,)P x y ,(,)P x y 是线段12P P 的分点,λ是实数,且12PP PP λ= ,则 121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩⇔121OP OP OP λλ+=+ 直线和圆斜率公式 :2121y y k x x -=-(111(,)P x y 、222(,)P x y ). 直线方程:(1)点斜式 11()y y k x x -=- (直线l 过点111(,)P x y ,且斜率为k ).(2)斜截式 y kx b =+(b 为直线l 在y 轴上的截距).(3)两点式 112121y y x x y y x x --=--(12y y ≠) (111(,)P x y 、222(,)P x y (1212,x x y y ≠≠))(4)截距式 1x y a b+=(a b 、分别为直线的横、纵截距,00a b ≠≠、) (5)一般式 0Ax By C ++=(其中A 、B 不同时为0). 直线0Ax By C ++=的法向量:(,)l A B '= ,方向向量:(,)l B A =-夹角公式:(1)2121tan ||1k k k k α-=+. (111:l y k x b =+,222:l y k x b =+,121k k ≠-) (2)12211212tan ||A B A B A A B B α-=+.(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠). 直线12l l ⊥时,直线l 1与l 2的夹角是2π.1l 到2l 的角:(1)2121tan 1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-) (2)12211212tan A B A B A A B B α-=+.(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l ⊥时,直线l 1到l 2的角是2π. 点到直线的距离 :0022||Ax By C d A B++=+(点00(,)P x y ,直线l :0Ax By C ++=).圆的四种方程:(1)圆的标准方程 222()()x a y b r -+-=. (2)圆的一般方程 220x y Dx Ey F ++++=(224D E F +->0).(3)圆的参数方程 cos sin x a r y b r θθ=+⎧⎨=+⎩.点与圆的位置关系:点00(,)P x y 与圆222)()(r b y a x =-+-的位置关系有三种:2200()()d a x b y =-+-, 则d r >⇔点P 在圆外; d r =⇔点P 在圆上; d r <⇔点P 在圆内.直线与圆的位置关系:直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种(22BA C Bb Aa d +++=): 0<∆⇔⇔>相离r d ; 0=∆⇔⇔=相切r d ;0>∆⇔⇔<相交r d . 两圆位置关系的判定方法:设两圆圆心分别为O 1,O 2,半径分别为r 1,r 2,d O O =21,则:条公切线外离421⇔⇔+>r r d ;条公切线外切321⇔⇔+=r r d ;条公切线相交22121⇔⇔+<<-r r d r r ;条公切线内切121⇔⇔-=r r d ;无公切线内含⇔⇔-<<210r r d .立体几何空间中的平行问题线面平行的判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。
立体几何中的向量方法——证明平行及垂直

立体几何中的向量方法(一)——证明平行与垂直1.直线的方向向量与平面的法向量确实定(1)直线的方向向量:在直线上任取一非零向量作为它的方向向量.(2)平面的法向量可利用方程组求出:设a ,b 是平面α两不共线向量,n 为平面α的法向量,则求法向量的方程组为⎩⎨⎧n ·a =0,n ·b =0.2.用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ,与平面α共面的两个不共线向量v 1和v 2,则l ∥α或l ⊂α⇔存在两个实数*,y ,使v =*v 1+y v 2.(3)设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1,u 2,则α∥β⇔u 1∥u 2.3.用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2=0.(2)设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2,则α⊥β⇔u 1⊥u 2⇔u 1·u 2=0.【思考辨析】判断下面结论是否正确(请在括号中打"√〞或"×〞)(1)直线的方向向量是唯一确定的.()(2)平面的单位法向量是唯一确定的.()(3)假设两平面的法向量平行,则两平面平行.()(4)假设两直线的方向向量不平行,则两直线不平行.()(5)假设a ∥b ,则a 所在直线与b 所在直线平行.()(6)假设空间向量a 平行于平面α,则a 所在直线与平面α平行.()1.以下各组向量中不平行的是()A .a =(1,2,-2),b =(-2,-4,4)B .c =(1,0,0),d =(-3,0,0)C .e =(2,3,0),f =(0,0,0)D .g =(-2,3,5),h =(16,24,40)2.平面α有一点M (1,-1,2),平面α的一个法向量为n =(6,-3,6),则以下点P 中,在平面α的是()A .P (2,3,3)B .P (-2,0,1)C .P (-4,4,0)D .P (3,-3,4)3.AB →=(1,5,-2),BC →=(3,1,z ),假设AB →⊥BC →,BP →=(*-1,y ,-3),且BP ⊥平面ABC ,则实数*,y ,z 分别为______________.4.假设A (0,2,198),B (1,-1,58),C (-2,1,58)是平面α的三点,设平面α的法向量n =(*,y ,z ),则*∶y ∶z =________.题型一 证明平行问题例1(2013·改编)如图,在四面体A -BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =22,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ =3QC .证明:PQ ∥平面BCD .如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ ;(2)是否存在λ,使平面EFPQ 与平面PQMN 所成的二面角为直二面角?假设存在,求出λ的值;假设不存在,说明理由.题型二 证明垂直问题例2 如下图,正三棱柱(底面为正三角形的直三棱柱)ABC —A 1B 1C 1的所有棱长都为2,D 为CC 1的中点.求证:AB 1⊥平面A 1BD .如下图,在四棱锥P -ABCD 中,PC ⊥平面ABCD ,PC =2,在四边形ABCD 中,∠B =∠C =90°,AB =4,CD =1,点M 在PB 上,PB =4PM ,PB 与平面ABCD 成30°角.(1)求证:CM ∥平面PAD ;(2)求证:平面PAB ⊥平面PAD .题型三 解决探索性问题例3 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1AC均为60°,平面AA1C1C⊥平面ABCD.(1)求证:BD⊥AA1;(2)求二面角D-A1A-C的余弦值;(3)在直线CC1上是否存在点P,使BP∥平面DA1C1,假设存在,求出点P的位置,假设不存在,请说明理由.如下图,四棱锥S—ABCD的底面是正方形,每条侧棱的长都是底面边长的2倍,P为侧棱SD上的点.(1)求证:AC⊥SD.(2)假设SD⊥平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC.假设存在,求SE∶EC的值;假设不存在,试说明理由.利用向量法解决立体几何问题典例:如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C为60°,AP=1,AD=3,求三棱锥E-ACD的体积.A组专项根底训练1.假设直线l的方向向量为a=(1,0,2),平面α的法向量为n=(-2,0,-4),则()A.l∥αB.l⊥αC.l⊂αD.l与α相交2.假设AB→=λCD→+μCE→,则直线AB与平面CDE的位置关系是()A.相交B.平行C.在平面D.平行或在平面3.A(4,1,3),B(2,-5,1),C(3,7,-5),则平行四边形ABCD的顶点D的坐标是() A.(2,4,-1) B.(2,3,1)C.(-3,1,5) D.(5,13,-3)4.a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),假设a,b,c三向量共面,则实数λ等于()A.627B.637C.607D.6575.如图,在长方体ABCD —A 1B 1C 1D 1中,AB =2,AA 1=3,AD =22,P 为C 1D 1的中点,M 为BC 的中点.则AM 与PM 所成的角为()A .60°B .45°C .90°D .以上都不正确6.平面α的三点A (0,0,1),B (0,1,0),C (1,0,0),平面β的一个法向量n =(-1,-1,-1),则不重合的两个平面α与β的位置关系是________.7.设点C (2a +1,a +1,2)在点P (2,0,0)、A (1,-3,2)、B (8,-1,4)确定的平面上,则a =________.8.如图,在正方体ABCD —A 1B 1C 1D 1中,棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =2a 3,则MN 与平面BB 1C 1C 的位置关系是________. 9.如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,PD ∥QA ,QA =AB=12PD .证明:平面PQC ⊥平面DCQ . 10.如图,在底面是矩形的四棱锥P -ABCD 中,PA ⊥底面ABCD ,E ,F 分别是PC ,PD 的中点,PA =AB =1,BC =2.(1)求证:EF ∥平面PAB ;(2)求证:平面PAD ⊥平面PDC .B 组 专项能力提升11.如图,正方形ABCD 与矩形ACEF 所在平面互相垂直,AB =2,AF =1,M 在EF 上,且AM ∥平面BDE ,则M 点的坐标为()A .(1,1,1)B .(23,23,1) C .(22,22,1) D .(24,24,1)12.设u =(-2,2,t ),v =(6,-4,4)分别是平面α,β的法向量,假设α⊥β,则t 等于()A .3B .4C .5D .613.在正方体ABCD —A 1B 1C 1D 1中,P 为正方形A 1B 1C 1D 1四边上的动点,O 为底面正方形ABCD 的中心,M ,N 分别为AB ,BC 的中点,点Q 为平面ABCD 一点,线段D 1Q 与OP 互相平分,则满足MQ →=λMN→的实数λ有________个.14.如下图,直三棱柱ABC —A 1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D 、E 、F 分别为B 1A 、C 1C 、BC 的中点.求证:(1)DE ∥平面ABC ;(2)B 1F ⊥平面AEF .15.在四棱锥P —ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E 、F 分别是AB 、PB 的中点.(1)求证:EF ⊥CD ;(2)在平面PAD 求一点G ,使GF ⊥平面PCB ,并证明你的结论.。
立体几何中的向量方法 gai

1.直线的方向向量与平面的法向量的确定
(1)直线的方向向量:在直线上任取一 作为它的方向向量. 非零 向量
(2)平面的法向量可利用方程组求出:设a,b是
平面α 内两不共线向量,n为平面α 的法向量,
n a 0 则求法向量的方程组为 n b 0.
解:设平面的法向量为n (x,y,z),
则n AB, n AC ( (2, 2,1) 0, x,y,z) (x,y,z) (4,5,3) 0 1 2 x 2 y z 0 x 即 , 取z 1,得 2 4 x 5 y 3 z 0 y 1 3 1 n ( , 1,1), | n | 2 2
1 2 2 求平面ABC的单位法向量为 ( , - ,) 3 3 3
平行关系:
设直线 l , m 的方向向量分别为 a , b , 平面 , 的法向量分别为 u, v ,则
线线平行
线面平行
l ∥ m a ∥ b a kb ; l ∥ a u a u 0 ;
2 a 2
C.a
D. a
1 2
由图易知A(a,0,0),B(a,a,0),
C(0,a,0),A′(a,0,a).
a a a a F (a, ,0), E ( , , ). 2 2 2 2 a 2 a a 2 a 2 | EF | (a ) ( ) (0 ) 2 2 2 2 a2 a2 2 a. 4 4 2
①如图①,AB、CD是二面角α—l—β的两个面
内与棱l垂直的直线,则二面角的大小θ=
AB, CD .
② 如图②③,n1,n2分别是二面角α —l—β 的两 个半平面α ,β 的法向量,则二面角的大小θ 满足 cosθ = cos〈n1,n2〉或-cos〈n1,n2〉 .
空间向量与立体几何公式大全

以下是部分空间向量与立体几何的公式:1. 向量的模:向量的长,可参考点点距离求模。
2. 向量的加法:三角形法则或平行四边形法则。
3. 向量的减法:三角形法则。
4. 向量的数乘:m*(x,y,z)=(mx,my,mz)。
5. 向量的积:向量m*向量n=m模*n模*cos<m,n>。
6. 向量的数乘:a=(x1,y1,z1),b=(x2,y2,z2) a+b=(x1+x2,y1+y2,z1+z2) a-b=(x1-x2,y1-y2,z1-z2) λa=(λx1,λy1,λz1) a·b=x1x2+y1y2+z1z2 a∥b:x1=λx2,y1=λy2,z1=λz2 a⊥b:x1x2+y1y2+z1z2=0。
7. 法向量与方向向量解答如下关系:线线平行:线L1方向向量为m,线L2方向向量为n,m=y*n;线面平行:法向量与方向向量垂直;面面平行:法向量平行;线线垂直:线L1方向向量为m,线L2方向向量为n,m*n=0;线面垂直:法向量与方向向量平行;面面垂直:法向量垂直;线线夹角:方向向量乘积公式求角;线面夹角:方向向量与法向量乘积公式求角;面面夹角:法向量乘积求角。
8. 点点距离:向量模长公式;点面距离:设点为o,取平面内点p,向量op*法向量n;线线距离:直线a,b,E、F为线a,b上点;直线ab距离d为=向量EF*公垂线方向向量n/向量n模;直线方向向量求法:(1)直线l:ax+by+c=0,则直线l的方向向量为=(-b,a)或(b,-a)。
(2)若直线l的斜率为k,则l的一个方向向量为=(1,k)。
(3)若A(x1,y1),B(x2,y2),则AB所在直线的一个方向向量为=(x2-x1,y2-y1)。
9. 法向量求法:法向量(a,b,c)与面内向量乘积为零,带入求解方程。
如需更多公式和信息,建议查阅数学书籍或相关网站获取。
立体几何中的向量方法1——法向量
(4)解方程组,取其中的一 个解,即得法向量。
练习:在空间直角坐标系中,已知 A(3, 0, 0), B(0, 4, 0) , C (0,0, 2) ,试求平面 ABC 的一个法向量. 解:设平面 ABC 的一个法向量为 n ( x, y, z ) 则 n AB , AC .∵ AB (3,4,0) , AC (3,0, 2) n 3 ( x, y, z ) ( 3,4,0) 0 3 x 4 y 0 y 4 x ∴ 即 ( x, y, z ) ( 3,0, 2) 0 3 x 2z 0 ∴ z 3 x 2 取 x 4 ,则 n (4, 3,6) ∴ n (4, 3,6) 是平面 ABC 的一个法向量.
B
D Q B R G D F C
⑵ BD⊥平面EFG
A
CE B u Nhomakorabea v
例1:已知A(0, 2,3), B (2, 0, -1), C (3,-4,0) 求平面ABC的法向量.
问题:如何求平面ABC的法向量呢?
求法向量的步骤:
(1)设出平面的法向量为 ( x, y, z) n
(2)找出(求出)平面内的 两个不共线的 向量的坐标a (a1, b1, c1 ),b (a2 , b2 , c2 )
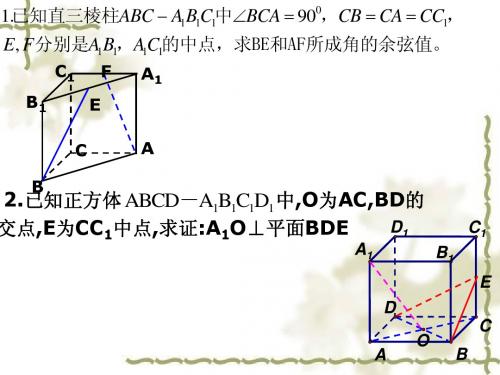
1.已知直三棱柱ABC A1B1C1中BCA 900,CB CA CC1, E, F 分别是A1B1,A1C1的中点,求BE和AF所成角的余弦值。
C1 B1 C B E A F
A1
2.已知正方体 ABCD-A1B1C1D1 中,O为AC,BD的 D1 交点,E为CC1中点,求证:A1O⊥平面BDE
立体几何的向量方法-空间向量求距离

BIG DATA EMPOWERS TO CREATE A NEW
ERA
向量的表示与运算
向量的表示
空间中一个点可以表示为一个有序实数对(x,y,z),与该点对应的向量可以表示为 $overrightarrow{OP} = (x,y,z)$。
向量的加法
对于任意两个向量$overrightarrow{a} = (a_1, a_2, a_3)$和$overrightarrow{b} = (b_1, b_2, b_3)$,它们的和为$overrightarrow{a} + overrightarrow{b} = (a_1 + b_1, a_2 + b_2, a_3 + b_3)$。
04
空间向量求距离的实例分析
BIG DATA EMPOWERS TO CREATE A NEW
ERA
球面距离问题
总结词
利用向量方法求球面上的两点之间的最 短距离
VS
详细描述
将球面上的两点分别表示为向量,通过向 量的模长和夹角计算两点之间的距离。具 体步骤包括将球面距离转化为平面距离, 利用向量的模长和夹角公式计算距离。
平面距离问题
总结词
利用向量方法求平面上的两点之间的最短距 离
详细描述
将平面上的两点分别表示为向量,通过向量 的模长和夹角计算两点之间的距离。具体步 骤包括将平面距离转化为直线距离,利用向 量的模长和夹角公式计算距离。
异面直线间的距离问题
总结词
利用向量方法求异面直线间的最短距离
详细描述
将异面直线分别表示为向量,通过向量的模 长和夹角计算直线之间的距离。具体步骤包 括将异面直线间的距离转化为平面距离,利
用向量的模长和夹角公式计算距离。
立体几何中向量知识点总结

立体几何中向量知识点总结一、向量的概念向量是几何研究的一个基本概念。
向量是具有大小和方向的量,通常用箭头表示,箭头的长度表示其大小,箭头的方向表示其方向。
在立体几何中,向量用来描述空间中的位移、速度、力和加速度等物理量。
向量既可以用几何的方法表示,也可以用代数的方法表示。
在数学上,向量是一个笛卡尔积的元素,是由一个起点和一个终点组成的有向线段,可以用其终点的坐标减去其起点的坐标得到。
例如,设A、B是平面上的两点,以这两点为起点和终点的有向线段a(即箭头)就是以点A为起点,点B为终点的有向线段,而以这两点为起点和终点的有向线段b就是以点B为起点,点A为终点的有向线段。
两有向线段a和b所表示的量,虽然线段的长度相等,但方向是相反的。
这两个向量的长度(或模)是相等的,表示它们的大小(或大小)相等。
但是,这两个有向线段之间不能互相等价,于是有向线段的不等价性是它们的有向性所决定的。
二、向量的表示在直角坐标系中,一个向量可以用坐标表示。
如果一个向量a的终点坐标是(x1, y1, z1),起点坐标是(x0, y0, z0),则用两点表示该向量为:a = (x1-x0,y1-y0,z1-z0)如果有向直线L通过两个不同的起终点坐标A(x0, y0, z0)和B(x1, y1, z1),则可以用向量AB表示这条有向线段,即:AB = (x1-x0,y1-y0,z1-z0)若直角坐标系中两点A(x0, y0, z0)与B(x1, y1, z1)之间的向量AB可以表示为a = (x1-x0,y1-y0,z1-z0)则称向量a是点A到点B的位移向量,通常简记为向量AB。
点A称为向量a的起点,记作A= a_;点B称为向量a的终点,记作B=a+a_ 。
a的起点到终点的位移向量(或矢量)仍记作AB,即AB=a。
我们在平面直角坐标系中规定一个正方向,就是一个单位长度的向量,我们记作i。
同样,我们在平面直角坐标系中的另一个正方向,第二个单位长度的向量记作j。
(整理)立体几何证明的向量公式和定理证明

a
b
精品文档
精品文档
文字 语言
性 质 定 理 图形
语言
如果两个平面互相垂直, 如果两条平行线中的一
如果两条直线同垂直于一 那么在一个平面内垂直于他 个平面,那么这两条直线平行。 们交线的直线垂直于另外一 条垂直于一个平面,那么另一
条也垂直于这个平面。 个平面。
符号 语言
文字语言
经过这条直线的平面和这个平面相
们的交线平行。
交,那么这条直线和交线平行。
性
图
质
形
定
语
理
言
符
a //
号 语 言
a
a
//
b
b
// a a // b b
其他 重要 结论
如果两个平面平行,则其中一 个平面内的任意一条直线平行于另 外一个平面。
(1)点 A 和平面 内任
意一点 B 构成一个向量
AB ; (2)平面 的法向量 n
d | AB n | |n|
高考数学专题——立体几何
综合近几年的高考题可知,本章高考命题的形式比较稳定,难易适中。主要考线线、线面及面
面的平行与垂直,三垂线定理及逆定理的应用,以及空间角和距离的计算。从解答题来看,一般
(3) sin h l
2 找平面角 三垂线法(斜线射影) 垂面法(平行于公共棱 的面)
技巧:多找中点,中位线,平 (4)三角余弦定理:
(3)射影面积法
行四边形等,或实行拓展补图等。
cos cos1 cos2
距 离
点面距离 线面距离 面面距离
两异面直线间的距离
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向量法解立体几何
用传统的方法解立体几何需要烦琐的分析、复杂的计算。
而用向量法解题思路清晰、过程简洁。
对立体几何的常见问题都可以起到化繁为简,化难为易的效果。
一. 证明两直线平行
已知两直线a 和b , b D C a B A ∈∈,,,,则⇔b a //存在唯一的实数λ使CD AB λ=
二. 证明直线和平面平行
1.已知直线αα∈∈⊄E D C a B A a ,,,,,且三点不共线,则a ∥⇔α存在有序实数对μλ,使CE CD AB μλ+=
2.已知直线,,,a B A a ∈⊄α和平面 α的法向量n ,则a ∥n AB ⊥⇔α
三.证明两个平面平行
已知两个不重合平面βα,,法向量分别为n m ,,则α∥n m //⇔β
四.证明两直线垂直 已知直线b a ,。
b D C a B A ∈∈,,,,则0=•⇔⊥CD AB b a
五.证明直线和平面垂直
已知直线α和平面a ,且A 、B a ∈,面α的法向量为m ,则m AB a //⇔⊥α
六.证明两个平面垂直
已知两个平面βα,,两个平面的法向量分别为n m ,,则n m ⊥⇔⊥βα
七.求两异面直线所成的角
已知两异面直线b a ,,b D C a B A ∈∈,,,,则异面直线所成的角θ
为:CD
AB •=θcos
八.求直线和平面所成的角
A
B
已知A,B 为直线a 上任意两点,n 为平面α的法向量,则a 和平面α所成的角θ为:
1.
⎪⎭
⎫ ⎝⎛•2,0π
时-=2πθ 2.
⎪⎭⎫ ⎝⎛∈ππ,2
时2πθ-= 九.求二面角
1.已知二面角βα--l ,且l CD l AB D C B A ⊥⊥∈∈,,,,且βα,则二面角的平面角θ
的大小为:=θ
2.已知二面角,βα--l n m ,分别为面βα,的法向量,则二面角的平面角θ的
大小与两个法向量所成的角相等或互补。
即-=πθ
注:如何判断二面角的平面角和法向量所成的角的关系。
(1)通过观察二面角锐角还是钝角,再由法向量的成的角求之。
(2)通过观察法向量的方向,判断法向量所成的角与二面角的平面角相等还是互补。
十.求两条异面直线的距离
已知两条异面直线b a ,,
m 是与两直线都垂直的向量,b B a A ∈∈,则两条
异面直线的距离d = 十一.求点到面的距离
已知平面α和点A,B 且αα∈∉B A ,,m 为平面α的法向量,则点A 到平面α
的距离d =。
