地基弹性系数取值
地基系数K30(2011-7-18)

地基系数K30
地基系数K30是表示土体表面在平面压力作用下产生的可压缩性的大小。
它是用直径为300mm 的刚性承载板进行静压平板载荷试验,取第一次加载测得的应力—位移(σ—s)曲线上s 为1.25mm 所对应的荷载σ,按K30=σs/1.25计算得出,单位:MPa/m。
K30平板载荷试验适用于粒径不大于载荷板直径1/4的各类土和土石混合填料。
影响K30测试结果的因素很多,但含水量变化是造成K30测试结果偶然误差的主要因素,也就是说K30测试结果具有时效性。
一般来说,控制在最佳含水量附近施工,路基压实系数较高,路基质量好,基床表面刚度较大,K30测试结果较高。
但是由于受季节及天气气温变化的影响,其水分的蒸发程度不同,含水量差别较大,因而含水量为一变量。
实践证明,碾压完毕后,路基含水量高时,K30测试结果就小;含水量低时,K30测试结果就大。
由于击实土处于不饱和状态,含水量对其力学性质的影响很大,这就造成K30测试结果因含水量变化而离散性大、重复性差,为此,现场测试应消除土体含水量变化的影响。
常用的地基沉降计算方法

常用的地基沉降计算方法
一、弹性模型法
弹性模型法是地基沉降计算的一种常用方法,它基于弹性体理论,直接应用中等体积条件,利用K值表面积比来估算计算地基沉降。
1.原理及公式
弹性模型法是假设地基是一种脆性材料,按照体积稳定原理,当在地基上发生荷载时,地基沉降量s可表示为:
s=K·q/F
其中:
s:地基沉降量,m;
K:沉降系数,m/t;
q:表面单位荷载,t/m2;
F:表面积,m2
2.计算方法
(1)选择沉降系数K。
一般情况下,K的取值可根据工程案例计算,也可以参考试验结果或文献资料中给出的K值,另外,也可根据地基材料的弹性模量E和泊松比μ确定:
K=1.8(G/E)1/2+2.8(μ/E)1/3
其中:G为地基材料的弹性模量,Pa;E是弹性模量,Pa;μ是泊松比。
(2)确定计算点位及坐标系。
根据工程实际情况确定计算点位及确
定坐标系,通常坐标系以空间坐标系为准;
(3)计算沉降量s。
根据系数K和地基单位面积荷载q计算沉降量s,计算公式为:
s=K·q/F
其中:K为沉降系数,m/t;q为地基单位面积荷载,t/m2;F为表面积,m2
(4)结果分析。
各种土体基床系数取值

各种土体基床系数取值各种土体基床系数取值基床系数: 基床反力系数(温克尔系数) 弹性半空间地基上某点所受的法向压力与相应位移的比值。
又称温克尔系数基床反力系数K应如何取值?这个应该就是文克勒在1867年提出的文克勒地基模型(弹性地基梁)中的基床反力系数吧,文克勒假设:地基上任一点所受的压力强度p与该点的地基沉降量s成正比,p=ks ,这个比例系数k称为基床反力系数,简称基床系数。
就是把地基土体划分成许多的土柱,然后用一根独立的弹簧来代替,k就是弹簧刚度,就如楼主所说吧。
不过基床系数的确定比较复杂,它又不是单纯表征土的力学性质的计算指标,还受基底压力的大小和分布、压缩性、土层厚度、邻近荷载等等的影响。
有些书推荐按基础的预估沉降量或者载荷试验成果来确定。
K的取值可参阅说明书中的附表,在同一类土中,相对偏硬的土取大值,偏软的土取小值,若考虑垫层的影响K值还可取大些,当有多种土层时,应按土的变形情况取加权平均值。
K值的改变对荷载均匀的基础内力影响不大,但荷载不均匀时则会对内力产生一定的影响。
应适当调整K值,选择较理想的内力与变形的K值,并最好使垂直位【资料来源】中国船舶工业总公司第九设计院编写.弹性地基梁及矩形板计算.附录A:基床系数的参考数值表地基的一般特征土壤种类κ0值(千牛/米3)松软土壤流砂新填筑的砂土湿的软粘土弱淤泥质土壤或有机质土壤*981~4905981~4905981~49054905~9810中等密实土壤粘土及亚粘土????软塑的*????可塑的*砂????松散的*????中密的*????密实的*????石土中密的????黄土及黄土性亚粘土*9810~19620密实土壤紧密下卧层砂紧密下卧层砾石碎石砾砂硬塑土壤49050~98100极密实土壤人工夯实的亚粘土硬粘土98100~196200硬土壤软质岩石中等风化或强风化的坚硬岩石冻土层196200~981000硬质岩石完好的坚硬岩石人工桩基* 木桩:????打至岩层的桩????穿到弱土层达到密实砂层及粘土层的桩????软弱土层内摩擦桩钢筋混凝土桩:????打至岩层的桩????穿过弱土层及粘土层的桩49050~147150建筑材料砖块石砌体混凝土钢筋混凝土3924000~4905000注:1.凡有*号,原文注明适用于地基面积>10平米。
地下结构抗震计算地基弹簧系数取值方法研究_李英民

第1 期
李英民,等: 地下结构抗震计算地基弹簧系数取值方法研究
107
性地基上的框架,通过地基弹簧的弹性抗力模拟周围土层对结构的作用,常用于地下结构抗震简化计算方法 ( 反应位移法) 中。荷载-结构模型是一种最基本的地下结构设计模型,它计算简便,广泛应用于地下结构的 抗震计算。
荷载-结构计算模型中,地基弹簧系数的取值非常关键,对简化模型的可靠性和计算结果的正确性都有 很大影响。地下结构弹簧系数的取值可借鉴地基基床系数的取值方法,一般需要通过理论分析、现场原位试 验和室内试验获得,几类岩土工程勘察规范均给出了测试方法[4 ~ 6]。仲锁庆等[7]分析了现有基床系数的确 定方法和影响准确确定地基土基床系数的一些因素。屈成忠等[8]通过分析不同基床系数的计算方法,给出 了不同工况下基床系数的计算公式。Biot[9]和 Vesic[10]均提出了计算地基基床系数的方法。林皋[11]、黄先 锋[12]和地铁抗震设计规范[13]提出可通过有限元方法计算地基弹簧系数。虽然试验和有限元数值方法均能 确定地基弹簧系数,但对于地下结构抗震简化计算方法,给出经验公式比数值模拟和试验更为有效。可以借 鉴已有对地基基床系数计算公式的研究[9,10],但该公式仅能应用于法向地基弹簧系数,且未考虑成层土等更 接近实际的情况。文中在已有研究成果的基础上,建立了适用于地下结构抗震简化计算的法向和切向地基 弹簧系数的经验计算公式,以有限元分析结果为数据基础,对公式的系数进行了拟合,并将公式拓展用于成 层土体,最后对提出的公式进行了验证。
K
=
E ωB( 1 - υ2 )
( 1)
式中: E 和 υ 为土体的弹簧模量和泊松比; B 为基础宽度; ω 为系数,取决于基础的形状和刚度。
由于土体的泊松比一般在 0. 25 ~ 0. 4 之间,平方后数值更小,因此将式( 1) 中的系数合并,令:
[VIP专享]弹性地基的处理
![[VIP专享]弹性地基的处理](https://img.taocdn.com/s3/m/0caf059df12d2af90242e6e0.png)
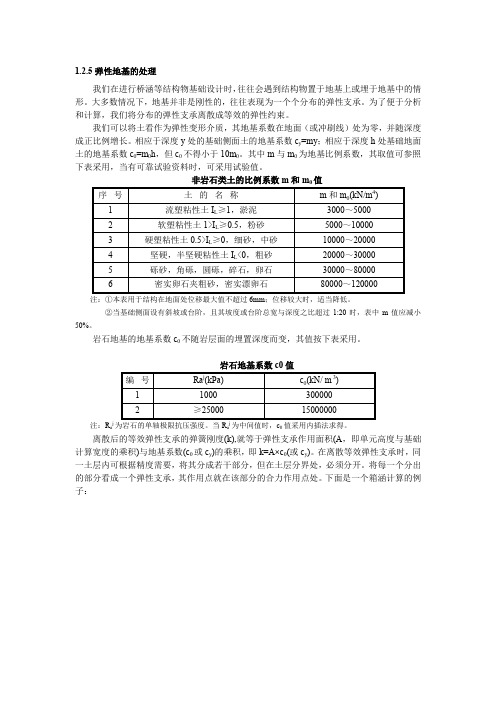
弹性地基的处理我们在进行桥涵等结构物基础设计时,往往会遇到结构物置于地基上或埋于地基中的情形。
大多数情况下,地基并非是刚性的,往往表现为一个个分布的弹性支承。
为了便于分析和计算,我们将分布的弹性支承离散成等效的弹性约束。
我们可以将土看作为弹性变形介质,其地基系数在地面(或冲刷线)处为零,并随深度成正比例增长。
相应于深度y处的基础侧面土的地基系数c y=my;相应于深度h处基础地面土的地基系数c0=m0h,但c0不得小于10m0。
其中m与m0为地基比例系数,其取值可参照下表采用,当有可靠试验资料时,可采用试验值。
非岩石类土的比例系数m和m0值序号土的名称m和m0(kN/m4) 1流塑粘性土I L≥1,淤泥3000~50002软塑粘性土1>I L≥0.5,粉砂5000~100003硬塑粘性土0.5>I L≥0,细砂,中砂10000~200004坚硬,半坚硬粘性土I L<0,粗砂20000~300005砾砂,角砾,圆砾,碎石,卵石30000~800006密实卵石夹粗砂,密实漂卵石80000~120000注:①本表用于结构在地面处位移最大值不超过6mm;位移较大时,适当降低。
②当基础侧面设有斜坡或台阶,且其坡度或台阶总宽与深度之比超过1:20时,表中m 值应减小50%。
岩石地基的地基系数c0不随岩层面的埋置深度而变,其值按下表采用岩石地基系数c0值编号Rj(kPa)c0(kN/m3)a110003000002≥2500015000000注:R a j为岩石的单轴极限抗压强度。
当R a j为中间值时,c0值采用内插法求得。
离散后的等效弹性支承的弹簧刚度(k),就等于弹性支承作用面积(A,即单元高度与基础计算宽度的乘积)与地基系数(c0或c y)的乘积,即k=A×c0(或c y)。
在离散等效弹性支承时,同一土层内可根据精度需要,将其分成若干部分,但在土层分界处,必须分开。
将每一个分出的部分看成一个弹性支承,其作用点就在该部分的合力作用点处。
各种土体基床系数取值

各种土体基床系数取值
各种土体基床系数取值
称为
不过基床系数的确定比较复杂,它又不是单纯表征土的力学性质的计算指标,还受基底压力的大小和分布、压缩性、土层厚度、邻近荷载等等的影响。
有些书推荐按基础的预估沉降量或者载荷试验成果来确定。
K的取值可参阅说明书中的附表,在同一类土中,相对偏硬的土取大值,偏软的土取小值,若考虑垫层的影响K值还可取大些,当有多种土层时,应按土的变形情况取加权平均值。
K值的改变对荷
•
中等密实土壤
砂松散的*
中密的*密实的*
石土中密的黄土及黄土性亚粘
土* 14715~2452524525~3924 0
24525~3924039240~4905 0
密实土壤紧密下卧层砂
紧密下卧层砾石碎石
砾砂硬塑土壤
49050~98100
人工夯实的亚粘土
极密实土壤
98100~196200
硬粘土
软质岩石
硬土壤
196200~981000
中等风化或强风化的坚硬岩石冻土层
硬质岩石完好的坚硬岩石981000~14715000 Array平
.本
性地基梁及矩形板计算》。
弹性地基的处理
1.2.5弹性地基的处理我们在进行桥涵等结构物基础设计时,往往会遇到结构物置于地基上或埋于地基中的情形。
大多数情况下,地基并非是刚性的,往往表现为一个个分布的弹性支承。
为了便于分析和计算,我们将分布的弹性支承离散成等效的弹性约束。
我们可以将土看作为弹性变形介质,其地基系数在地面(或冲刷线)处为零,并随深度成正比例增长。
相应于深度y处的基础侧面土的地基系数c y=my;相应于深度h处基础地面土的地基系数c0=m0h,但c0不得小于10m0。
其中m与m0为地基比例系数,其取值可参照下表采用,当有可靠试验资料时,可采用试验值。
注:①本表用于结构在地面处位移最大值不超过6mm;位移较大时,适当降低。
②当基础侧面设有斜坡或台阶,且其坡度或台阶总宽与深度之比超过1:20时,表中m值应减小50%。
岩石地基的地基系数c0不随岩层面的埋置深度而变,其值按下表采用。
岩石地基系数c0值注:R a j为岩石的单轴极限抗压强度。
当R a为中间值时,c0值采用内插法求得。
离散后的等效弹性支承的弹簧刚度(k),就等于弹性支承作用面积(A,即单元高度与基础计算宽度的乘积)与地基系数(c0或c y)的乘积,即k=A×c0(或c y)。
在离散等效弹性支承时,同一土层内可根据精度需要,将其分成若干部分,但在土层分界处,必须分开。
将每一个分出的部分看成一个弹性支承,其作用点就在该部分的合力作用点处。
下面是一个箱涵计算的例子:上图中,除m0以kN/m4单位外,其余以m为单位。
如图,将该箱分为17个单元,虽然整个结构都埋于土中,但由于需要研究箱体的受力,且箱体侧面是受到主动土压力,故在侧面不设弹性支承,而是将其考虑为荷载。
所以,只有6、7、8、9、10号单元受到弹性支承,它们分别是弹性支承1、2、3、4、5、6。
由于需要保持结构的稳定(维持结构的不可变性),故加上7号水平约束(非弹性支承)。
取1m长的箱涵进行计算。
1、6号弹簧,其作用宽度取所在单元宽度的一半,从而可计算它们的刚度为:k=m0h×A=20000×1.50×1.0×0.1=3000(kN/m)=300(t/m)2、3、4、5号弹簧,其作用宽度取所在两个单元宽度和的一半,从而可计算它们的刚度为:k=m0h×A=20000×1.50×1.0×0.2=6000(kN/m)=600(t/m)对于桩基础,由于往往会发生水平位移,故需要在侧向放置弹性支承。
各种土体基床系数取值

各种土体基床系数取值
各种土体基床系数取值
称为
不过基床系数的确定比较复杂,它又不是单纯表征土的力学性质的计算指标,还受基底压力的大小和分布、压缩性、土层厚度、邻近荷载等等的影响。
有些书推荐按基础的预估沉降量或者载荷试验成果来确定。
K的取值可参阅说明书中的附表,在同一类土中,相对偏硬的土取大值,偏软的土取小值,若考虑垫层的影响K值还可取大些,当有多种土层时,应按土的变形情况取加权平均值。
K值的改变对荷
•
中等密实土壤
砂松散的*
中密的*密实的*
石土中密的黄土及黄土性亚粘
土* 14715~2452524525~3924 0
24525~3924039240~4905 0
密实土壤紧密下卧层砂
紧密下卧层砾石碎石
砾砂硬塑土壤
49050~98100
人工夯实的亚粘土
极密实土壤
98100~196200
硬粘土
软质岩石
硬土壤
196200~981000
中等风化或强风化的坚硬岩石冻土层
硬质岩石完好的坚硬岩石981000~14715000 Array平
.本
性地基梁及矩形板计算》。
弹性抗力系数

1. 初始弹性系数A、A1是何含义?如何计算?
答:初始弹性系数A和A1表示滑面处弹性抗力的初始系数。
图4.2-1 初始弹性系数
计算土反力时,需要确定弹性抗力系数
(m法)
(C法)
(K法)
其中,A表示嵌固面处弹性抗力系数,取法如下:
图4.2-2 弹性系数示意图
式中:
h ——桩前上部覆土厚度
h1 ——桩后上部覆土厚度
m ——上部覆土的水平抗力系数的比例系数,由用户根据经验或试验获得,如无经验,可用《建筑基坑支护技术规程》中的公式计算:
d ——基坑底面处位移量(mm),按地区经验取值,无经验时可取10;
φ——土层的固结不排水(快)剪内摩擦角标准值(°);
c ——土层的固结不排水(快)剪粘聚力标准值(kPa)。
地基弹性系数取值

地基弹性系数取值集团企业公司编码:(LL3698-KKI1269-TM2483-LUI12689-ITT289-弹性地基的处理我们在进行桥涵等结构物基础设计时,往往会遇到结构物置于地基上或埋于地基中的情形。
大多数情况下,地基并非是刚性的,往往表现为一个个分布的弹性支承。
为了便于分析和计算,我们将分布的弹性支承离散成等效的弹性约束。
我们可以将土看作为弹性变形介质,其地基系数在地面(或冲刷线)处为零,并随深度成正比例增长。
相应于深度y 处的基础侧面土的地基系数c y =my ;相应于深度h 处基础地面土的地基系数c 0=m 0h ,但c 0不得小于10m 0。
其中m 与m 0为地基比例系数,其取值可参照下表采用,当有可靠试验资料时,可采用试验值。
非岩石类土的比例系数m 和m 0值注:①本表用于结构在地面处位移最大值不超过6mm ;位移较大时,适当降低。
②当基础侧面设有斜坡或台阶,且其坡度或台阶总宽与深度之比超过1:20时,表中m 值应减小50%。
岩石地基的地基系数c 0不随岩层面的埋置深度而变,其值按下表采用。
岩石地基系数c0值注:R a j 为岩石的单轴极限抗压强度。
当R a j 为中间值时,c 0值采用内插法求得。
离散后的等效弹性支承的弹簧刚度(k),就等于弹性支承作用面积(A,即单元高度与的乘积)与地基系数(c0或cy)的乘积,即k=A×c(或cy)。
在离散等效弹性支承时,同一土层内可根据精度需要,将其分成若干部分,但在土层分界处,必须分开。
将每一个分出的部分看成一个弹性支承,其作用点就在该部分的合力作用点处。
下面是一个箱涵计算的例子:上图中,除m以kN/m4单位外,其余以m为单位。
如图,将该箱分为17个单元,虽然整个结构都埋于土中,但由于需要研究箱体的受力,且箱体侧面是受到主动土压力,故在侧面不设弹性支承,而是将其考虑为荷载。
所以,只有6、7、8、9、10号单元受到弹性支承,它们分别是弹性支承1、2、3、4、5、6。
各种土体基床系数取值

各种⼟体基床系数取值各种⼟体基床系数取值各种⼟体基床系数取值基床系数: 基床反⼒系数(温克尔系数) 弹性半空间地基上某点所受的法向压⼒与相应位移的⽐值。
⼜称温克尔系数基床反⼒系数K应如何取值?这个应该就是⽂克勒在1867年提出的⽂克勒地基模型(弹性地基梁)中的基床反⼒系数吧,⽂克勒假设:地基上任⼀点所受的压⼒强度p与该点的地基沉降量s成正⽐,p=ks ,这个⽐例系数k称为基床反⼒系数,简称基床系数。
就是把地基⼟体划分成许多的⼟柱,然后⽤⼀根独⽴的弹簧来代替,k就是弹簧刚度,就如楼主所说吧。
不过基床系数的确定⽐较复杂,它⼜不是单纯表征⼟的⼒学性质的计算指标,还受基底压⼒的⼤⼩和分布、压缩性、⼟层厚度、邻近荷载等等的影响。
有些书推荐按基础的预估沉降量或者载荷试验成果来确定。
K的取值可参阅说明书中的附表,在同⼀类⼟中,相对偏硬的⼟取⼤值,偏软的⼟取⼩值,若考虑垫层的影响K值还可取⼤些,当有多种⼟层时,应按⼟的变形情况取加权平均值。
K值的改变对荷载均匀的基础内⼒影响不⼤,但荷载不均匀时则会对内⼒产⽣⼀定的影响。
应适当调整K值,选择较理想的内【资料来源】中国船舶⼯业总公司第九设计院编写.弹性地基梁及矩形板计算.附录A:基床系数的参考数值表地基的⼀般特征⼟壤种类κ0值(千⽜/⽶3)松软⼟壤流砂新填筑的砂⼟湿的软粘⼟弱淤泥质⼟壤或有机质⼟壤*981~4905981~4905981~49054905~9810中等密实⼟壤粘⼟及亚粘⼟软塑的*可塑的*砂松散的*中密的*密实的*⽯⼟中密的黄⼟及黄⼟性亚粘⼟*9810~19620密实⼟壤紧密下卧层砂紧密下卧层砾⽯碎⽯砾砂硬塑⼟壤49050~98100极密实⼟壤⼈⼯夯实的亚粘⼟硬粘⼟98100~196200硬⼟壤软质岩⽯中等风化或强风化的坚硬岩⽯冻⼟层196200~981000硬质岩⽯完好的坚硬岩⽯⼈⼯桩基* ⽊桩:打⾄岩层的桩穿到弱⼟层达到密实砂层及粘⼟层的桩软弱⼟层内摩擦桩钢筋混凝⼟桩:打⾄岩层的桩穿过弱⼟层及粘⼟层的桩49050~147150建筑材料砖块⽯砌体混凝⼟钢筋混凝⼟3924000~4905000注:1.凡有*号,原⽂注明适⽤于地基⾯积>10平⽶。
各种土体基床系数取值

各种土体基床系数取值各种土体基床系数取值基床系数: 基床反力系数(温克尔系数) 弹性半空间地基上某点所受的法向压力与相应位移的比值。
又称温克尔系数基床反力系数K应如何取值这个应该就是文克勒在1867年提出的文克勒地基模型(弹性地基梁)中的基床反力系数吧,文克勒假设:地基上任一点所受的压力强度p与该点的地基沉降量s成正比, p=ks ,这个比例系数k称为基床反力系数,简称基床系数。
就是把地基土体划分成许多的土柱,然后用一根独立的弹簧来代替,k就是弹簧刚度,就如楼主所说吧。
不过基床系数的确定比较复杂,它又不是单纯表征土的力学性质的计算指标,还受基底压力的大小和分布、压缩性、土层厚度、邻近荷载等等的影响。
有些书推荐按基础的预估沉降量或者载荷试验成果来确定。
K的取值可参阅说明书中的附表,在同一类土中,相对偏硬的土取大值,偏软的土取小值,若考虑垫层的影响K值还可取大些,当有多种土层时,应按土的变形情况取加权平均值。
K值的改变对荷载均匀的基础内力影响不大,但荷载不均匀时则会对内力产生一定的影响。
应适当调整K值,选择较理想的内力与变形的K值,并最好使垂直位移不出现负值。
【资料来源】顾晓鲁等主编.地基与基础(第三版).北京:中国建筑工业出版社,2003基床系数κ 值表 12-2-1黄土及黄土类粉质粘土×10^4~×10^4桩基软弱土层内摩擦桩×10^4~×10^4穿过软弱土层达到密实砂层或粘性土层的桩×10^4~×10^4打到岩层的支承桩800×10^4【资料来源】中国船舶工业总公司第九设计院编写.弹性地基梁及矩形板计算.附录A:基床系数的参考数值表地基的一般特征土壤种类κ0值(千牛/米3)松软土壤流砂新填筑的砂土湿的软粘土弱淤泥质土壤或有机质土壤*981~4905981~4905981~49054905~9810中等密实土壤粘土及亚粘土软塑的* 可塑的*砂松散的*中密的* 密实的*石土中密的黄土及黄土性亚粘土*9810~1962019620~0~1471514715~25~3924024525~40~49050密实土壤紧密下卧层砂紧密下卧层砾石碎石砾砂硬塑土壤49050~98100极密实土壤人工夯实的亚粘土硬粘土98100~196200 硬土壤软质岩石中等风化或强风化的坚硬岩石冻土层196200~981000硬质岩石完好的坚硬岩石981000~人工桩基*木桩:打至岩层的桩穿到弱土层达到密实砂层及粘土层的桩软弱土层内摩擦桩钢筋混凝土桩:打至岩层的桩穿过弱土层及粘土层的桩49050~1471509050~10~4905049050~147150建筑材料砖块石砌体混凝土钢筋混凝土3924000~49050004905000~484600~7484800~注:1.凡有*号,原文注明适用于地基面积>10平米。
土的弹性模量参考值

静止侧压力系数K0参考值土类液限w L塑性指数静止侧压力系数K0饱和松砂0.46饱和紧砂0.34干紧砂(e=0.6)0.49干松砂(e=0.6)0.64压实残积黏土9 0.42压实残积黏土74% 31 0.66原状有机质土61% 45 0.57原状高岭土37% 23 0.64~0.70原状海相黏土34% 16 0.48灵敏性黏土10 0.52泊松比v的参考值弹性模量E的参考值在弹性阶段,E=Eo=Es(1-2μ^2/(1-μ)),土力学上有相关说明。
有经验说是E=(2~5)·Es(未考证出处)变形模量的定义在表达式上和弹性模量是一样的E=ζ/ε,对于变形模量ε是指应变,包括弹性应变εe和塑性应变εp,对于弹性模量而言,ε就是指εe(计算变形模量时,应变ε包括了弹性应变和塑性应变)。
岩土的弹性模量要远大于压缩模量和变形模量,而压缩模量又大于变形模量。
弹性模量>压缩模量>变形模量。
弹性模量也叫杨氏模量(岩土体在弹性限度内应力与应变的比值)压缩模量是有侧限的,杨氏模量是无侧限的。
同样的土体,同样的荷载,有侧限的土体应变小,所以压缩模量更大才对。
这只是弹性理论上的关系,对土体这种自然物不一定适用。
土体计算中所用的称为“弹性模量”不一定是在弹性限度内。
E——弹性模量;Es——压缩模量;Eo——变形模量。
弹性模量=应力/弹性应变,它主要用于计算瞬时沉降。
压缩模量和变形模量均=应力/总应变。
压缩模量是通过现场取原状土进行实验室有侧限压缩实验得出的,而变形模量则是通过现场的原位载荷试验得出的,它是无侧限的。
弹性模量要远大于压缩模量和变形模量,而压缩模量又大于变形模量。
地堪报告中,一般给出的是土的压缩模量Es与变形模量Eo,而一般不会给出弹性模量E。
数值模拟中一般用Eo,E(50),达到峰值应力(应变)50%时的割线模量。
Es(勘查报告中提供),有侧限,E=2.0~5.0Es(看别人这么弄的)。
地基文克尔系数K常用值

1~1.5 松砂
1.5~2.5 中密砂或松散砾石
2.5~4 密砂或中密砾石
4~5 黄土及黄土性粉质粘土
5~10 紧密砾石
5~15 砾石, 含淤泥
6~15 1~3 砂土, 级配良好
5~8 1~3 砂土, 级配差
6~15 砂土, 含粘土
3~8 ቤተ መጻሕፍቲ ባይዱ 砂土, 含淤泥
基床系数K的含义:地基产生单位变形时所需的压力强度。
K值 (x10000 kN/m^3) 地基土种类与特征
0.1~0.5 淤泥质、有机质土或新填土
0.5~10 软弱粘土
1~2 粘土及粉质粘土,软塑
2~4 粘土及粉质粘土,可塑
----- 砾石和砂土参考值 -------
K值(x10000 kN/m^3) 地基土种类,特征
密实的 松散的
15~20 5~10 砾石, 级配良好
10~20 5~10 砾石, 级配差
8~15 砾石, 含粘土
10~20 硬粘土或人工夯实粉质粘土
20~100 软质岩石和中、强风化的坚硬岩石
100~1500 完好的坚硬岩石
400~500 砖
500~600 块石砌体
800~1500 混凝土与钢筋混凝土
地基弹性系数取值

弹性地基的处理我们在进行桥涵等结构物基础设计时,往往会遇到结构物置于地基上或埋于地基中的情形。
大多数情况下,地基并非是刚性的,往往表现为一个个分布的弹性支承。
为了便于分析和计算,我们将分布的弹性支承离散成等效的弹性约束。
我们可以将土看作为弹性变形介质,其地基系数在地面(或冲刷线)处为零,并随深度成正比例增长。
相应于深度y处的基础侧面土的地基系数c y=my;相应于深度h处基础地面土的地基系数c0=m0h,但c0不得小于10m0。
其中m与m0为地基比例系数,其取值可参照下表采用,当有可靠试验资料时,可采用试验值。
非岩石类土的比例系数m和m值注:①本表用于结构在地面处位移最大值不超过6mm;位移较大时,适当降低。
②当基础侧面设有斜坡或台阶,且其坡度或台阶总宽与深度之比超过1:20时,表中m值应减小50%。
岩石地基的地基系数c0不随岩层面的埋置深度而变,其值按下表采用。
岩石地基系数c0值注:R a j为岩石的单轴极限抗压强度。
当R a为中间值时,c0值采用内插法求得。
离散后的等效弹性支承的弹簧刚度(k),就等于弹性支承作用面积(A,即单元高度与基础计算宽度的乘积)与地基系数(c0或c y)的乘积,即k=A×c0(或c y)。
在离散等效弹性支承时,同一土层内可根据精度需要,将其分成若干部分,但在土层分界处,必须分开。
将每一个分出的部分看成一个弹性支承,其作用点就在该部分的合力作用点处。
下面是一个箱涵计算的例子:上图中,除m0以kN/m4单位外,其余以m为单位。
如图,将该箱分为17个单元,虽然整个结构都埋于土中,但由于需要研究箱体的受力,且箱体侧面是受到主动土压力,故在侧面不设弹性支承,而是将其考虑为荷载。
所以,只有6、7、8、9、10号单元受到弹性支承,它们分别是弹性支承1、2、3、4、5、6。
由于需要保持结构的稳定(维持结构的不可变性),故加上7号水平约束(非弹性支承)。
取1m长的箱涵进行计算。
弹性地基梁法(全面版)资料

弹性地基梁法(全面版)资料弹性地基梁法整体式平底板的平面尺寸远较厚度为大,可视为地基上的受力复杂的一块板。
目前工程实际仍用近似简化计算方法进行强度分析。
一般认为闸墩刚度较大,底板顺水流方向弯曲变形远较垂直水流方向小,假定顺水流方向地基反力呈直线分布,故常在垂直水流方向截取单宽板条进行内力计算。
按照不同的地基情况采用不同的底板应力计算方法。
相对密度Dr >0.5的砂土地基或粘性土地基,可采用弹性地基梁法。
相对密度Dr 0.5的砂土地基,因地基松软,底板刚度相对较大,变形容易得到调整,可以采用地基反力沿水流流向呈直线分布、垂直水流流向为均匀分布的反力直线分布法。
对小型水闸,则常采用倒置梁法。
(一)弹性地基梁法该法认为底板和地基都是弹性体,底板变形和地基沉降协调一致,垂直水流方向地基反力不呈均匀分布(图1),据此计算地基反力和底板内力。
此法考虑了底板变形和地基沉降相协调,又计入边荷载的影响,比较合理,但计算比较复杂。
当采用弹性地基梁法分析水闸闸底板应力时,应考虑可压缩土层厚度T 与弹性地基梁半长L /2之比值的影响。
当L T 2小于0.25时,可按基床系数法(文克尔假定)计算;当L T 2大于2.0时,可按半无限深的弹性地基梁法计算;当2T /L 为0.25-2.0时,可按有限深的弹性地基梁计算。
弹性地基梁法计算地基反力和底板内力的具体步骤如下:(1)用偏心受压公式计算闸底纵向(顺水流方向)地基反力。
(2)在垂直水流方向截取单宽板条及墩条,计算板条及墩条上的不平衡剪力。
以闸门槽上游边缘为界,将底板分为上、下游两段,分别在两段的中央截取单宽板条及墩条进行分析,如图1(a )所示。
作用在板条及墩条上的力有:底板自重(q 1)、水重(q 2)、中墩重(G 1/b i )及缝墩重(G 2/b i ),中墩及缝墩重中(包括其上部结构及设备自重在内),在底板的底面有扬压力(q 3)及地基反力(q 4),见图1(b )所示。
弹性抗力系数

1. 初始弹性系数A、A1是何含义?如何计算?
答:初始弹性系数A和A1表示滑面处弹性抗力的初始系数。
图4.2-1 初始弹性系数
计算土反力时,需要确定弹性抗力系数
(m法)
(C法)
(K法)
其中,A表示嵌固面处弹性抗力系数,取法如下:
图4.2-2 弹性系数示意图
式中:
h ——桩前上部覆土厚度
h1 ——桩后上部覆土厚度
m ——上部覆土的水平抗力系数的比例系数,由用户根据经验或试验获得,如无经验,可用《建筑基坑支护技术规程》中的公式计算:
d ——基坑底面处位移量(mm),按地区经验取值,无经验时可取10;
φ——土层的固结不排水(快)剪内摩擦角标准值(°);
c ——土层的固结不排水(快)剪粘聚力标准值(kPa)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弹性地基的处理
我们在进行桥涵等结构物基础设计时,往往会遇到结构物置于地基上或埋于地基中的情形。
大多数情况下,地基并非是刚性的,往往表现为一个个分布的弹性支承。
为了便于分析和计算,我们将分布的弹性支承离散成等效的弹性约束。
我们可以将土看作为弹性变形介质,其地基系数在地面(或冲刷线)处为零,并随深度成正比例增长。
相应于深度y处的基础侧面土的地基系数c y=my;相应于深度h处基础地面土的地基系数c0=m0h,但c0不得小于10m0。
其中m与m0为地基比例系数,其取值可参照下表采用,当有可靠试验资料时,可采用试验值。
非岩石类土的比例系数m和m
注:①本表用于结构在地面处位移最大值不超过6mm;位移较大时,适当降低。
②当基础侧面设有斜坡或台阶,且其坡度或台阶总宽与深度之比超过1:20时,表中m值应减小50%。
岩石地基的地基系数c0不随岩层面的埋置深度而变,其值按下表采用。
岩石地基系数c0值
注:R a j为岩石的单轴极限抗压强度。
当R a j为中间值时,c0值采用内插法求得。
离散后的等效弹性支承的弹簧刚度(k),就等于弹性支承作用面积(A,即单元高度与基础计算宽度的乘积)与地基系数(c0或c y)的乘积,即k=A×c0(或c y)。
在离散等效弹性支承时,同一土层内可根据精度需要,将其分成若干部分,但在土层分界处,必须分开。
将每一个分出的部分看成一个弹性支承,其作用点就在该部分的合力作用点处。
下面是一个箱涵计算的例子:
上图中,除m0以kN/m4单位外,其余以m为单位。
如图,将该箱分为17个单元,虽然整个结构都埋于土中,但由于需要研究箱体的受力,且箱体侧面是受到主动土压力,故在侧面不设弹性支承,而是将其考虑为荷载。
所以,只有6、7、8、9、10号单元受到弹性支承,它们分别是弹性支承1、2、3、4、5、6。
由于需要保持结构的稳定(维持结构的不可变性),故加上7号水平约束(非弹性支承)。
取1m长的箱涵进行计算。
1、6号弹簧,其作用宽度取所在单元宽度的一半,从而可计算它们的刚度为:k=m0h×A=20000×1.50×1.0×0.1=3000(kN/m)=300(t/m)
2、3、4、5号弹簧,其作用宽度取所在两个单元宽度和的一半,从而可计算它们的刚度为:k=m0h×A=20000×1.50×1.0×0.2=6000(kN/m)=600(t/m)
对于桩基础,由于往往会发生水平位移,故需要在侧向放置弹性支承。
下面是桩基础计算的例题:
图为一直径2m的桩,将其在地面或局部冲刷线以下部分划分为4个单元,它分别位于三种土层中。
图中1、2、3、4即为等效弹性支承,它们作用的位置分别是由所在单元边界处的地基系数构成的三角形或梯形(即上图中右边的实线图形)的形心。
分别计算4个弹性支承的弹簧刚度。
弹性支承1:
k1=0.5m1h1×A1=0.5×18000×0.9(2+1)×3=72900(kN/m)=7290(t/m)
弹性支承2:
k2=0.5[m2h1+m2×(h1+h2)]×A2=0.5×(18000+70000)×0.9(2+1)×4=475200(kN/m)=47520(t/m)
弹性支承3:
k3=0.5[m2×(h1+h2)+m2×(h1+h2+h3)]×A3
=0.5×(70000+110000)×0.9(2+1)×4=972000(kN/m)=97200(t/m)
弹性支承4:
k4=0.5[m3×(h1+h2+h3)+m3×(h1+h2+h3+h4)]×A4
=0.5×(44000+60000)×0.9(2+1)×4=561600(kN/m)=56160(t/m)
在进行结构的基础设计时,遇到结构物置于地基上或埋于地基中的情况时,多数情况下,地基,往往表现为一个个分布的弹性支承。
为了便于计算,将分布的弹性支承离散成等效的弹性约束。
在桥博中,需要用户计算出相应的弹性系数。
可以参考《地基基础》相关教程中的方法计算,如可按类似于m法计算:
首先,将土看作为弹性变形介质,根据相关规范等查取针对某一土层的地基系数随深度变化的比例系数m值,然后计算出地基系数C z=m*z,其中:z是指深度。
对于基础底部的地基系数C0=m0*h,m0为基础底部竖向地基系数的比例系数,h为基础的入土深度。
然后,将土层离散,对于不同的土层,需要根据土层的顶、底面作为划分面。
根据地基系数C值,以及单元土层的面积A(土层单元厚度*基础横向的宽度),即可得弹性系数k z=C z*A(对于分层土,需要按三角形或者梯形计算土层单元顶、底面的C z值,取平均,作用位置位三角形或者梯形的形心位置),或者k0=C0*A。
